1.
Что такое момент
инерции?
Отношение
вращающего
момента к угловой
скорости.
2.
Что такое
передаточная
функция?
Отношение
выходного
сигнала к входному.
3.
Что такое переходная
функция?
Реакция
системы на
единичный
ступенчатый
импульс.
3.
Что такое весовая
функция?
Реакция
системы на
функцию Дирака
(единичный
импульс в
бесконечность).
4.
Определение
наблюдаемости.
Система
наблюдаема
если нет двух
одинаковых
начальных
условий, которые
приводят систему
к одному и тому
же конечному
состоянию.
5.
Определение
управляемости.
Система
управляема
если выбором
соответствующего
управляющего
воздействия
её можно из
любого начального
состояния
перевести в
любое конечное
состояние за
конечное время.
6.
Зачем надо
проверять на
наблюдаемость
и управляемость.
Если
мы проверим
систему на
наблюдаемость,
а она не наблюдаема
то мы не сможем
потом выбрать
управляющее
воздействие,
так как мы выбираем
его после оценки
состояния
системы (в
наблюдателе),
а если она не
наблюдаема,
то мы и не можем
его выбрать.
А
если система
не управляема,
то мы соответственно
не можем ею
управлять, а
нас это не
устраивает.
7.
Где на схеме
замкнутой
системы наблюдатель,
а где сам объект?
Верху
сам объект, а
снизу наблюдатель.
И вообще всюду,
где стоят над
переменными
тильды (волнистые
линии), то это
относится к
наблюдателю,
все остальное
к объекту.
8.
От чего зависит
управление?
Управление
зависит от
переменных
состояния
системы:
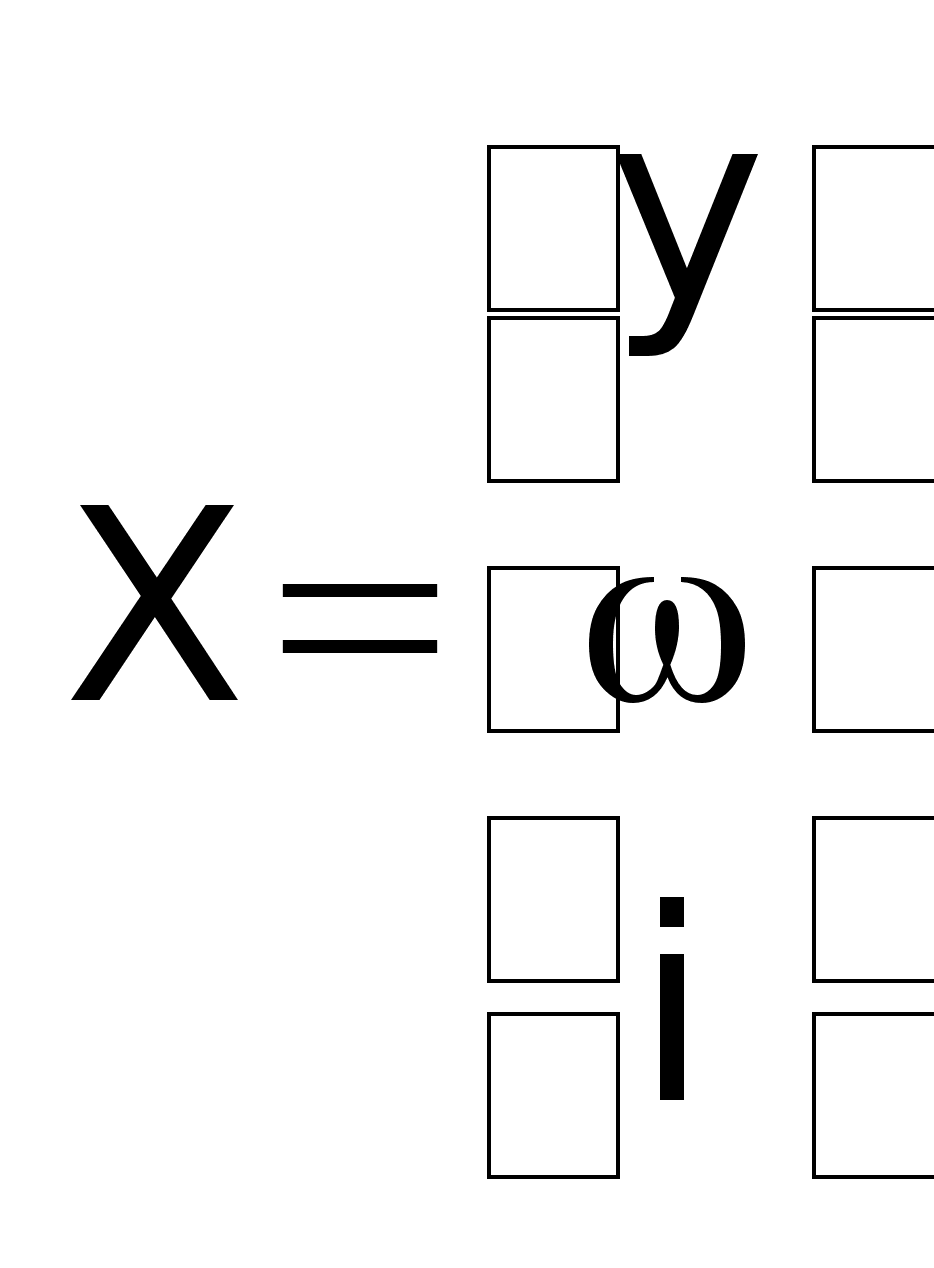 Объясняется
это тем, что на
регулятор мы
подаем именно
переменные
состояния, а
на его выходе
получаем управляющее
воздействие,
которое мы
потом подаем
на объект: U=-RX. Где
R-матрица регулятора.
Объясняется
это тем, что на
регулятор мы
подаем именно
переменные
состояния, а
на его выходе
получаем управляющее
воздействие,
которое мы
потом подаем
на объект: U=-RX. Где
R-матрица регулятора.
9.
Где на схеме
оценка состояния?
Всюду
где стоят над
переменными
тильды, то это
относится к
наблюдателю,
все остальное
к объекту. А
наблюдатель
и дает нам оценку
состояния.
10.
Зачем находим
матрицу Acr и
Ach?
Матрицу
Acr находим для
того, что бы
посмотрев её
в 3й степени
убедиться что,
переходный
процесс в объекте
заканчивается
за 3 такта (отсюда
и третья степень).
Матрицу
Ach находим для
того, что бы
посмотрев её
в 3й степени
убедиться что,
переменные
состояния
совпадают с
их оценкой.
11.
Что связывает
матрица A0?
Она
связывает
вектор XX который
равен:
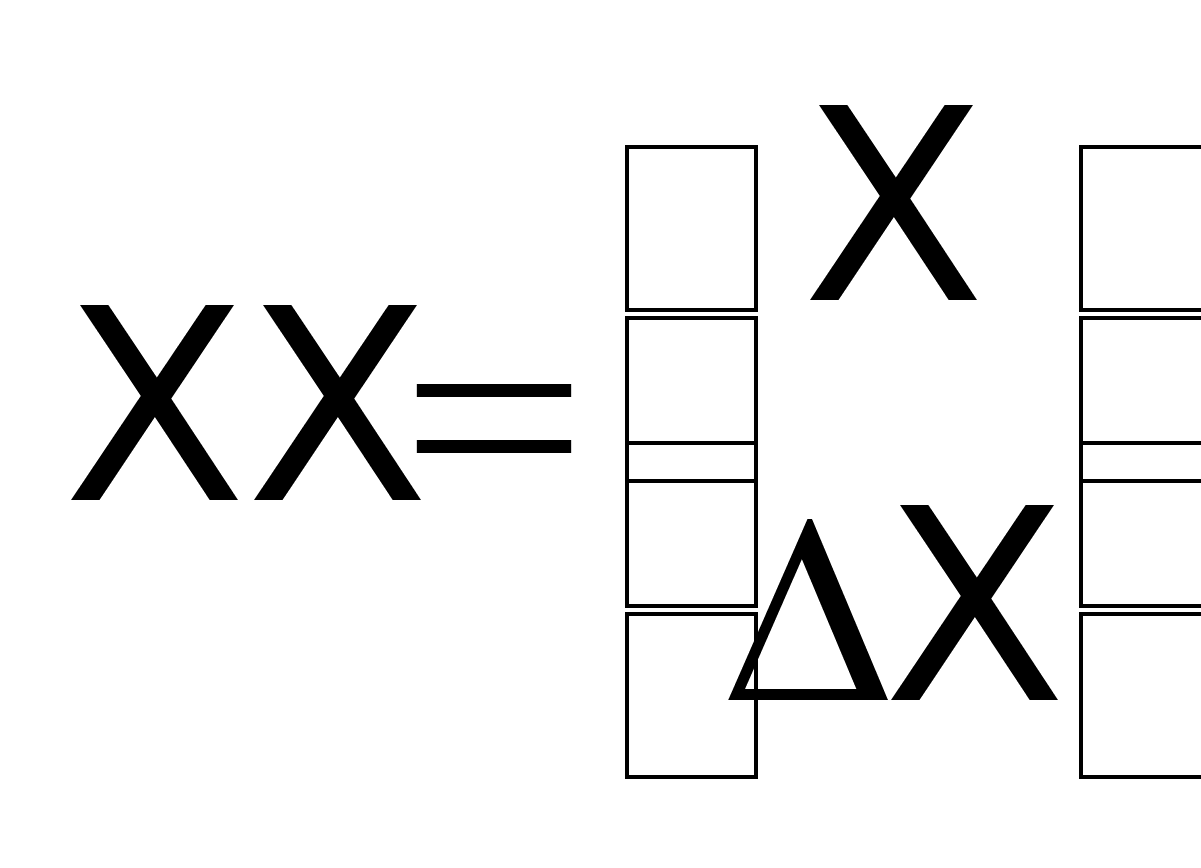 ,
где ,
где
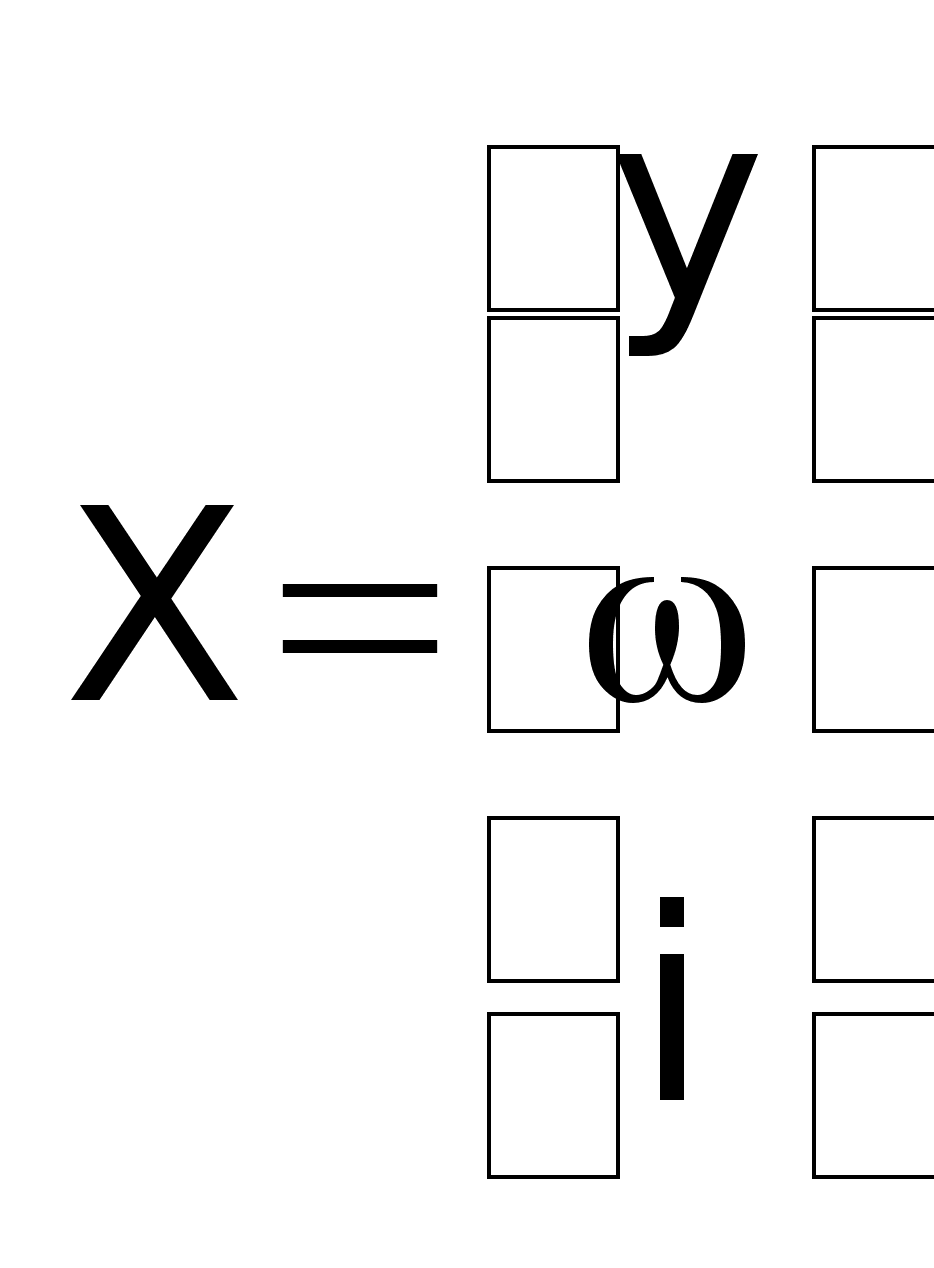 и и
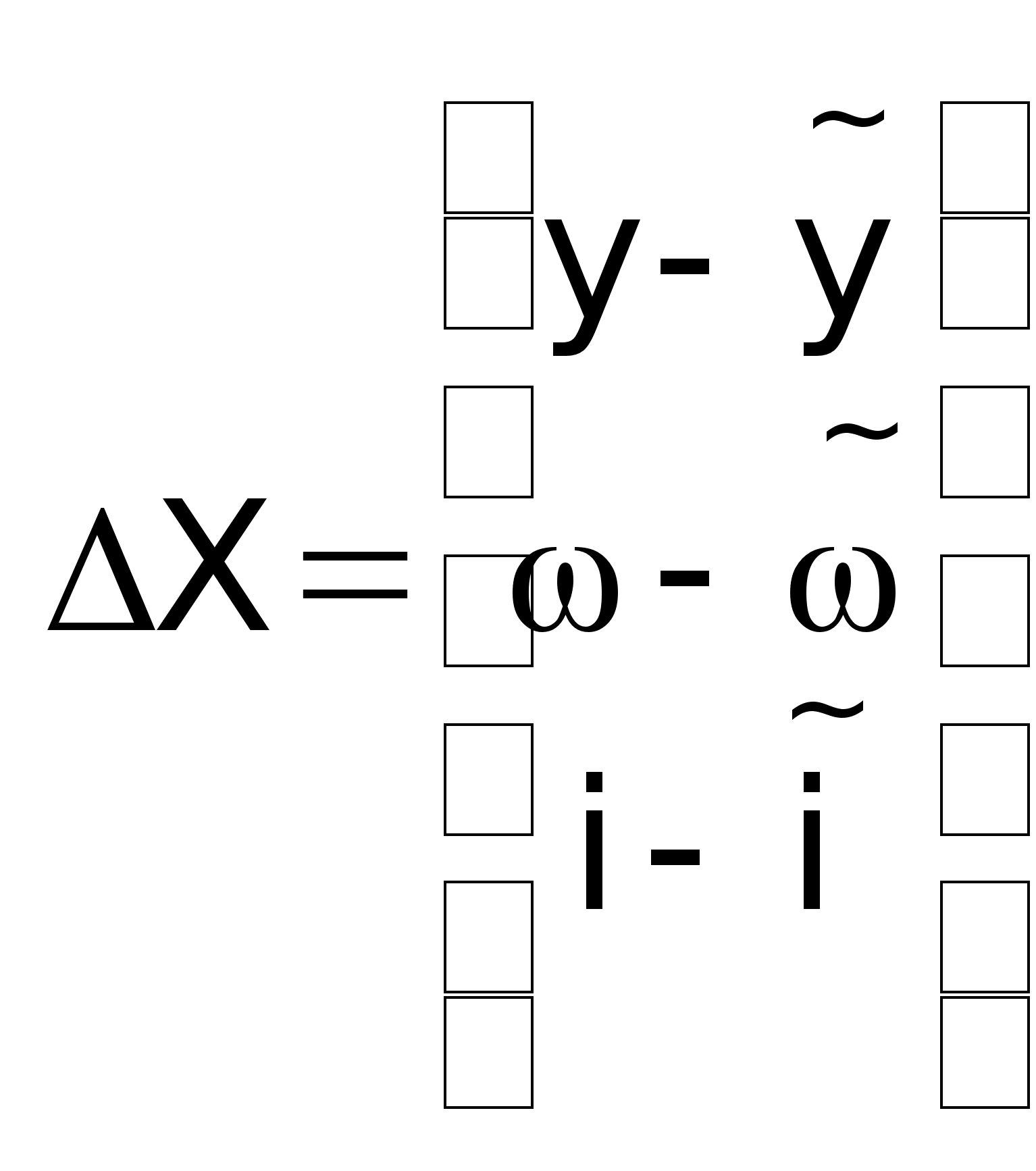 . .
Так
вот она связывает
этот вектор
на ком шаге
и этот же вектор
на к+1 шаге, т.е.:
XX(k+1)=A0XX(k),
(*)-запомните
что это уравнение
звездочка.
12.
Как с помощью
матрицы A0
получить таблицу?
Мы
знаем начальные
данные:
0
wноминальная
iноминальный
0
0
(последние три
цифры это начальное
состояние
наблюдателя)
0
Так
вот: зная эти
начальные
данные (они на
нулевом такте,
т.е. при к=0), подставляем
их в уравнение
(*)(да это именно
то уравнение
которое вы
должны были
запомнить),
получаем значение
вектора XX на
к+1 такте, т.е. в
нашем случае
на 1 такте, и так
далее по кругу,
вычисляем
значения вектора
XX на всех тактах
и видим что за
6 тактов процесс
полностью
заканчивается.
13.
Как написать
передаточную
функцию по
дифуру?
Передаточная
функция представляет
собой дробь,
числитель
которой получается
путем замены
производных
степенями р
в правой части
дифура, а знаменатель
- в левой.
14.
Как по передаточной
функции найти
выходной сигнал
зная входной?
Выходной
сигнал получается
так:
его
амплитуда равна
амплитуде
входного сигнала
домноженного
на модуль
передаточной
функции на
частоте входного
сигнала.
а
к фазе входного
сигнала надо
прибавить
значение фазовой
характеристики,
опять же на
частоте входного
сигнала.
(это
всё справедливо
для синусоидального
входного сигнала).
15.
Если матрица
R=(1 2 3) то чему будет
равно управляющее
воздействие?
Оно
равно:
U=-R*X
т.е. в нашем случае:
U=-(1 2 3)*X.
16.
Почему изображение
переходной
функции мы
получаем деля
изображение
передаточной
на р.
Потому
что изображение
единичной
ступеньки (а
как уже говорилось,
переходная
функция есть
реакция на
единичную
ступеньку)
равно 1/p.
17.
Как построили
структурную
схему объекта
зная уравнения?
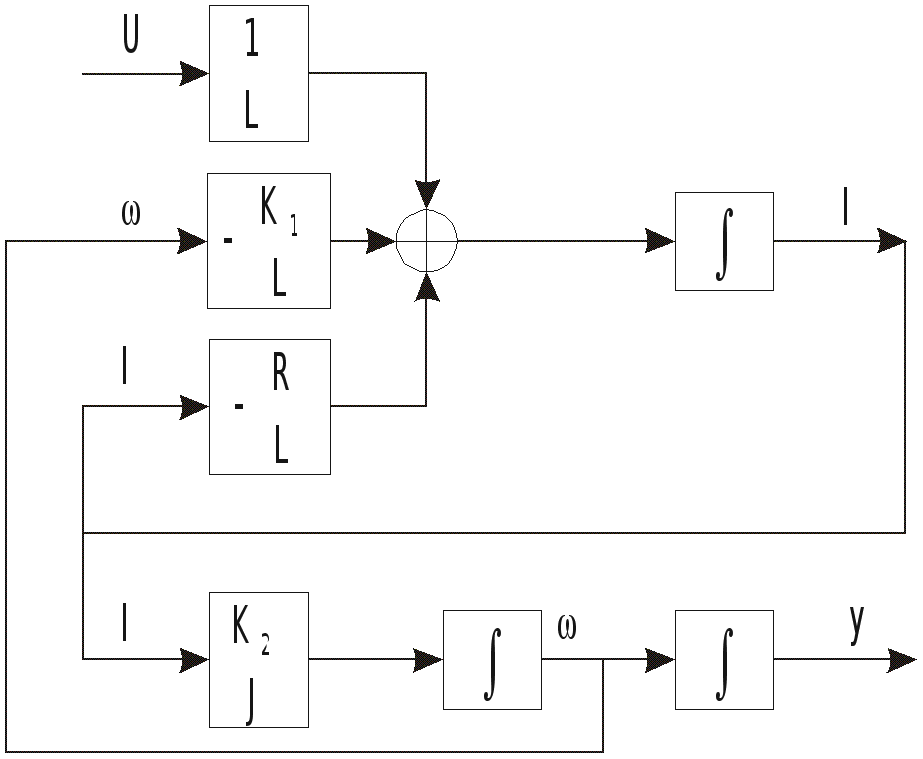
Начинаем
строить её с
нижнего дифура.
Принцип
таков:
Берем
три входных
сигнала u, w, i, пропускаем
через звенья
с передаточными
коэффициентами
равными коэффициентам
перед ними в
дифуре, суммируем
их, смотрим что
получилось
если производная
то пропускаем
сигнал через
интегратор,
получаем сам
сигнал, далее
соединяем ветви
с одинаковыми
сигналами. Так
делаем со всеми
дифурами, в
итоге получаем
вход, куда мы
подаем U, и выход
- y.
18.
За сколько
тактов заканчивается
переходный
процесс при
выборе матрицы
управления?
Он
заканчивается
за минимальное
число тактов,
которое равно
порядку системы,
в нашем случае
- 3.
19.
А за сколько
тактов состояние
наблюдателя
совпадет с
состоянием
объекта?
20.
А почему переходный
процесс в замкнутой
системе с
наблюдателем
и регулятором
заканчивается
за 2n тактов?
Потому
что там уже
есть и наблюдатель
и система, а
состояние
наблюдателя
совпадет с
состоянием
объекта через
три такта, а
переходный
процесс в объекте
закончиться
еще через три
такта, вот и
получили 3+3=6
тактов.
21.
Что такое ранг
матрицы?
Это
порядок наибольшего
минора определитель
которого не
равен нулю.
1. Составить
структурную
схему объекта
управления.
Исходные
данные:
|
Номер
варианта
|
15
|
|
Модель
|
ДПМ-12А
|
|
Мощность,
Вт
|
-
|
|
Напряжение,
В
|
14
|
|
Ток,
А
|
0,11
|
|
Скорость
вращения, об/мин
|
6000
|
|
Вращающий
момент, Нм
|
0,0018
|
|
Момент
инерции, кгм2
|
0,003
|
|
Сопротивление,
Ом
|
28
|
|
Индуктивность,
Гн
|
-
|
Объект
управления
– электрический
привод с двигателем
постоянного
тока, описываемый
уравнениями:
уравнение
электрической
цепи двигателя:
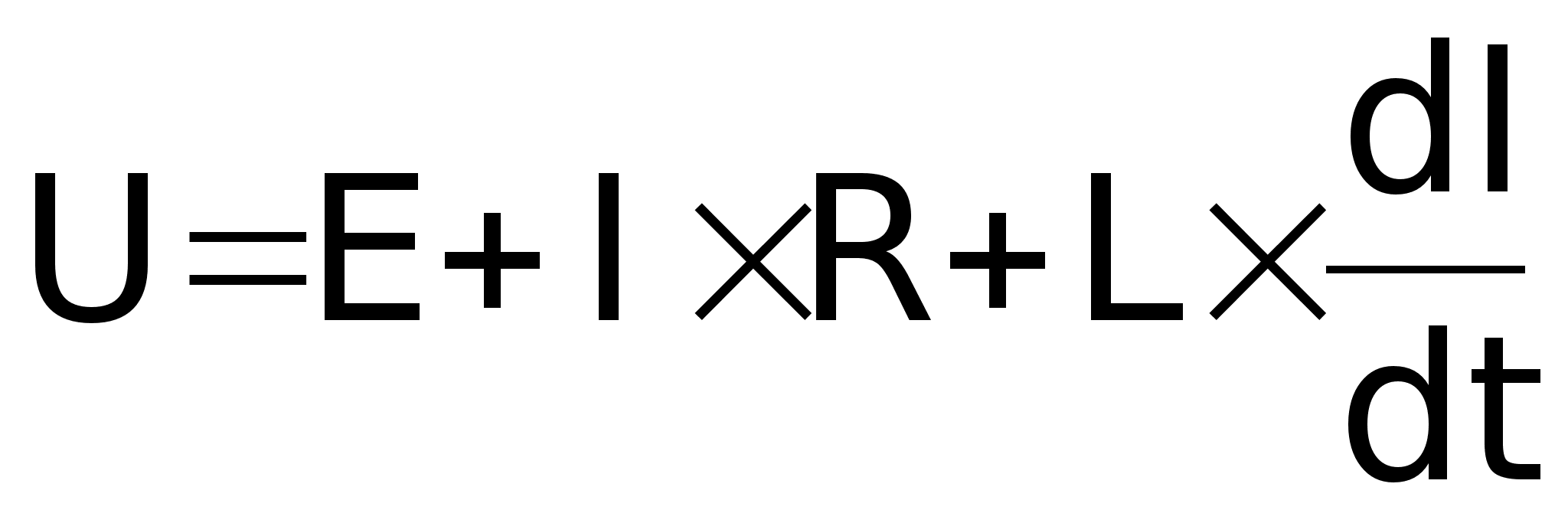
уравнение
моментов:
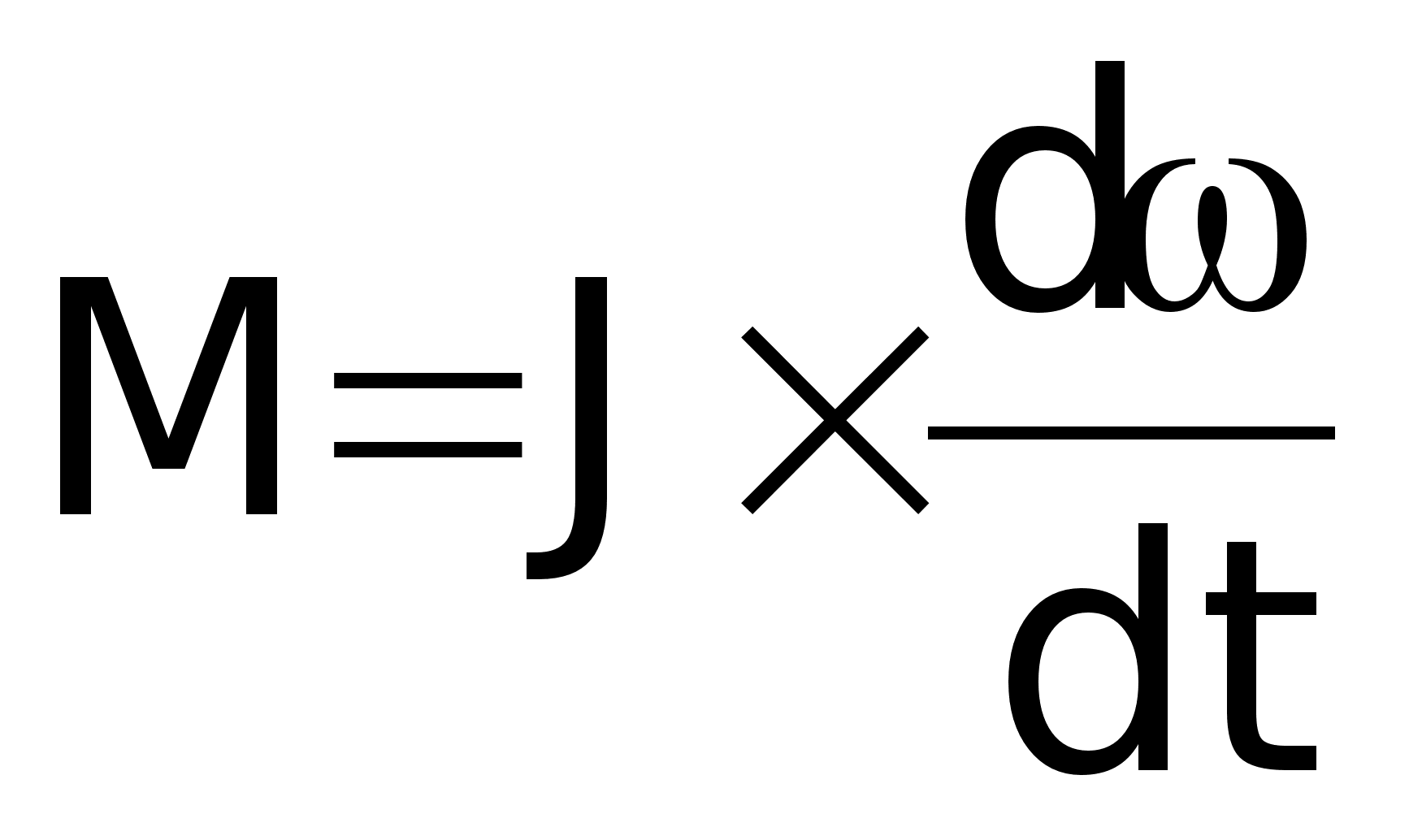
уравнение
редуктора:
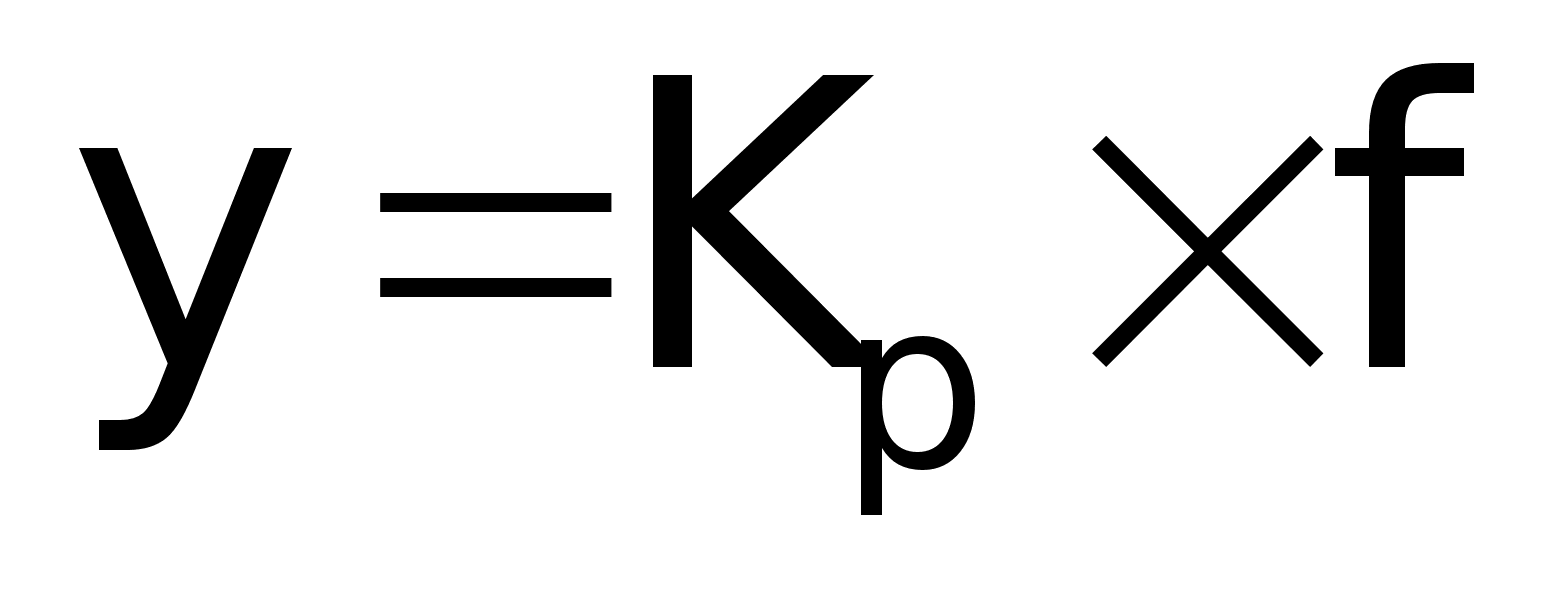
где:
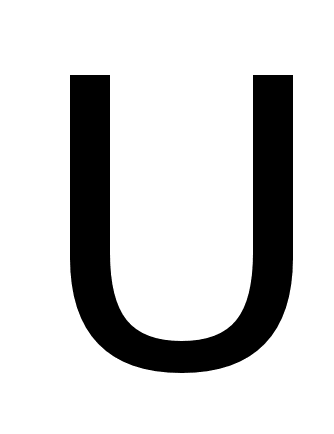 - напряжение
на якоре двигателя.
- напряжение
на якоре двигателя.
 - ток якоря.
- ток якоря.
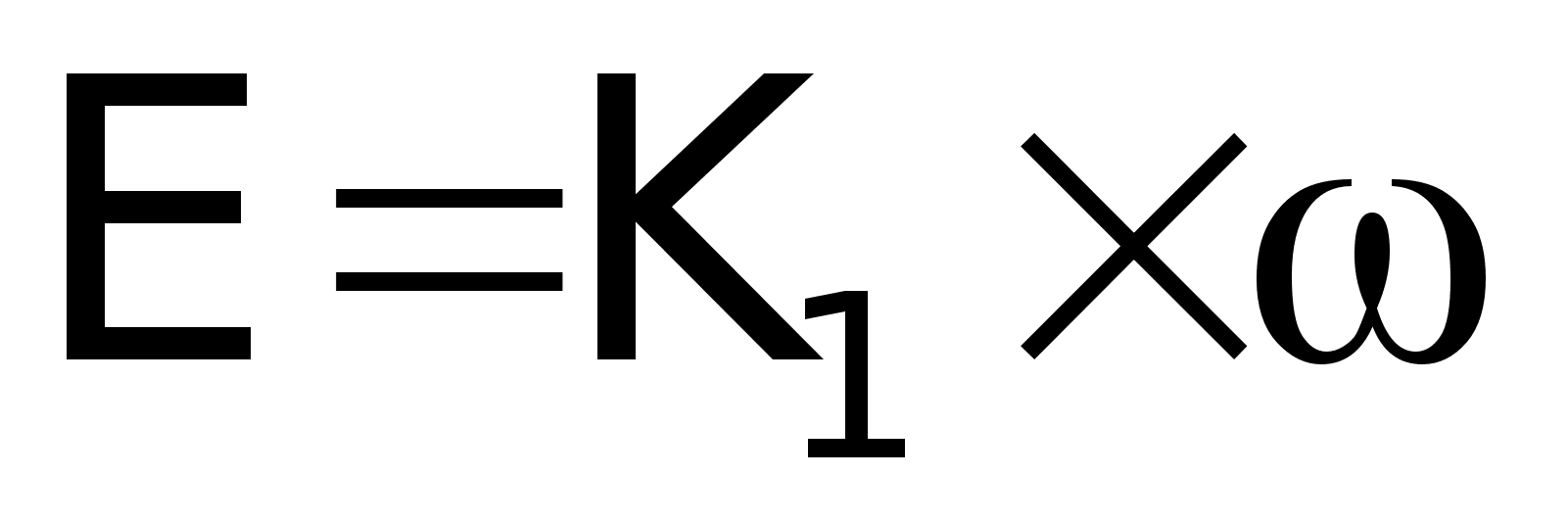 - ЭДС вращения.
- ЭДС вращения.
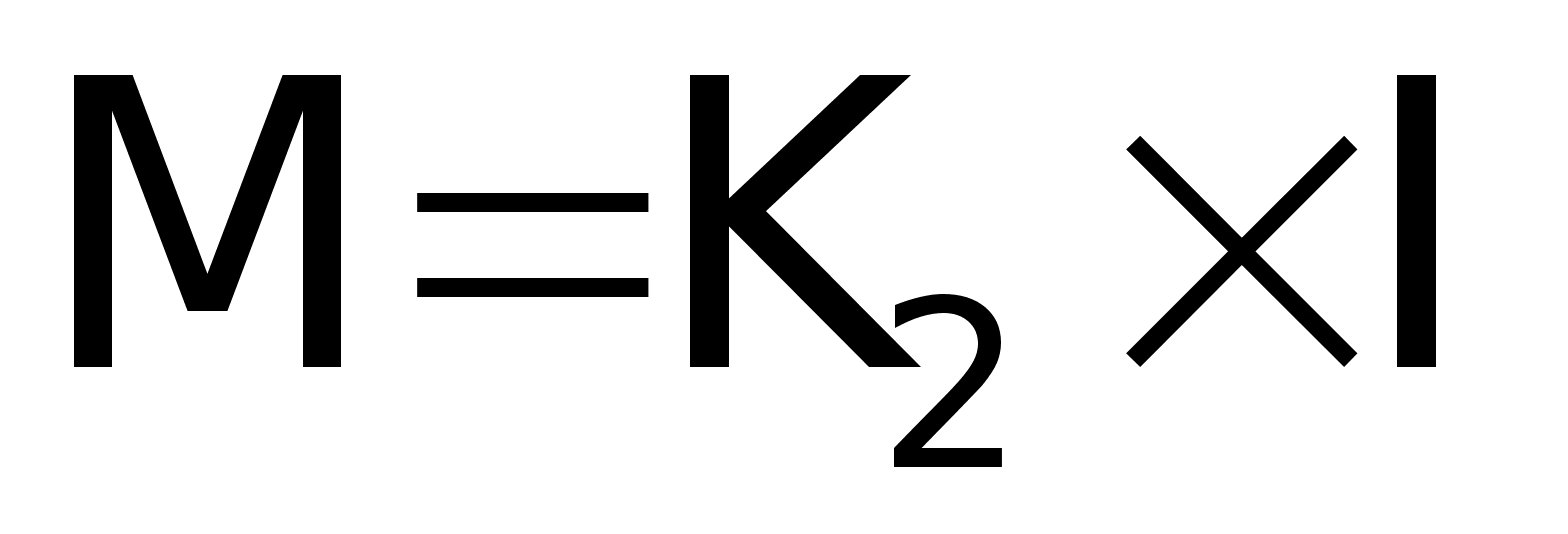 - момент,
развиваемый
двигателем.
- момент,
развиваемый
двигателем.
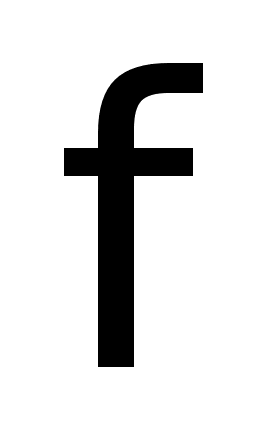 - угол
поворота вала
двигателя.
- угол
поворота вала
двигателя.
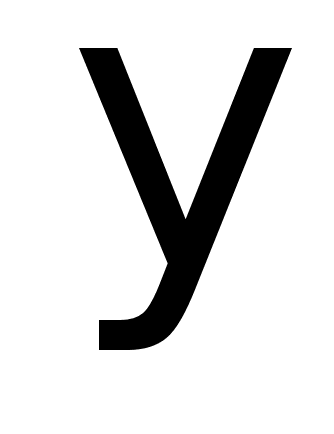 - угол
поворота вала
редуктора.
- угол
поворота вала
редуктора.
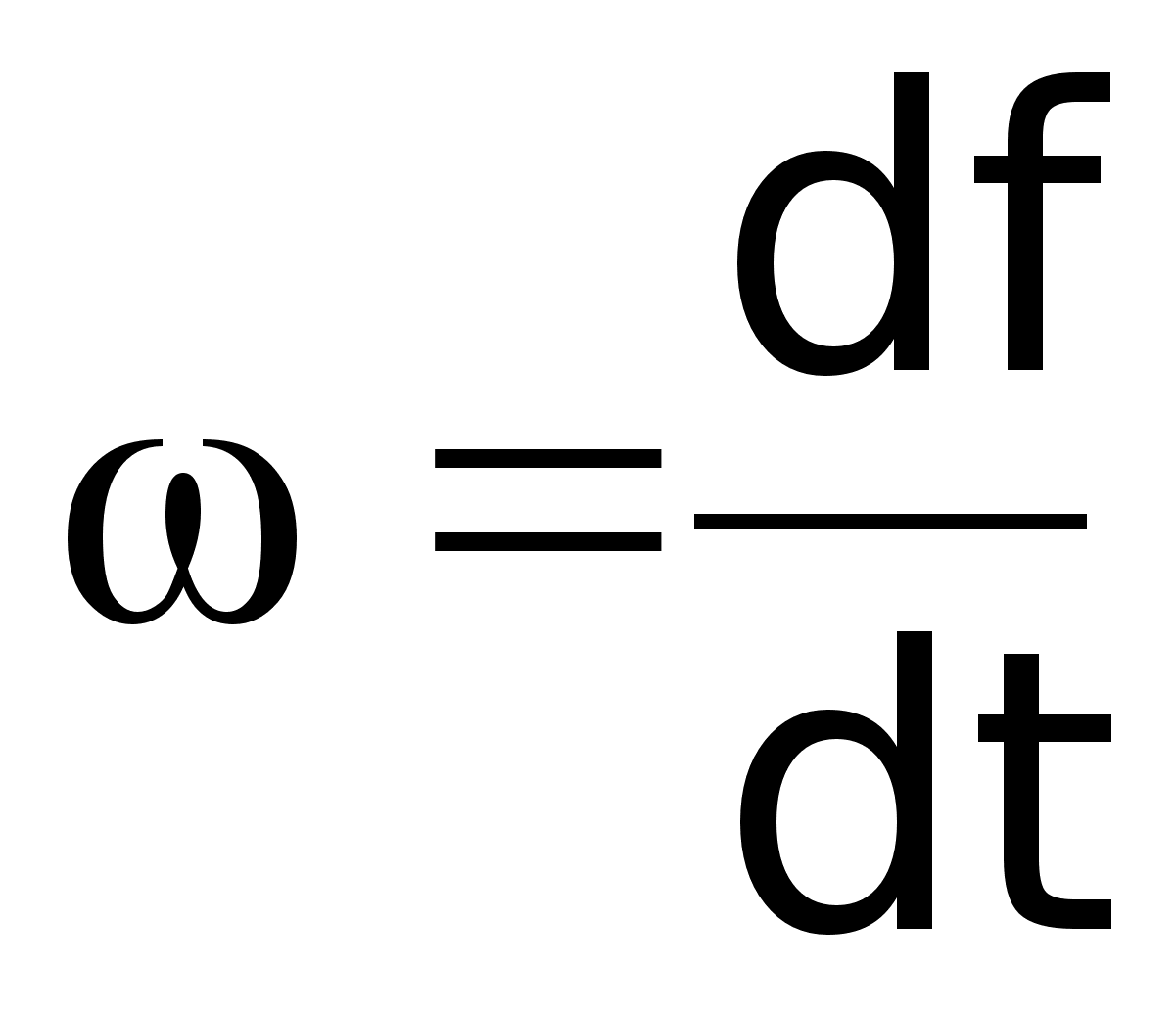 - угловая
скорость.
- угловая
скорость.
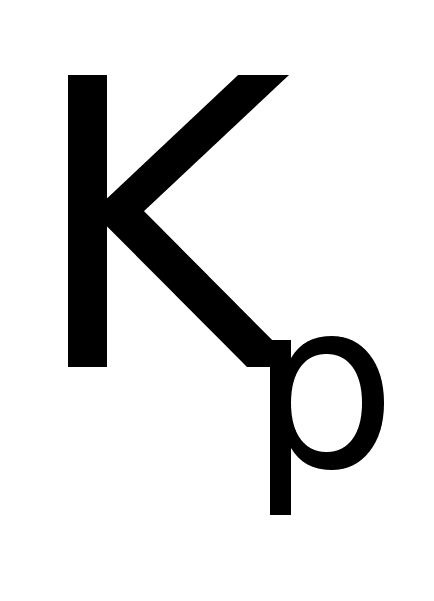 - коэффициент
передачи редуктора.
- коэффициент
передачи редуктора.
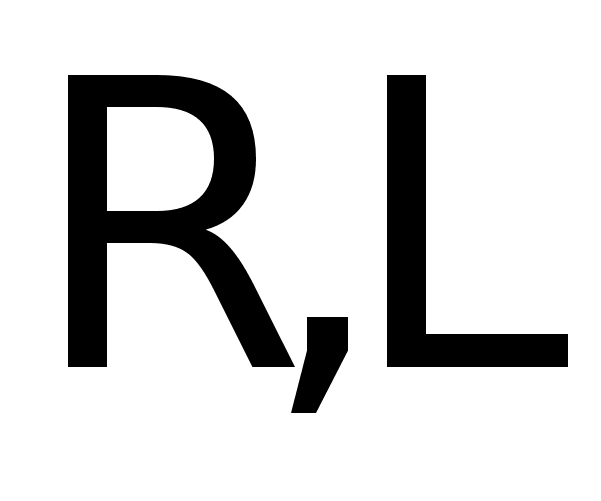 - сопротивление
и индуктивность
якоря.
- сопротивление
и индуктивность
якоря.
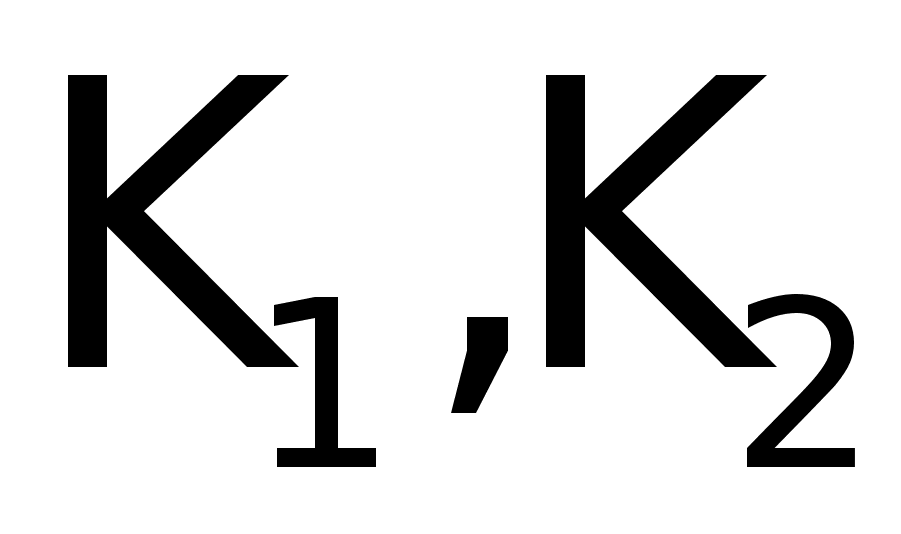 - конструктивные
параметры
двигателя.
- конструктивные
параметры
двигателя.
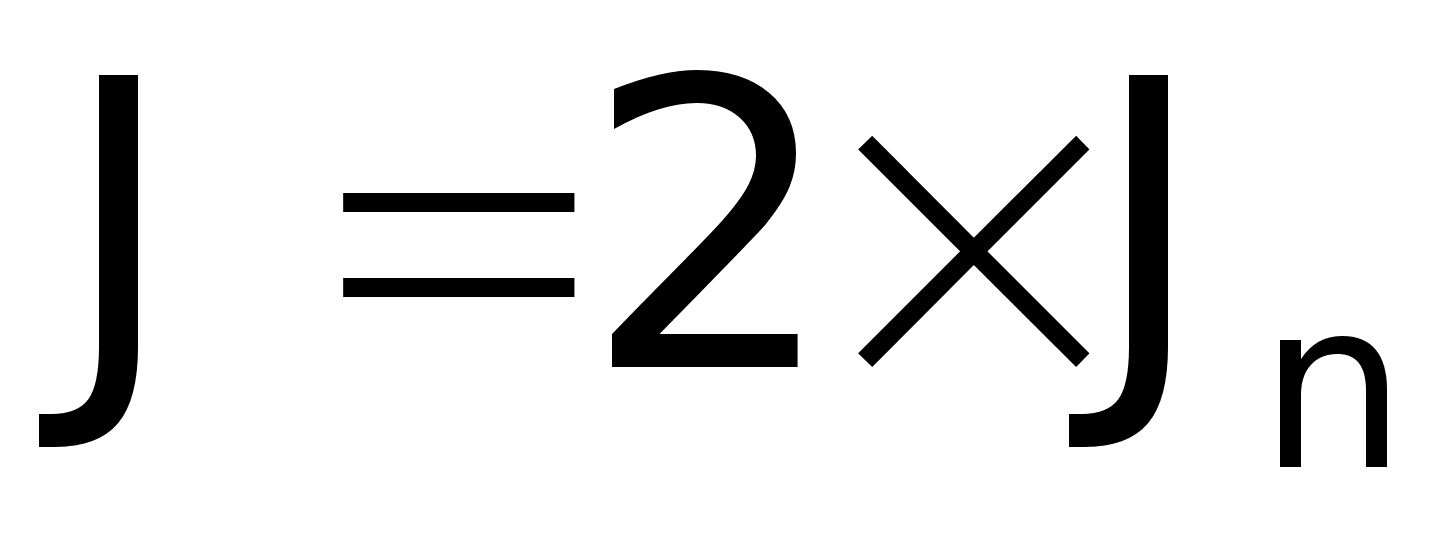 - момент
инерции.
- момент
инерции.
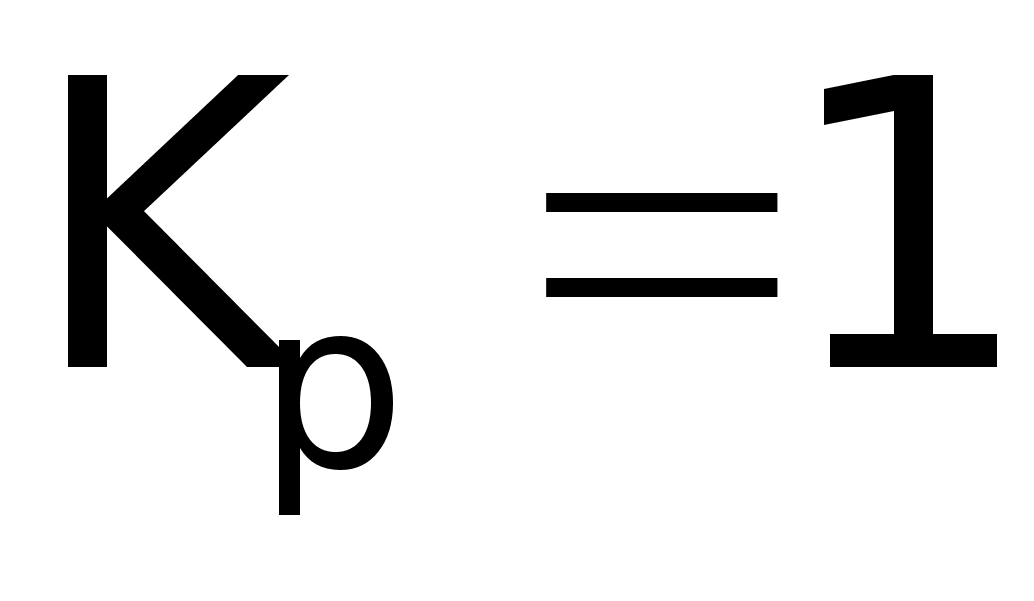
Рассчитаем
коэффициенты
К1, К2:
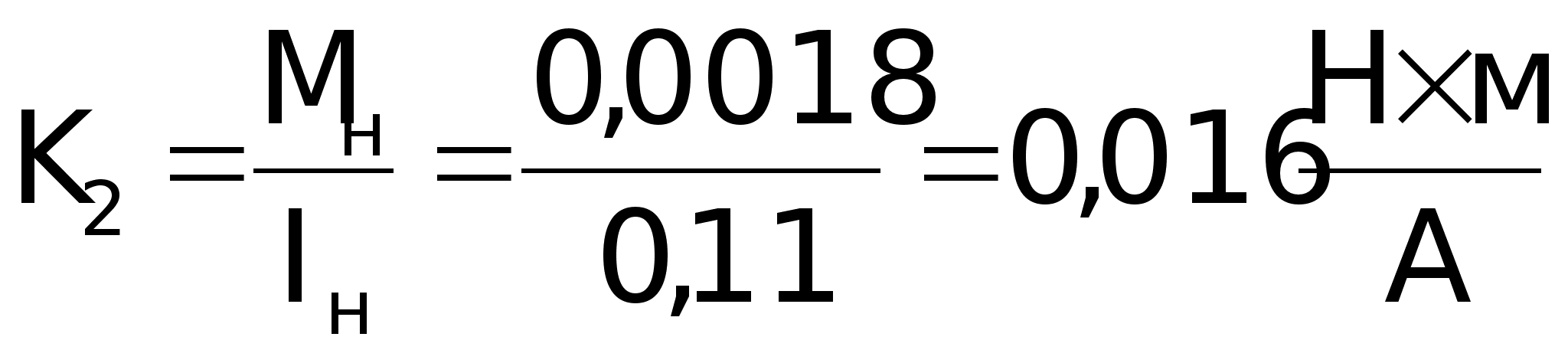
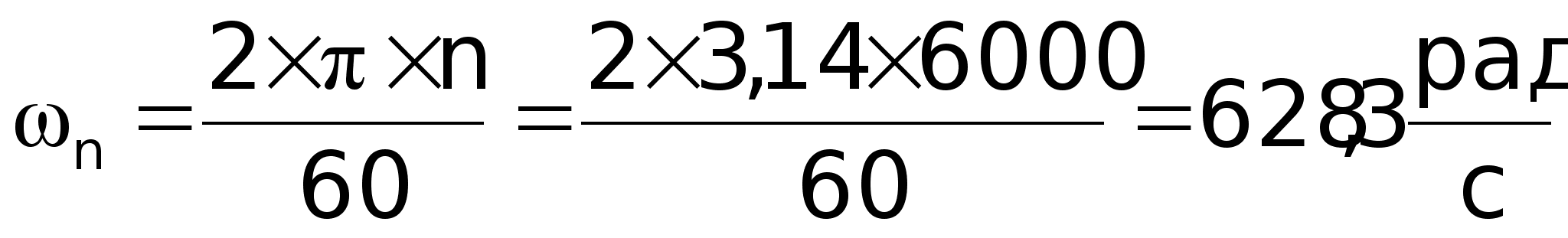
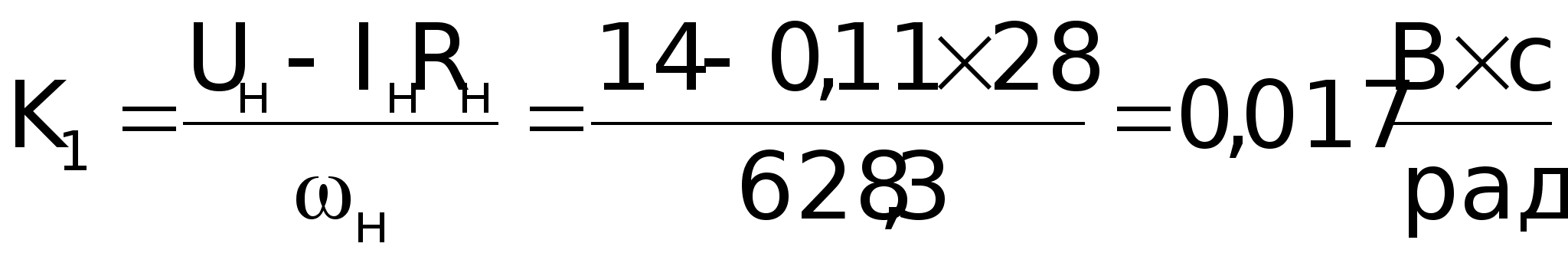
Найдем
индуктивность
якоря:
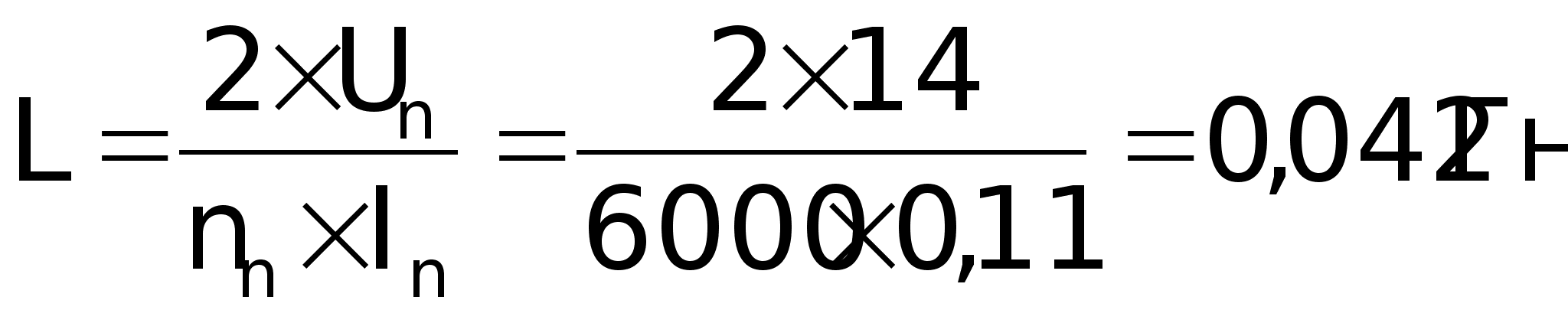
Запишем
систему уравнений
описывающих
систему:
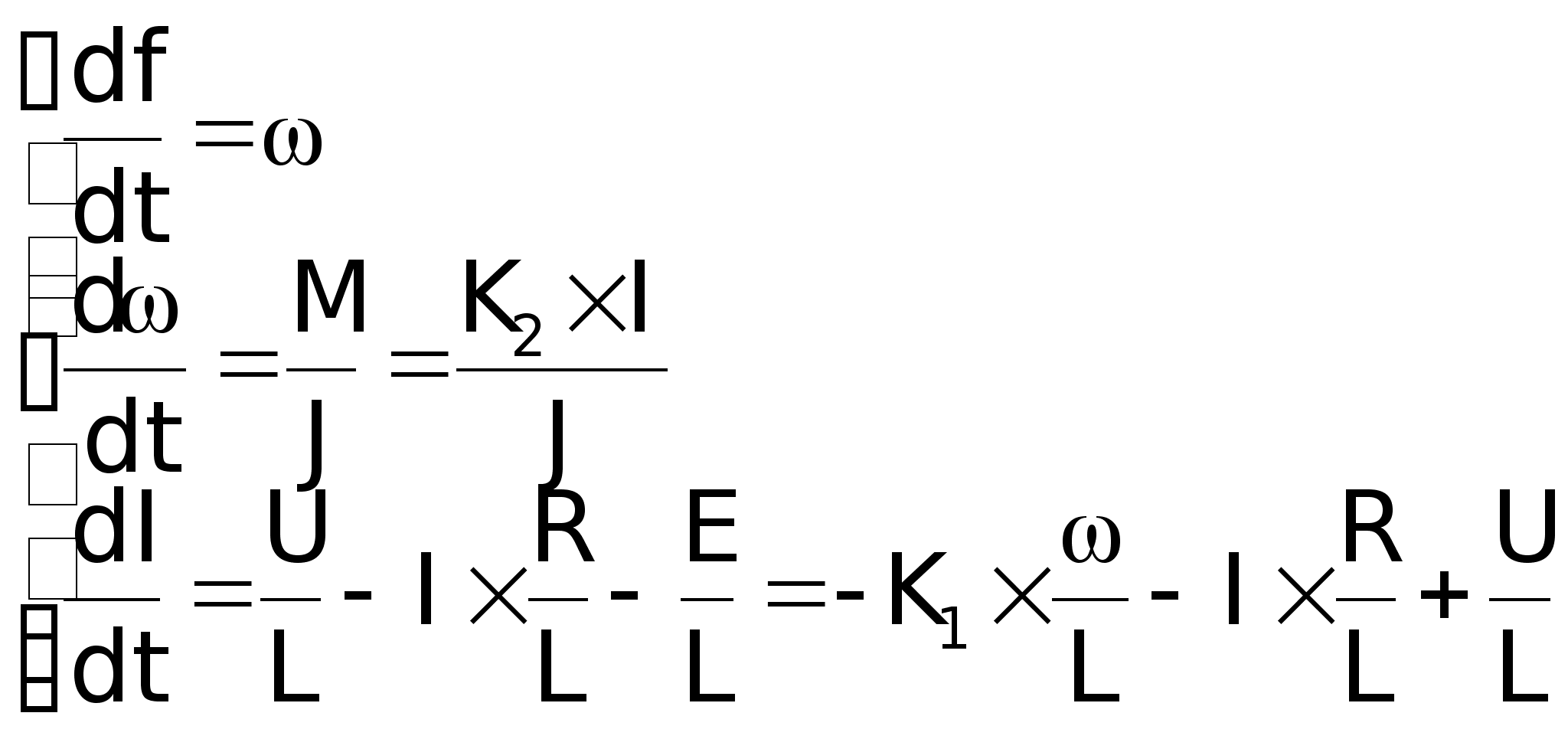
Структурная
схема объекта
управления:
Система
дифференциальных
уравнений в
форме Коши:
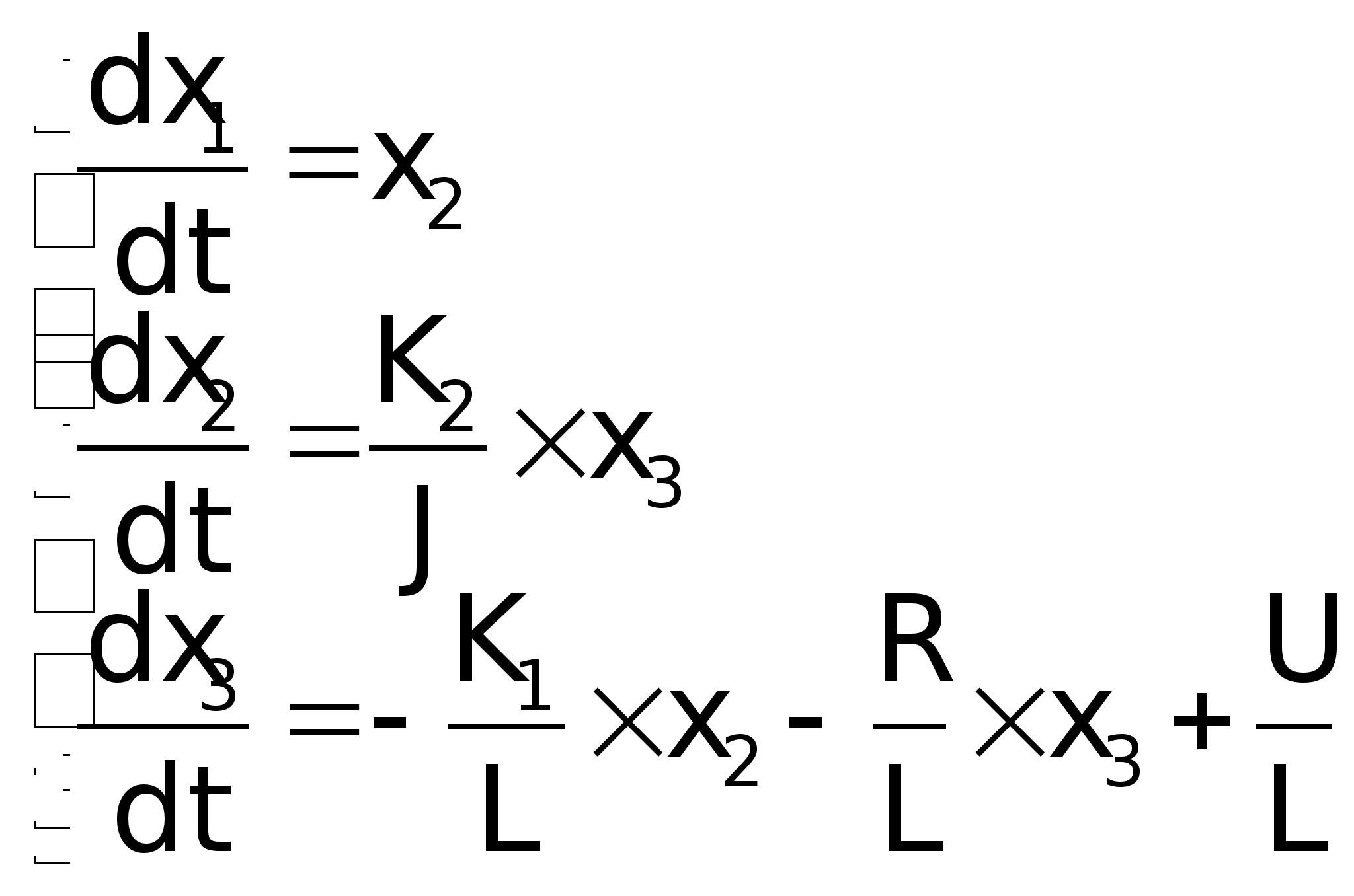
где:
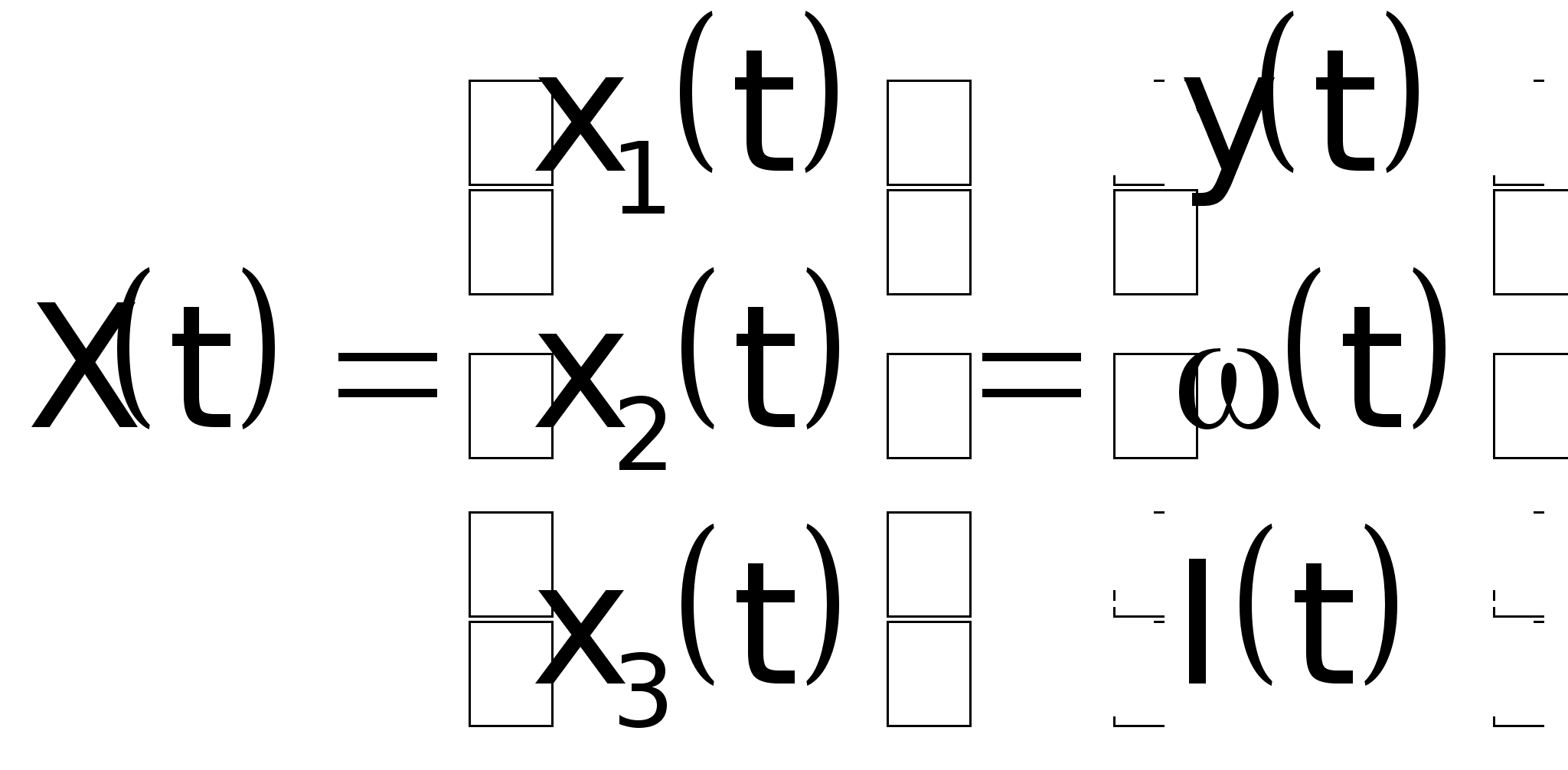
2.
Определить
передаточную
функцию объекта
управления.
Из написанной
выше системы
выразим:
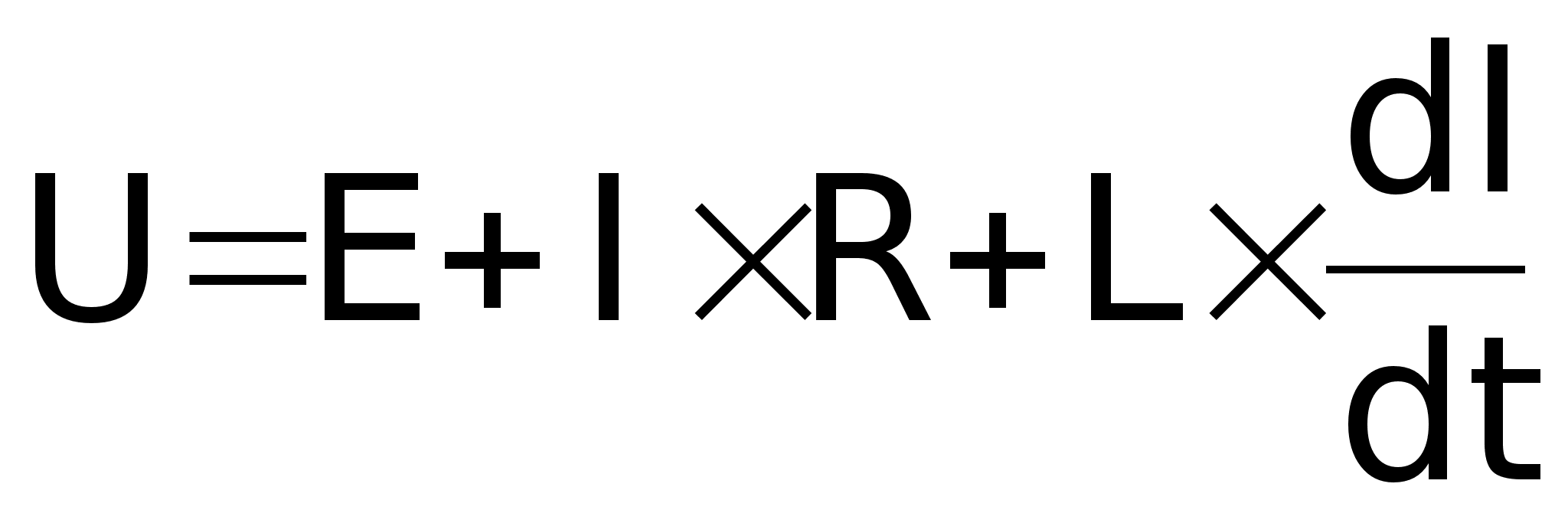
далее:

Передаточная
функция:
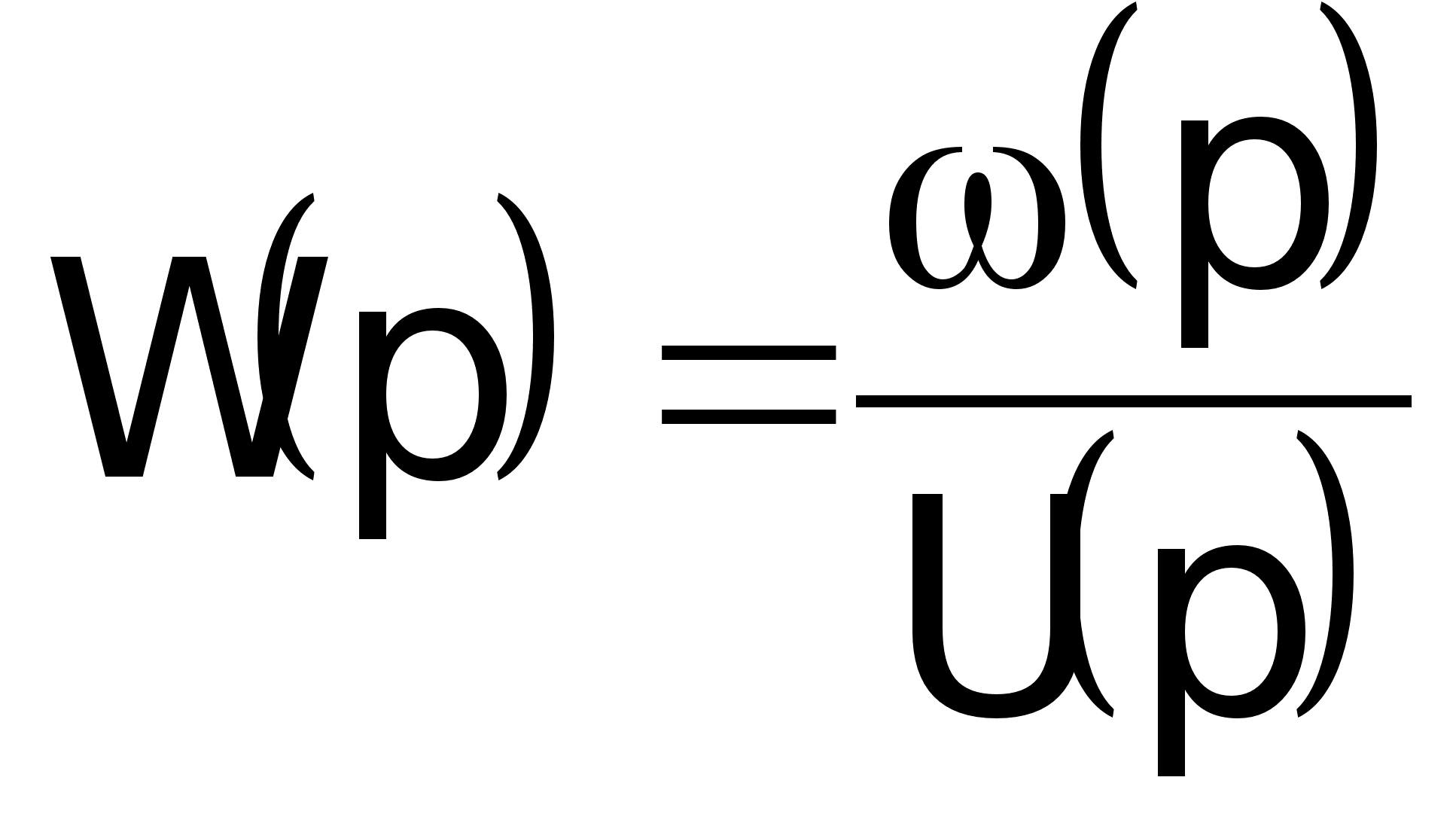
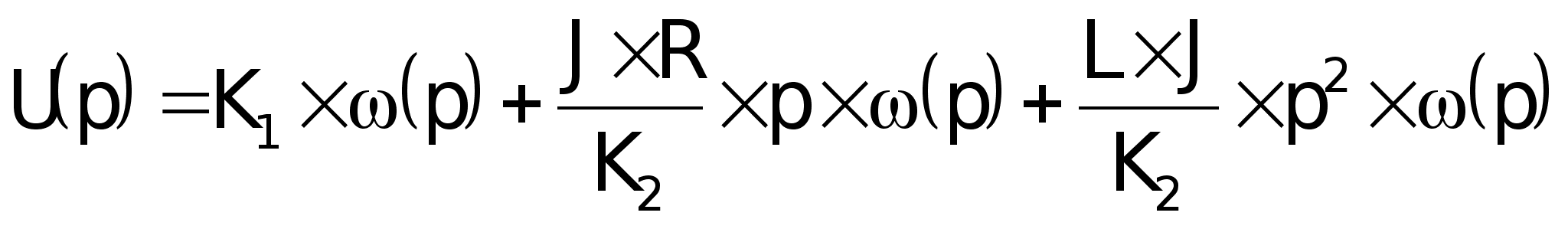
после
подстановки:
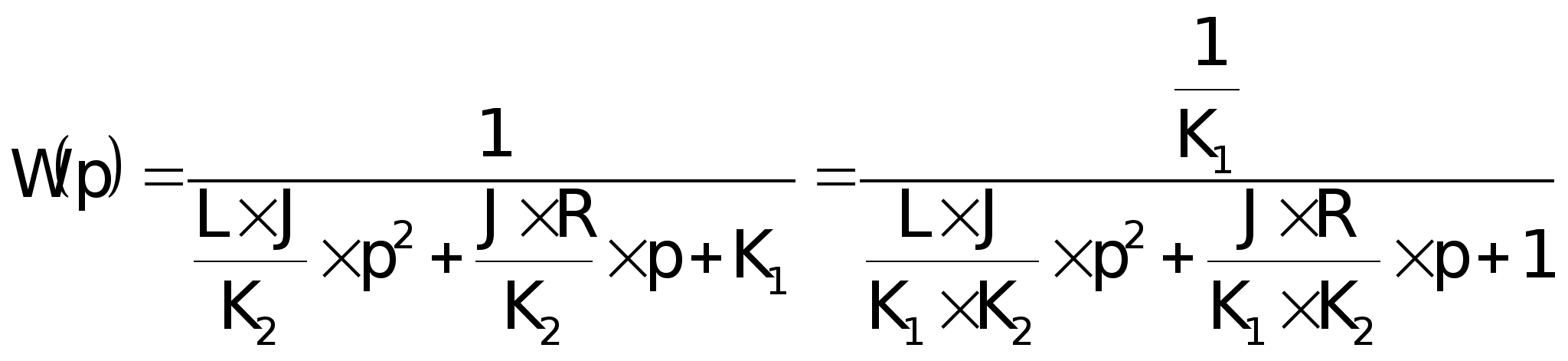
после
подстановки
моих значений:
 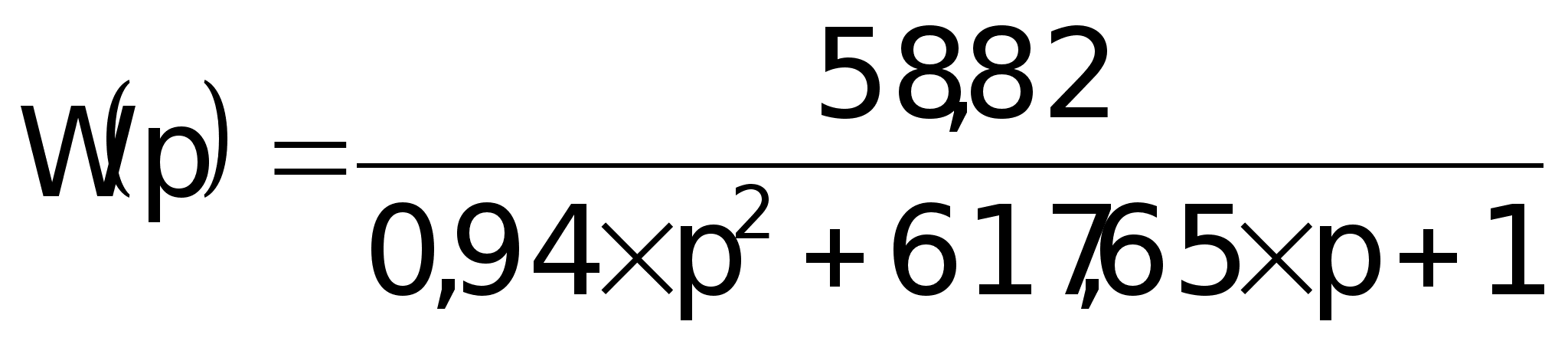 ; ;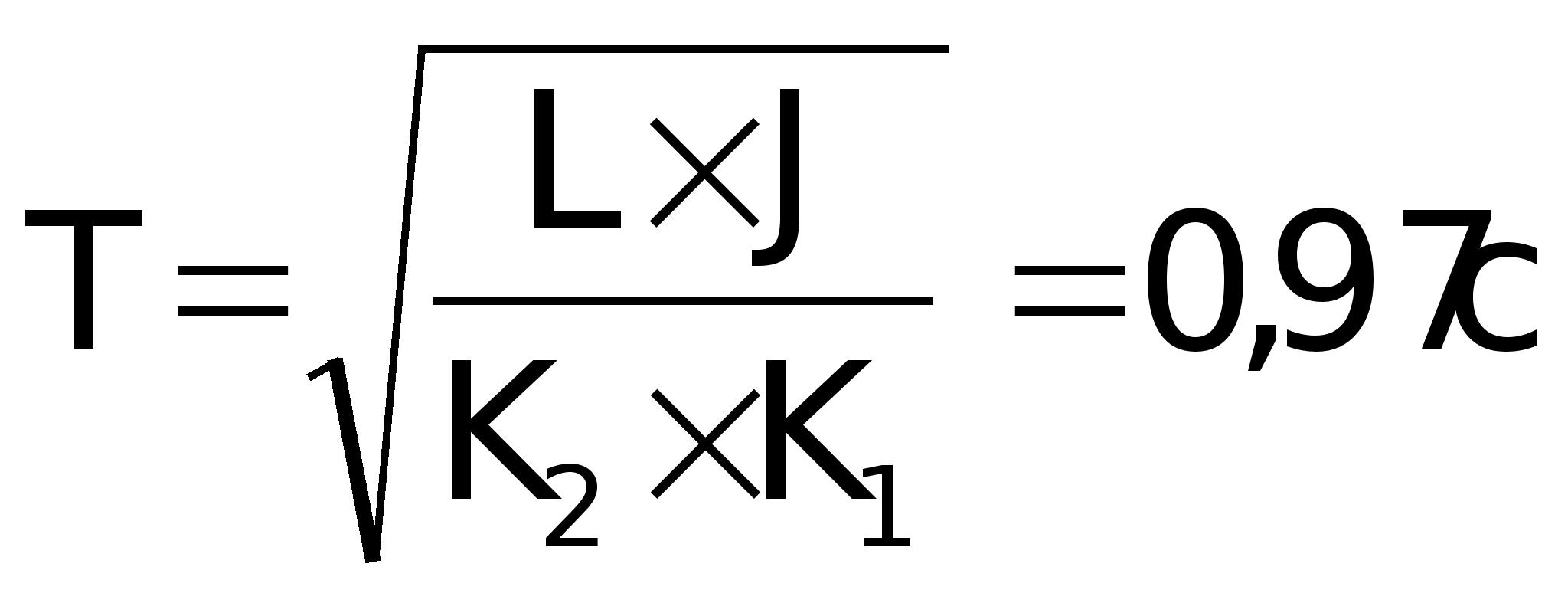 ; ;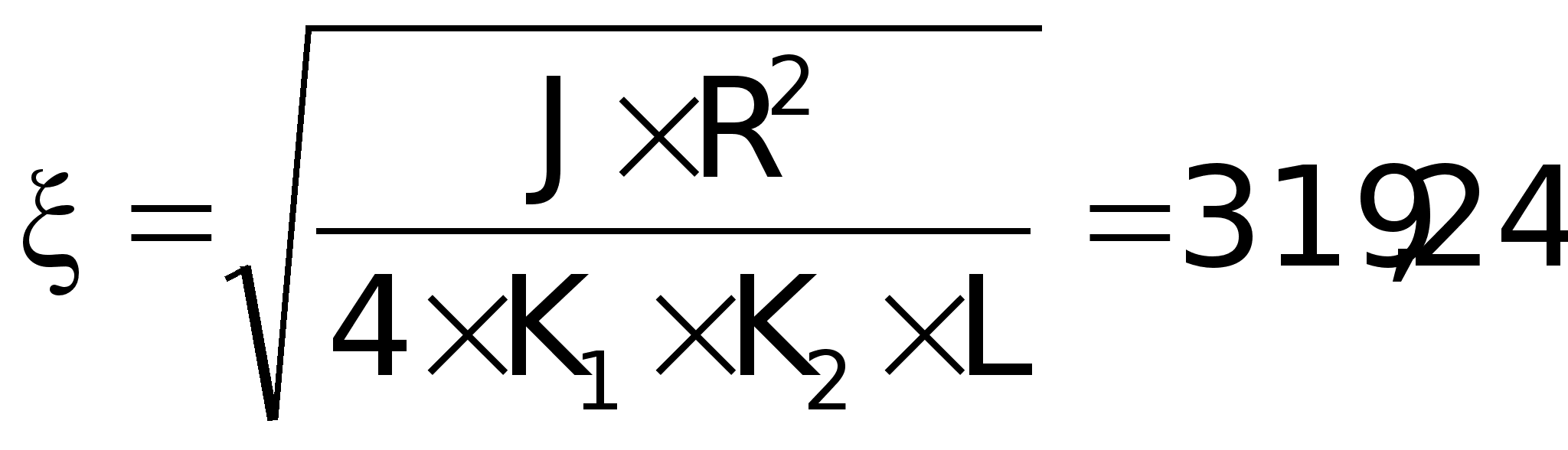
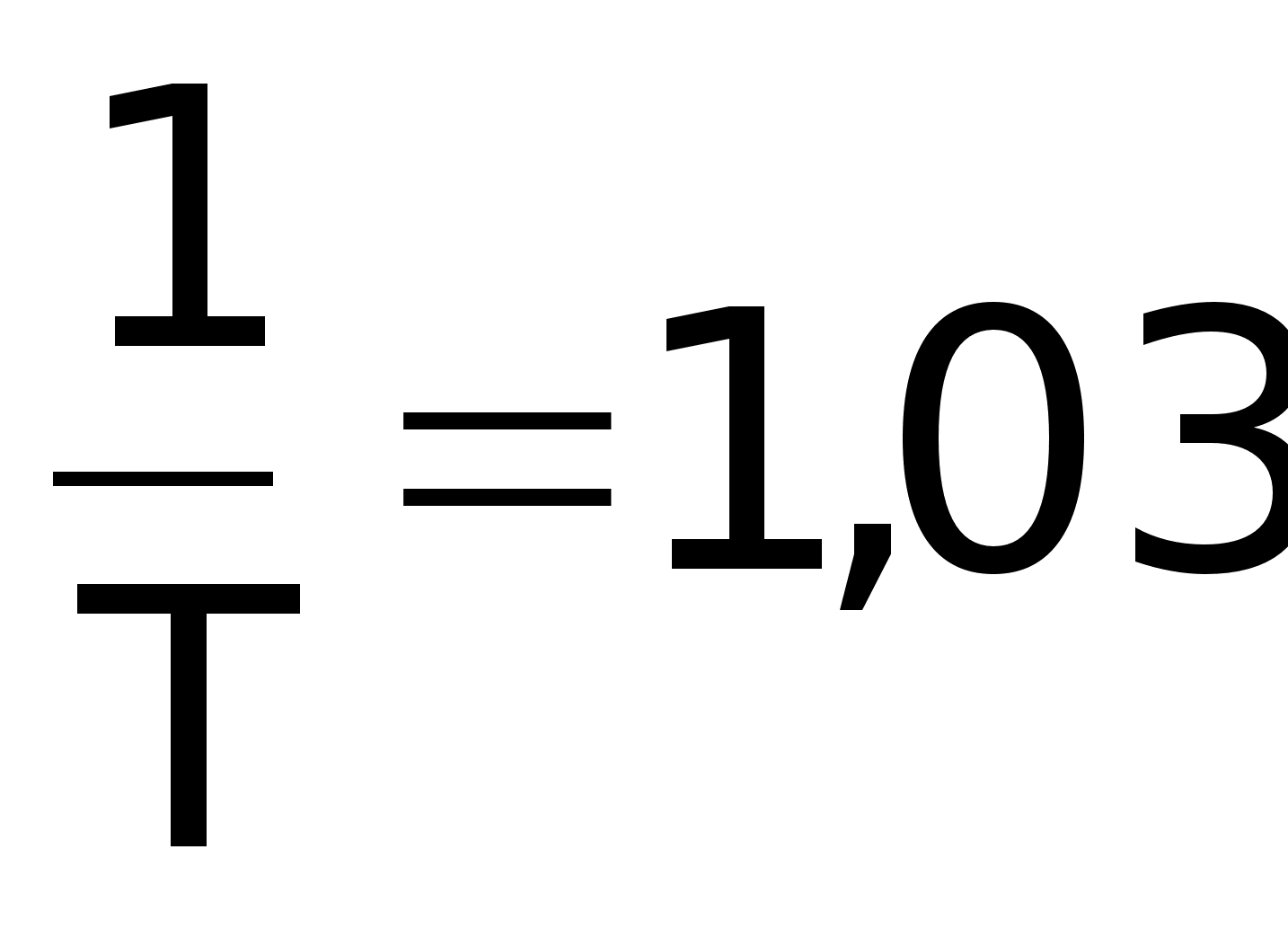
т.к.
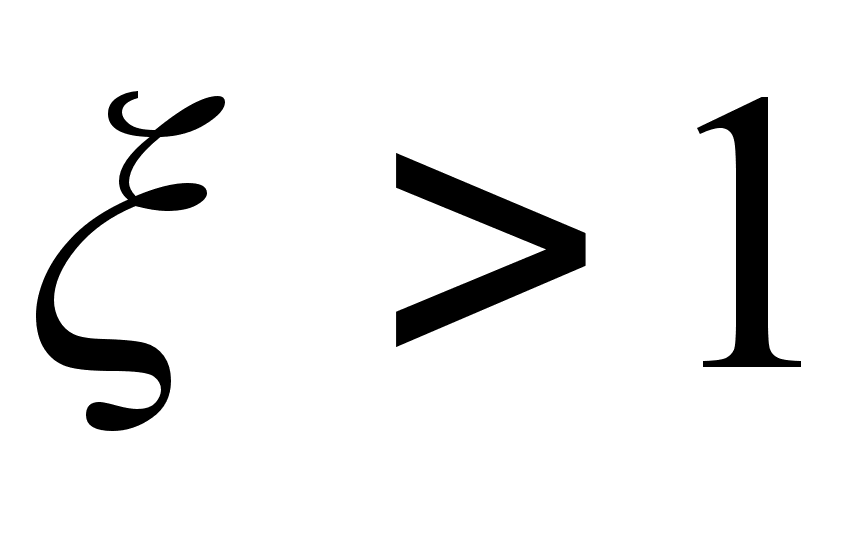 ,
то представим
передаточную
функцию в виде: ,
то представим
передаточную
функцию в виде:
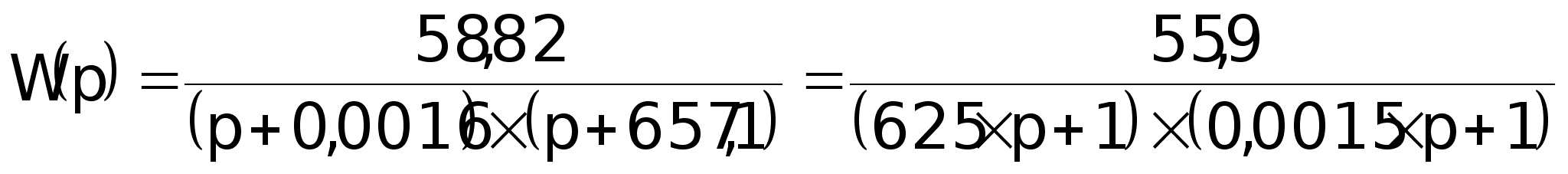
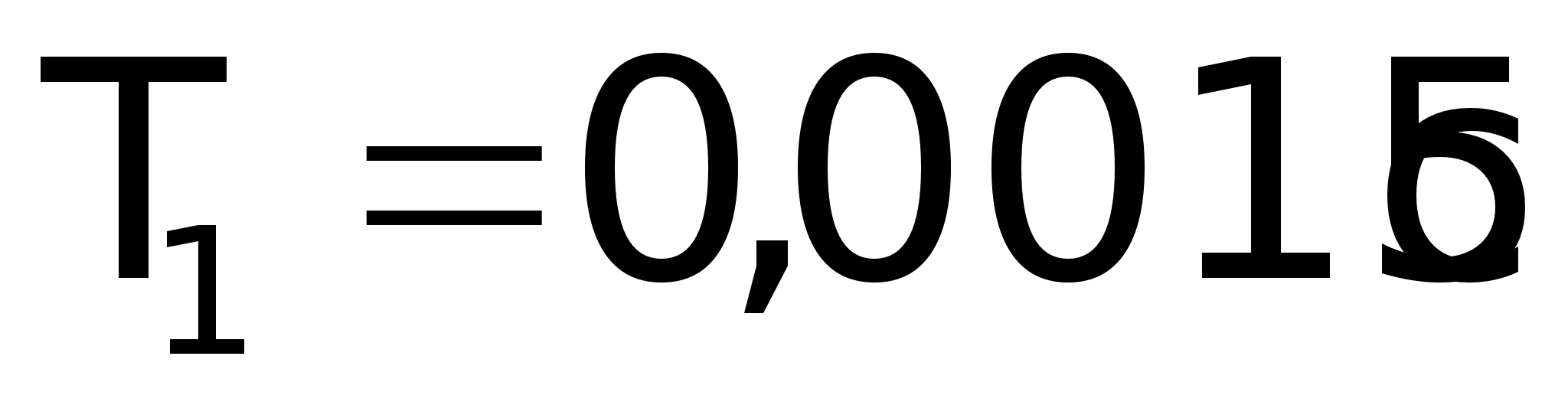 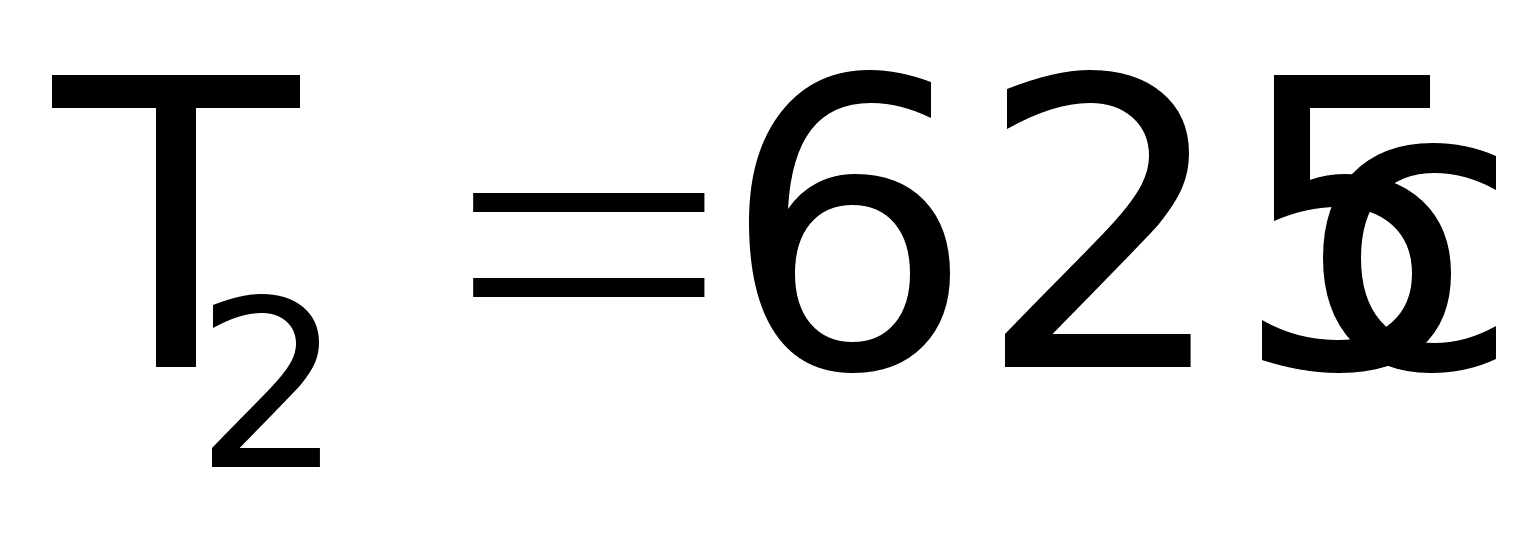 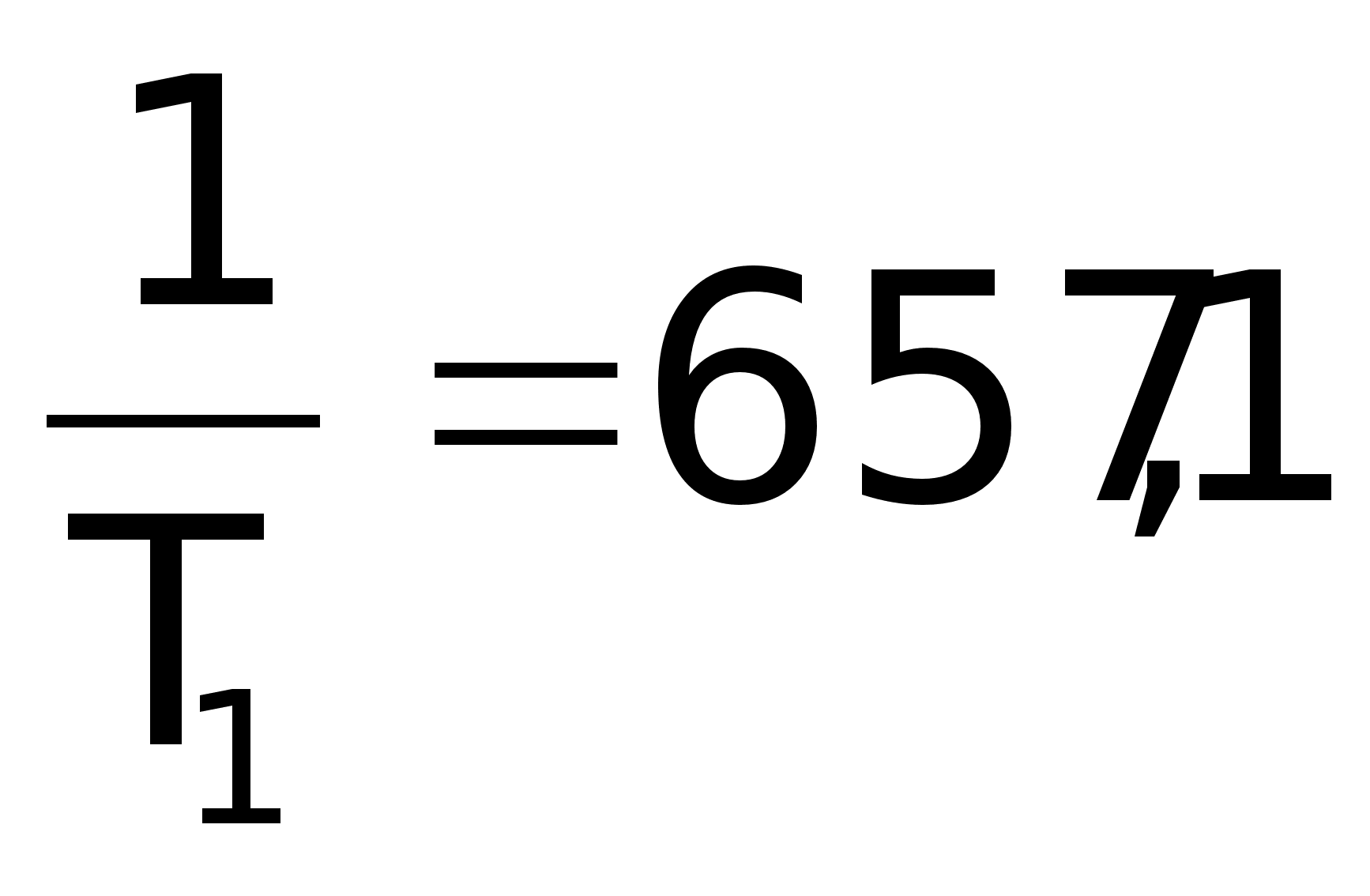 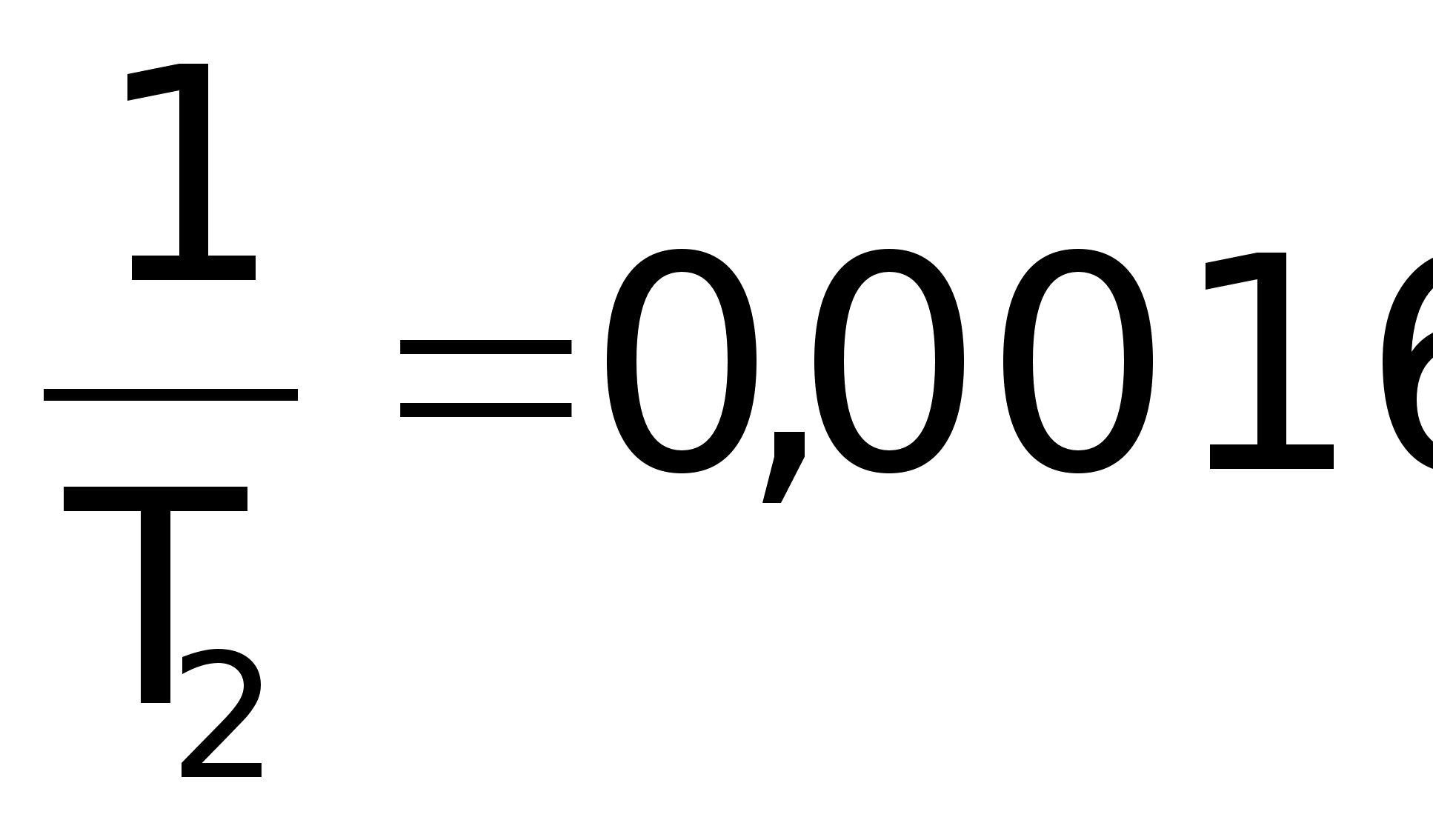
3. Построить
логарифмические
и переходные
характеристики
объекта.
Изображение
переходной
характеристики:
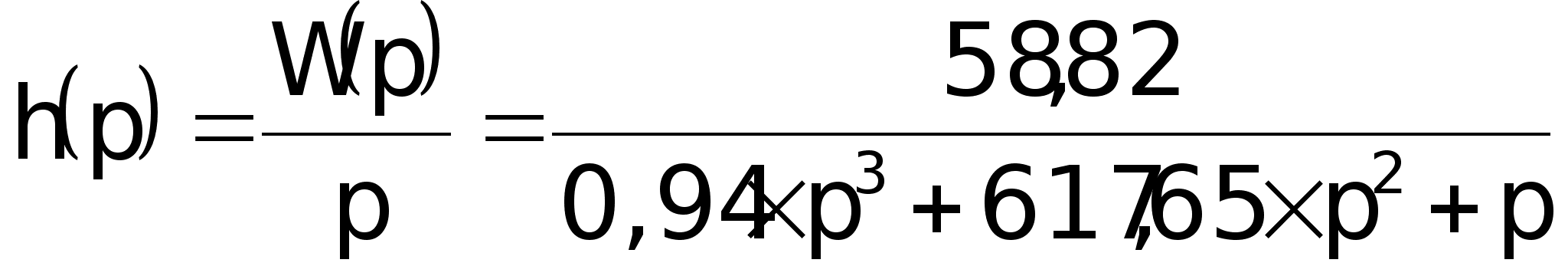
Воспользовавшись
программой
RLT.EXE (обратное
преобразование
Лапласа), получаем
оригинал переходной
характеристики:
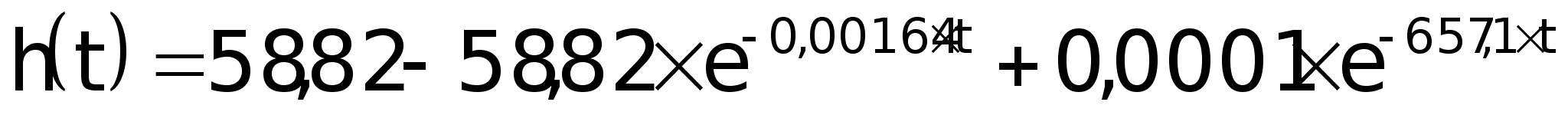
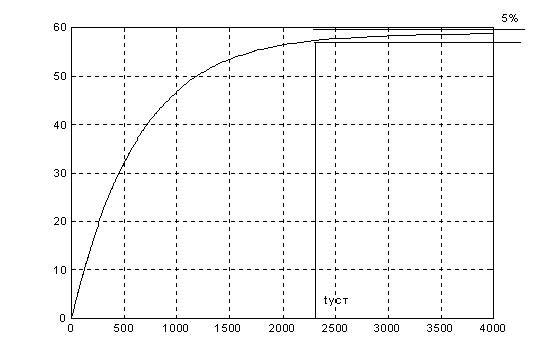
График
переходной
функции.
4. Составить
уравнения
состояния
непрерывного
объекта.
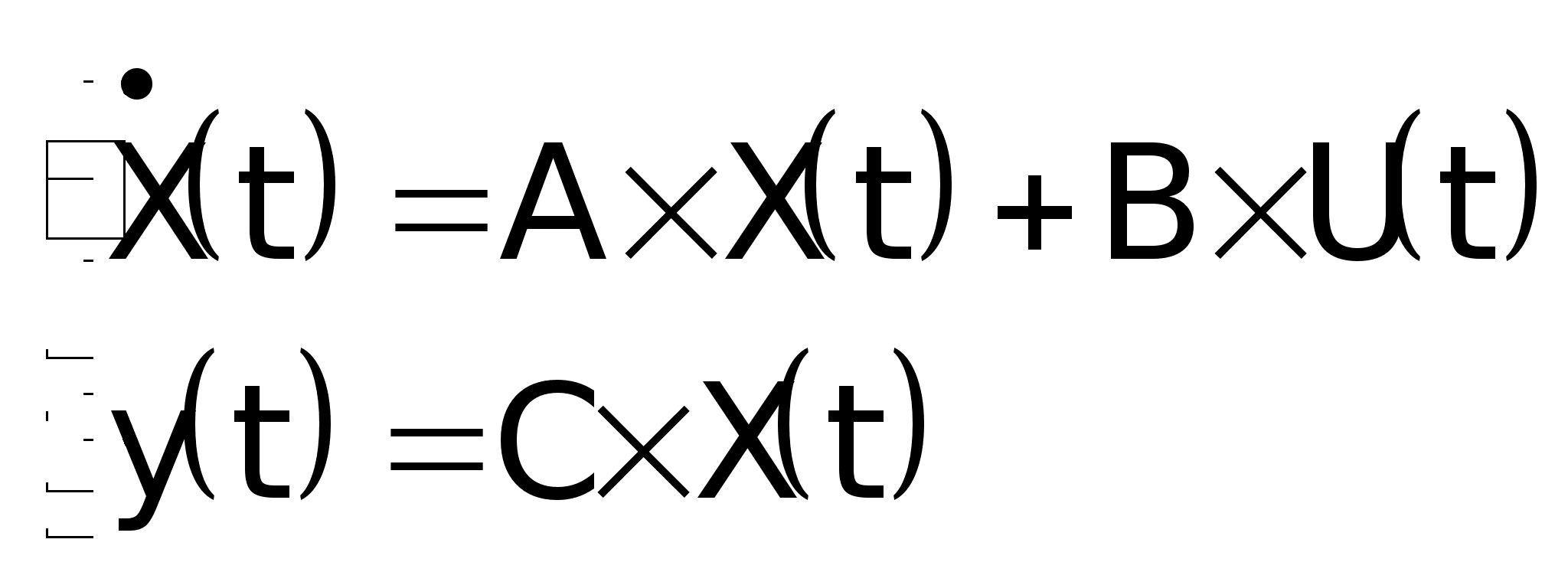
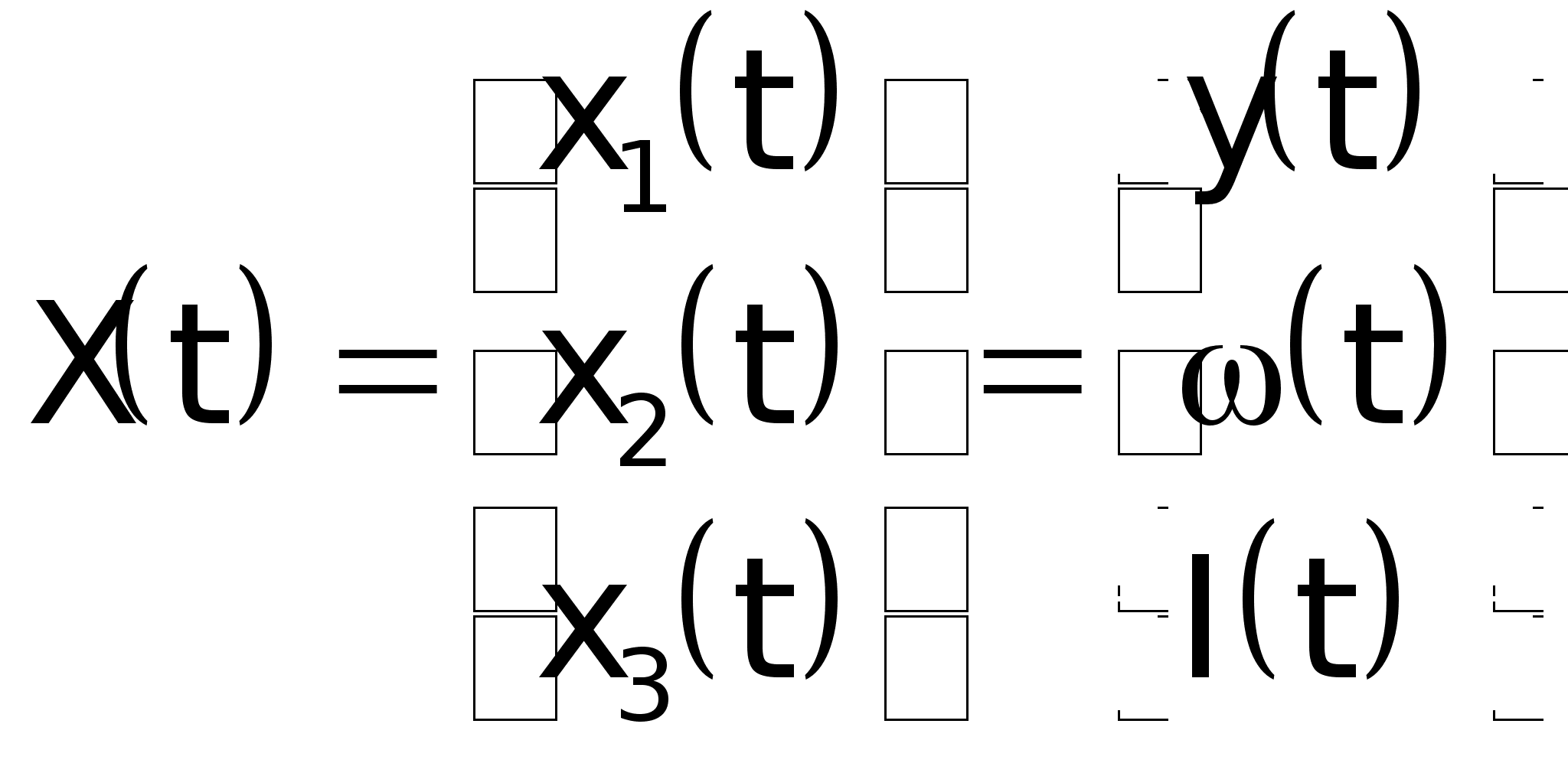
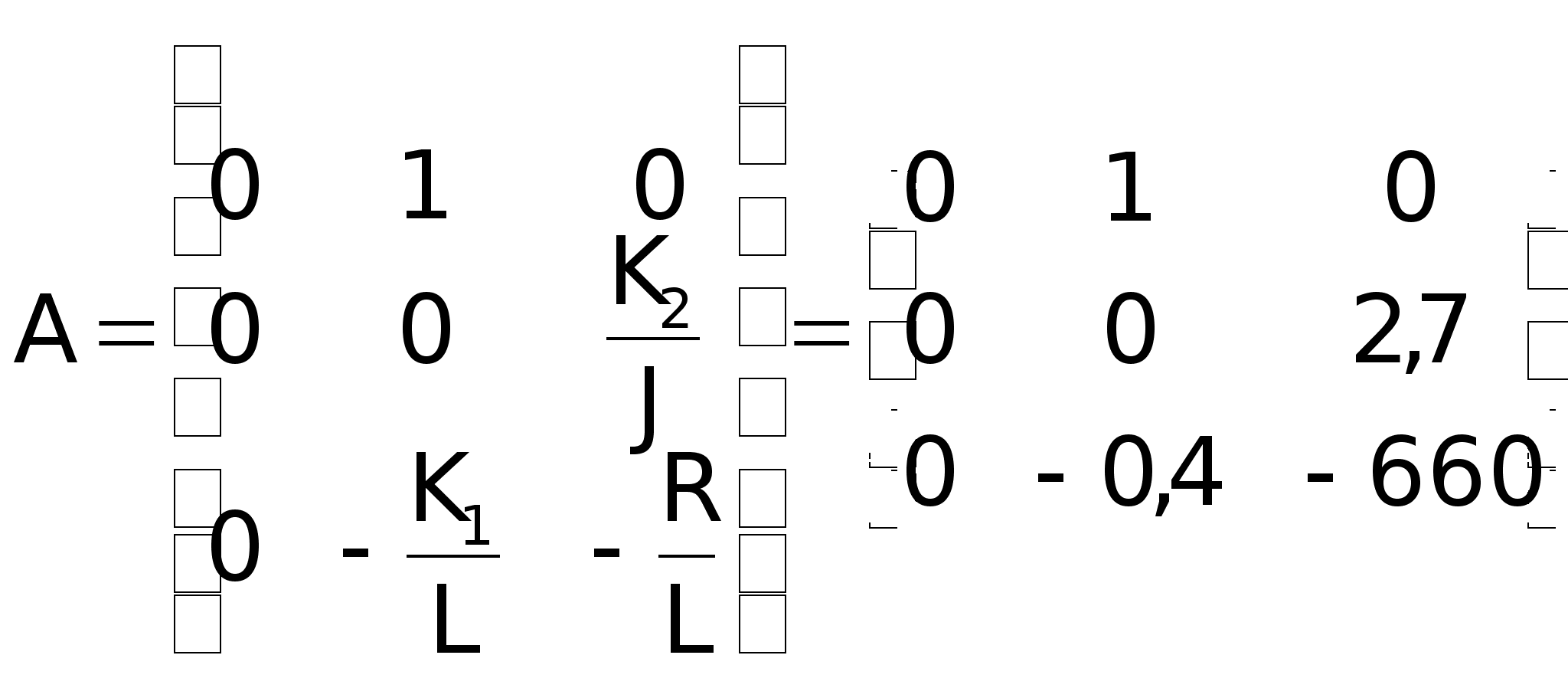
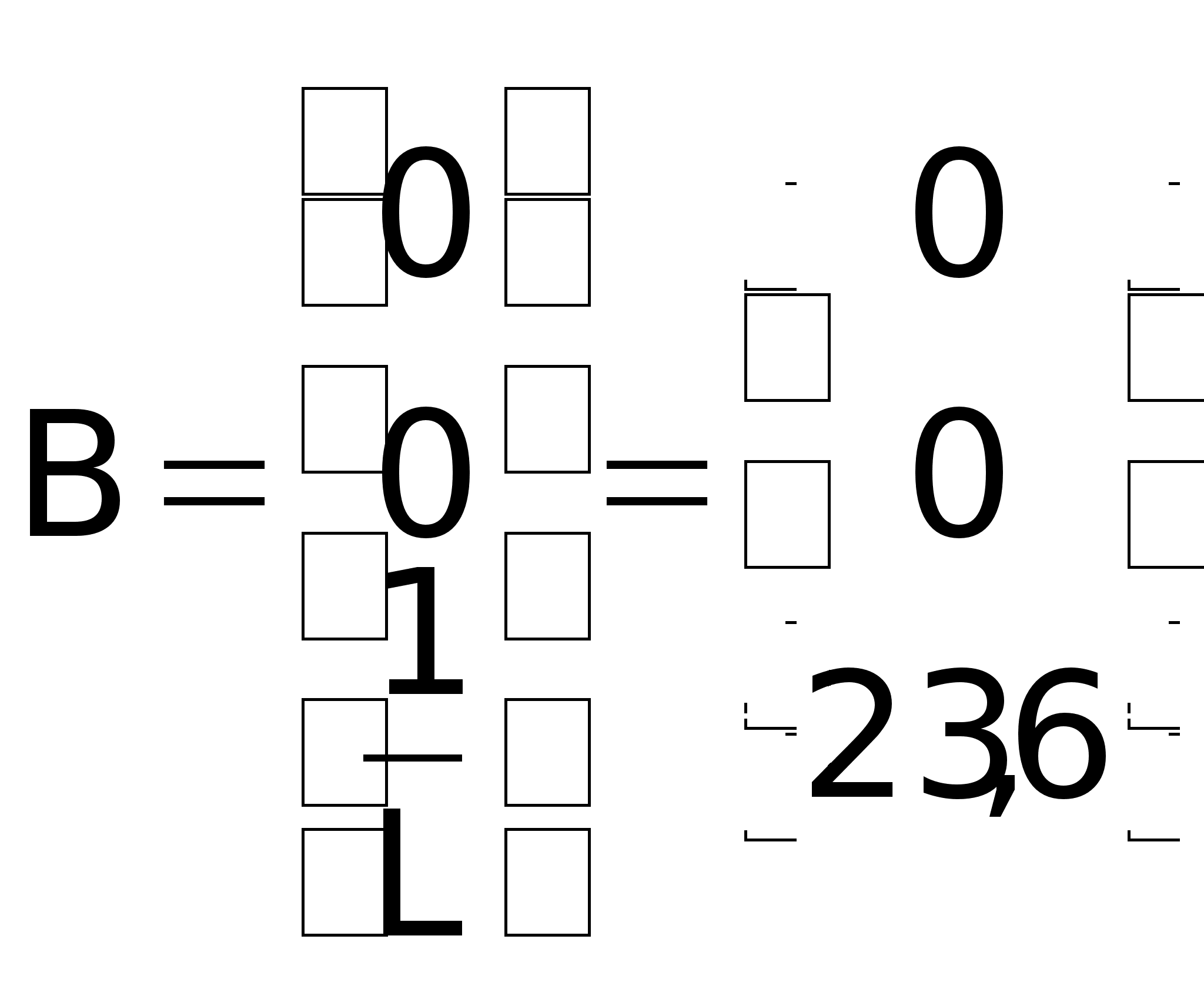 ; ;
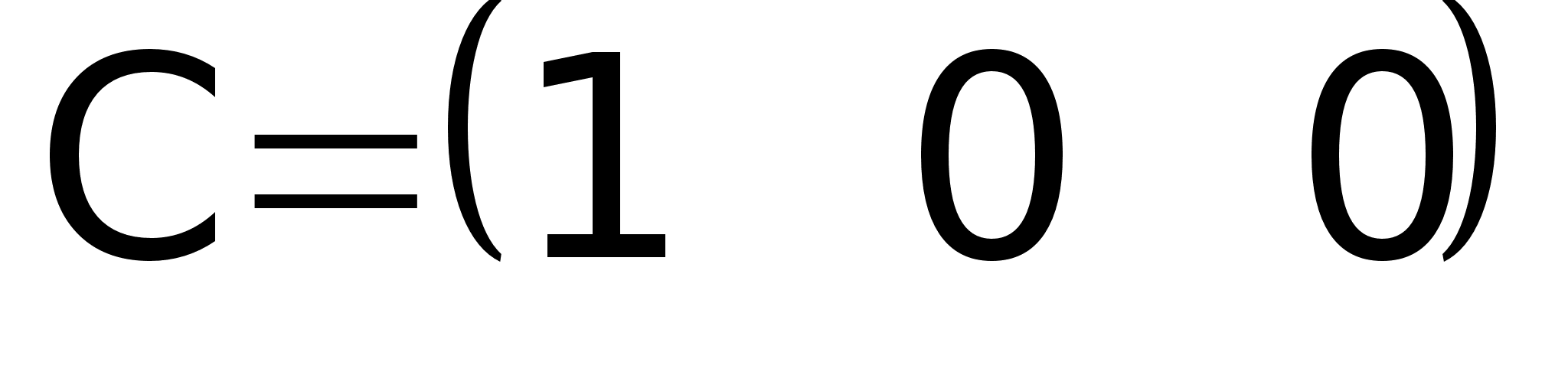
5. Определить
период квантования
управляющей
ЦВМ.
Воспользовавшись
программой,
которая помогает
построить
переходную
характеристику,
получаем время
переходного
процесса:
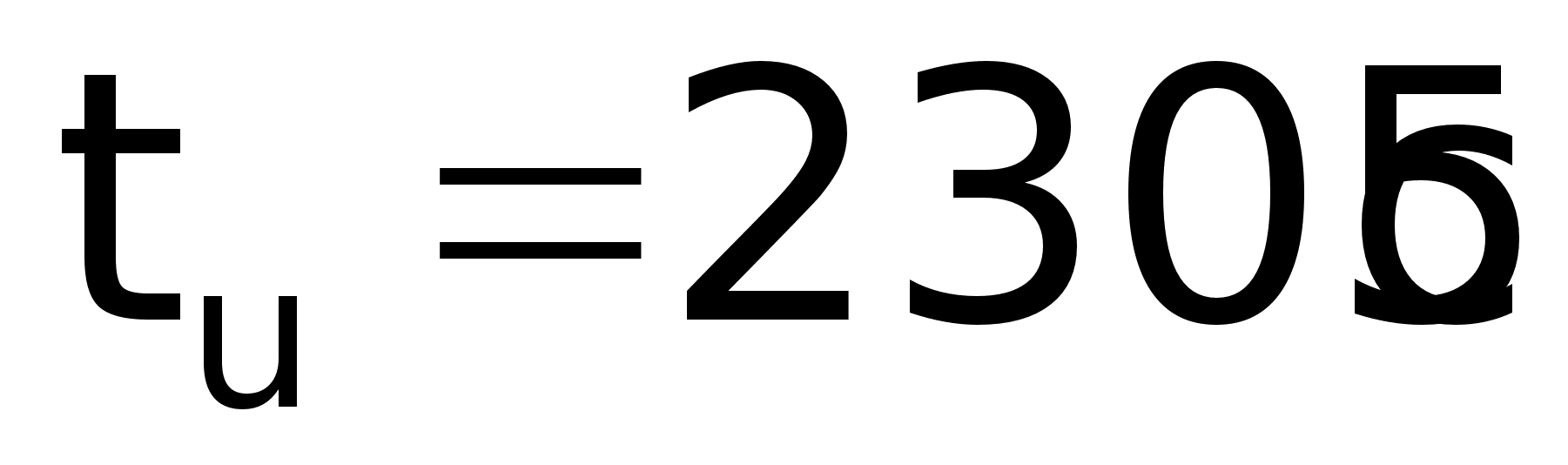
а соответственно
период квантования
центральной
ЦВМ составит:
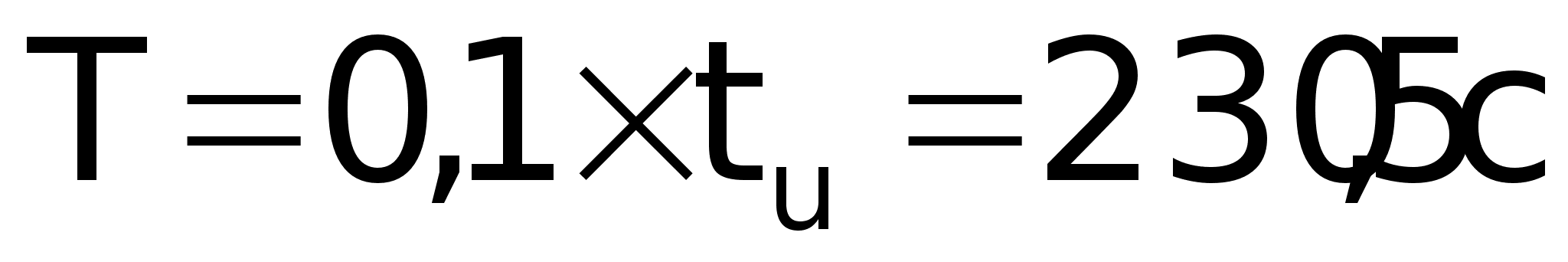
Получили
большое время
дискретизации,
для того, что
бы в расчетах
воспользоваться
программой
SNT2.EXE уменьшим
его до:
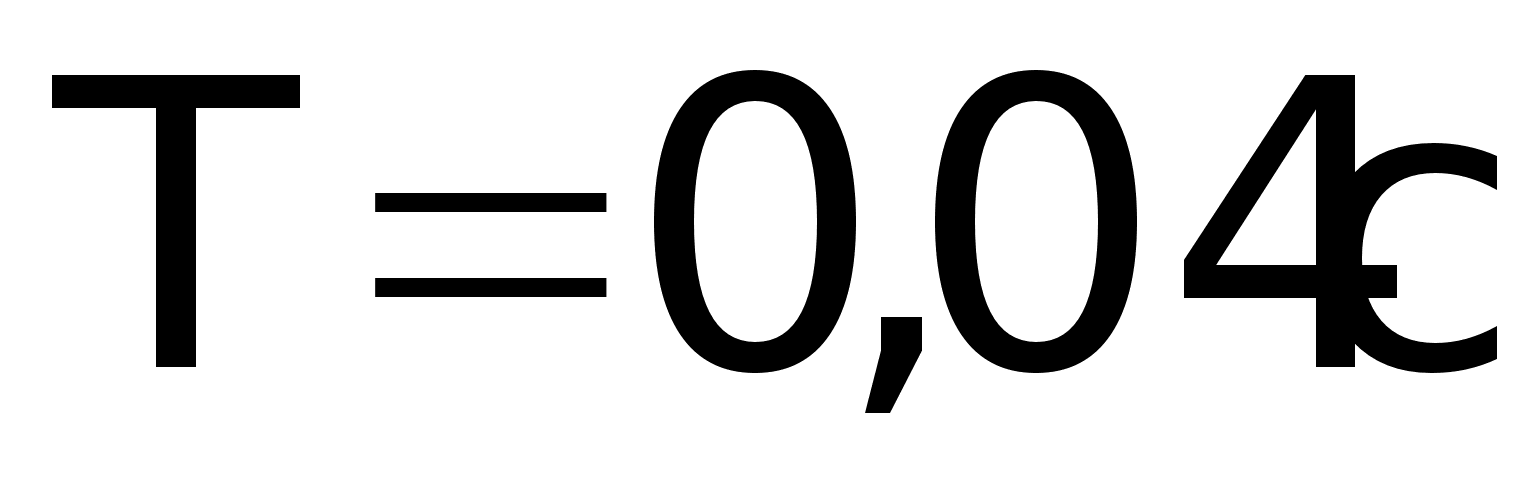
6. Составить
уравнения
состояния
дискретной
модели объекта.
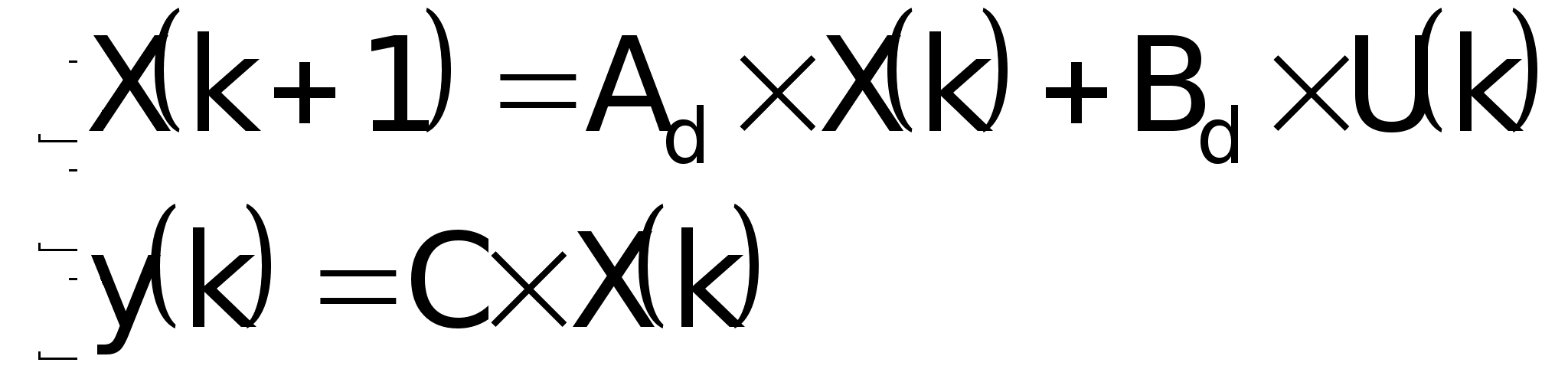
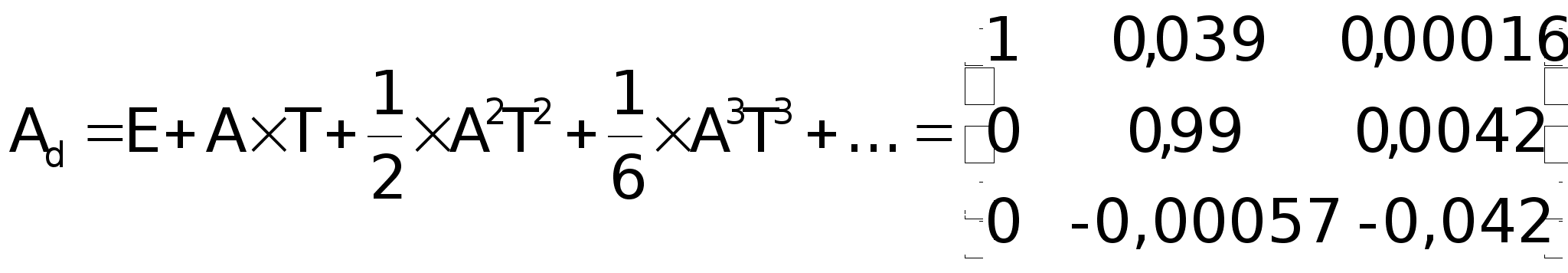
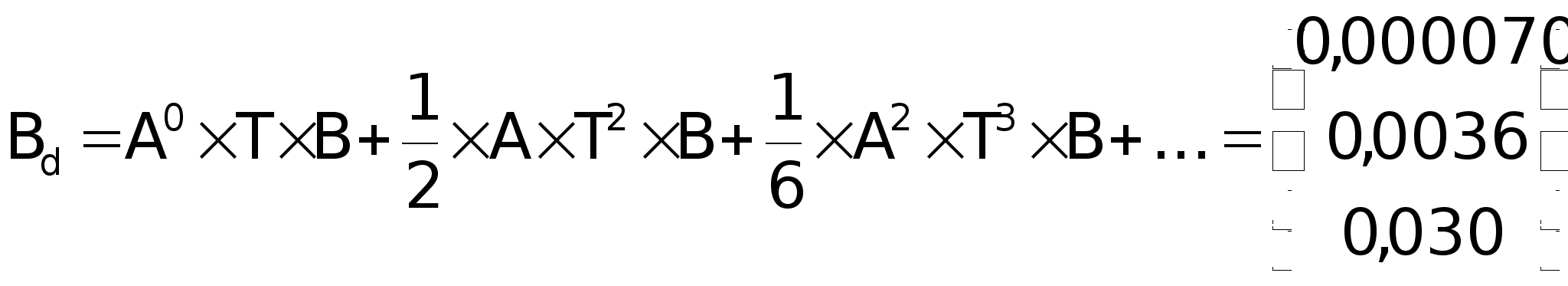
Матрица
управляемости
дискретной
модели объекта:
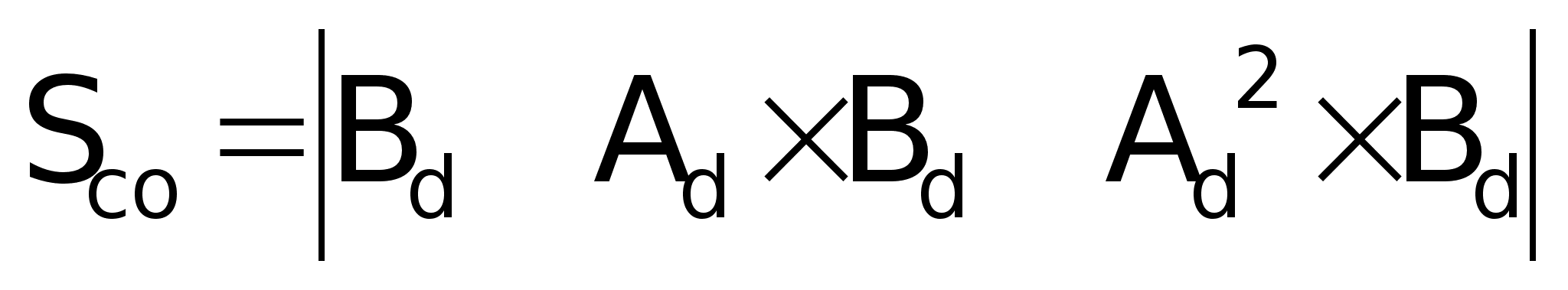
в числах:
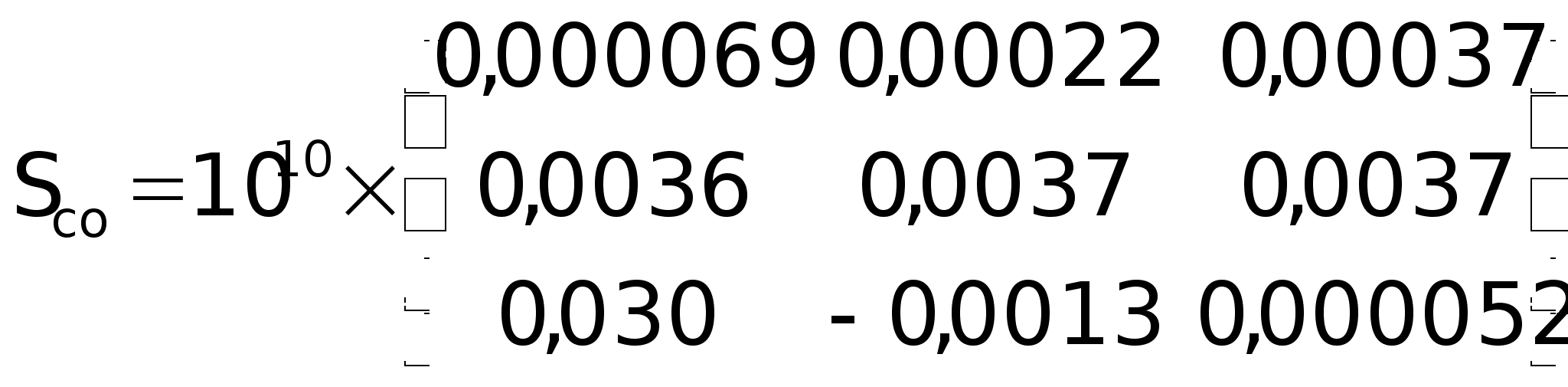

т.е. система
полностью
управляема.
Матрица
наблюдаемости
дискретной
модели объекта:
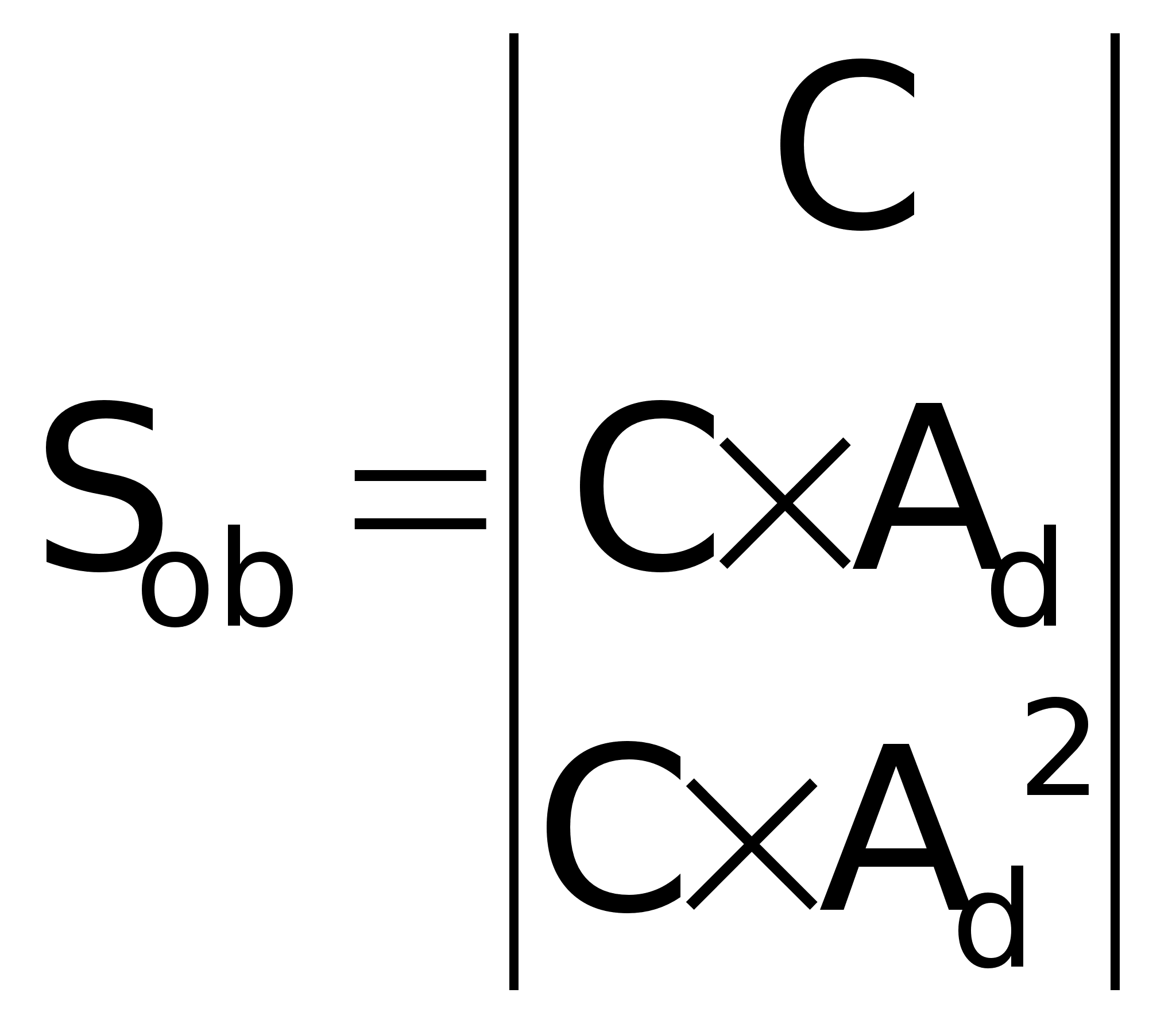
в числах:
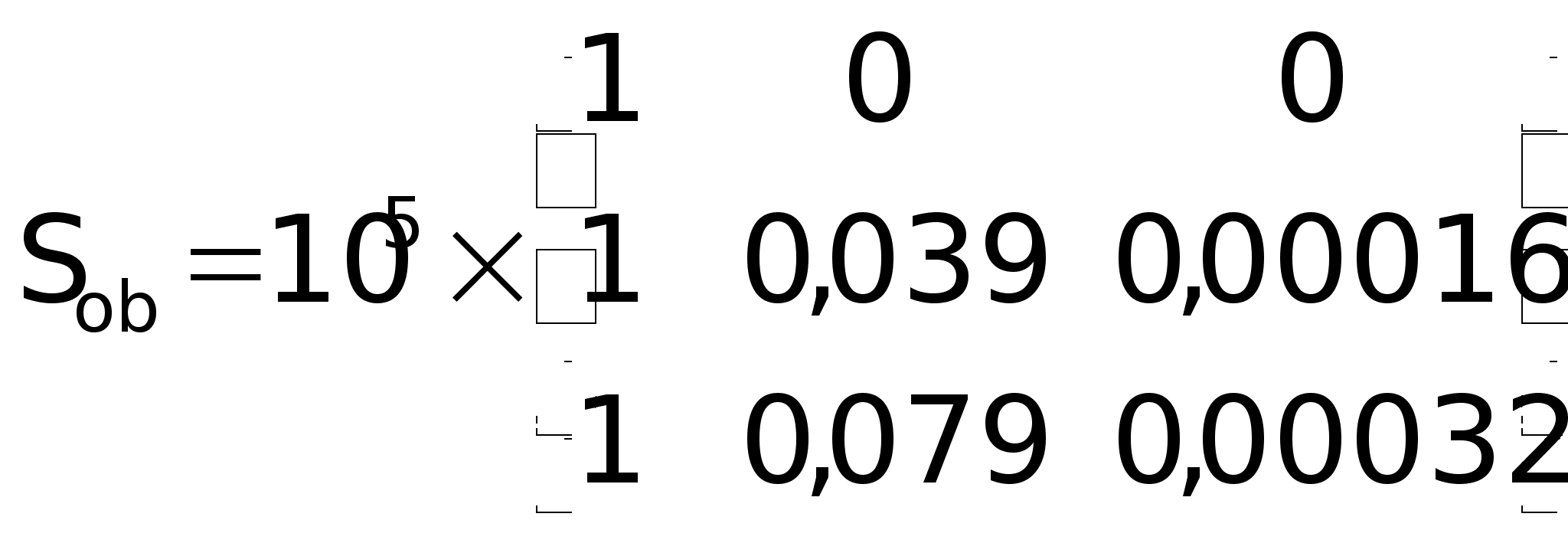

т.е. система
полностью
наблюдаема.
7. Рассчитать
параметры
цифрового
регулятора
состояния.
Матрица
управления
из условия
окончания
переходного
процесса за
минимальное
число тактов:
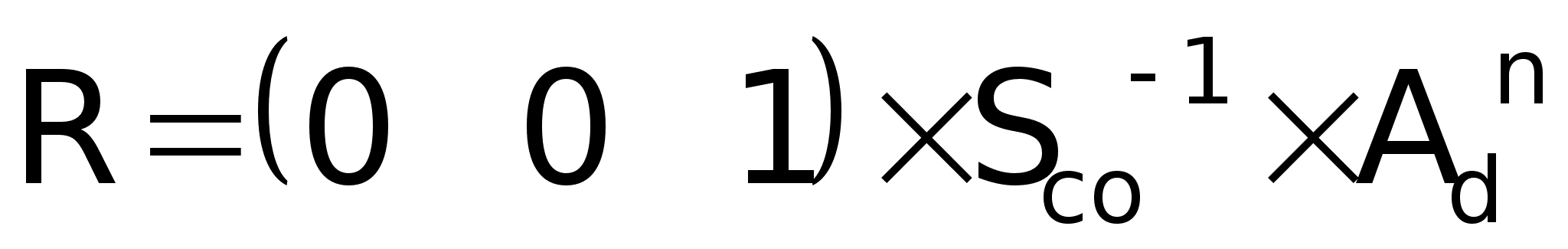
где:
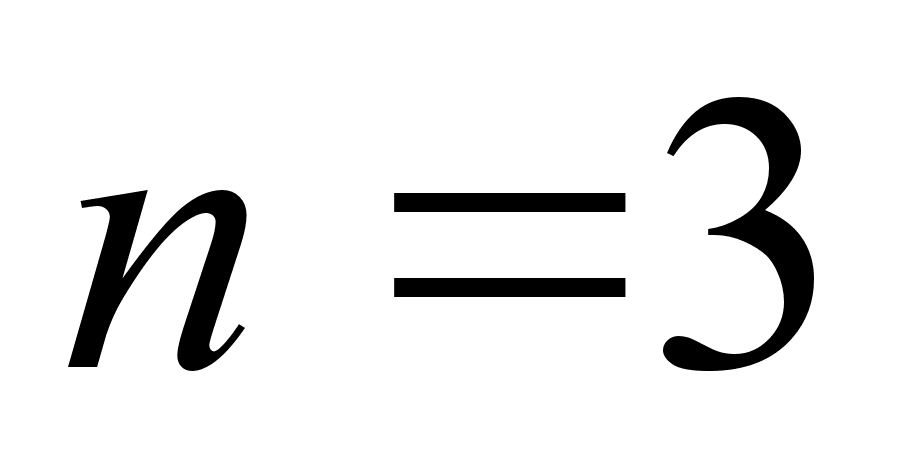
в числах:
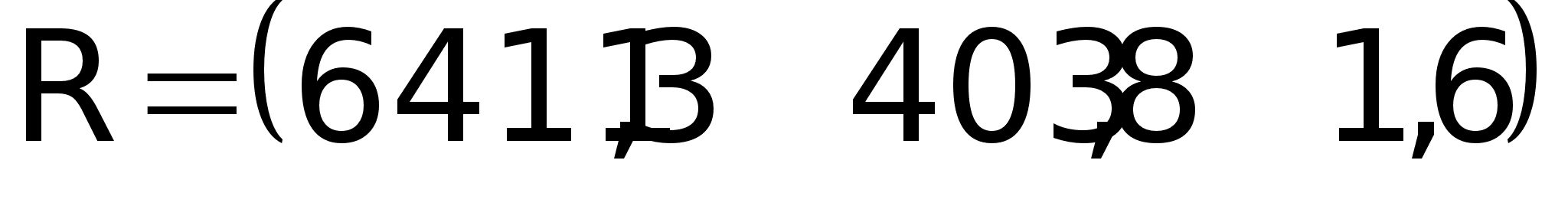
8. Рассчитать
параметры
оптимального
быстродействию
наблюдателя
состояния и
составить его
структурную
схему.
Вектор
обратной связи
наблюдателя:
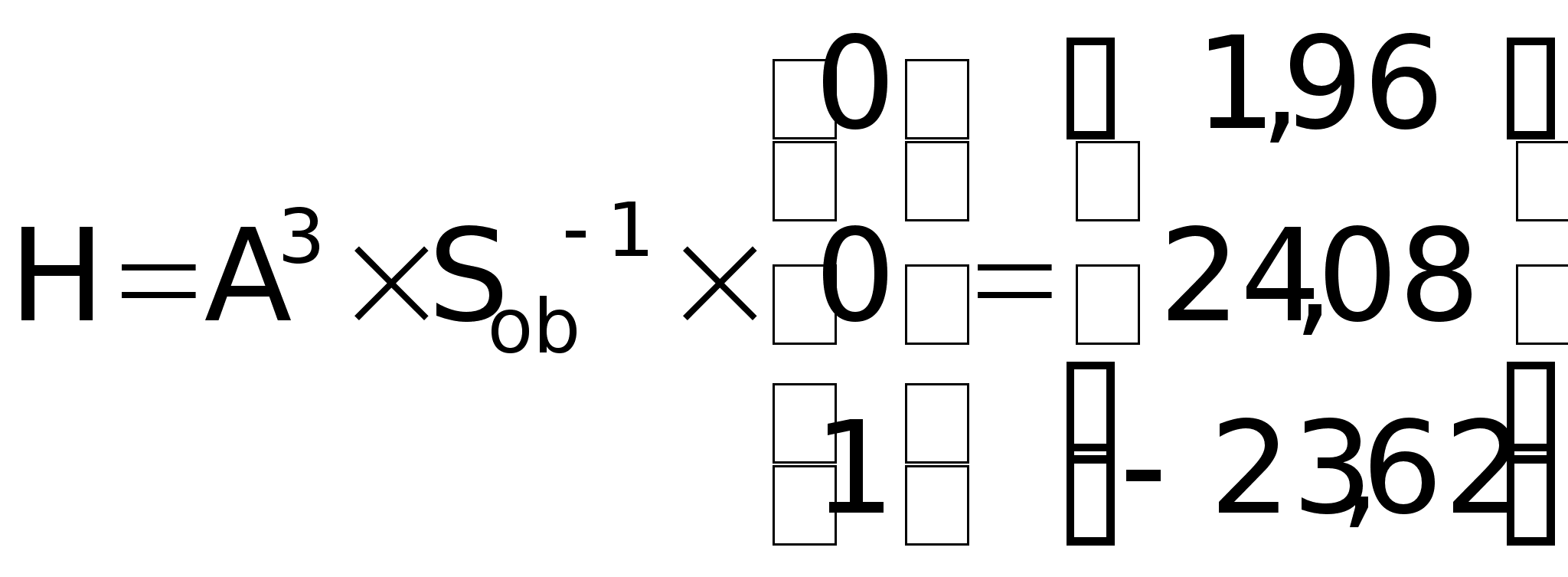
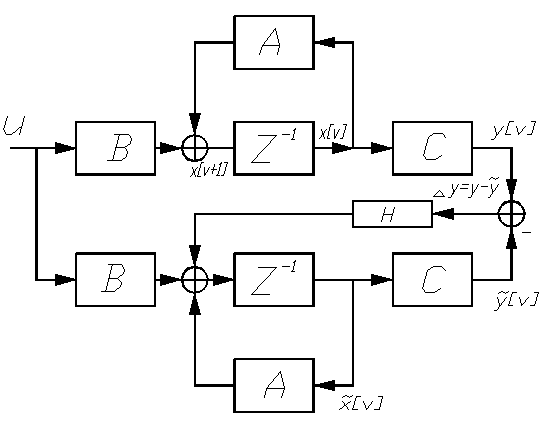
Структурная
схема наблюдателя:
9. Записать
уравнения
состояния
замкнутой
цифровой системы
и составить
её структурную
схему.
Уравнения
состояния
наблюдателя:
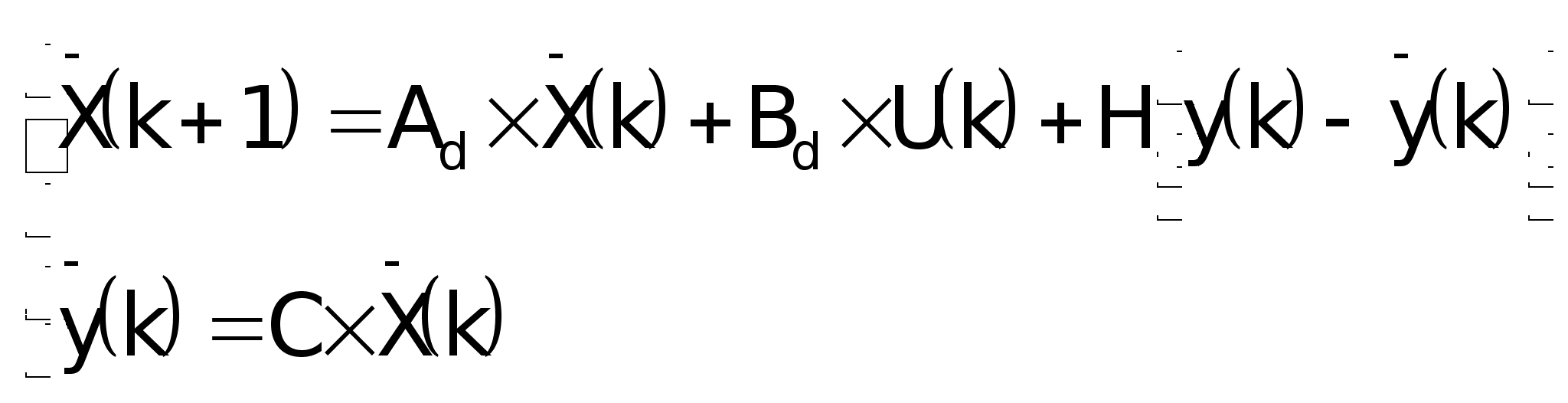
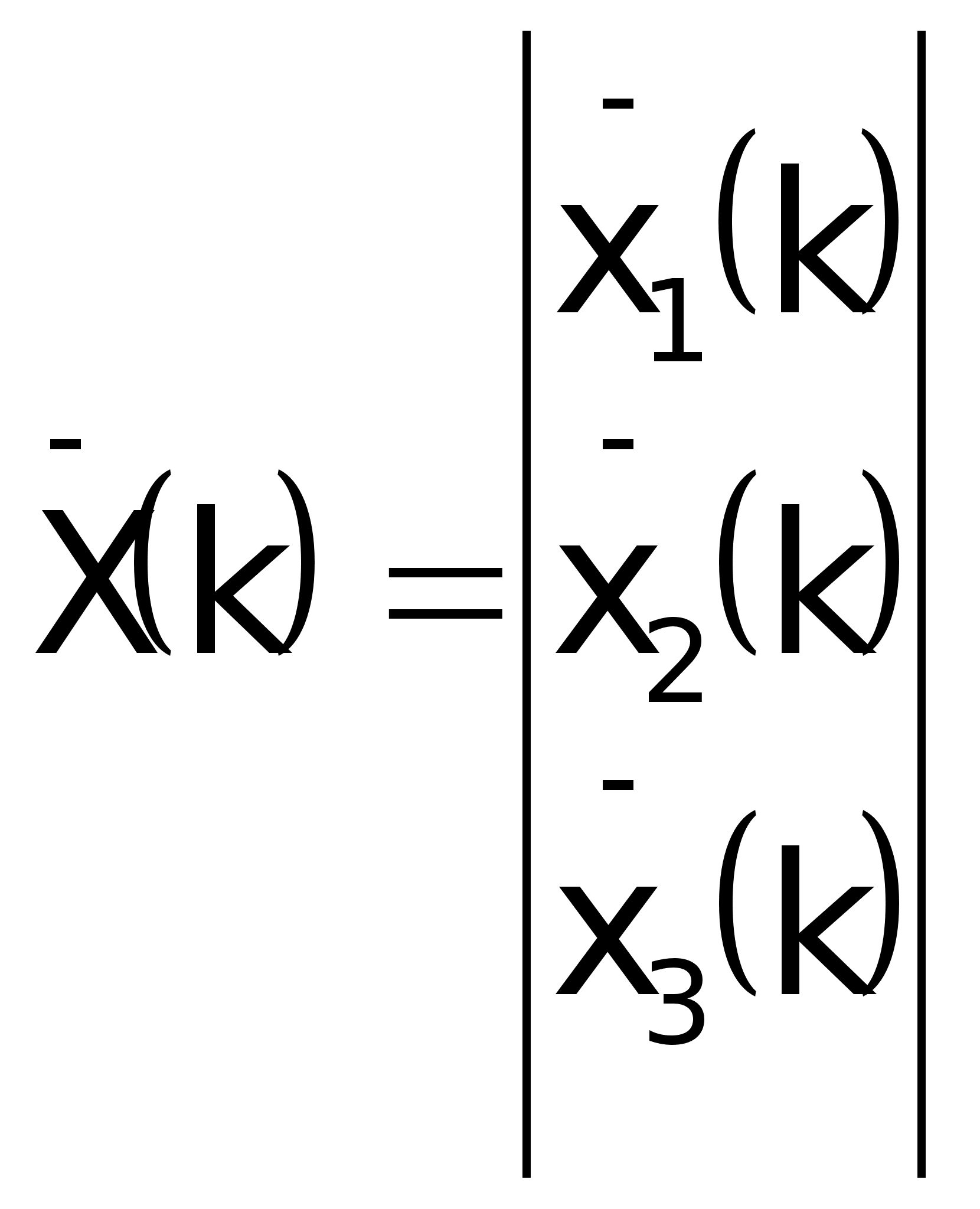
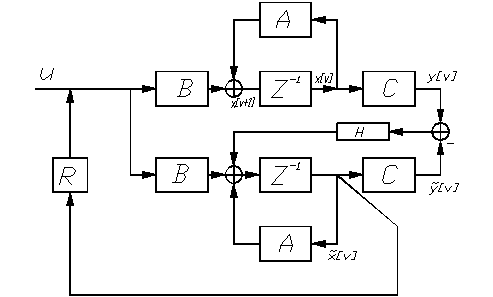
Структурная
схема замкнутой
цифровой системы,
с наблюдателем:
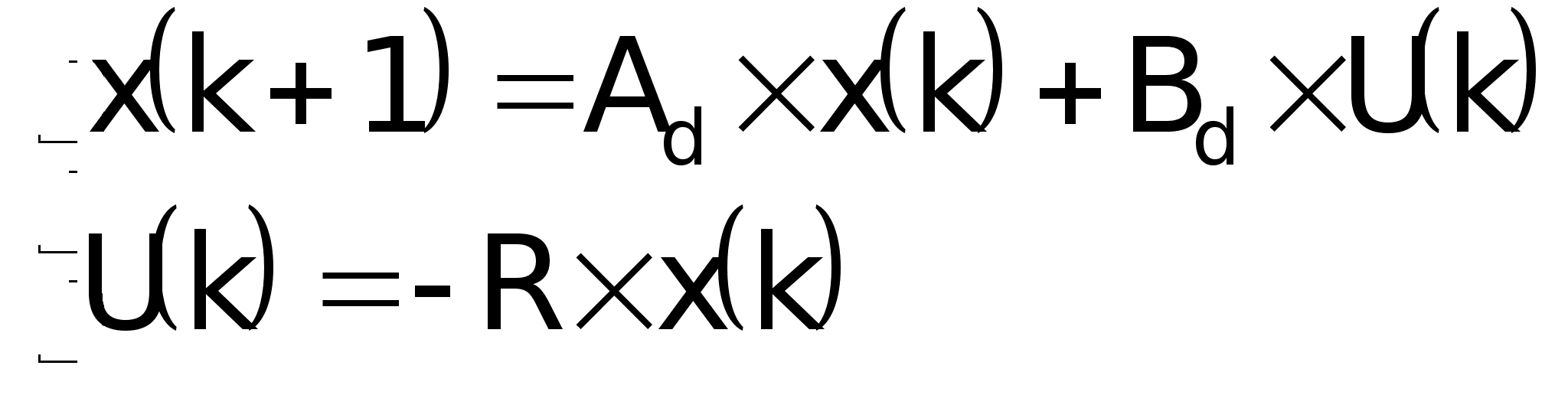
Матрица
замкнутой
системы с регулятором
состояния:
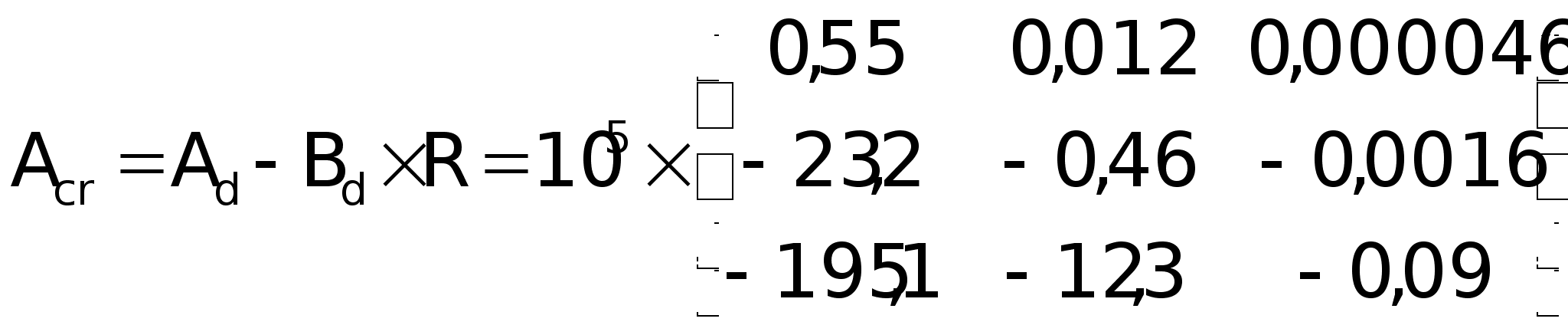
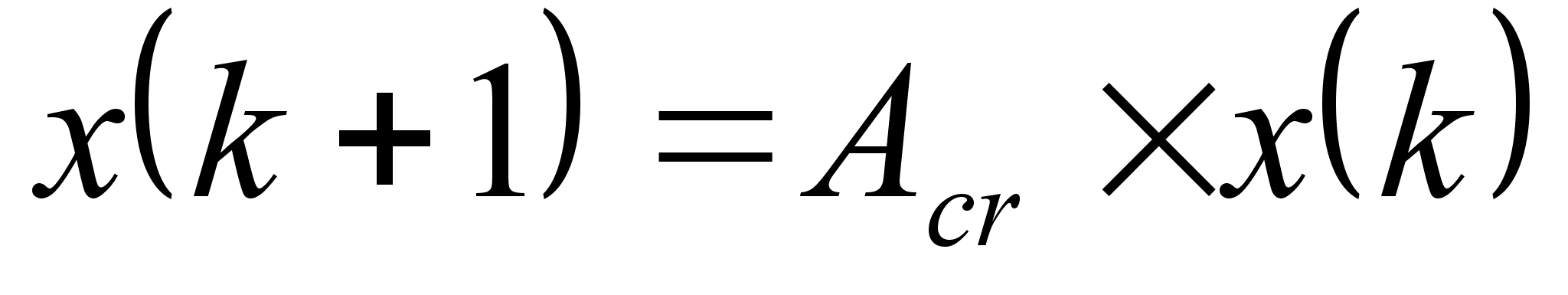
Если
посмотреть
матрицу
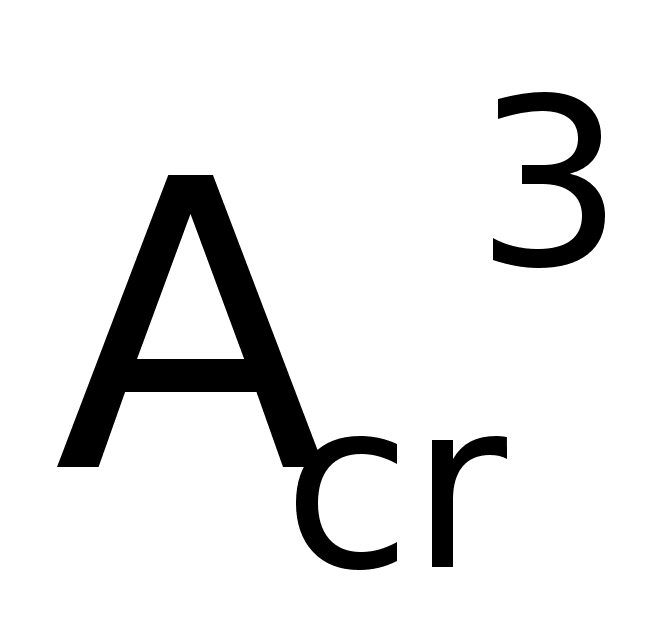 то увидим, что
она очень мала,
т.е. за три такта
процесс полностью
устанавливается.
то увидим, что
она очень мала,
т.е. за три такта
процесс полностью
устанавливается.
Собственная
матрица наблюдателя:
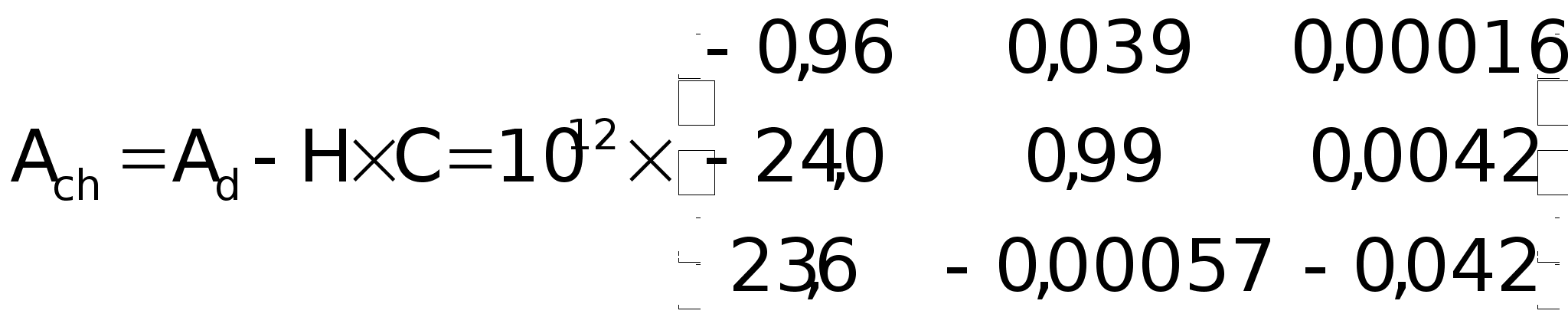
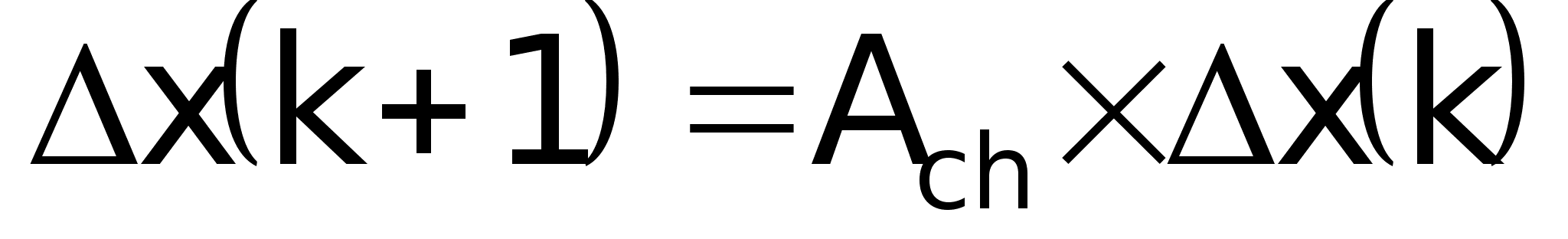
Если
посмотреть
матрицу
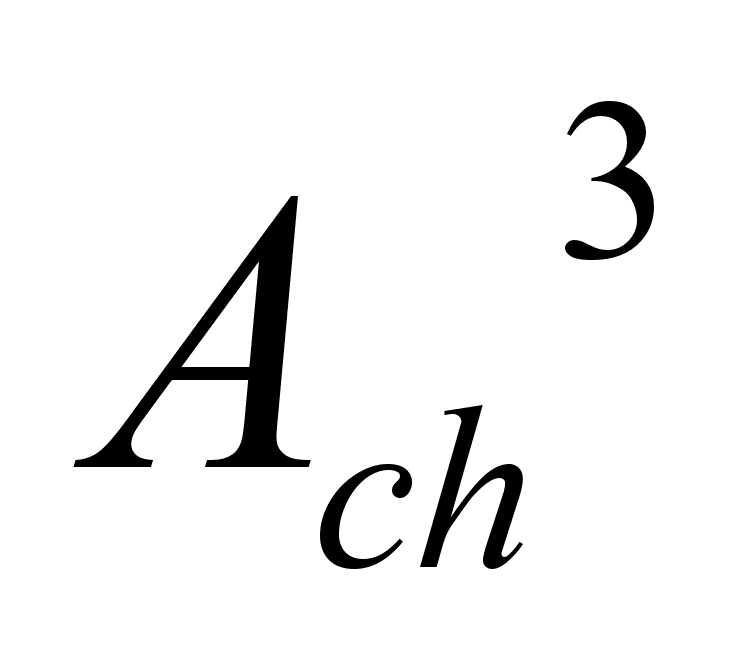 то увидим, что
она очень мала,
т.е. за три такта
процесс полностью
устанавливается.
то увидим, что
она очень мала,
т.е. за три такта
процесс полностью
устанавливается.
Вектор
состояния
замкнутой
системы с регулятором
и наблюдателем:
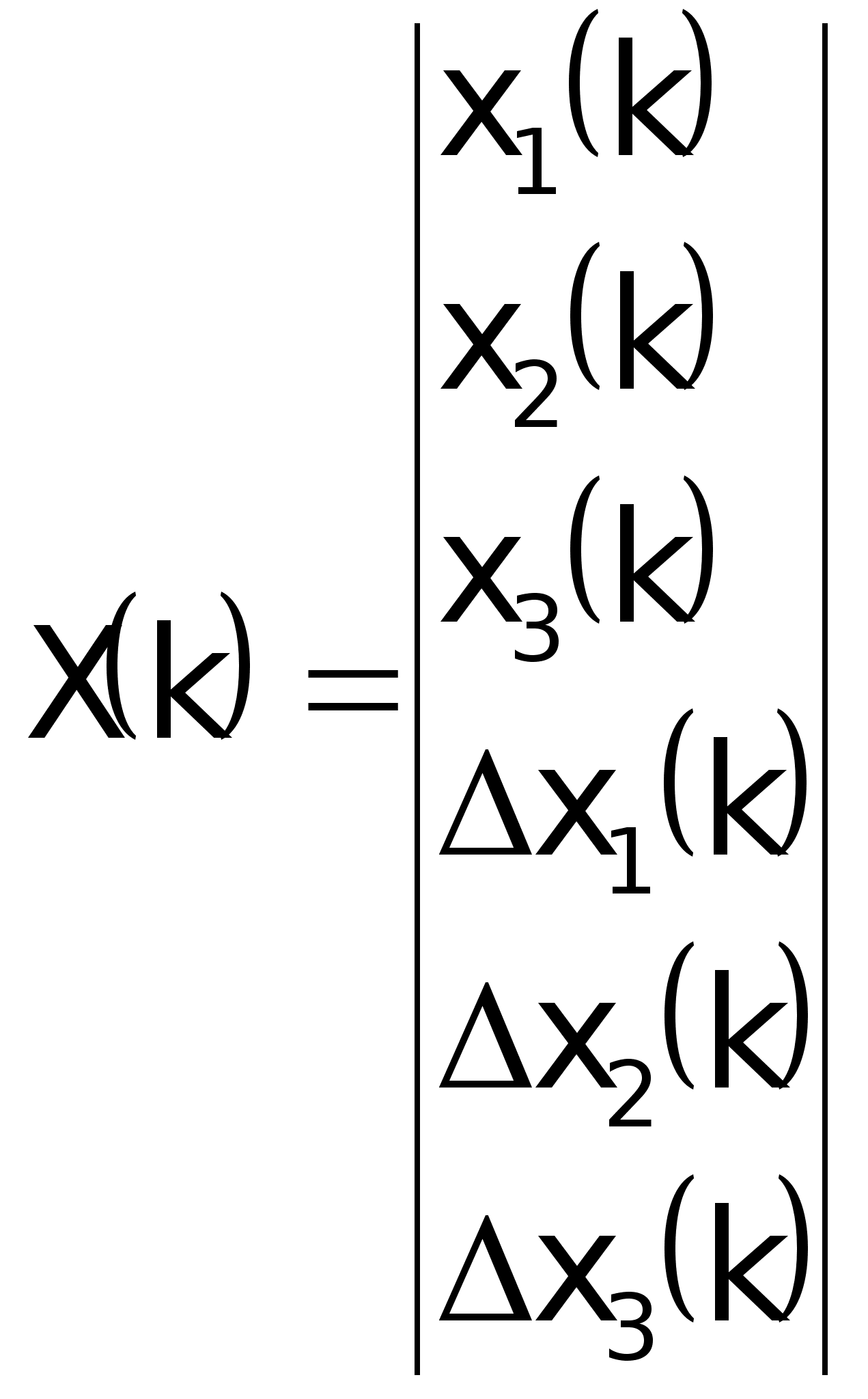
где:
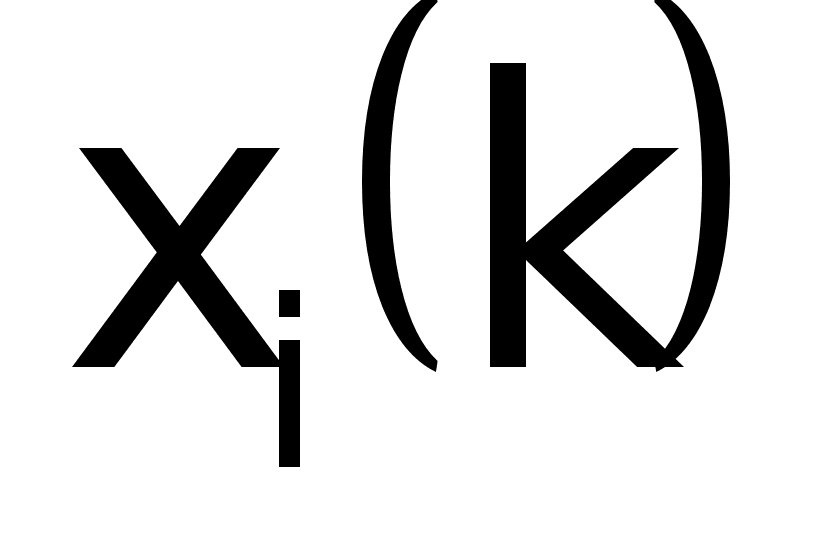 - переменные
состояния
объекта.
- переменные
состояния
объекта.
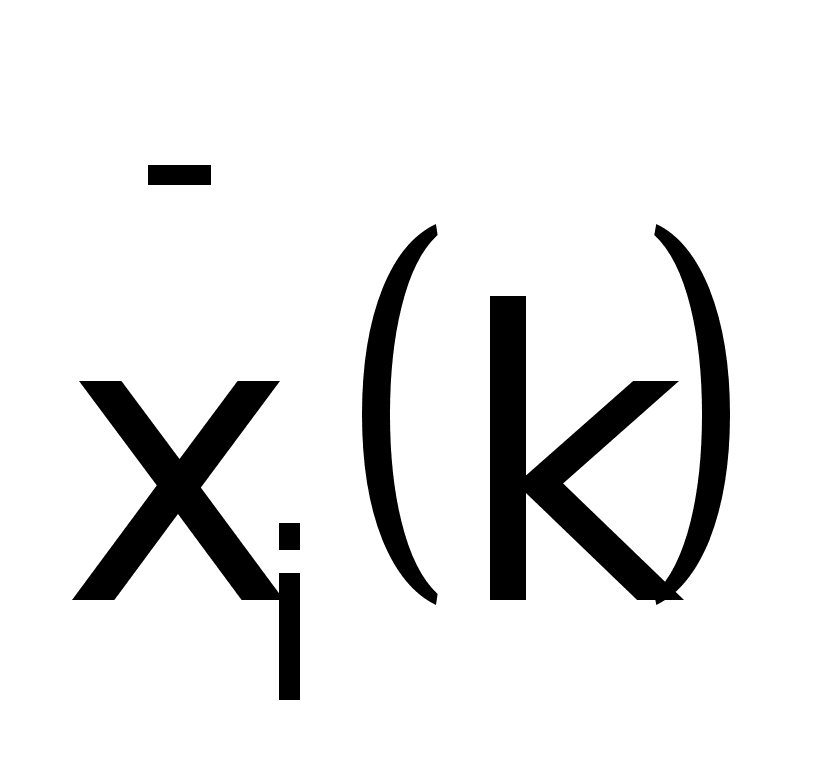 - переменные
состояния
наблюдателя.
- переменные
состояния
наблюдателя.
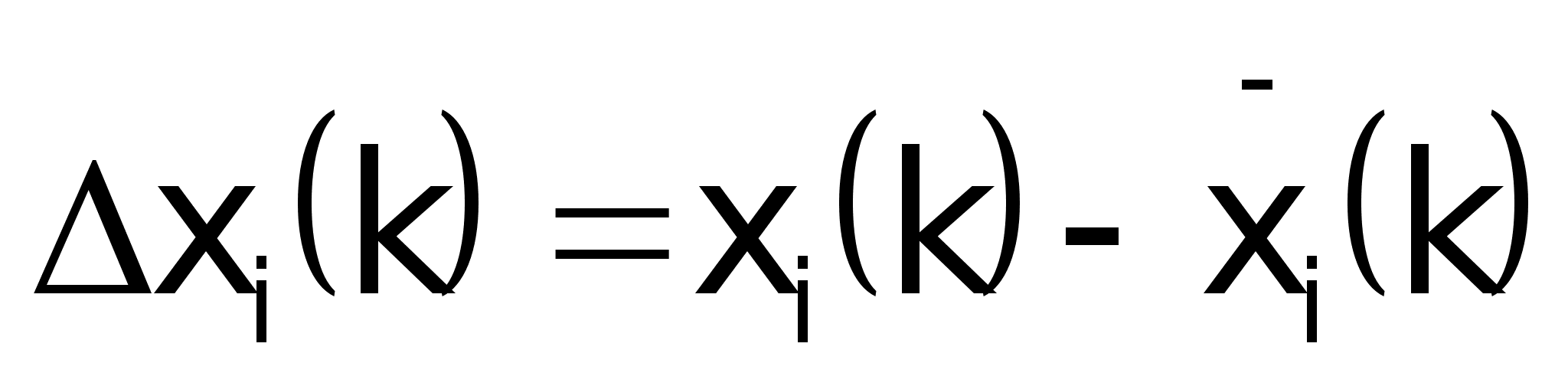
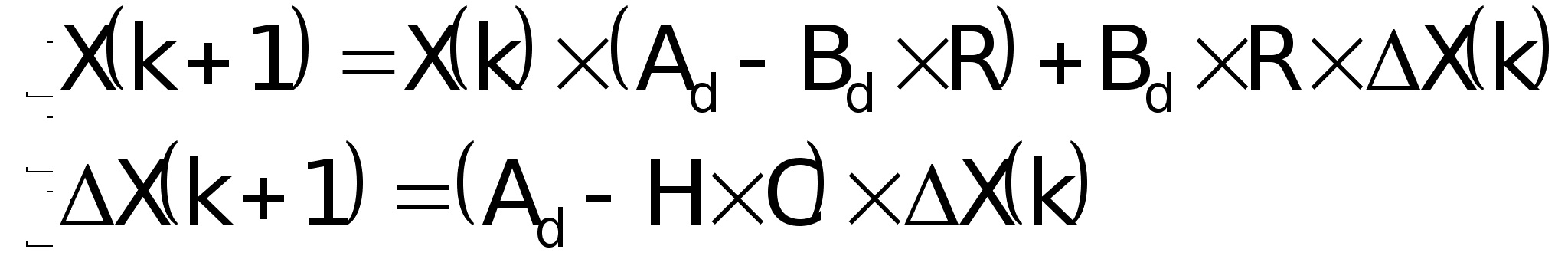
Матрица
замкнутой
системы с регулятором
состояния и
наблюдателем:
 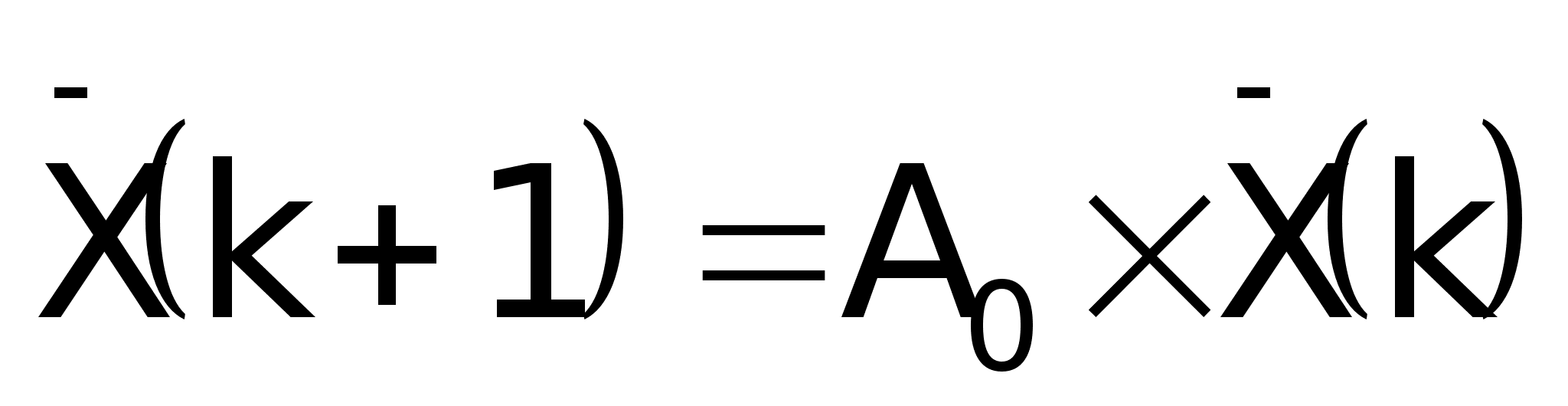
10. Рассчитать
и построить
графики сигналов
в цифровой
системе с
наблюдателем
и регулятором
состояния.
Вектор
начальных
условий:
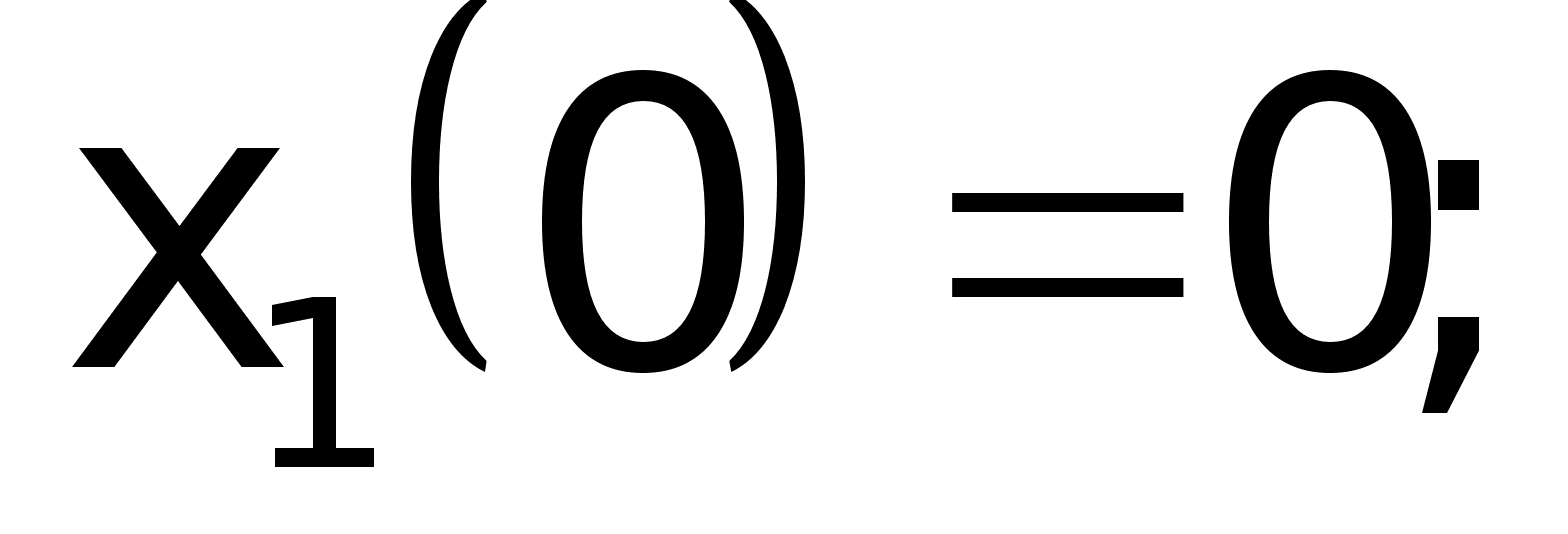
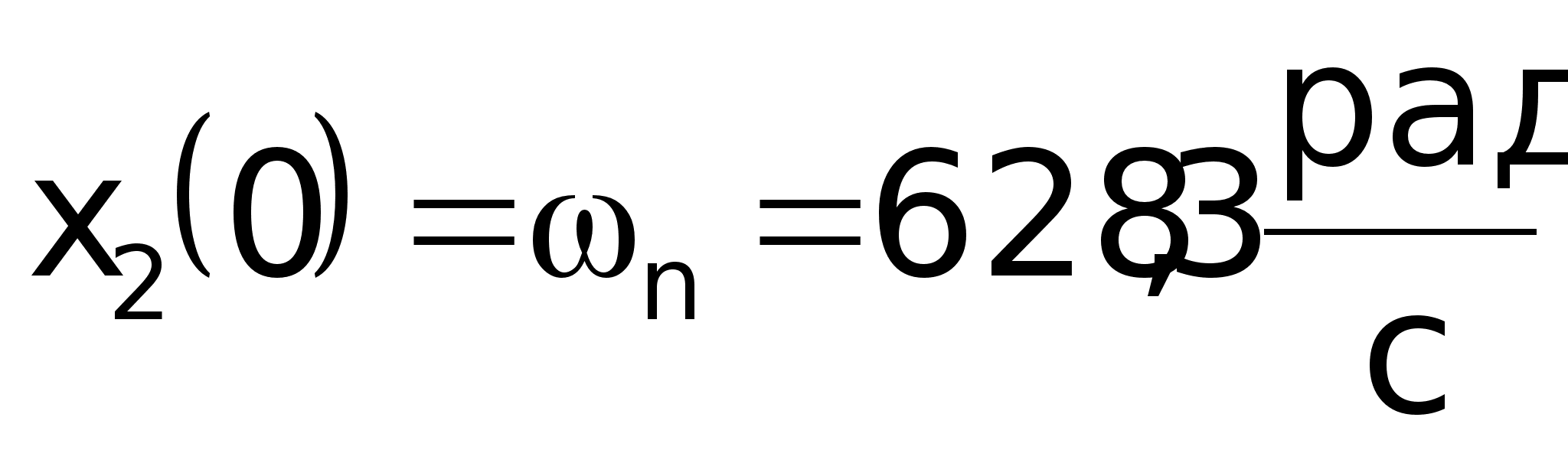
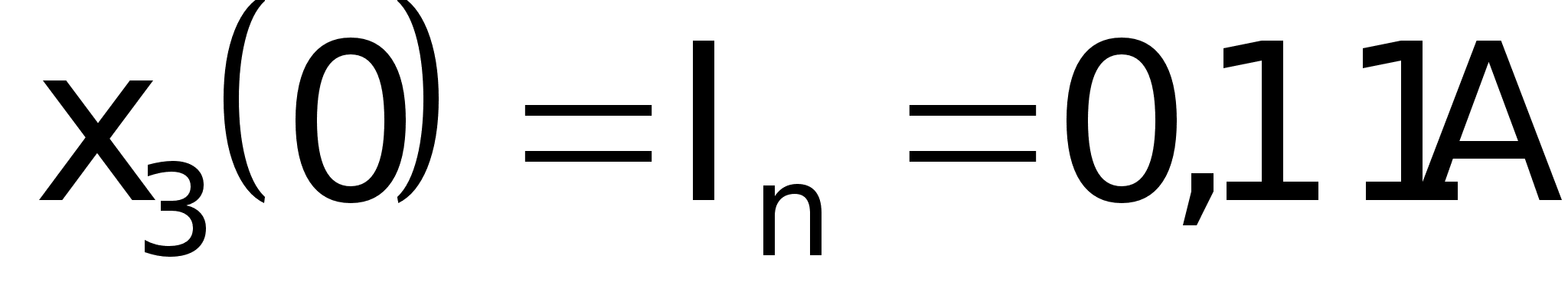
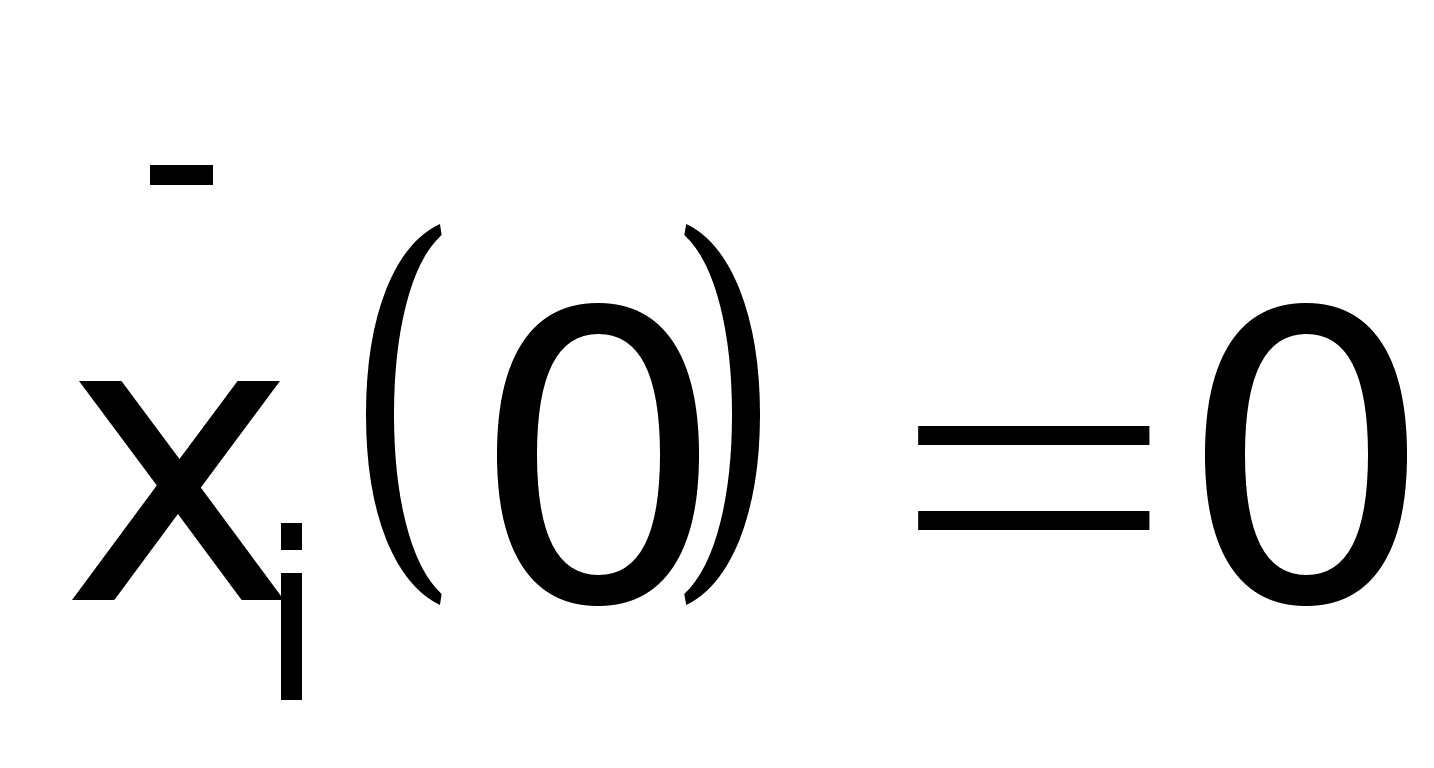
Решение
уравнений
состояния
представим
в виде таблицы:
|
|
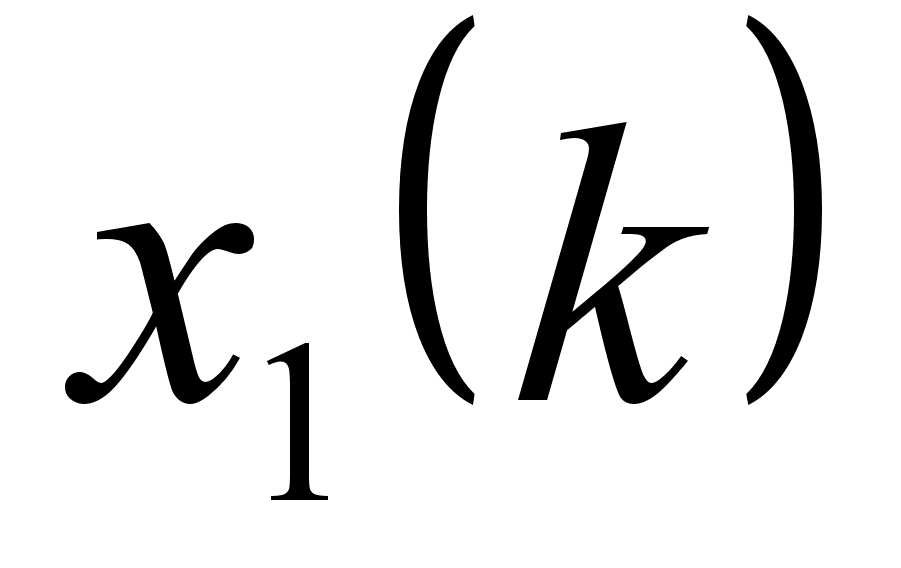
|
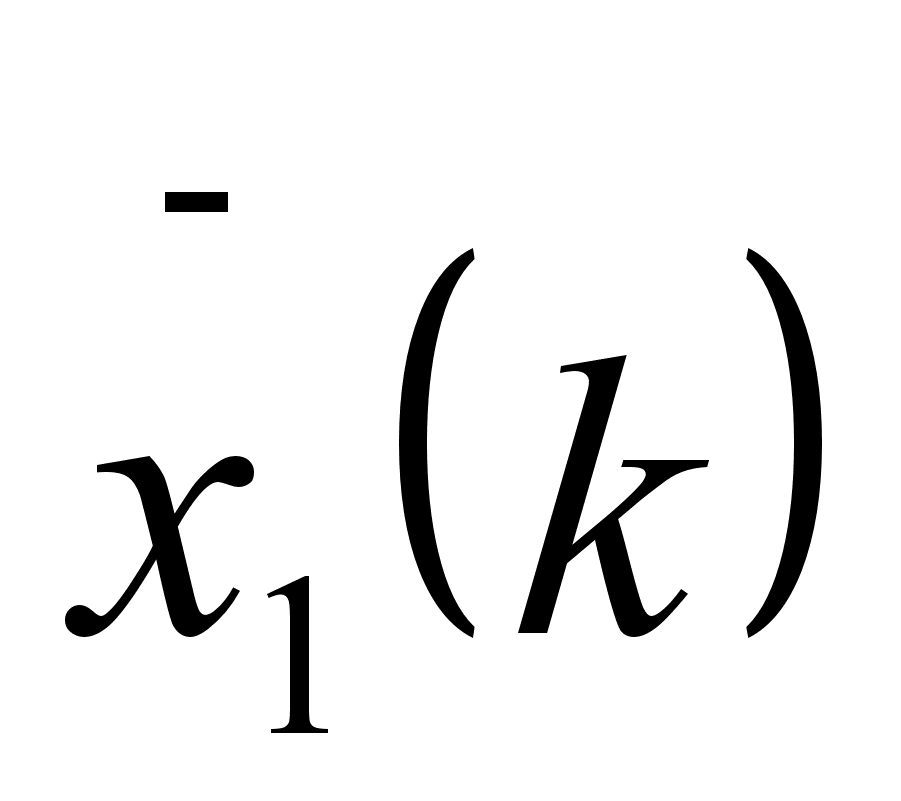
|
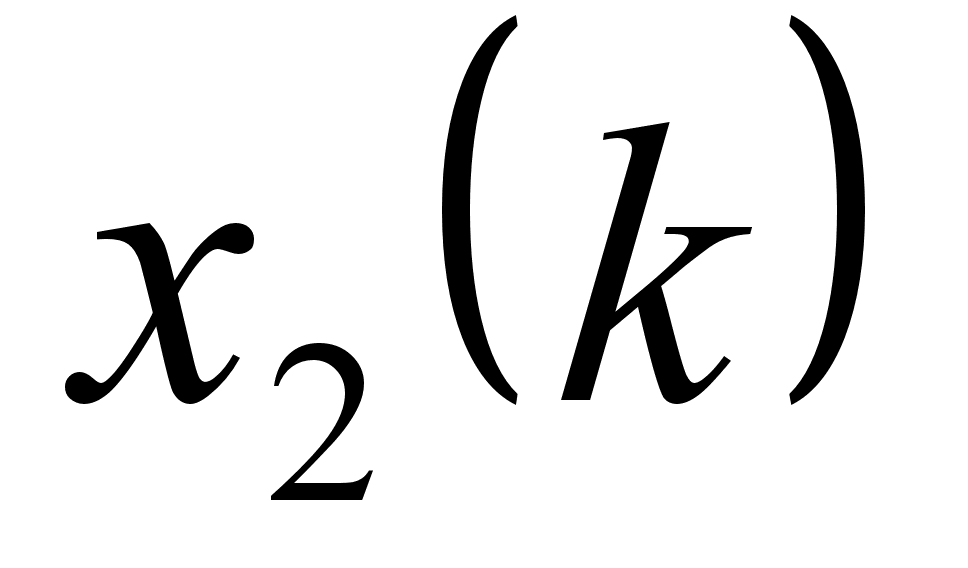
|
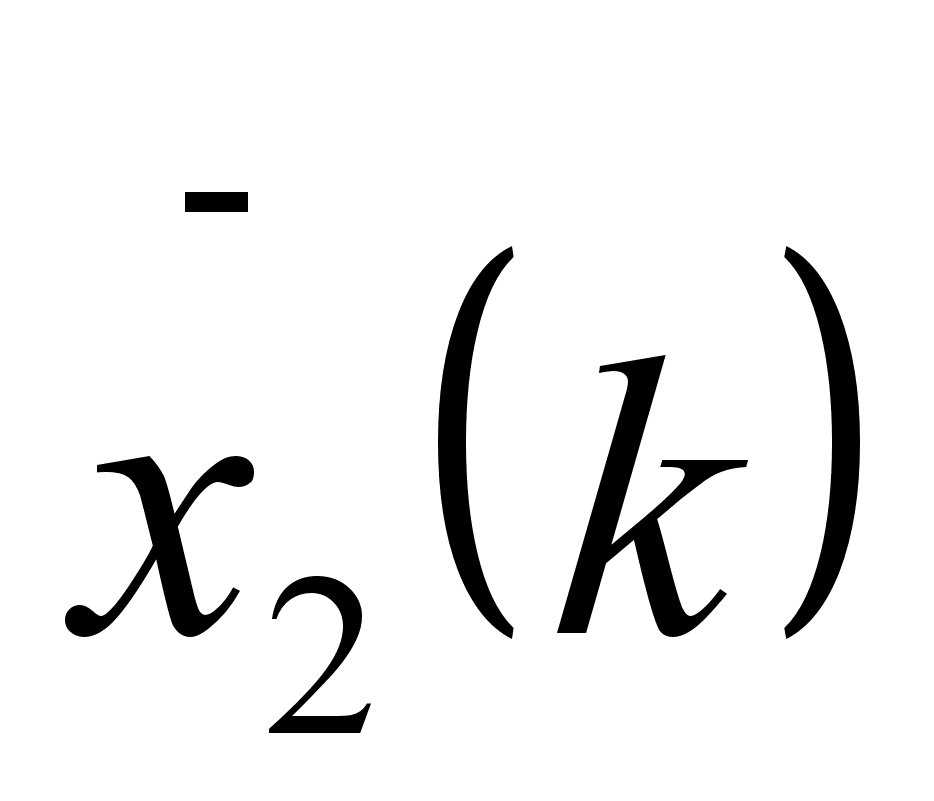
|
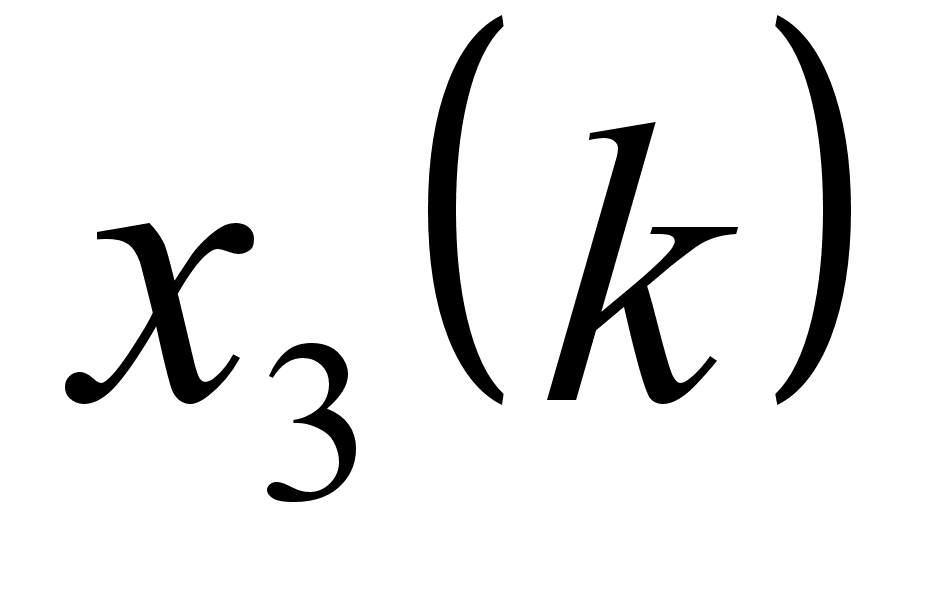
|
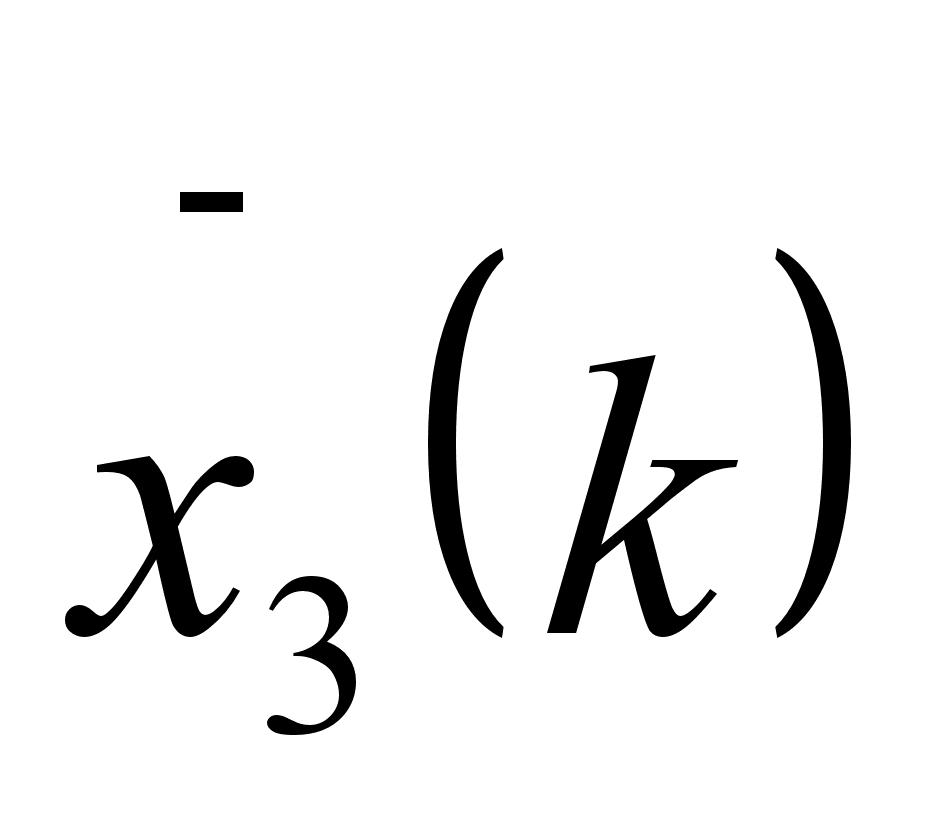
|
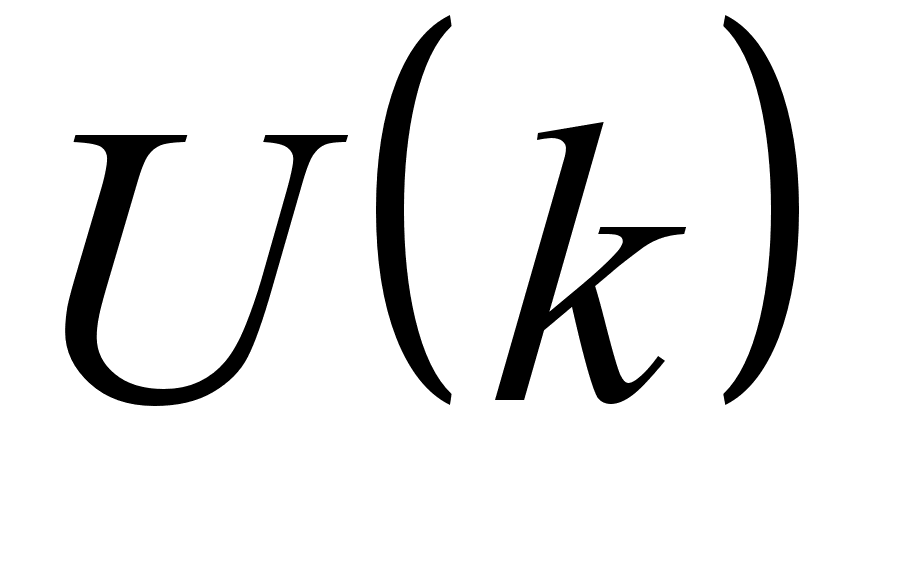
|
|
0
|
0
|
628,3
|
0,11
|
0
|
0
|
0
|
0
|
|
1
|
25
|
0
|
630
|
0
|
-0,36
|
0
|
0
|
|
2
|
50
|
49
|
630
|
610
|
-0,34
|
-0,059
|
-5,6105
|
|
3
|
36
|
36
|
-1,4103
|
-1,4103
|
-1,7104
|
-1,7104
|
3,6105
|
|
4
|
2,8
|
2,8
|
-170
|
-170
|
1,2104
|
1,2104
|
3,3104
|
|
5
|
0,058
|
0,058
|
-4,7
|
-4,7
|
520
|
520
|
710
|
|
6
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
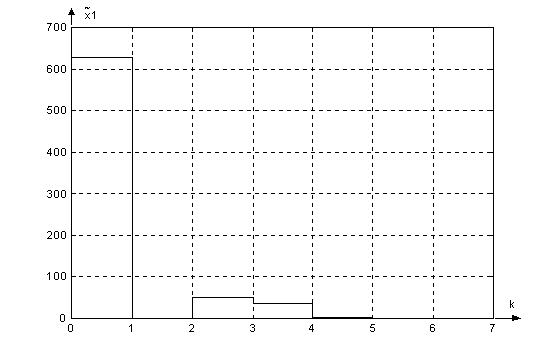
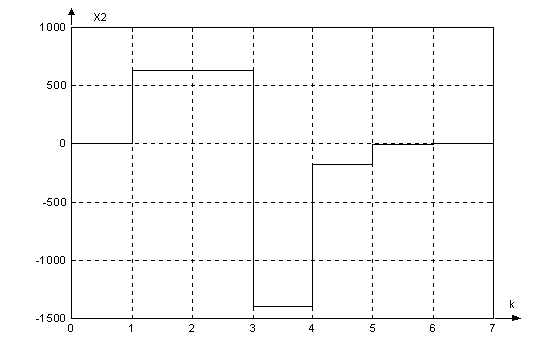
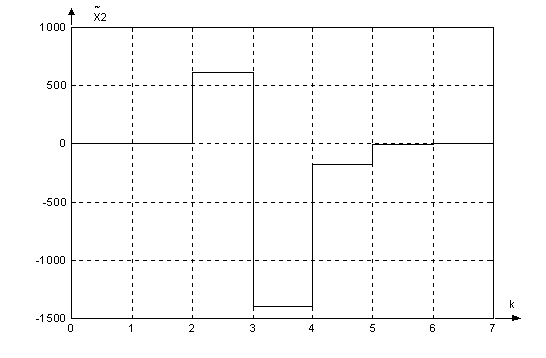
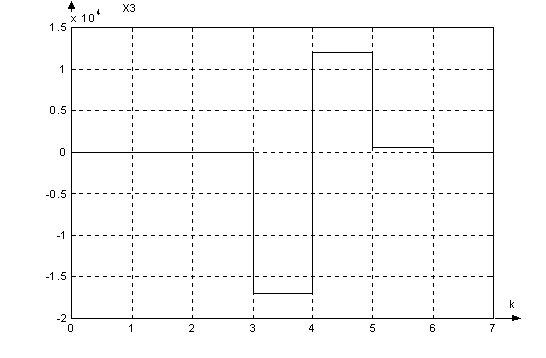
Графики
сигналов в
цифровой системе
с наблюдателем:
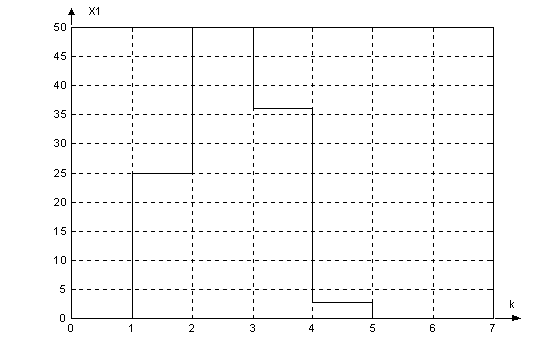
 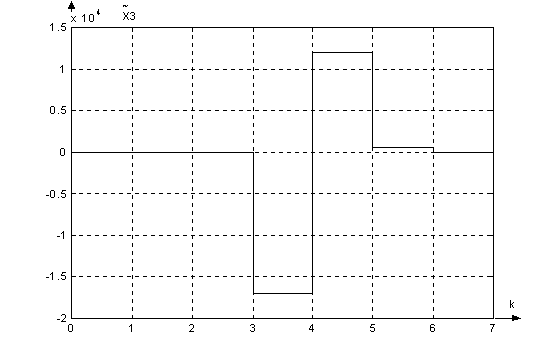
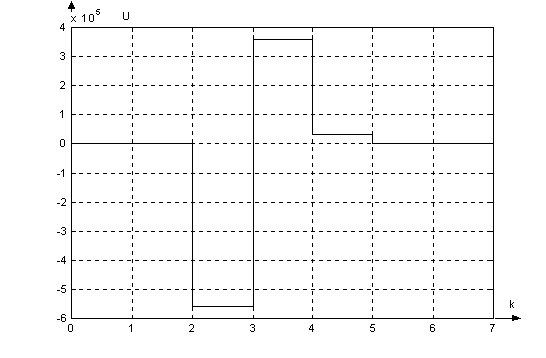
|