Реферат: Естествознание

ЧАСТЬ 1. ЕСТЕСТВОЗНАНИЕ - СОСТАВНАЯ ЧАСТЬ ОБЩЕЙ КУЛЬТУРЫ ЧЕЛОВЕЧЕСТВА.

1. ЕСТЕСТВЕННО - НАУЧНАЯ И ГУМАНИТАРНАЯ КУЛЬТУРЫ

Ученые и специалисты насчитывают более 170 определений понятия культура. Это свидетельствует о универсальности данного явления человеческого общества. Понятием культура обозначают и обычные явления, и сорта растений и умственные качества человека, и образ жизни, и систему положительных ценностей и так далее. В таком контексте все созданное человеком есть культура.

Мы используем одно из определений культуры, которое связано с ее инструментальной трактовкой. Культура - это система средств человеческой деятельности, благодаря которой реализуются действия индивида, групп, человечества в их взаимодействии с природой и между собой. Эти средства создаются людьми , постоянно меняются и совершенствуются. Принято выделять три типа культуры: материальную, социальную и духовную.

Материальная культура -совокупность средств бытия человека и общества. Она включает разнообразные факторы: орудия труда, технику, благосостояние человека и общества. Социальная культура - это система правил поведения людей в различных видах общения. Она включает этикет, профессиональную, правовую, религиозную и т. д. разновидности деятельности человека. Более подробно содержательная часть первой и второй культур изучается в других дисциплинах. Духовная культура - это составная часть культурных достижений человечества. Основные виды духовной культуры - мораль, право, мировоззрение, идеология, искусство, наука и т.д. Каждый из этих видов духовной культуры состоит из относительно самостоятельных частей. Эти части взаимосвязаны и относятся к духовной культуре человечества.

Под наукой в настоящее время понимают ту сферу человеческой деятельности, функция которой - выра­ботка и теоретическая систематизация объективных знаний о действитель­ности. Система наук условно делится на естественные, общественные и технические науки.

В науке принято выделять систему знаний о природе - естествознание, которое является предметом естественнонаучной культуры и систему знаний о позитивно значимых ценностях бытия индивида, групп , государства, человечества - гуманитарные науки или гуманитарную культуру. До того, как наука оформилась в самостоятельную часть культуры человечества, знания о природе и ценностях общественной жизни входили в иные состояния духовной культуры : практический опыт, мудрость, народная медицина, натурфилософия и т.д.

Взаимосвязь естественнонаучной и гуманитарной культур заключается в следующем:

- они имеют единую основу, выраженную в потребностях и интересах человека и человечества, в создании оптимальных условий для самосохранения и самосовершенствования;

- осуществляют взаимообмен достигнутыми результатами;

- взаимно координируют в процессе развития человечества;

- являются самостоятельными ветвями единой системы знаний науки и духовной культуры в целом.

Мы являемся свидетелями того, как социологи, юристы, экономисты, менеджеры и другие специалисты - гуманитарии начинают применять в своей работе системный подход, идеи и методы кибернетики и теории информации, знание фундаментальных законов естествознания и в частности физики.

Поясним вышесказанное примерами из практики. Юрист разбирает дело о столкновении судов. Конечно, ему нужно знать законы, приняты в мировой практике судовождения. Но, с другой стороны, если он не знает, что такое масса, радиус поворота, скорость, ускорение и т. д. , он не сможет реально применить свои профессиональные знания.

Социолог изучает общественное мнение путем опроса. Но как он сможет оценить степень достоверности результатов, если не имеет представление о теории вероятности и теории погрешностей. Без знания этих разделов естественных наук, результаты его предсказаний не будут представлять практической ценности.

Менеджер рекламирует изделие какого - то предприятия. Хорошо известно, что на выставках или просмотрах первые вопросы всегда касаются технических сторон изделия. Конечно, полностью ответить на такие вопросы может только специалист, имеющий хорошую фундаментальную естественнонаучную подготовку. Однако разбираться в этих вопросах должен и менеджер.

Существует и другая сторона рассматриваемого вопроса. Наука часто обвиняется в тех грехах, в которых повинна не столько она сама, сколько та система институтов, в рамках которой она функционирует и развивается. В настоящее время очевидно, что развитие науки может приводить к отрицательным последствиям влияющем на все человечество в целом. Актуальным становится вопрос о социальной ответственности всех людей, а не только ученых за возможность использования из открытий и достижений. В настоящее время сформировалась направление, называемое этикой науки, дисциплине, изучающей нравственные основы научной деятельности.

В качестве примера можно привести пример из истории второй мировой войны. Р.Оппенгеймера называют отцом атомной бомбы. Он являлся координатором и руководителем проекта создания атомной бомбы. Она была создана и испытана сначала в Неваде, а потом и в Хиросиме и Нагасаке. Позднее Оппенгеймер, осознавая тяжесть ответственности, ушел из проекта и стал заниматься деятельностью, направленной на предотвращение использования атомных бомб.

Вышесказанное утверждает нас в мысли, что представляется весьма важным познакомится с основными концепциями естествознания. Это необходимо для того, чтобы: во первых, сознательно применять их в своей деятельности, во вторых, чтобы получить более ясное и точное представление о современной научной картине мира, которую дает естествознание.

Необходимость применения естественно научных методов и законов в практической деятельности гуманитарных специальностей и привело к постановке того курса, который мы будем изучать: Физика для гуманитариев.

Курс состоит из нескольких частей. В первой части мы рассмотрим основы естественнонаучного метода познания, математический аппарат естествознания, виды материи , т.е. общие для всех разделов естествознания вопросы.

Во второй части , самой большой по объему, мы изучим раздел под общей темой: Физика для гуманитариев. Он состоит из трех частей: физики необходимого, физики непрерывного и физики возможного.

В третьей части мы рассмотрим концепции самоорганизации материи.

2. НАУЧНЫЙ МЕТОД ПОЗНАНИЯ. ОПЫТ, ГИПОТЕЗА, ЗАКОН, ТЕОРИЯ.

Что такое на­учный метод познания? На чем он базируется? Что лежит в его основе и чем он отличается от других методов познания?

Способ получить частичные ответы на вопросы придуман несколько сотен лет назад. Наблюдение, размышление и опыт составляют так называемый научный метод познания, который и позволяет давать ответы на многие интересующие нас вопросы. Основой научного метода является опыт - пробный камень всех наших знаний. Опыт, эксперимент - это един­ственный судья научной истины.

Проводя наблюдения каких-либо природных явлений, невозможно охватить все процессы, с этими явлениями связанные. Поэтому нужно отбросить все второстепенные факты и выделить основные, т.е. суть явления. Этот процесс называется аб­страгированием или построением модели явления. В размышлениях создается основа наблюдаемого явления, его модель. Что является существенным для данного явления, а что несуще­ственным, вопрос неоднозначный и сложный. Не всегда он решается сразу, на первых этапах наблюдения и размышления. На этом этапе нельзя, как говорится в старой поговорке, “выплеснуть младенца из купели вместе с водой”.

В создаваемой модели должны быть учтены главные характе­ристики и основные параметры изучаемого явления. Построенная модель должна не только верно описывать наблюдаемое это явление, но и хорошо прогнозировать его развитие в новых условиях. Предсказания теории проверяются экспериментом или опытом - важнейшей частью научного метода познания.

С самого начала необходимо договорится, что подразумеваться под тем или иным термином. В понятие “опыт” будем вкладывать смысл наблюдения за явлением при контролируемых условиях, т.е. наблюдения с возможностью контролировать, воспроизводить и изменять желаемым образом внешние условия. Существенна возможность создавать как обычные, так и искусственные (т.е. в природе не встречающиеся) условия. Физика, химия, биология и ряд других наук назы­ваются естественными именно потому, что в их основе лежит опыт.

Для объяснения экспериментальных фактов привлекаются гипотезы. Гипотеза - это предположение, позволяющее объяс­нить и количественно описать наблюдаемое явление. Описать что-либо количественно можно лишь на языке математики.

Между явлениями природы существуют устойчивые, повторяющиеся связи - проявления законов природы. Качественная формулировка законов может быть иногда дана без привлечения математического аппарата. Законы, записанные на языке формул позволяют перейти к более высокой ступени познания. Эту ступень называют теорией. Т.е. при определенных условиях выдвинутая гипотеза может перейти в теорию, в основе которой лежат законы. Теория дает представление о закономерностях и существенных связях в определенной области.

Законы естественных наук устанавливают количественные соотношения между наблюдаемыми явлениями, т.е. имеют матема­тическую формулировку. Не всегда эта формулировка бывает явной. Например, всем при­вычна следующая, казалось бы, качественная формулировка первого за­кона Ньютона: “Существуют такие системы отсчета, которых тело сохраняет состоя­ние покоя или прямолинейного равномерного движения, если на него не действуют другие тела, или действие других тел взаимно компенсируется”. Но строго сформулировать, что такое прямолинейное равномерное движение, можно лишь на языке математических формул. Т.е. даже качественная формулировка закона подразумевает введение количественных понятий.

Естествознание, изучающее количественные (т.е. точные) соотношения природных явлений, относится к точным наукам. Понятие “точное” требует комментариев. Точные науки, как правило оперируют не с абсо­лютно точными, а с приближенными величинами. При количественном описании любого наблю­даемого явления всегда оговаривают, с какой степенью точности имеют дело, т.е. приводят погрешности измеряемых величин.

Когда гипотеза перерастает в теорию, т. е. в форму научных знаний, дающих целостное представление о закономерностях и существенных связях опреде­ленной области действительности? Какой путь она должна пройти? Ответ на этот вопрос частично дан. Гипотезы должны быть проверены фактами, опытами, здравым смыслом. В своей области они должны объяснять всю совокуп­ность имеющихся явлений. Но этого мало. Для того, чтобы стать теорией, ги­потеза должна сформулировать количественные отношения между наблюдаемыми явлениями. Фактически это означает формулировку законов. Непременным условием превращения гипотезы в теорию является предсказание новых, до сих пор не наблюдавшихся и из известных теорий не следующих, явлений, и подтверждение этих предсказаний в специально поставленных экспериментах.

Переход гипотезы в теорию зачастую не обходится без драм. Классиче­скими являются примеры Николая Коперника (1473-1543) и Джордано Бруно (1548-1600). Н.Коперник выдвинул гипотезу о гелиоцентрической системе мира, в которой планеты вращаются вокруг Солнца по орбитам. Эта гипо­теза позволяла достаточно точно и просто описывать и предсказывать наблюдаемые движения планет. Однако сам Коперник не утверждал, что наша система и есть гелиоцентрическая. Для него модель гелиоцентрической системы мира нужна была только для более удобного описания движения планет. Гелиоцен­трическая система противоречила Библии, в которой говорилось, что Иисус Навин остановил вращение Солнца вокруг Земли. Развивая гелиоцентриче­скую космологию, Бруно выдвинул идею множественности миров во Все­ленной, центрами которых являются звезды. Д. Бруно утвердил мысль о том, что гелиоцентрическая система не является гипотезой Копер­ника, а космологической теорией, опирающейся на факт движения планет вокруг Солнца. И именно поэтому был обвинен в ереси и сожжен в 1600 году на Площади Роз в Риме.

Естественнонаучная теория дает объяснение целой области явлений в при­роде с единой точки зрения. Квинтэссенцией теории являются законы, устанавливающие количественные связи, соотношения между различными наблюдаемыми в опыте величинами.

Нужно различать законы природы и законы науки. Первые проявляются в особенностях протекания природных явлений и процессов и во взаимосвязи некоторых величин. Они неизменны и всегда выполняются. Научные законы - это попытка описать законы природы на языке математических формул и точных формулировок. В дальнейшем речь будет идти только о них. Научные законы не точны и не постоянны. На определенных этапах раз­вития науки возникает необходимость уточнения наблюдаемых в опыте явлений и пересмотра законов или границ их применимости. Постоянная проверка опытных фак­тов на базе новых экспериментальных методик, позволяющих увеличить точность проведения эксперимента, необходима всегда на любом уровне знаний. Расхождение экспериментальных данных и существующих законов позволяет выдвигать новые гипотезы и строить новые теории.

3. МАТЕРИЯ И ФОРМЫ ЕЕ СУЩЕСТВОВАНИЯ.

В основе всех естественнонаучных дисциплин лежит понятие материи, за­коны движения и изменения которой изучаются. В зависимости от того, как мы определим это понятие, мы и будем рассматривать проявление раз­личных теорий. Для понимания естественнонаучных теорий, в частности концепций современной физики, приемлемым является определе­ние, данное В.И. Лениным в монографии “Материализм и эмпириокрити­цизм”. “Материя - есть философская категория для обозначения объективной реальности, которая отображается нашими ощущениями, существует неза­висимо от них. Материя - это основа (субстанция, субстрат) всех реально существующих в мире свойств, связей и форм движения, бесконечное мно­жество всех существующих в мире объектов и систем”.

В этом определении есть два основных момента. Во-первых, материя суще­ствует объективно, независимо от нас, от чьего-то субъективного сознания или ощущения. Во-вторых, материя копируется, отображается нашими ощущениями и, следовательно, познаваема. Мы здесь исходим из материа­листического единства мира из первичности материи.

Материя несотворима и неуничтожаемая. Она бесконечна. Неотъемлемым атрибутом материи является ее движение, как форма существования мате­рии, ее важнейший атрибут. Движение в самом общем виде - это всякое изменение вообще. Движение материи абсолютно, тогда как всякий покой относителен. Понять эту мысль проще всего при рассмотрении простейших видов движения. Например, тело покоится относительно Земли, но относи­тельно Солнца оно движется.

Формами существования материи являются про­странство и время. Материя неотъемлема от них. Современная наука оперирует такими струк­турными уровнями, как элементарные частицы и поля, атомы и молекулы, макроскопические тела, геологические системы, планеты и звезды, галактики и метагалактики; совокупности организмов, способных к воспроизводству и, наконец, общество. Мы будем изучать только первые структурные уровни- поля и частицы, макро­скопические тела.

Различают ряд основных форм движения материи: механическую, физиче­скую (включая тепловую, гравитационную, ядерную и т.д.), химиче­скую, биологическую, общественную. Высшие формы движения включают в себя более низшие, но не сводятся только к ним. Так, ядерные процессы невозможно описать только формулами классической механики.

В настоящем курсе будут рассмотрены лишь простые формы движения материи - механическая, физическая и химическая. Для описания материи и ее дви­жения необходимо ввести количественные меры этих величин исходя из поставленных задач. Масса является количественной мерой материи и вводится как для микро- и макрообъектов, так и для полей. Одной из количественных мер движения материи является энергия. Она имеет много форм: механиче­ская, тепловая, ядерная, химическая и т.д. Поскольку материя не существует без дви­жения, а движение без материи между количественными характеристиками меры и движения материи должна существовать связь. Эта связь была установлена в начале нашего века А. Эйнштейном (1879-1955) в работах по теории относи­тельности.

Мы будем рассматривать два вида материи - вещество и поле. К первому отнесем элементарные частицы, атомы, молекулы, все построенные из них макросистемы. Ко второму отнесем особую форму материи, физическую систему с бесконечным числом степеней свободы. Примерами физических полей могут служить электромагнитные и гравитационные поля, поля ядер­ных сил, а также волновые поля.

4. ПОСТУЛАТИВНОСТЬ ОСНОВНЫХ ЗАКОНОВ ЕСТЕСТВО­ЗНАНИЯ, ГРАНИЦЫ ИХ ПРИМЕНИМОСТИ.

Для описания поведения простых и сложных систем нужно установить “правила игры”, т.е. законы которым подчиняются те или иные вид движе­ния материи. В некоторых науках, которые не относятся к естественным, на­пример геометрия, поступают следующим образом. Сначала формулиру­ются аксиомы, а потом из них делаются выводы (теоремы). Логика построения естественных наук другая, нельзя сразу ввести законы и смотреть, что из них следует. Так поступить нельзя, поскольку исследователю неизвестны все законы естествознания. Одной из задач является именно их установление и формулирование. Но, ответив на каждый вопрос, исследователь неизбежно ставит несколько новых. Чем больше познается, тем шире становятся границы непознанного. Установленные на определенном этапе развития науки законы, всегда являются приближенными. По мере накопления знаний, новых экспериментальных фактов, явлений и увеличения точности измерений появляются данные, не укладываю­щиеся в рамки имеющихся законов и эти законы пересматриваются.

Есть и другая сторона этого вопроса. Для точной формулировки законов ес­тествознания, в особенности физики, требуются новые определения и по­нятия, знание специальных разделов математики. Исааку Ньютону (1643-1727) для описания законов механики потребовалось создать совершенно новые для своего времени разделы высшей математики: дифференциальное и интегральное исчисление. Физики часто сталкивались с ситуацией, когда имевшегося математического аппарата оказывалось недостаточно для получе­ния количественных формулировок полученного закона и требовалось создавать специальный математически аппарат. Пример с Ньютоном и Лейбни­цем и созданием дифференциального и интегрального исчисления является классическим.

В этом разделе мы рассмотрим самые общие представления о том, как устанавливаются законы естествознания, как они применяются и чем они ограни­чены. Уже говорилось, что опыт - единственный судья истины. Законы ес­тествознания постулируются на основании наблюдаемых опытных фактов. Сначала идет процесс накопления знаний в определенной области. Эти результаты анализируются и делается некоторое предположение. Это предположение не выводится из других законов. Оно возникает само по себе на основании опыта. Сделанное умозаключение, сформулированное в виде математической формулы, становится частью гипотезы. Если последующие опыты подтверждают правильность этого предположения, оно становится законом.

Проиллюстрируем сказанное несколькими примерами. Закон всемирного тяготения, был открыт И. Ньютоном не потому, что, как любят писать в популярной литературе, ему “упало на голову яблоко”.. Закон родился в результате анализа трех законов движения планет И. Кеплера (1571-1630). Законы Кеплера позволяли рассчитывать с высокой точностью движения планет. Ньютон показал, что эти законы могут быть получены на основании одного закона - закона всемирного тяготения:

, где G - константа, m₁ и m₂ - массы тел, r - расстояние между ними.

Анализируя опыты, Ш.О. Кулон в 1785 году сформулировал закон взаимодействия зарядов, позже названный его именем:

,

где q₁ и q₂ - заряды, r - расстояние между ними; константа определяется выбором системы единиц. До Кулона этот закон ни в каком виде не формулировался.

Уже отмечалось, что все научные законы всегда приближенные. Почему же сразу не удается открыть “правильный закон”? Почему всегда приходится начинать с каких-то приближений? Во-первых, для “точной” формулировки закона зачастую бывает еще не готов соответствующий математический аппарат, а, во-вторых, экспериментальные данные всегда бывают недостаточно точны. Точность измерений определяется с одной стороны нашими приборами, а с другой стороны - некоторыми фундаментальными запретами, связанными с природой явления. Существует, например, соотношение неопределенностей Гейзенберга, которое ограничивает точность одновременного измерения импульса и координаты частицы.

Приведем пример. Реально мы можем измерить массу волчка с точностью до долей микрограмма. Измеряя массу покоящегося и вращающегося волчка мы всегда будем получать один результат. Отсюда, казалось бы, можно было вывести закон, что масса тела постоянна и не зависит от его скорости. Но оказывается масса от скорости зависит когда скорости становятся сравнимыми с скоростью света.

Сказанное приводит нас к выводу, что законы и теории не абсолютны. Они развиваются по мере накопления знаний. Фундаментальные законы естествознания описывают огромное количество явлений в разных областях. И все они подчиняются некоторым общим правилам. Рассмотрим их.

Во первых, законы сами по себе не меняются. Именно поэтому они и называются фундаментальными. Иначе никакая наука не могла бы развиваться. Но, надо помнить о том, что закон написан для определенной области явлений.

Всякий раз, когда с определенной степенью точности подтверждается какой-либо закон, можно утверждать, что закон окончателен и ни какой результат его не опровергнет в той области, для которой он написан. Однако может так случится, что появление новых экспериментальных данных или теорий приведет к тому, что закон окажется приближенным. Иначе говоря, увеличение точности измерений может обнаружить неточность даже самых незыблемых законов.

Нильс Бор (1885-1962) анализируя положения квантовой механики сформулировал ”Принцип соответствия” новой и старой теорий. Этот принцип применим к любым теориям в естествознании. Сущность его заключается в том, что всякая новая теория должна содержать в себе старую как частный случай, к которому она сводится при определенных условиях.

Проще всего принцип соответствия проиллюстрировать примером из классической механики и механики теории относительности. Созданная А.Эйнштейном специальная теория относительности содержит в себе классическую механику Ньютона, в которую она переходит при скоростях движения V, малых по сравнению, с скоростью света -C. Математически это записывается как V<<C. Законы специальной теории относительности переходят в законы классической механики и движения тел при малых скоростях описывается, по-прежнему, законами Ньютона. Только тогда когда скорость станет сравнима с скоростью света, требуется привлечение новых законов. Например, когда скорость тела не превосходит 1000 км/с масса тела постоянна с точностью до 10^{- 5} .

Еще один пример: законы классической и квантовой физики приведут к одним и тем же уравнениям для движения частицы, имеющей массу много больше массы атома.

Таким образом, при формулировке законов необходимо задавать границы их применимости. Законы и теории должны описывать всю совокупность явлений в той области, для которой они сформулированы. Они не должны противоречить известным фактам. Более того, они обязательно должны предсказывать новые, неизвестные ранее явления. Наконец, никакой закон не должен нарушать принцип причинности. Это значит, что нельзя что-то изменить в событии которое уже случилось. Можно повлиять только на будущее, но никак не на прошлое.

В заключение отметим, что новые фундаментальные законы невозможно вывести в рамках старых теорий. Стремление некоторых авторов сделать это не имеет под собой никакого основания и зачастую связано лишь с большим желанием авторов “пооригинальничать” и внести свой “вклад в науку”.

5. РАЗДЕЛЫ ЕСТЕСТВОЗНАНИЯ.

Слово естествознание представляет из себя сочетание двух слов: естество (природа) и знание. В настоящее время под естествознанием подразумевается в основном точное знание о том, что в природе, во Вселенной действительно есть или по крайней мере возможно. Первоначально к физике Аристотель относил проблемы устройства, происхождения, организации всего, что есть во Вселенной, даже жизни. Само слово физика, греческое по происхождению, близко к русскому слову природа. Таким образом, первоначально естествознание называлось физикой.

В своем развитии наука прошла четыре стадии развития. На первой стадии формулировались общие представления о природе, окружающем мире как о чем-то целом. В этой стадии произошло развитие натурфилософии (философии природы) ставшей вместилищем идей и догадок, которые к 13-15 векам стали зачатками естественных наук. В 15-17 веках последовала аналитическая стадия - мысленное расчленение и выделение частностей, превратившая физику, астрономию, химию, биологию действительно в науки. Позднее, ближе к нашему времени, наступила синтетическая стадия изучения природы, характеризуемая воссозданием целостной картины мира на основе ранее познанных частностей. Сегодня пришло время обосновать не только принципиальную целостность всего естествознания, но пояснить, почему именно физика, химия и биология стали основными и самостоятельными разделами науки о природе. Т.е. в настоящее время осуществляется целостная интегрально - дифференциальная стадия развития естествознания, как единой науки о природе.

Все описанные стадии изучения природы по существу представляют звенья одной цепи. Каждый из разделов естествознания прощел через эти стадии. Рассмотрев в следующей части коротко историю развития физики мы видим, что она тоже прошла все описанные стадии. Отличие имеется лишь в том, что описание этапов развития физики мы будем давать с точки зрения развития методов подхода к изучаемым явлениям. В физике сейчас также наступает интеграционная стадия, характеризуемая тем, что проводятся попытки создать единые теории, объединяющие различные разделы. Примером тому может служить попытка создать единую теорию поля.

Рассмотрим главные разделы естествознания и связь между ними. Мы уже говорили о движении материи. В порядке возрастания сложности мы приводили следующие формы движения: механическую, физическую, химическую, биологическую, общественную. Все формы движения связаны между собой. Высшие содержат в себе низшие, составными части, но ни в коем случае не сводятся только к ним. Например, нельзя ядерные силы свести к механическим. Различные виды движений, существующих в природе изучают различные разделы естествознания: ФИЗИКА, ХИМИЯ, БИОЛОГИЯ, ПСИХОЛОГИЯ и другие разделы.

В каждом из разделов естествознания имеются свои законы, которые не могут быть сведены к законам других разделов, однако, теории, описывающие сложные структуры, опираются на теории и законы для простых структур. При этом, как правило, по мере усложнения структур и разделов естествознания их законы становятся менее точными, формулировки приближаются к качественным. Чем ниже уровень раздела естествознания, тем сложнее и точнее математические формулировки его законов. Наиболее сложны для понимания законы физики - фундаменте всех естественных наук.

В этом разделе мы попытаемся показать связь физики с другими науками, очертим круг фундаментальных задач, возникающих в пограничных областях и на стыке наук. Однако, мы коснемся связей физики с техникой, физики с промышленностью, физики с общественной жизнью и физики с искусством. Связь с последнем прослеживается на многих исторических примерах, когда выдающиеся скульпторы, архитекторы и живописцы прошлого были одновременно и крупными учеными.

Химия испытывает на себе влияние физики, пожалуй сильнее, чем любая другая наука. На заре своего развития она играла важную роль в становлении физики. Эти науки взаимодействовали очень сильно, они были практически неразделимы. Теория атомного строения вещества получила основательное подтверждение именно в химических опытах. Под теорией неорганической химии подвел черту Д.И.Менделеев (1834-1907), создав свою периодическую систему химических элементов. Эта система выявила немало удивительных связей между различными элементами. Она предсказала существование многих тогда еще неизвестных химических элементов. Однако, объяснение системы Менделеева возможно только с опорой на теорию строения атома, т.е. на физическую теорию. В настоящее время в неорганической химии остались два раздела: физическая химия и квантовая химия. Сами названия этих разделов говорят о тесной связи с физикой.

Другая ветвь химии - органическая химия, химия веществ, связанных с жизненными процессами. Одно время предполагали, что органические вещества столь сложны, что их нельзя синтезировать. Однако, развитие физики и неорганической химии изменило ситуацию. В настоящее время научились синтезировать сложные органические соединения, необходимые в жизненных процессах. Главной задачей органической химии является анализ и синтез веществ, образующихся в биологических системах, живых организмах. Отсюда вытекает тесная связь химии и физики с другим разделом естествознания, с биологией.

Изучение живых организмов позволяет увидеть множество чисто физических явлений: циркуляцию и гидродинамику протекания крови, давление в сосудах и т.д. Биология - очень широкое поле деятельности для приложения физических и химических теорий. Например, как осуществляется зрение, что происходит в глазе. Как квант света взаимодействует с сетчаткой. Однако, эти вопросы не основные в биологии, не они лежат в сущности всего живого. Фундаментальные процессы, изучаемые в биологии лежат глубже, в понимании функционирования клеток, их биохимических циклов. В конечном итоге, в понимании того, что есть жизнь. Понятие жизни не удается свести только к химическим или физическим процессам.

Психология изучает отражение действительности в процессах деятельности человека и животных. Эта наука лежит на грани естественных и общественных наук. Казалось бы, какая связь может быть у нее с физикой. Давайте рассмотрим пару примеров. Одной из ветвью психологии является физиология ощущений. Она рассматривает взаимосвязь между поведением человека и его ощущениями. Почему красный цвет вызывает тревожные ощущения, а зеленый наоборот. Недаром запрещающий цвет светофора - красный, а разрешающий - зеленый. Ответ может дать физика. Днем максимум излучения солнца приходится на зеленый цвет. День - самое безопасное время суток, и в процессе эволюции у живых организмов выработалась положительная реакция на зеленый цвет. В сумерках максимум излучения солнца сдвинут в красную область. Сумерки - самое опасное время суток, когда хищные животные выходят на охоту. Естественно, что в процессе эволюции выработалось отрицательная реакция на этот цвет.

Другой пример из области криминалистики, которую условно также можно отнести к ветви психологии, поскольку она рассматривает поведения людей в сложных ситуациях, приводящих к криминальным случаям. Когда доктор Ватсон спросил, знает ли Шерлок Холмс о теории Коперника и о строении солнечной системы, Холмс ответил, что наверно знал, но постарался об этом забыть. Тем не менее, доктором Ватсоном было установлено, что Холмс обладает глубокими знаниями в области химии и ряда разделов физики. Действительно, сейчас ни один криминалист не может обойтись без такого раздела физики, как механика, точнее ее прикладного раздела - баллистики, а также ряда других.

В заключении этого раздела упомянем еще один момент, выявляющий связь физики с другими разделами естествознания. Все приборы, используемые в опытах и экспериментах созданы специалистами с техническим (т.е. физическим) образованием. Принцип действия этих приборов основан на физических законах. В конечном итоге, тестер для измерения напряжения или тока , томограф, получающий пространственную картину внутренних органов, микроанализатор, определяющий уровень загрязненности окружающей среды или потребляемой пищи, требуют от работающих определенных знаний. С одной стороны - это знание основных принципов работы прибора, с другой стороны - умение оценивать степень точности параметров, которые измеряет данный прибор.

6. МАТЕМАТИЧЕСКИЙ АППАРАТ ЕСТЕСТВОЗНАНИЯ.

"Тот, кто хочет решать вопросы естественных наук без помощи математики, ставит неразрешимую задачу. Следует измерять то, что измеримо, и делать таковым то, что таковым не является" - сказал выдающийся итальянский физик и астроном Г. Галилей. Законы естествознания отражают количественную взаимосвязь между явлениями. В силу этого они требуют формулировок не только в качественном, но и в количественном виде, т.е. на языке формул.

Математика начинается с простейшего счета (тривиальная арифметика), простейших измерений (обычная геометрия и тригонометрия) и оперирования простыми формулами (алгебра). По мере своего развития естествознание требует все более сложного математического аппарата. Неправые те, кто говорит, что основные законы могут быть сформулированы с использованием только этих операций. Даже введение такого понятия, как скорость или ускорение, не говоря о законах, в которых они используются, уже требует знание раздела высшей математики - дифференциального исчисления. Наиболее сложным разделом естествознания с точки зрения использования математического аппарата для описания теорий и законов является физика. В этом разделе мы введем некоторые определения, которые будут широко использоваться в дальнейшем при описании теорий и законов физики. Конечно, речь пойдет лишь о минимально необходимом математическом аппарате: дифференциальном и интегральном исчислении и векторной алгебре. Всегда нужно помнить, что изучение подавляющего большинства естественнонаучных законов и теорий, как бы ни были они просты на первый взгляд, требует знания специальных разделов высшей математики.

Например, всем известна формулировка закона сохранения заряда - в замкнутой системе алгебраическая сумма зарядов не меняется. Чтобы понять, отражением какого процесса симметрии является этот закон, нам потребовалось бы изучить такие разделы высшей математики, как теория групп, векторный анализ, теорию функций комплексного переменного.

Для успешного усвоения дальнейшего материала читатель должен быть знаком с арифметикой, алгеброй, геометрией, тригонометрией и с началами математического анализа. Нужно хорошо представлять себе, что такое функция, производная, интеграл, и что такое вектор.

Начнем с элементов векторной алгебры. Все изучаемые процессы и явления происходят в окружающем нас трехмерном пространстве. Иногда мы будем абстрагироваться и рассматривать одномерные процессы (например, перемещение вдоль координатной оси). Задать положение тела или материальной точки в пространстве проще всего с помощью декартовой системы координат. Она задается тремя взаимно перпендикулярными осями X , Y и Z как это показано на рис.6.1. Любая точка А может быть задана тремя проекциями на оси координат: A_x , A_y , A_z . Если точка А перемещается в пространстве, т.е. ее положение меняется со временем, то меняются и ее проекции на оси. В этом случае они являются функциями времени: x(t), y(t) и z(t). Вектором называется отрезок в пространстве, который имеет длину и направление. В дальнейшем векторы мы будем выделять стрелочкой наверху или жирным шрифтом. Например: A , или . Модуль (или длину) вектора, которая является скаляром, будем обозначать той же буквой без стрелочки, без выделения шрифтом или под знаком “модуля”: A , B , .

В физике положение точки в пространстве принято задавать с помощью специального вектора, который называется радиусом-вектором и обозначается r . Жирный шрифт означает, что мы имеем дело с векторной, а не с скалярной величиной. Так же, как и любой вектор, радиус-вектор определяется длиной r и направлением в пространстве. Радиус-вектор соединяет начало координат с выбранной точкой. Поскольку эта точка может перемещаться с течением времени в пространстве, радиус-вектор также является функцией времени r = r (t ). Радиус-вектор можно задать тремя проекциями на координатные оси и ортам. Орт - единичный вектор, направленный вдоль оси координат. Договоримся обозначать орты e _x , e _y , e _z . Так как орты не меняют своего направления в пространстве и их длина всегда равна единице, они являются константами, т.е. не меняются. Проекции радиуса-вектора на оси координат обозначаются либо, как r _x (t), r _y (t), r _z (t) , либо просто x(t), y(t), z(t). С учетом введенных обозначений радиус- вектор r (t) записывается:

r (t) = e _x x(t) + e _y y(t) + e _z z(t) (6.1)

В случае прямолинейного движения можно одну из осей (например, ось X) направить вдоль направления движения, и написанное выражение сведется к уравнению лишь для одной проекции. Такое движение, задаваемое лишь одним уравнением x = x(t) , называется одномерным. Если движение можно задать двумя уравнениями, например, x = x(t) и y = y(t) , то такое движение совершается в плоскости (X,Y) и называется двумерным.

Рассмотрим основные действия, которые можно проводить с векторами, в том числе и с радиусом-вектором. Вектора можно складывать и вычитать по правилу параллелограмма или треугольника. Вектор можно умножать на скалярную величину, на число . В результате последней операции получится новый вектор, длина которого в больше прежнего. Эти операции легко записываются с использованием (6.1).

r = r₁ + r₂ = (e _x x₁ + e _y y₁ + e _z z₁ ) + (e _x x₁ + e _y y₁ + e _z z₁ ) =

=e _x (x₁ +x₂ ) + e _y (y₁ + y₂ ) + e _z (z₁ + z₁ ) (6.2)

= (e _x x + e _y y + e _z z ) = e _x x + e _y y + e _z z (6.3)

Наряду с описанными, существуют еще операции умножения вектора на вектор. Их две: скалярное и векторное произведение векторов. Из их названий ясно, что результатом скалярного произведения векторов является скаляр, а результатом векторного произведения - вектор. Операция деления на вектор не определена.

Скалярным произведением векторов называется произведение их длин на косинус угла между ними. Скалярное произведение векторов A и B обозначается (AB ) или A B. Если эти векторы заданы в проекциях на координатные оси, то для их скалярного произведения получится выражение:

(AB ) = (e _x A_x + e _y A_y + e _z A_z ) (e _x B_x + e _y B_y + e _z B_z ) =

= (e _x e _x )A_x B_x + (e _x e _y )A_x B_y + (e _x e _z )A_x B_z +

+ (e _y e _x )A_y B_x + (e _y e _y )A_y B_y + (e _y e _z )A_y B_z +

+ (e _z e _x )A_z B_x + (e _z e _y )A_z B_y + (e _z e _z )A_z B_z =

=A_x B_x +A_y B_y +A_z B_z (6.4).

При выводе (6.4) мы воспользовались тождествами:

(e _x e _x ) = (e _y e _y ) = (e _z e _z ) = 1;

(e _x e _y )=(e _y e _z )=(e _z e _x )=0 (6.5).

Введем понятие проекции вектора А на вектор В , которую обозначают A_B :

. Соответственно, проекция вектора В на вектор А равна: 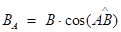, и для скалярного произведения векторов получим выражение: (АВ ) = .

Векторным произведением векторов A и B называется вектор С , численно равный произведению модулей векторов A и B на синус угла между ними. Вектор С перпендикулярен обоим векторам, т.е. перпендикулярен плоскости, в которой они лежат. Таких направлений существует два, см. рис.6.3. Из них выбирают одно по правилу правого буравчика: если вращать ручку буравчика от вектора A к вектору B в направлении меньшего угла, то поступательное движение буравчика укажет направление векторного произведения С . Записывается векторное произведение или . Величина векторного произведения равна , т.е. длина отрезка С численно равна площади параллелограмма, образованного отрезками А и B , см. рис.5.3. Таким образом, в окончательном виде получаем:

, где - единичный вектор, перпендикулярный векторам и .

Векторы, в том числе и радиус-вектор, могут меняться во времени, т.е. они являются функциями времени. Вектор может меняться разными способами. Во-первых, может меняться его длина (модуль) при неизменном направлении вектора в пространстве. Во-вторых, не меняясь по величине вектор может менять свое направление в пространстве. Наконец, вектор может меняться как по длине, так и по направлению. Проекции вектора на оси координат также являются функциями времени, т.е. переменными функциями. Переменные по какому- либо параметру функции могут быть продифференцированы или проинтегрированы по этому параметру. Дифференцирование и интегрирование векторных функций, в принципе, ничем не отличается от дифференцирования и интегрирования скалярных. Дифференцирование или интегрирование вектора можно свести к дифференцированию или интегрированию каждой из его проекций на оси координат. Производная радиуса-вектора по времени записывается в следующем виде: . То же самое можно записать в других обозначениях: .Здесь и в дальнейшем для удобства и краткости производную по времени будем обозначать точкой над функцией. Приращение (полный дифференциал) радиуса-вектора будет равен:

. Аналогично определяется и операция интегрирования векторной функции:

.Как видно из (6.8) и (6.10), специфика интегрирования и дифференцирования векторных функций состоит лишь в необходимости проводить эти операции трижды, по разу для каждой проекции.

В некоторых случаях для упрощения описания явления вместо трехмерных векторов рассматривают двумерные и даже одномерные. Это возможно, если движение тела является, к примеру, плоским или прямолинейным. В общем случае такое упрощение описания происходит, если движение тела можно задать менее чем тремя параметрами.

Еще одно понятие, которое нам надо ввести- вероятность. Все знают, что вероятность выпадения “орла” при бросании монеты равна 1/2. Но что это значит? Означает ли это, что при двух бросаниях монеты один раз выпадет “орел” , а второй раз “решка”, или это что-то другое? Введем строгое понятие вероятности, а потом рассмотрим задачу с бросанием монеты.

Пусть у нас имеется система, в которой может реализоваться S какиx-то событий. При бросании монеты S=2. Одно событие - выпадение “орла”, второе - выпадение “решки”. В общем случае число событий может быть любым. Например, при бросании кости имеется 6 событий. Это выпадение одной из 6 цифр от 1 до 6. Мы проводим над системой N измерений. В каждом измерении регистрируем одно из S событий. Пусть N>>S. При измерении i события (i принадлежит множеству s, 1<i<S) мы получили его значение N_i раз. Относительной частотой выпадения i события называется величина N_i /N. Если устремить число измерений (т.е. N)к бесконечности, то относительная частота выпадения события будет равна вероятности выпадения или измерения этого события P(i):

P(i) = lim N_i /N при N -> (6.11).

Значит, если нам известна вероятность выпадения какого-то события, то при очень большом числе измерений N у нас событие i выпадет P(i) N раз. Значит, если мы бросаем монету 1 раз , мы ничего не сможем сказать, какой стороной она упадет. Но, если мы бросаем монету очень много раз (например 10000) то мы можем утверждать, что примерно 5000 раз выпадет “орел”, а 5000 раз- “решка.

Сумма вероятностей выпадения всех событий всегда будет нормирована и равна 1. Действительно, поскольку SN_i =N, то имеем: SP(i)= S(N_i /N)=(SN_i )/N=1.

Число событий может быть конечно, а может быть и бесконечно. Например, соседние скорости атомов в газе отличаются на бесконечно малую величину. В этом случае вероятность Р будет непрерывной функцией. Для газа, например, это будет функция распределения атомов по скоростям, известная из школьного курса как функция распределения Максвелла.

В заключении этого раздела сделаем акцент на двух моментах.

Первое. Математический аппарат современной физики и всего естествознания в целом огромен и очень сложен. В рамках курса невозможно даже просто перечислить все разделы, которые используются в науке. В этом разделе затронут лишь минимум некоторых разделов математики, необходимых для понимания фундаментальных законов естествознания: алгебры, геометрии, тригонометрии, математического анализа, дифференциального и интегрального исчисления, аналитической геометрии, векторного анализа, теории вероятностей.

Второе. В некоторых учебниках по естествознанию, написанных в основном людьми, не имеющими фундаментальной естественнонаучной подготовки , делаются попытки изложить все естествознание, опираясь на одну только арифметику. Это глубоко ошибочный подход. Без введения понятий переменной величины и функции и соответствующего математического аппарата невозможно не только описать, но даже просто осмыслить тот или иной закон естествознания. Во всех областях естественных и даже общественных наук имеются т. н. "динамические законы", т. е. законы, в которых что-либо меняется. Но даже самый простой динамический параметр скорость, невозможно ввести, не используя языка высшей математики - дифференциального исчисления. Ведь скорость -это производная исследуемой величины по времени.