|
§1. ЧИСЛЕННОЕ РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ.
1п. Общий вид нелинейного уравнения
F(x)=0
Нелинейные уравнения могут быть двух видов:
1. Алгебраические
an
xn
+ an-1
xn-1
+… + a0
= 0
2. Трансцендентные- это уравнения в которых х является аргументом тригонометрической, логарифмической или показательной функции.
Значение х0
при котором существует равенство f(x0
)=0 называется корнем
уравнения.
В общем случае для произвольной F(x) не существует аналитических формул определения корней уравнения. Поэтому большое значение имеют методы, которые позволяют определить значение корня с заданной точностью. Процесс отыскания корней делиться на два этапа:
1. Отделение корней, т.е. определение отрезка содержащего один корень.
2. Уточнение корня с заданной точностью.
Для первого этапа нет формальных методов, отрезки определяются или табуляцией или исходя из физического смысла или аналитическими методами.
Второй этап, уточнение корня выполняется различными итерационными методами, суть которых в том, что строится числовая последовательность xi
сходящихся к корню x0
Выходом из итерационного процесса являются условия:
1. │f(xn
)│≤ε
2. │xn
-xn-1
│≤ε
рассмотрим наиболее употребляемые на практике методы: дихотомии, итерации и касательных.
2 п. Метод половинного деления.
Дана монотонная, непрерывная функция f(x), которая содержит корень на отрезке [a,b], где b>a. Определить корень с точностью ε, если известно, что f(a)*f(b)<0
Суть метода
Данный отрезок [a,b] делится пополам, т.е. определяется x0
=(a+b)/2, получается два отрезка [a,x0
] и [x0
,b], далее выполняется проверка знака на концах, полученных отрезков для отрезка, имеющего условия f(a)*f(x0
)≤0 или f(x0
)*f(b)≤0 снова проводится деление пополам координатой х, снова выделение нового отрезка и так продолжается процесс до тех пор пока │xn
-xn-1
│≤ε
Приведем ГСА для данного метода
3п. Метод итерации.
Дана непрерывная функция f(x), которая содержит единственный корень на отрезке [a,b], где b>a. Определить корень с точностью ε.
Суть метода
Дано f(x)=0 (1)
Заменим уравнение (1) равносильным уравнением x=φ(x) (2).
Выберем грубое, приближенное значение x0
, принадлежащее[a,b], подставим его в правую часть уравнения (2), получим:
Реклама

x1
= φ(x0
) (3) ,
далее подставим х1
в правую часть уравнения (3) получим:
x2
= φ(x1
) (4)
x3
= φ(x2
) (5)
Проделаем данный процесс n раз получим xn
=φ(xn-1
)
Если эта последовательность является сходящейся т.е. существует предел
x*
=lim xn
, то данный алгоритм позволяет определить искомый корень.
Выражение (5) запишем как x*
= φ(x*
) (6)
Выражение (6) является решением выражения (2), теперь необходимо рассмотреть в каких случаях последовательность х1
…хn
является сходящейся.
Условием сходимости является если во всех токах x принадлежит [a,b] выполняется условие:
Приведем ГСА для метода итерации:
4 п. Метод касательных (Ньютона).
Дана непрерывная функция f(x), которая содержит единственный корень на отрезке [a,b], где b>a при чем определены непрерывны и сохраняют знак f`(x) f``(x). Определить корень с точностью ε.
Суть метода
1.
Выбираем грубое приближение корня х0
(либо точку a, либо b)
2.
Наити значение функции точке х0
и провести касательную до пересечения с осью абсцисс, получим значение х1
3.
Определить значение функции в точке х1
, через эту точку провести касательную получим точку х2
4.
Повторим процесс n раз 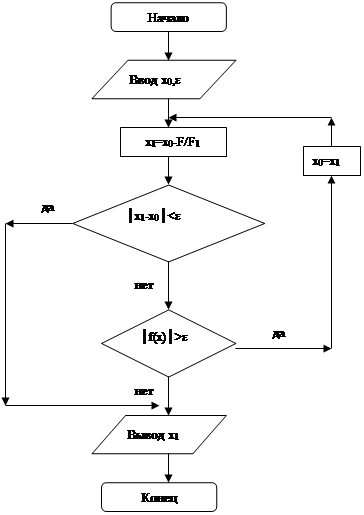 Если процесс сходящийся то xn
можно принять за искомое значение корня Если процесс сходящийся то xn
можно принять за искомое значение корня
Условиями сходимости являются:
│f(xn
)│≤ε
│xn
-xn-1
│≤ε
Приведем ГСА метода касательных:
5п. Задание для РГР
Вычислить корень уравнения
На отрезке [2,3] с точностью ε=10-4
методами половинного деления, итерации, касательных.
6 п. Сравнение методов
Эффективность численных методов определяется их универсальностью, простотой вычислительного процесса, скоростью сходимости.
Наиболее универсальным является метод половинного деления, он гарантирует определение корня с заданной точностью для любой функции f(x), которая меняет знак на [a,b]. Метод итерации и метод Ньютона предъявляют к функциям более жесткие требования, но они обладают высокой скоростью сходимости.
Метод итерации имеет очень простой алгоритм вычисления, он применим для пологих функций.
Метод касательных применим для функций с большой крутизной, а его недостатком является определение производной на каждом шаге.
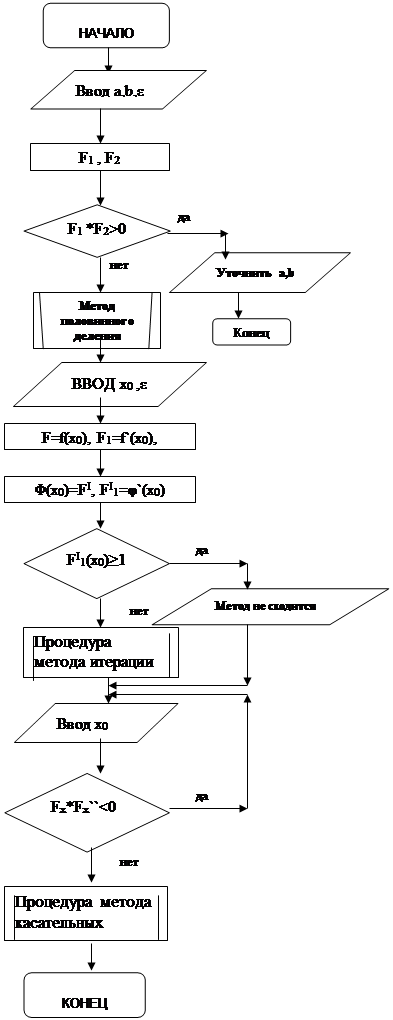
ГСА головной программы, методы оформлены подпрограммами.
Программа по методам половинного деления, итерации и метода Ньютона.
CLS ‑
a = 2: b = 3: E = .0001
DEF FNZ (l) = 3 * SIN(SQR(l)) + .35 * l - 3.8
Реклама

F1 = FNZ(a): F2 = FNZ(b)
IF F1 * F2 > 0 THEN PRINT "УТОЧНИТЬ КОРНИ": END
GOSUB 1
x0 = a
IF ABS((-3 * COS(SQR(x))) / (.7 * SQR(x))) > 1 THEN PRINT "НЕ СХОДИТСЯ"
DEF FNF (K) = -(3 * SIN(SQR(x)) - 3.8) / .35
GOSUB 2
x0 = b
F = FNZ(x0)
DEF FND (N) = (3 * COS(SQR(N)) / (2 * SQR(N))) + .35 _
IF F * (-4.285 * (-SQR(x0) * SIN(SQR(x)) - COS(SQR(x))) / (2 * x * SQR(x))) < then print “не сходится”:end
GOSUB 3
END
'=========Метод половинного деления========
1 x = (a + b) / 2: T = T + 1
F3 = FNZ(x)
IF ABS(F3) < E THEN 5
IF F1 * F3 < 0 THEN b = x ELSE a = x
IF ABS(b - a) > E THEN 1 ‑
5 PRINT "X="; x, "T="; T
RETURN
'=========Метод итерации==========
2 x0 = a
12 X2 = FNF(x0): S = S + 1
IF ABS(X2 - x0) > E THEN x0 = X2: GOTO 12
PRINT "X="; X2, "S="; S
RETURN
'========Метод касательных=======
3 x0 = b
23 D = D + 1
F = FNZ(x0): F1 = FND(x0)
X3 = x0 - F / F1
IF ABS(X3 - x0) < E THEN 100
IF ABS(F) > E THEN x0 = X3: GOTO 23
100 PRINT "X="; X3, "D="; D
RETURN
Ответ
x= 2,29834 T=11
x=2,29566 S=2
x=2,29754 D=2
где T,S,D-число итерации для метода половинного деления, итерации, касательных соответственно.
|