 .
ЛИНЕЙНЫЕ МЕТОДЫ
ОПТИМИЗАЦИИ,
ЗАДАЧА ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ,
ЕЕ ПОСТАНОВКА
И СВОЙСТВА .
ЛИНЕЙНЫЕ МЕТОДЫ
ОПТИМИЗАЦИИ,
ЗАДАЧА ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ,
ЕЕ ПОСТАНОВКА
И СВОЙСТВА
1.1 Постановка
задачи линейного
программирования
В экономике
помимо соотношений
затрат, выпуска,
спроса, предложения
и т.п., часто
возникает
необходимость
выбора одного
из возможных
вариантов
функционирования
экономической
системы. Экономически
оправдано в
таких условиях
ставить вопрос
о выборе наилучшего
варианта. Что
понимать под
лучшим вариантом
задается в виде
критерия (цели).
В количественном
выражении
критерий представляет
собой функциональную
зависимость
от переменных
показателей,
в дальнейшем
будем ее называть
целевой (критериальной)
функцией. Наилучший
вариант в таком
случае соответствует
наибольшему
(экстремальному,
оптимальному)
значению функции.
В экономических
задачах, как
правило, область
изменения
переменных
параметров
ограничена
и оптимальное
значение целевой
функции требуется
найти на ограниченном
множестве.
Область исследования,
заключающаяся
в нахождении
алгоритмов
решения подобных
задач, образует
направление,
которое называется
математическим
программированием.
Экономические
требования
накладывают
свои особенности:
в практических
задачах число
переменных
и ограничений
достаточно
велико, целевая
функция не
всегда дифференцируема.
Поэтому методы
классического
анализа для
отыскания
экстремумов
к задачам
математического
программирования
часто неприменимы.
Возникает
необходимость
разработки
специальных
методов решения
задач математического
программирования
и, следовательно,
как всегда в
таких случаях,
появляются
новые направления,
требующие
упорядочения,
классификации.
Классификация
задач происходит
в зависимости
от экономических
условий, видов
ограничений,
переменных
и параметров,
методов решения.
Традиционно
в математическом
программировании
выделяют следующие
основные разделы.
Линейное
программирование
- целевая функция
линейна, множество,
на котором
ищется экстремум
целевой функции,
задается системой
линейных равенств
и неравенств.
В свою очередь
в линейном
программировании
существуют
классы задач,
структура
которых позволяет
создать специальные
методы их решения,
выгодно отличающиеся
от методов
решения задач
общего характера.
Так, в линейном
программировании
появился раздел
транспортных
задач, блочного
программирования
и др.
Н
лист
Кп-км-п-44-2203-99
 елинейное
программирование
- нелинейны
целевая функция
и ограничения.
Нелинейное
программирование
принято подразделять
следующим
образом: елинейное
программирование
- нелинейны
целевая функция
и ограничения.
Нелинейное
программирование
принято подразделять
следующим
образом:
- выпуклое
программирование
- когда выпукла
целевая функция,
если рассматривается
задача ее минимизации
(либо выпуска,
если ищется
максимум), и
выпукло множество,
на котором
решается
экстремальная
задача;
выпуклое
программирование
- когда выпукла
целевая функция,
если рассматривается
задача ее минимизации
(либо выпуска,
если ищется
максимум), и
выпукло множество,
на котором
решается
экстремальная
задача;
- квадратичное
программирование
- когда целевая
функция квадратичная,
а ограничения
- линейные равенства
и неравенства.
Многоэкстремальные
задачи - здесь
обычно выделяют
специализированные
классы задач,
часто встречающихся
в приложениях,
например, задачи
о минимизации
на выпуклом
множестве
вогнутых функций.
Важным разделом
математического
программирования
является
целочисленное
программирование
- когда на переменные
накладываются
условия целочисленности.
Первой из
"неклассических"
задач оптимизации
была подробно
исследована
задача отыскания
экстремума
линейной функции
на множестве,
заданном линейными
неравенствами
и равенствами.
Раздел теории
оптимизации,
изучающий такие
задачи, получил
название "линейное
программирование".
В данном
разделе изучается
задача линейного
программирования,
которая задается
следующим
образом.
1. Задача решается
относительно
переменных
.
В дальнейшем
они будут
записываться
в виде либо
вектора-столбца
(
X1)
X = ( .. )
( Xn)
либо вектора-строки
х = (х1,
..., хn).
Предполагается,
что вектор х
должен удовлетворять
системе n
линейных неравенств
a11x1+ ….
+a1nxn <= b1
am1x1+….+amnxn<=bm
(1)
3. В экономических
задачах присутствует
дополнительное
необходимое
условие: координаты
вектора х должны
быть неотрицательными:
X
>= 0 (2)
где 0 - нулевой
вектор-столбец
размерности
n.
4. Целевая
функция представляет
собой линейную
функцию переменных
X1,…..,Xn
P1X1+…..PmXn=f(x1,….,xn)
(3)
Лист
Кп-км-п-44-2203-99

5 .
Общая задача
линейного
программирования
(ЛП) состоит в
выборе вектора
х, удовлетворяющего
системе неравенств
(1),
(2)
и максимизирующего
целевую функцию
( 3 ).
Математически
задача ЛП
записывается
следующим
образом: .
Общая задача
линейного
программирования
(ЛП) состоит в
выборе вектора
х, удовлетворяющего
системе неравенств
(1),
(2)
и максимизирующего
целевую функцию
( 3 ).
Математически
задача ЛП
записывается
следующим
образом:
P1X1+…..+PnXn
max
(x1<….xn) (4)
при условиях
{a11x1+…….+a1nxn<=b1}
{……………………………
} (5)
{am1x1+…….+amnxn<=bm}
x1>=0, x2>=0,……,xn>=0
(6)
или
n
E pixi max
J=1 x1,..,xn
при условиях
n
{ E a1jxj<=bi
j=1
{…………
n
{ E a1jxj<=bj
j=1
{…………
n
{ E mjxj<=bm
x1,….,xn >=0
Задача Линейного
Программирования
в матричной
форме записывается
следующим
образом. Обозначим
через b
вектор-столбец
правой части
СЛН
(b1)
B = (….)
(bm)
через А - матрицу
коэффициентов
СЛН:
a11…..a1n
……..
A = ……..
Лист
Кп-км-п-44-2203-99
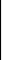
 am1…..amn
am1…..amn
ч   ерез
р - вектор-строку
коэффициентов
целевой функции.
Напомним, выражение
(р, х) означает
скалярное
произведение
векторов р и
х. Тогда в матричном
виде задача
ЛП записывается: ерез
р - вектор-строку
коэффициентов
целевой функции.
Напомним, выражение
(р, х) означает
скалярное
произведение
векторов р и
х. Тогда в матричном
виде задача
ЛП записывается:
(P,X)max(x)
при условии:
Ax<=b
x>=0
Таким образом,
в задаче Линейного
Программирования
константами
(параметрами)
являются коэффициенты
матрицы А, вектор
правой части
В и коэффициенты
целевой функции
- вектор P.
Подлежит определению
вектор х*=х1,..,,хn,),
который удовлетворяет
ограничениям
( 8 ),
( 9):
Ах* < В
х*>0,
и доставляет
максимум целевой
функции ( 7):
max(p,x)=
(р, х*).
Это матричная
запись задачи
ЛП на максимум
в стандартной
форме.
Запись задачи
линейного
программирования
( 4) -
(6)
или (7)
- (9) называют
записью ЗЛП
в стандартной
форме.
Иногда, исходя
из практических
требований,
отдельные
ограничения
на переменные
х,, ..., х„ могут
иметь вид точного
равенства
n
E aijxj=bi
I=1
(10)
Это значит,
что решение
требуется
искать среди
векторов х,
координаты
которых удовлетворяют
i-му
ограничению
как точному
равенству.
Чтобы привести
в этом случае
задачу к стандартному
виду, уравнение
(10)
достаточно
заменить на
систему из двух
^неравенств:
{ E ai jxj<=bi
{ E aij xj>=bi (11)
или
{ E aij xj<=bi
{ E aij xj<= -bi (12)
Лист
Кп-км-п-44-2203-99
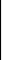

У равнение
( 11)
и система (
12 ) или эквивалентны.
Задача линейного
программирования
вида: равнение
( 11)
и система (
12 ) или эквивалентны.
Задача линейного
программирования
вида:
mах
(р, х)
Ах=B
(
13 )
х>0
называется
задачей линейного
программирования
в канонической
форме.
Чтобы привести
задачу линейного
программирования
в стандартной
фюрме к форме
канонической,
следует ввести
дополнительные
переменные
ui,ui>=0,i=1,2,….,m
, такие,
что
E aij xj+ui=bi, i=1,….,m
Причем целевая
функция при
этом должна
оставаться
неизменной.
Для этого запишем
целевую функцию
в виде:
EpjXj+0*u1+0*u2+…..0*um
Здесь коэффициенты
при переменных
u1,….,um
полагаются
равными нулю.
Тогда задача
(7)
- (9)
в каноническом
виде принимает
вид:
( n )
( E PjXj ) max
x
( j=1 )
(14)
при условиях:
n
E
aijxj+ui=bi, i=1,…..,m (15)
j=1
x1,…..,xn>=0 u1,…..um>=0 (16)
Стандартная
задача линейного
программирования
на минимум
(матричная
запись) записывается
в виде:
(p,x) max
x (17)
при условиях:
ax>=b
x>=0
(18)
или в записи
в виде неравенств:
Лист
Кп-км-п-44-2203-99
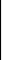

E pjXj
min x1..xn pjXj
min x1..xn
при ограничениях:
E aij xj>=bi
…………..
E
aij xj>=bm
X1….xn>=0
Таким образом,
не важно, в какой
форме получаются
линейные ограничения:
в форме равенств
или в форме
неравенств.
Эквивалентными
преобразованиями
возможно привести
неравенства
к равенствам
и наоборот.
Необходимость
преобразований
обычно связана
с тем, какой
применяется
метод решения.
1.3 Транспортная
задача
Пусть некоторый,
однородный
товар (продукт)
хранится на
M
складах и
потребляется
в N
пунктах (например,
магазинах).
Известны следующие
параметры:
ai - запас
продукта на
-ом
складе,
ai>0, i=1,….,m
bj-
потребность
в продукте в
-ом
пункте,
bj>0,j=1,….,n
Cij -
стоимость
перевозки
единичного
количества
товара с -го
склада в
-й
пункт,
. Планируется
полностью
перевезти товар
со складов и
полностью
удовлетворить
потребности
в пунктах назначения.
При этом предполагается,
что суммарные
запасы равны
суммарным
потребностям:
m n
E ai = E bj
(19)
i=1 j=1
Транспортная
задача ставится
как каноническая
задача ЛП следующего
специального
вида:
m n
E E CijXij
min (20)
i=1 j=1
при условиях:
Лист
Кп-км-п-44-2203-99
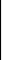

n
E xij=ai,i=1,…,m
(21)
J=1
n
E xij=bj,j=1,….,n
(22)
I=1
Xij>=0, i=1,…..m j=1,….n
(23)
где - количество
товара, перевозимого
с I-го
склада в J-ый
пункт. Иными
словами, требуется
так организовать
перевозки
продукта со
складов в пункты
потребления,
чтобы при полном
удовлетворении
потребностей
минимизировать
суммарные
транспортные
расходы. Заметим,
что условие
( )
является необходимым
и достаточным
для существования
решения транспортной
задачи.
Лист
Кп-км-п-44-2203-99

4 .
Анализ задачи
или модели. .
Анализ задачи
или модели.
4.1 Определение
опорного плана
транспортной
задачи
Для решения
транспортной
задачи разработано
несколько
методов, каждый
из которых
отличается
от другого
методом заполнения
матрицы перевозок.
Существуют
два типа транспортной
задачи:
открытая и
закрытая.
Транспортная
задача называется
открытой если
сумма запасов
товара на складах
отличается
от суммы потребностей
товаров у магазинов.
Транспортная
задача называется
закрытой , если
сумма запасов
товара на складах
равняется сумме
потребностей
магазинов.
Решение существует
только для
закрытой транспортной
задачи, поэтому
если транспортная
задача открытая
, то ее надо привести
к закрытому
типу. Для этого
в случае , если
запас товара
на складах
превышает
потребность
магазинов, то
вводят фиктивного
потребителя,
который выбирает
весь избыток
товара. В случае
же, если существует
дефицит товара,
т.е. потребность
магазинов
больше, чем
запас товаров
на складах, то
вводят фиктивного
поставщика,
с фиктивным
запасом товара
на складе. В
обоих случаях
в матрице тарифов
перевозок |C|
данному
складу или
магазину
проставляется
нулевая цена
перевозки.
Метод минимального
элемента
Алгоритм
метода минимального
элемента состоит
в следующем.
Просматривается
вся матрица
тарифов перевозок,
и из нее выбирается
позиция с наименьшим
значением
тарифа C,
затем просматриваются
значения наличия
запасов на
складе
A и потребности
у потребителя
B,
затем в данную
клетку записывается
величина D=MIN(A,B).
Из запасов
соответствующего
склада и потребностей
магазина вычитается
величина D
. Если запас
товара на складе
исчерпан, то
эта строка
исключается
из дальнейшего
рассмотрения.
Если потребность
магазина в
товаре удовлетворена
полностью, то
этот столбец
исключается
из дальнейшего
рассмотрения.
Может быть
случай , когда
одновременно
исключаются
и строка и столбец,
этот случай
называется
вырожденным.
В дальнейшем
весь процесс
повторяется
до тех пор , пока
не будет исчерпан
весь запас
товаров на
складах и не
будет удовлетворена
потребность
всех магазинов.
По полученной
матрице перевозок
вычисляется
целевая функция
задачи Z.
Лист
Кп-км-п-44-2203-99


Метод Фогеля
Метод состоит
в следующем.
Просматриваются
все строки и
столбцы матрицы
тарифов, вычисляется
разность между
двумя наименьшими
элементами
в строке или
в столбце. Затем
из всех этих
разностей
выбирается
строка или
столбец с
максимальной
разность. В
выбранной
строке или
столбце , как
и в методе
минимального
элемента, заполняется
клетка с наименьшим
значением
тарифа. Затем
обнулявшаяся
строка или
столбец исключаются
из рассмотрения
и весь процесс
повторяется
до полного
исчерпания
запаса товаров
на складах. По
полученной
матрице перевозок
вычисляется
целевая функция
Z.
Метод двойного
предпочтения
В начальной
своей стадии
этот метод
похож на метод
минимального
элемента , но
для столбцов.
Просматривается
первый столбец
матрицы тарифов,
в нем находится
наименьший
элемент. Затем
проверяется
, минимален ли
этот элемент
в своей строке.
Если элемент
минимален в
своей строке,
то по методу
минимального
элемента в эту
клетку заносится
значение D=MIN(A,B),
соответствующие
запас и потребность
уменьшаются
на эту величину.
Обнулившаяся
строка или
столбец исключаются
из рассмотрения
и процесс
повторяется,
начиная с первого
неисключенного
столбца. Если
найденный
минимальный
элемент не
минимален в
своей строке,
то происходит
переход к следующему
столбцу и так
до тех пор, пока
не будет найден
такой элемент.
По полученной
матрице перевозок
вычисляется
целевая функция
Z. Этот
метод требует
интенсивных
операции обмена
с памятью , поэтому
более громоздок
по сравнению
с остальными
и требует больших
вычислительных
ресурсов.
Как и любая
задача линейного
программирования,
необходимо
построить
первоначальный
опорный план
для решения
задачи. Одним
из методов
построения
исходного
опорного плана
является так
называемый
метод «северо-западного»
угла.
Лист
Кп-км-п-44-2203-99


Метод северо-западного
угла
Метод состоит
в следующем.
Просматривается
матрица тарифов
перевозок C
, начиная
с левого верхнего
угла (клетки).
В эту клетку
записывается
величина D=MIN(A,B).
Она вычитается
из запасов и
потребностей
соответствующего
склада и магазина.
Обнулившаяся
строка или
столбец исключаются
из рассмотрения,
затем процесс
опять повторяется
для левой верхней
клетки оставшейся
матрицы и так
до тех пор пока
весь запас
товаров не
будет исчерпан.
Полученный
опорный план
не оптимален,
поэтому его
дальнейшее
решение продолжают
одним из вышерассмотренных
методов.
Лист
Кп-км-п-44-2203-99

2 .
Предмодельный
анализ. .
Предмодельный
анализ.
2.1 Анализ
существующих
аналогов и
подсистем
Программное
обеспечение
для решения
задач линейного
программирования
и в частности,
транспортной
задачи разработано
уже в конце
60-ых – начале
70-ых годов и было
реализовано
как пакет программ
– библиотек.
Данный пакет
задач был реализован
на таких алгоритмических
языках как
Алгол, Фортран.
В западных
разработках
в основном
применялся
алгоритмический
язык Кобол. С
появлением
персональных
компьютеров
данный пакет
был перемещен
на ПК, с учетом
особенностей
реализации
трансляторов
вышеперечисленных
языков на ПК.
Также дополнительно
были реализованы
пакеты программ,
в основном
усилиями вузов
на языках Паскаль,
Си. Перенос
программного
обеспечения
на ПК открыл
новые возможности
в решении задач
линейного
программирования
и наглядного
отображения
результатов
вычислении,
что отсутствовало
на больших
вычислительных
системах –
мэйнфреймах.
Ход вычислении
и его результаты,
особенно для
многомерных
задач с большим
числом переменных
можно было
наглядно отобразить
на мониторе.
Кроме того
появление
интерактивных
программ, программ
, в ход которых
человек- оператор
мог активно
вмешаться,
корректировать
промежуточные
результаты
, изменить методику
расчетов, значительно
облегчал и
ускорял разработку
нового программного
обеспечения.
С развитием
аппаратного
обеспечения
совершенствовалось
и программное
обеспечение.
Алгоритмические
языки тоже
совершенствовались
согласно потребностям
экономики,
науки и т.д.
Особо бурное
развитие программного
обеспечения
началось с
появлением
операционной
системы Windows.
Почти все
существующее
программное
обеспечение
и алгоритмические
языки были
перенесены
на эту операционную
платформу.
Возможности
Windows усилили
интерактивную
сторону этих
алгоритмических
языков, перейдя
на объектно-ориентированный
принцип построения
алгоритмов,
что позволяло
использовать
уже наработанное
программное
обеспечение
без больших
изменений.
Одним из бурно
развивающихся
алгоритмических
языков является
Pascal и
его диалекты.
Первоначально
этот язык был
создан для
обучения студентов
основам программирования,
ввиду своей
простоты и
наглядности
конструкции.
Он был создан
Никлаусом
Виртом, и послужил
основой для
целого семейства
паскале-подобных
языков –
Modula, Classcal, Object Pascal.
Наиболее
развитую систему
программирования
на языке Pascal
построила
фирма Borland
– Turbo Pascal. Первоначально
она была реализована
для DOS,
с появлением
Windows ,
она была перенесена
в нее. И наконец,
была выпущена
новая версия
для Windows
– Delphi.
Лист
Кп-км-п-44-2203-99


5.2 Среда разработки
Delphi
Без баз данных
сегодня невозможно
представить
работу большинства
финансовых,
промышленных,
торговых и
прочих организаций.
Потоки информации,
циркулирующие
в мире, который
нас окружает,
огромны. Во
времени они
имеют тенденцию
к увеличению.
Не будь баз
данных, мы давно
захлебнулись
бы в информационной
лавине. Базы
данных позволяют
информацию
структурировать,
хранить и извлекать
оптимальным
для пользователя
образом.
Поскольку
использование
баз данных
является одним
из краеугольных
камней, на которых
построено
существование
различных
организаций,
пристальное
внимание
разработчиков
приложений
баз данных
вызывают инструменты,
при помощи
которых такие
приложения
можно было бы
создавать.
Выдвигаемые
к ним требования
в общем виде
можно сформулировать
как:
"быстрота,
простота,
эффективность,
надежность".
Среди большого
разнообразия
продуктов для
разработки
приложений
Delphi занимает
одно из ведущих
мест. Delphi и
отдают предпочтение
разработчики
с разным стажем,
привычками,
профессиональными
интересами.
С помощью Delphi
написано
колоссальное
количество
приложений,
десятки фирм
и тысячи
программистов-одиночек
разрабатывают
для Delphi дополнительные
компоненты.
В основе такой
общепризнанной
популярности
лежит тот факт,
что Delphi, как
никакая другая
система программирования,
удовлетворяет
изложенным
выше требованиям.
Действительно,
приложения
с помощью Delphi
разрабатываются
быстро, причем
взаимодействие
разработчика
с интерактивной
средой Delphi
не вызывает
внутреннего
отторжения,
а наоборот,
оставляет
ощущение комфорта.
Delphi -приложения
эффективны,
если разработчик
соблюдает
определенные
правила (и часто
- если не соблюдает).
Эти приложения
надежны и при
эксплуатации
обладают
предсказуемым
поведением.
Н
Лист
Кп-км-п-44-2203-99
 о
вот проста ли
Delphi?
И да, и нет. Она
лишь кажется
простой, поскольку
многие "подводные
камни" скрыты
от разработчика.
Однако чем
больше изучаешь
ее, тем больше
становится
ясной ее глубина,
которая одновременно
и вызывает
уважение, и
пугает. Лишь
со временем
приходит понимание
того, что для
написания
действительно
мощных и функциональных
приложений
требуется
постоянное
изучение Delphi. о
вот проста ли
Delphi?
И да, и нет. Она
лишь кажется
простой, поскольку
многие "подводные
камни" скрыты
от разработчика.
Однако чем
больше изучаешь
ее, тем больше
становится
ясной ее глубина,
которая одновременно
и вызывает
уважение, и
пугает. Лишь
со временем
приходит понимание
того, что для
написания
действительно
мощных и функциональных
приложений
требуется
постоянное
изучение Delphi.


Б лок-схема
меню определение
опорного плана
(Transtask.pas) лок-схема
меню определение
опорного плана
(Transtask.pas)
 1
1
 2
2

3
  Да
Да
нет

4
Да
5
нет

6
Да
7

нет

8
Да
9
 нет
нет
Лист
Кп-км-п-44-2203-99



 10
10
 11
11
12


13
  Да
Да
14
нет
 15
15
16


Лист
Кп-км-п-44-2203-99


Блок-схема
подпрограммы
решения методом
минимального
элемента MINIELEM
1

2

3
4
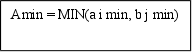
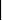
 5
5
6
Да
 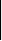
7
 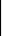
нет
8
Да
  9
9
нет

Лист
Кп-км-п-44-2203-99


 10
10
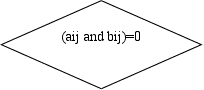
11
Да
 12
12
13

Лист
Кп-км-п-44-2203-99


Блок-схема
подпрограммы
решения транспортной
задачи
Transsolver
 1
1
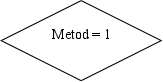  2
2
Да
3
  нет
нет
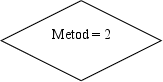
4
Да
 5
5
 нет
нет
6
 7
7
нет


8

Лист
Кп-км-п-44-2203-99


unit
Unit1;
interface
uses
Windows,
Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs,
Grids;
type
TForm1
= class(TForm)
StringGrid1:
TStringGrid;
private
{
Private declarations }
public
{
Public declarations }
end;
var
Form1:
TForm1;
word:string;
words:TStringList;
i:integer;
implementation
{$R
*.DFM}
Form1.slString=TStringList.Create;
for
i:=1 to 8 do
begin
word:=IntTostr(i);
words.add(word)
end
end.
Лист
Кп-км-п-44-2203-99


unit
TransTask;
interface
uses
Windows,
Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs,
StdCtrls,
ExtCtrls, Grids, ComCtrls, Math;
type
TfmTransTask
= class(TForm)
pgcTransTask:
TPageControl;
tbsAbout:
TTabSheet;
tbsData:
TTabSheet;
tbsTarif:
TTabSheet;
tbsSolve:
TTabSheet;
Label1:
TLabel;
edProviderCount:
TEdit;
spnProviderCount:
TUpDown;
Label2:
TLabel;
stgProvider:
TStringGrid;
Label3:
TLabel;
Label4:
TLabel;
edCustomerCount:
TEdit;
spnCustomerCount:
TUpDown;
stgCustomer:
TStringGrid;
Label5:
TLabel;
lblTypeTask:
TLabel;
lblProviderGruz:
TLabel;
lblCustomerGruz:
TLabel;
stgTarif:
TStringGrid;
stgSolve:
TStringGrid;
rgMetod:
TRadioGroup;
rbMinelem:
TRadioButton;
rbFogel:
TRadioButton;
rbTwoWall:
TRadioButton;
btnSolve:
TButton;
btnPrint:
TButton;
Label6:
TLabel;
Label7:
TLabel;
Label8:
TLabel;
Label9:
TLabel;
btnLoadData:
TButton;
btnLoadDataC:
TButton;
lblProvider:
TLabel;
lblCustomer:
TLabel;
lblTupeTask:
TLabel;
lblMsg:
TLabel;
Label10:
TLabel;
lblZ:
TLabel;
procedure
FormCreate(Sender: TObject);
procedure
edProviderCountChange(Sender: TObject);
procedure
edCustomerCountChange(Sender: TObject);
procedure
btnLoadDataClick(Sender: TObject);
procedure
btnLoadDataCClick(Sender: TObject);
procedure
btnSolveClick(Sender: TObject);
procedure
btnPrintClick(Sender: TObject);
Лист
Кп-км-п-44-2203-99
 private
private
 { Private declarations }
{ Private declarations }
public
{
Public declarations }
end;
var
fmTransTask:
TfmTransTask;
a,b:
array of integer;// наличие
груза у поставщиков
//
и спрос у потребителей
c:
array of array of integer; // матрица
тарифов перевозок
d:
array of array of integer;// матрица
перевозок
(решение)
z,m,n:integer;
//число поставщиков
и потребителей
s:string;
implementation
{$R
*.DFM}
procedure
ShowSolve;
var
i,j:integer;
begin
for
i:= 0 to m-1 do
for
j:= 0 to n-1 do
fmTransTask.stgSolve.Cells[j+1,i+1]:=IntToStr(d[i,j]);
fmTransTask.lblZ.Caption:=IntToStr(z);
end;
procedure
Minelem;
label
l1;
var
i,j,imin,jmin,cmin:integer;
set_i:set
of 0..255;
set_j:set
of 0..255;
begin
//
создаем множество
индексов
set_i:=[];
for
i:=0 to m-1 do include(set_i,i);
set_j:=[];
for
j:=0 to n-1 do include(set_j,j);
z:=0;
repeat
//
поиск первоначального
минимального
ьэлемента в
матрице тарифов
for
i:= 0 to m-1 do
for
j:= 0 to n-1 do
if
(i in set_i) and (j in set_j) then
begin
cmin:=c[i,j];
goto
l1
end;
l1:
//
поиск минимального
элемента в
//
в матрице тарифов
c
for
i:= 0 to m-1 do
for
j:= 0 to n-1 do
if
(i in set_i) and (j in set_j) then
if
c[i,j]<=cmin then
begin
Лист
Кп-км-п-44-2203-99
 cmin:=c[i,j];
cmin:=c[i,j];
 imin:=i;
imin:=i;
jmin:=j
end;
//
определение
величины поставки
d[imin,jmin]:=min(a[imin],b[jmin]);
//
определяем
исключаемую
строку столбец
a[imin]:=a[imin]-d[imin,jmin];
if
a[imin]=0 then
exclude(set_i,imin);
b[jmin]:=b[jmin]-d[imin,jmin];
if
b[jmin]=0 then
exclude(set_j,jmin);
z:=z+d[imin,jmin]*cmin
until
(set_i=[]) and (set_j=[]);
ShowSolve
end;
procedure
Fogel;
var
i,j:integer;
cminprev,cmin:integer;
SubCol,SubRow:array
of array of integer;
set_i,set_j:set
of 0..255;
imin,jmin:integer;
imax,jmax:integer;
SubRowMax,SubColMax:integer;
begin
//
размещаем
массивы
SetLength(SubRow,m);
for
i:= 0 to m-1 do SetLength(SubRow[i],2);
SetLength(SubCol,n);
for
j:= 0 to n-1 do SetLength(SubCol[j],2);
set_i:=[];
for
i:=0 to m-1 do include(set_i,i);
set_j:=[];
for
j:=0 to n-1 do include(set_j,j);
repeat
//
цикл по строкам
for
i:= 0 to m-1 do
if
i in set_i then
begin
//
ищем первоначальный
минимальный
элемент в строке
for
j:= 0 to n-1 do
if
j in set_j then
begin
cmin:=c[i,j];
break
end;
//
ищем 1-ое наименьшее
значение в
строке
for
j:= 0 to n-1 do
Лист
Кп-км-п-44-2203-99
 if j in set_j then
if j in set_j then
 if c[i,j]<=cmin
then
if c[i,j]<=cmin
then
begin
cmin:=c[i,j];
SubRow[i,1]:=j
end;
cminprev:=cmin;
//
ищем первоначальный
минимальный
элемент в строке
for
j:= 0 to n-1 do
if
(j in set_j) and (j<>SubRow[i,1]) then
begin
cminprev:=c[i,j];
break
end;
//
ищем 2-ое наименьшее
значение в
строке
for
j:= 0 to n-1 do
if
(j in set_j) and (j<>SubRow[i,1]) then
if
c[i,j]<=cminprev then
cminprev:=c[i,j];
//
Вычисляем
разность между
двумя наименьшими
SubRow[i,0]:=cminprev-cmin;
end;
//
цикл по столбцам
for
j:= 0 to n-1 do
if
j in set_j then
begin
//
ищем первоначальный
минимальный
элемент в столбце
for
i:= 0 to m-1 do
if
i in set_i then
begin
cmin:=c[i,j];
break
end;
//
ищем 1-ое наименьшее
значение в
столбце
for
i:= 0 to m-1 do
if
i in set_i then
if
c[i,j]<=cmin then
begin
cmin:=c[i,j];
SubCol[j,1]:=i
end;
cminprev:=cmin;
//
ищем первоначальный
минимальный
элемент в столбце
for
i:= 0 to m-1 do
if
(i in set_i) and (i<>SubCol[j,1]) then
begin
cminprev:=c[i,j];
break
end;
//
ищем 2-ое наименьшее
значение в
столбце
for
i:= 0 to m-1 do
if
(i in set_i) and (i<>SubCol[j,1]) then
if
c[i,j]<=cminprev then
cminprev:=c[i,j];
//
Вычисляем
разность между
двумя наименьшими
SubCol[j,0]:=cminprev-cmin;
end;
Лист
Кп-км-п-44-2203-99
 //отыскиваем
максимальное
значение в
строке
//отыскиваем
максимальное
значение в
строке
 // сперва
находим начальный
наибольший
элемент
// сперва
находим начальный
наибольший
элемент
for
i:= 0 to m-1 do
if
i in set_i then
begin
SubRowMax:=Subrow[i,0];
break
end;
//
Теперь просматриваем
всю строку
for
i:= 0 to m-1 do
if
i in set_i then
if
SubRow[i,0]>=SubRowMax then
begin
SubRowMax:=SubRow[i,0];
imax:=i
end;
//отыскиваем
максимальное
значение в
строке
//
сперва находим
начальный
наибольший
элемент
for
j:= 0 to n-1 do
if
j in set_j then
begin
SubColMax:=SubCol[j,0];
break
end;
//
Теперь просматриваем
всю строку
for
j:= 0 to n-1 do
if
j in set_j then
if
SubCol[j,0]>=SubColMax then
begin
SubColMax:=SubCol[j,0];
jmax:=j
end;
//
сравниваем
максимальное
значение разности
по строкам и
столбцам
if
SubRowMax>SubColMax then
begin
d[imax,SubRow[imax,1]]:=min(a[imax],b[SubRow[imax,1]]);
a[imax]:=a[imax]-d[imax,SubRow[imax,1]];
b[SubRow[imax,1]]:=b[SubRow[imax,1]]-d[imax,SubRow[imax,1]];
if
a[imax]=0 then Exclude(set_i,imax);
if
b[SubRow[imax,1]]=0 then
Exclude(set_j,SubRow[imax,1]);
z:=z+d[imax,SubRow[imax,1]]*c[imax,SubRow[imax,1]];
if
set_i=[] then set_j:=[];
if
set_j=[] then set_i:=[]
end
else
begin
d[SubCol[jmax,1],jmax]:=min(a[SubCol[jmax,1]],b[jmax]);
a[SubCol[jmax,1]]:=a[SubCol[jmax,1]]-d[SubCol[jmax,1],jmax];
b[jmax]:=b[jmax]-d[SubCol[jmax,1],jmax];
if
a[SubCol[jmax,1]]=0 then Exclude(set_i,SubCol[jmax,1]);
if
b[jmax]=0 then
Exclude(set_j,SubCol[jmax,1]);
z:=z+d[SubCol[jmax,1],jmax]*c[SubCol[jmax,1],jmax];
if
set_i=[] then set_j:=[];
if
set_j=[] then set_i:=[]
end
Лист
Кп-км-п-44-2203-99
 until (set_i=[]) and (set_j =
[]);
until (set_i=[]) and (set_j =
[]);
 ShowSolve
ShowSolve
end;
procedure
TwoWall;
var
RowMin,ColMin:integer;
i,j,jj,j0:integer;
imin,jmin:integer;
set_i,set_j:set
of 0..255;
begin
set_i:=[];
for
i:=0 to m-1 do include(set_i,i);
set_j:=[];
for
j:=0 to n-1 do include(set_j,j);
repeat
//
начинаем цикл
по столбцам
for
j:= 0 to n-1 do
if
j in set_j then
begin
//
находим начальный
минимальный
элемент строки
for
i:= 0 to m-1 do
if
i in set_i then
begin
RowMin:=c[i,j];
break
end;
//
теперь просматриваем
весь столбец
for
i:=0 to m-1 do
if
i in set_i then
if
c[i,j]<=RowMin then
begin
RowMin:=c[i,j];
imin:=i
end;
//
минимальный
элемент в j-ом
столбце найден
//
проверяем ,
минимальный
ли он в своей
строке
j0:=j;
for
jj:= 0 to n-1 do
if
jj in set_j then
if
c[imin,jj]< RowMin then
j0:=jj;
//
проверяем по
индексу не тот
ли это элемент
if
j=j0 then
begin
d[imin,j]:=min(a[imin],b[j]);
a[imin]:=a[imin]-d[imin,j];
b[j]:=b[j]-d[imin,j];
if
a[imin]=0 then exclude(set_i,imin);
if
b[j]=0 then exclude(set_j,j);
z:=z+d[imin,j]*c[imin,j];
end
end
until
(set_i=[]) and (set_j=[]);
ShowSolve
e
Лист
Кп-км-п-44-2203-99
 nd; nd;

procedure
TfmTransTask.FormCreate(Sender: TObject);
var
i,j:integer;
begin
m:=3;
n:=3;
SetLength(a,m);
for
i:= 0 to m-1 do a[i]:=0;
SetLength(b,n);
for
j:= 0 to n-1 do b[j]:=0;
SetLength(c,m);
for
i:= 0 to m-1 do SetLength(c[i],n);
for
i:= 0 to m-1 do
for
j:= 0 to n-1 do
c[i,j]:=0;
SetLength(d,m);
for
i:= 0 to m-1 do SetLength(d[i],n);
for
i:= 0 to m-1 do
for
j:= 0 to n-1 do
d[i,j]:=0;
for
i:= 1 to m do
begin
stgProvider.Cells[i-1,0]:=IntToStr(i);
str(a[i-1],s);
stgProvider.Cells[i-1,1]:=s;
end;
for
j:= 1 to n do
begin
stgCustomer.Cells[j-1,0]:=IntToStr(j);
str(b[j-1],s);
stgCustomer.Cells[j-1,1]:=s;
end;
for
i:= 1 to m do
stgTarif.Cells[0,i]:=IntToStr(i);
for
j:= 1 to n do
stgTarif.Cells[j,0]:=IntToStr(j);
for
i:= 1 to m do
stgSolve.Cells[0,i]:=IntToStr(i);
for
j:= 1 to n do
stgSolve.Cells[j,0]:=IntToStr(j);
end;
procedure
TfmTransTask.edProviderCountChange(Sender: TObject);
var
i:integer;
b
Лист
Кп-км-п-44-2203-99
 egin egin
 stgProvider.ColCount:=StrToInt(edProviderCount.Text);
stgProvider.ColCount:=StrToInt(edProviderCount.Text);
stgTarif.RowCount:=stgProvider.ColCount+1;
stgSolve.RowCount:=stgTarif.RowCount;
m:=StrToInt(edProviderCount.Text);
SetLength(a,m);
SetLength(c,m);
for
i:= 0 to m-1 do SetLength(c[i],n);
SetLength(d,m);
for
i:= 0 to m-1 do SetLength(d[i],n);
stgProvider.Cells[stgProvider.ColCount-1,0]:=edProviderCount.Text;
stgTarif.Cells[0,stgProvider.ColCount]:=edProviderCount.Text;
stgSolve.Cells[0,stgProvider.Colcount]:=edProviderCount.Text;
end;
procedure
TfmTransTask.edCustomerCountChange(Sender: TObject);
var
i:integer;
begin
stgCustomer.ColCount:=StrToInt(edCustomerCount.Text);
stgTarif.ColCount:=stgCustomer.ColCount+1;
stgSolve.ColCount:=stgTarif.ColCount;
n:=StrToInt(edCustomerCount.Text);
SetLength(b,n);
SetLength(c,m);
for
i:= 0 to m-1 do SetLength(c[i],n);
SetLength(d,m);
for
i:= 0 to m-1 do SetLength(d[i],n);
stgCustomer.Cells[stgCustomer.ColCount-1,0]:=edCustomerCount.Text;
stgTarif.Cells[stgCustomer.ColCount,0]:=edCustomerCount.Text;
stgSolve.Cells[stgCustomer.Colcount,0]:=edCustomerCount.Text;
end;
procedure
TfmTransTask.btnLoadDataClick(Sender: TObject);
var
i,j:integer;
suma,sumb:integer;
begin
for
i:= 0 to m-1 do
if
stgProvider.Cells[i,1]<>'' then
a[i]:=StrToInt(stgProvider.Cells[i,1])
else
a[i]:=0;
suma:=0;
for
i:= 0 to m-1 do suma:=suma+a[i];
lblProvider.Caption:=IntToStr(suma);
for
j:= 0 to n-1 do
if
stgCustomer.Cells[j,1]<>'' then
b[j]:=StrToInt(stgCustomer.Cells[j,1])
else
b[j]:=0;
sumb:=0;
for
j:= 0 to n-1 do sumb:=sumb+b[j];
lblCustomer.Caption:=IntToStr(sumb);
if
sumb<>suma then
Лист
Кп-км-п-44-2203-99
 begin
begin
 lblTypeTask.Caption:='Открытая';
lblTypeTask.Caption:='Открытая';
If
sumb>suma then
lblMsg.Caption:='Создать
фиктивного
поставщика
с грузом '+IntToStr(sumb
-suma);
if
sumb
lblMsg.Caption:='Создать
фиктивного
потребителя
со спросом '+
IntToStr(suma-sumb)
end
else
begin
lblTypeTask.Caption:='Закрытая';
lblMsg.Caption:=''
end;
btnSolve.Enabled:=True
end;
procedure
TfmTransTask.btnLoadDataCClick(Sender: TObject);
var
i,j:integer;
begin
for
i:= 0 to m-1 do
for
j:= 0 to n-1 do
if
stgTarif.Cells[j+1,i+1]<>'' then
c[i,j]:=StrToInt(stgTarif.Cells[j+1,i+1]);
end;
procedure
TfmTransTask.btnSolveClick(Sender: TObject);
begin
if
rbMinelem.Checked then Minelem;
if
rbFogel.Checked then Fogel;
if
rbTwoWall.Checked then TwoWall
end;
procedure
TfmTransTask.btnPrintClick(Sender: TObject);
var
i,j:integer;
out:TextFile;
begin
AssignFile(out,'rezult.txt');
Rewrite(out);
writeln(out,'Исходные
данные транспортной
задачи');
writeln(out,'потребность
потребителей');
for
j:= 0 to n-1 do write(out,b[j]:8);
writeln(out);
writeln(out,'Матрица
тарифов перевозок');
for
i:= 0 to m-1 do
begin
write(out,a[i]:8);
for
j:= 0 to n-1 do write(out,c[i,j]:8);
writeln(out)
end;
writeln(out,'Матрица
перевозок
(решение)');
for
i:= 0 to m-1 do
begin
Лист
Кп-км-п-44-2203-99
 for j:= 0 to n-1 do
write(out,d[i,j]:8);
for j:= 0 to n-1 do
write(out,d[i,j]:8);

Лист
Кп-км-п-44-2203-99
writeln(out)
end;
CloseFile(out);
end;
End.
7.8 Инструкция
Аппаратные
и программные
требования
Для нормальной
работы программы
необходим
персональный
компьютер
совместимый
с IBM PC ,
с процессором
не ниже
486, тактовой
частотой 120 Мгц,
оперативной
памятью не
менее 8 МБ, занимаемое
место на диске
после инсталляции
5 МБ.
Операционная
система Windows
95,98,NT.
Инсталляция
и запуск программы.
В
Лист
Кп-км-п-44-2203-99

 ключите
компьютер,
после загрузки
Windows вставьте
дискету в дисковод
на которой
находиться
дистрибутив
программы.
После чего
запустите файл
setup.exe
для инсталляции
программы на
ваш компьютер.
После установки
программы
выберите в меню
пуск папку
Transtask и
запустите
программу.
После запуска
программы на
экране появиться
заставка "О
программе"
, выберите вкладку
исходные данные
и начинайте
работу. ключите
компьютер,
после загрузки
Windows вставьте
дискету в дисковод
на которой
находиться
дистрибутив
программы.
После чего
запустите файл
setup.exe
для инсталляции
программы на
ваш компьютер.
После установки
программы
выберите в меню
пуск папку
Transtask и
запустите
программу.
После запуска
программы на
экране появиться
заставка "О
программе"
, выберите вкладку
исходные данные
и начинайте
работу.
4 .3
Критерии
качества модели .3
Критерии
качества модели
К
основным критериям
качества любой
модели относятся
такие как:
критерий
адекватности;
чувствительности;
устойчивости
модели.
Критерий
адекватности
Под
адекватностью
модели понимается
ее способность
наиболее точно
отражать все
свойства и
характеристики
моделируемой
среды. В качестве
критериев
адекватности
можно выбрать
, например, величину
отличия (абсолютных
и относительных)
входных и выходных
характеристик
модели и реального
объекта, сравнительная
оценка реакции
модели и объекта
и т.д.
Критерий
чувствительности
Под
критерием
чувствительности
понимают степень
воздействия
изменения
параметров
модели на результаты
выдаваемые
моделью. Изменение
параметров
можно моделировать
меняя коэффициенты
в системе уравнений
, описывающих
модель, характер
изменения
входных данных
и т.д.
Критерий
устойчивости
Критерий
устойчивости
– это количественная
или качественная
оценка, которая
характеризует
исследуемую
модель как
устойчивую
или неустойчивую.
П
Лист
Кп-км-п-44-2203-99
 од
устойчивостью
системы или
модели понимают
способность
модели , находящейся
в состоянии
равновесия
, возвращаться
в исходное
состояние после
того как на нее
было оказано
входное воздействие
на ее входные
данные и основные
параметры. В
математической
формулировке
это звучит как
устойчивость
решения систему
уравнений
описывающих
модель при
изменений
аргументов.
Разработана
математическая
теория, позволяющая
на основе
коэффициентов
уравнении дать
оценку предполагаемому
решению уравнения
и оценит его
как устойчивое
или неустойчивое. од
устойчивостью
системы или
модели понимают
способность
модели , находящейся
в состоянии
равновесия
, возвращаться
в исходное
состояние после
того как на нее
было оказано
входное воздействие
на ее входные
данные и основные
параметры. В
математической
формулировке
это звучит как
устойчивость
решения систему
уравнений
описывающих
модель при
изменений
аргументов.
Разработана
математическая
теория, позволяющая
на основе
коэффициентов
уравнении дать
оценку предполагаемому
решению уравнения
и оценит его
как устойчивое
или неустойчивое.

Лист
Кп-км-п-44-2203-99

6 .
Тестирование
и отладка .
Тестирование
и отладка
6.1 Синтаксическая
отладка
Синтаксическая
отладка предназначена
для устранения
ошибок в языковых
конструкциях
на этапе написания
исходного
текста программы.
Большинство
интегрированных
пакетов разработки
программного
обеспечения
содержат встроенные
средства проверки
прямо в ходе
написания кода
программы.
Средства проверки
не только находят
синтаксические
ошибки, но также
делают подсказки
или дают рекомендации
для написания
данной конструкции.
Второй этап
, на котором
выявляются
синтаксические
ошибки – это
компиляция,
когда компилятор
строка за строкой
анализирует
исходный код
и выдает листинг
синтаксических
ошибок.
Семантическая
отладка осуществляется
для проверки
семантики
языковых конструкции
и является
одним из этапов
синтаксической
отладки.
Тестовые
отчеты и анализ
тестирования
При
сдаче программного
обеспечения
в эксплуатацию
необходима
провести его
тестовый прогон
в области допустимых
значении входных
параметров.
Для этого , в
основном проводят
ручной обсчет
одного или
нескольких
вариантов
решения задачи
и затем сверяют
воспроизводим
ость результатов
моделью. Адекватностью
модели служит
полная воспроизводим
ость тестовых
данных.
Лист
Кп-км-п-44-2203-99

6 .2
Семантическая
отладка .2
Семантическая
отладка
Семантическая
отладка - это
процесс нахождения
и исправления
ошибок связанных
с неправильным
указанием
логических
страниц данных.
Семантическая
отладка подразумевает
в себя проверку
поэтапного
хода выполнения
программы. Это
можно выявить
при тестирование
программы
правильно ли
мы задали тип
False или True
.
В Delpfi
при выполнении
операций в
логических
выражениях
поддерживается
две различные
модели:
При полной
схеме всегда
вычисляются
все операнды
и выполняются
все операции
выражения, даже
если его результат
будет известен
уже после первой
операции.
При использовании
короткой схемы
вычисление
операндов и
результатов
операций выполняется
строго с лева
на право и
прекращается,
как только
выполнение
дальнейших
действий перестанет
оказывать
влияние на
конечный результат
всего выражения.
6.4 Оптимизация
программы
В
ходе отладки
программного
пакета возникает
вопрос о таких
показателях
как скорость
(быстродействие)
работы программы,
объем занимаемого
места на диске,
необходимый
объем оперативной
памяти
Лист
Кп-км-п-44-2203-99

О писание
блок-схемы
программы
Transtask.pas писание
блок-схемы
программы
Transtask.pas
|
№ п/п
|
Содержание
|
|
1
|
Начало
|
|
2
|
Вызов
главной формы
|
|
3
|
Выбор
метода решения
|
|
4
|
Метод
минимального
элемента
|
|
5
|
Вызывается
процедура
metod
1
|
|
6
|
Метод
Фогеля
|
|
7
|
Вызывается
процедура
metod
2
|
|
8
|
Метод
двойного
предпочтения
|
|
9
|
Вызывается
процедура
metod
3
|
|
10
|
Ввод
размерности
таблицы перевозок
m,n
|
|
11
|
Отображение
пустой таблицы
перевозок
m*n
|
|
12
|
Ввод
таблицы данных:Вектор
А, Вектор В,
Матрица С
|
|
13
|
Проверяется
открытая задача
|
|
14
|
Да.
Введение
фиктивного
поставщика
или потребителя.
|
|
15
|
Нет.
Решение транспортной
задачи.
|
|
16
|
Отображение
результатов
решения
|
|
17
|
Конец
|
Описание
Блок-схемы меню
определение
опорного плана.
|
№ п.п
|
Содержание
|
|
1
|
Начало
|
|
2
|
Метод
минимального
элемента
|
|
3
|
Вызывается
программа
miniem
|
|
4
|
Метод
Фогеля
|
|
5
|
Вызывается
программа
Fogel
|
|
6
|
Метод
двойного
предпочтения
|
|
7
|
Вызывается
программа
Double
Pref
|
|
8
|
Конец
|
Лист
Кп-км-п-44-2203-99

О писание
блок-схемы
Определение
опорного плана
транспортной
задачи методом
минимального
элемента. писание
блок-схемы
Определение
опорного плана
транспортной
задачи методом
минимального
элемента.
|
№ п.п
|
Содержание
|
|
1
|
Начало
|
|
2
|
Выбор
минимального
тарифа
|
|
3
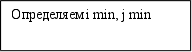
|
Определяем
i
min,
j min.
|
|
4
|
A
min = Min(a i min, b j min)
|
|
5
|
Корректируем
элементы исходного
массива
|
|
6
|
A
i min =0
|
|
7
|
Исключаем
строку i
min
|
|
8
|
B
j min = 0
|
|
9
|
Исключаем
столбец j
min
|
|
10
|
Заносим
в матрицу
перевозок
значение A
min
|
|
11
|
Проверяем
(a
i j and b i j) = 0
|
|
12
|
Вычисление
целевой функции
Z
|
|
13
|
Конец
|
Лист
Кп-км-п-44-2203-99

Рецензия
на курсовой
проект
Студента
группы П-44
Голубовского
Дениса Николаевича
Тема:
Нахождение
опорного плана
транспортной
задачи
Председатель
руководитель
курсового
проекта Тлисова
Л.Б
5
Лист
Кп-км-п-44-2203-99
.1 Тестирование
программ
Тестирование
алгоритмов
и программ --
одна из наиболее
сложных и
ответственных
задач в процессе
их отладки.
Времени для
тестирования
мало, но и спешка
в работе недопустима,
слишком дорого
обходятся
неудачные
попытки предъявить
решение задачи.
Проверка корректности
алгоритмов,
равно как и
составление
авторами задачи
достаточно
полного набора
корректных
тестов -- наборов
данных для
задачи и ответов
к ним -- далеко
не всегда
представляют
собой простую
проблему.
В
задачах на
этапе тестирования
программ есть
много общего
-- и те и другие
должны обеспечить
корректность
алгоритмов.
Но есть и различия.
Автор задачи
не ограничен
во времени, но
должен предусмотреть
все возможные
огрехи участника.
Специфика
положения
тестирующего,
связана с коварством
составителя
тестов, от которого
можно ожидать,
например,
непредвиденной
глубины рекурсии,
разрядности,
точности вычислений
или размерности
наборов данных.
Поэтому будет
неправильно,
успешно решив
задачу для
нарисованного
на листочке
бумаги примера.
Будьте
внимательны!
Всегда есть
опасность
получить по
существу правильный,
но не тот ответ.
Кроме того,
способ описания
ответа может
послужить
намеком на
используемый
автором алгоритм
решения задачи.
Проверка
алгоритма на
данных максимальной
установленной
размерности:
по количеству
перечисленных
в условиях
задачи объектов,
по количеству
связей между
ними, по разрядности
и точности
машинного
представления
числовых параметров
и пр. Такая проверка
нужна для выявления
и отсева неэффективных
- медленно работающих
или нерационально
использующих
память программ.
Известны случаи,
когда, в принципе,
правильно
работающий
алгоритм приводил
к ошибочному
ответу из-за
ошибок переполнения
-- в условиях
задачи оговаривается
диапазон или
разрядность
исходных данных,
но не разрядность
промежуточных
результатов
или ответа.
Типичным примером
грубой ошибки
такого рода
может служить
нахождение
опорного плана
транспортной
задачи. Проверка
работоспособности
алгоритма в
вырожденных
случаях: срабатывание
пустого или
состоящего
из единственного
элемента цепного
списка, работа
программы с
графом, не содержащим
дуг и т.п. В некоторых
случаях, например,
при декомпозиции
задачи, когда
решение задачи
сводится к
решению задачи
меньшей размерности
переход от
начального
i=0 уменьшением
на единицу
может привести
к непредусмотренному
эффекту выхода
за границы
зарезервированной
памяти. Результат
работы на нижней
границе размерности
легко просчитывается,
иногда он будет
получен как
и в общем случае,
иногда удобней
вручную просчитать
его и предусмотреть
особую ветку
программы, но
никогда о нем
не следует
забывать.
Следует
иметь ввиду,
что построение
авторами заданий
тестов, особенно,
значительной
размерности
представляет
собой непростую
задачу. Возможно
несколько
подходов к
построению
тестов.
С  оставление
тестов вручную.
Это возможно,
когда решение
задачи не
представляет
собой вычислительной
сложности (вся
сложность --
логическая).
Задача "Путь
на кубе" раздела
"Геометрия"
-- пример именно
такой задачи.
Во всех остальных
случаях подобный
путь тупиковый.
У участников
олимпиады
иногда выбора
нет, но не забывайте
проверить
случаи вырожденной
и максимальной
размерности
хотя бы в тривиальном
варианте (матрица
из нулей и единиц
не содержит
нулей или единиц,
в ней единственная
строка или
единственный
столбец, в графе
нет дуг, или
граф полный). оставление
тестов вручную.
Это возможно,
когда решение
задачи не
представляет
собой вычислительной
сложности (вся
сложность --
логическая).
Задача "Путь
на кубе" раздела
"Геометрия"
-- пример именно
такой задачи.
Во всех остальных
случаях подобный
путь тупиковый.
У участников
олимпиады
иногда выбора
нет, но не забывайте
проверить
случаи вырожденной
и максимальной
размерности
хотя бы в тривиальном
варианте (матрица
из нулей и единиц
не содержит
нулей или единиц,
в ней единственная
строка или
единственный
столбец, в графе
нет дуг, или
граф полный).
П рименение
случайных
чисел. Такие
генераторы
тестов удобно
конструировать
для числовых
последовательностей,
матриц или
графов. Достаточно
задать один
-- два параметра
настройки
датчика случайных
чисел и в вашем
распоряжении
замечательные
тесты. При
построении
матрицы из 0-1
таким параметром
будет доля
единиц среди
элементов
матрицы, координаты
очередной
единицы определяются
в результате
испытания с
равномерным
распределением
среди элементов
этой матрицы,
при построении
графа -- среднее
число дуг, выходящих
из вершины. рименение
случайных
чисел. Такие
генераторы
тестов удобно
конструировать
для числовых
последовательностей,
матриц или
графов. Достаточно
задать один
-- два параметра
настройки
датчика случайных
чисел и в вашем
распоряжении
замечательные
тесты. При
построении
матрицы из 0-1
таким параметром
будет доля
единиц среди
элементов
матрицы, координаты
очередной
единицы определяются
в результате
испытания с
равномерным
распределением
среди элементов
этой матрицы,
при построении
графа -- среднее
число дуг, выходящих
из вершины.
Лист
Кп-км-п-44-2203-99

Колледж
информационных
технологий
и экономики
КБГУ
К УРСОВОЙ
ПРОЕКТ УРСОВОЙ
ПРОЕКТ
По дисциплине
Компьютерное
моделирование
Наименование
учебного предмета
На тему:
Нахождение
опорного плана
транспортной
задачи
Студента
Голубовского
Дениса Николаевича
Группа П-44
Специальность
2203 “Программное
обеспечение
ВТ и АС”
Председатель
руководитель
курсового
проектирования
Тлисова
Л.Б
Оценка
_________ Подпись_________________
Дата___________
1 .2
Описание целей
моделирования
их приоритеты. .2
Описание целей
моделирования
их приоритеты.
Цель - Это
образ несуществующего,
но желаемого
с точки зрения
рассматриваемой
проблемы состояния
среды.
Система
- Средство достижения
цели, т,е всё
то, что нужно
для достижения
цели.
Модель служит
для исследования
.
Требования
к модели:
наглядность
обозримость
доступность
для исследования
- простота
исследования
Моделирование
является
экспериментальной
и прикладной
методологией
имеющая целью:
описание
поведения
системы
по строительные
теории и гипотезы
которые могут
объяснить
наблюдаемое
поведение.
Использовать
эти теории для
предсказания
будущего поведения
системы, т.е
тех воздействий
которые могут
быть вызваны
изменением
в системе или
изменение
способов её
функционирования.
Данные с
которыми приходиться
иметь дело ,
часто представляются
в виде таблицы.
Это может быть
связано либо
с тем, что объём
таблиц ограничен
и в них можно
привести лишь
некоторые
данные.
Цель интерполяции
состоит в отыскании
значения функции
в некоторой
промежуточной
точке по отношению
к табличным
данным.
лист
Кп-км-п-44-2203-99

2
лист
Кп-км-п-44-2203-99
.2 Анализ технического
обеспечения
среды моделирования.
ЭВМ широко
применяется
для решения
научных, технических
и экономических
задач. Они способны
производить
вычисления
очень быстро,
выводить очень
точные результаты,
заполнять
большие массивы
информации
и производить
длинные и сложные
последовательные
вычисления
без вмешательства
человека.
Современный
компьютер имеет
следующие
основные компоненты:
центральный
процессор ,
который выполняет
арифметические
и логические
операции и
организует
процесс выполнения
программ.
Память служащая
для хранения
информации
В  нешние
устройства
для управления
компьютеров
и ввода - вывода
информации. нешние
устройства
для управления
компьютеров
и ввода - вывода
информации.
|