Сахалинский Государственный Университет
Институт Естественных Наук
План урока алгебры
Тема: Значения тригонометрических функций. Решение простейших тригонометрических уравнений.
Чуванова Г. М.
Меркулов М. Ю.
411
12.05.03
|
|
Руководитель:
Выполнил:
Группа:
Дата:
Оценка:
Южно-Сахалинск
2003г.
Тема: Значения тригонометрических функций. Решение простейших тригонометрических уравнений.
Тип: урок по изучению нового материала
Цель урока: вычисление значений тригонометрических функций, изучение метода решения простейших тригонометрических уравнений, повторение изученного ранее
Структура урока
Организационный момент
Домашнее задание 19(3,6), 20(2,4)
Постановка цели
Актуализация опорных знаний
Свойства тригонометрических функций
Формулы приведения
Новый материал
Значения тригонометрических функций
Решение простейших тригонометрических уравнений
Закрепление
Решение задач
Цель урока: сегодня мы будем вычислять значения тригонометрических функций и решать простейшие тригонометрические уравнения
АОЗ
Вызов двух учеников к доске. Задание:
Пилюков Дмитрий:
SIN (p + t) = -SIN t
COS (p + t) = -COS t
SIN (p/2 – t) = COS t
SIN (p/2 + t) = COS t
COS (p/2 – t) = SIN t
COS (3p/2 + t) = SIN t
SIN (-t) = SIN t
|
Ким Олеся
SIN (p - t) = SIN t
COS (p - t) = -COS t
SIN (3p/2 – t) = COS t
SIN (3p/2 + t) = -COS t
COS (p/2 + t)= -SIN t
COS (3p/2 – t) = SIN t
COS (-t) = COS t
|
Устный опрос:
В: Какие из тригонометрических функций являются четными, какие нечетными:
О: Косинус – четная, синус, тангенс, котангенс – нечетные
В: Когда в формулах приведения функция меняется на кофункцию?
О: когда p/2 или 3p/2 добавляются к аргументу
В: Когда функция не меняется на кофункцию в формулах приведения?
О: Когда добавляется ±p
В: В каких четвертях тангенс принимает положительные значеня?
О: В I и III
В: В каких четвертях котангенс принимает положительные значеня?
О: В I и III
В: Какое число является наименьшим положительным периодом синуса и косинуса?
О: 2p
В: Назовите основное тригонометрическое тождество.
О: SIN2
x + COS2
x = 1
В: Чему равно произведение тангенса на котангенс?
О: Единице
Новый материал:
Пусть SIN t = -3/5 и t лежит в III четверти
SIN2
t + COS2
t = 1
COS2
t = 1 – SIN2
t
 т. .к. коинус в III четверти имеет знак -, то
COS t = -Ö1 - SIN t
  COS t = -Ö1 – 9/25 = -Ö16/25 = -4/5
TG t = SIN t / COS t =3/4
CTG t = 1 / TG t = 4/3
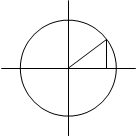
Катет, противолежащий углу в 30 градусов или p/6 равен половине гипотенузы, а т. к. у нас единичная окружность и катет равен синусу угла, то SIN 30° = 1/2.
  COS 30° = Ö1 - SIN 30°
COS 30° = Ö1 – 1/4
 COS 30° = Ö3/2
 SIN 60° = COS (90° - 30°) = COS 30° = Ö3/2
COS 60° = SIN (90° - 30°) = SIN 30° = 1/2
Если угол прямоугольного треугольника равен 45°, то катеты равны:
SIN2
45° + COS2
45° = 1
 2SIN2
45° = 1
SIN 45° = Ö2/2
 COS 45° = Ö2/2
Полезно записать значения этих углов в таблицу:
| T |
SIN t |
COS t |
TG t |
CTG t |
| 0 |
0 |
1 |
0 |
- |
  30°, p/6 |
½ |
Ö3/2 |
Ö3/3 |
Ö3 |
| 45°, p/4 |
Ö2/2 |
Ö2/2 |
1 |
1 |
   60°, p/3 |
Ö3/2 |
½ |
Ö3 |
Ö3/3 |
| 90°, p/2 |
1 |
0 |
- |
0 |
Решение простейших тригонометрических уравнений
Возьмем уравнение SIN t = 0. Вращающаяся точка Pt
имеет ординату 0в точках 0, p, 2p
Т. к. период синуса равен 2p, то вращающаяся точка будет иметь ординату 0 также и в точках -p, -2p, 3p, 4p, т. е. в точках pk, kÎZ
Таким образом, решение уравнения SIN t = 0 можно записать в виде t = pk, kÎZ
Запишем еще решения простейших уравнений:
SIN t = 1, t = p/2 + 2pk, kÎZ
SIN t = -1, t = 3p/2 + 2pk, kÎZ
COS t = 0, t = p/2 + pk, kÎZ
COS t = 1, t = 2pk, kÎZ
COS t = -1, t = p + 2pk, kÎZ
Решение задач
№18
1) SIN 135° = SIN (90° + 45°) = COS 45° = Ö2/2
2) COS 135° = COS (90° + 45°) = -SIN 45° = Ö2/2
3) COS 120° = COS (90° + 30°) = -SIN 30° = -1/2
4) TG 150° = TG (90° + 60°) = -TG 60° = -Ö3
9) TG 3/4p = TG (p/2 + p/4) = -CTG p/4 = -1
10) CTG 4/3p = CTG (p + p/3) = CTG p/3 = -Ö3
16) SIN2
402° + SIN2
48° + TG2
225° = SIN2
(360° + 42°) + SIN2
(90° - 42°) + TG2
(180° + 45°) = SIN2
42° + COS2
42° + TG2
45° = 1 + 1 = 2
№20
1) SIN t = 12/13 ; p/2 < t < p
  COS t = -Ö1 – SIN2
= -Ö25/169 = -5/13
TG t = SIN t / COS t = -12/5
CTG t = 1 / TG t = -5/12
   3) TG t = 5/2 ; p < t < 3p/2
COS t = -Ö1 / (1 + TG2
t) = -Ö1 / (1 + 25/4) = -2/Ö29
  SIN t = TG t COS t = 5/2 (-2/Ö29) = -5/Ö29
CTG t = 1 / TG t =2/5
Самостоятельная работа
I вариант
Найти знак:
16.5) sin (13/5p)
16.7) cos(-4/3p)
Вычислить:
18.12) cos (3/2p)
18.13) tg (5/4p)
Найти COS t и SIN t, если TG t = -5/12, COS t < 0
Упростить:
SIN2
t / (COS t – 1) =
1 – COS2
t + TG2
t COS2
t
Существует ли такое t, что
1) SIN t = 0,5, COS t = 0,5
2) TG t = 5, CTG t =1/5
II вариант
Найти знак:
16.8) cos (5/4p)
16.9) ctg(-3/4p)
Вычислить:
18.12) ctg (7/6p)
18.13) sin (11/6p)
Найти COS t и SIN t, если TG t = -5/12, COS t < 0
Упростить:
COS2
t / (SIN t – 1)
1 – SIN2
t + CTG2
t SIN2
t
Существует ли такое t, что
1) TG t = -2/9, CTG t = -9/2
2) SIN t = 0,6, COS t =0,8
|
