Маткаримов П.Ж.
Рассматриваются методика и алгоритм решения задачи гидроупругости для грунтовых плотин, взаимодействующих с водной средой.
Рассматриваемая проблема представляется актуальной при проектировании гидросооружений, так как включает в себя совершенствование модели сооружения, модели взаимодействия и алгоритмизацию поиска собственных значений системы “плотина-водохранилище”. На сегодняшний день методы исследования задач гидроупругости, т.е. совместных колебаний конструкции и жидкости весьма разнообразны. Применение тех или иных методов решения рассматриваемых задач диктуется многими обстоятельствами: характером задачи, целью исследования, принятой схематизацией явления, требуемой точностью, возможностью вычислительных средств и др.
Изложим постановку и методику решения задач гидроупругости, связанных с определением динамических характеристик упругих грунтовых плотин, взаимодействующих с полубесконечным слоем жидкости. Динамические характеристики (собственные частоты, формы колебаний) являются основными регламентирующими характеристиками (паспортом) сооружений, позволяющими заранее судить о его динамических свойствах и его поведении при различных воздействиях
Опираясь на современные достижения науки в этой области и основываясь на имеющихся материалах по влиянию жидкости на напряженно-деформированное состояние гидротехнических сооружений при динамических и сейсмических воздействиях, при формулировании задачи жидкость считаем идеальной и несжимаемой, волнообразование на свободной поверхности не учитываем. Тогда потенциал скорости движения жидкости 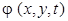 должен удовлетворять уравнению Лапласа должен удовлетворять уравнению Лапласа
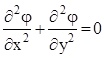 (1) (1)
и граничным условиям [1, 2]:
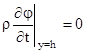 ; ; 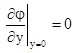 и и 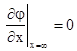 , , 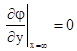 ; (2) ; (2)
на напорной грани 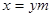 (где (где 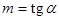 ), скорости частиц жидкости и точек грани плотины по направленнию нормали n одинаковы ), скорости частиц жидкости и точек грани плотины по направленнию нормали n одинаковы
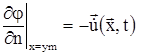 (3) (3)
Тогда выражение для потенциала скоростей, удовлетворяющего уравнению (1) и условиями (2)-(3), будет иметь вид [2]
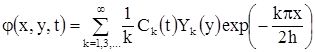 , ,
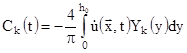 , , 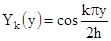
Далее рассматривается динамическая задача гидроупругости для грунтовых плотин. При этом для постановки задачи используется вариационное уравнение Лагранжа, основанное на принципе Даламбера:
 (4) (4)
и кинематическое граничное условие в основании:
Реклама

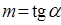 , , 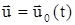 . (5) . (5)
Здесь 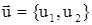 , , 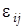 , , 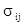 - соответственно, компоненты вектора перемещений, тензоров деформаций и напряжений; - соответственно, компоненты вектора перемещений, тензоров деформаций и напряжений; 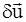 , , 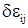 - изохронные вариации перемещений и деформаций; - изохронные вариации перемещений и деформаций; 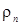 -плотность материала элементов рассматриваемой системы; -плотность материала элементов рассматриваемой системы; 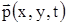 - гидродинамическое давление воды. - гидродинамическое давление воды.
Физические свойства тела описываются соотношениями между напряжениями и деформациями вида
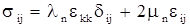 (6) (6)
Величины 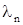 и и 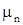 являются константами Ламе (индекс n относится к телу, с соответствующими механическими характеристиками). являются константами Ламе (индекс n относится к телу, с соответствующими механическими характеристиками).
В соотношении Коши учитываются только линейные члены
 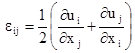 , i, j=1,2,3 (7) , i, j=1,2,3 (7)
Все задачи, поставленные в данной работе, решаются на базе метода конечных элементов (МКЭ). В частном случае, когда рассматриваются гармонические колебания полное смещение 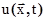 и потенциал скорости и потенциал скорости 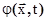 можно представить в виде можно представить в виде
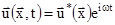 , , 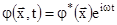 , (8) , (8)
где 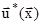 - упругие перемещения стенки плотины, зависящие только от координаты - упругие перемещения стенки плотины, зависящие только от координаты 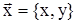 . .
Собственные колебания грунтовой плотины с учетом водной среды водохранилища представляют собой упорядочное движение грунтовой плотины, протекающее при отсутствии внешних воздействий. Решение проблемы заключается в следующем: ищется нетривиальное решение уравнения (4) при однородных кинематических условиях в виде (5).
Постановка (8) в (4) сводит данную задачу к действительной вариационной задаче о собственных значениях в виде
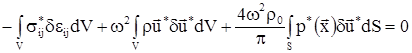 (9) (9)
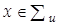 , , 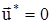
где 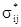 - амплитуда напряжений, - амплитуда напряжений, 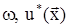 - искомая собственная частота и форма колебаний плотины с учетом водной среды, - искомая собственная частота и форма колебаний плотины с учетом водной среды, 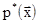 - гидродинамическое давление воды на стенку плотины, которое имеет вид - гидродинамическое давление воды на стенку плотины, которое имеет вид
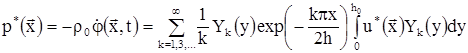 (10) (10)
При этом для решения вариационной задачи (9) используется закон Гука, геометрические соотношения Коши (7) и стандартная процедура МКЭ с использованием треугольного конечного элемента с линейной аппроксимацией поля перемещений внутри элемента.
При этом для i-го узла n-го конечного элемента первые вариации работ упругих, инерционных сил и гидродинамического давления относительно ui
будут иметь вид
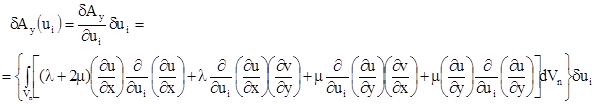 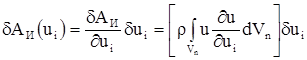 , (11) , (11)
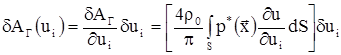 , ,
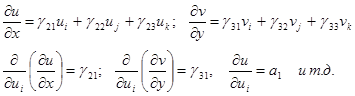
Здесь l, m - константы Ламе, r, r0
- плотность материала сооружений и воды.
После интегрирования этих выражений получим строки матриц жесткости, массы и присоединённой массы воды, соответствующие перемещениям ui
для n-го элемента. Если эти операции повторить для узлов j и k, а также для перемещения v, то мы получим матрицы жесткости и массы порядка 6´6 для n-го конечного элемента и соответствующие матрицы масс от воды к узлам конечного элемента (если эти узлы соприкасаются с водой). Таким образом, сформировав для каждого конечного элемента свою матрицу [K], [M], [Mв
] и объединив их, получим алгебраическую задачу на собственные значения для рассматриваемого сооружения с учетом взаимодействия с водой:
Реклама

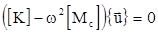 , (12) , (12)
где [K]-матрица жесткости плотины, [Mc
]=[M]+[Mв
] - суммарная матрица массы плотины и массы воды, w и {u} - искомые собственная частота и собственный вектор плотины, взаимодействующей с водой.
Решая уравнение (12) методом Мюллера и квадратного корня определим собственную частоту и форму колебания гидроупругой системы “грунтовая плотина с водой”. Такая постановка и методика решения задачи о собственных колебанях гидроупругих систем позволяют получить, в отличие от известных работ, более реальную картину динамики системы.
С помощью изложенного выше алгоритма исследованы собственные колебания грунтовых плотин, взаимодействующих с водной соедой.
Анализ полученных результатов позволяет сделать вывод о том, что учет взаимодействия воды с плотиной приводит к уменьшению частот собственных колебаний и для первых восьми частот составляет от 2 до 10% в зависимости от вида плотины. Эти отклонения зависят от многих факторов: от высоты плотины, характера форм колебаний сооружения, а также от значения коэффициента откоса, контактирующего с водой. При этом самым значимым фактором является крутизна верхового откоса, определяемая коэффициентом откоса - с увеличением коэффициента откоса соответственно уменьшается влияние воды на динамические характеристики плотины. Для вертикальной стенки значение гидродинамического давления воды является определяющим.
Список литературы
1. Кульмач П.П. Гидродинамика гидротехнических сооружений (Основные плоские задачи). -М.: Изд-во АН СССР. –1963. 190 с.
2. Шульман С.Г. Расчеты сейсмостойкости гидросооружений с учетом влияния водной среды. М.: Энергия, 1976. 336 с.
|