Общая
постановка
задачи управляемости.
Для
задачи ОУ характерно
наличие динамического
объекта. Динамический
объект- объект,
состояние
которого меняется
со временем.
Состояние
любого динамического
объекта в момент
времени
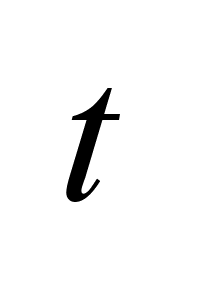 характеризуется
параметрами характеризуется
параметрами
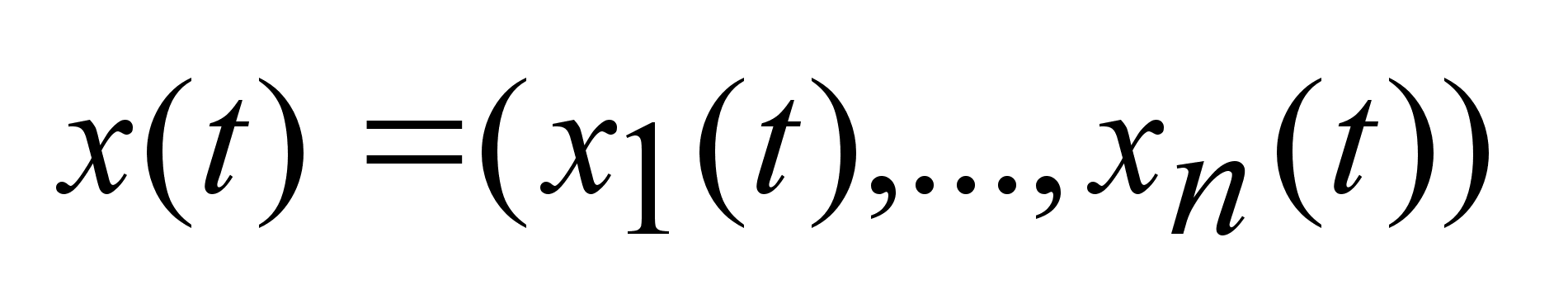 .
Такие параметры
наз. Фазовые
координаты,
а сам вектор-
фазовый вектор. .
Такие параметры
наз. Фазовые
координаты,
а сам вектор-
фазовый вектор.
Предполагается,
что движением
объекта можно
управлять.
Набор параметров
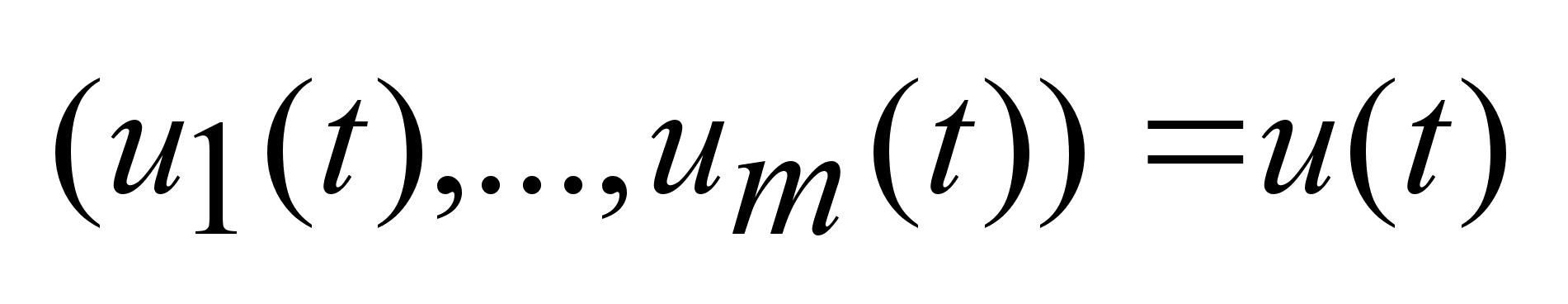 -
параметры
управления,
u(t)-
вектор управления.
Положение
объекта
зависит только
от того, какое
управление
было до момента
времени -
параметры
управления,
u(t)-
вектор управления.
Положение
объекта
зависит только
от того, какое
управление
было до момента
времени
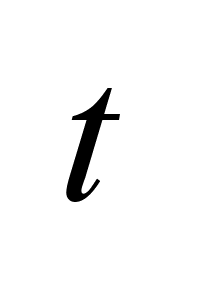 ,
и не зависит
от того, какое
управление
будет в будущем.
В зависимости
от описания
дин. Объекта
рассматриваются
различные
задачи. ,
и не зависит
от того, какое
управление
будет в будущем.
В зависимости
от описания
дин. Объекта
рассматриваются
различные
задачи.
Состояние
динамического
объекта описывается
диф. уравнением
1)
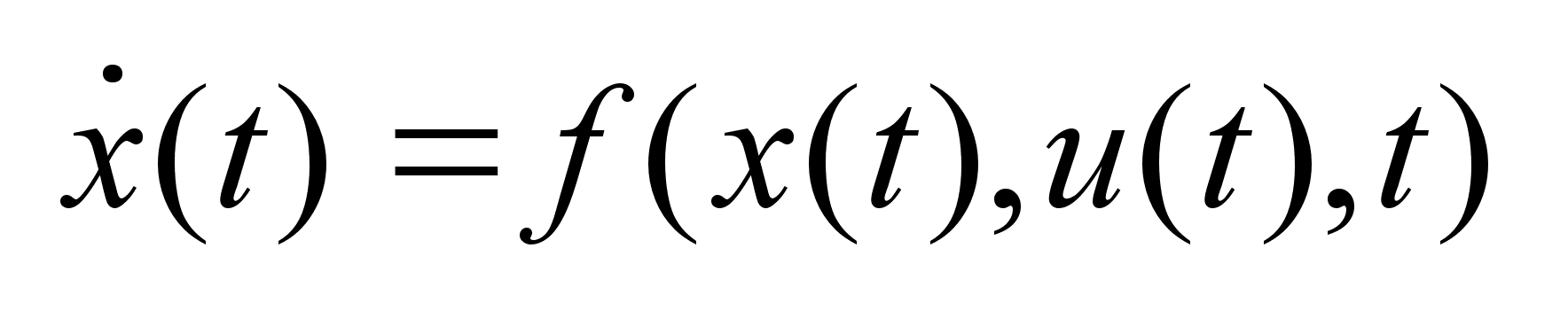 -
эта система
решается приближенным
методом. -
эта система
решается приближенным
методом.
2)
x(t)
должны принадлежать
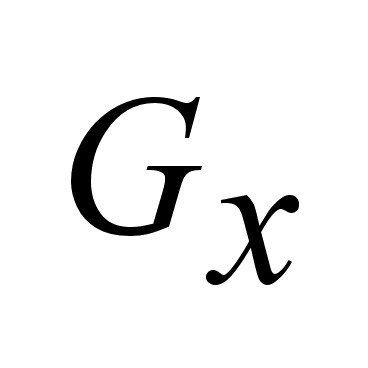 , ,
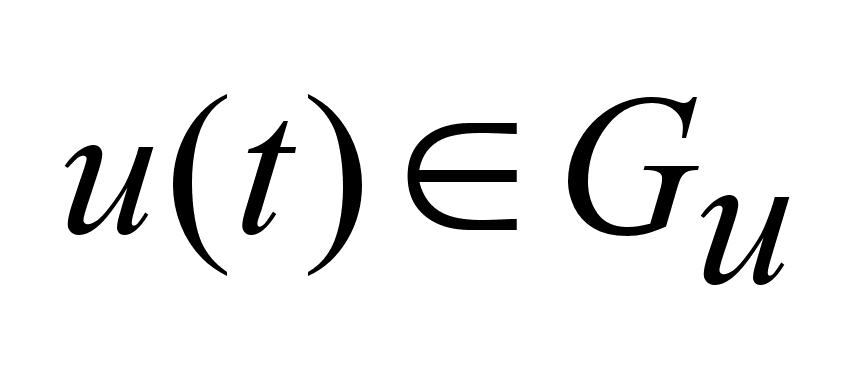 .
Класс допустимых
управлений
x(t), .
Класс допустимых
управлений
x(t),
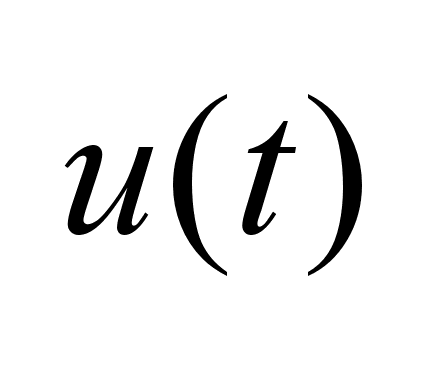 не
можат быть
произвольным. не
можат быть
произвольным.
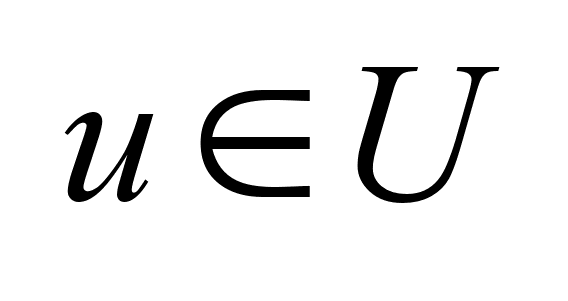 ,
как правило
мн-во замкнуто
и ограничено,
а это не позволяет
применять класс
вариационого
исчесления,
кроме этого
на ,
как правило
мн-во замкнуто
и ограничено,
а это не позволяет
применять класс
вариационого
исчесления,
кроме этого
на
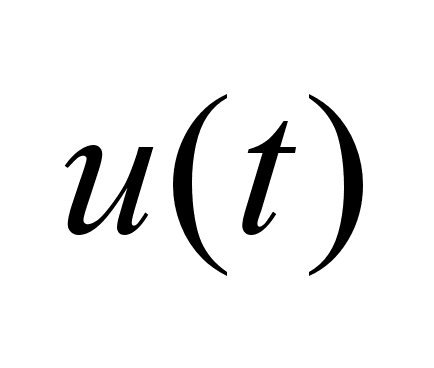 могут
быть наложены
ограничения
по времени. могут
быть наложены
ограничения
по времени.
3)Начальное
и конечное
состояние
объекта.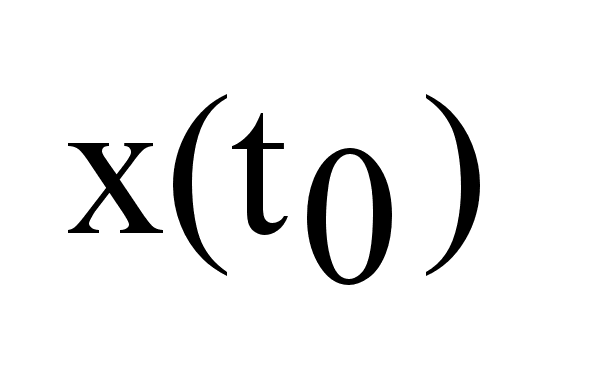 на
интервале на
интервале
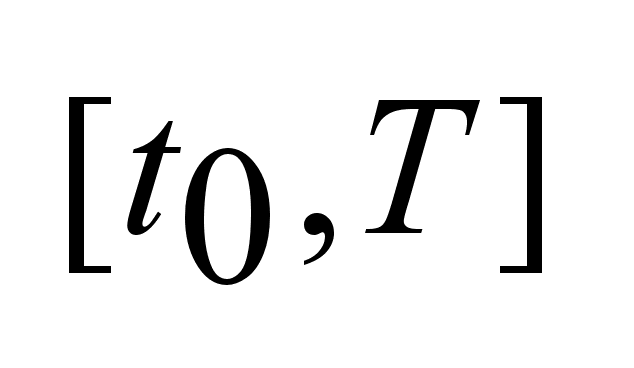 , ,
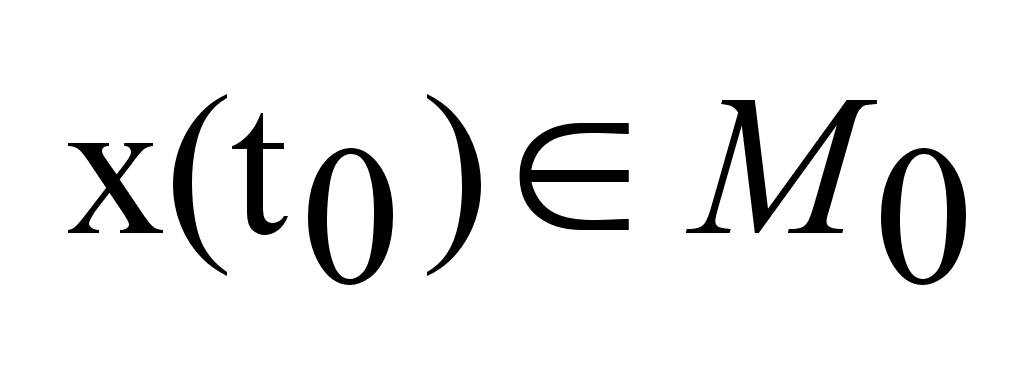 , ,
 .Задача
управления
заключается
в том, чтобы
динамический
объект, описываемый
системой (1),
удовлетворяющий
условиям (2),
перенести за
промежуток
времени .Задача
управления
заключается
в том, чтобы
динамический
объект, описываемый
системой (1),
удовлетворяющий
условиям (2),
перенести за
промежуток
времени
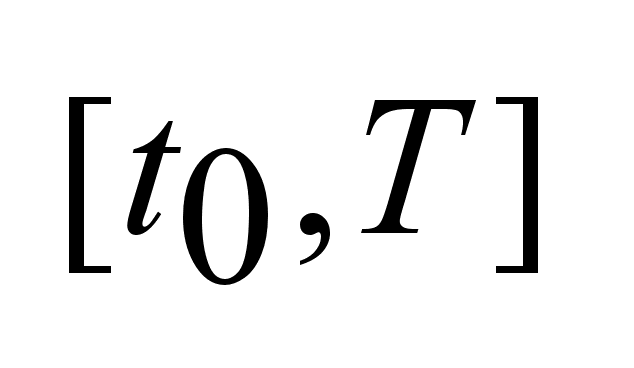 ,
из состояния ,
из состояния
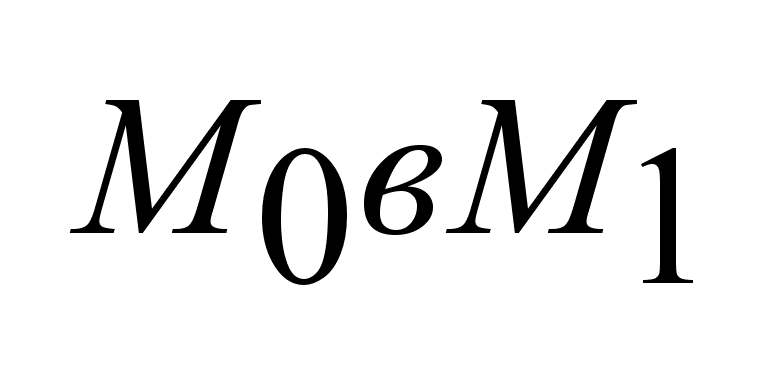 .Это
может быть
достигнуто
разными способами. .Это
может быть
достигнуто
разными способами.
4)
Критерий управления.
Это некоторый
функционал
вида
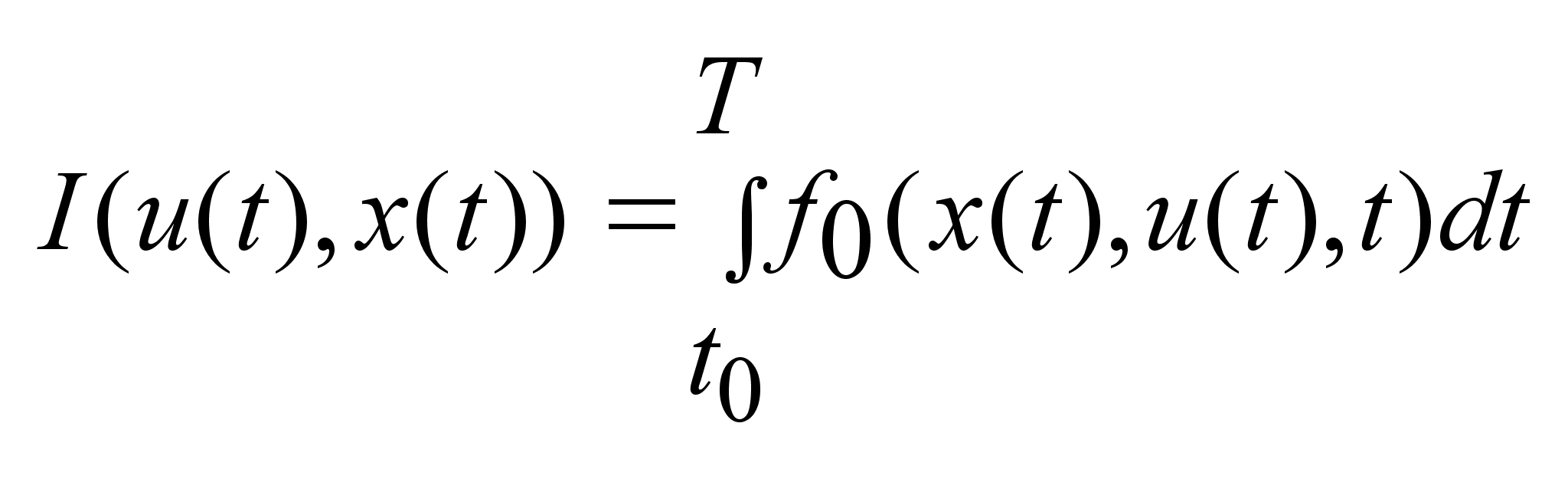 .
Находим такие .
Находим такие
 ,
что ,
что
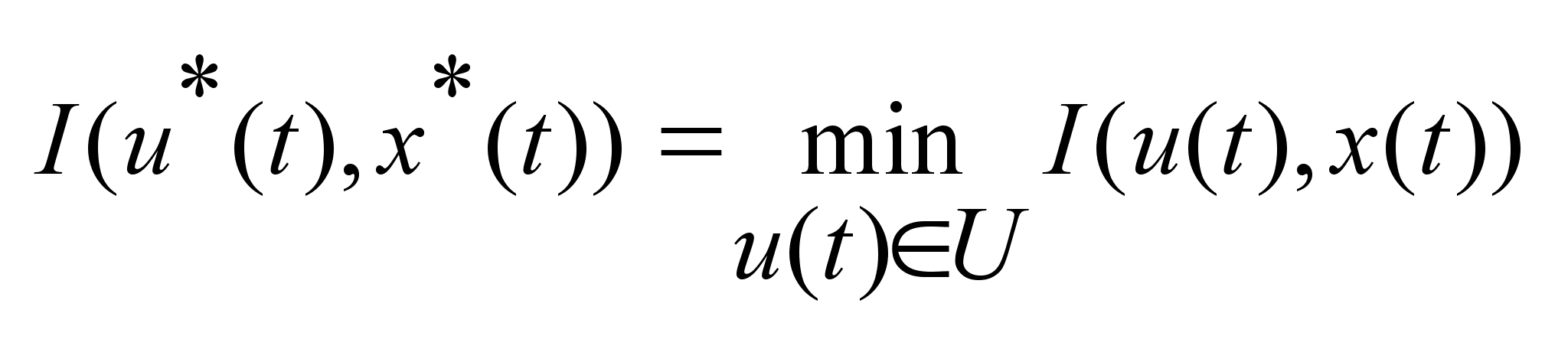
2.
Основные вопросы
в теории ОУ.
1)
Управляемость.
Можно ли осуществить
перевод динамического
объекта из
состояния
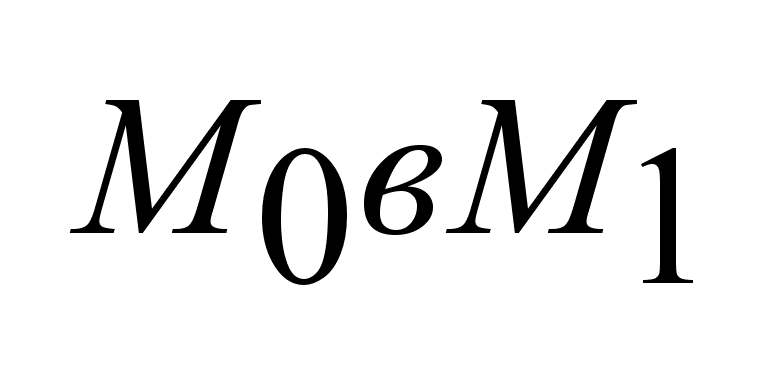 ,
за промежуток
времени ,
за промежуток
времени
 . .
Существует
ли ОУ.
3)
Необходимые
условия оптимальности-
принцип максимума
Понтрягина.
4)
Достаточные
условия ОУ.
5)
Единственность
ОУ.
3.
Постановка
линейной задачи.
Линейная
задача имеет
вид: Рассматриваем
динамический
объект, поведение
которого описывается
системой (1)
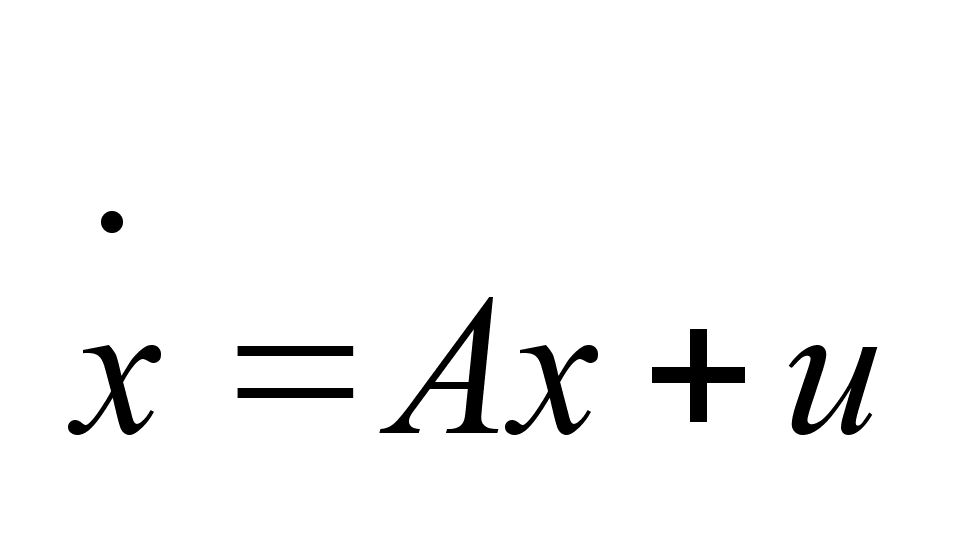 ,
x-
n-мерный
вектор, , A-матрица
nxn,
u
имеет ту же
размерность,
что
и ,
x-
n-мерный
вектор, , A-матрица
nxn,
u
имеет ту же
размерность,
что
и
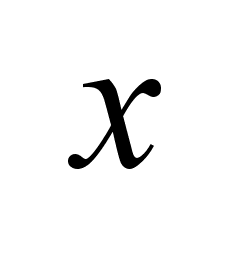 , ,
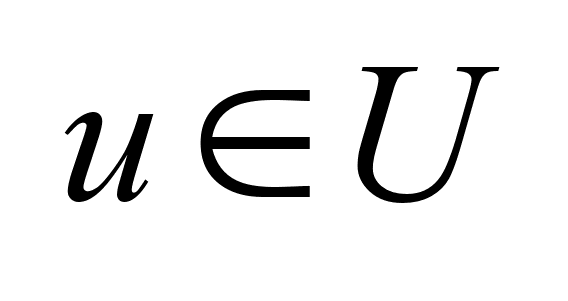 , ,
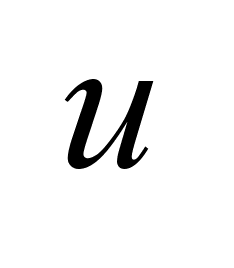 -замкнуто
и ограничено.
Допустимое
управление
u(t)
на отр.I
осуществляет
переход из
начального
мн-ва -замкнуто
и ограничено.
Допустимое
управление
u(t)
на отр.I
осуществляет
переход из
начального
мн-ва
 в конечное
множество
в конечное
множество
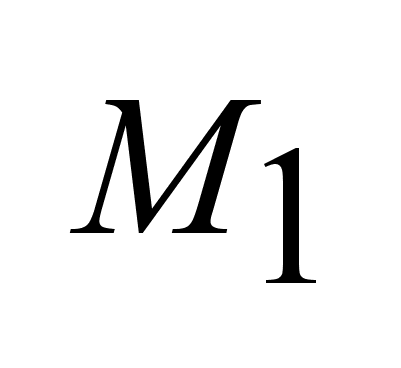 ,
если существует
решение уравнения
(1), удовлетворяющее
граничным
условиям ,
если существует
решение уравнения
(1), удовлетворяющее
граничным
условиям
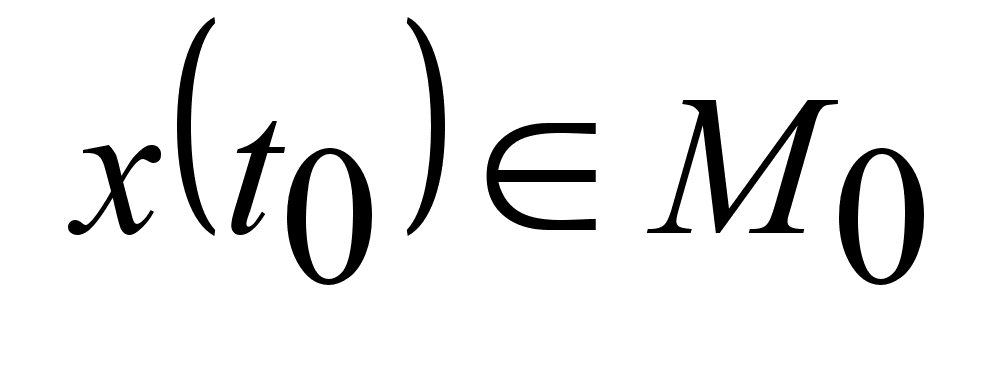 и и
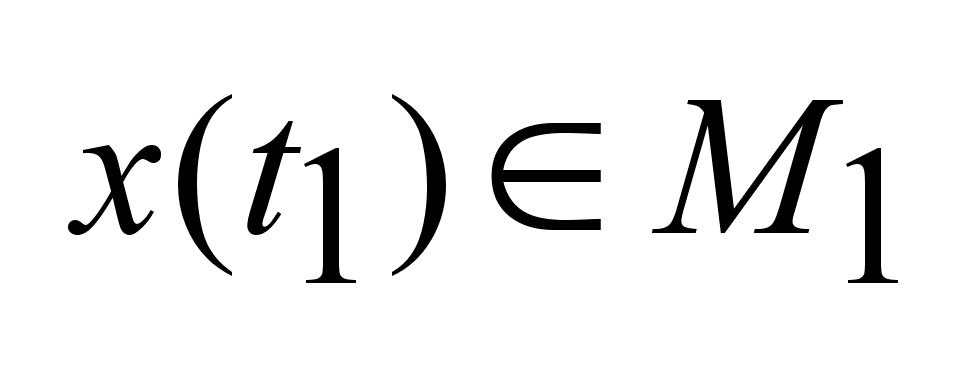 .
Цель управления
-
перевод динамический
объекта из .
Цель управления
-
перевод динамический
объекта из
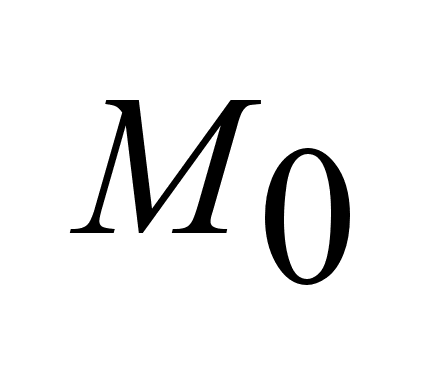 в в
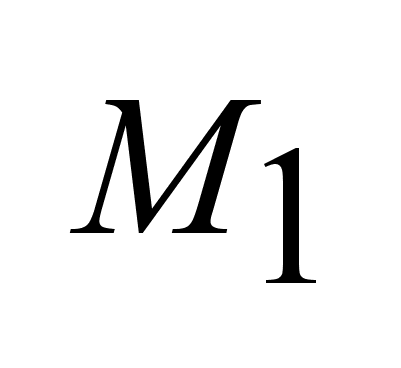 ,
а качество
определяет
функционал.
Таким функционалом
явл. время,
следовательно
задача быстродействия
заключается
в нахождении
такого допустимого
управления,
которое осуществляет
переход из
множества ,
а качество
определяет
функционал.
Таким функционалом
явл. время,
следовательно
задача быстродействия
заключается
в нахождении
такого допустимого
управления,
которое осуществляет
переход из
множества
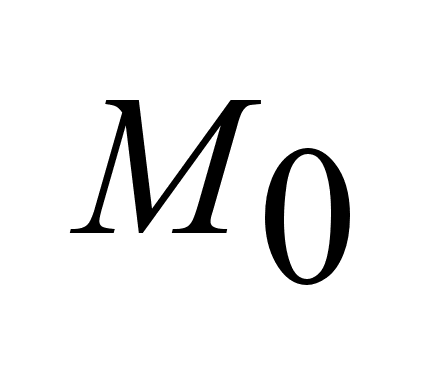 в в
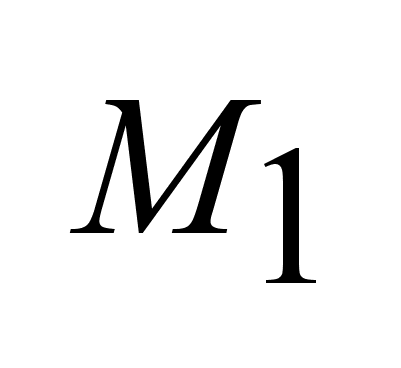 за
наименьшее
время. за
наименьшее
время.
4.
Пространство
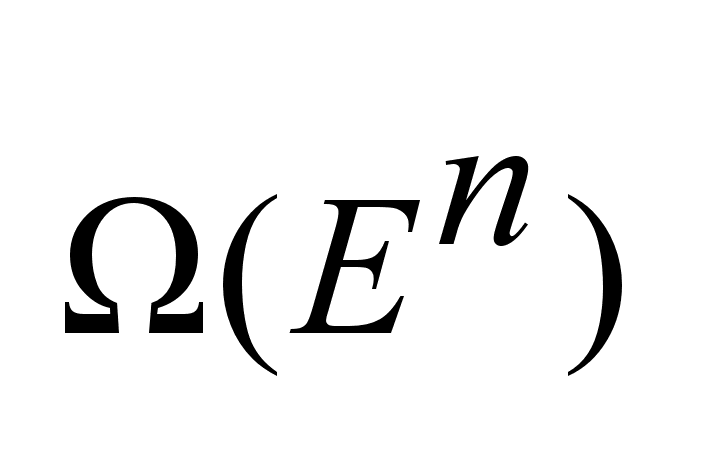 ,
алгебраическая
сумма ,
алгебраическая
сумма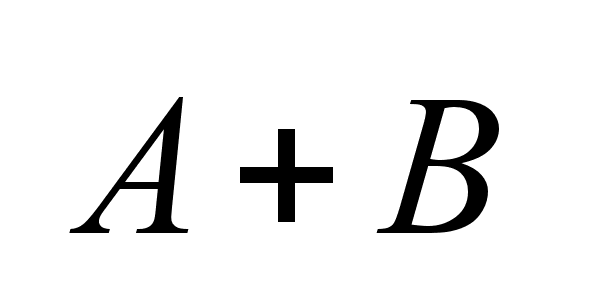 ,
произведение
множества на
число ,
произведение
множества на
число
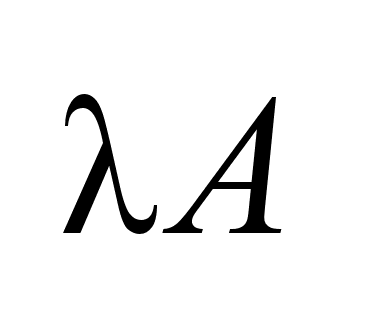 . .
Пространство
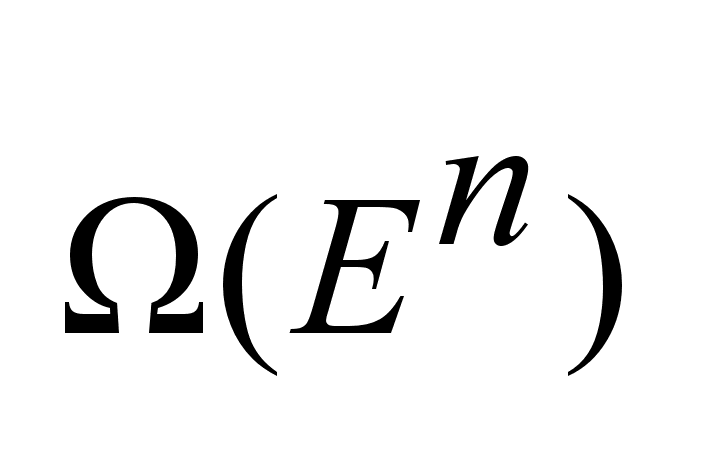 -пространство
состоящее из
всевозможных
не пустых компактных
подмножеств
пр-ва -пространство
состоящее из
всевозможных
не пустых компактных
подмножеств
пр-ва
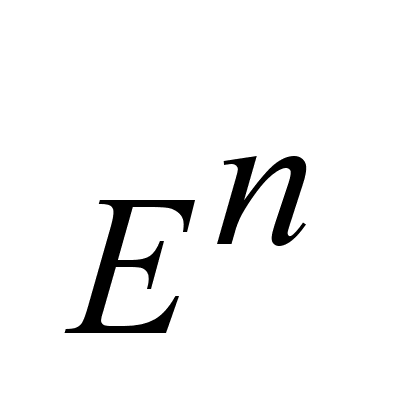 . .
Мн-во
F
компактное,
если оно замкнуто
и ограничено.
Мн-во
F
ограничено,
если оно содержится
в шарк некоторого
радиуса.
Мн-во
F
замкнуто,
если оно содержит
все свои предельные
точки.
Точка
f
предельная
точка F,
если в любой
ее окрестности
содержится
хотя бы одна
точка мн-ва F
отличная
от f.
Операции:1)
алгебраической
суммой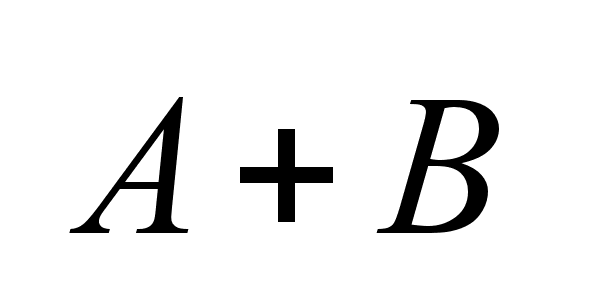 наз.
мн-во C
такое, что любой
элемент наз.
мн-во C
такое, что любой
элемент
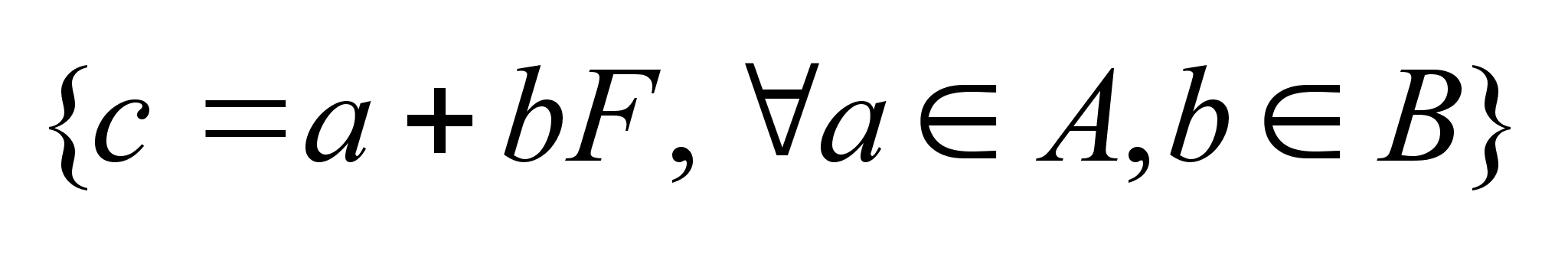 , ,
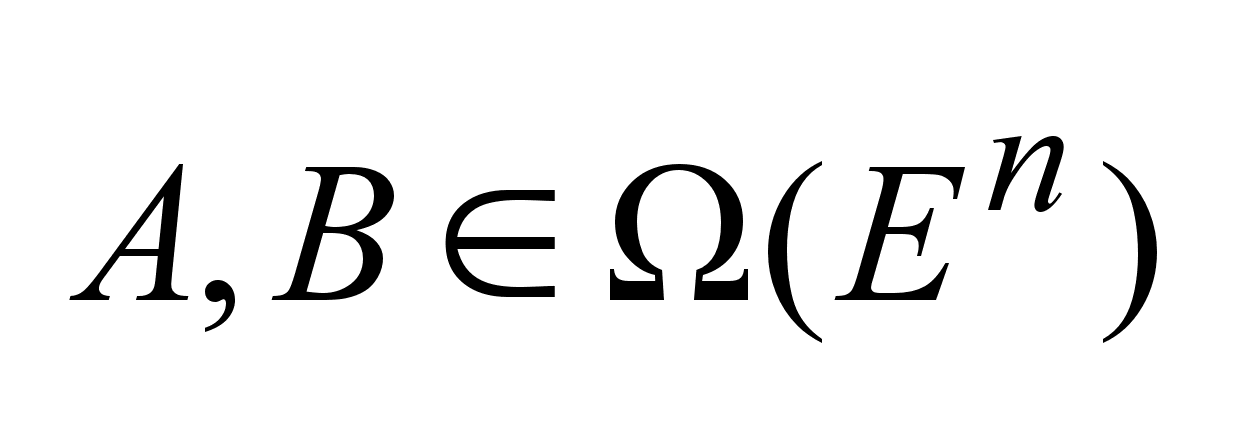 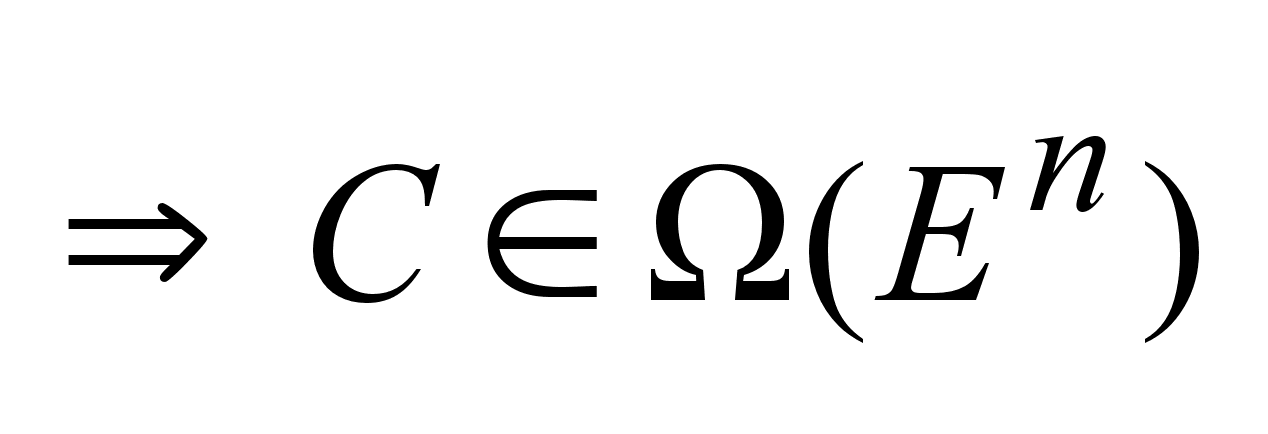 . .
2)
произведением
множества на
число
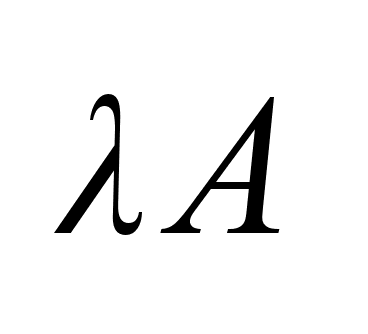 наз. мн-во C
такое, что любой
элемент
наз. мн-во C
такое, что любой
элемент
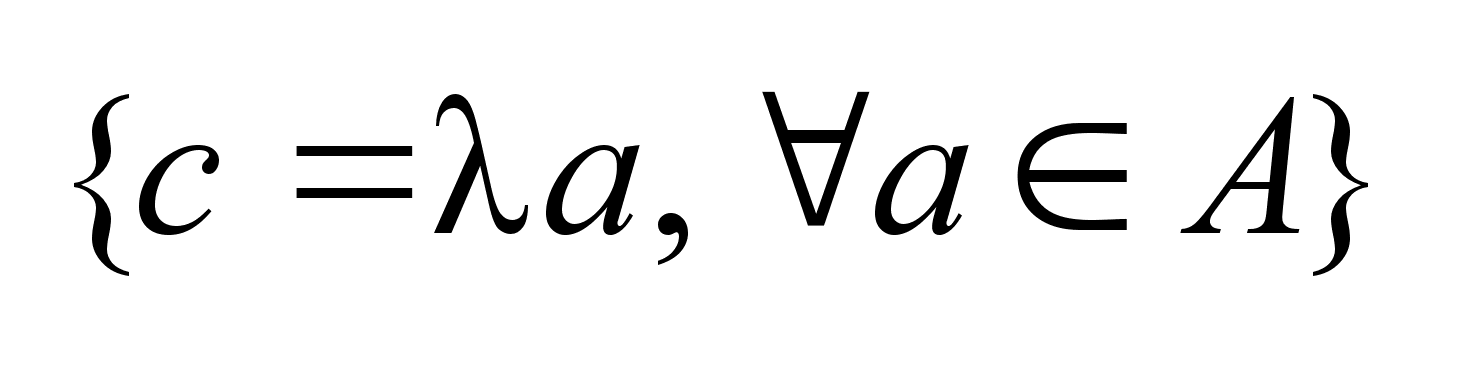 . .
5. ,
хаусдорффова
норма, лемма
про определенность
хаус. нормы. ,
хаусдорффова
норма, лемма
про определенность
хаус. нормы.
 -это
минимальный
радиус шара
с центром в
начале координат,
где -это
минимальный
радиус шара
с центром в
начале координат,
где
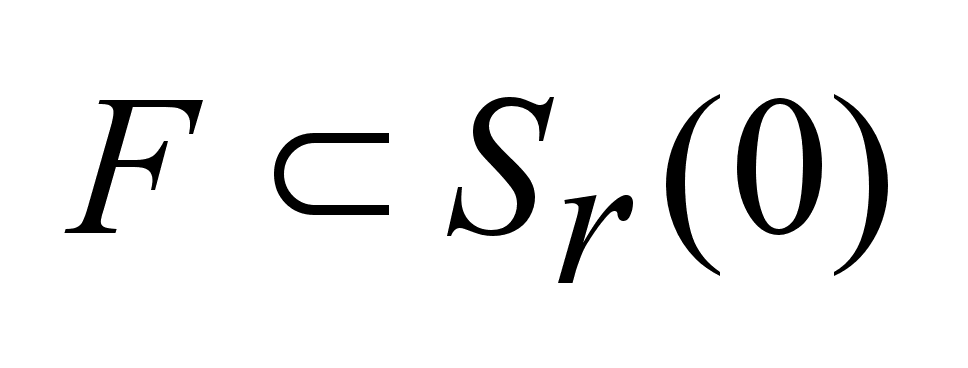 . .
Хаусдорффова
норма- это расстояние
между мн-ми A
и B:
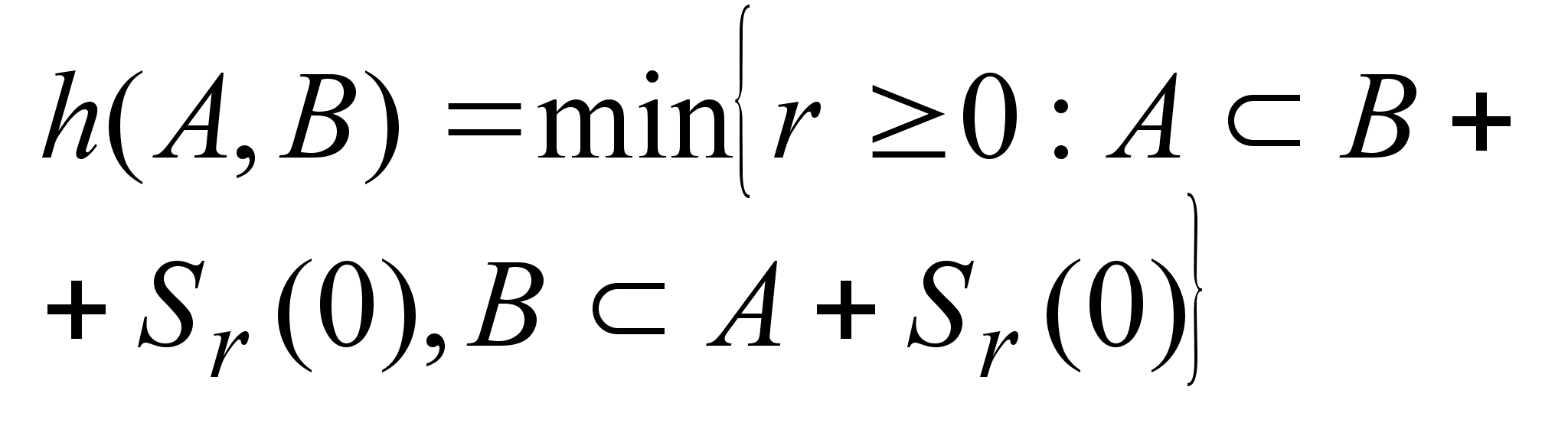 -расстояние
между мн-ми A
и B
(
-расстояние
между мн-ми A
и B
(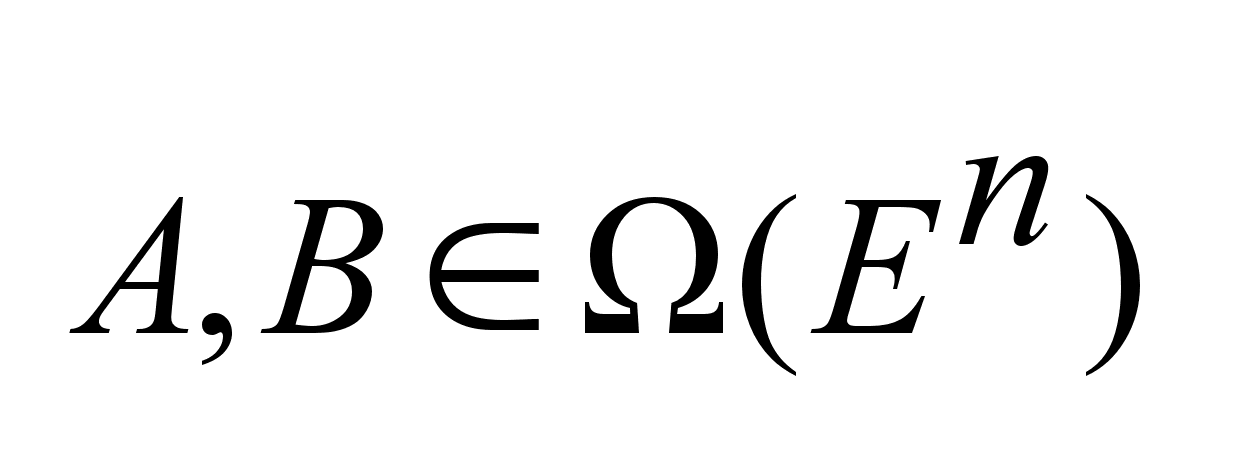 )
явл. наименьшее
положительное
число r. )
явл. наименьшее
положительное
число r.
Лемма:
Пусть
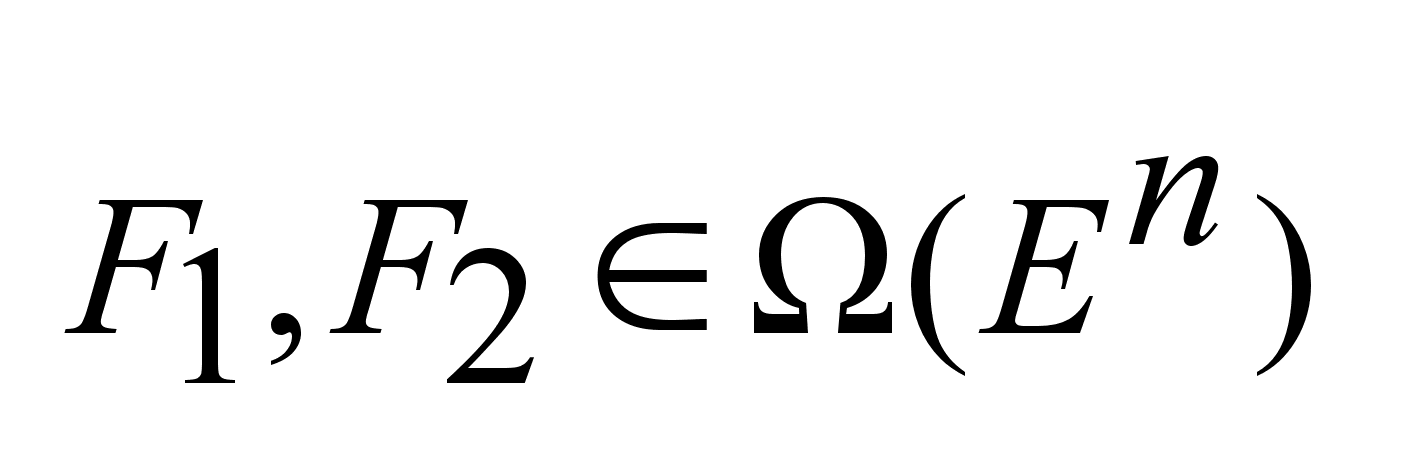 -
выпуклы, тогда
хаусдорффова
норма -
выпуклы, тогда
хаусдорффова
норма
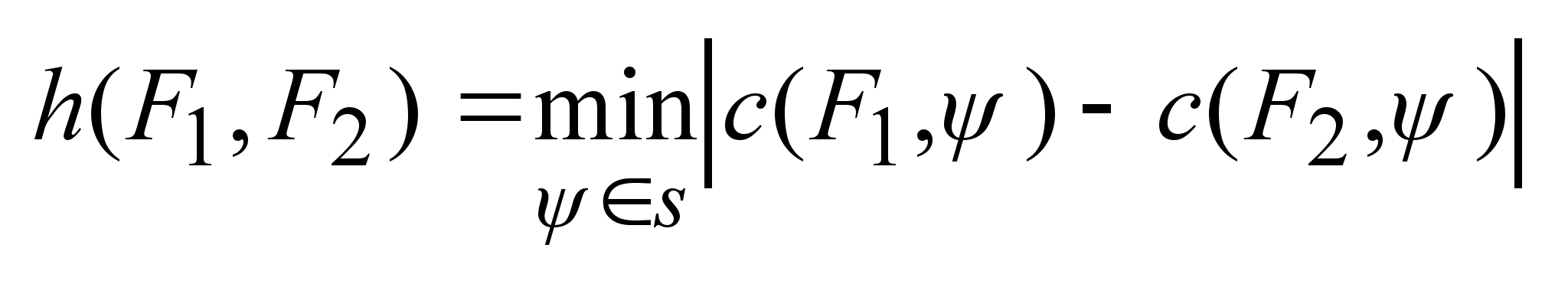 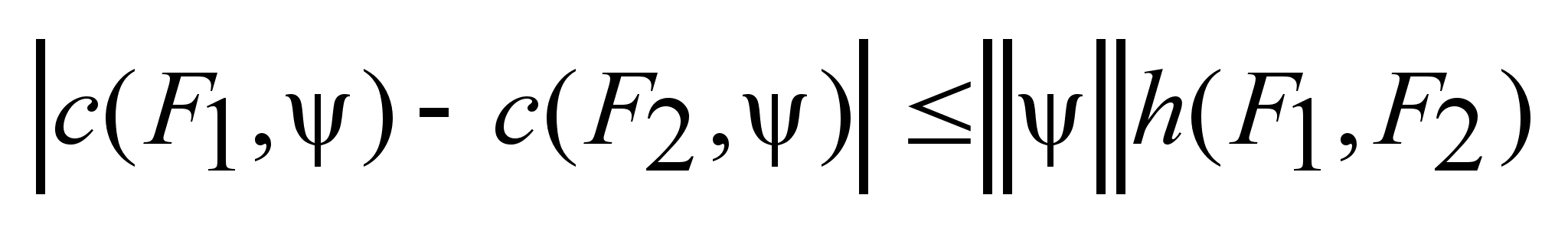
6.
Опорные
функции.
Задано
множество
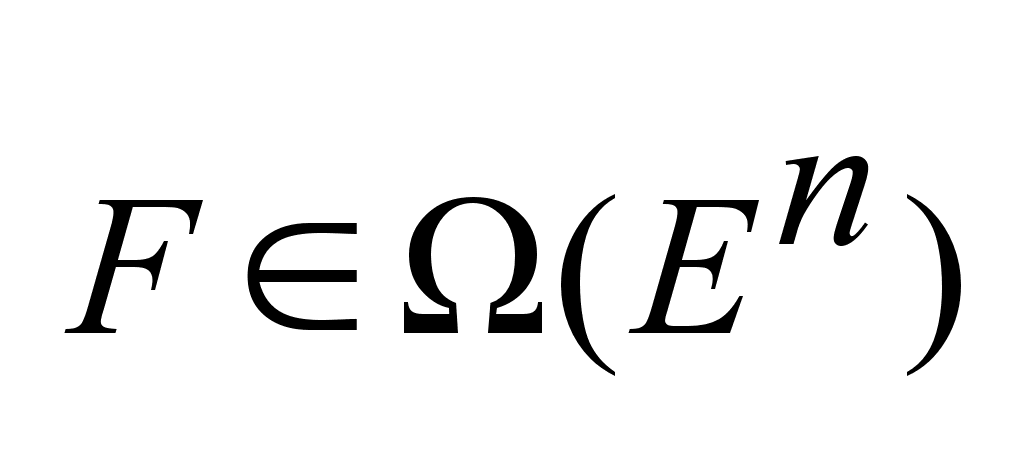 и
вектор и
вектор
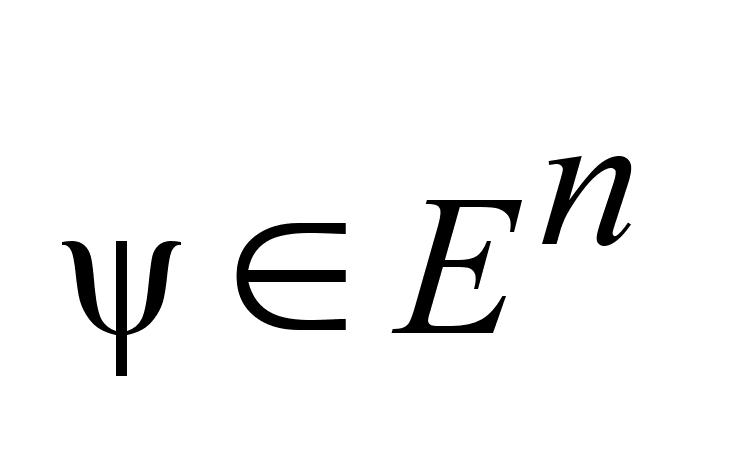 . Для этих двух
элементов можно
определить
опорную функцию
следующим
образом
. Для этих двух
элементов можно
определить
опорную функцию
следующим
образом
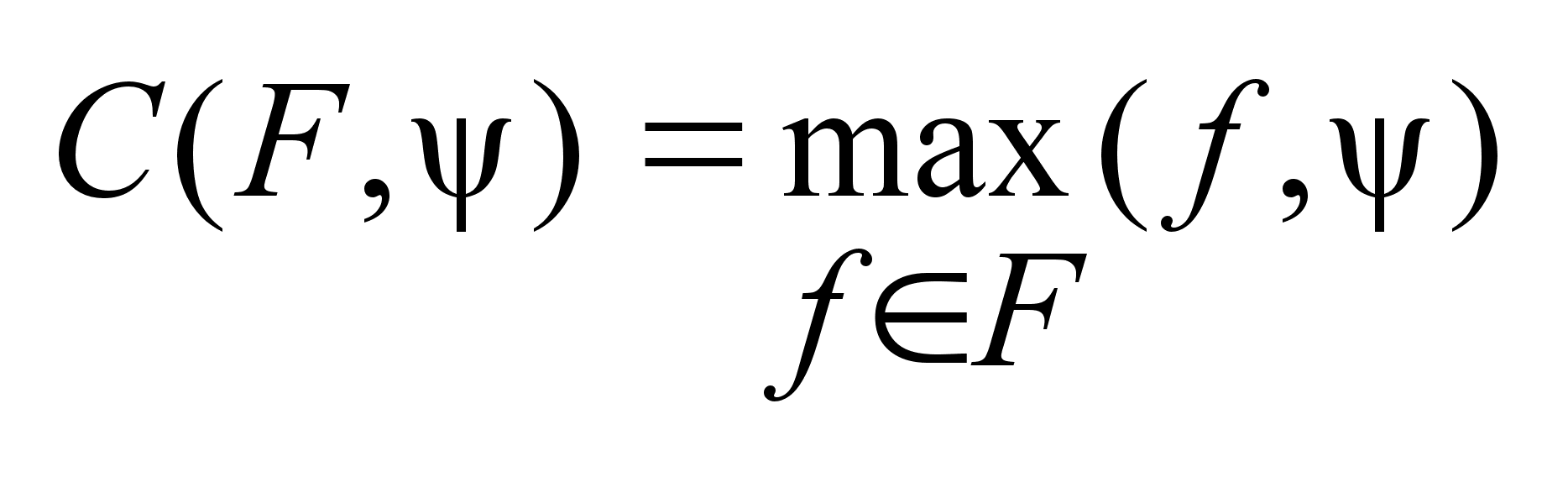 ,
где C
опорная функция. ,
где C
опорная функция.
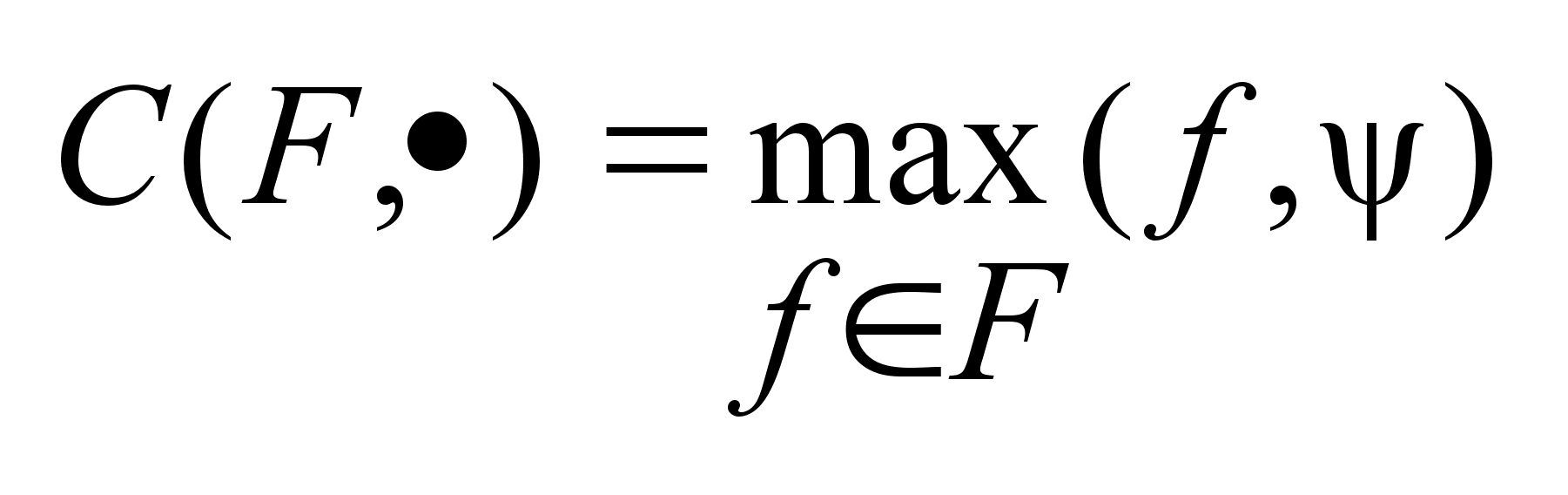 , ,
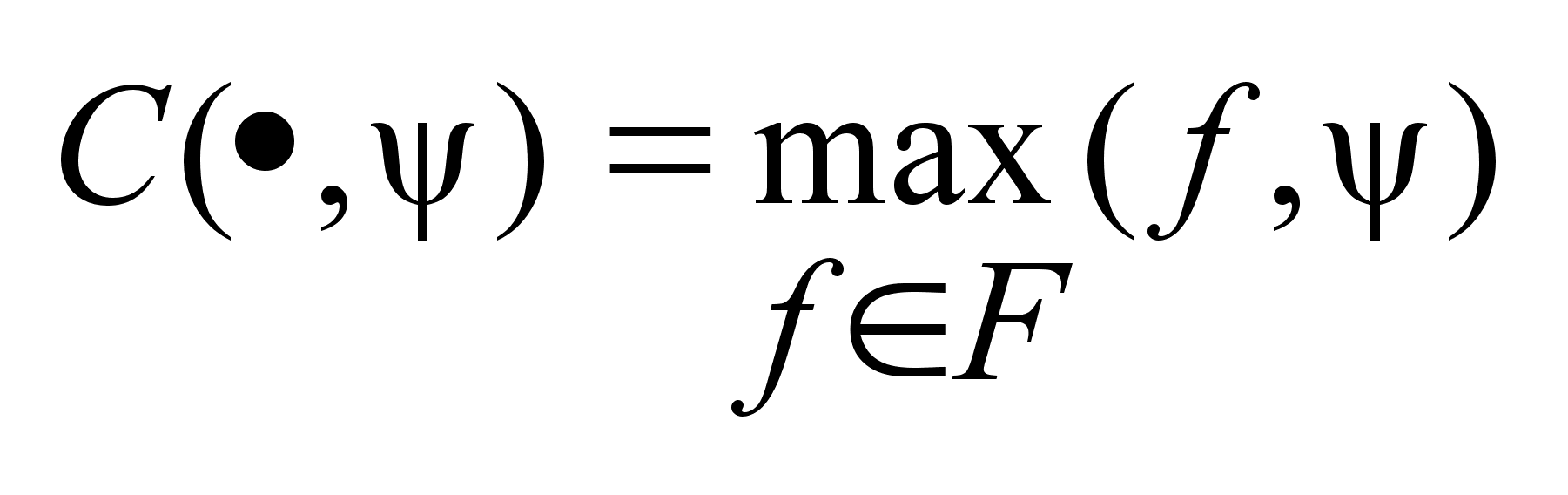
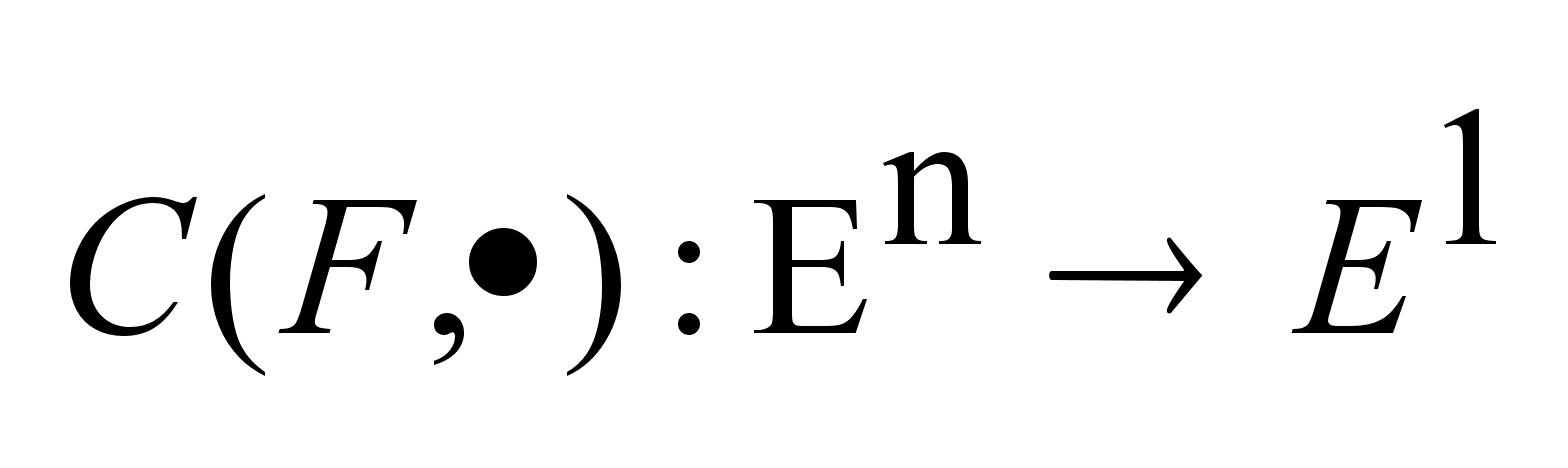 , ,
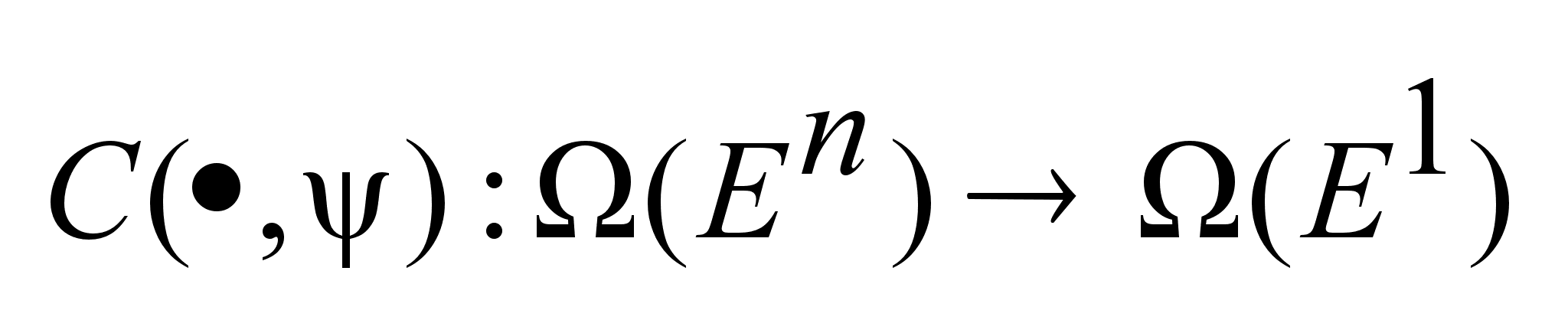 . .
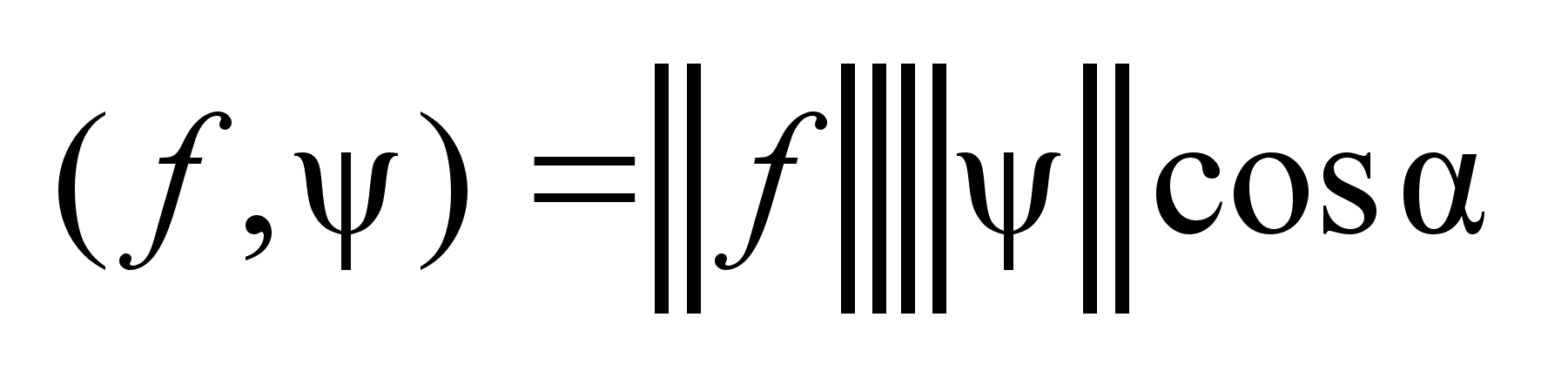 , ,
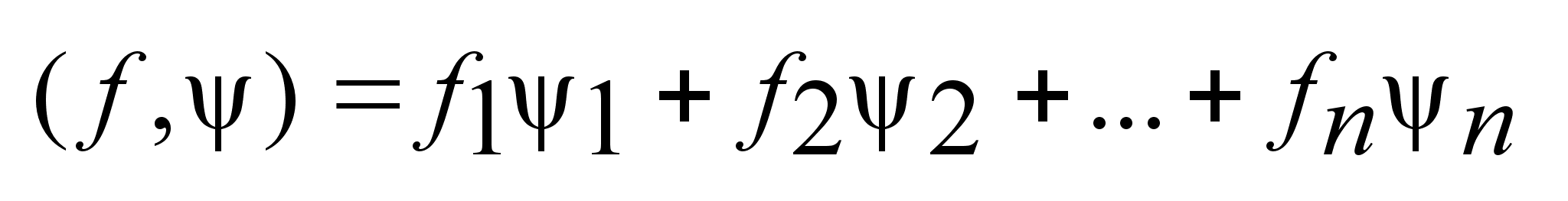 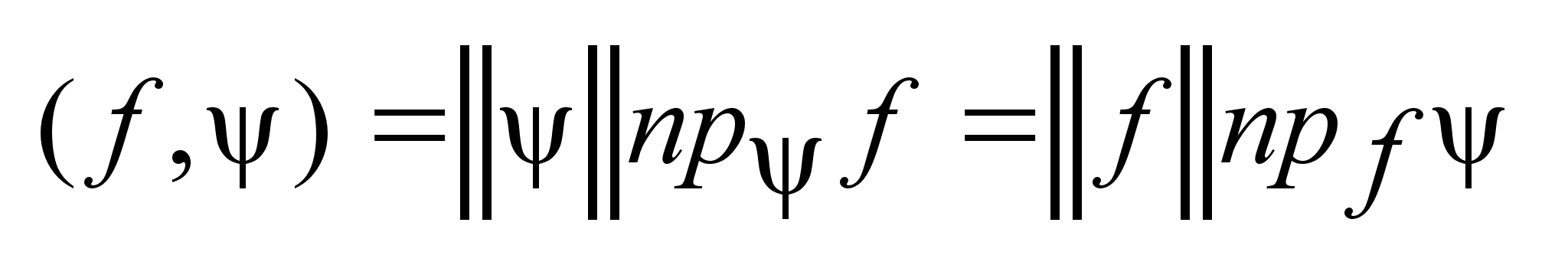 . .
Пусть
 -некоторый
фиксированный
вектор, а -некоторый
фиксированный
вектор, а
 один
из векторов
множества F,
на котором
опорная функция
достигает
максимум: один
из векторов
множества F,
на котором
опорная функция
достигает
максимум:
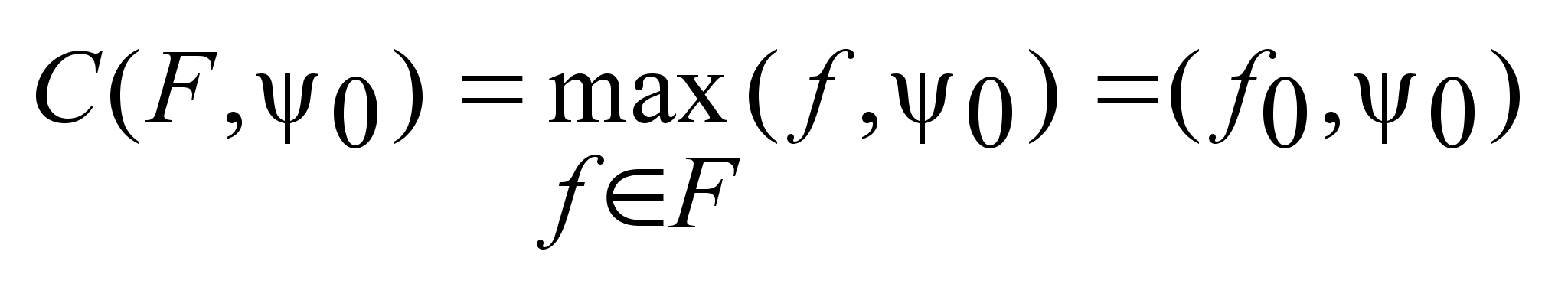 .
В этом случае .
В этом случае
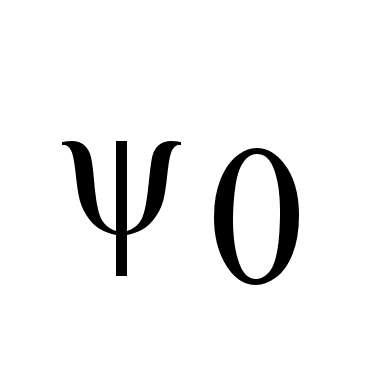 наз.
опорным вектором
мн-ва F
в точке наз.
опорным вектором
мн-ва F
в точке
 .
А совокупность
всех векторов .
А совокупность
всех векторов
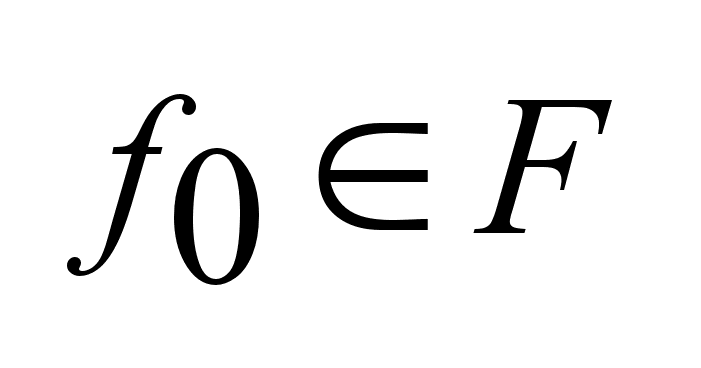 наз.
опорным множеством
к множеству
F
в
направлении наз.
опорным множеством
к множеству
F
в
направлении
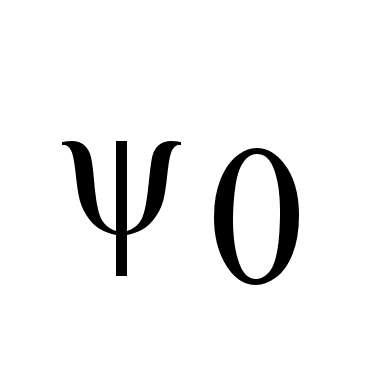 .Гиперплоскость .Гиперплоскость
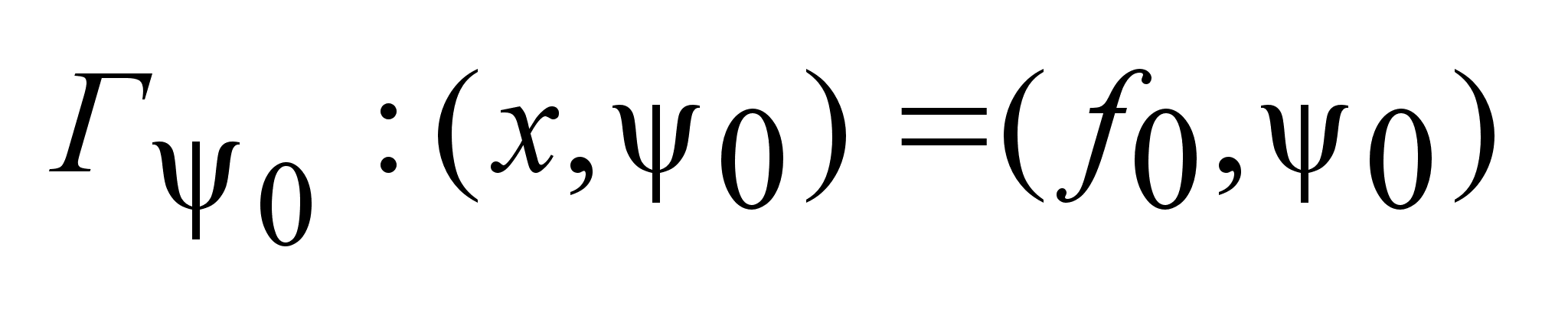 -
наз. опорной
гиперплоскостью
к множеству
F
в направлении -
наз. опорной
гиперплоскостью
к множеству
F
в направлении
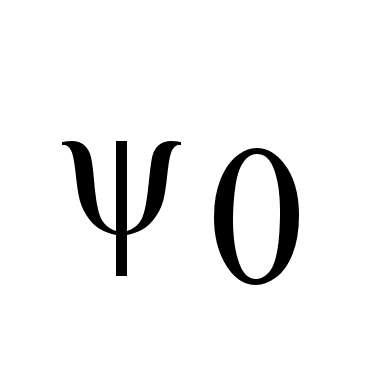 .
Гиперплоскость .
Гиперплоскость
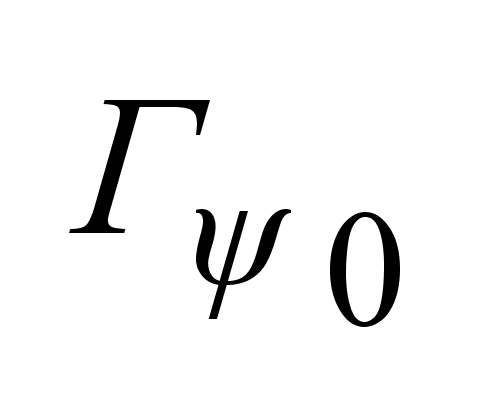 разбивает
разбивает
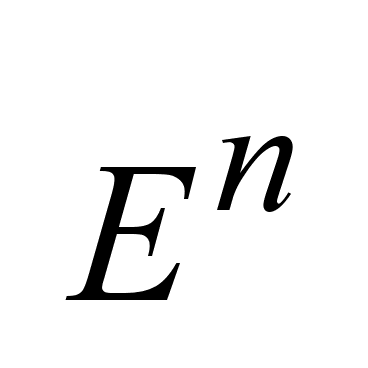 на
два подпространства,
при этом множество
F
находится в
отрезке получаемый
относительно на
два подпространства,
при этом множество
F
находится в
отрезке получаемый
относительно
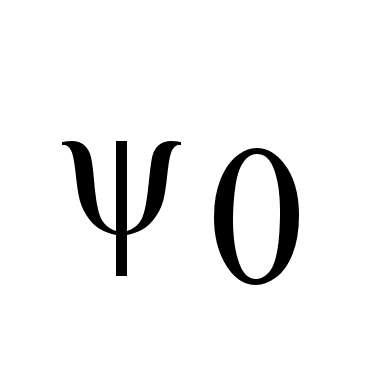 ,
т.к. для всех
точек ,
т.к. для всех
точек
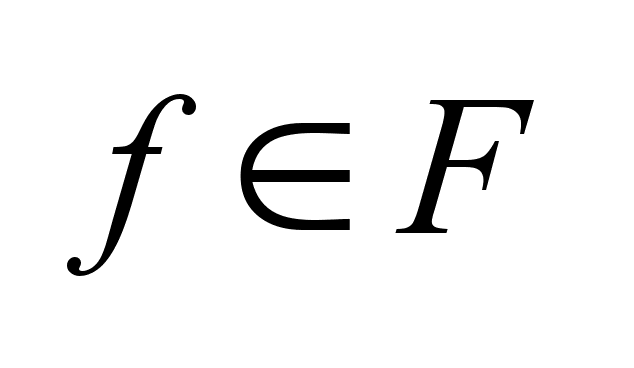 выполняется
неравенство выполняется
неравенство
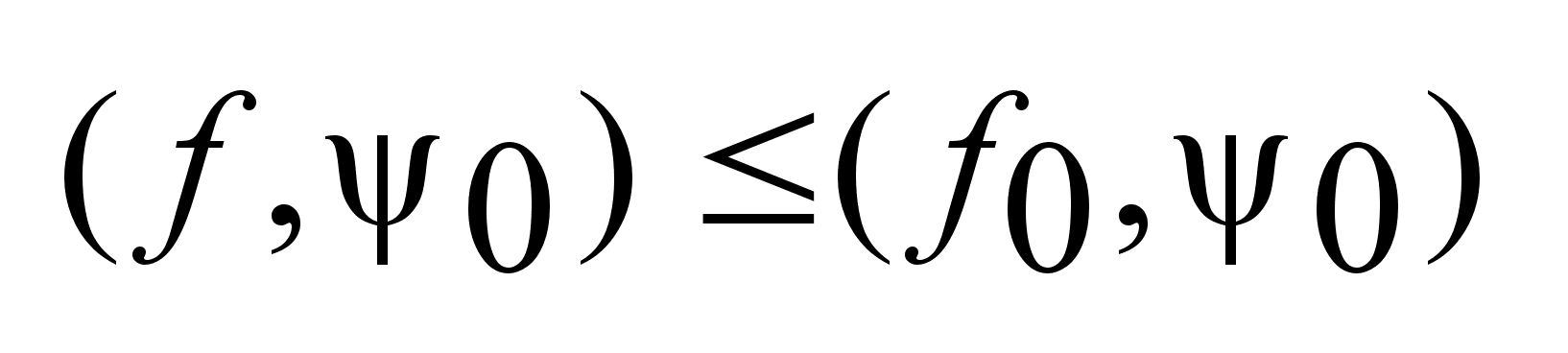 .
Если считать,
что .
Если считать,
что
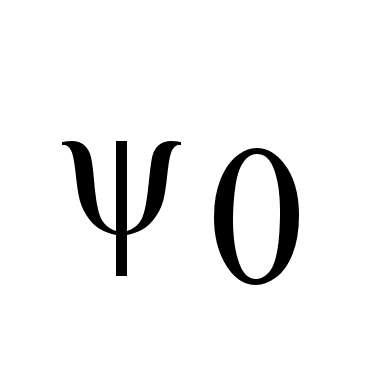 -
единичный
вектор, -
единичный
вектор,
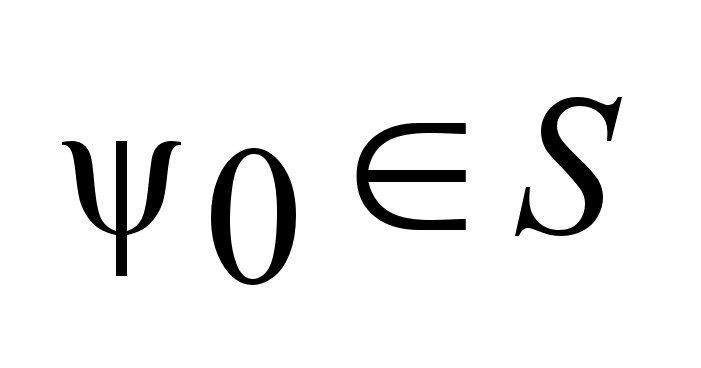 , ,
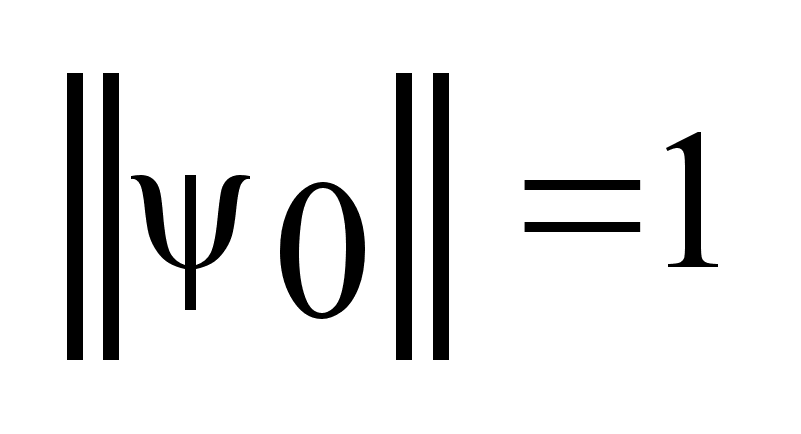 .
опорных .
опорных
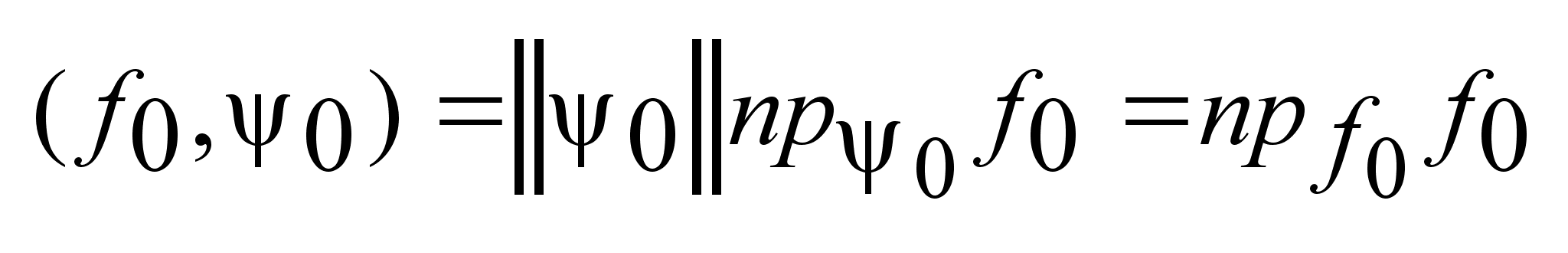
7.
Свойства
опорной функции.
1.
Опорные
функция- положительно
однородная
по переменной
 . .
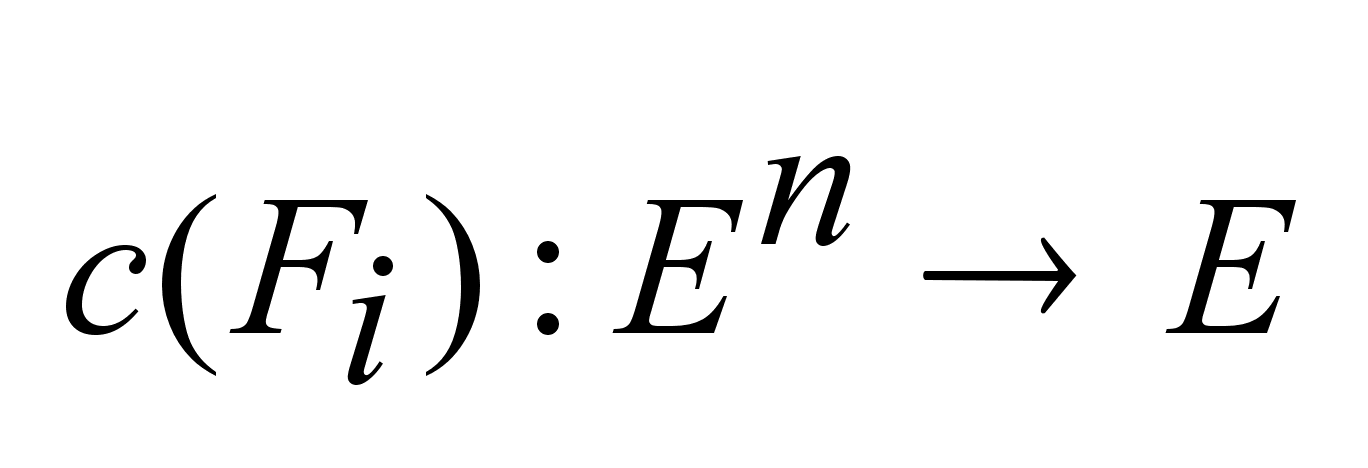 .
Это значит что .
Это значит что
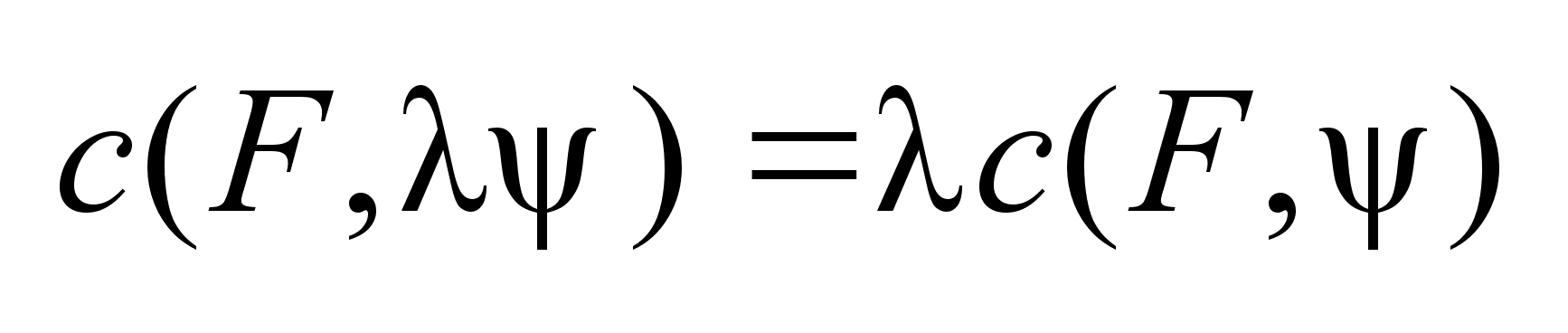 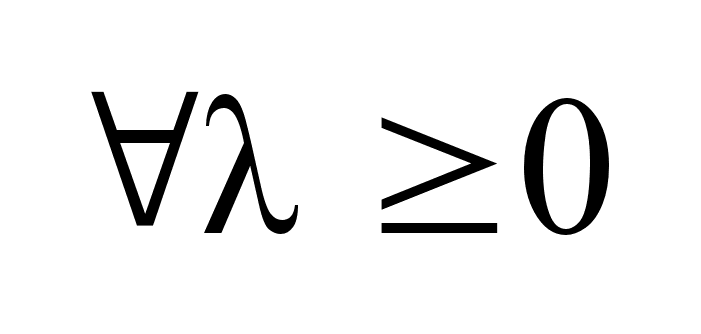 , ,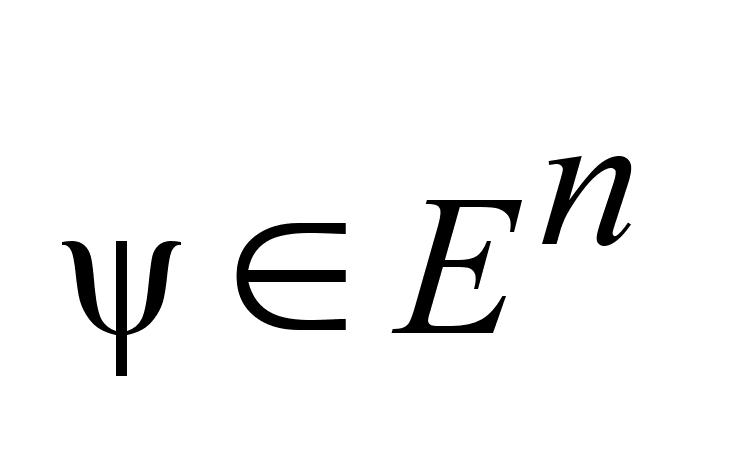 . .
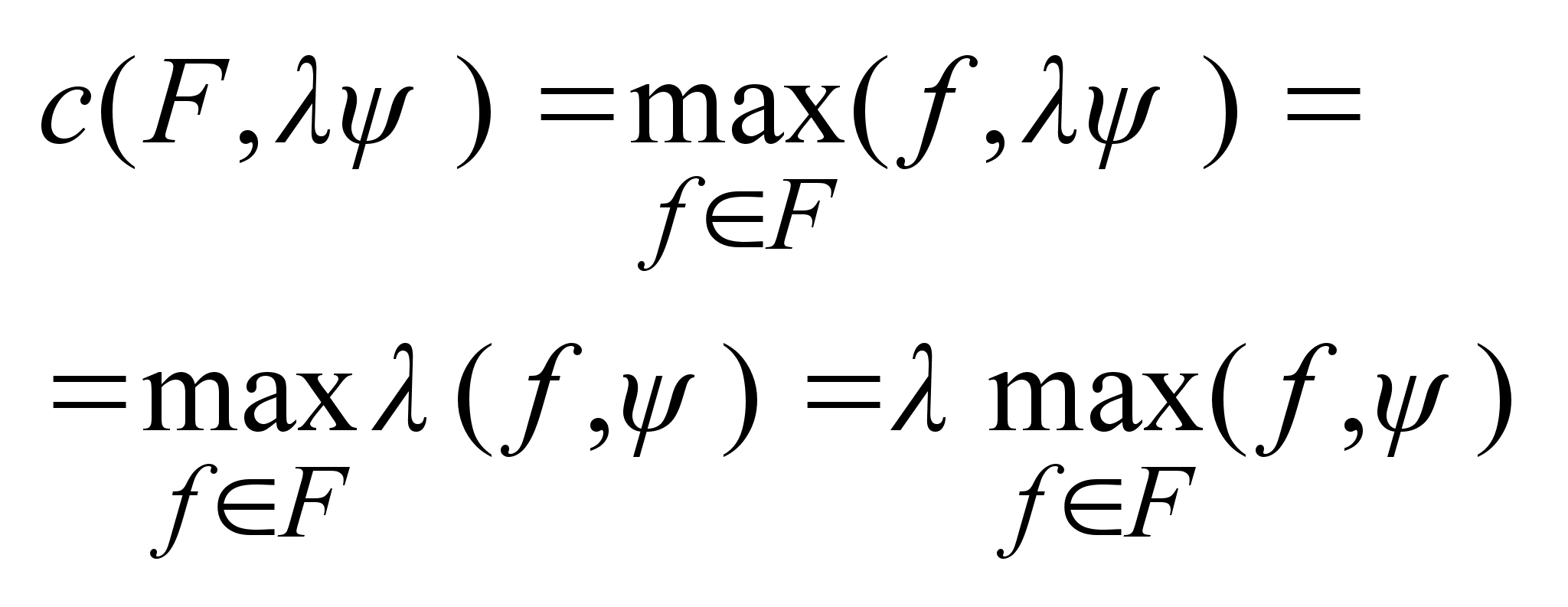
2.
Для
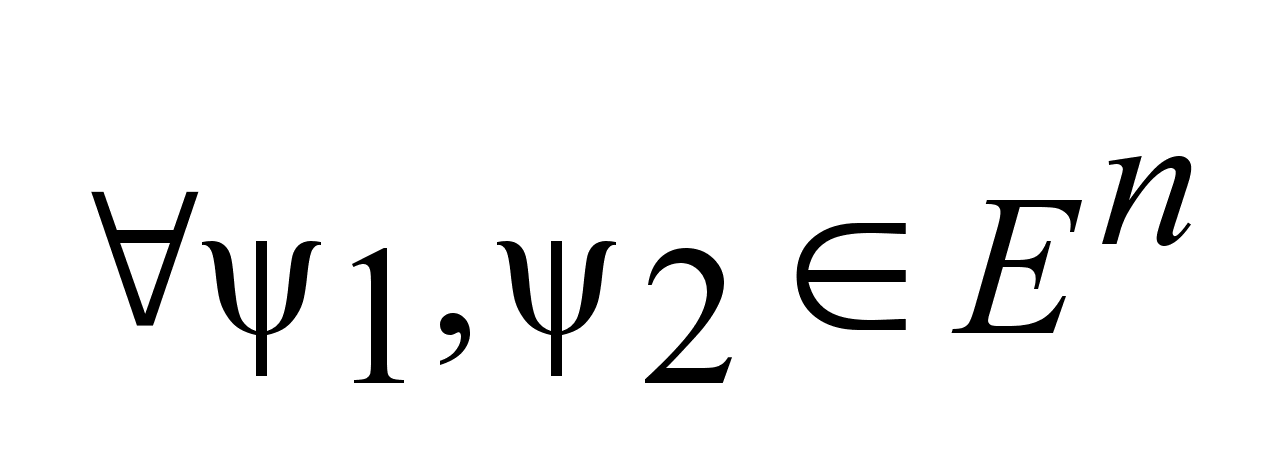 опорные
функции удовлетворяют
неравенству: опорные
функции удовлетворяют
неравенству:
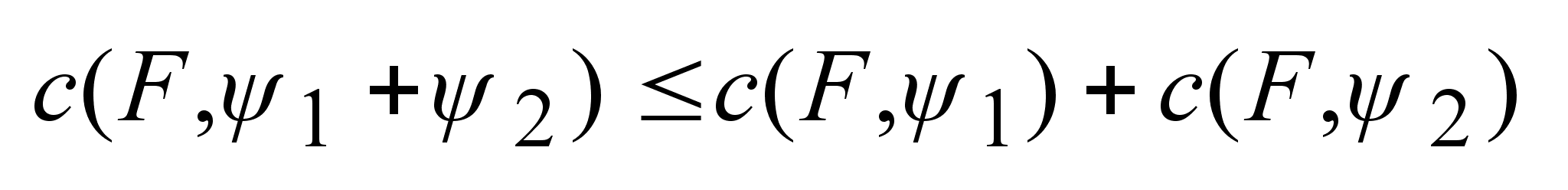 3.
Два
множества 3.
Два
множества
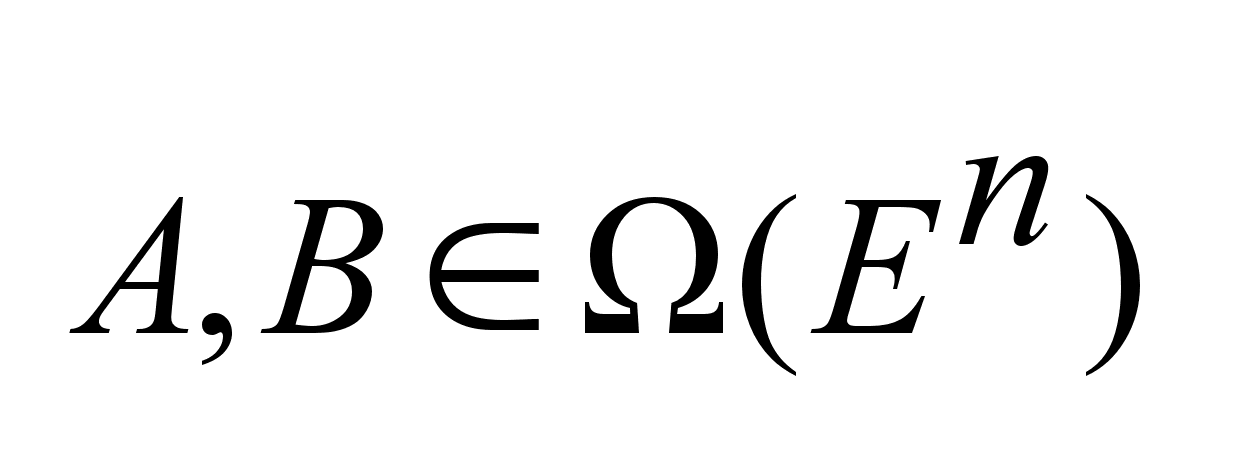 и
и
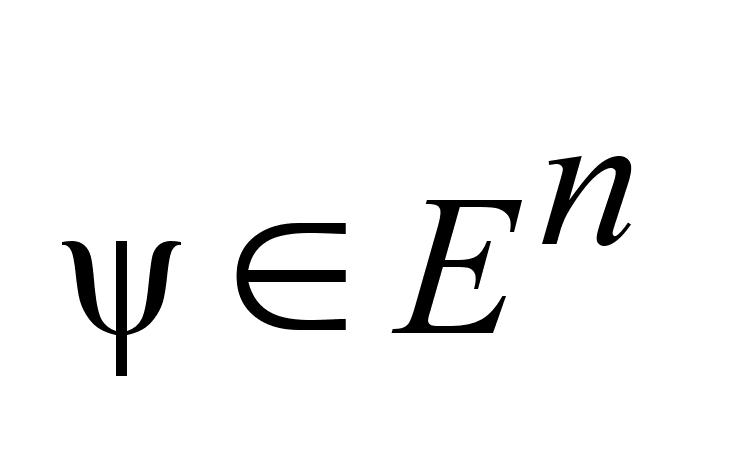 , ,
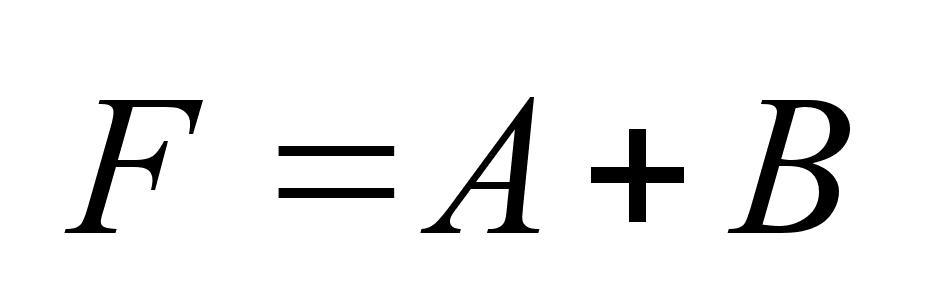 , ,
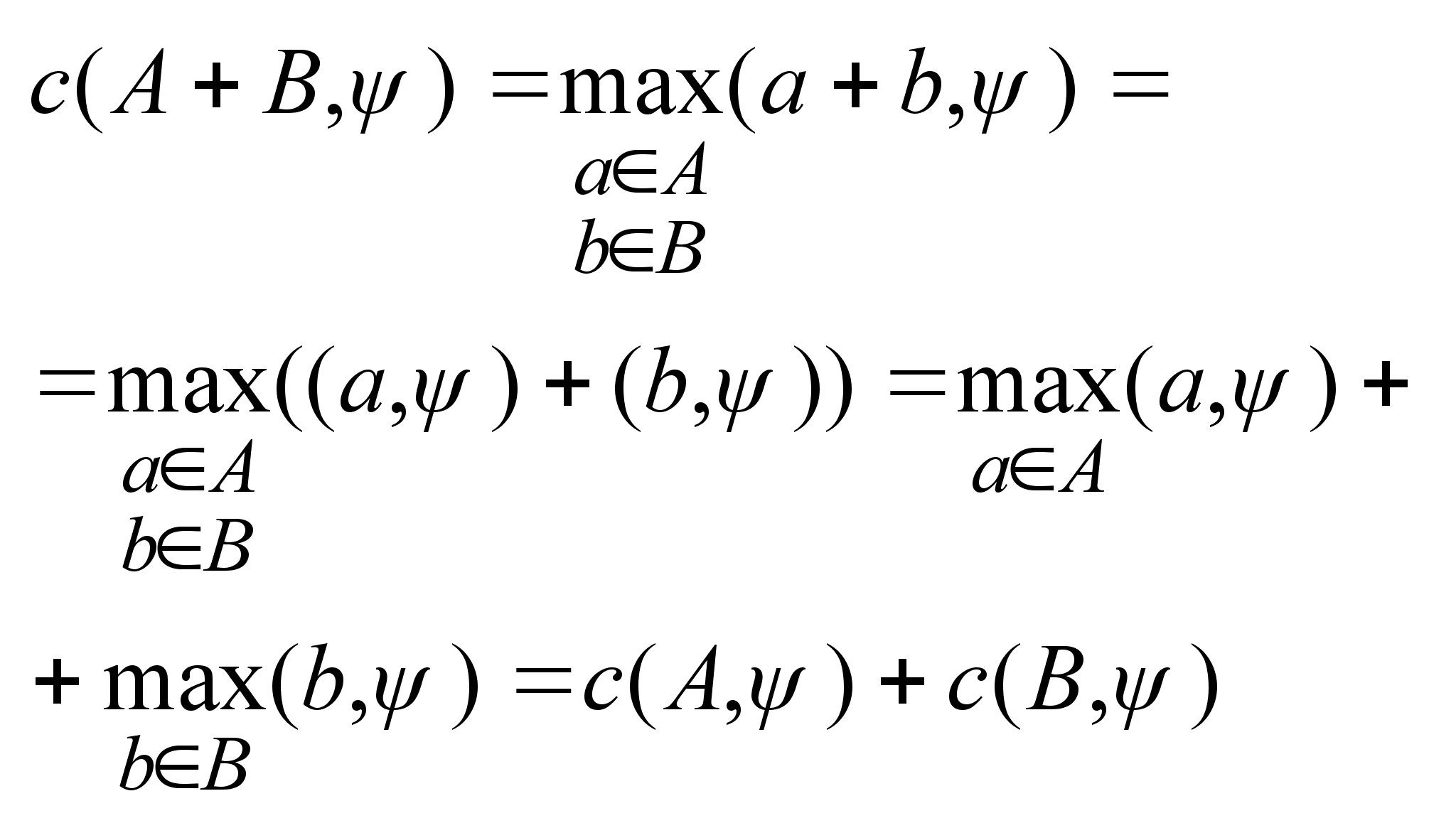 Пусть
матрица A
размера n
на
n, Пусть
матрица A
размера n
на
n,
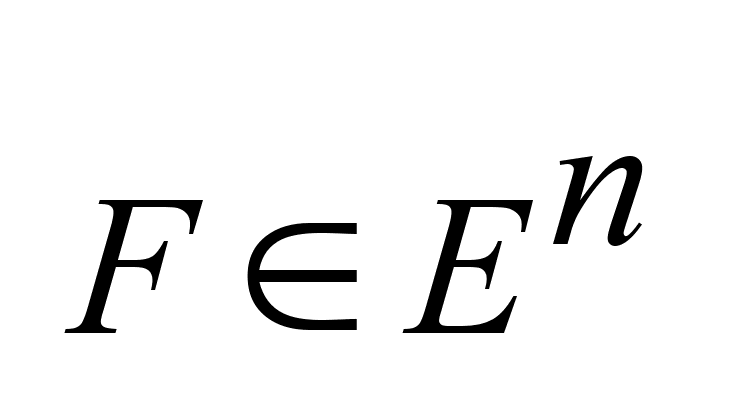 и
рассмотрим
лин. образ множества
F
при лин. преобразовании
A
и
наз. и
рассмотрим
лин. образ множества
F
при лин. преобразовании
A
и
наз.
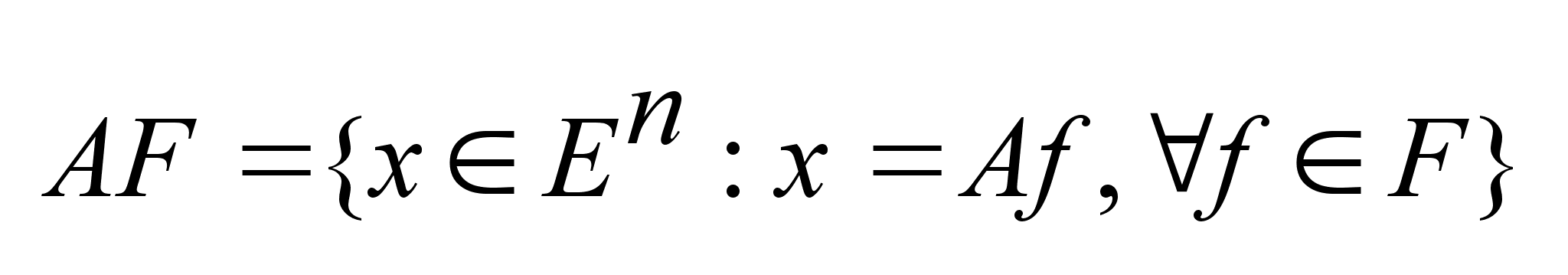 . .
4.
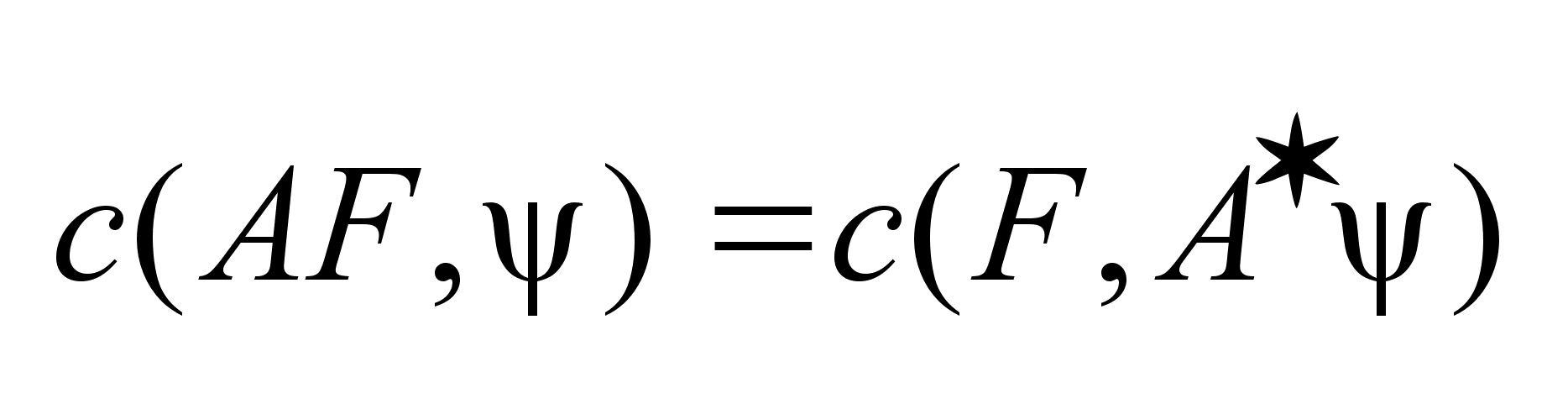 ,где ,где
 -матр.
сопряженная
с матр. -матр.
сопряженная
с матр.
 . .
5.
Опорная
функция положительная
и однородная
по первому
аргументу.
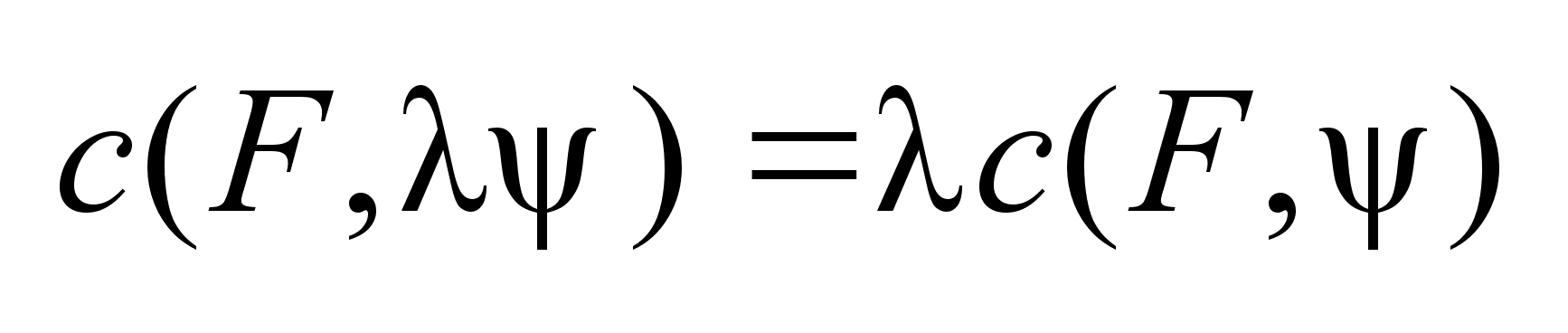 ,
,
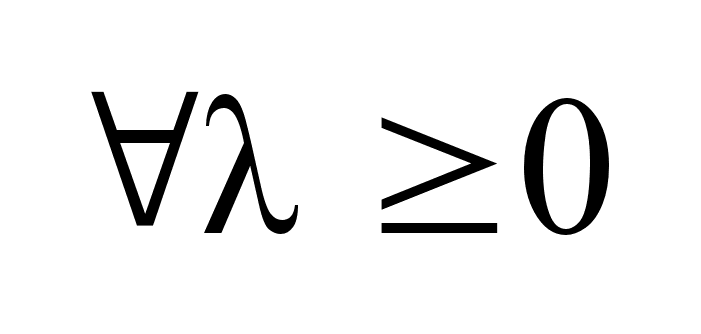 .
Пусть .
Пусть
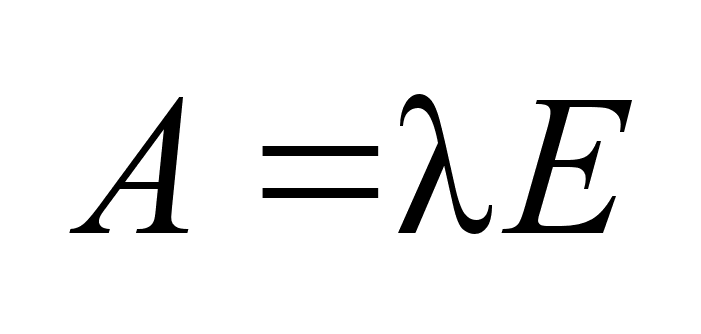 и пользуемся
: 1) условием
однородности:
и пользуемся
: 1) условием
однородности:
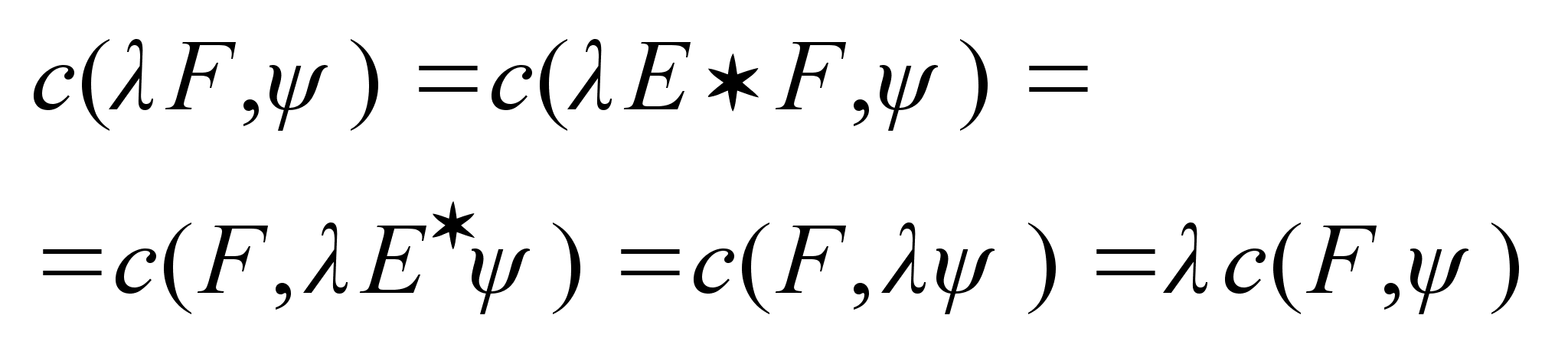 6.
Пусть
задано множество 6.
Пусть
задано множество
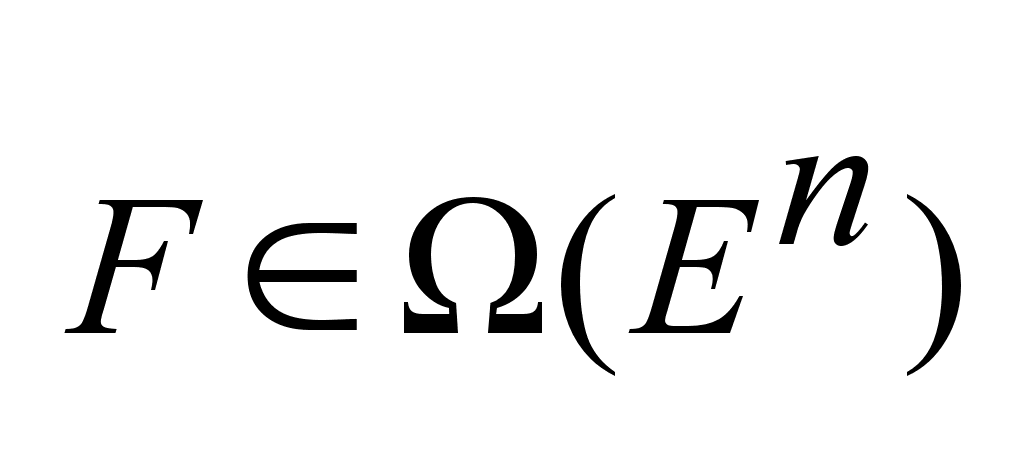 и
его опорная
фун. и
его опорная
фун.
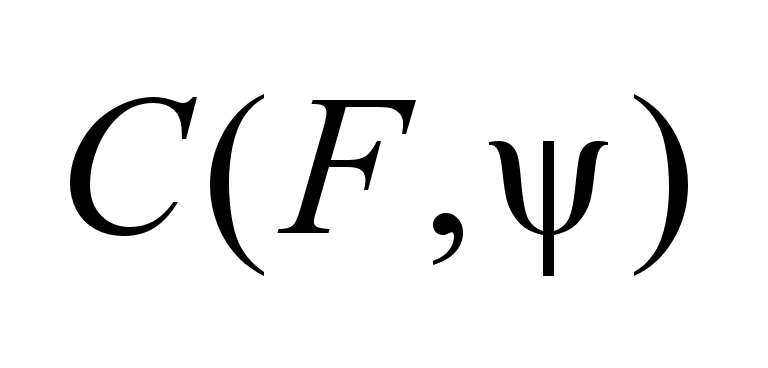 . Выпуклая оболочка
мн-ва F
. Выпуклая оболочка
мн-ва F
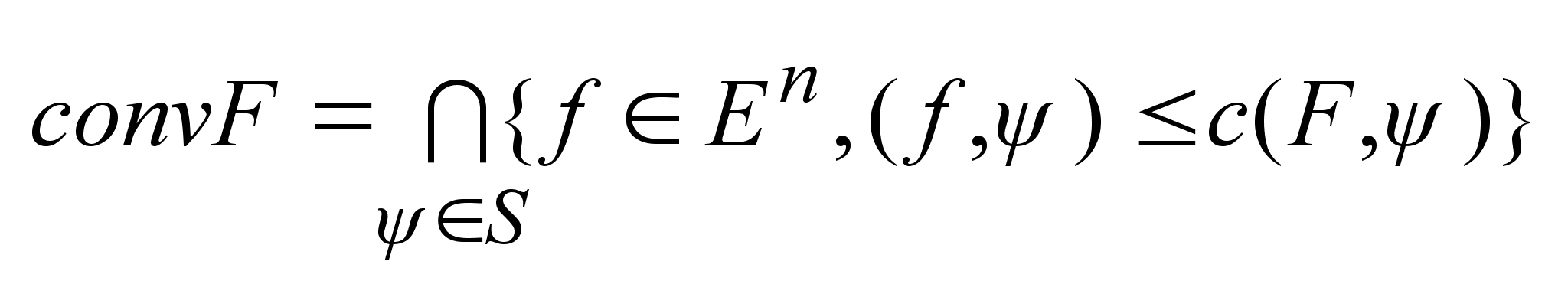 , ,
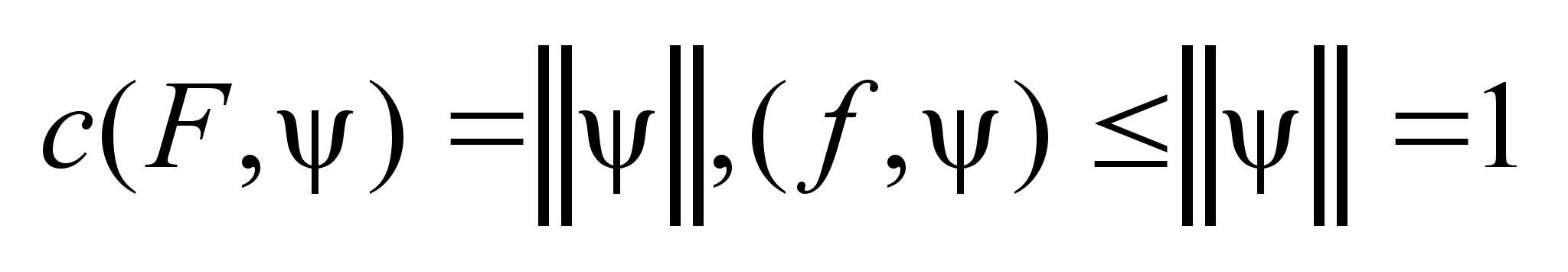 . .
7.
Если
 и
A=B,
то опорная
фун. и
A=B,
то опорная
фун.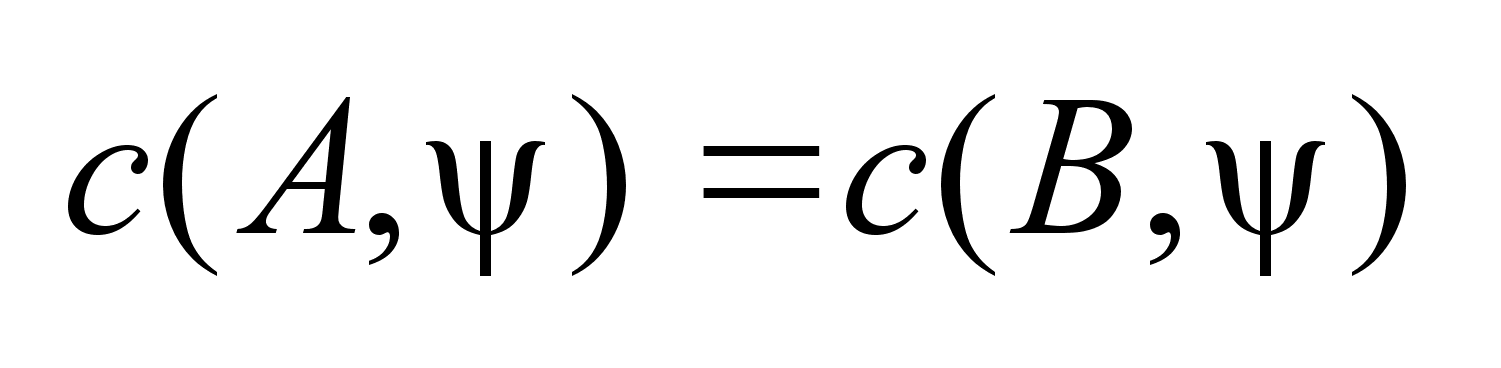 .
И наоборот,
если .
И наоборот,
если
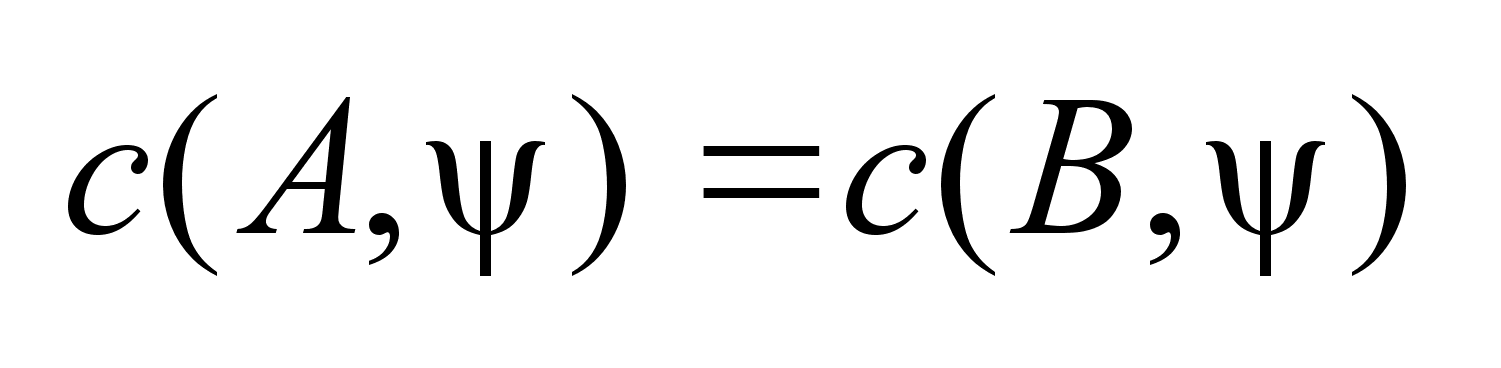 ,то ,то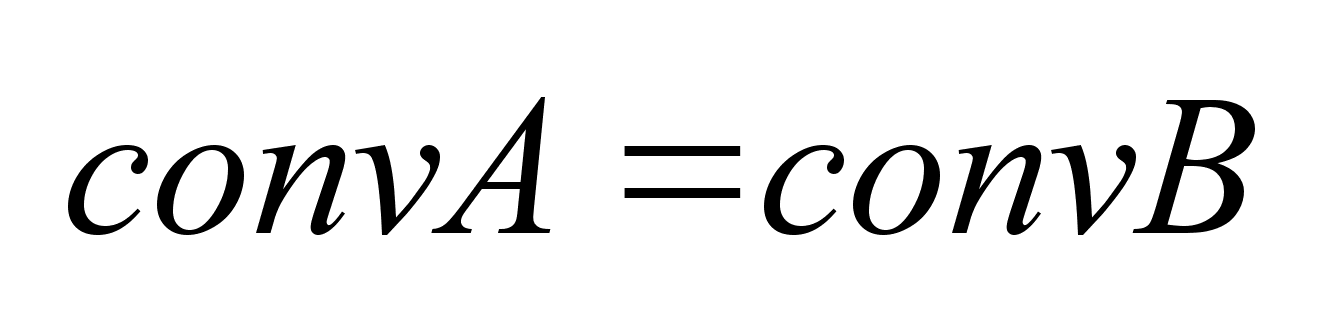 .
Следствие:
Выпуклые мн-ва
равны тогда
и только тогда,
когда равны
их опорные
функции. .
Следствие:
Выпуклые мн-ва
равны тогда
и только тогда,
когда равны
их опорные
функции.
8.
Если
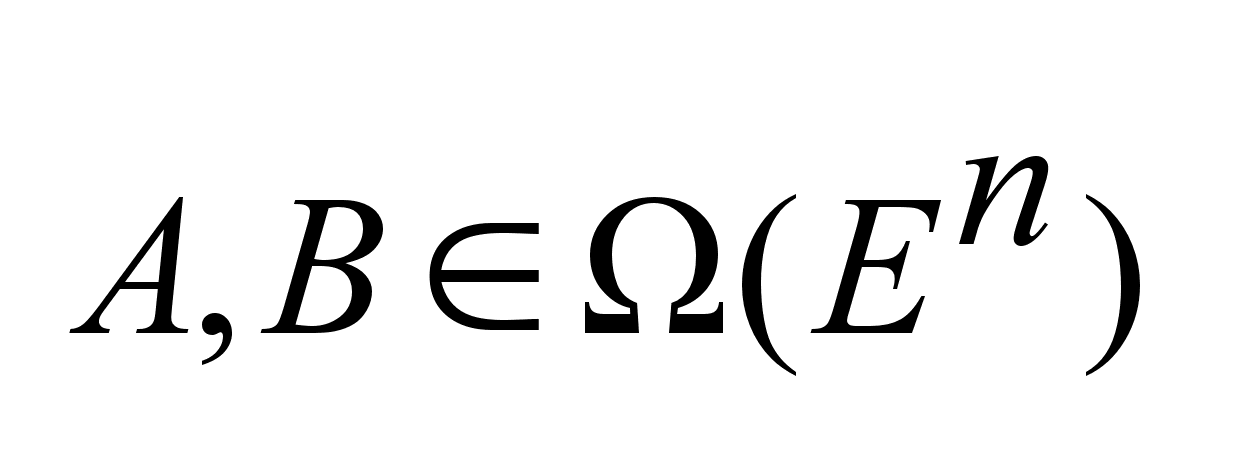 и и
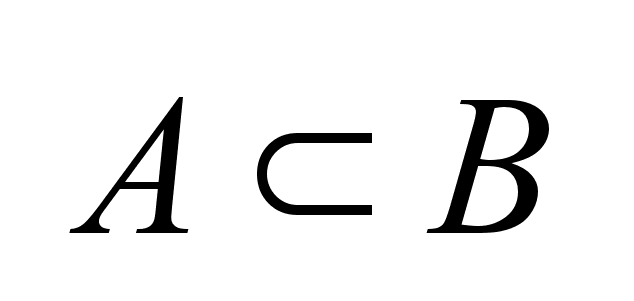 .
В этом случае .
В этом случае
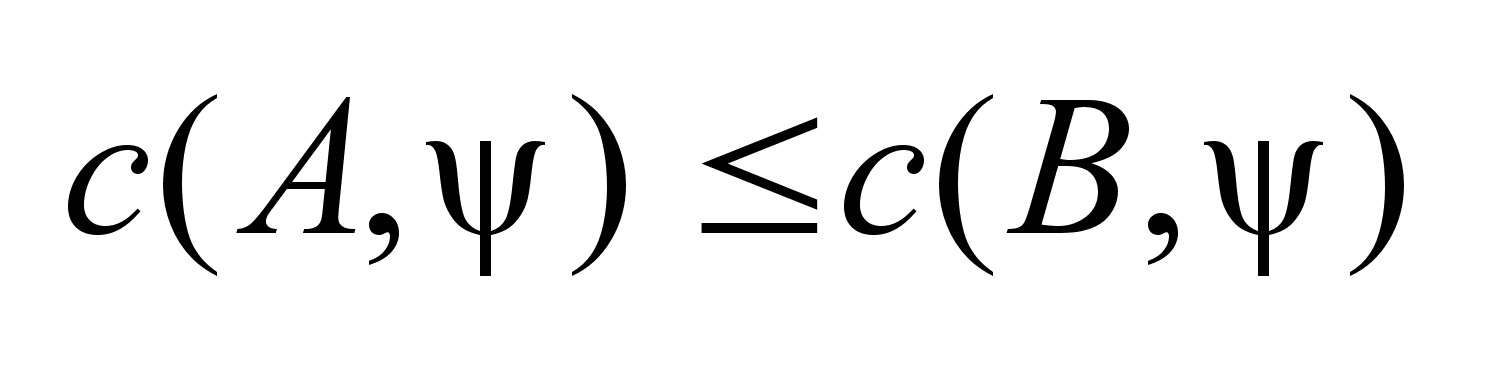 .
Если .
Если
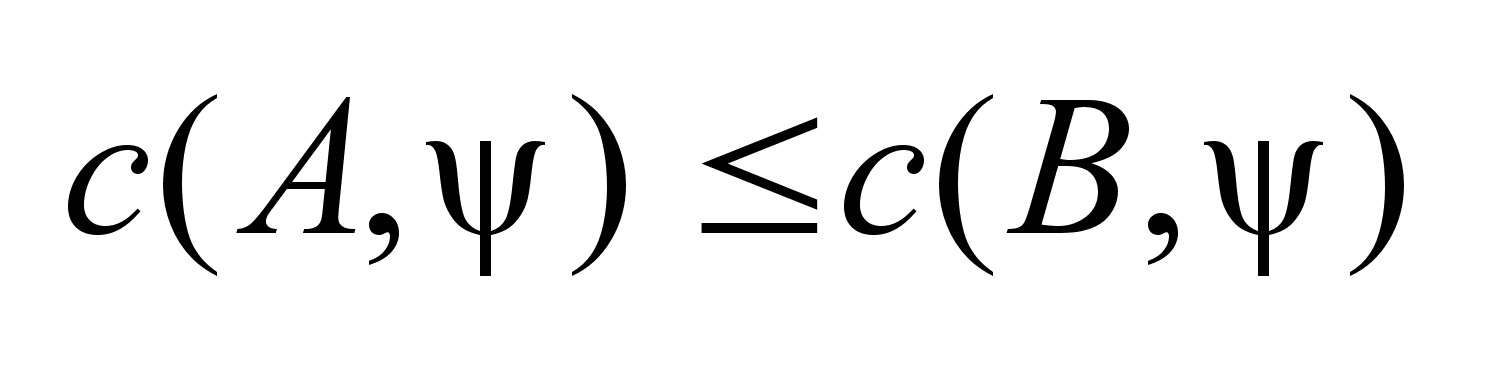 ,то ,то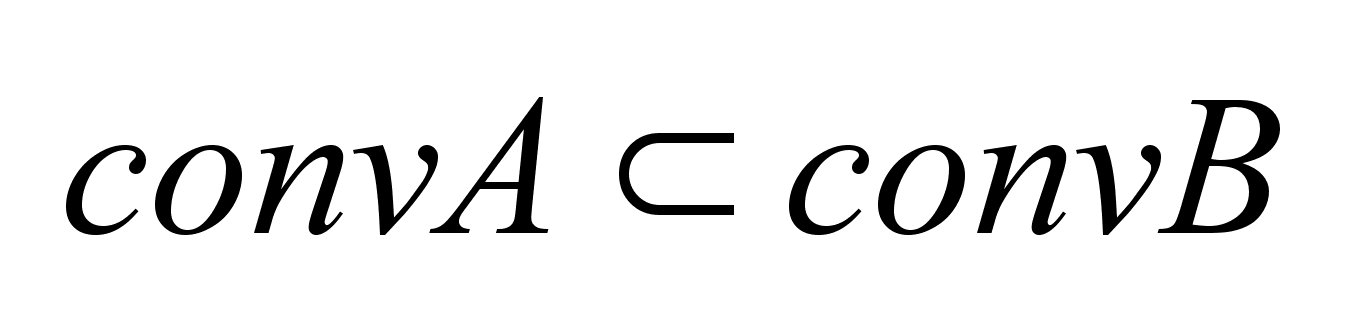 .
Следствие:
Выпуклые мн-ва .
Следствие:
Выпуклые мн-ва
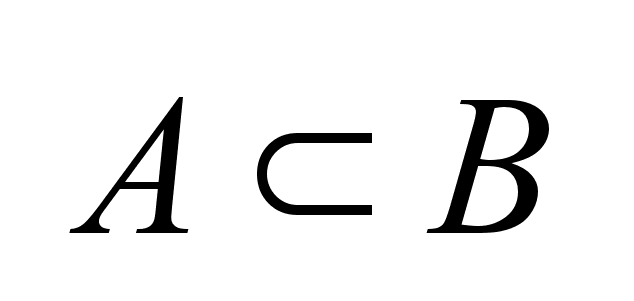 тогда и только
тогда, когда
равны их опорные
функции
тогда и только
тогда, когда
равны их опорные
функции
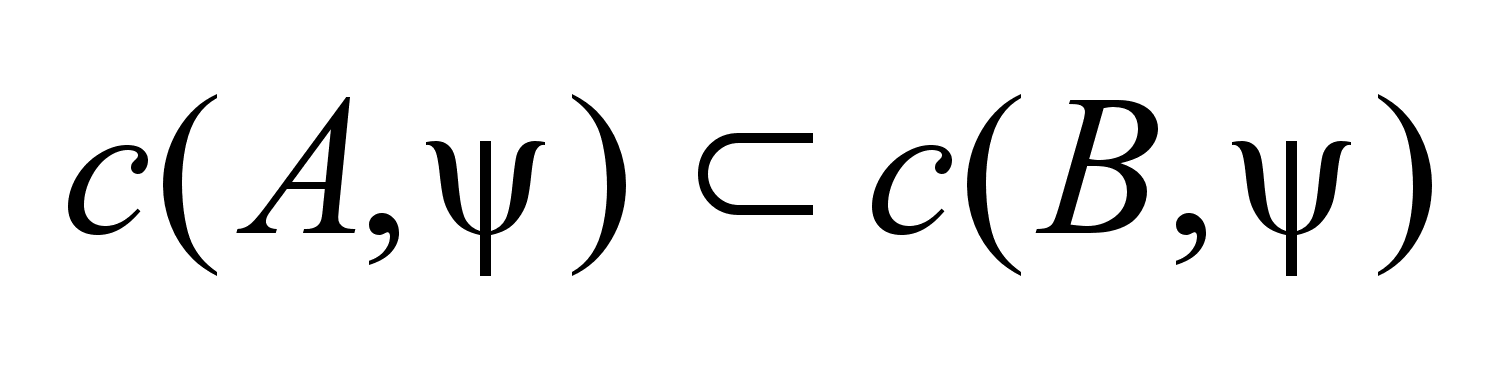 . .
9.
Пусть
задано множество
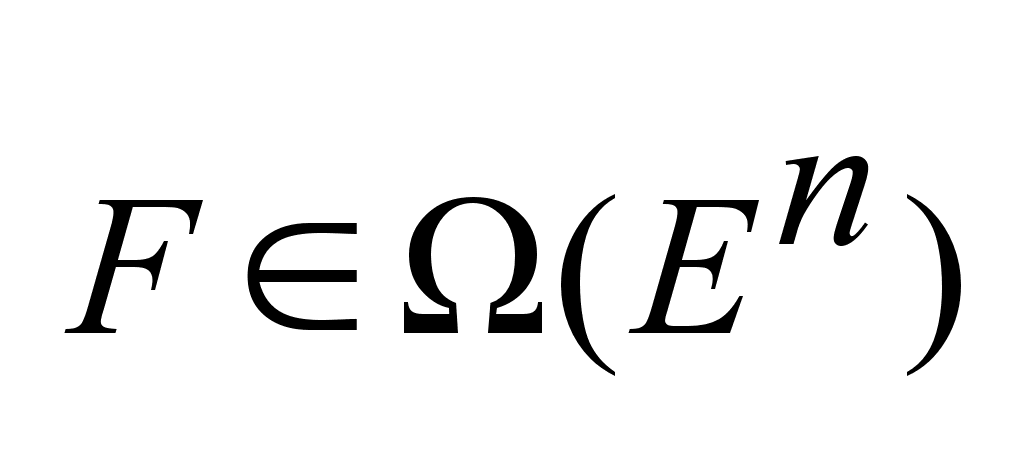 ,
тогда ,
тогда
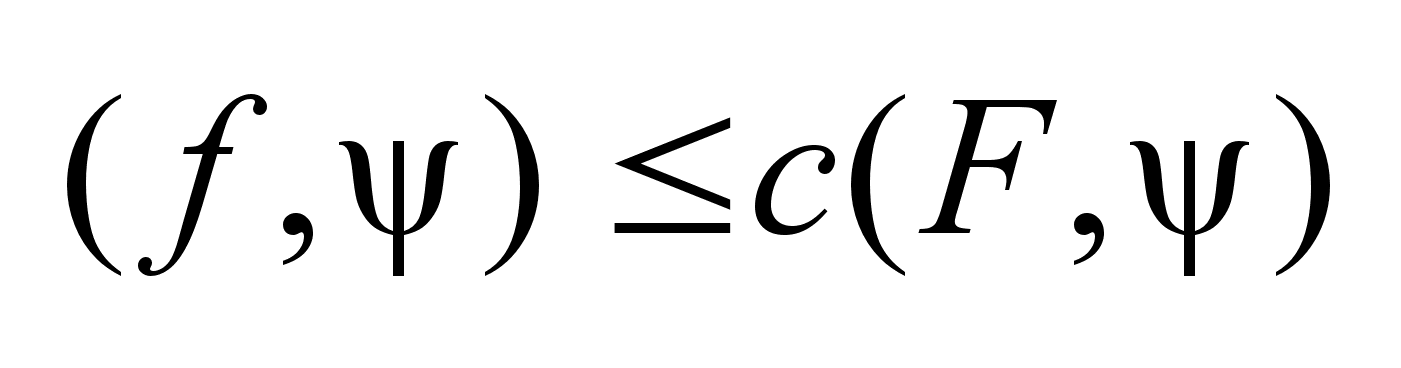 .
В обратную
сторону: .
В обратную
сторону:
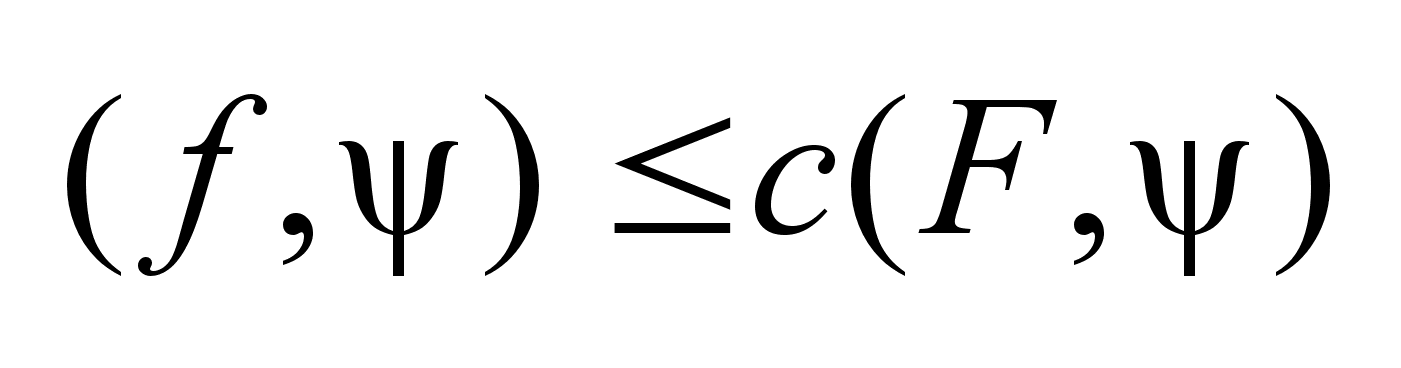 ,
когда ,
когда
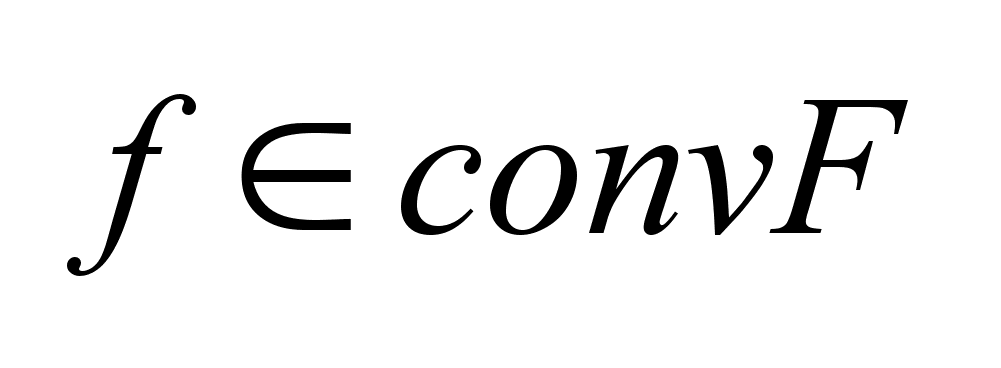 .
Следствие:
Точка .
Следствие:
Точка
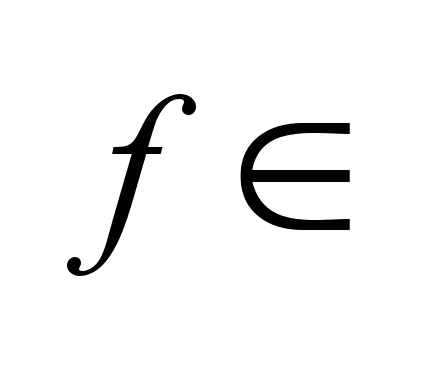 выпуклому мн-ву
выпуклому мн-ву
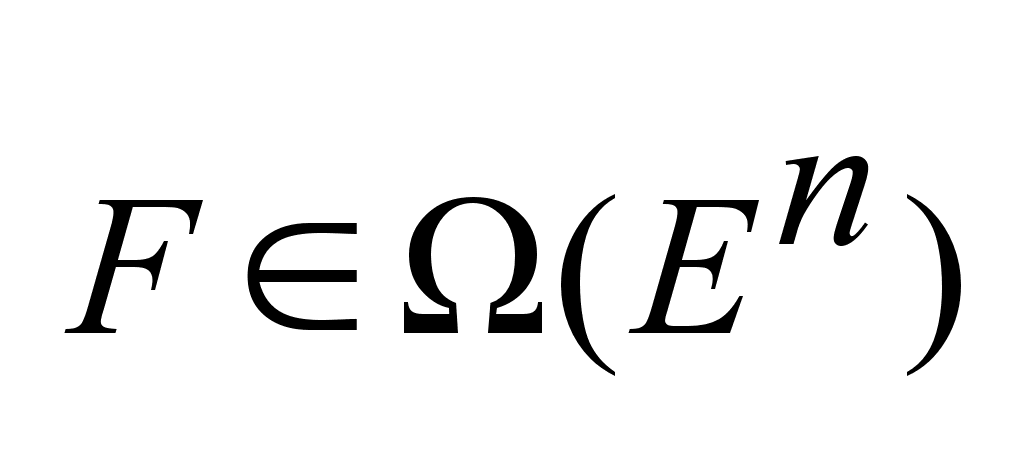 , тогда и только
тогда , когда
, тогда и только
тогда , когда
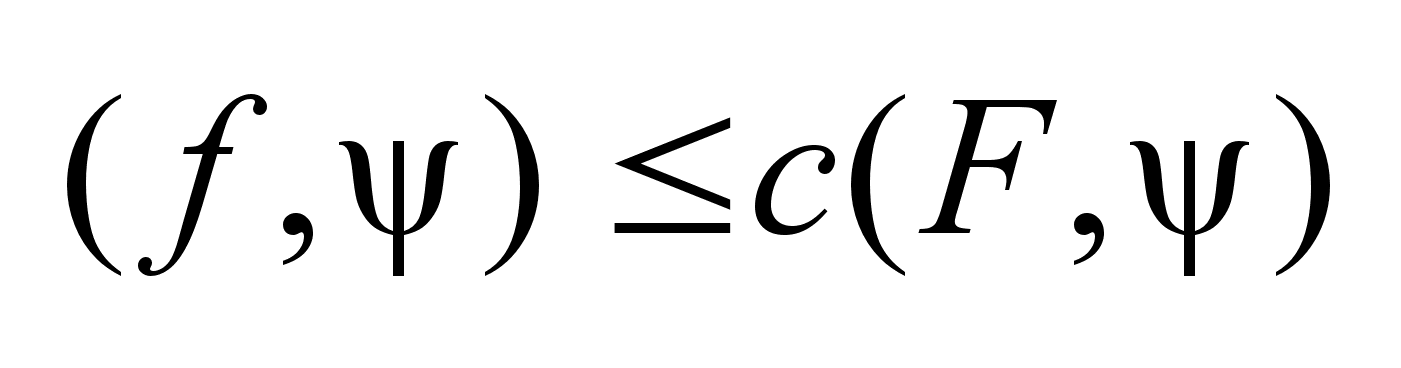 . .
10.
Пусть
задано множество
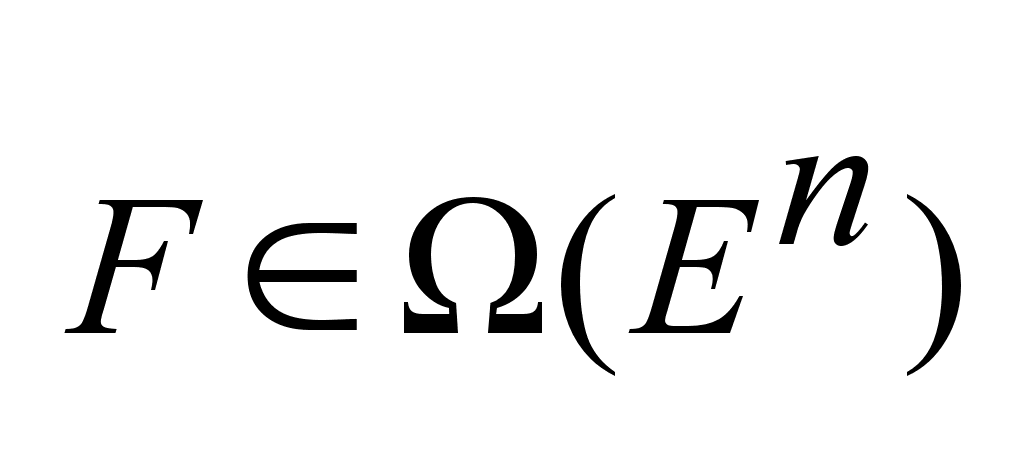 ,
а ,
а
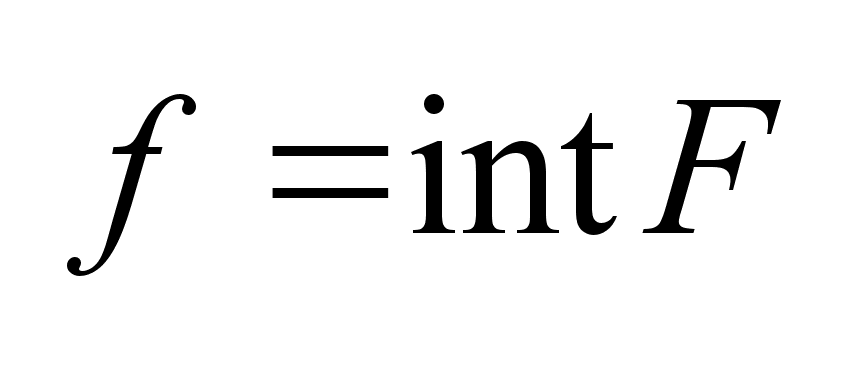 ,
тогда ,
тогда
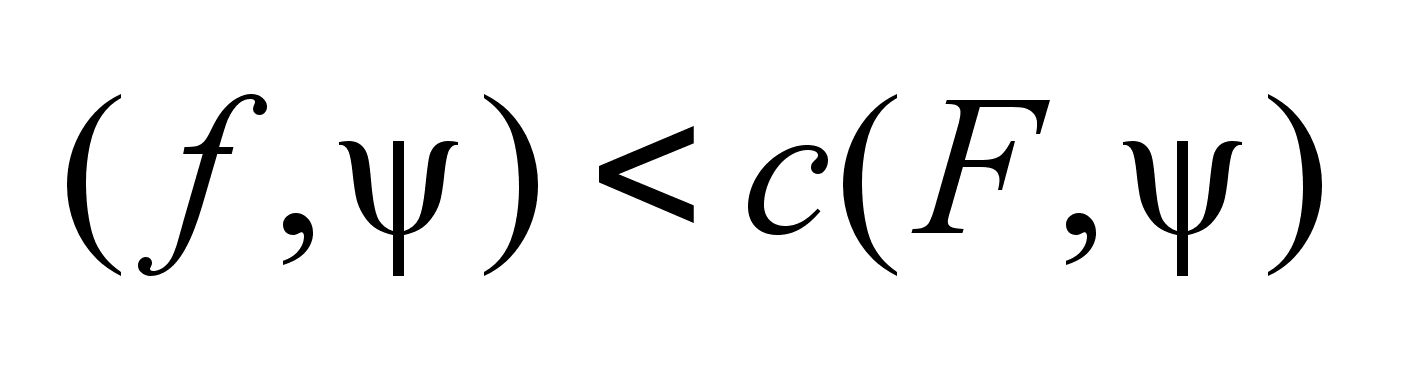 . .
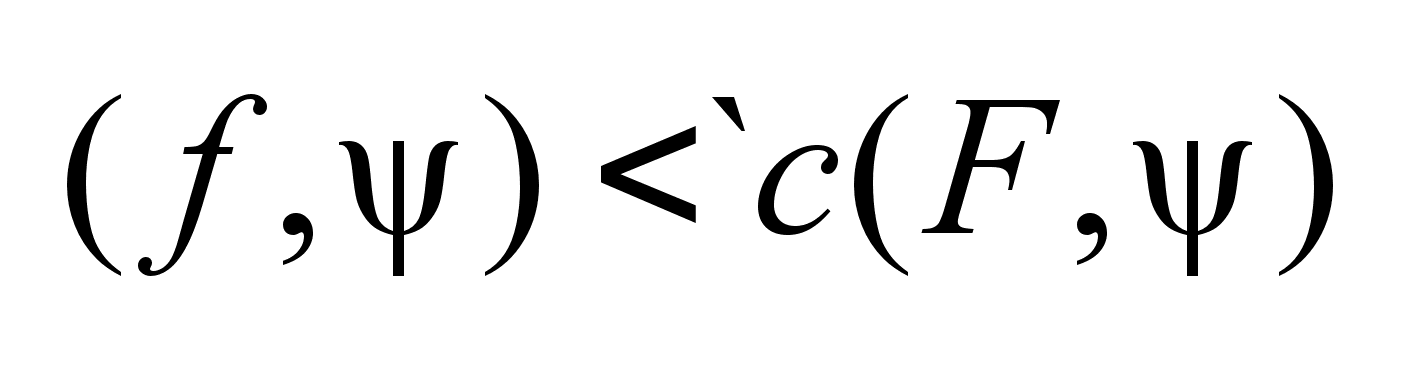 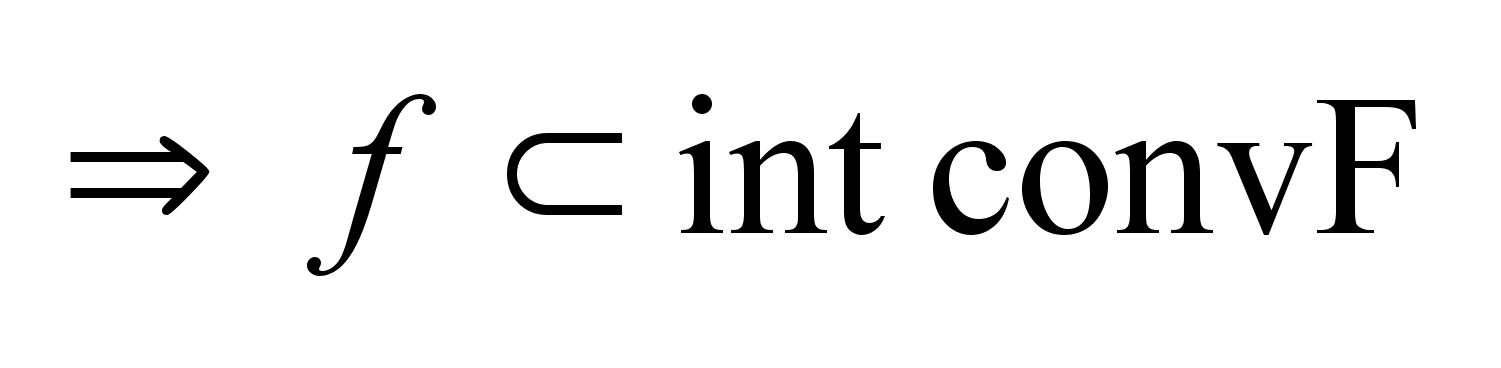 .
Следствие:
Пусть задано
множество .
Следствие:
Пусть задано
множество
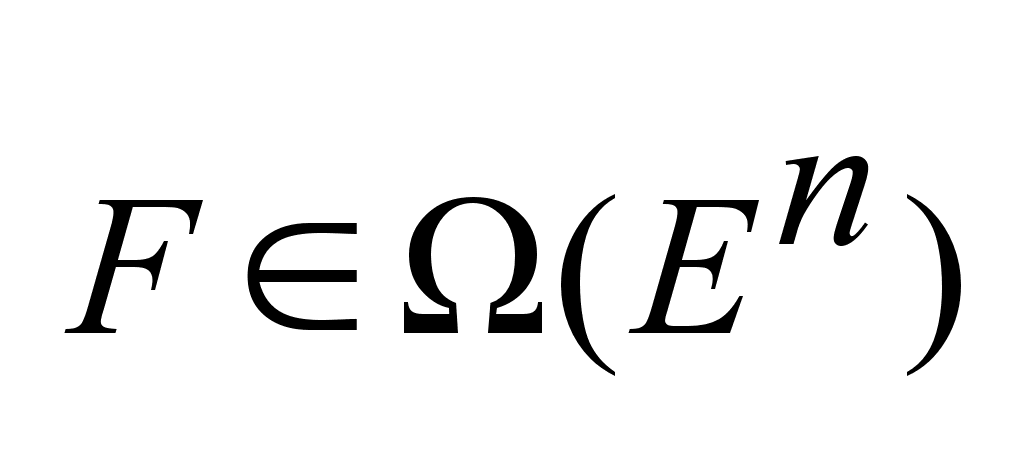 , ,
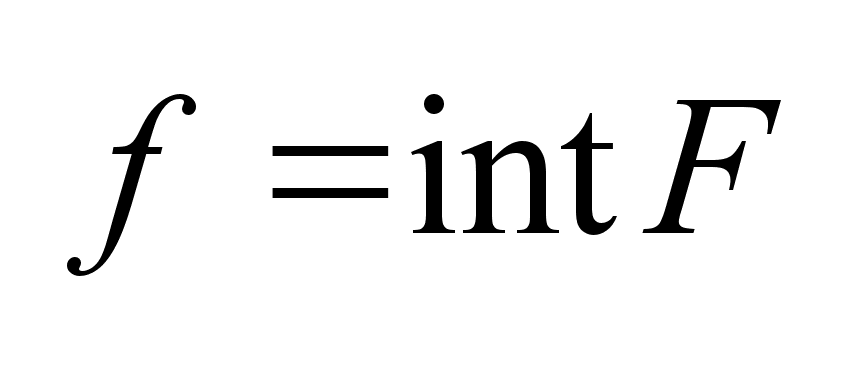 ,
тогда и только
тогда, когда ,
тогда и только
тогда, когда
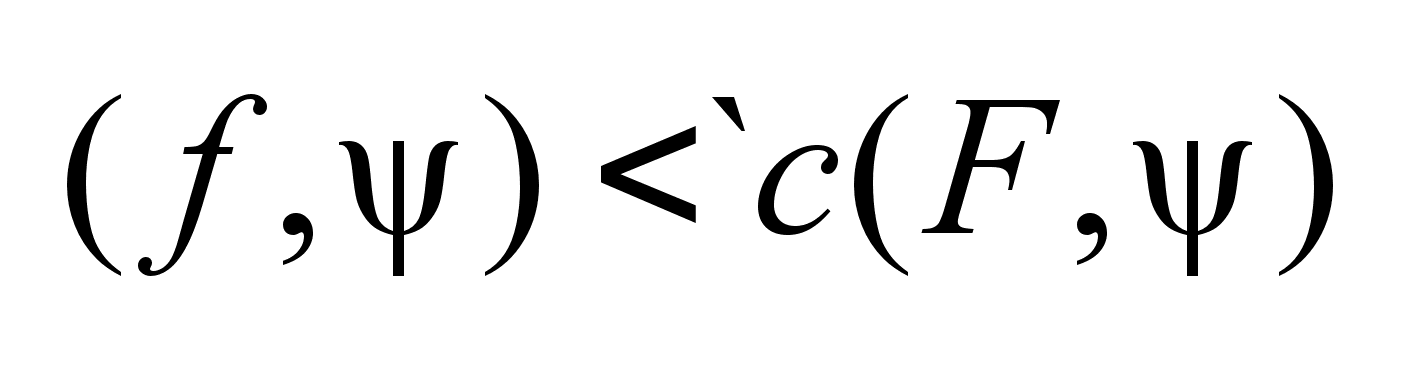 . .
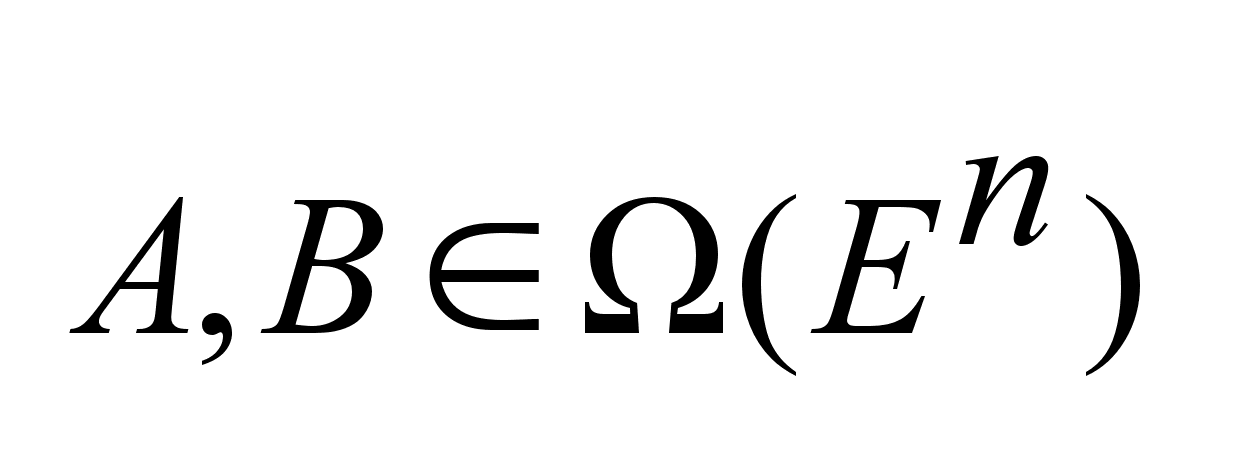 и
если
и
если
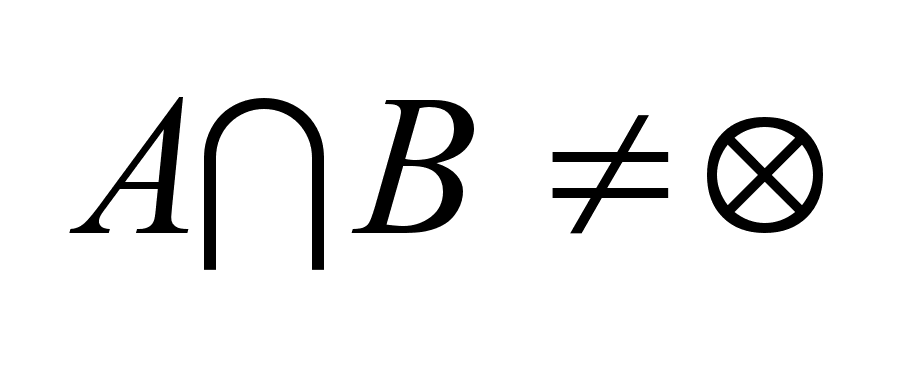 ,
то ,
то
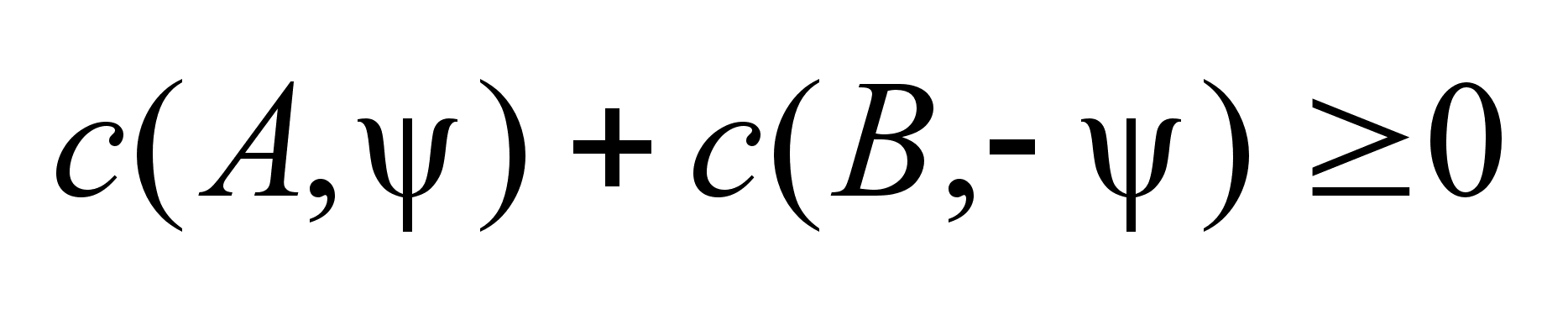 .
И наоборот:
Если .
И наоборот:
Если
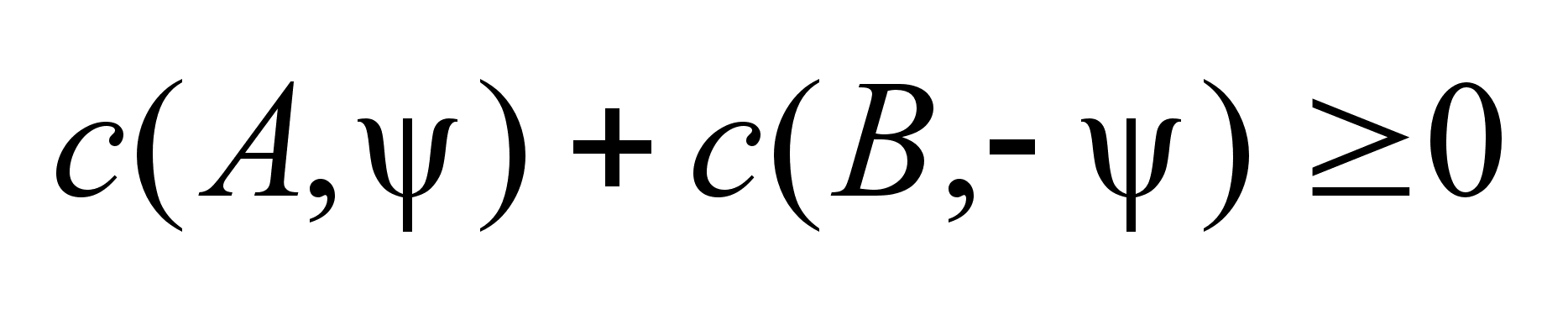 ,то ,то
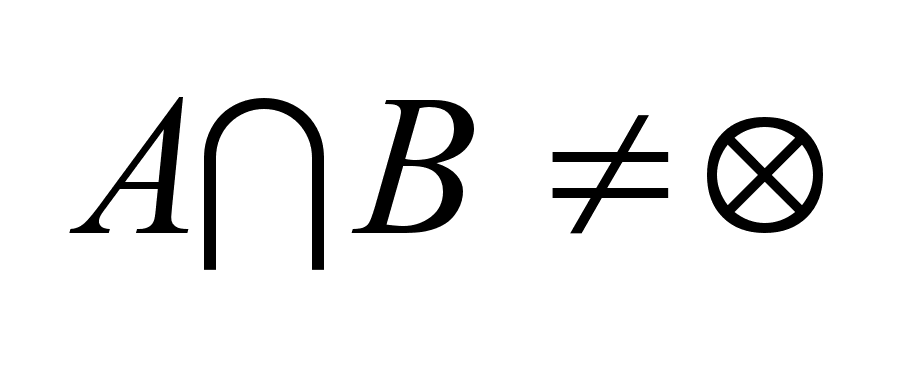 .Следствие:
Два вып. Мн-ва
пересекаются
тогда и только
тогда, когда .Следствие:
Два вып. Мн-ва
пересекаются
тогда и только
тогда, когда
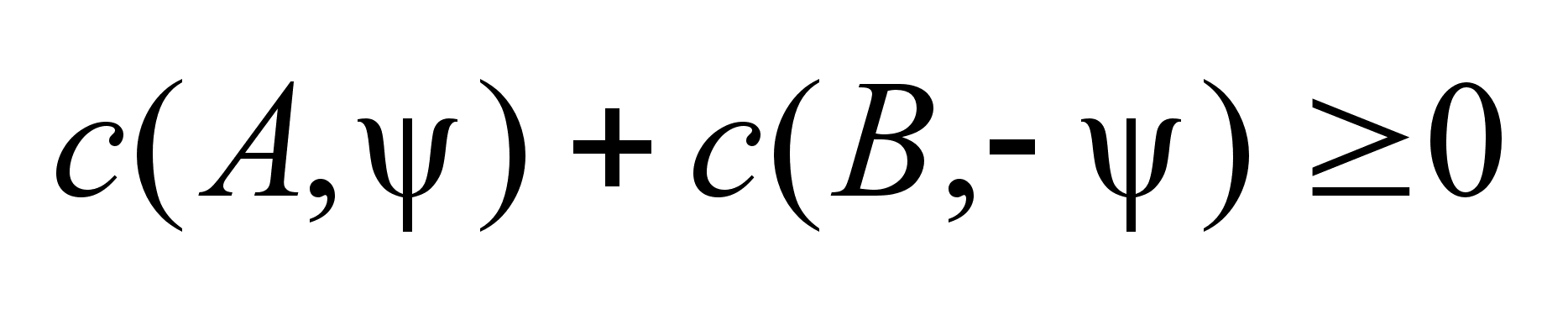 . .
8.
Непрерывные
функции. Условия
Липшица. Лемма
1,2 об условиях
Липшица для
опорных функций.
Пусть
 -два
метрических
пространства
с метриками -два
метрических
пространства
с метриками
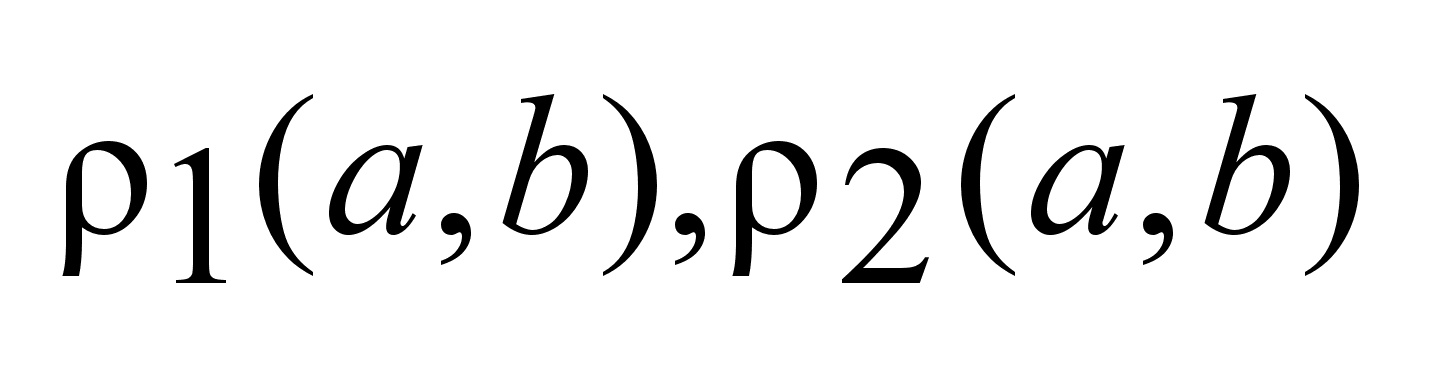 и
пусть f
отображает и
пусть f
отображает
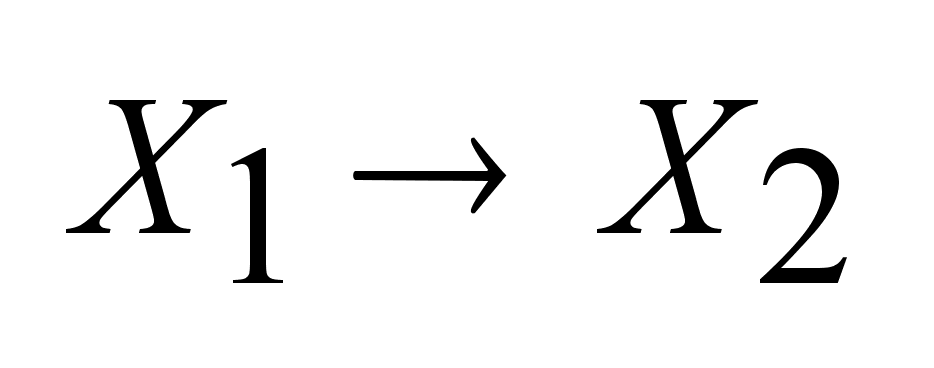 .
f
непрерывна
в точке .
f
непрерывна
в точке
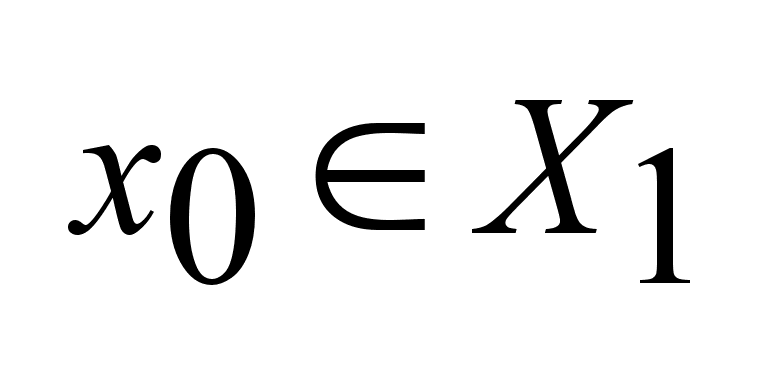 ,
если ,
если
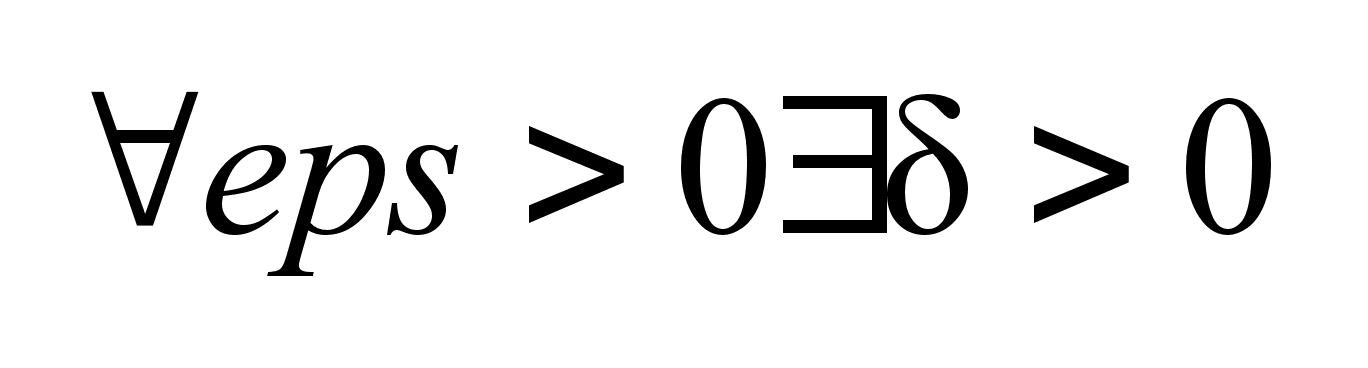 такое
что
такое
что
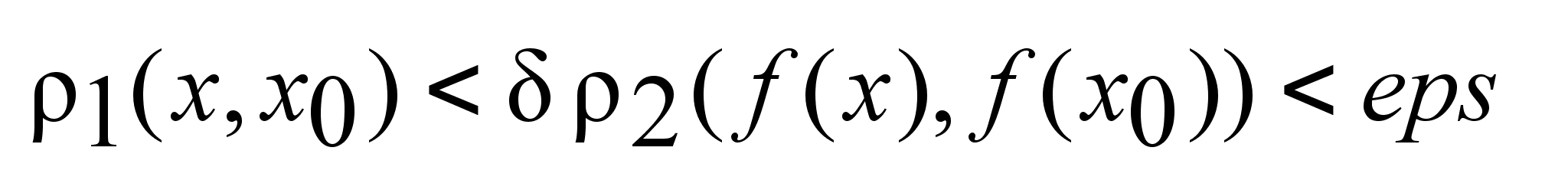 Условие
Липшица:
Функция f,
отображающая
Условие
Липшица:
Функция f,
отображающая
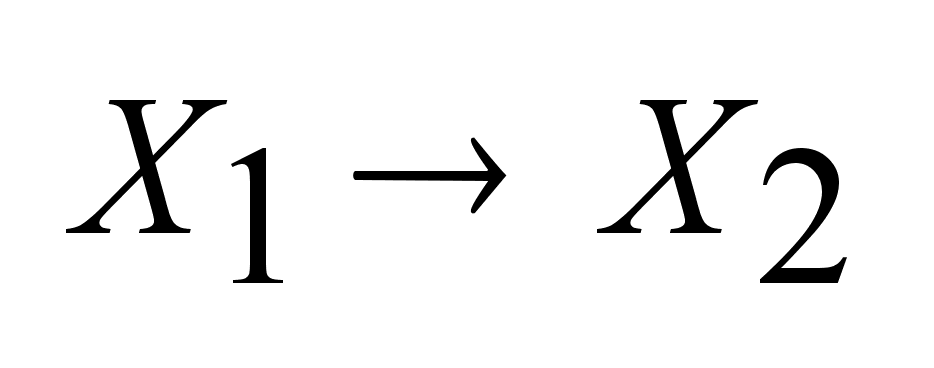 ,
удовлетворяет
условию Липшица
с const
L
, если для любых
двух точек ,
удовлетворяет
условию Липшица
с const
L
, если для любых
двух точек
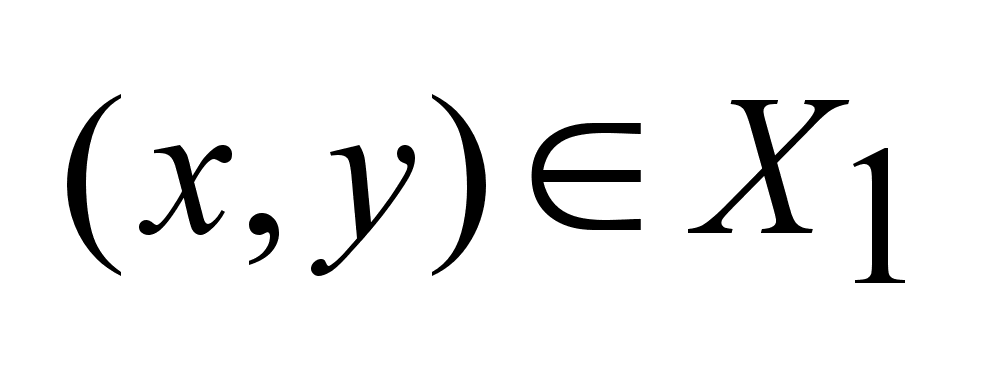 ,
выполняется
неравенство ,
выполняется
неравенство
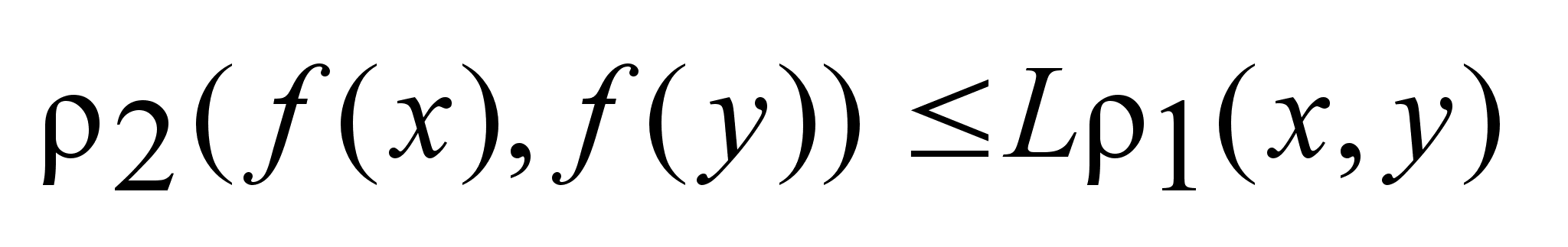 ,для опорных
функций
,для опорных
функций
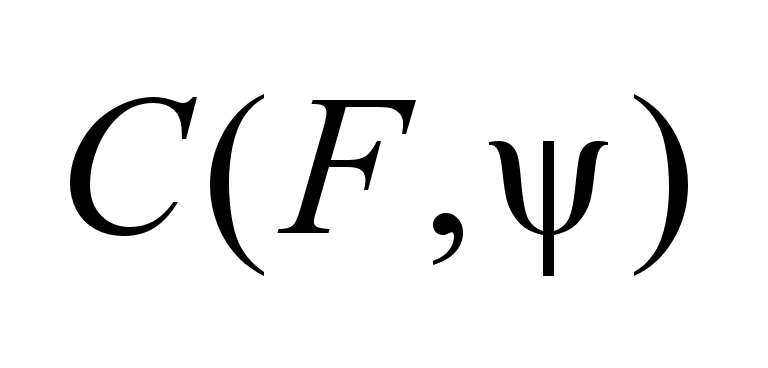 , ,
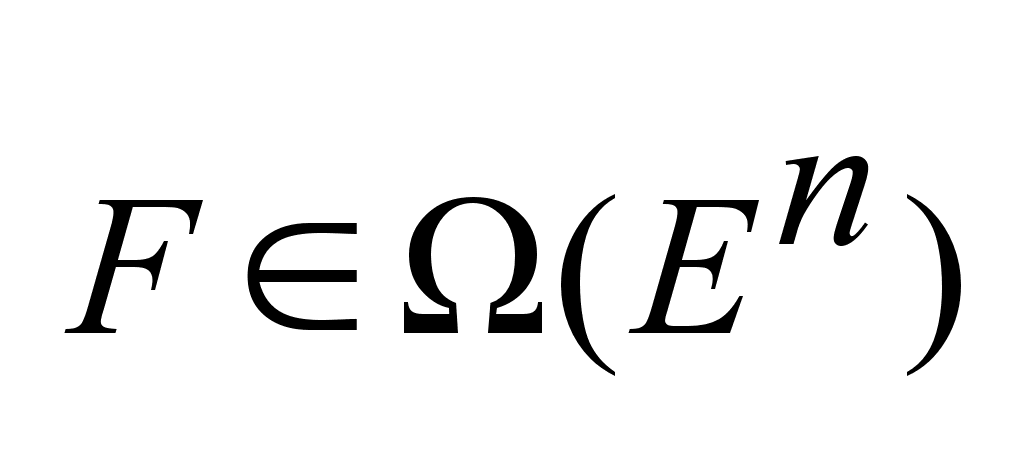 , ,
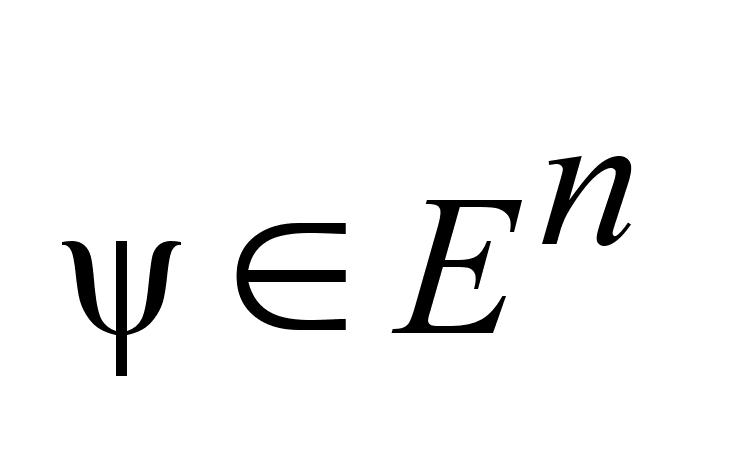 : :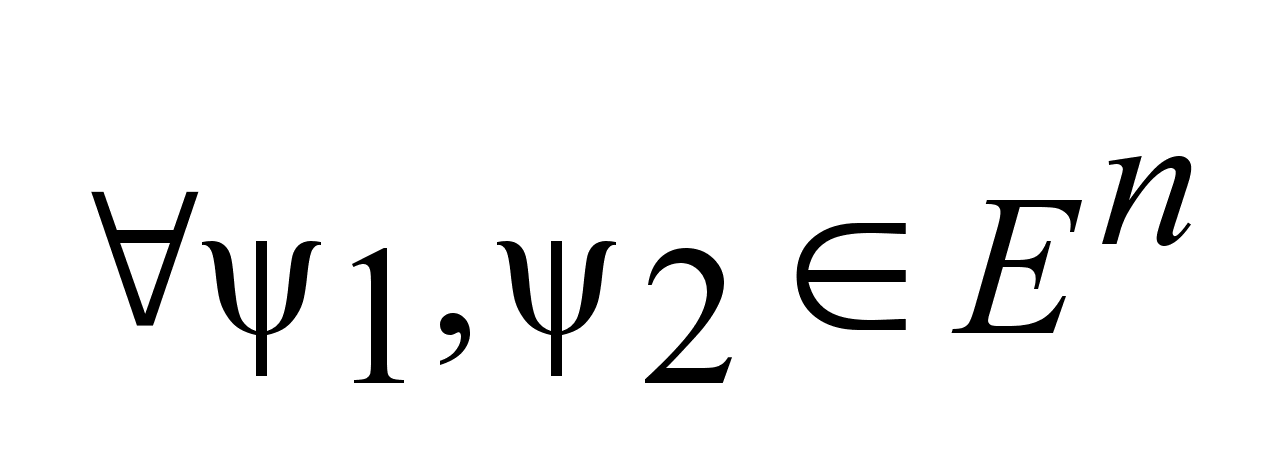 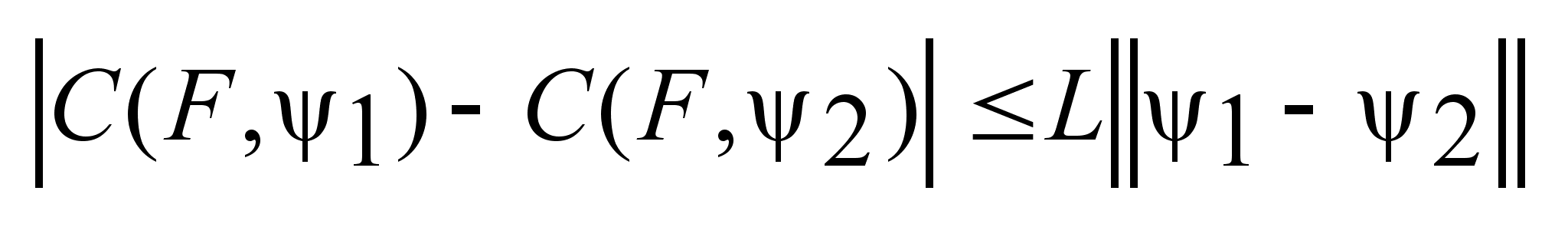
Лемма:
Опорная функция
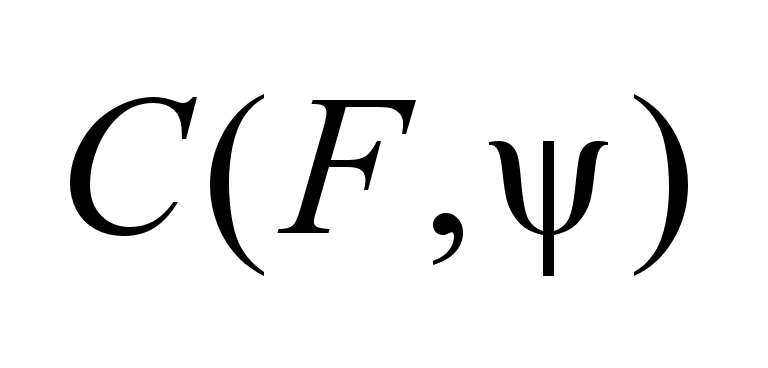 удовлетворяет
условию Липшеца
по f
с const
L=
удовлетворяет
условию Липшеца
по f
с const
L=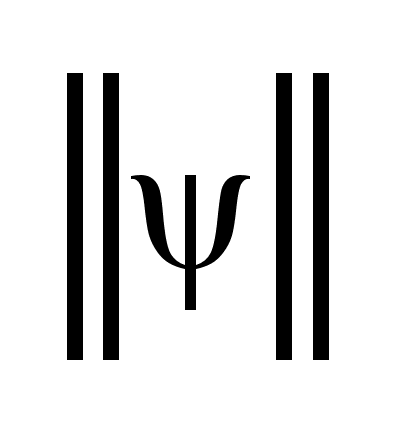 . .
Лемма:
Пусть
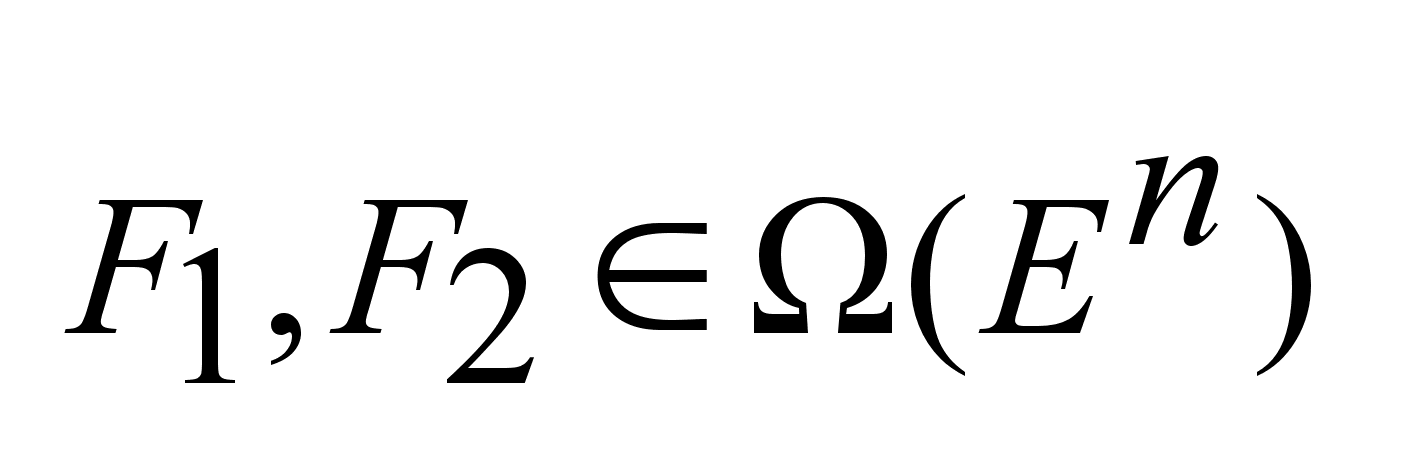 -
выпуклы, тогда
хаусдорффова
норма -
выпуклы, тогда
хаусдорффова
норма
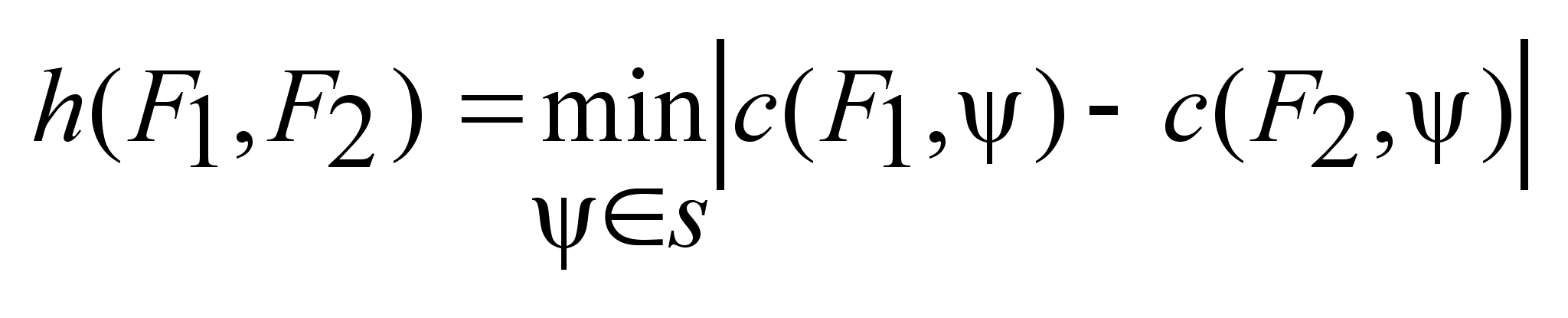 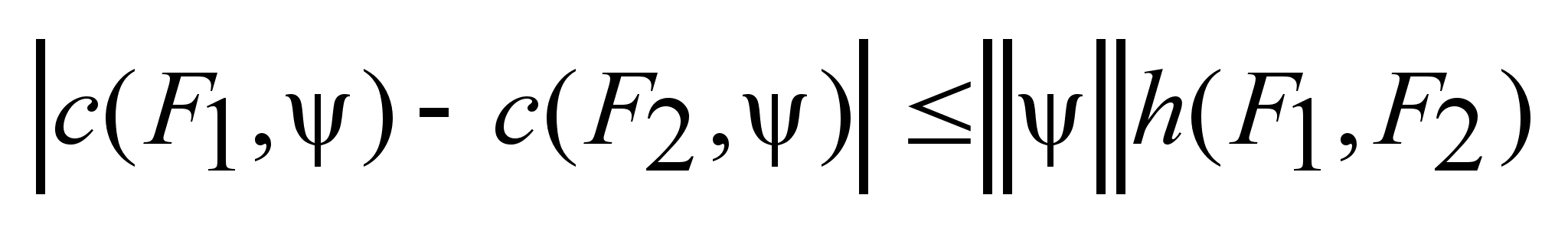
9.
Многозначные
отображения.
Многозначным
отображением
будем называть
функцию
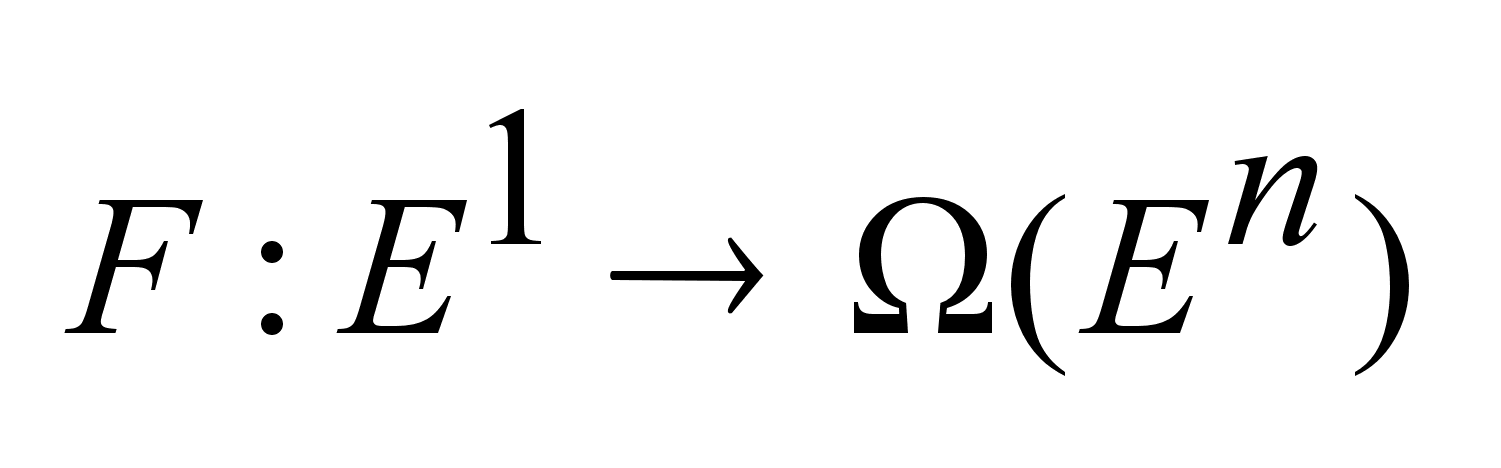 у
которой аргументом
является число,
а значением
некоторые
множества у
которой аргументом
является число,
а значением
некоторые
множества
10.
Непрерывные
и равномерно
непрерывные
многозначные
отображения.
Многозначное
отображение
F(t)
непрерывно
в точке
 ,
если для ,
если для
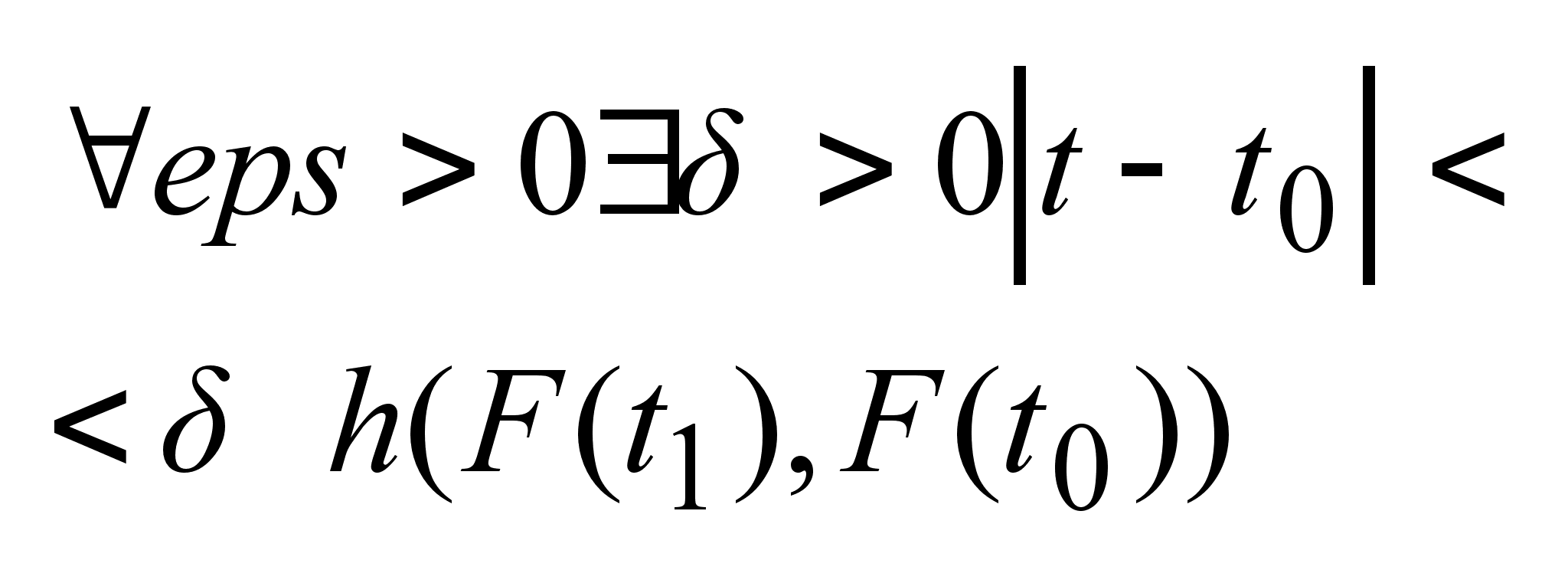 . .
Лемма:
Пусть
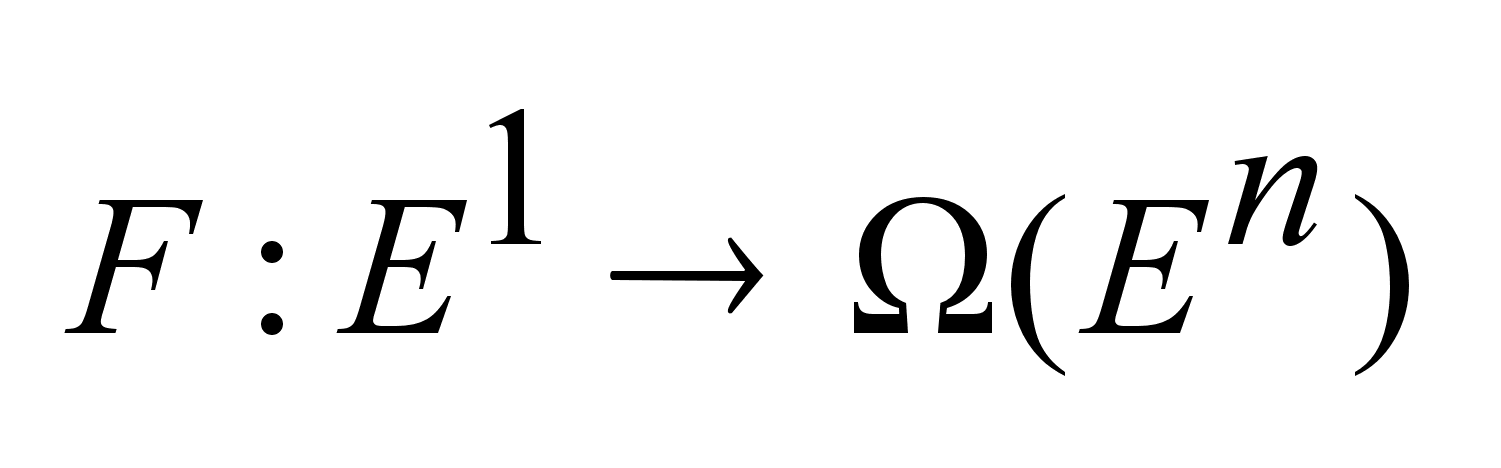 непрерывное
многозначное
отображение
, когда непрерывное
многозначное
отображение
, когда
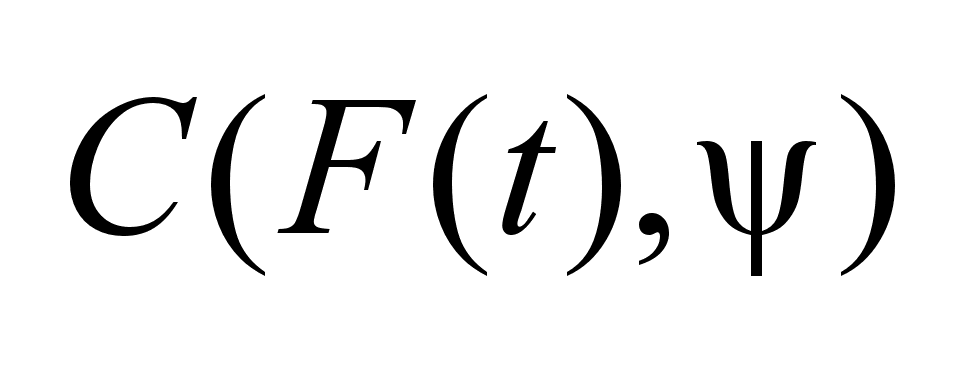 непрерывна
по t
при всяком
фиксированном непрерывна
по t
при всяком
фиксированном
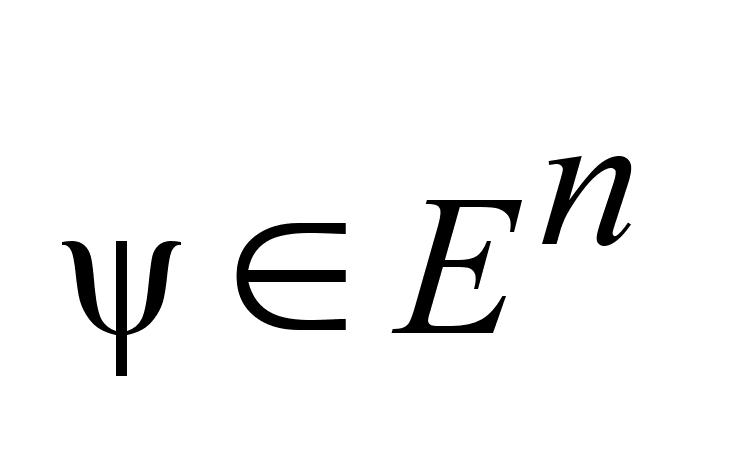 ,
более того ,
более того
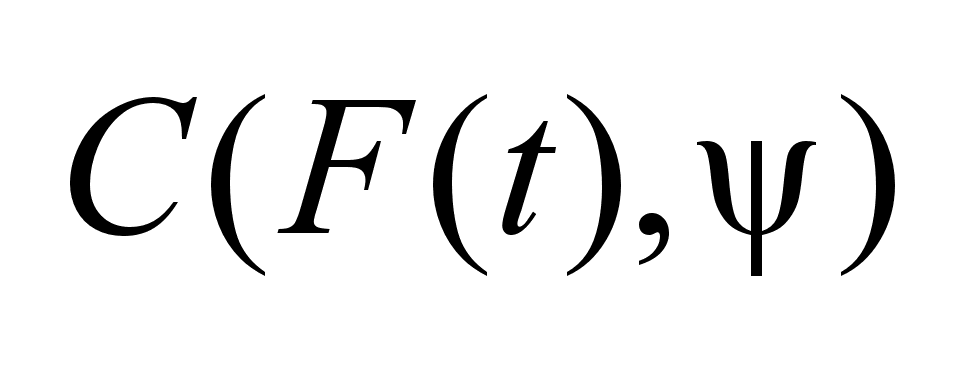 равномерно
непрерывно
по t равномерно
непрерывно
по t
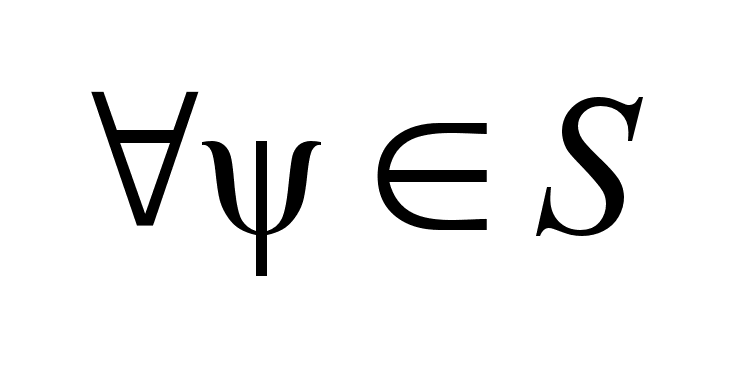 . .
Если
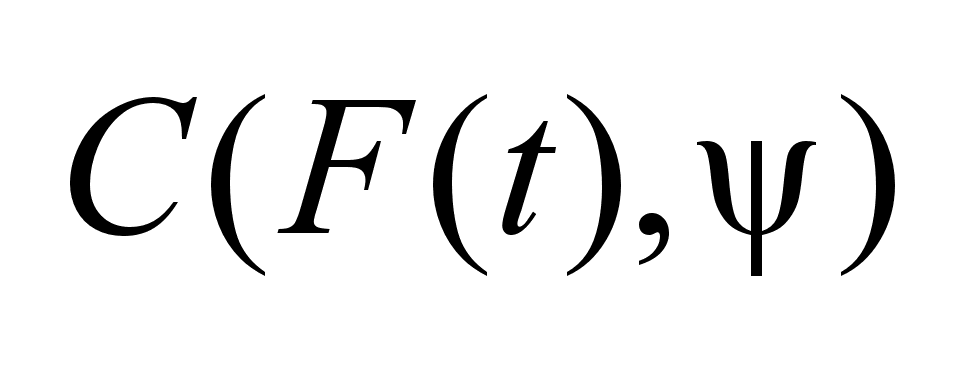 равномерно
непрерывно
по t
равномерно
непрерывно
по t
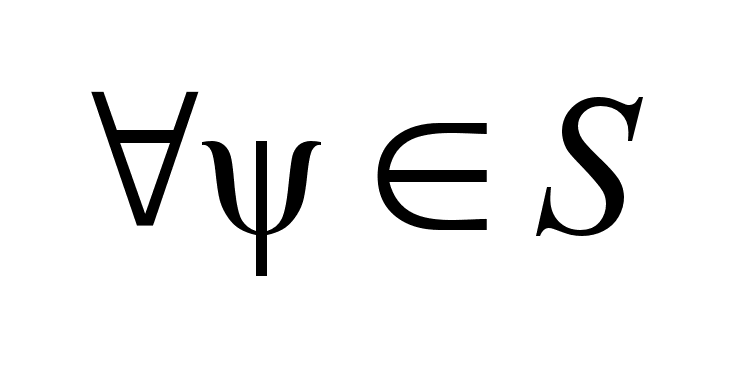 ,
то многозначное
отображение
conv
F(t) непрерывно. ,
то многозначное
отображение
conv
F(t) непрерывно.
11.
Измеримые
многозначные
отображения.
Лемма о равномерной
непрерывности
многозначного
отображения.
Функция
f(t)
отображающая
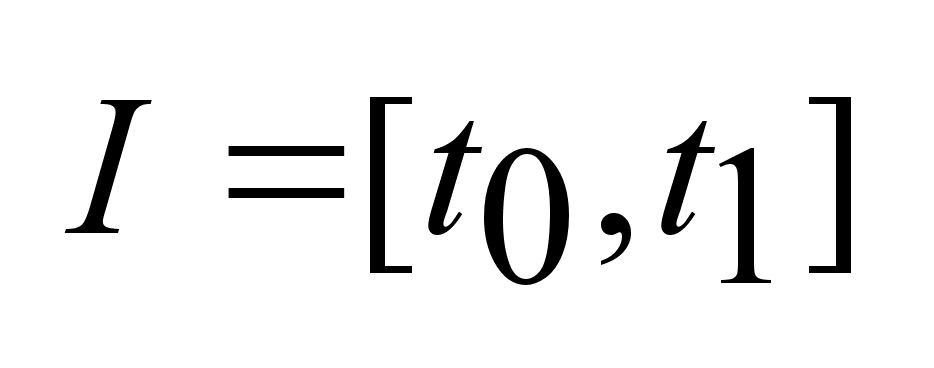 в
некоторое
метрическое
пр-во в
некоторое
метрическое
пр-во
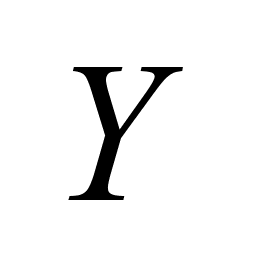 с
метрикой с
метрикой
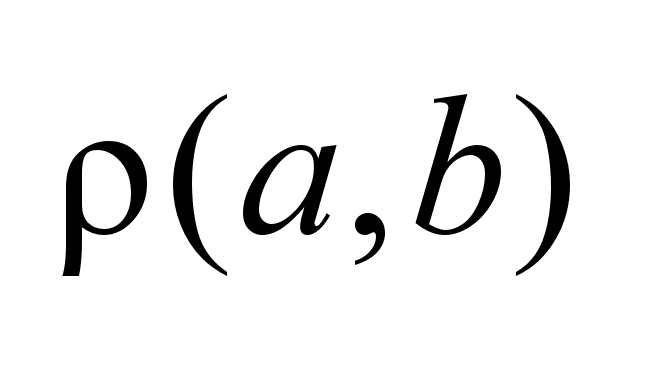 называется
измеримой, если
праобраз любого
шара называется
измеримой, если
праобраз любого
шара
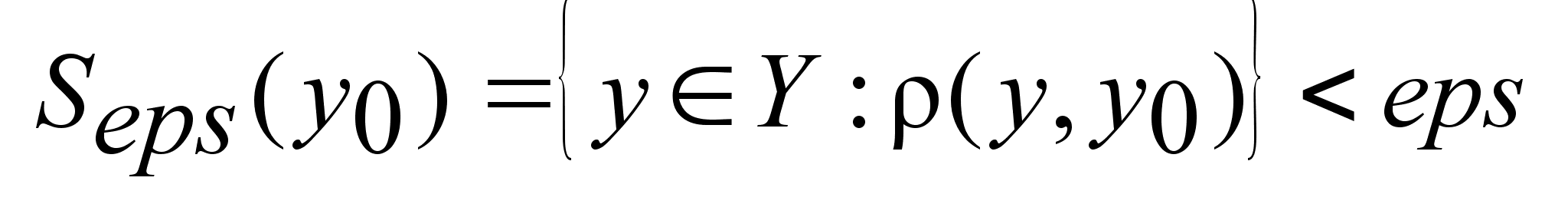 есть
мн-во измеримое. есть
мн-во измеримое.
12.
Интеграл
от многозначного
отображения.
Теорема о
непрерывности
от многозначного
отображения.
F-многозначное
отображение,
такое что F:
I 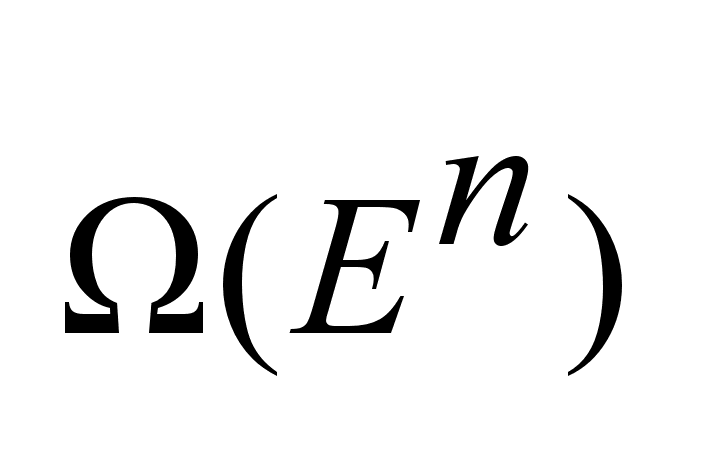 ,
где ,
где
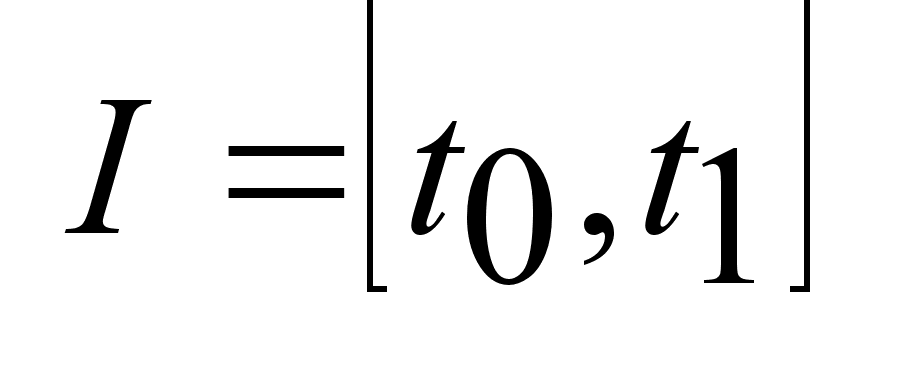 ,
,
 -замкнутое,
ограниченное,
не пустое, компактное
множество. -замкнутое,
ограниченное,
не пустое, компактное
множество.
Интегралом
от многозначного
отображения
на отрезке I
называется
множество G
(G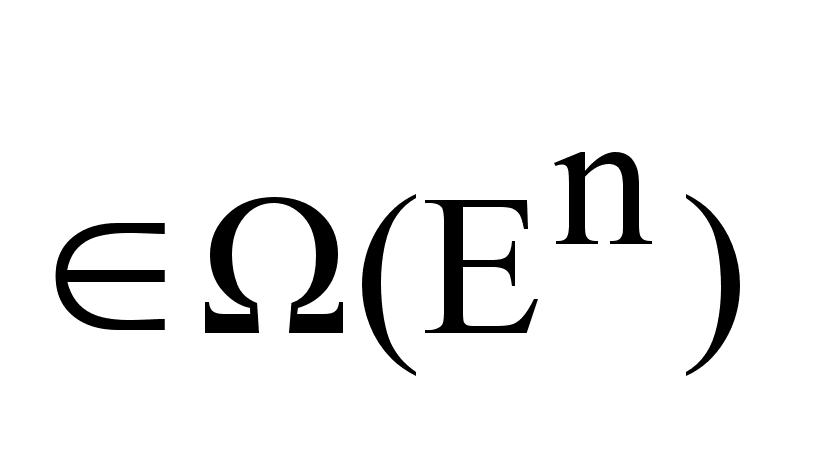 )
вида: )
вида:
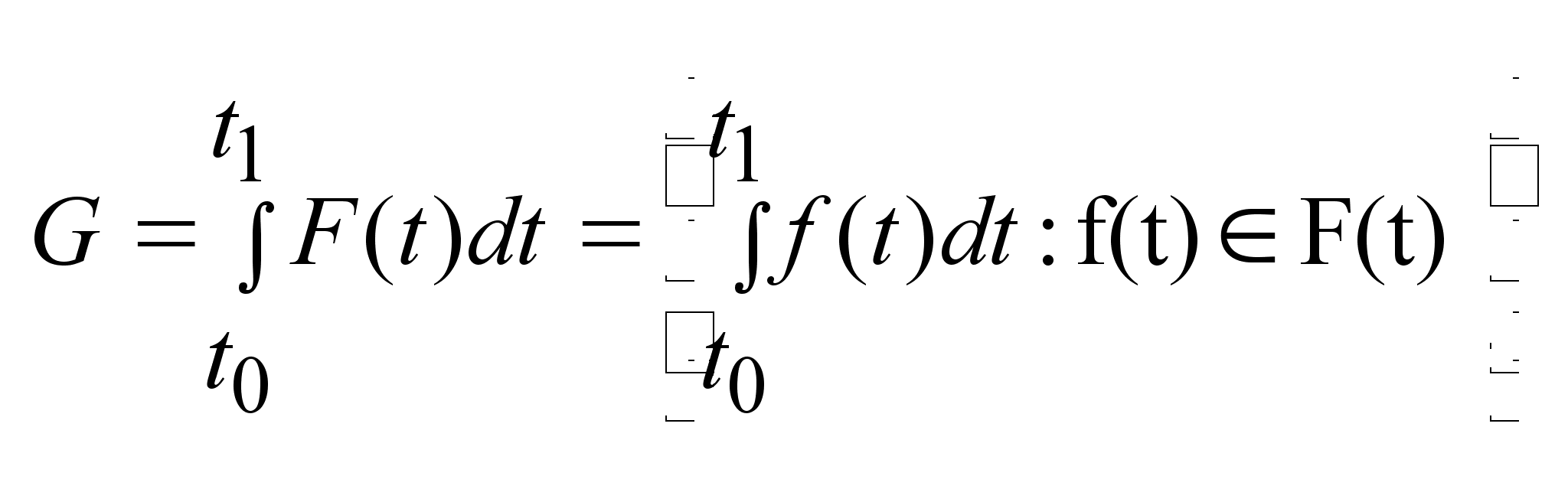 .
Это мн-во значений
интеграла по
всем однозначным
ветвям отображения .
Это мн-во значений
интеграла по
всем однозначным
ветвям отображения
F(t)
.
Теорема
3:
Пусть многозначное
отображение
F(t)
измеримо и
удовлетворяет
условию:
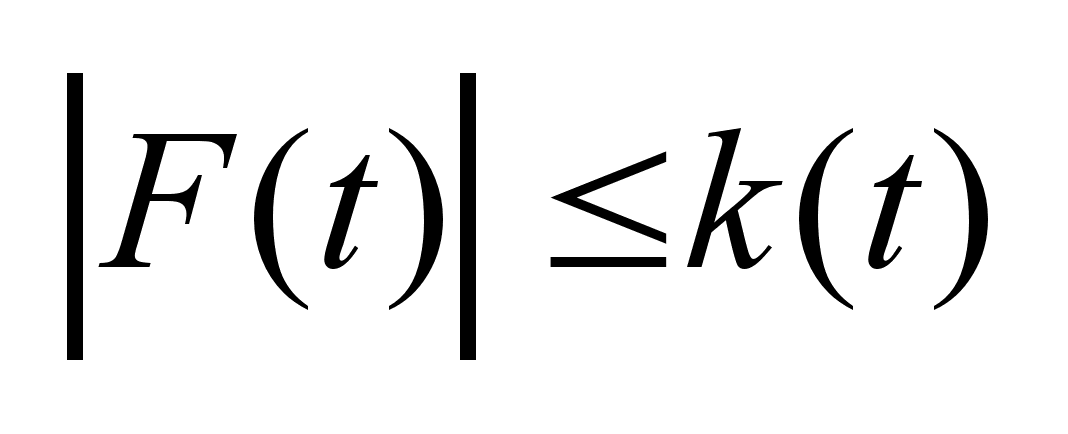 ,
где k(t)-
скалярная
функция, интегрируемая
по Лебегу на
отрезке I и
измерима, тогда ,
где k(t)-
скалярная
функция, интегрируемая
по Лебегу на
отрезке I и
измерима, тогда
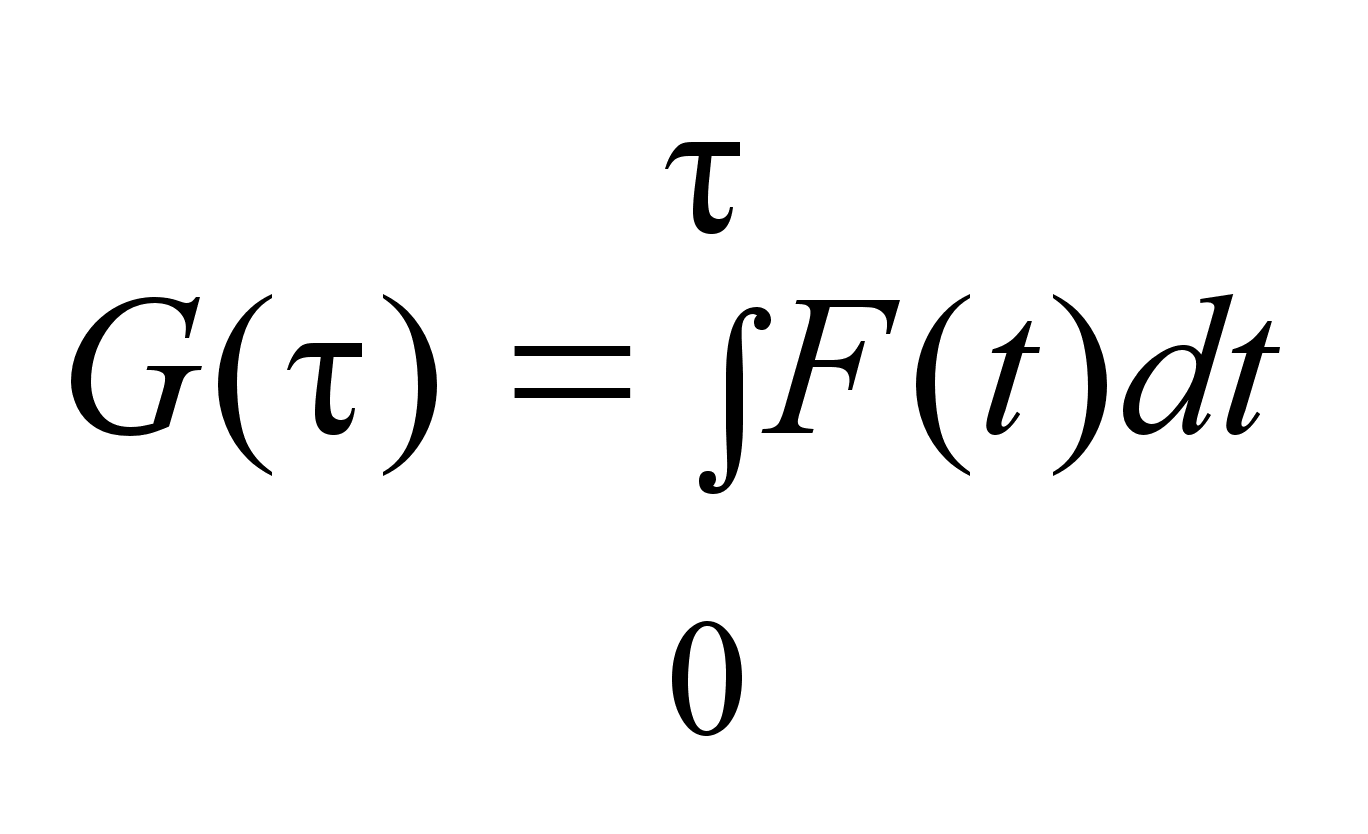 непрерывна
на отр. I
. непрерывна
на отр. I
.
Опорная
функция
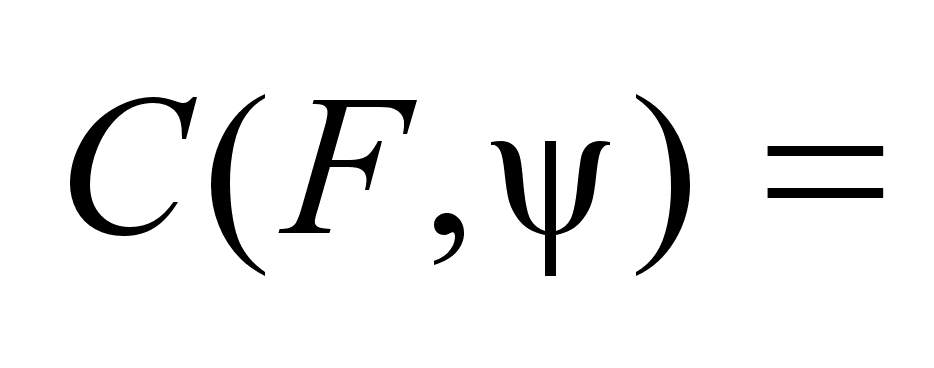 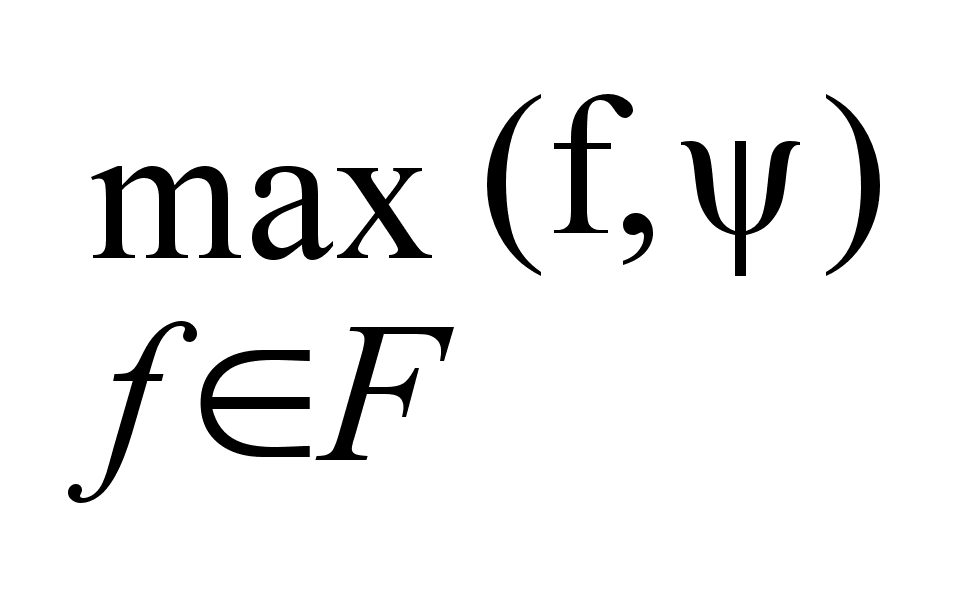 ,
где
F ,
где
F , ,
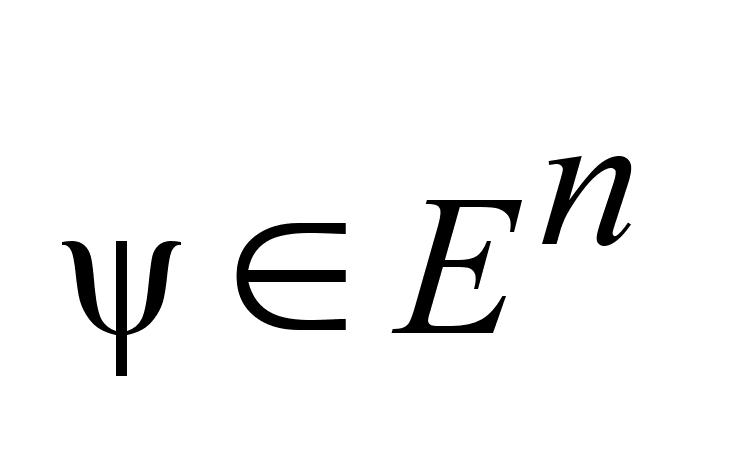 . .
13.
Теоремы
1, 2 о других видах
многозначных
отображений.
F-многозначное
отображение,
такое что F:
I 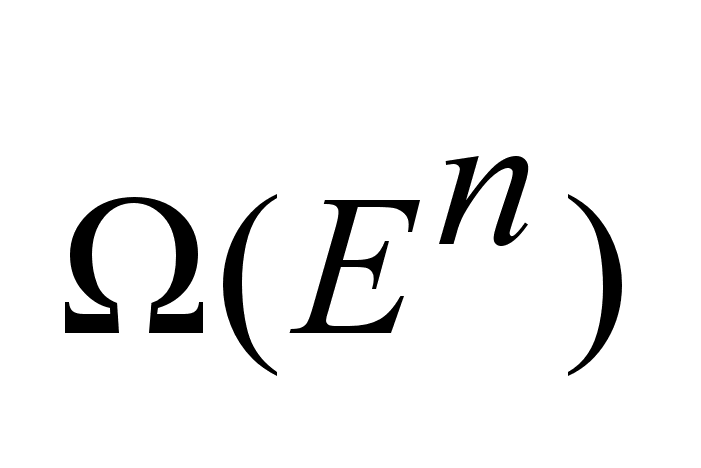 ,
где ,
где
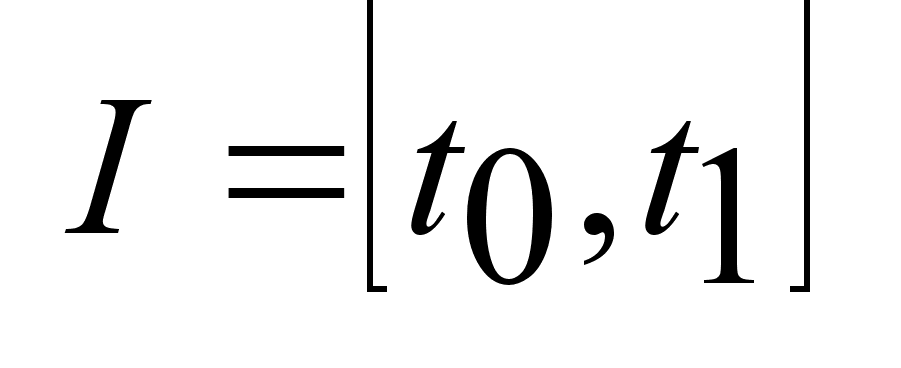 ,
,
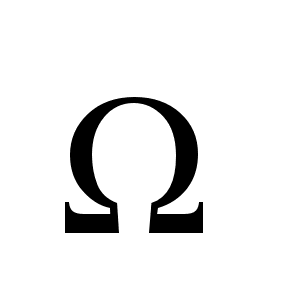 -замкнутое,
ограниченное,
не пустое, компактное
множество. -замкнутое,
ограниченное,
не пустое, компактное
множество.
Интегралом
от многозначного
отображения
на отрезке I
называется
множество G
(G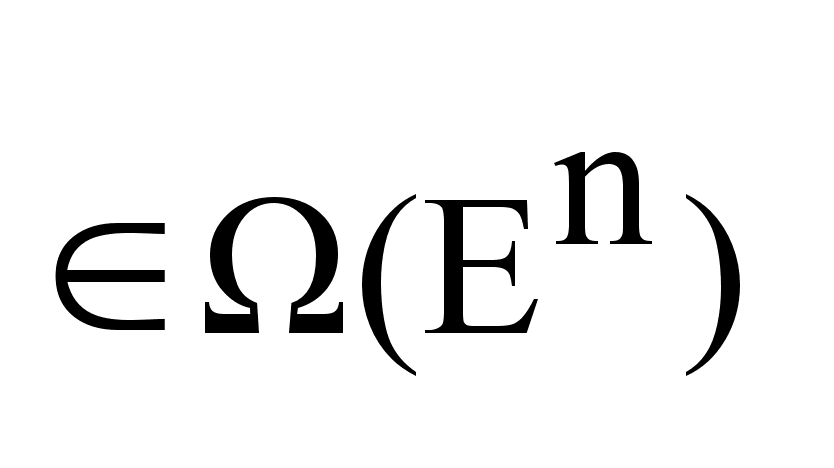 )
вида: )
вида:
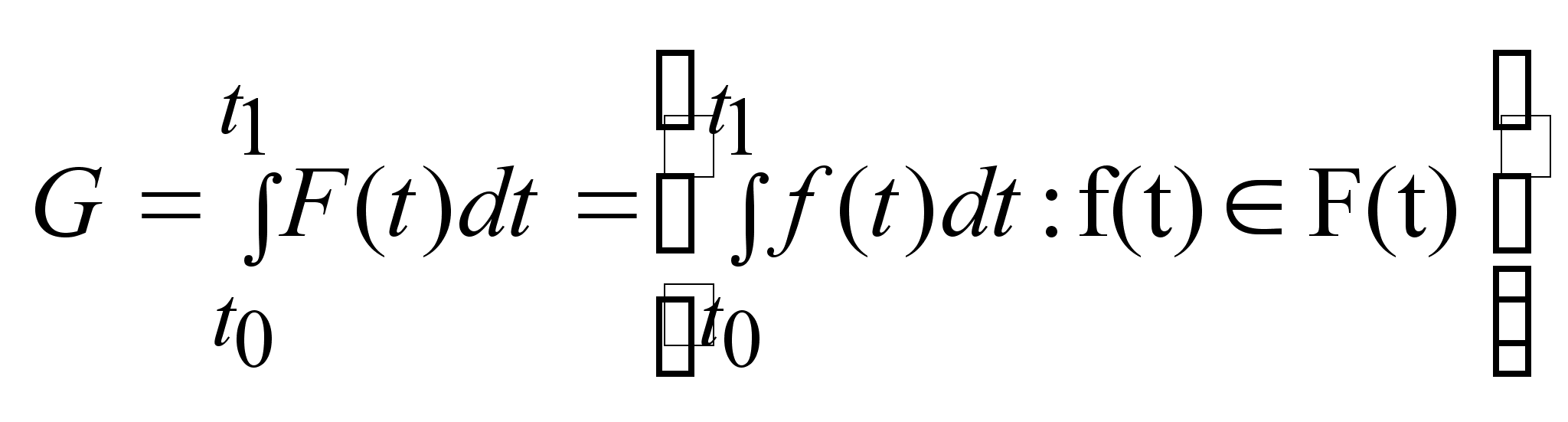 .
Это мн-во значений
интеграла по
всем однозначным
ветвям отображения .
Это мн-во значений
интеграла по
всем однозначным
ветвям отображения
F(t)
.
Теорема
1:
Пусть
многозначное
отображение
F(t)
измеримо и
удовлетворяет
условию:
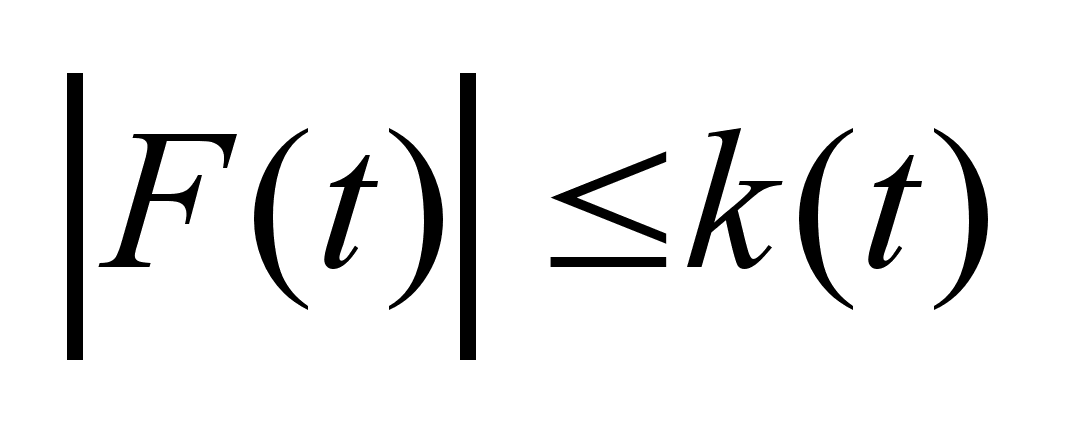 ,
где k(t)-
скалярная
функция, интегрируемая
по Лебегу на
отрезке I и
измерима, тогда
G является
не пустым, компактным
множеством
в пространстве ,
где k(t)-
скалярная
функция, интегрируемая
по Лебегу на
отрезке I и
измерима, тогда
G является
не пустым, компактным
множеством
в пространстве
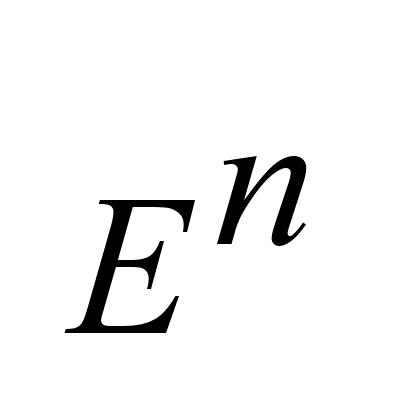 , ,
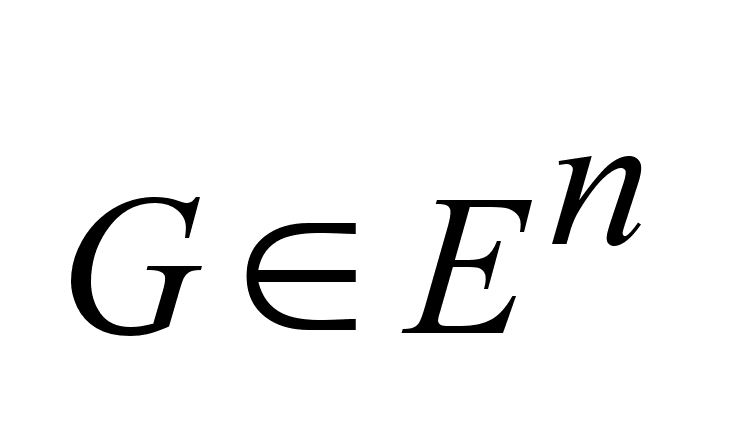 и
выпукло. и
выпукло.
Теорема
2 :
Пусть
многозначное
отображение
F(t)
измеримо и
удовлетворяет
условию:
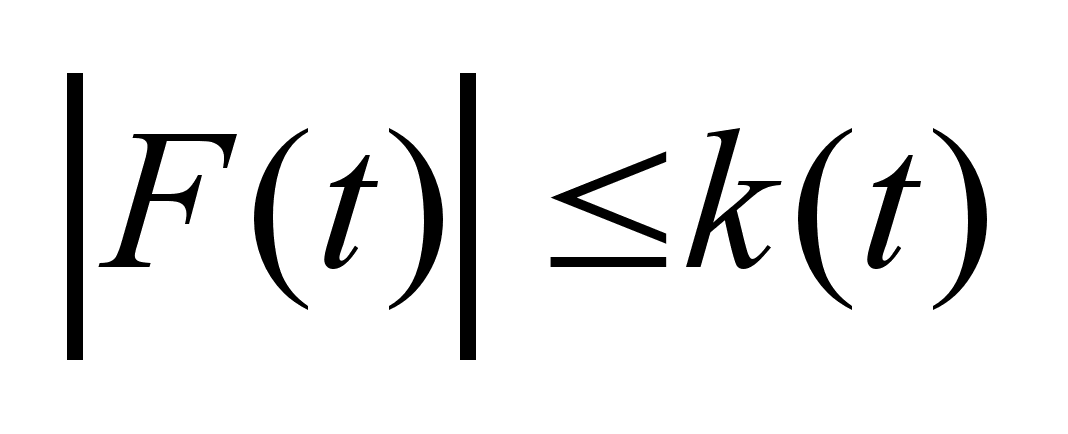 ,
где k(t)-
скалярная
функция, интегрируемая
по Лебегу на
отрезке I и
измерима, тогда
опорная функция ,
где k(t)-
скалярная
функция, интегрируемая
по Лебегу на
отрезке I и
измерима, тогда
опорная функция
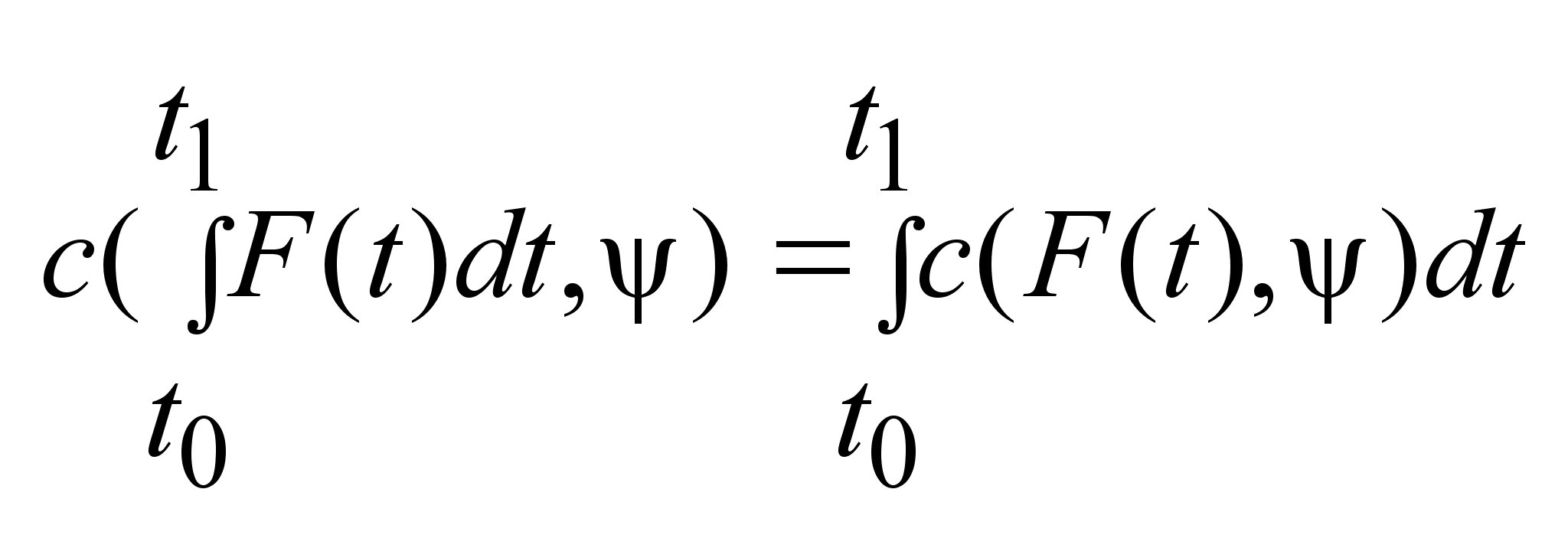 . .
14.
Линейная задача
быстродействия.
Определение
абс. непрерывной
функции. Теорема
Каратеодори.
Рассматриваем
динамический
объект, поведение
которого описывается
системой (1)
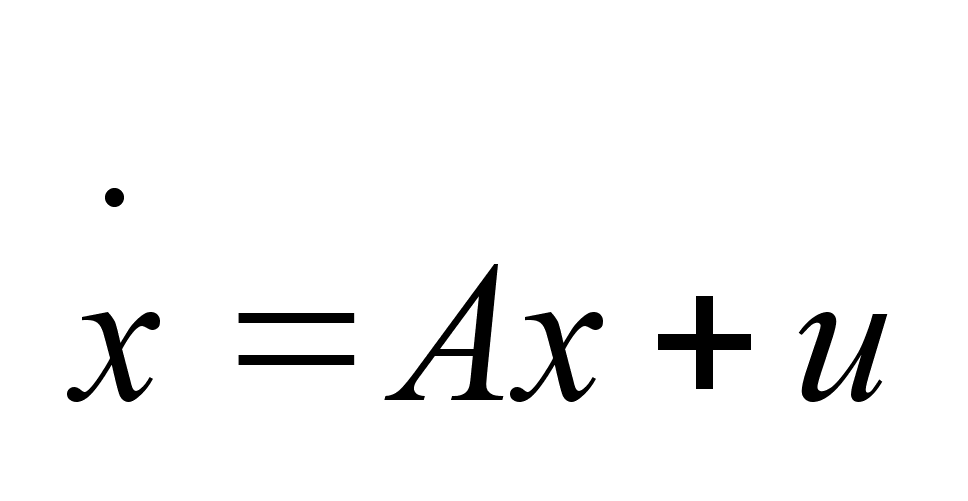 ,
x-
n-мерный
вектор, ,
x-
n-мерный
вектор,
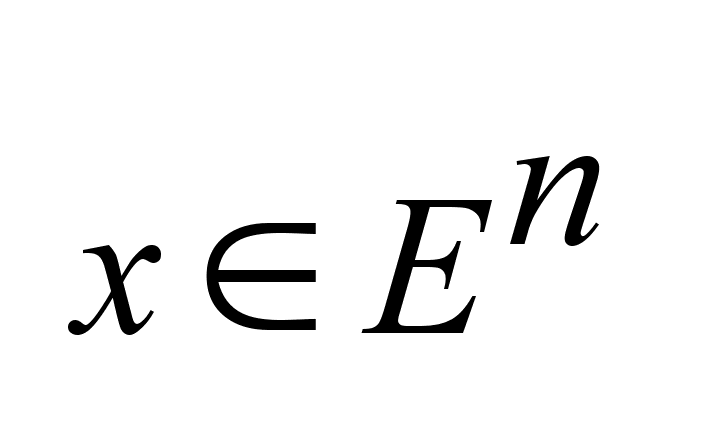 ,
A-матрица
nxn,
u
имеет ту же
размерность,
что
и ,
A-матрица
nxn,
u
имеет ту же
размерность,
что
и
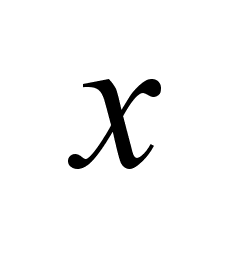 , ,
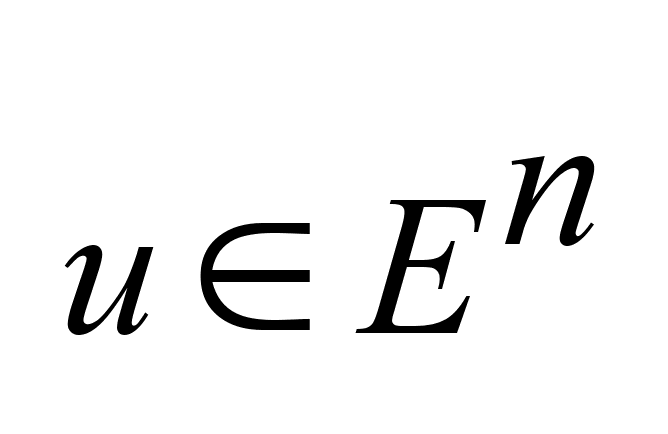 .Задано .Задано
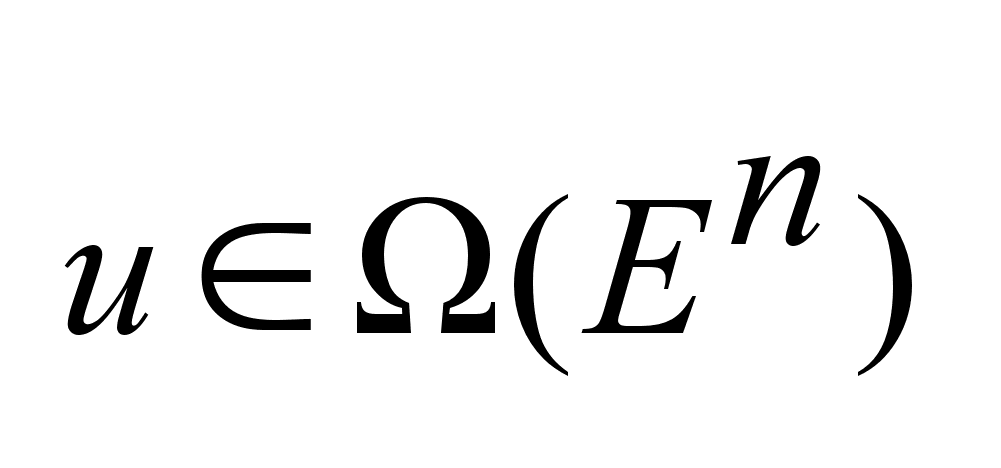 ,
u:
I ,
u:
I 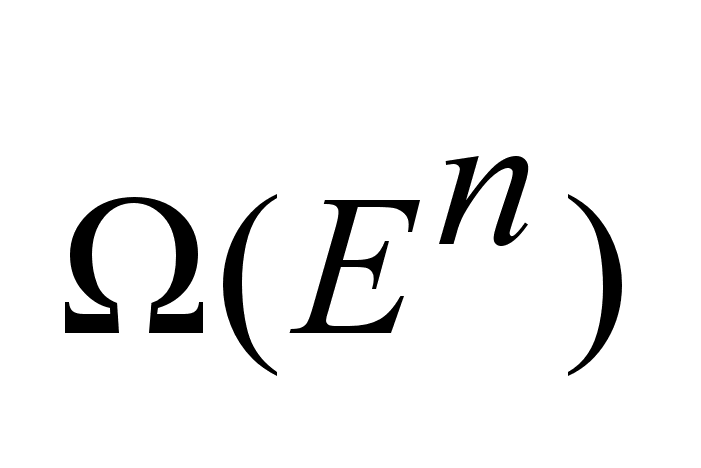 и полагается,
что u(t)
измеримо
и
и полагается,
что u(t)
измеримо
и
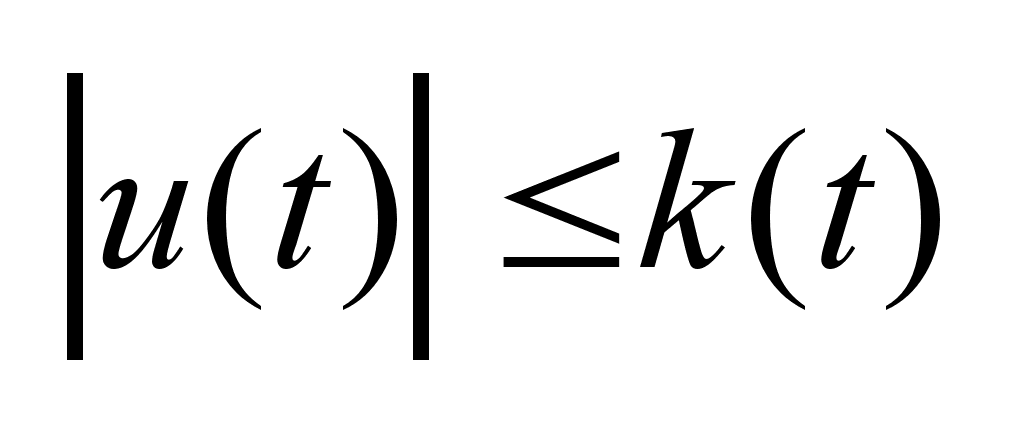 -
где
k(t)
скалярная
функция интегрируемая
по Лебегу на
отрезке I .Функция
u(t)-
называется
допустимым
управлением,
если измерима
и является
однозначной
ветвью
(2)
u(t) -
где
k(t)
скалярная
функция интегрируемая
по Лебегу на
отрезке I .Функция
u(t)-
называется
допустимым
управлением,
если измерима
и является
однозначной
ветвью
(2)
u(t) U(t)
-
ограничения
на управления
. В фазовом
пространстве U(t)
-
ограничения
на управления
. В фазовом
пространстве
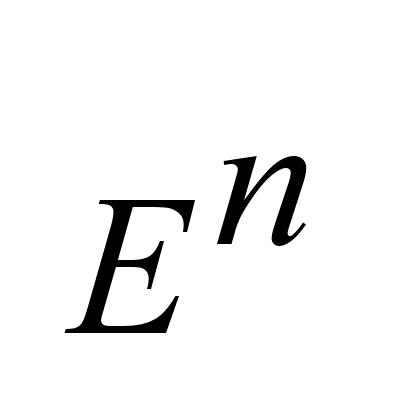 заданы
два не пустых
множества заданы
два не пустых
множества
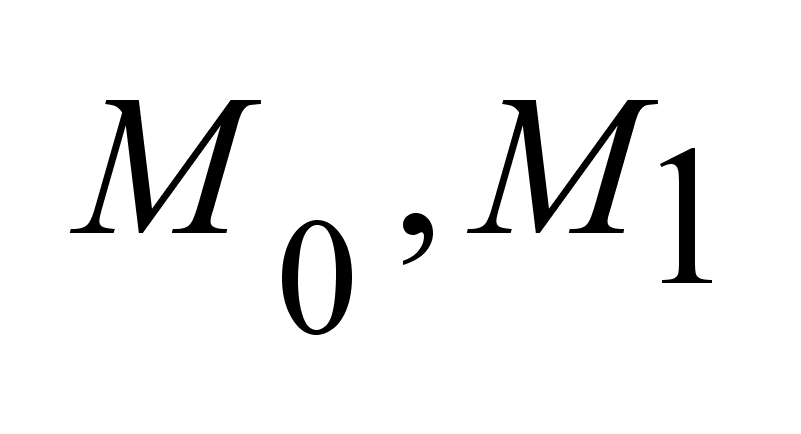 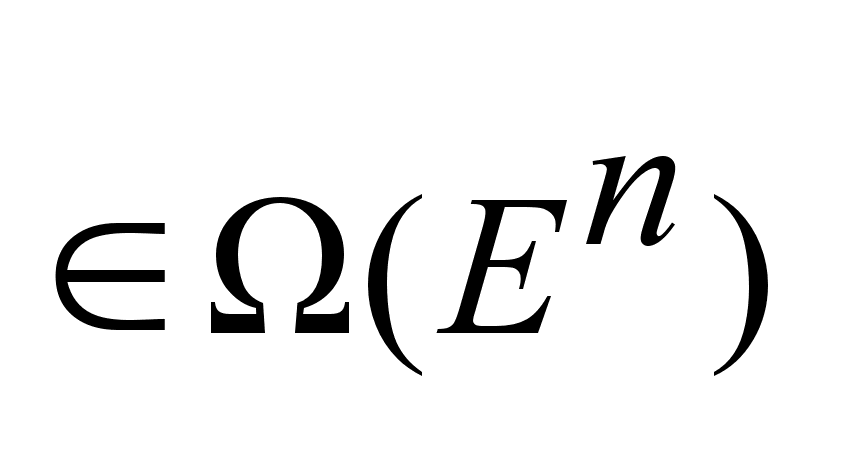 .
Допустимое
управление
u(t)
на отр.I
осуществляете
переход из
начального
мн-ва .
Допустимое
управление
u(t)
на отр.I
осуществляете
переход из
начального
мн-ва
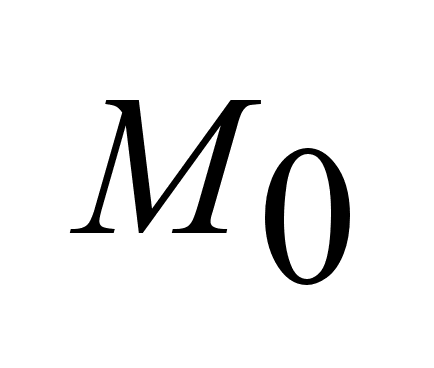 в конечное
множество
в конечное
множество
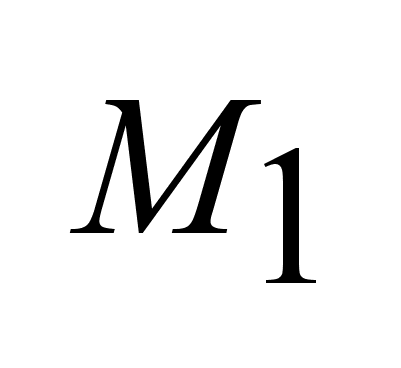 ,
если существует
решение уравнения
(1), удовлетворяющее
граничным
условиям (4) ,
если существует
решение уравнения
(1), удовлетворяющее
граничным
условиям (4)
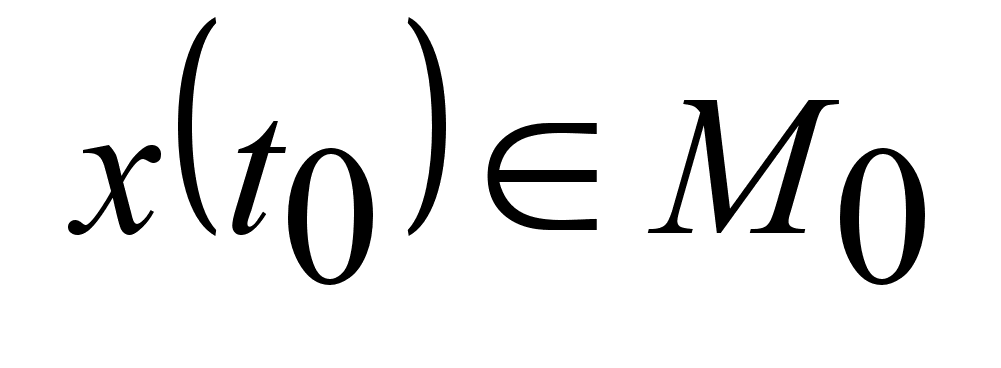 и и
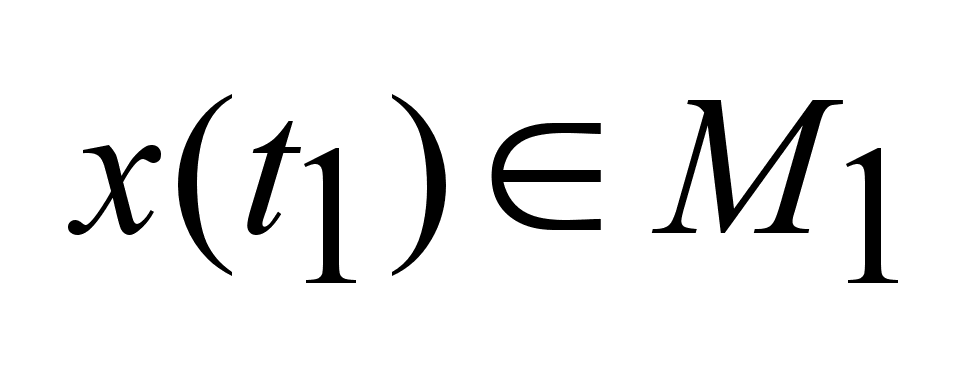 .
Цель управления-
перевод динамический
объекта из .
Цель управления-
перевод динамический
объекта из
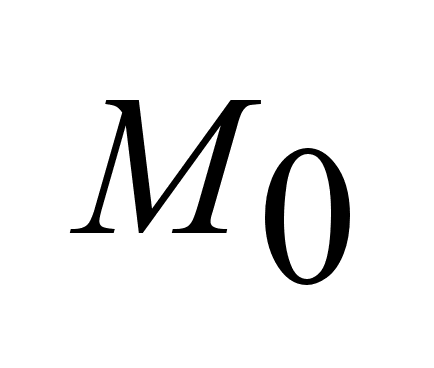 в в
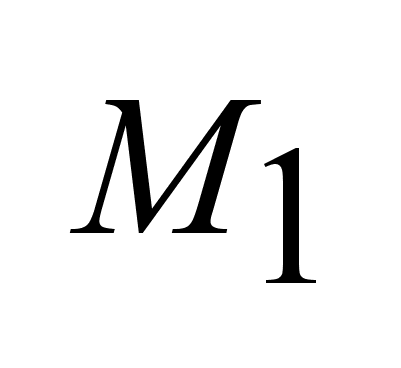 ,
а качество
определяет
функционал.
Таким функционалом
явл. время,
следовательно ,
а качество
определяет
функционал.
Таким функционалом
явл. время,
следовательно
задача
быстродействия
заключается
в нахождении
такого допустимого
управления,
которое осуществляет
переход из
множества
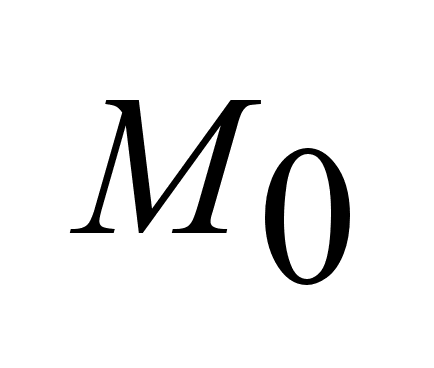 в в
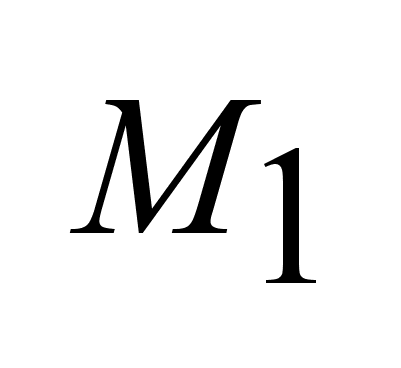 за
наименьшее
время. за
наименьшее
время.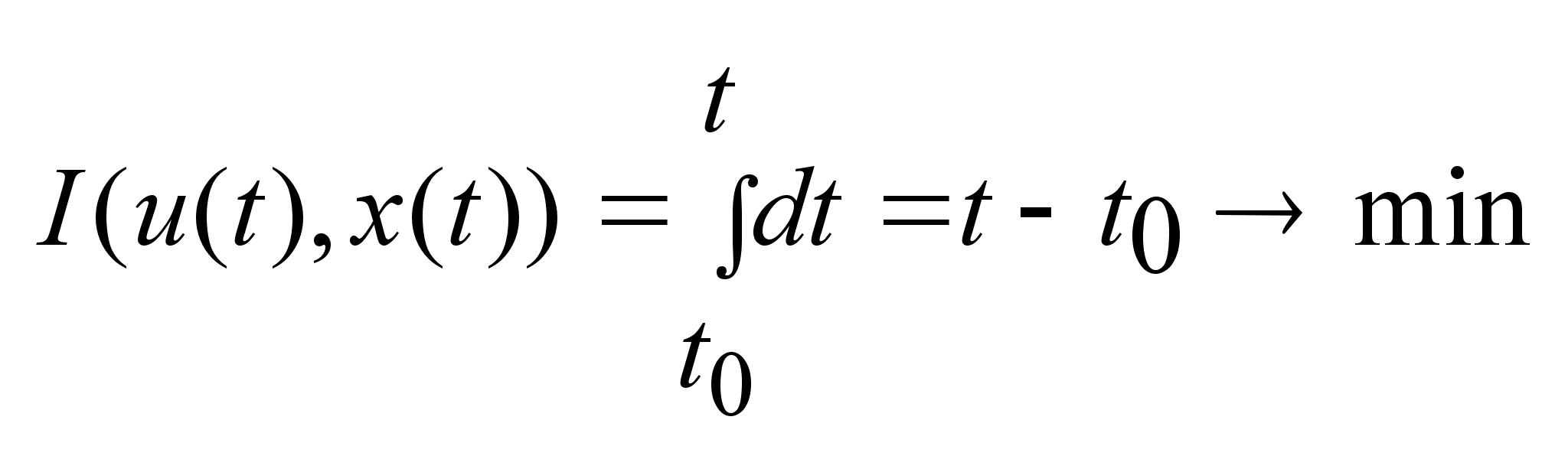 (4).
(4).
Рассмотрим
систему линейных
дифференциальных
уравнений:
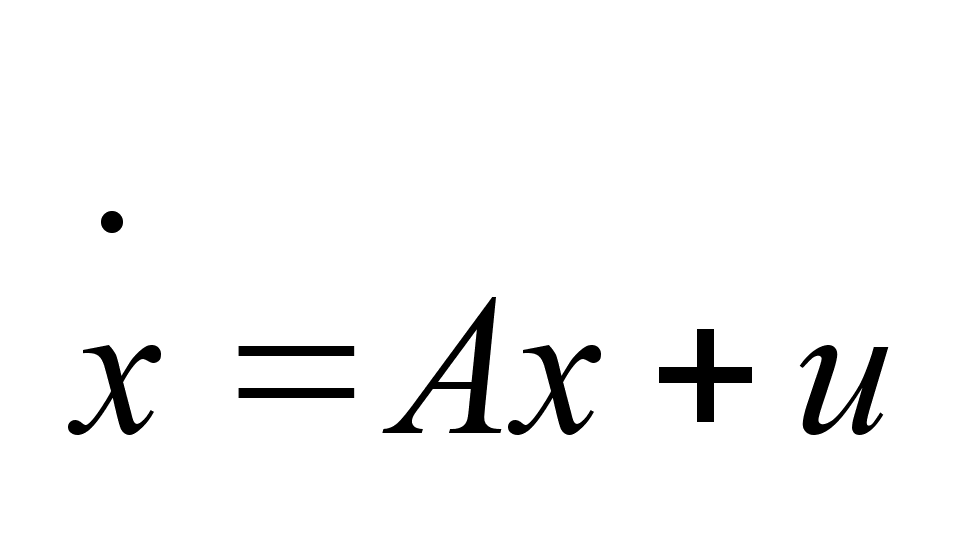 , ,
 ,
где u
известное .
Решение задачи
Коши записывается
в виде: ,
где u
известное .
Решение задачи
Коши записывается
в виде:
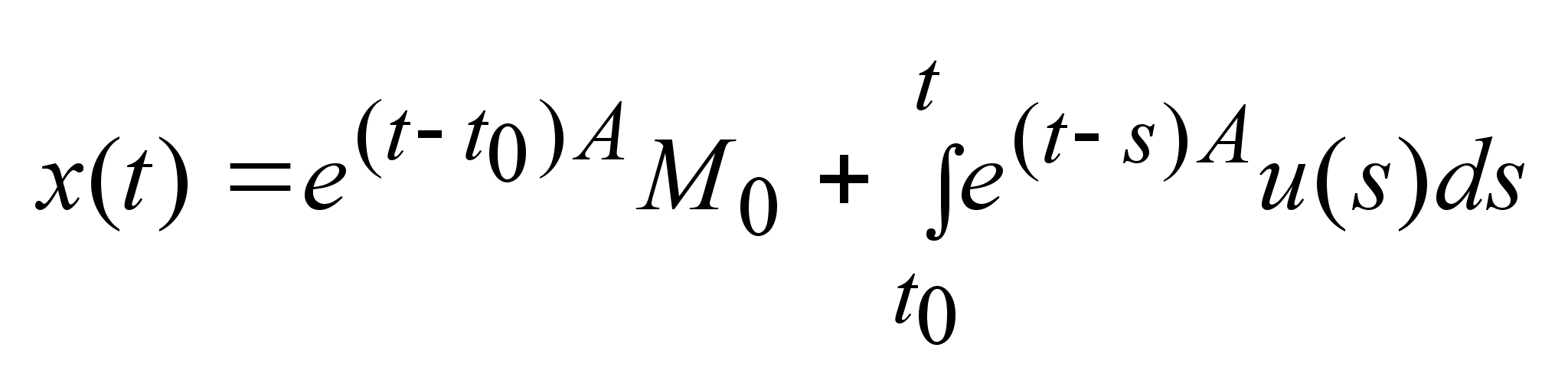 ,
оно справедливо,
если u-
непрерывная. ,
оно справедливо,
если u-
непрерывная.
Вычислим
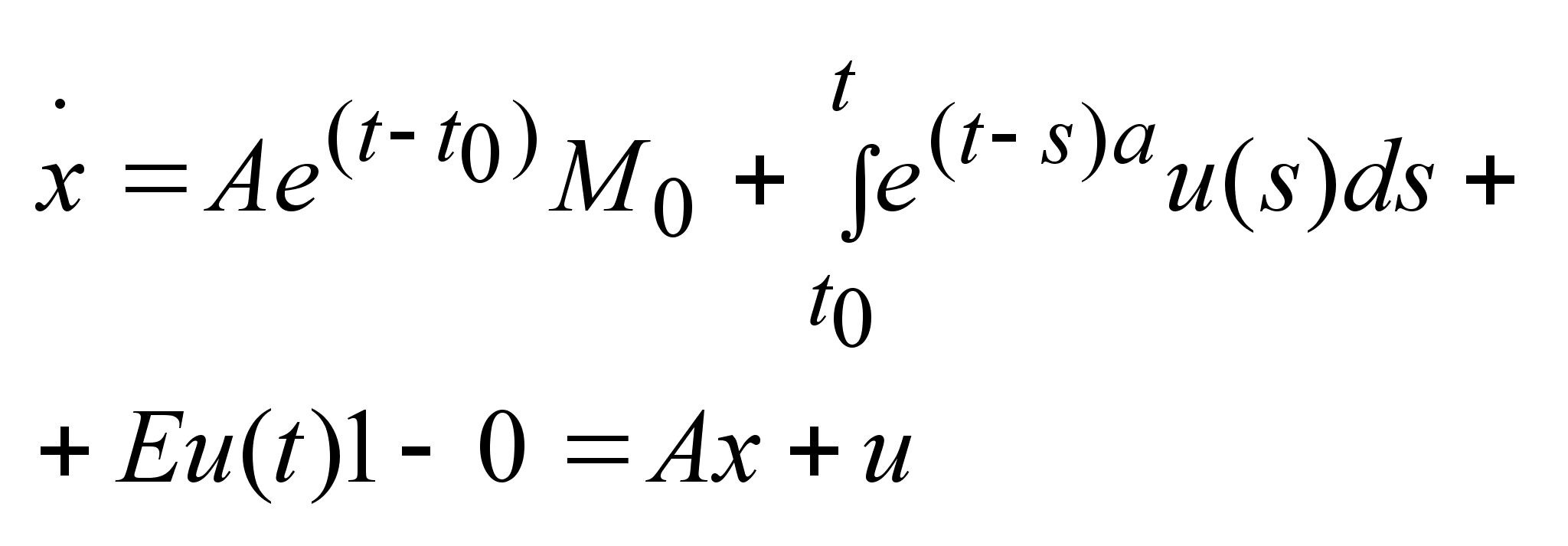 (это
следует из (это
следует из
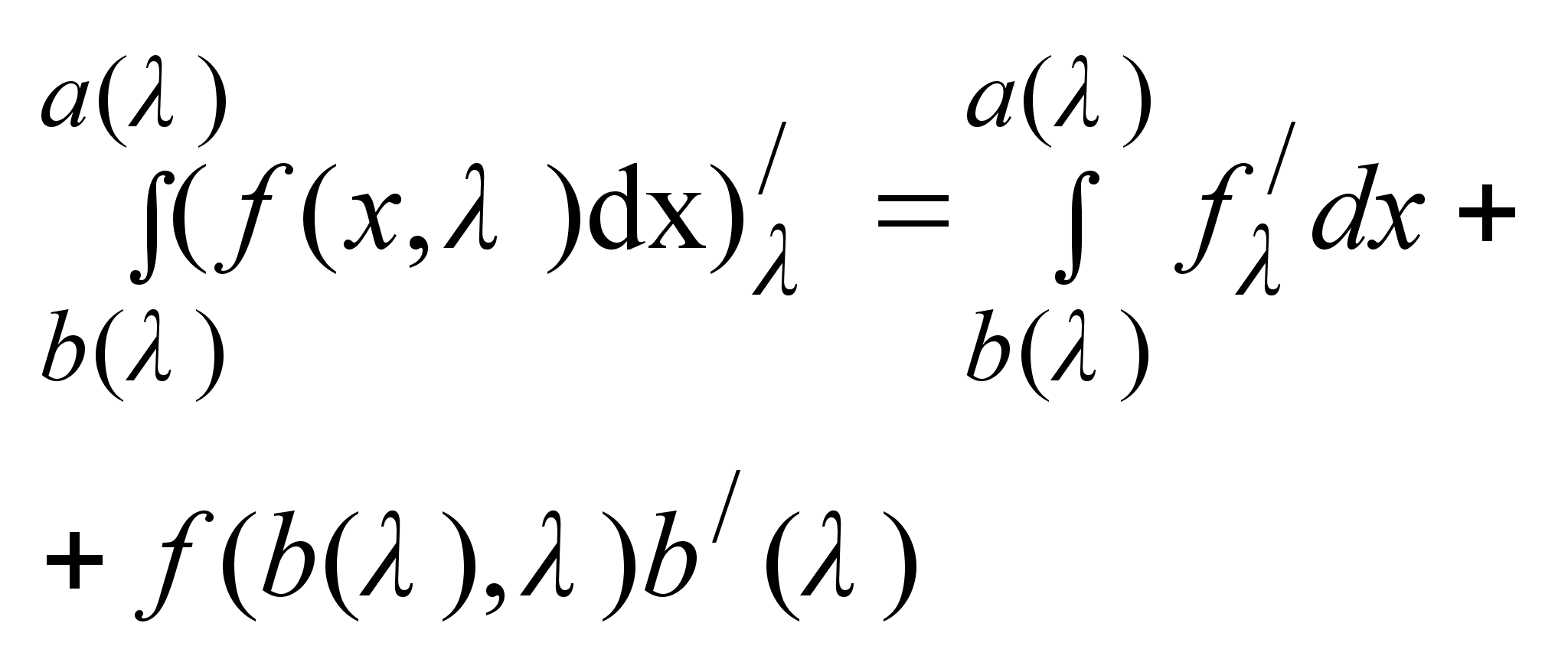 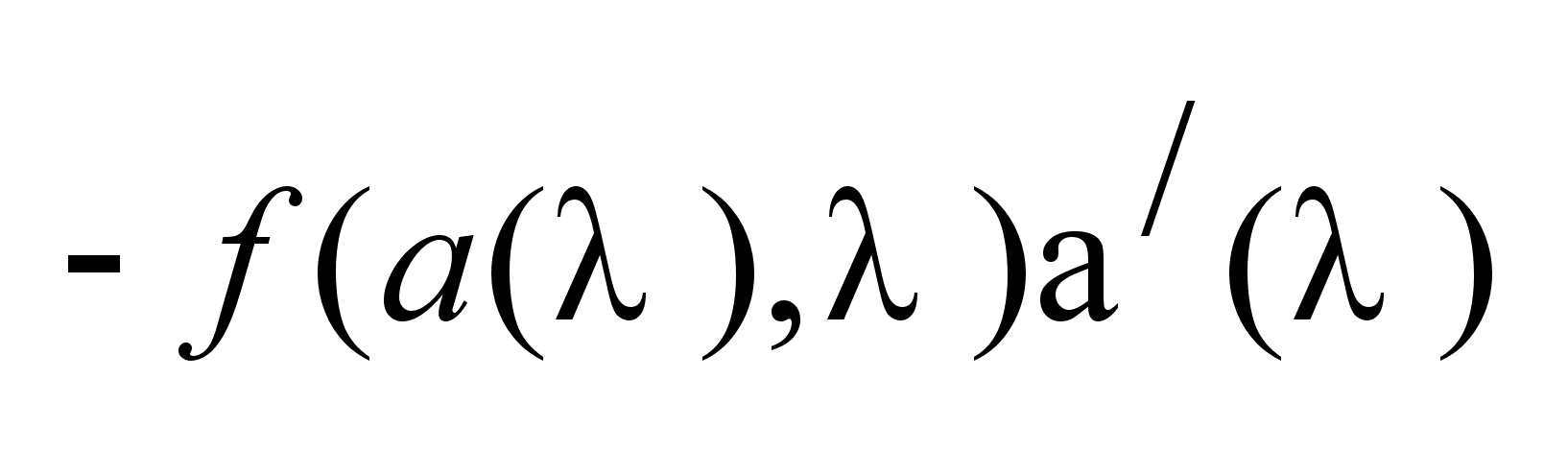 ). ).
Определение:
Функцию x(t)
наз. абсолютно
непрерывной
на отр. I,
если ее производная
существует
для почти всех
t,
принадлежащих
I, интегрируемая
по Лебегу производная
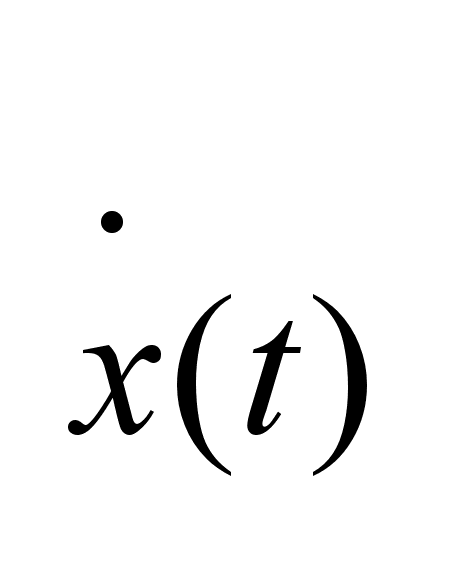 и
выполняется
условие: и
выполняется
условие:
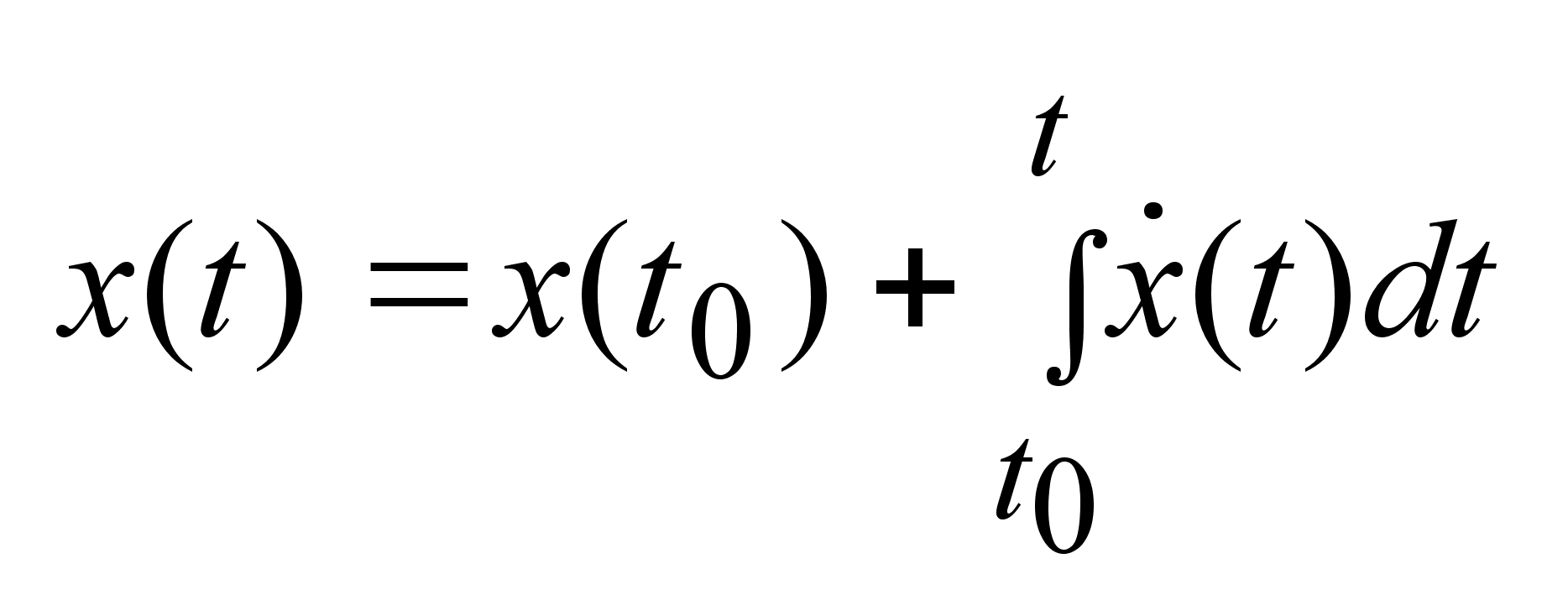 . .
Если
имеем измеримое
допустимое
управление
u(t), то решение
системы (1) также
можно определить
с помощью формулы
Коши, но в этом
случае x(t) не
будет непрерывно
дифференцируема,
а будет абсолютно
непрерывной.
Теорема
Каратеородори:
Если функция
u(t)
интегрируемая
по Лебегу на
отр. I,
то для любого
начального
значения
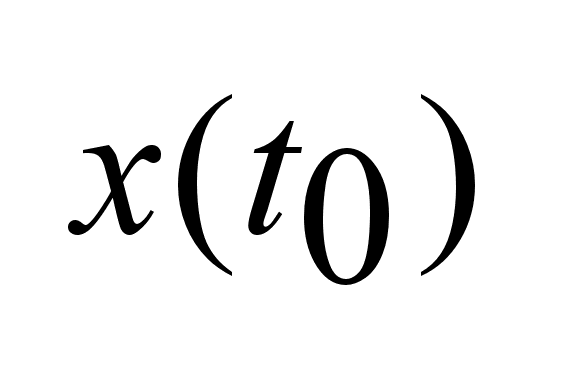 существует
и при том единое
абс. непрерывное
решение задачи
Коши, которая
задается
формулой
Коши. существует
и при том единое
абс. непрерывное
решение задачи
Коши, которая
задается
формулой
Коши.
15.
Множество
достижимости
и его свойства.
Рассматриваем
динамический
объект, поведение
которого описывается
системой (1)
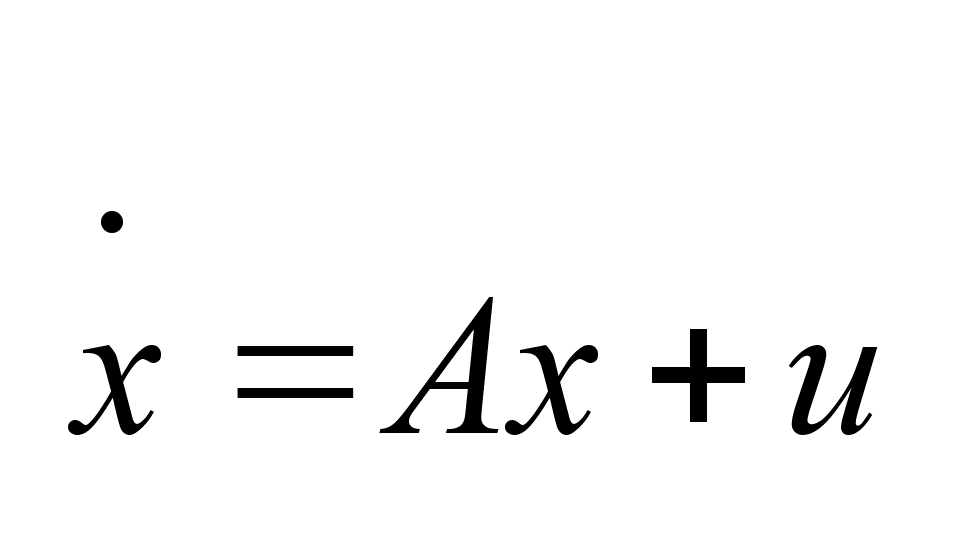 ,
x-
n-мерный
вектор, ,
x-
n-мерный
вектор,
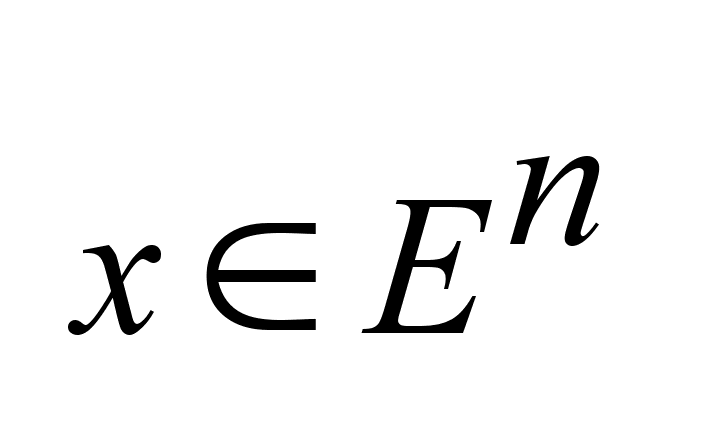 ,
A-матрица
nxn,
u
имеет ту же
размерность,
что
и ,
A-матрица
nxn,
u
имеет ту же
размерность,
что
и
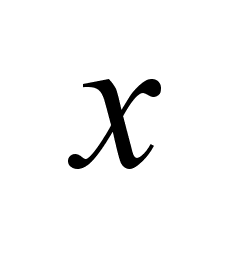 , ,
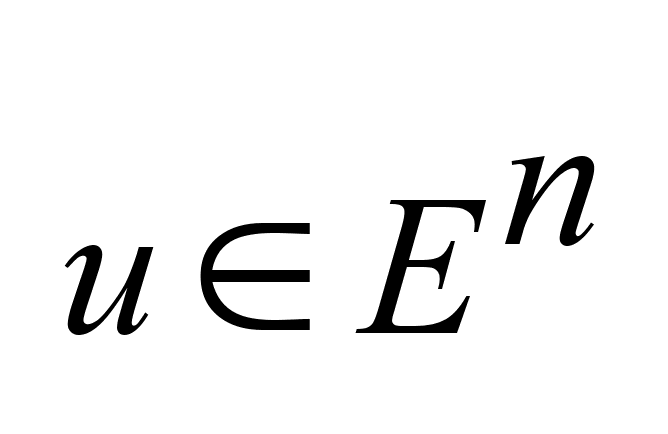 .Задано .Задано
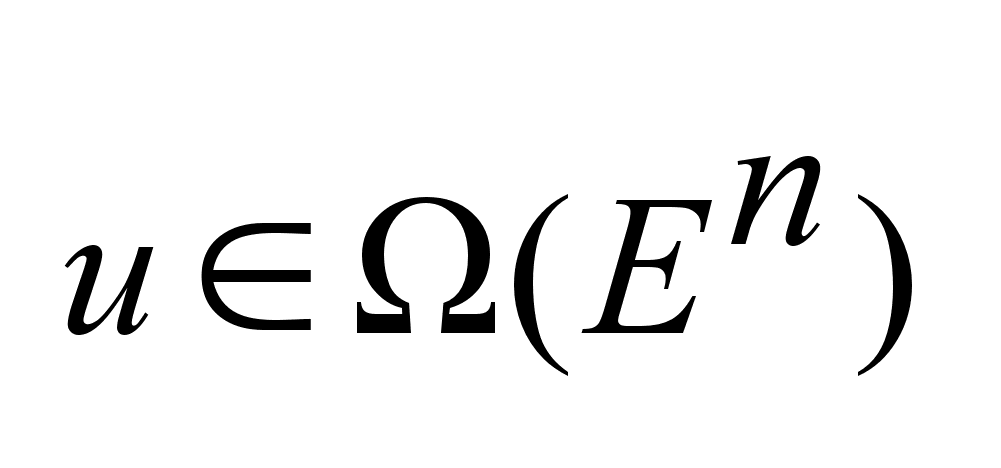 ,
u:
I ,
u:
I 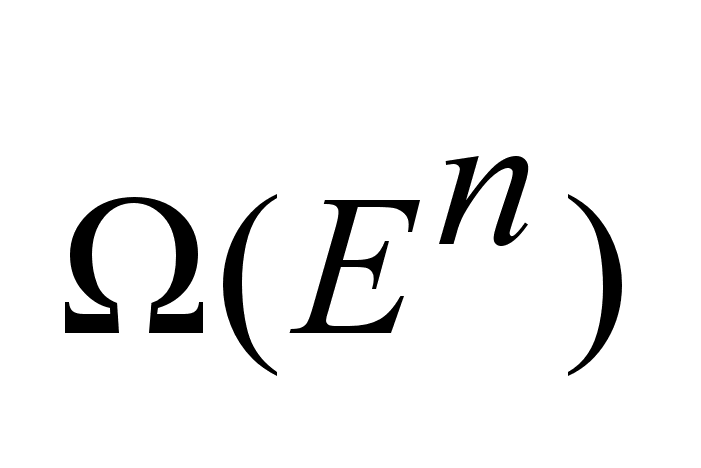 и полагается,
что u(t)
измеримо
и
и полагается,
что u(t)
измеримо
и
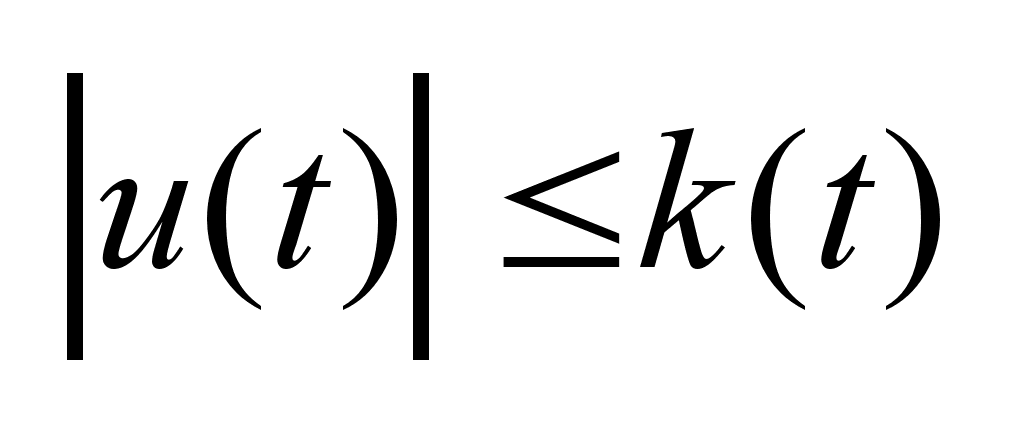 -
где
k(t)
скалярная
функция интегрируемая
по Лебегу на
отрезке I .Функция
u(t)-
называется
допустимым
управлением,
если измерима
и является
однозначной
ветвью (2) u(t) -
где
k(t)
скалярная
функция интегрируемая
по Лебегу на
отрезке I .Функция
u(t)-
называется
допустимым
управлением,
если измерима
и является
однозначной
ветвью (2) u(t) U(t)-
ограничения
на управления
. В фазовом
пространстве U(t)-
ограничения
на управления
. В фазовом
пространстве
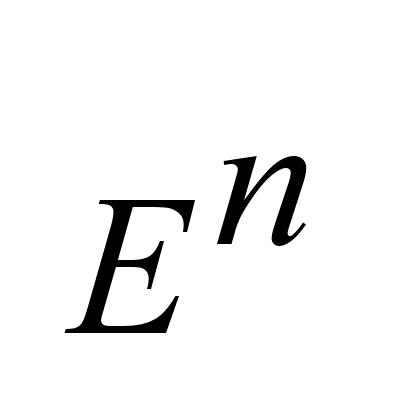 заданы
два не пустых
множества заданы
два не пустых
множества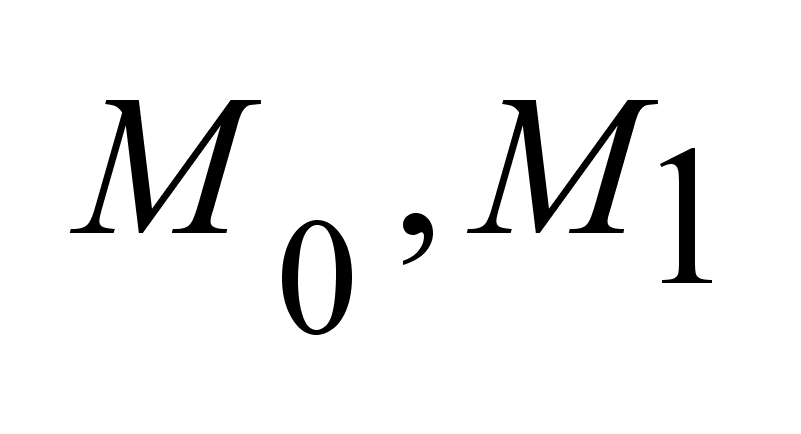 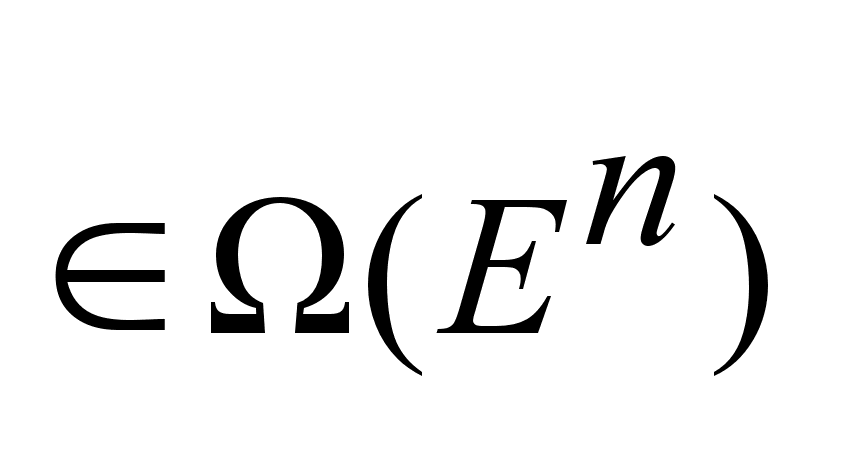 .
Допустимое
управление
u(t)
на отр.I
осуществляете
переход из
начального
мн-ва .
Допустимое
управление
u(t)
на отр.I
осуществляете
переход из
начального
мн-ва
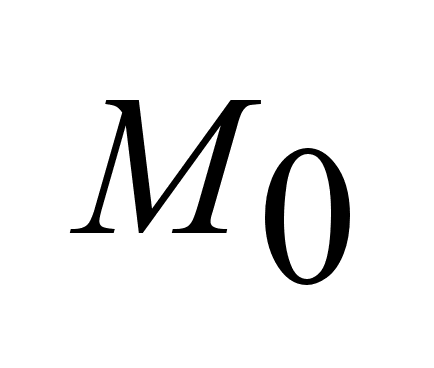 в конечное
множество
в конечное
множество
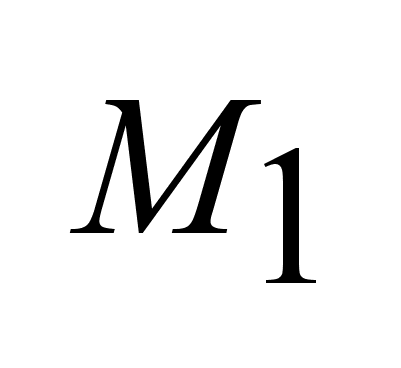 ,
если существует
решение уравнения
(1), удовлетворяющее
граничным
условиям (4) ,
если существует
решение уравнения
(1), удовлетворяющее
граничным
условиям (4)
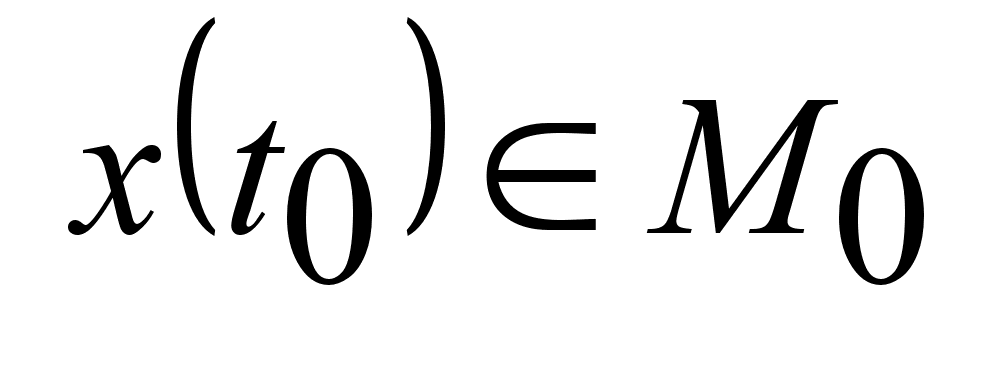 и и
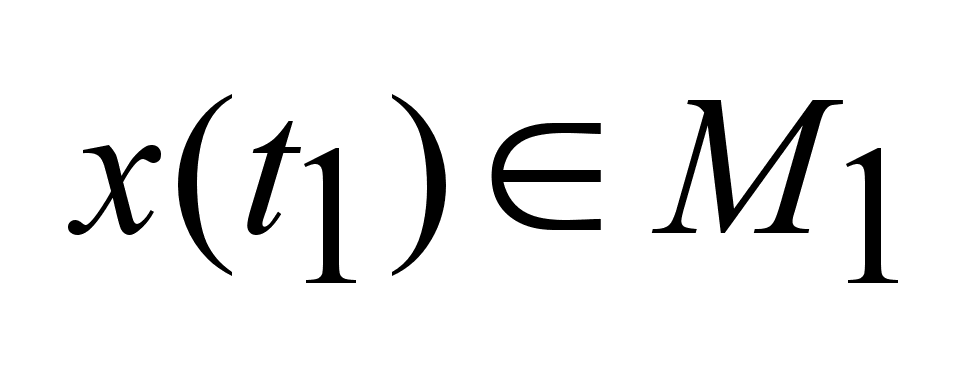 .
Цель управления-
перевод динамический
объекта из .
Цель управления-
перевод динамический
объекта из
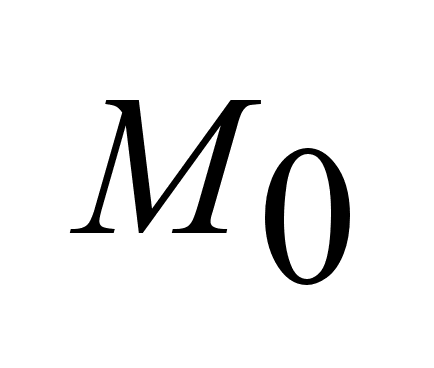 в
в
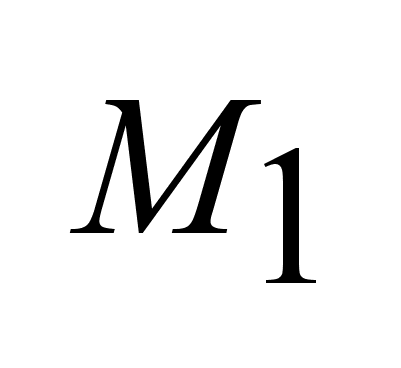 ,
а качество
определяет
функционал.
Таким функционалом
явл. время,
следовательно ,
а качество
определяет
функционал.
Таким функционалом
явл. время,
следовательно
задача
быстродействия
заключается
в нахождении
такого допустимого
управления,
которое осуществляет
переход из
множества
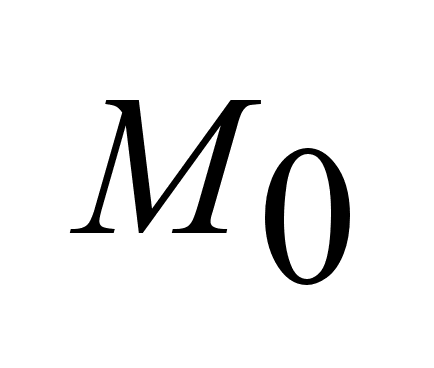 в
в
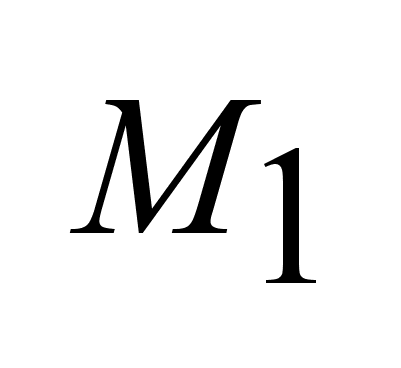 за
наименьшее
время. за
наименьшее
время.
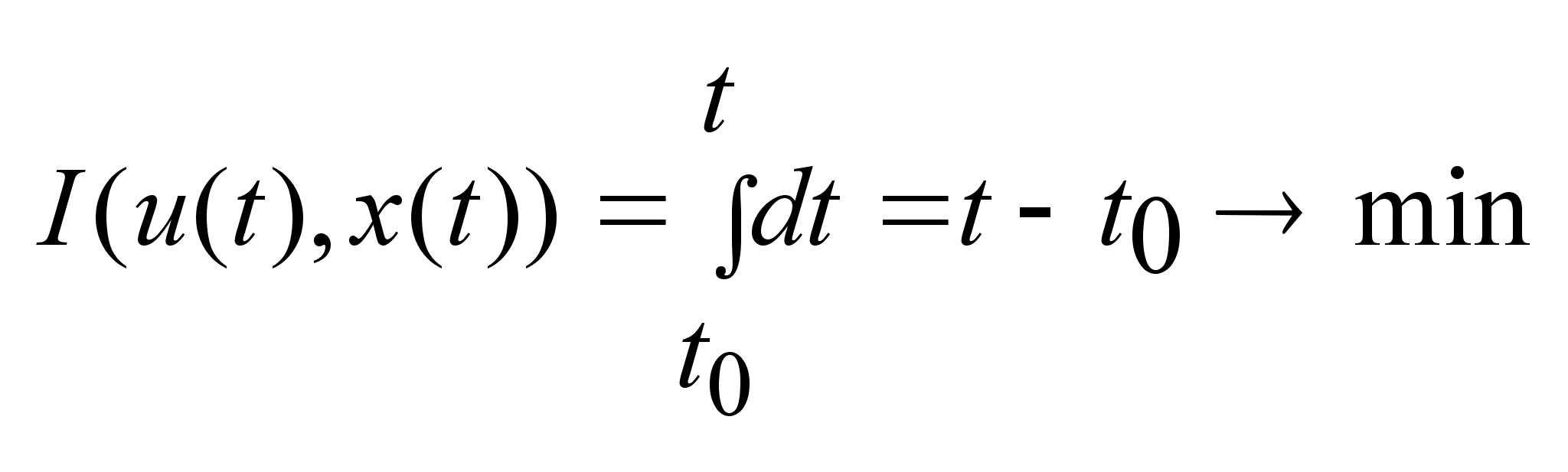 (4).
(4).
Введем
понятия мн-ва
достижимости:
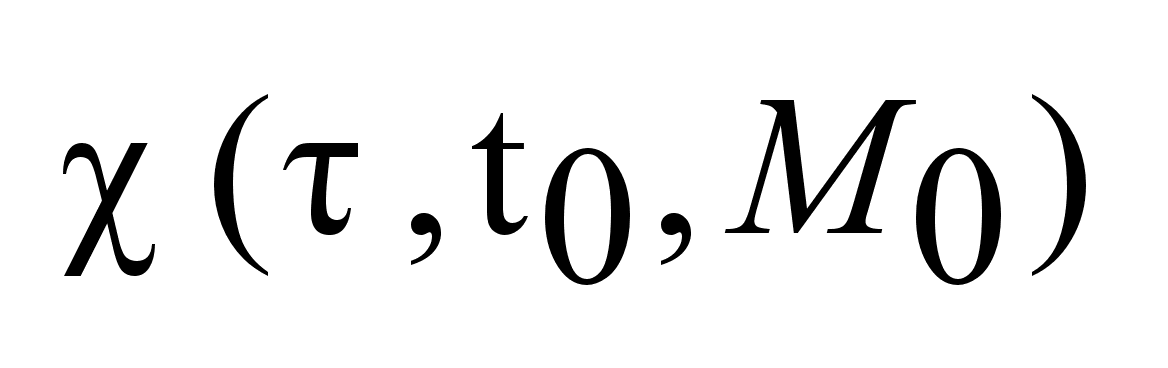 -это
множество все
точек фазового
пространства -это
множество все
точек фазового
пространства
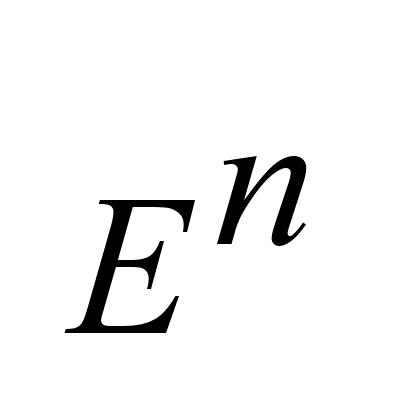 ,
в котором можно
перейти на
отр. ,
в котором можно
перейти на
отр.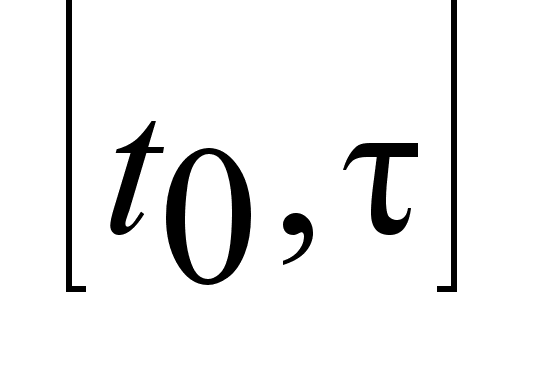 из начального
множества
из начального
множества
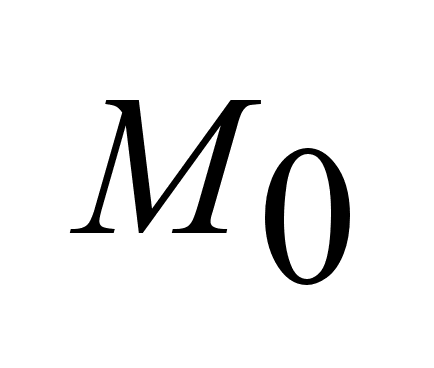 по
решениям (1) при
всех допустимых
значениях
управления
u(t)
в
момент времени по
решениям (1) при
всех допустимых
значениях
управления
u(t)
в
момент времени
 . .
Рассмотрим
свойства
множества
достижимости:
1)
Используем
формулу Коши: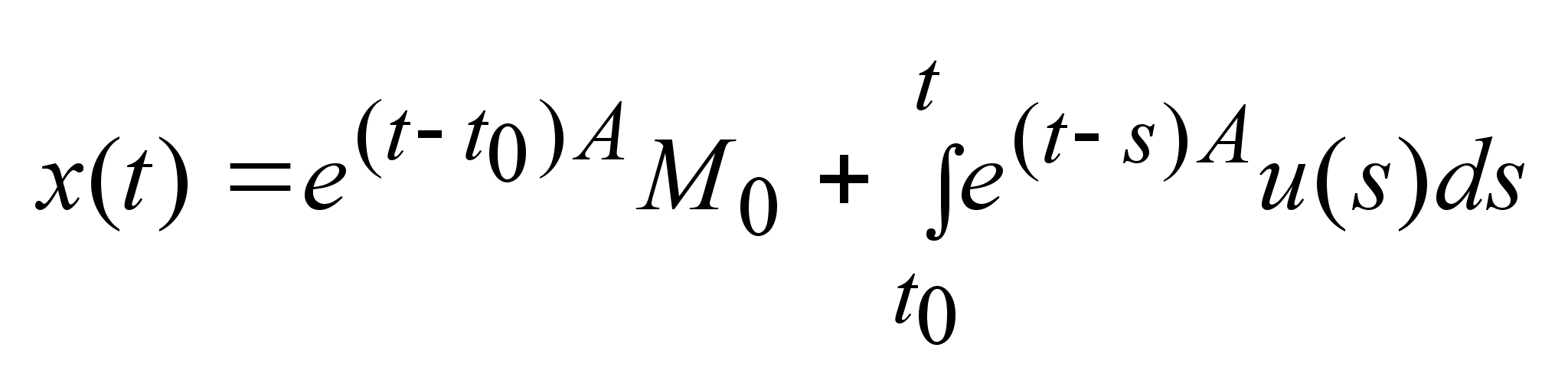
 , ,
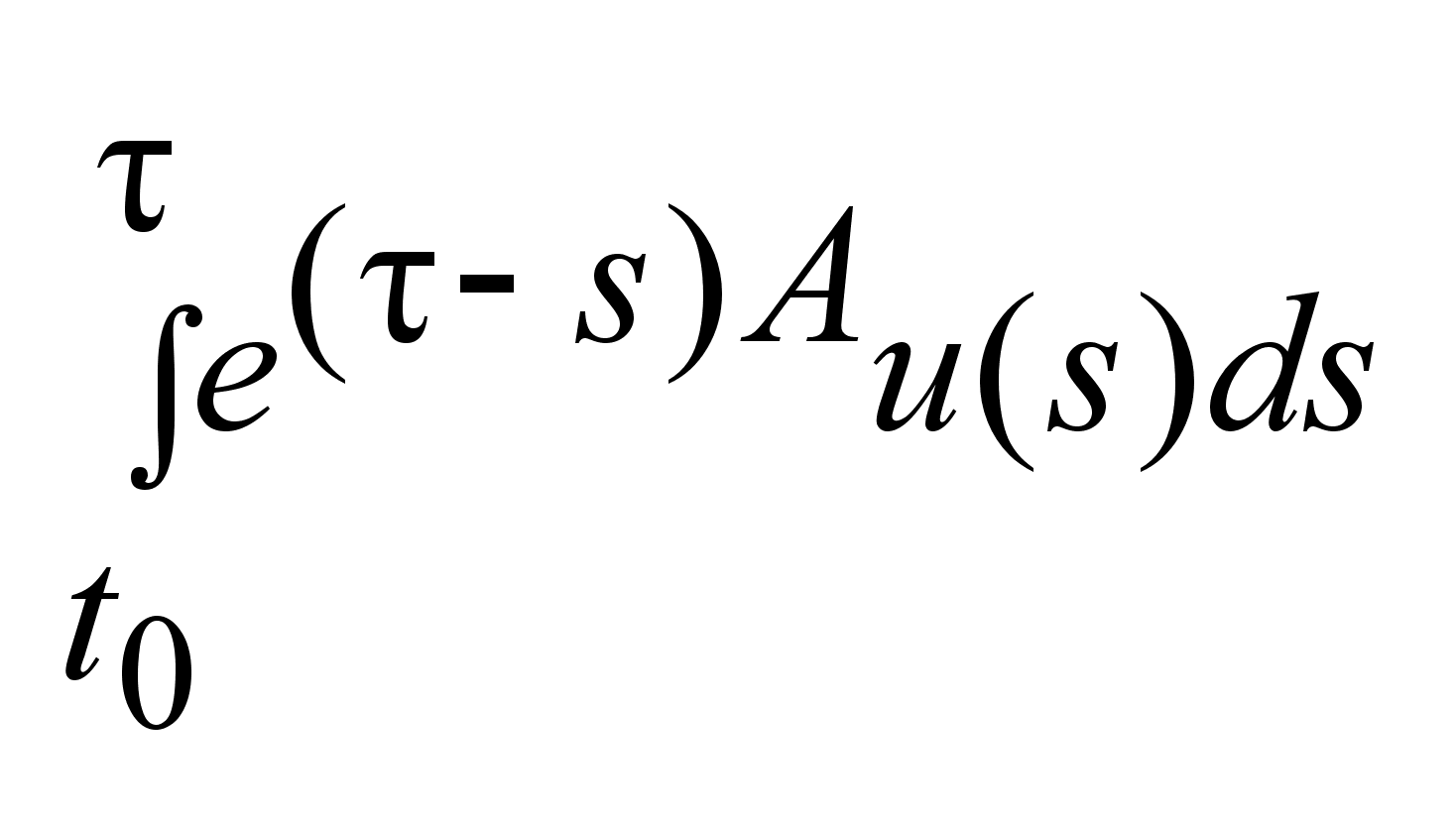 -интеграл
от многозначного
отображения.
Доказательство
непосредственно
подставлением
в
уравн (1). -интеграл
от многозначного
отображения.
Доказательство
непосредственно
подставлением
в
уравн (1).
2)
Множество
достижимости
является не
пустым, компактным
подмножеством
пр-ва
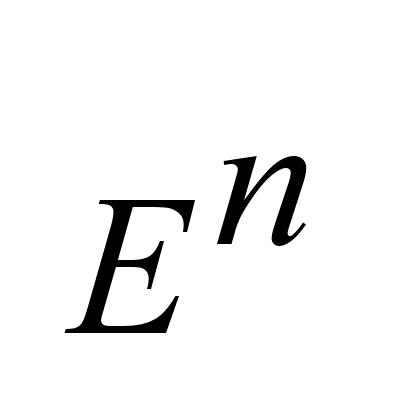 . .
 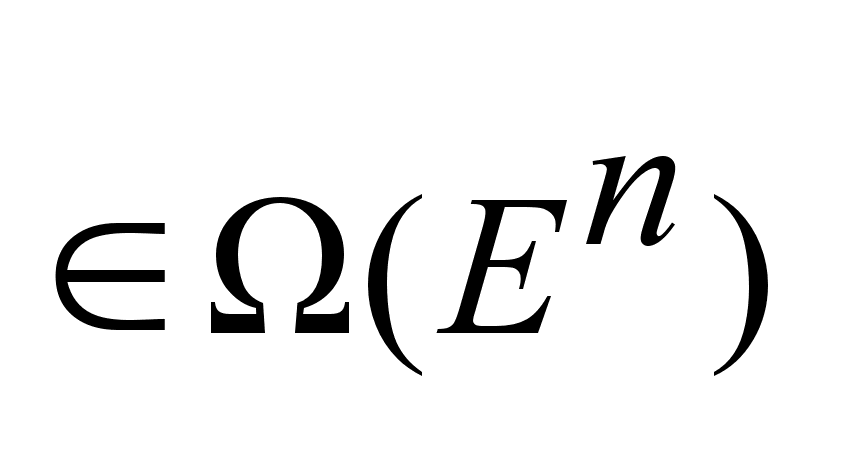 . .
Доказательство
следует из
формулы Коши
и 1-ой теоремы
для интеграла
многозначных
отображений.
3)
Если начальное
множество
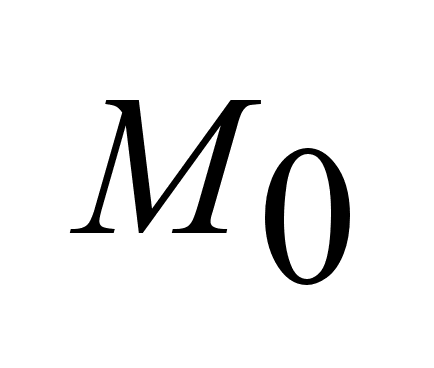 выпукло,
то множество
достижимости выпукло,
то множество
достижимости
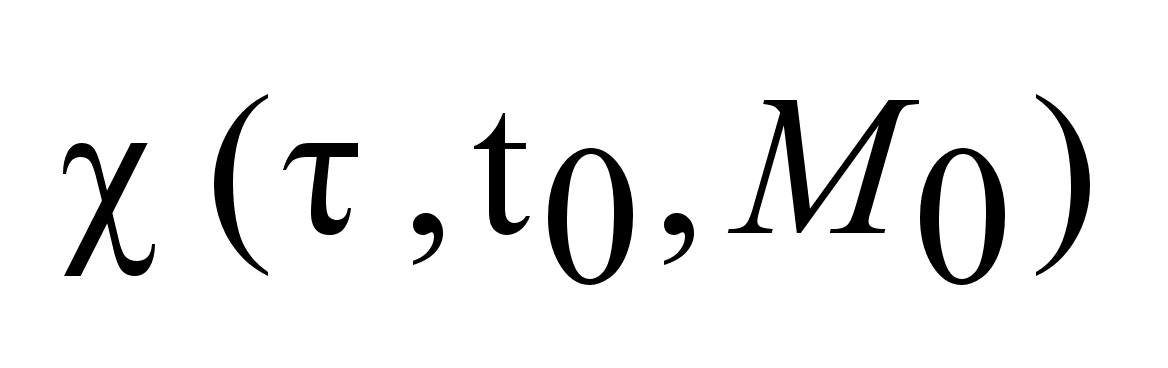 также
выпукло. Доказательство
следует из
формулы также
выпукло. Доказательство
следует из
формулы
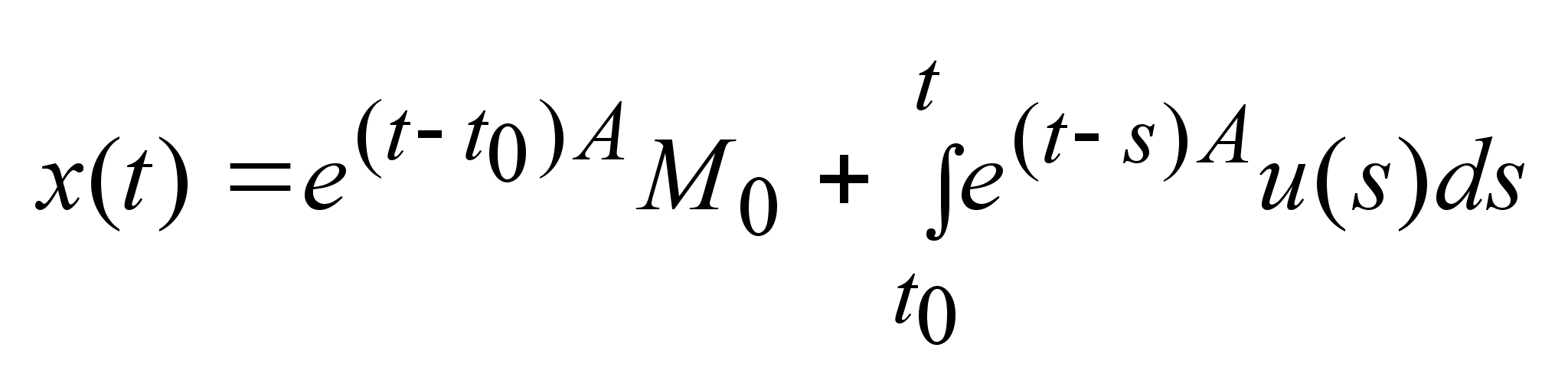 и теоремы о
выпуклости
интеграла от
многозначного
отображения.
и теоремы о
выпуклости
интеграла от
многозначного
отображения.
4)
Опорная функция
множества
достижимости
имеет вид:
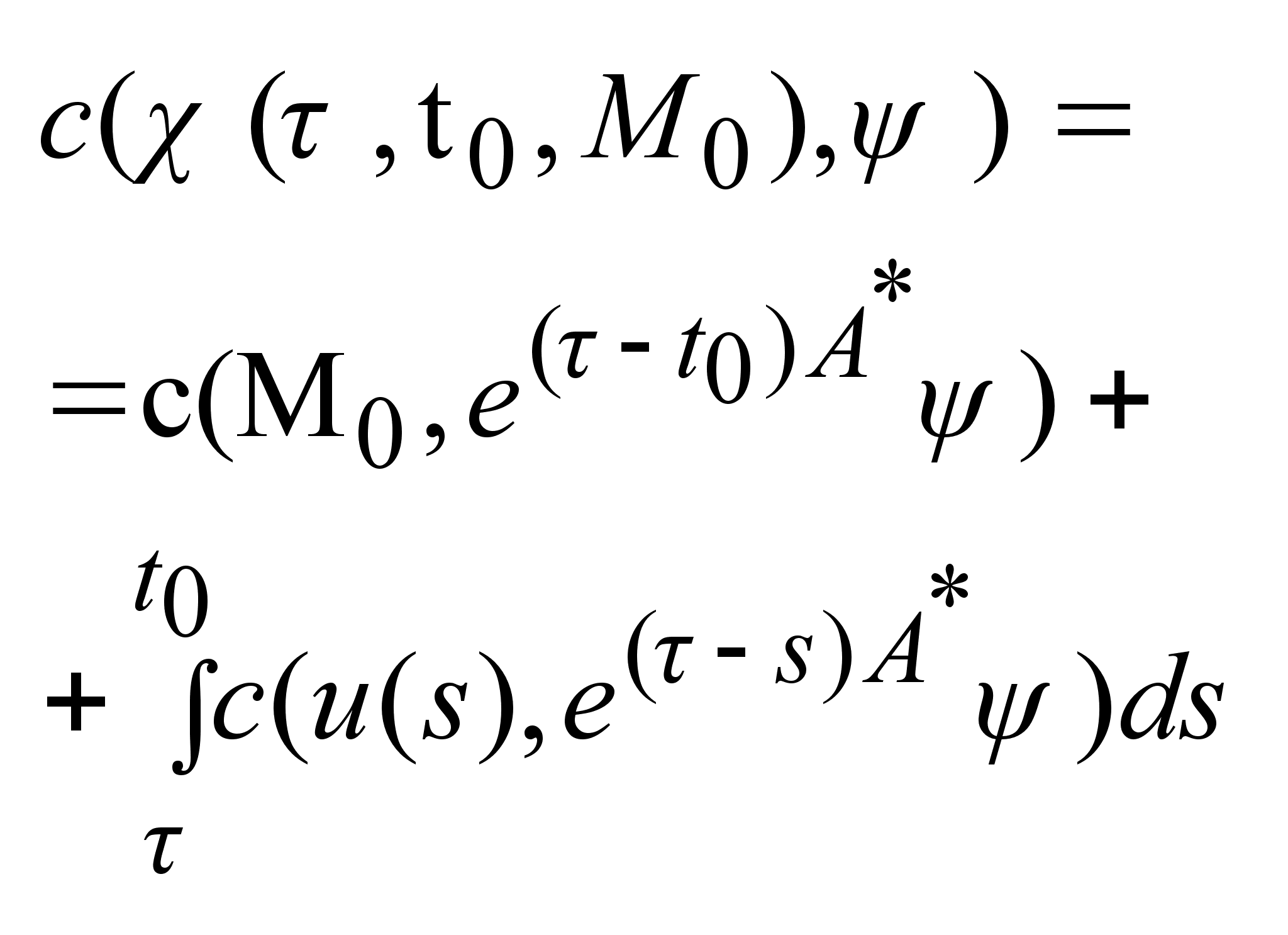 ,
u(s)=U. Доказательство
следует из
формулы ,
u(s)=U. Доказательство
следует из
формулы
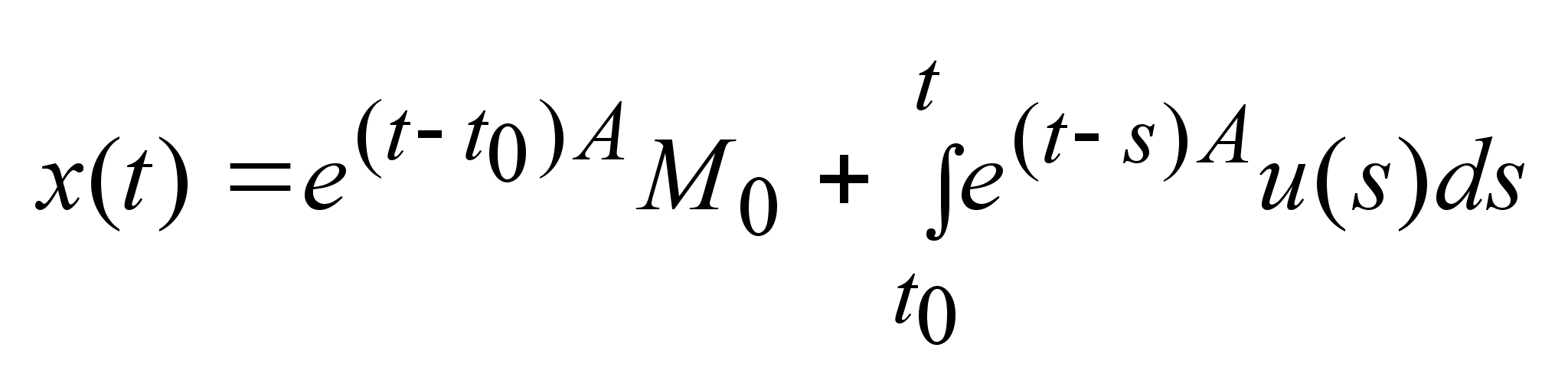 ,
свойств (3), (4) опорных
функций , теоремы
2 и того факта,
что ,
свойств (3), (4) опорных
функций , теоремы
2 и того факта,
что
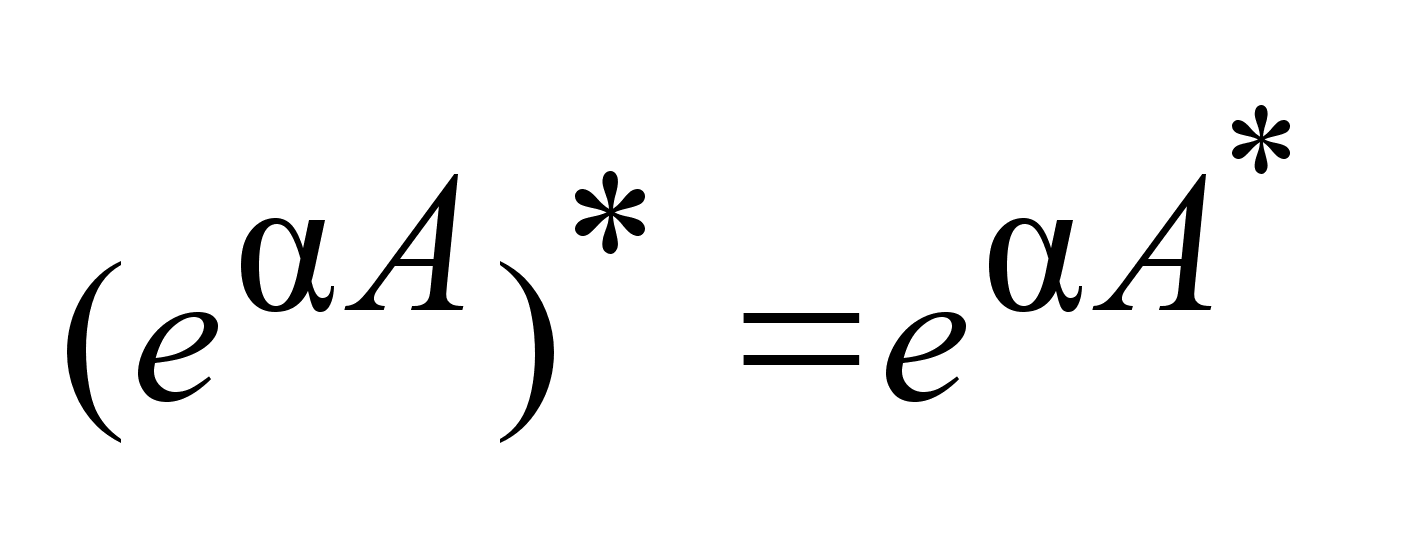 . .
Доказательство:
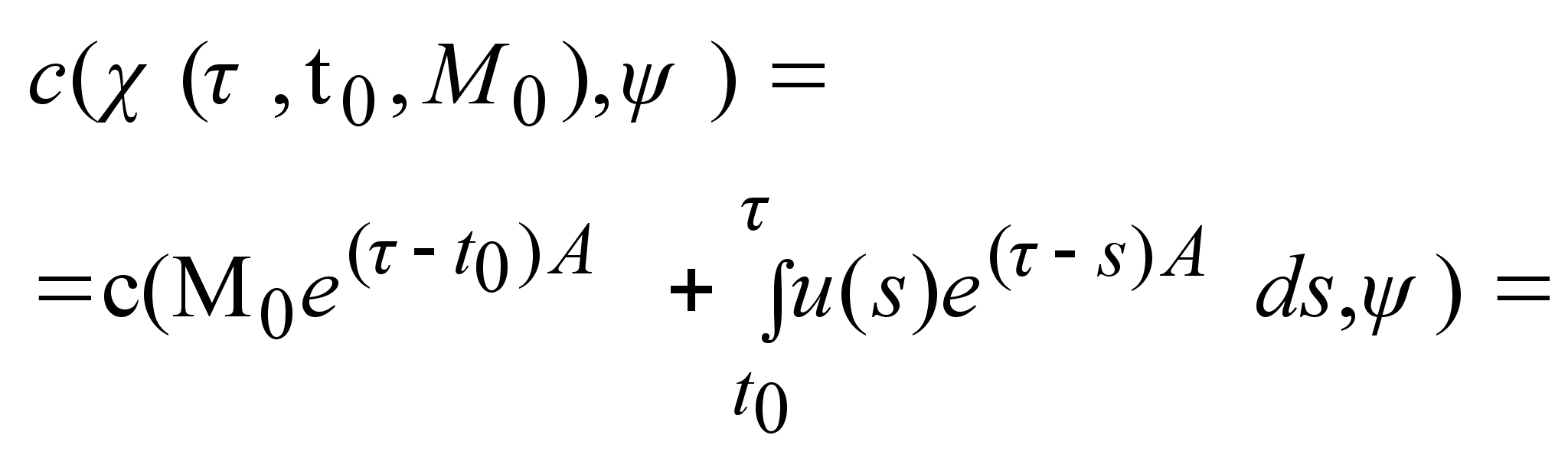 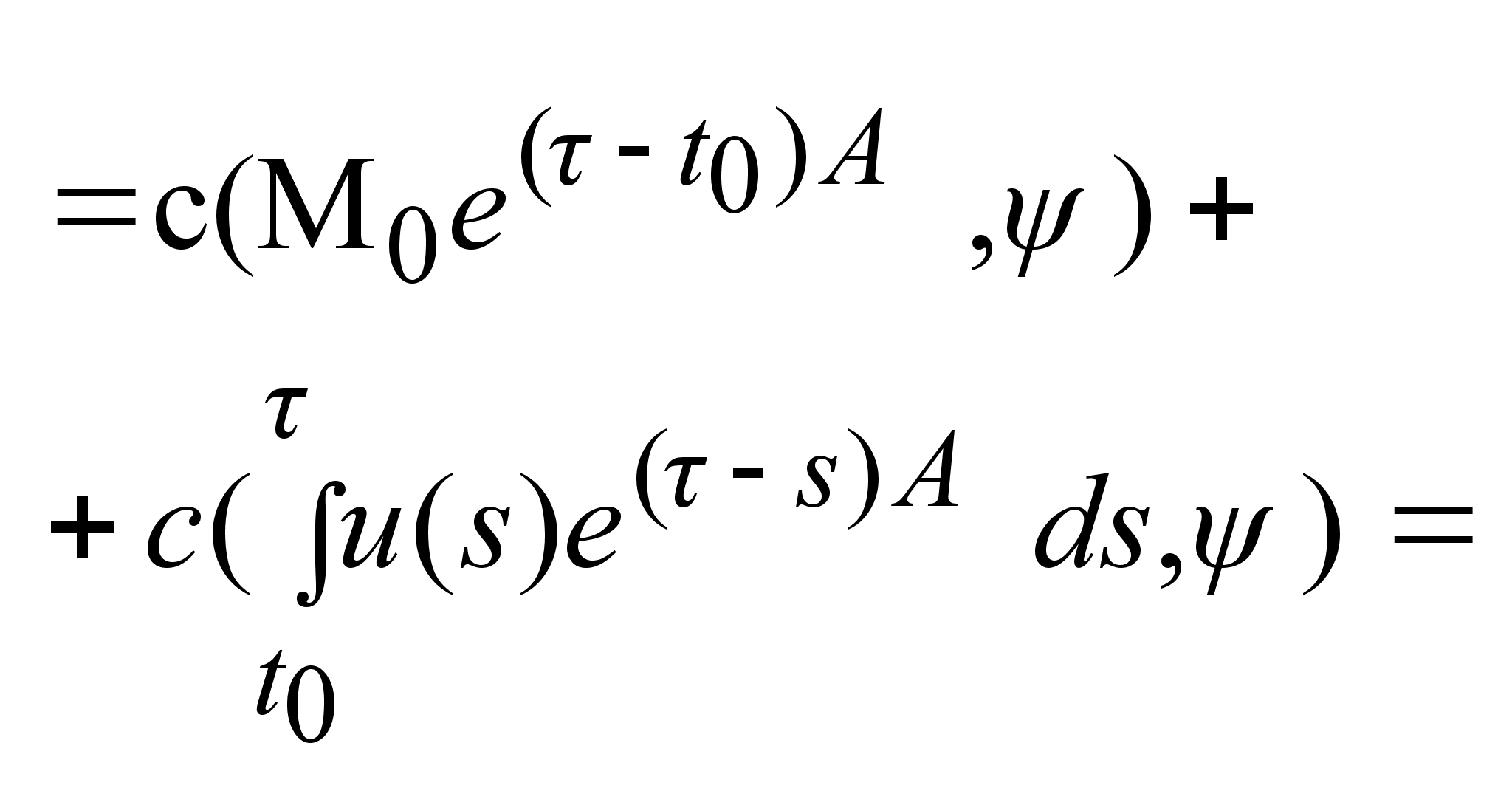
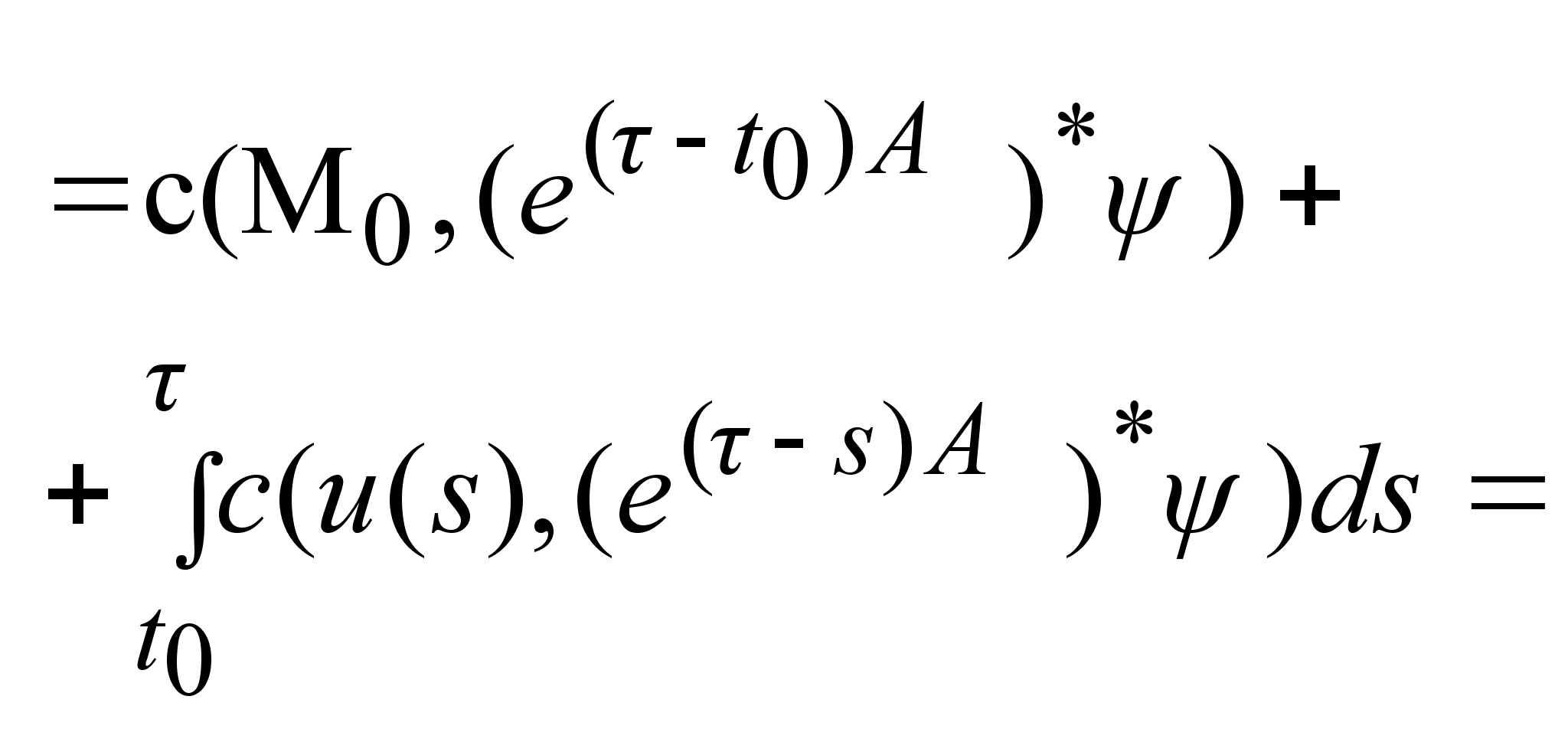 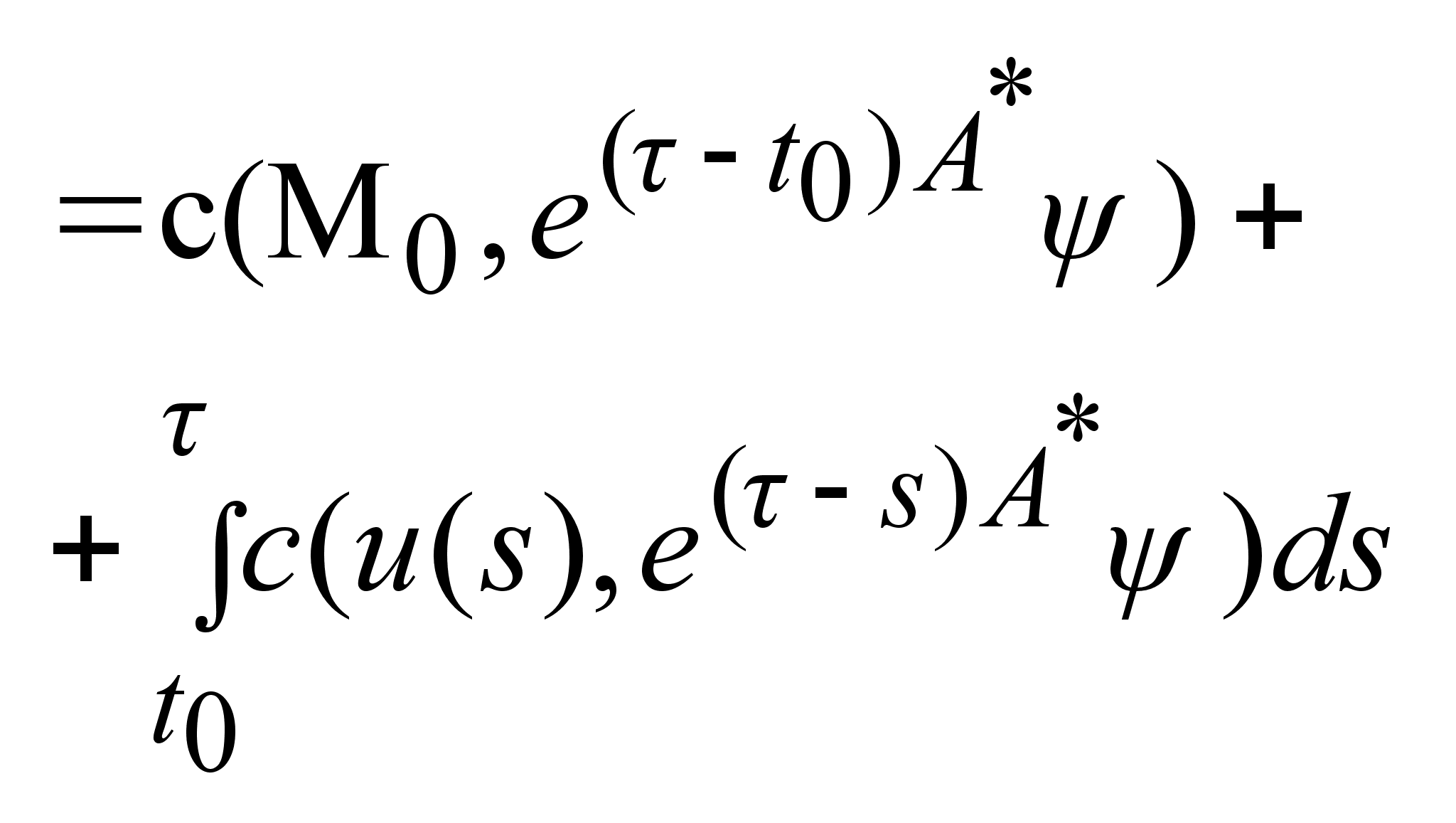 . .
5)
Мн-во
достижимости:
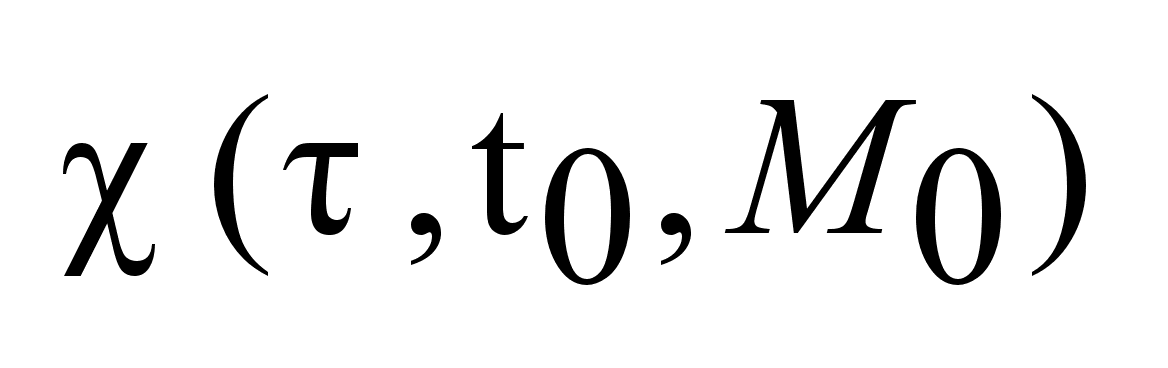 :
I :
I  непрерывно
зависит от
аргумента непрерывно
зависит от
аргумента
 .
Множество
достижимости
имеет вид : .
Множество
достижимости
имеет вид :
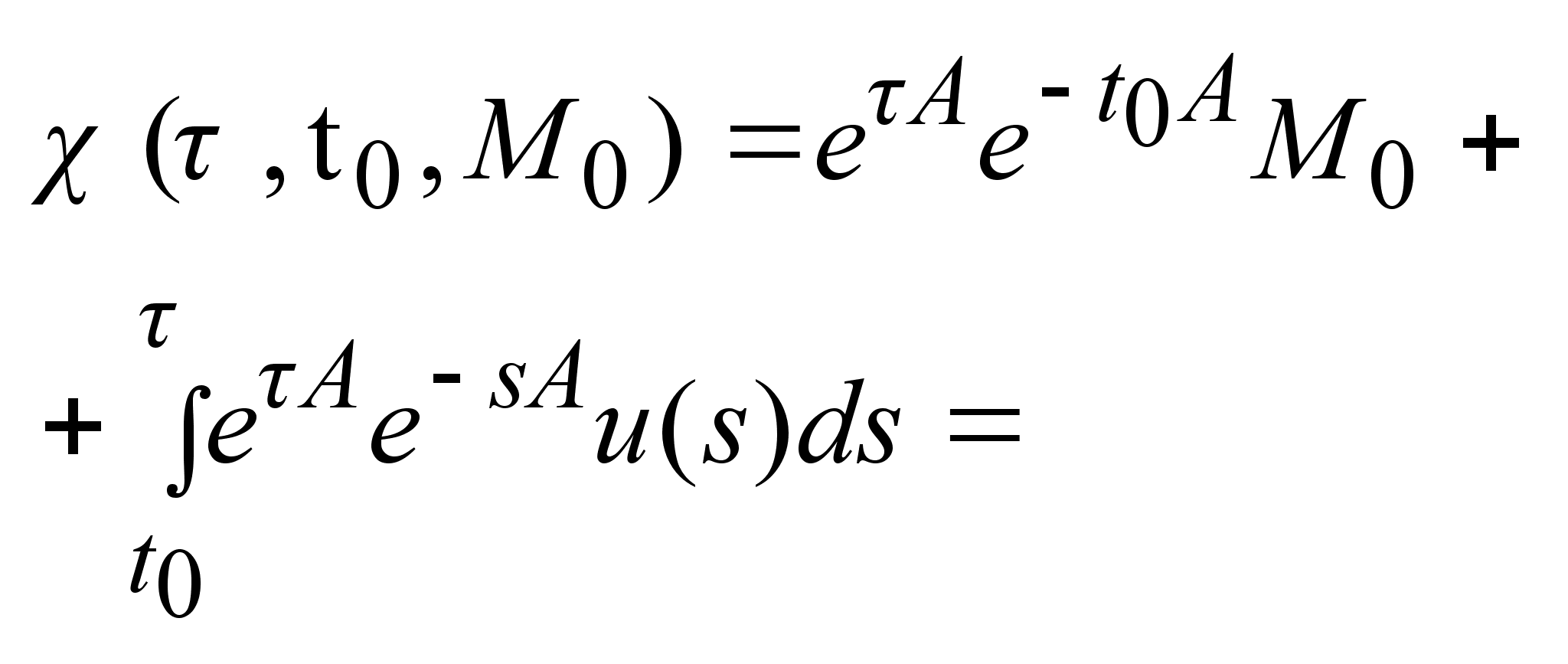 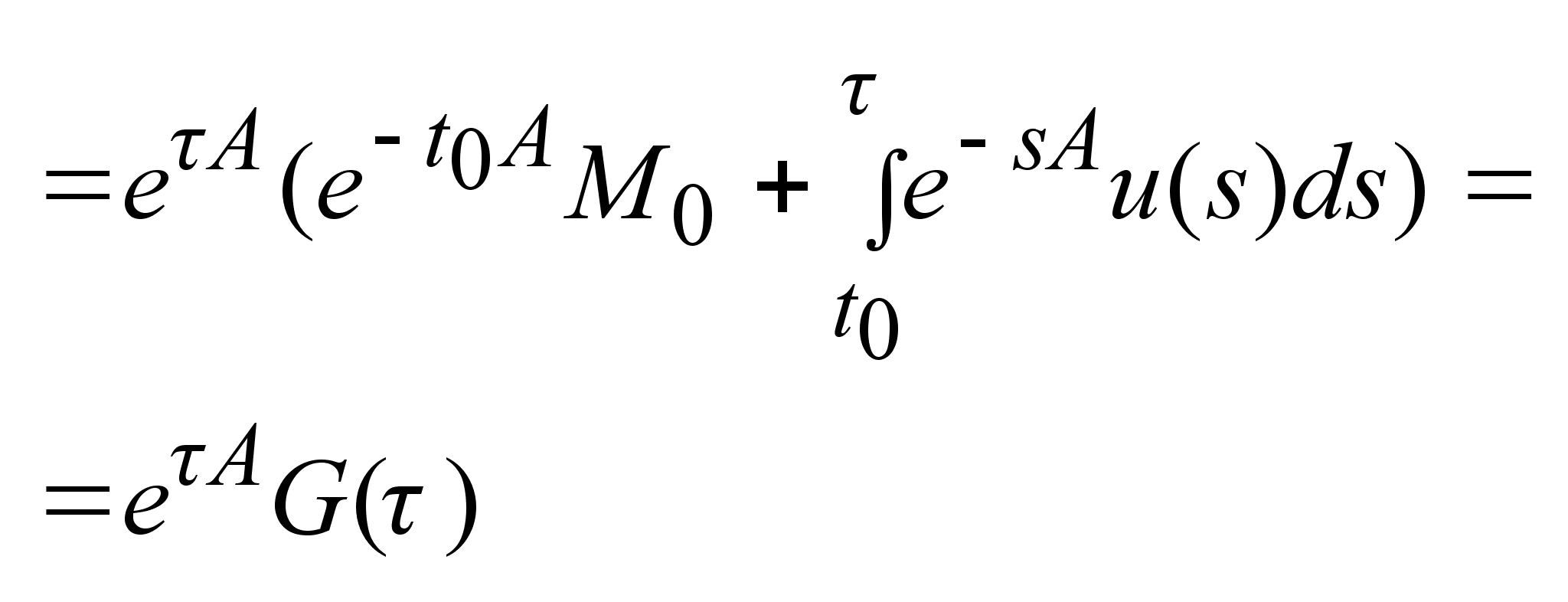  -непрерывна
по теореме 3,
матрица -непрерывна
по теореме 3,
матрица
 также
непрерывна
по также
непрерывна
по
 ,
следовательно
линейное отображение
непрерывная
функция. ,
следовательно
линейное отображение
непрерывная
функция.
Пример:
Найти мн-во
достижимости
для управляемого
объекта, описываемого
уравнением: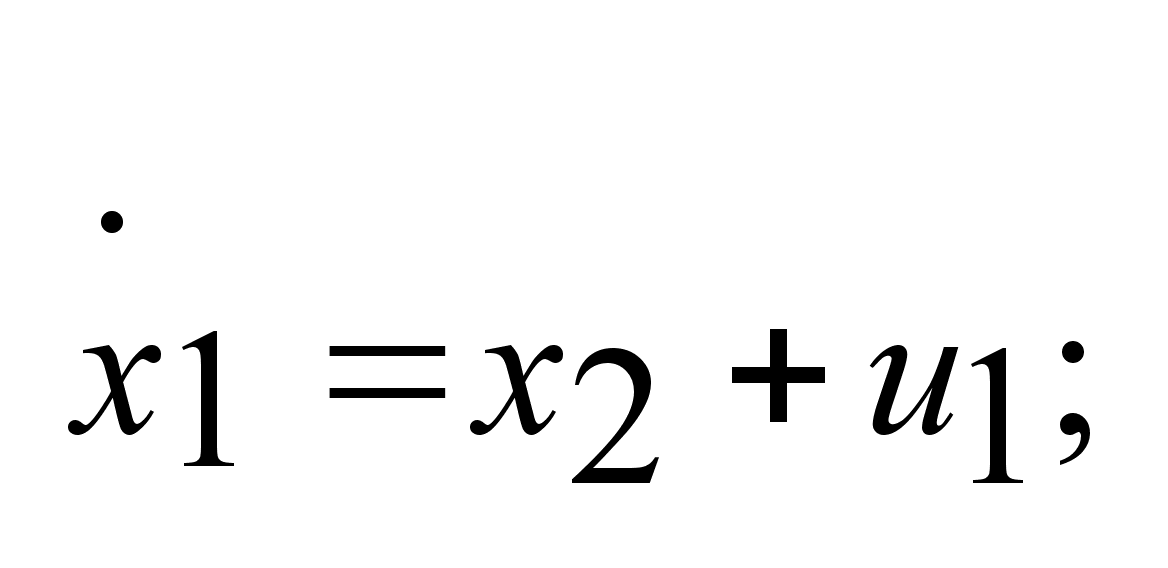 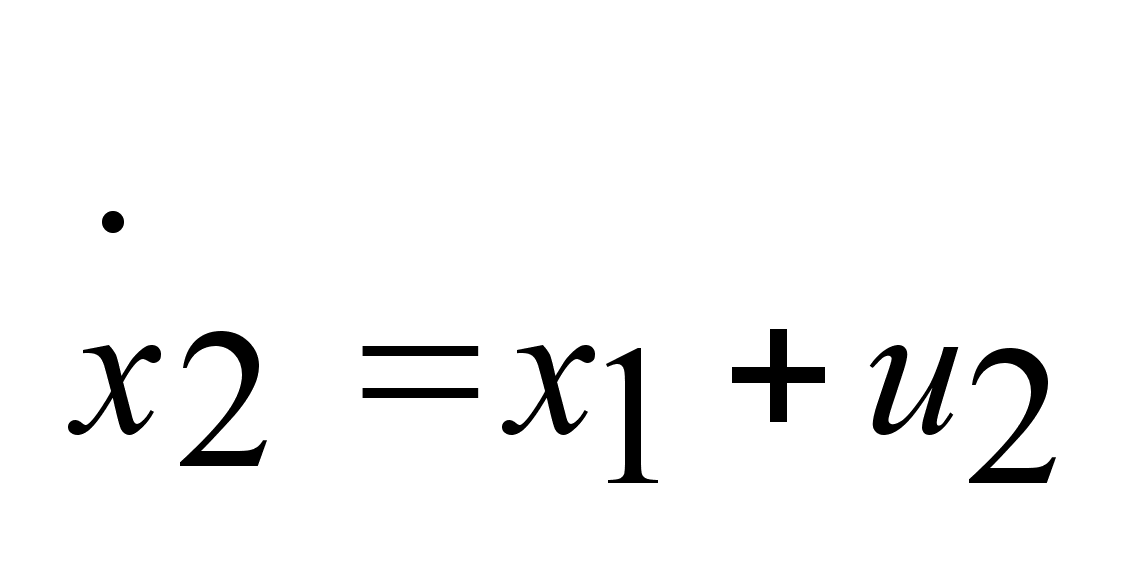 . .
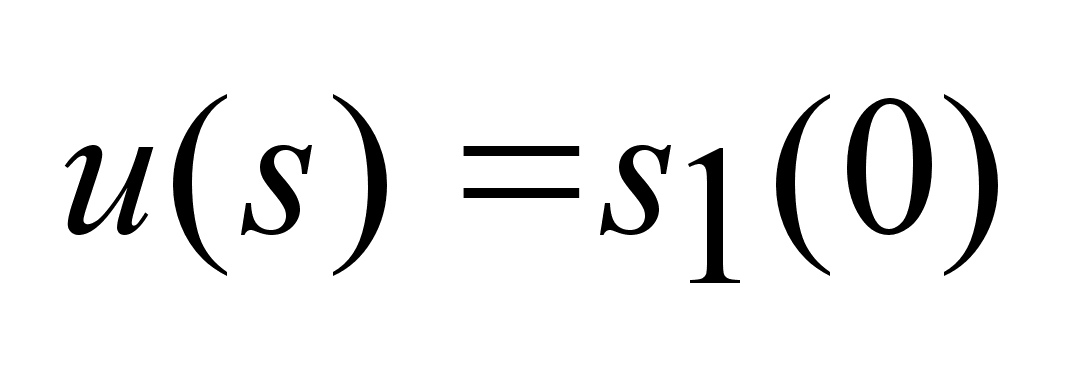 ,
,
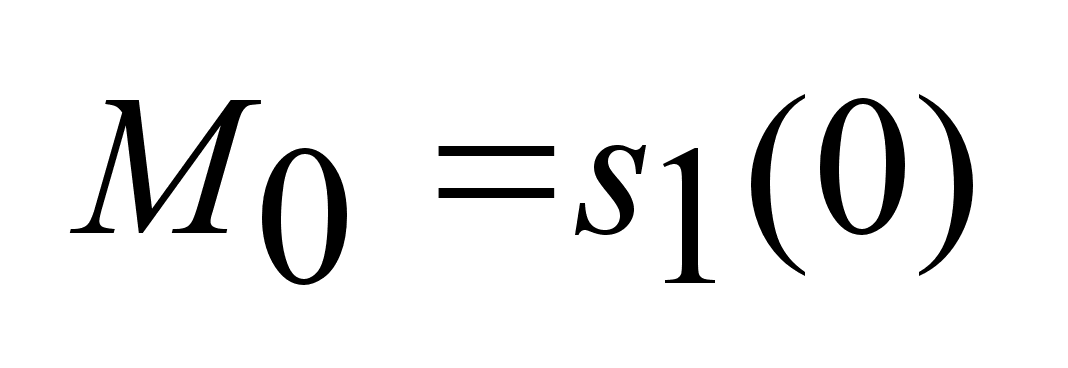 и и
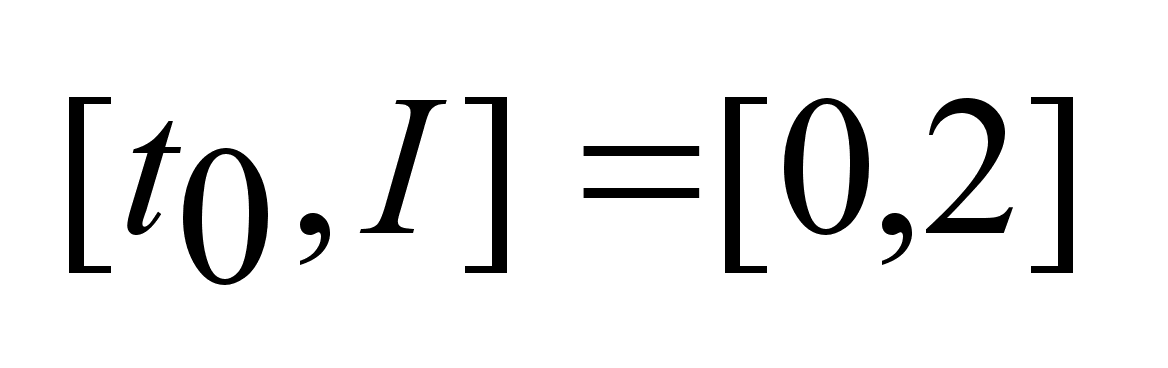 ,
I ,
I 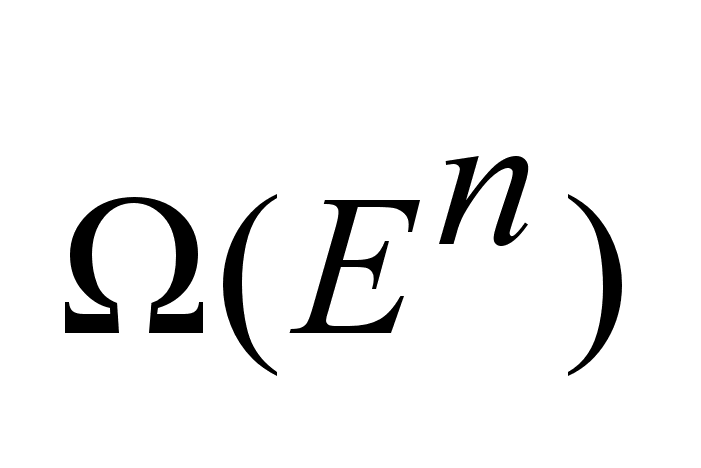 . .
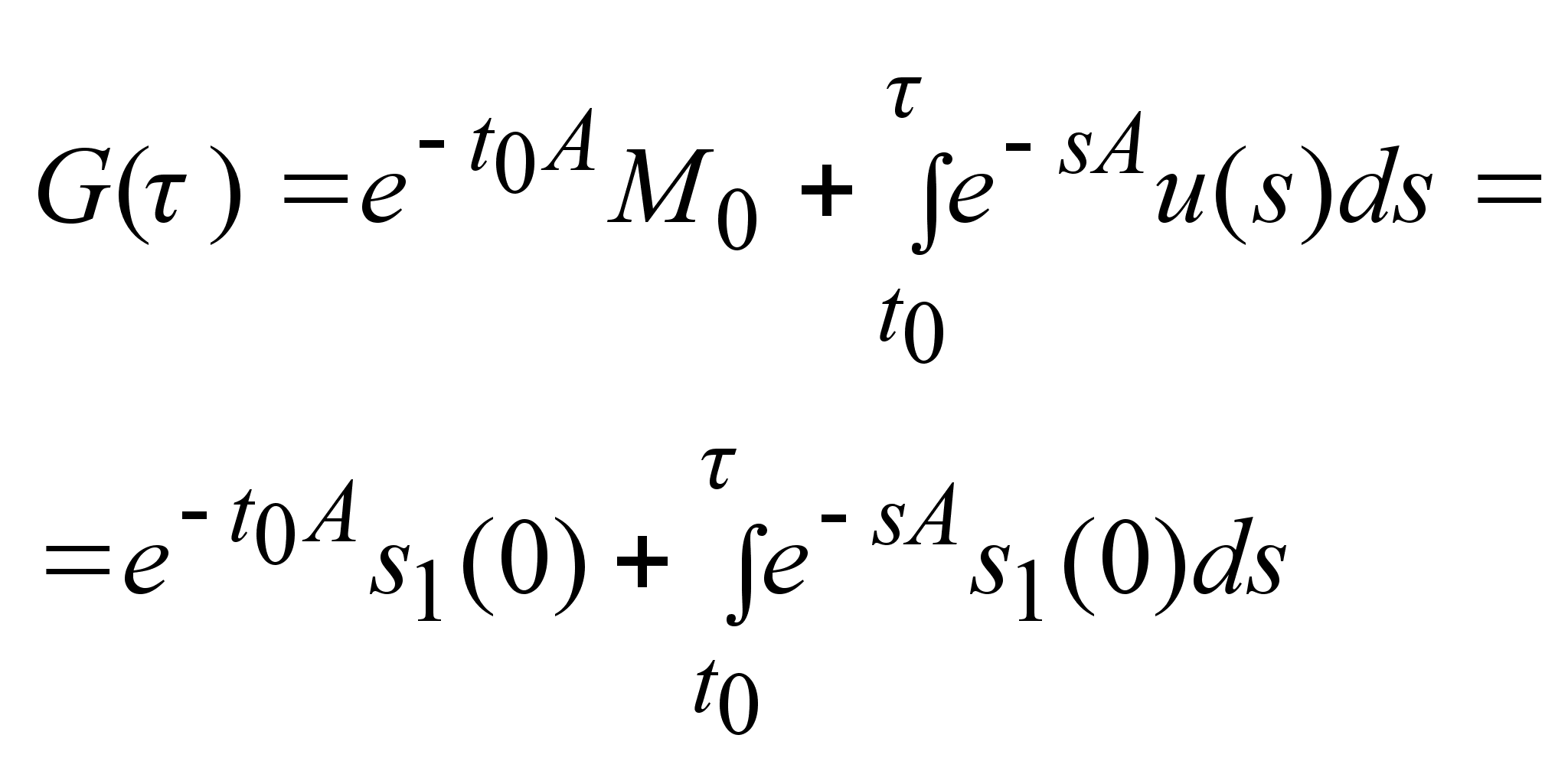 , ,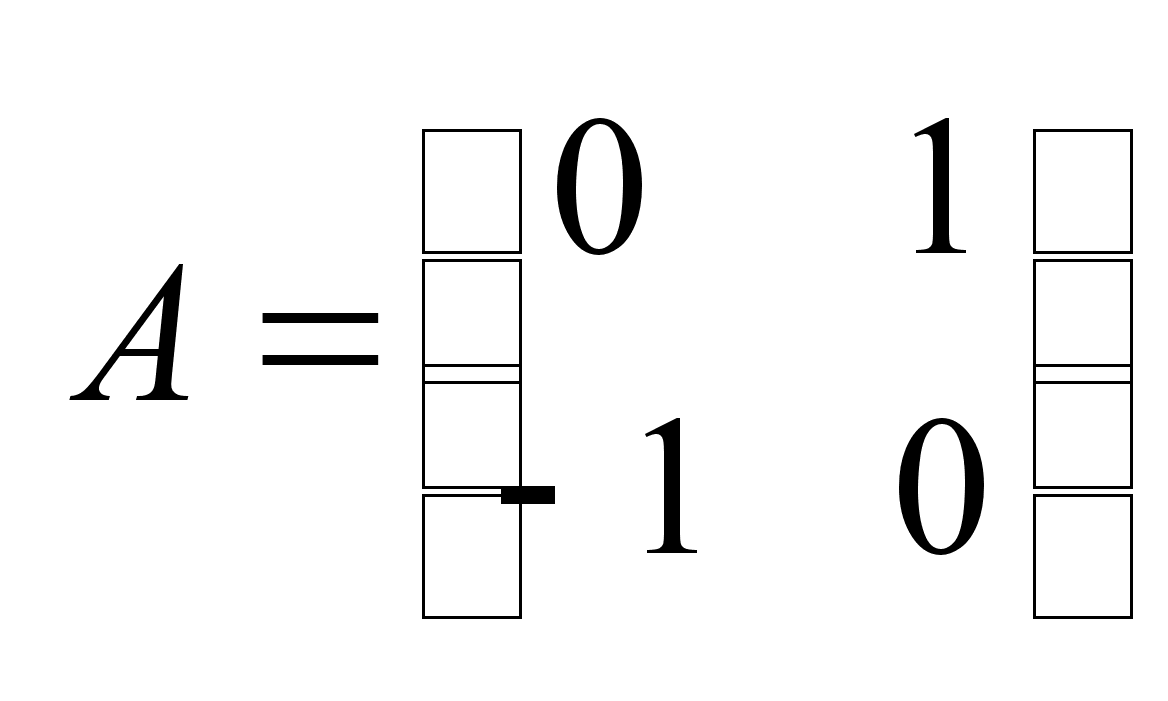 , ,
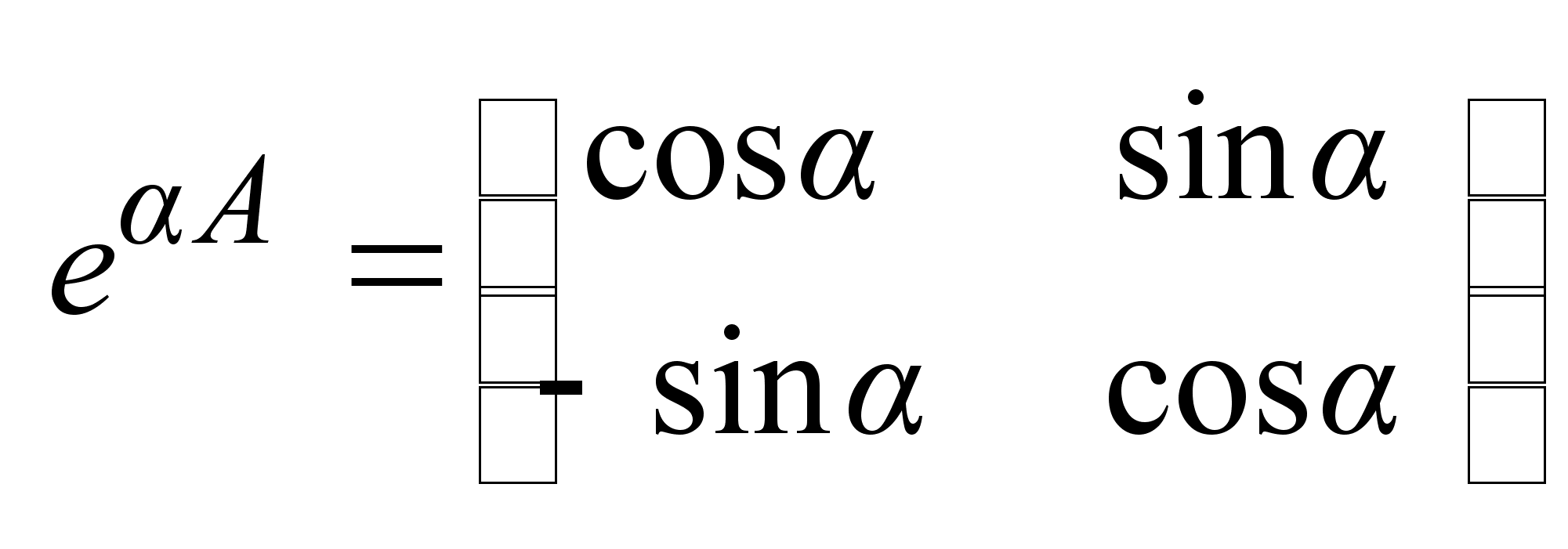 , ,
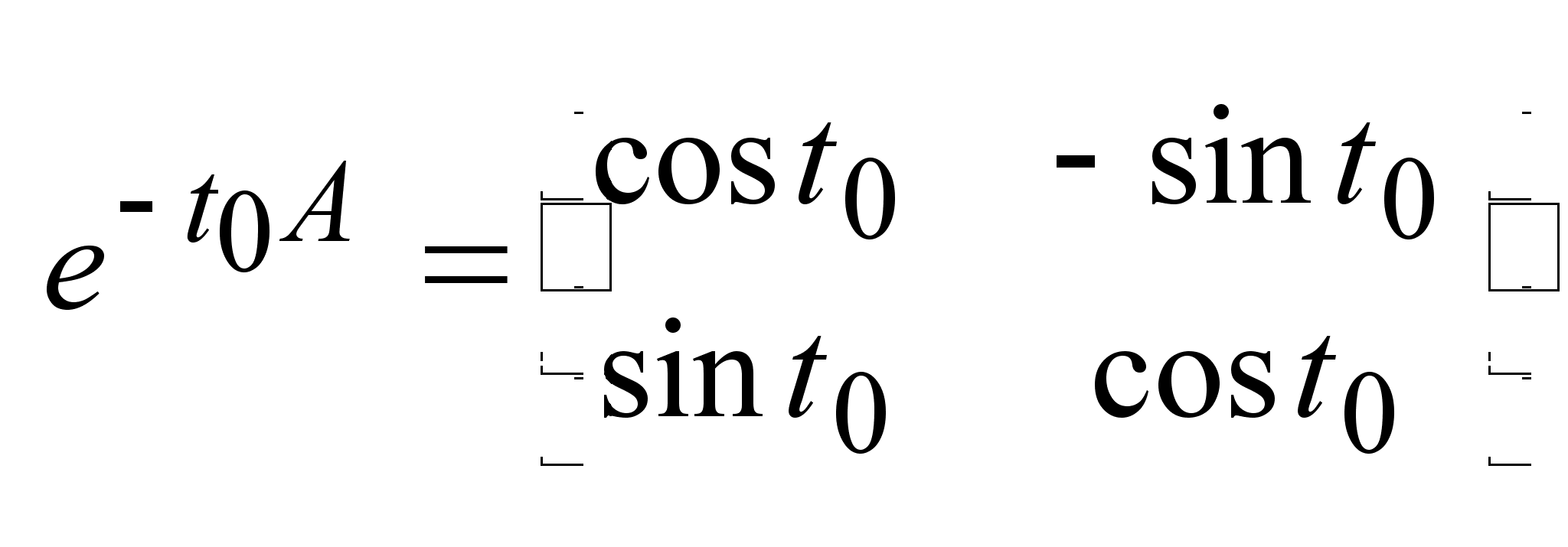 , ,
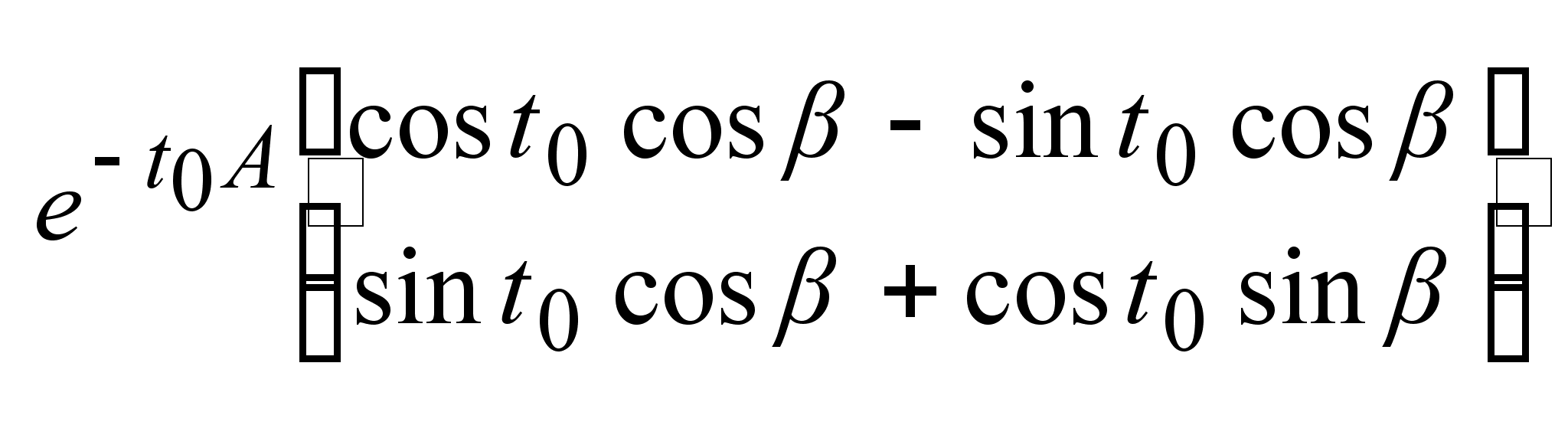 , ,
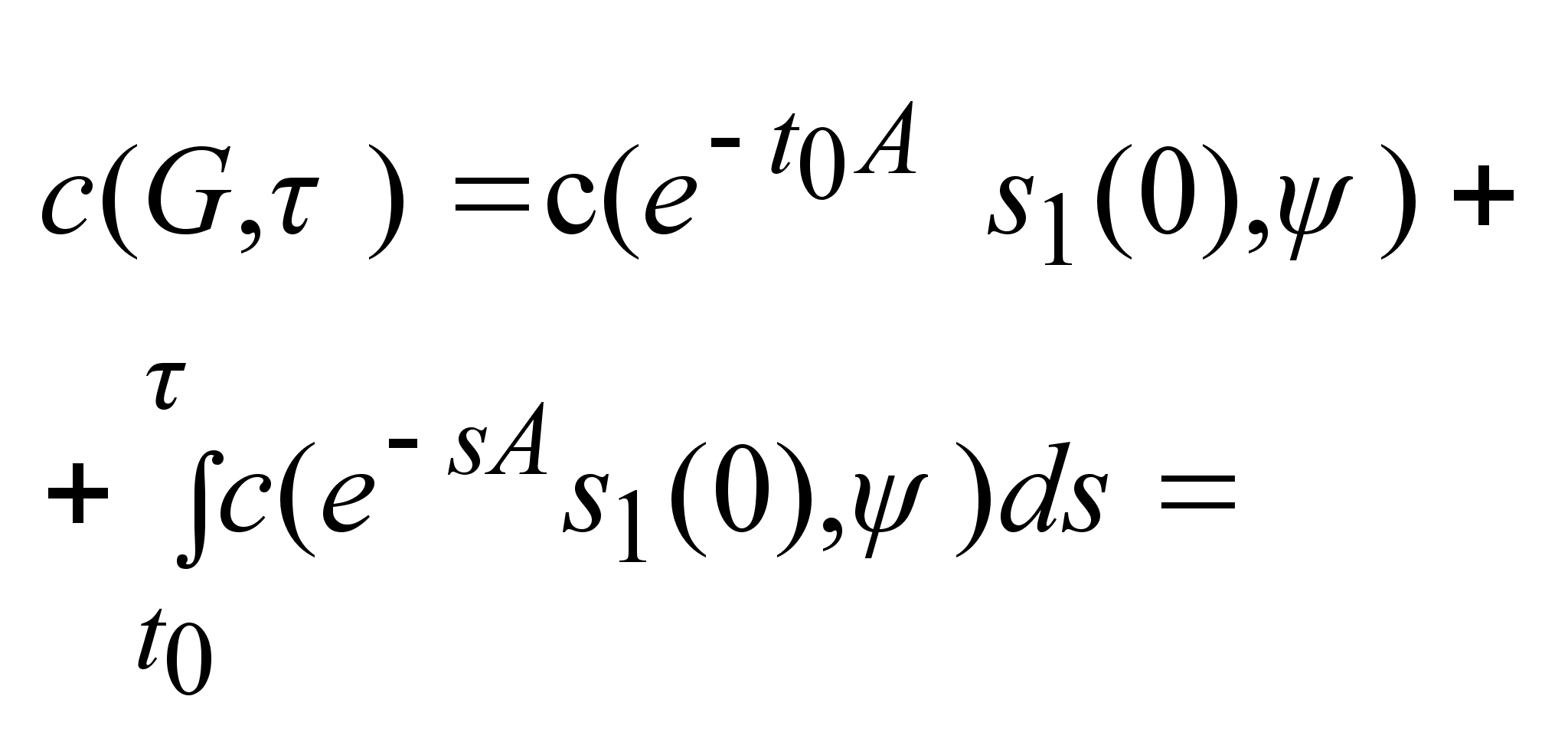 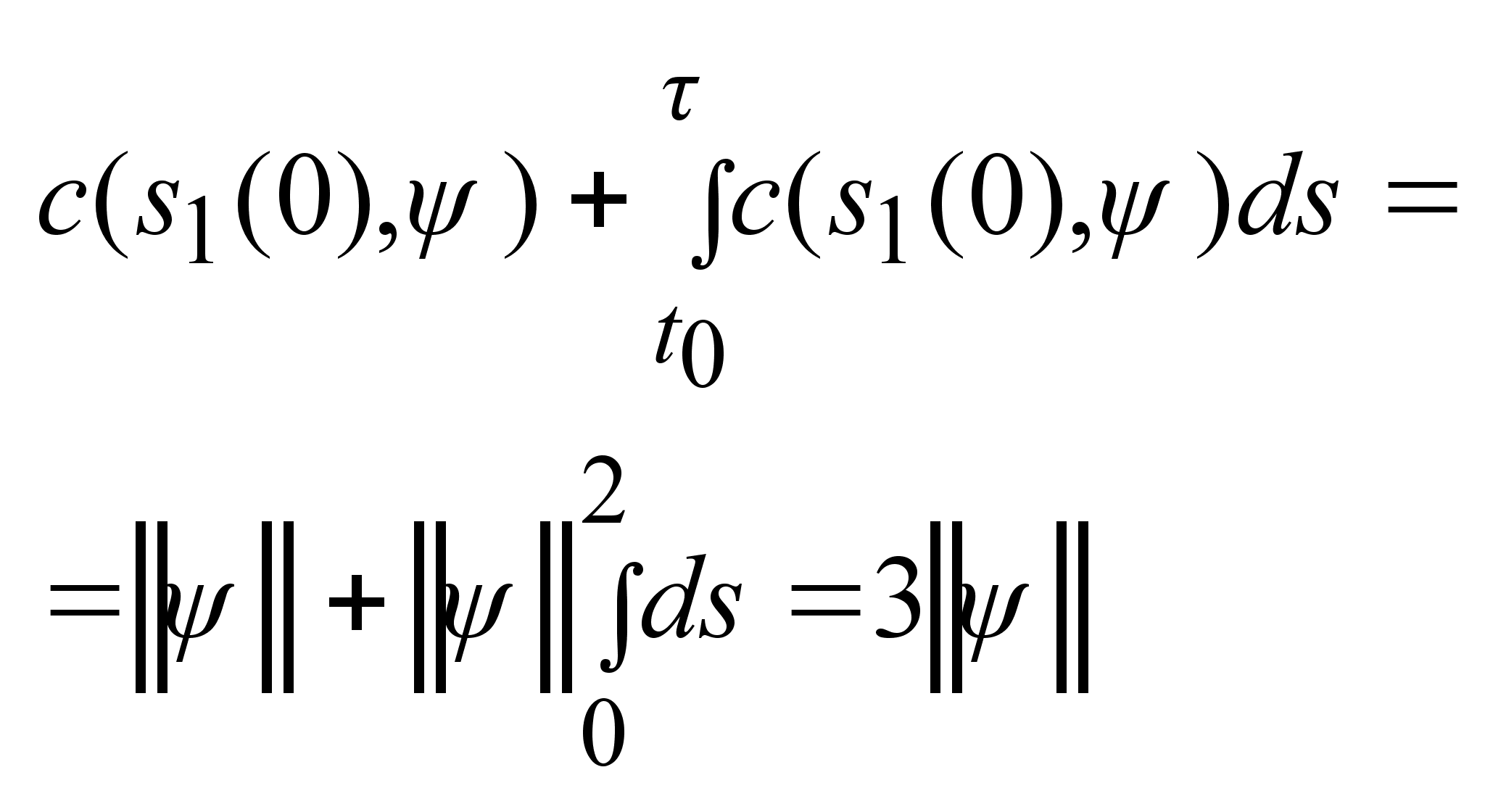 . .
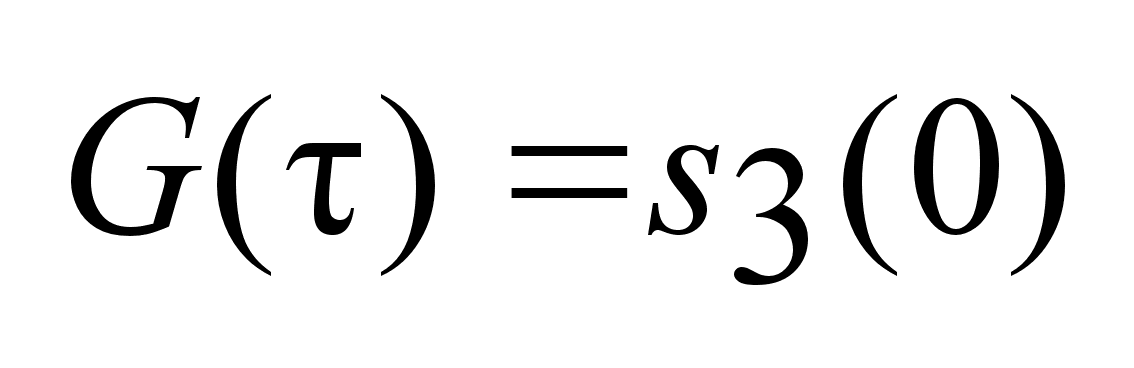 , ,
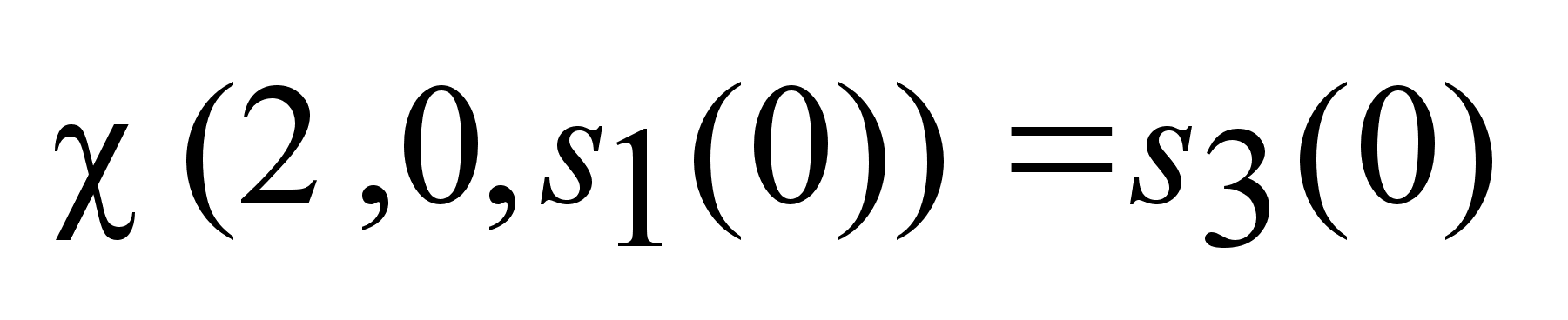 . .
16.
Общая
задача управляемости.
Теорема об
управляемости.
Рассмотрим
вопрос:
«Оптимален
ли объект?»
Рассматриваем
динамический
объект, поведение
которого описывается
системой (1)
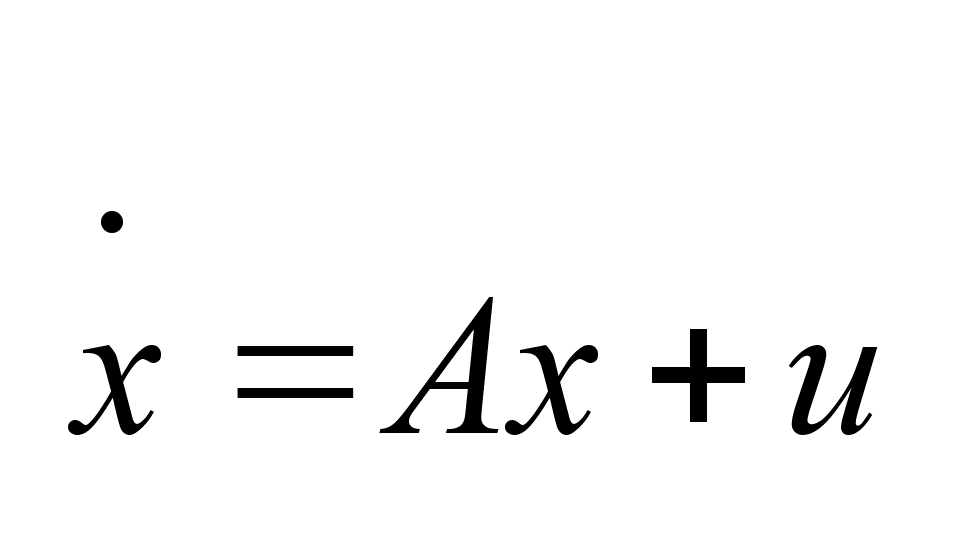 ,
x-
n-мерный
вектор, ,
x-
n-мерный
вектор,
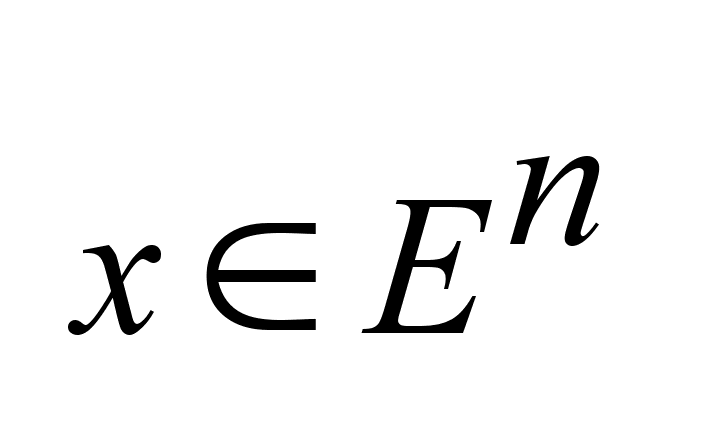 ,
A-матрица
nxn,
u
имеет ту же
размерность,
что
и ,
A-матрица
nxn,
u
имеет ту же
размерность,
что
и
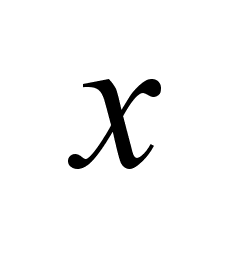 , ,
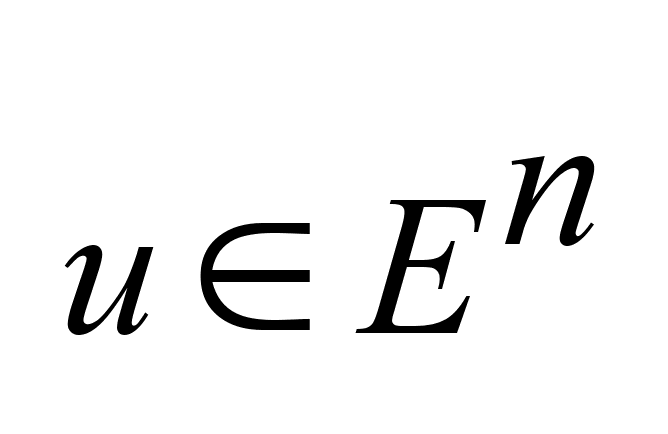 .Задано .Задано
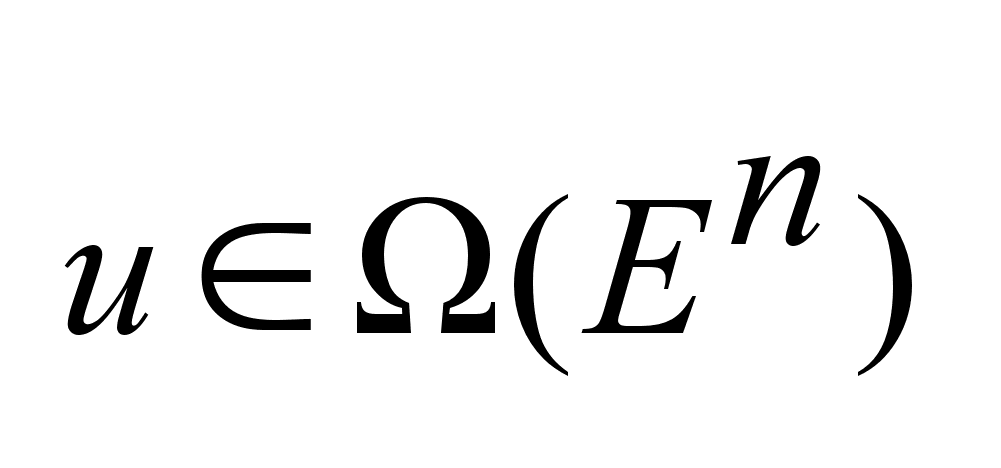 ,
u:
I ,
u:
I 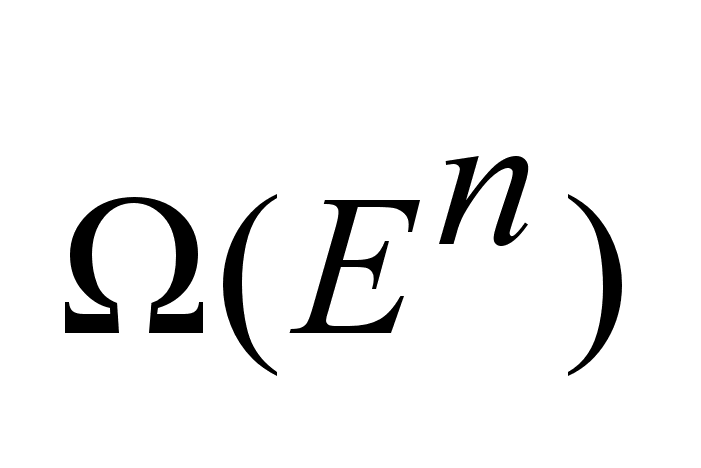 и полагается,
что u(t)
измеримо
и
и полагается,
что u(t)
измеримо
и
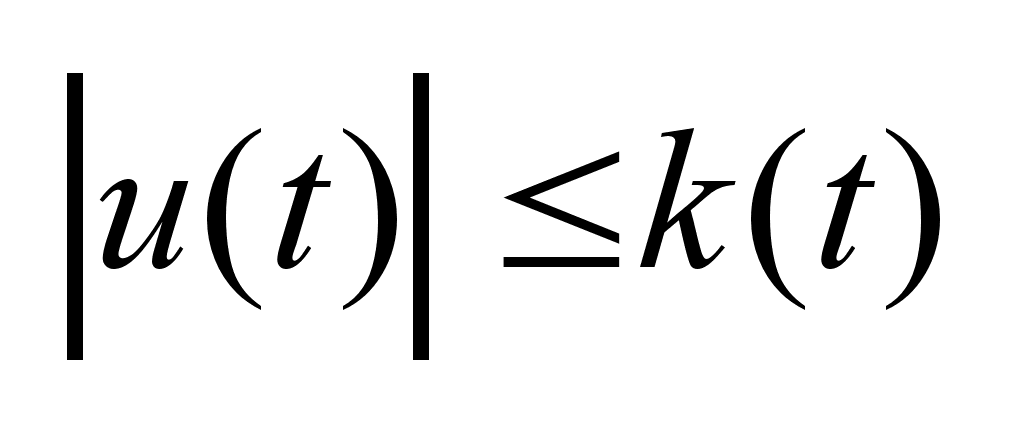 -
где
k(t)
скалярная
функция интегрируемая
по Лебегу на
отрезке I .Функция
u(t)-
называется
допустимым
управлением,
если измерима
и является
однозначной
ветвью из
многозначного
отображения
U
(2) u(t) -
где
k(t)
скалярная
функция интегрируемая
по Лебегу на
отрезке I .Функция
u(t)-
называется
допустимым
управлением,
если измерима
и является
однозначной
ветвью из
многозначного
отображения
U
(2) u(t) U(t)-
ограничения
на управления
. В фазовом
пространстве U(t)-
ограничения
на управления
. В фазовом
пространстве
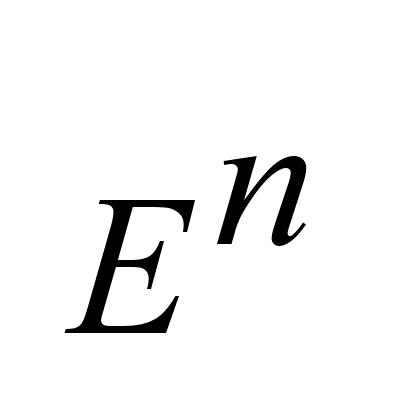 заданы
два не пустых
множества заданы
два не пустых
множества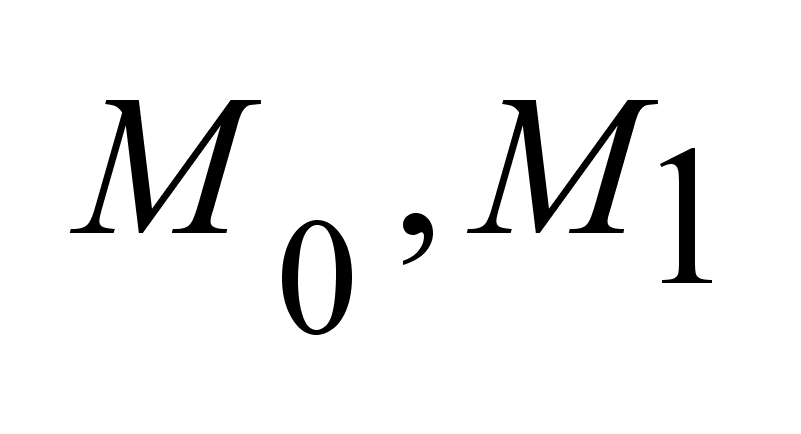 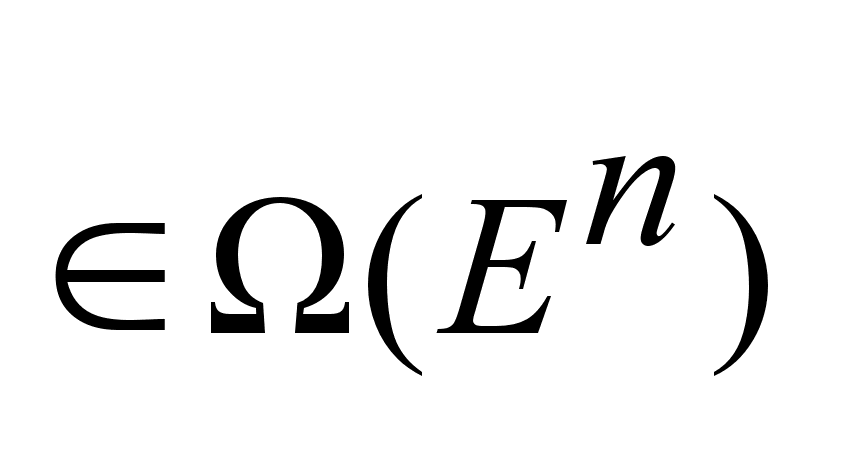 .
Допустимое
управление
u(t)
на отр.I
осуществляете
переход из
начального
мн-ва .
Допустимое
управление
u(t)
на отр.I
осуществляете
переход из
начального
мн-ва
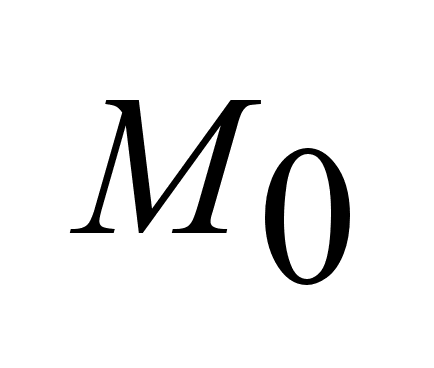 в конечное
множество
в конечное
множество
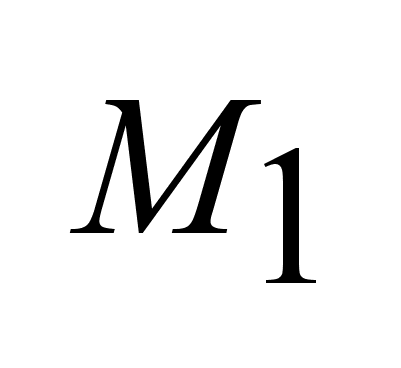 ,
если существует
решение уравнения
(1), удовлетворяющее
граничным
условиям (4) ,
если существует
решение уравнения
(1), удовлетворяющее
граничным
условиям (4)
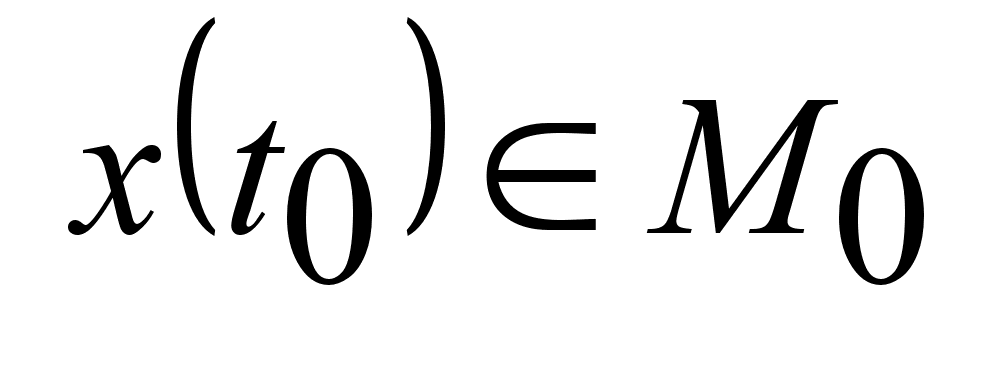 и и
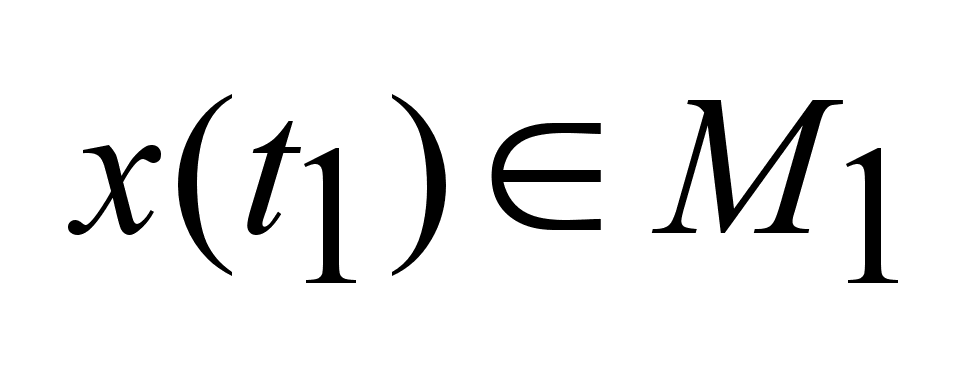 .
Цель управления-
перевод динамический
объекта из .
Цель управления-
перевод динамический
объекта из
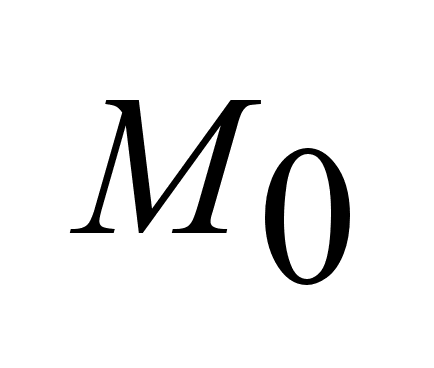 в в
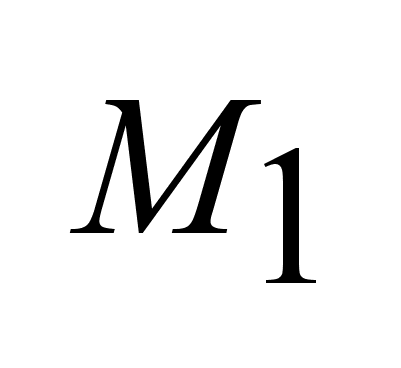 ,
а качество
определяет
функционал.
Таким функционалом
явл. время,
следовательно ,
а качество
определяет
функционал.
Таким функционалом
явл. время,
следовательно
задача
быстродействия
заключается
в нахождении
такого допустимого
управления,
которое осуществляет
переход из
множества
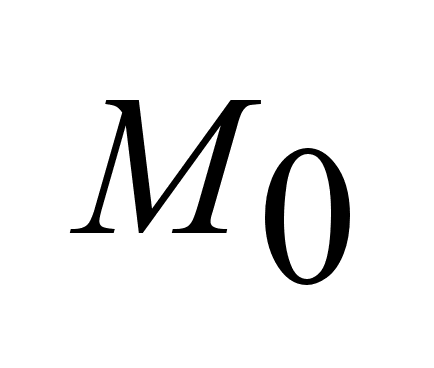 в в
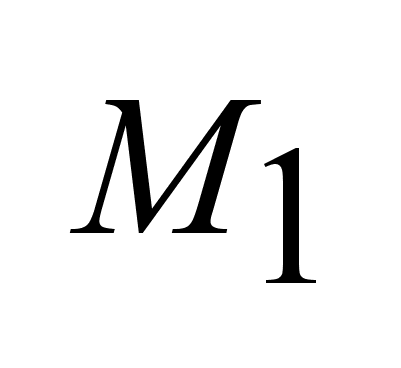 за
наименьшее
время. за
наименьшее
время.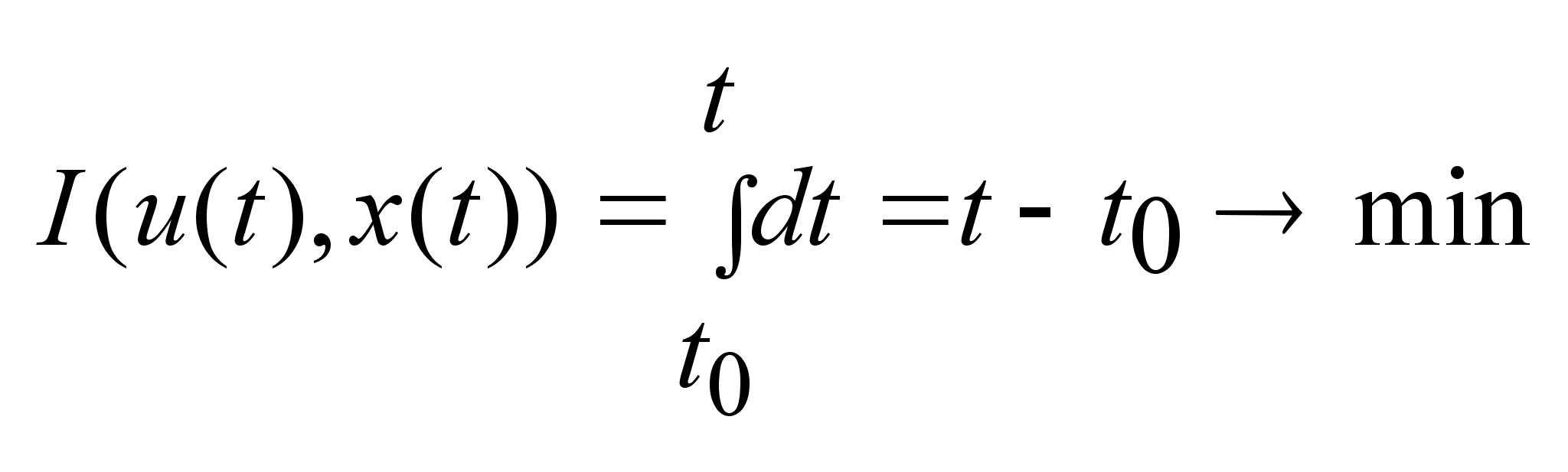 (4).
(4).
Задача
управления-
решение вопроса
:
существует
хотя бы одно
допустимое
управление
u(t)
, переводящий
динамический
объекта из
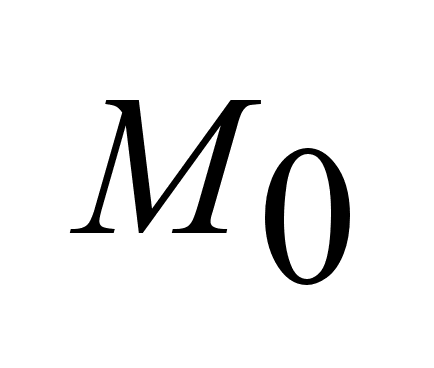 в в
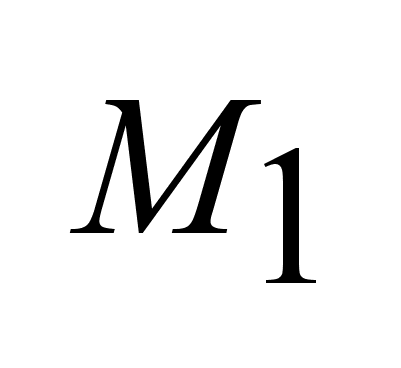 ,
на отр. времени
I.
Это соответствует
решению краевой
задачи: ,
на отр. времени
I.
Это соответствует
решению краевой
задачи:
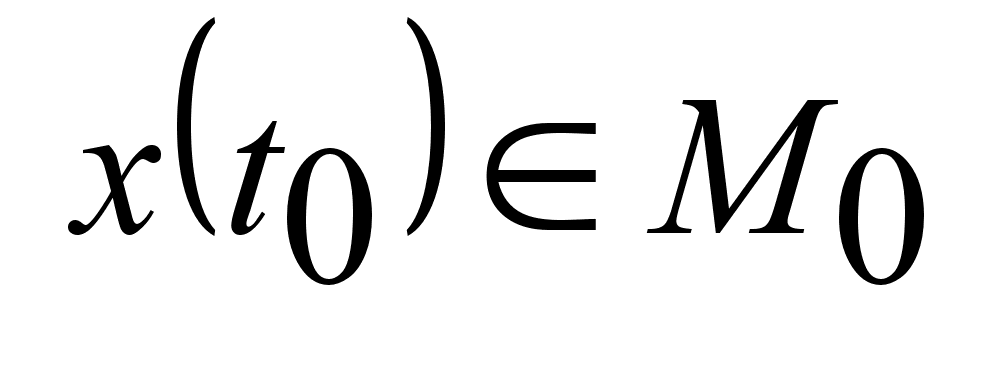 , ,
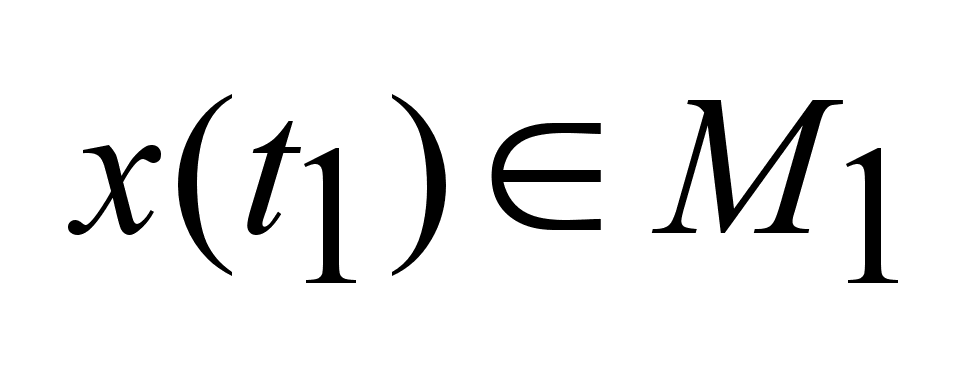 . .
Определим
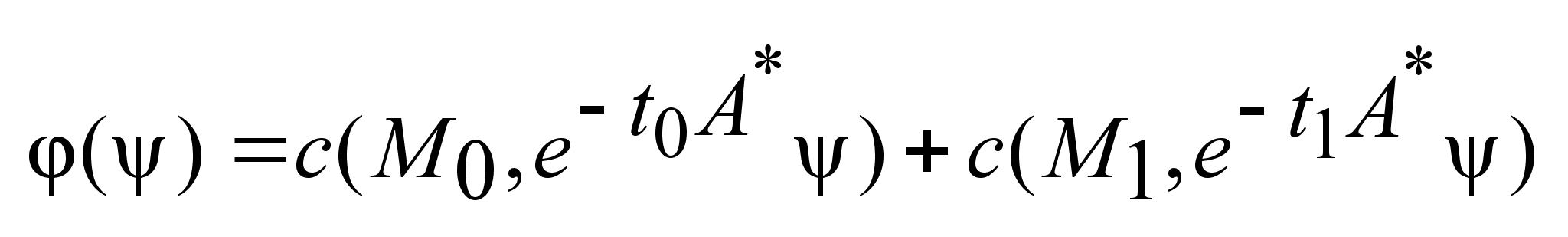 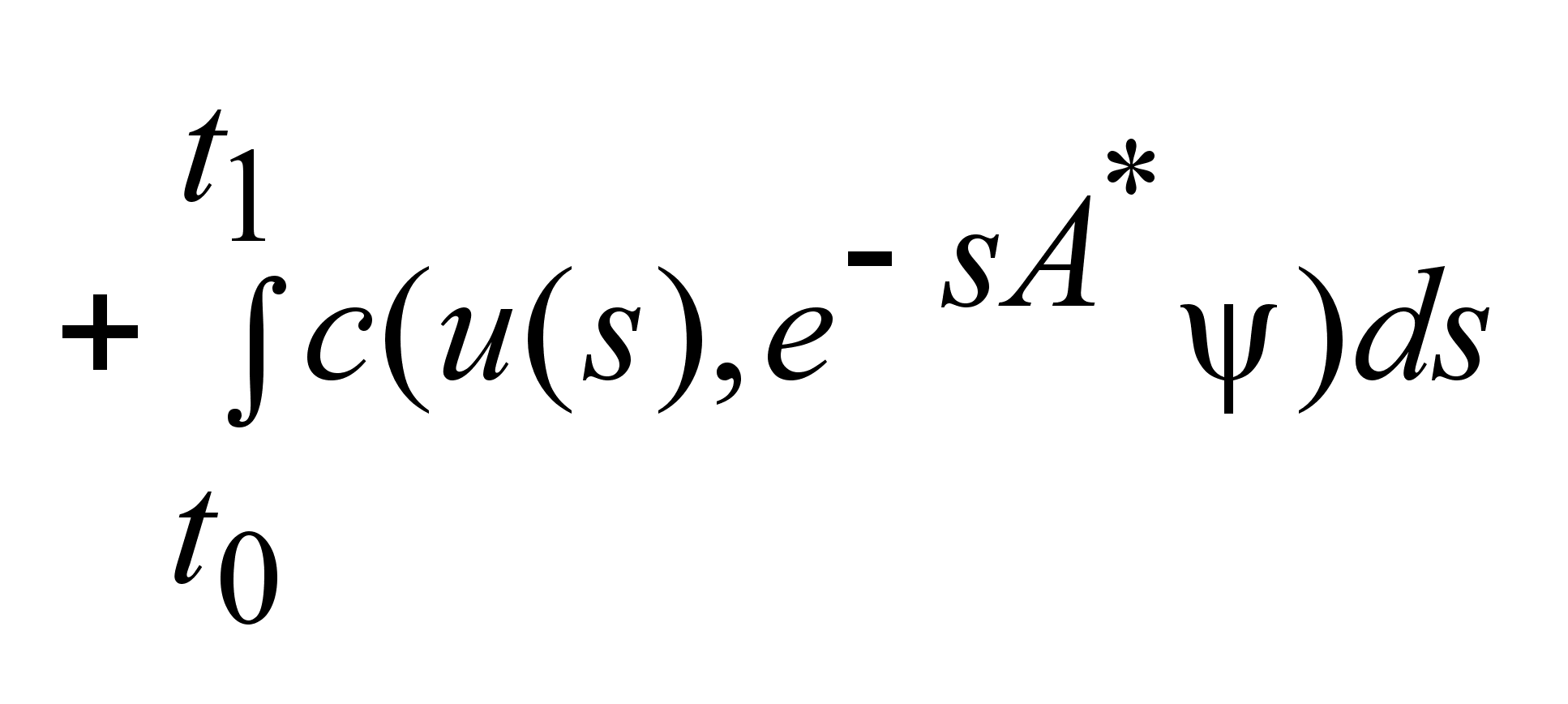 таким
образом. таким
образом.
Теорема
об уравляемости.Если
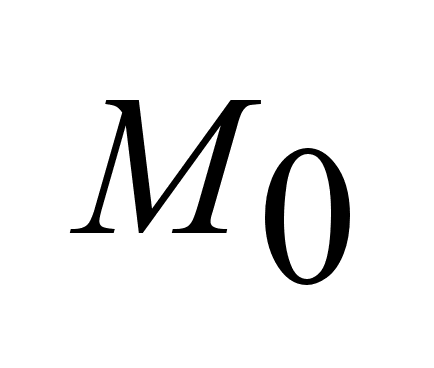 и и
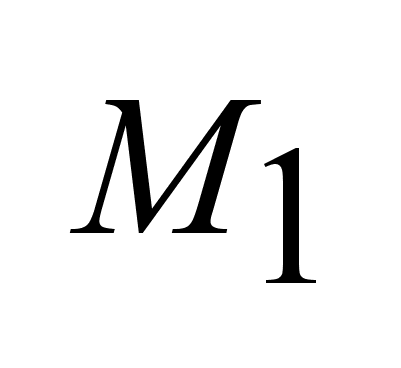 выпуклы,
то объект явл.
управляемым
на отр. I
из мн-ва выпуклы,
то объект явл.
управляемым
на отр. I
из мн-ва
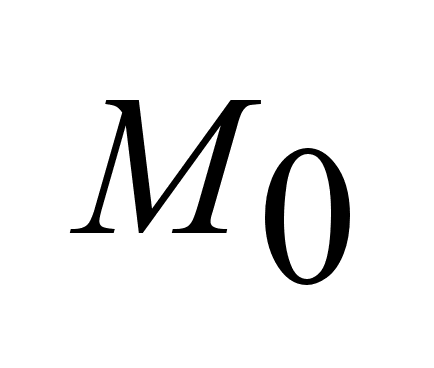 в
в
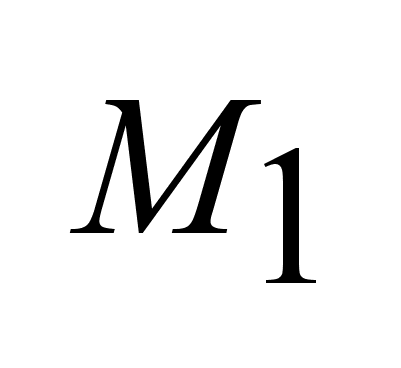 ,
тогда и только
тогда, когда
для ,
тогда и только
тогда, когда
для
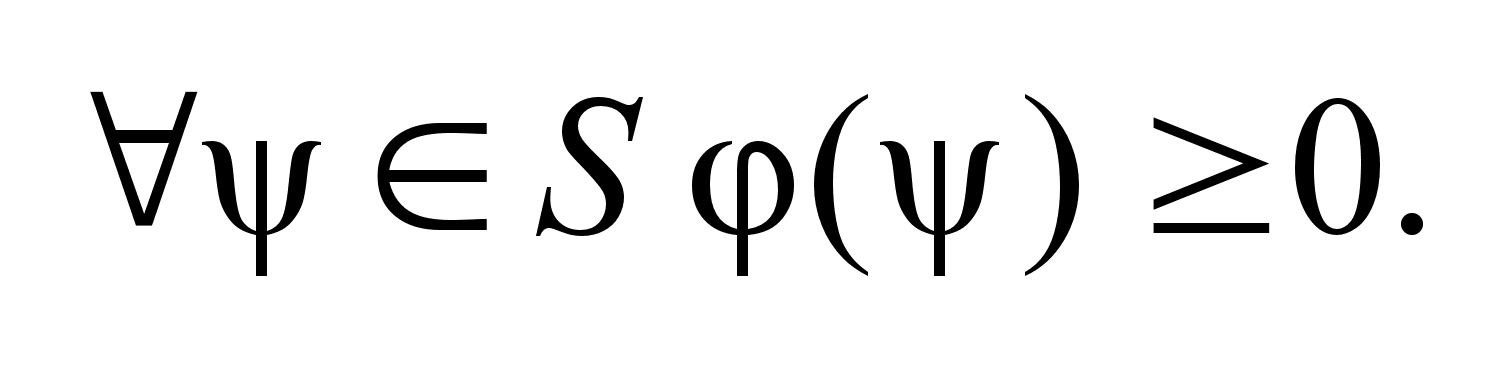
Док-во:
Очевидно, объект
управляем тогда
и только тогда,
когда множество
достижимости
и
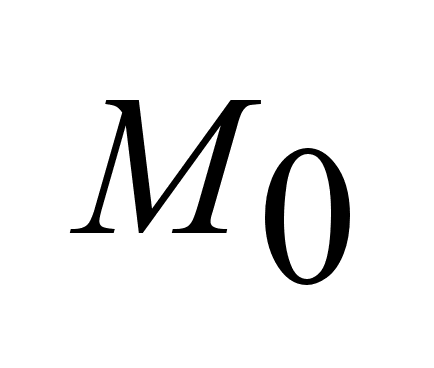 пересекаются.
Т.к.
пересекаются.
Т.к.
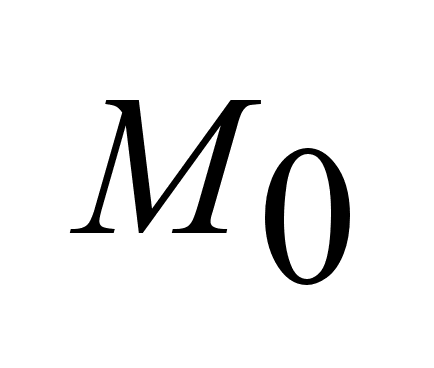 и и
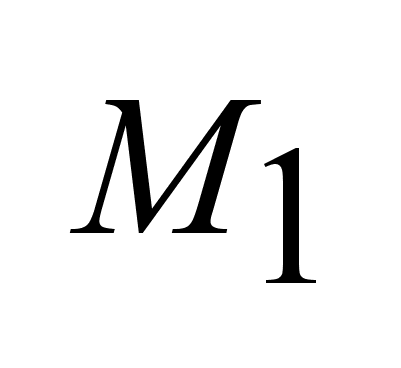 выпуклы,
то для него
применим следствие
из 11 св-ва опорных
фун-ий
(
выпуклы,
то для него
применим следствие
из 11 св-ва опорных
фун-ий
(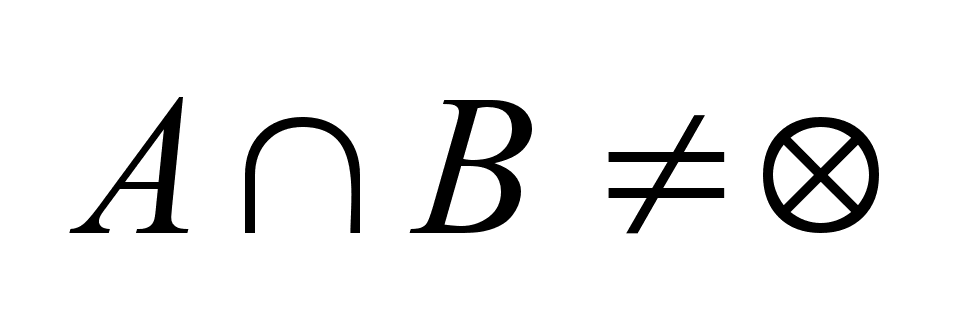 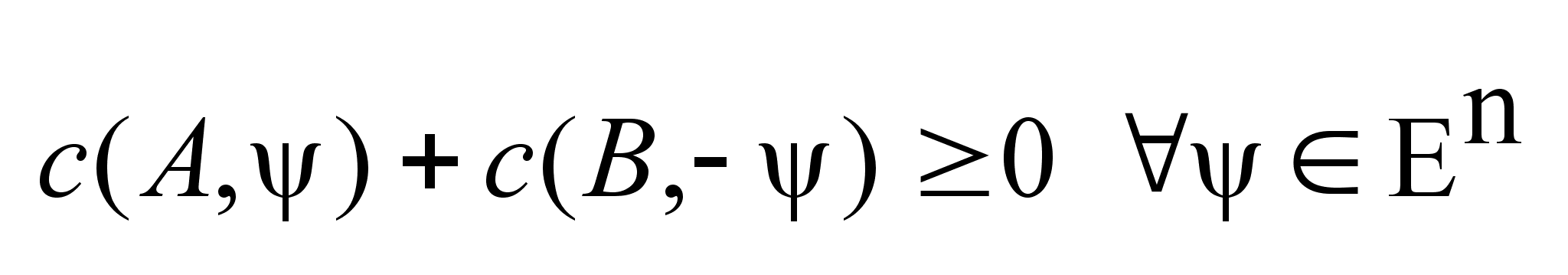 ). ).
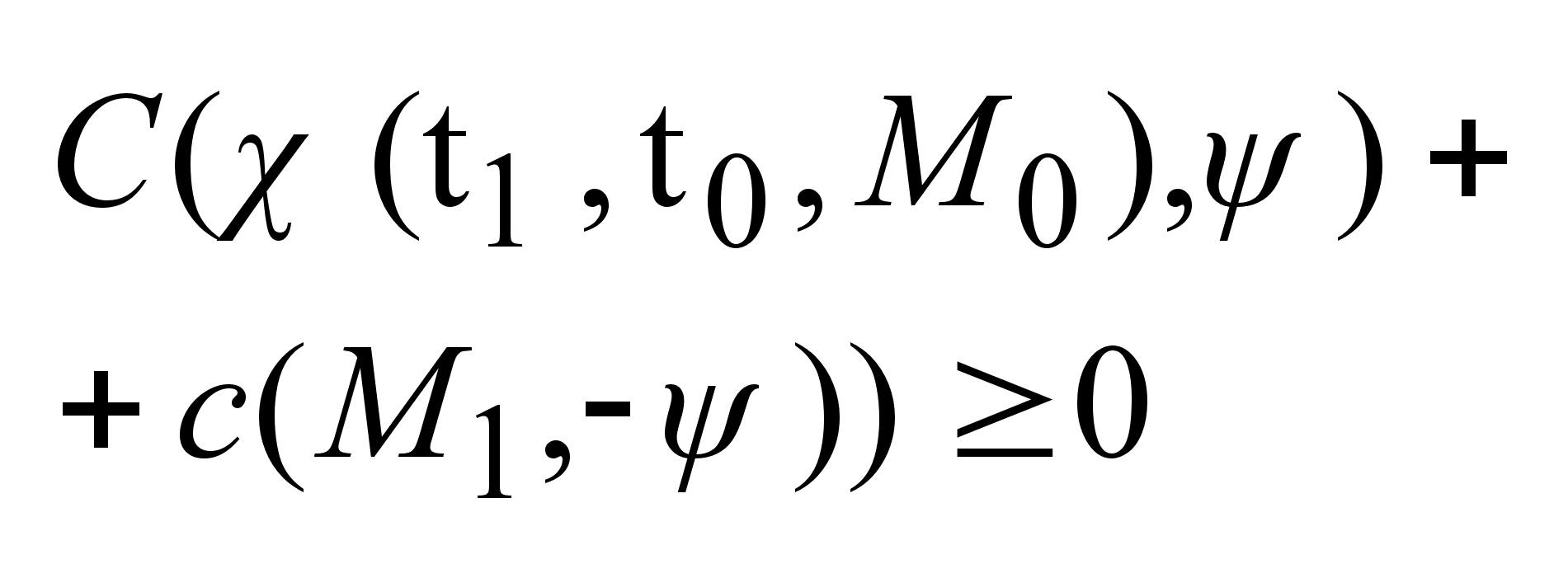 , , ; ;
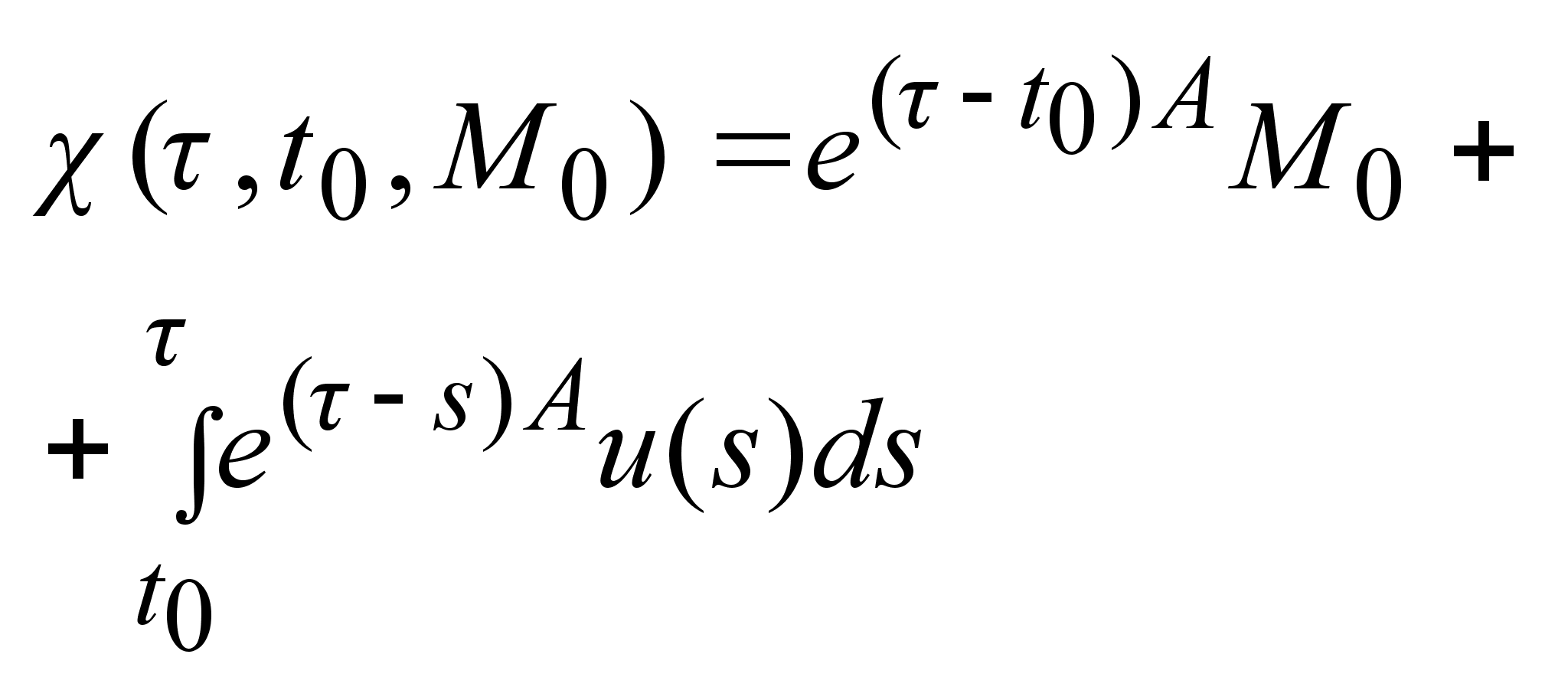
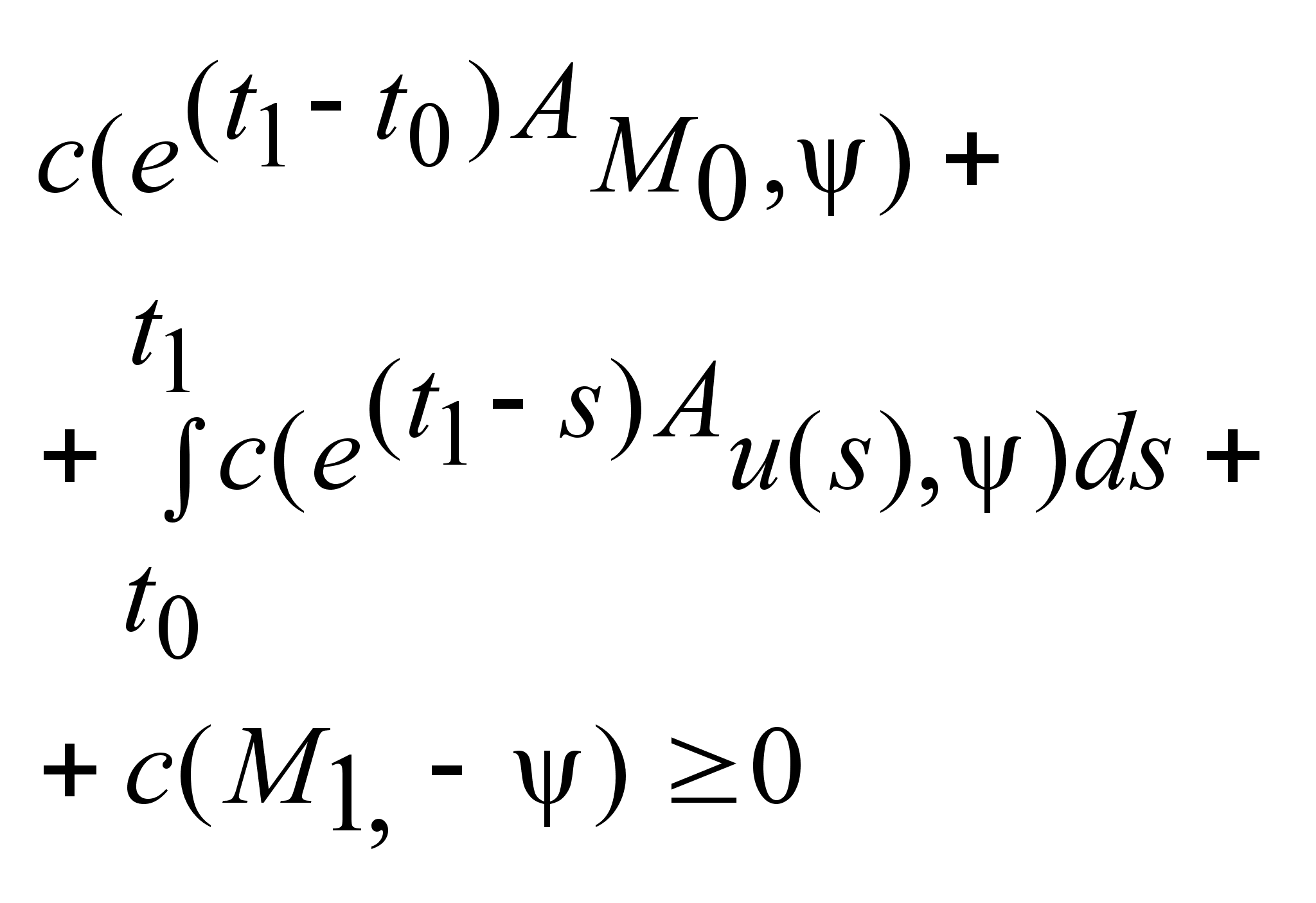 ; ;
Bocпользуемся
еще одним св-ом
опрных функий:
если
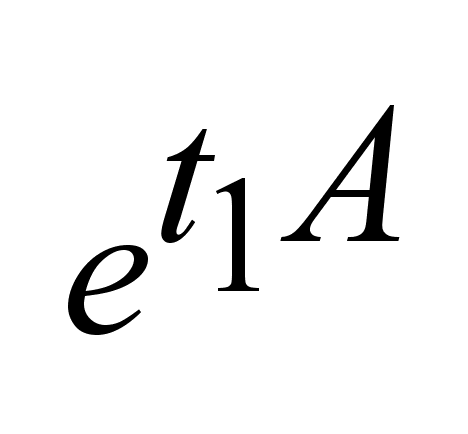 -
невырожденная
матрица, то
можно воспользоваться
св-вом , что -
невырожденная
матрица, то
можно воспользоваться
св-вом , что
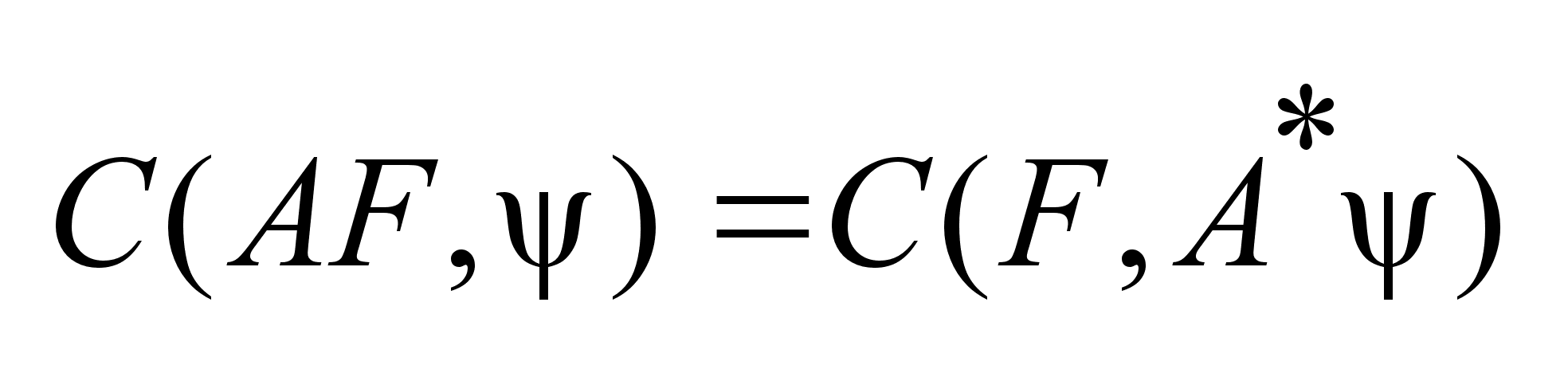 : :
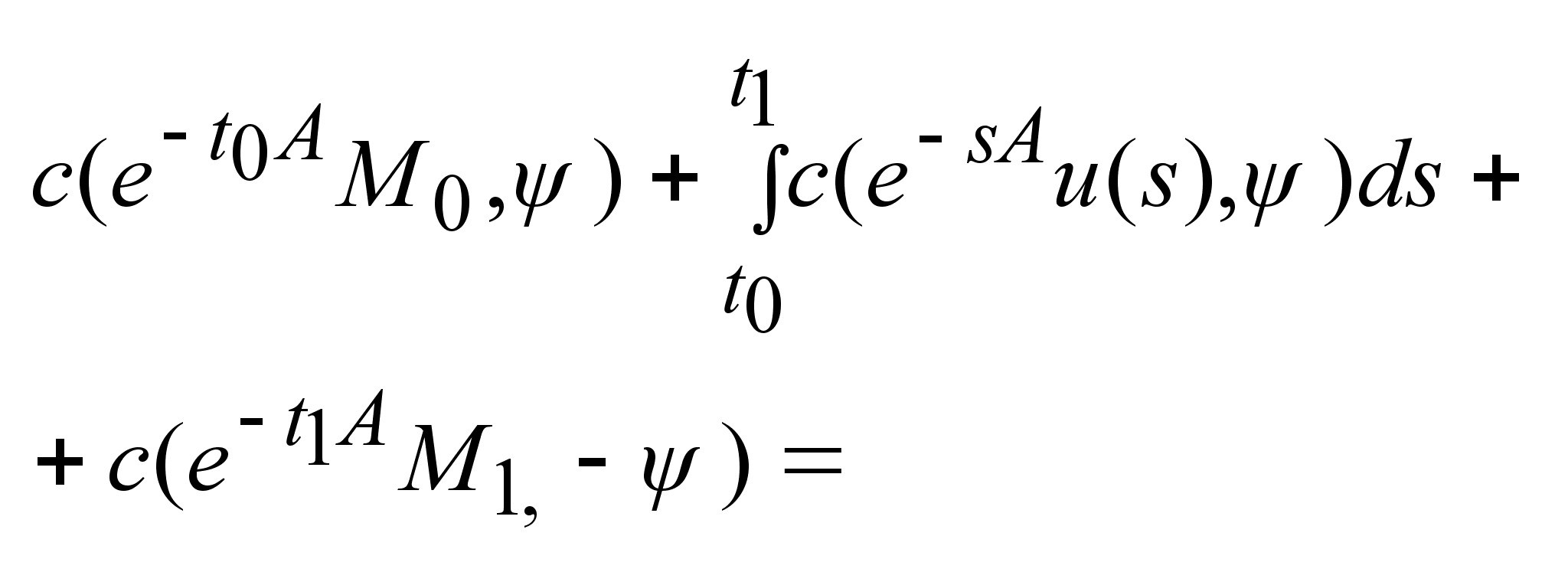 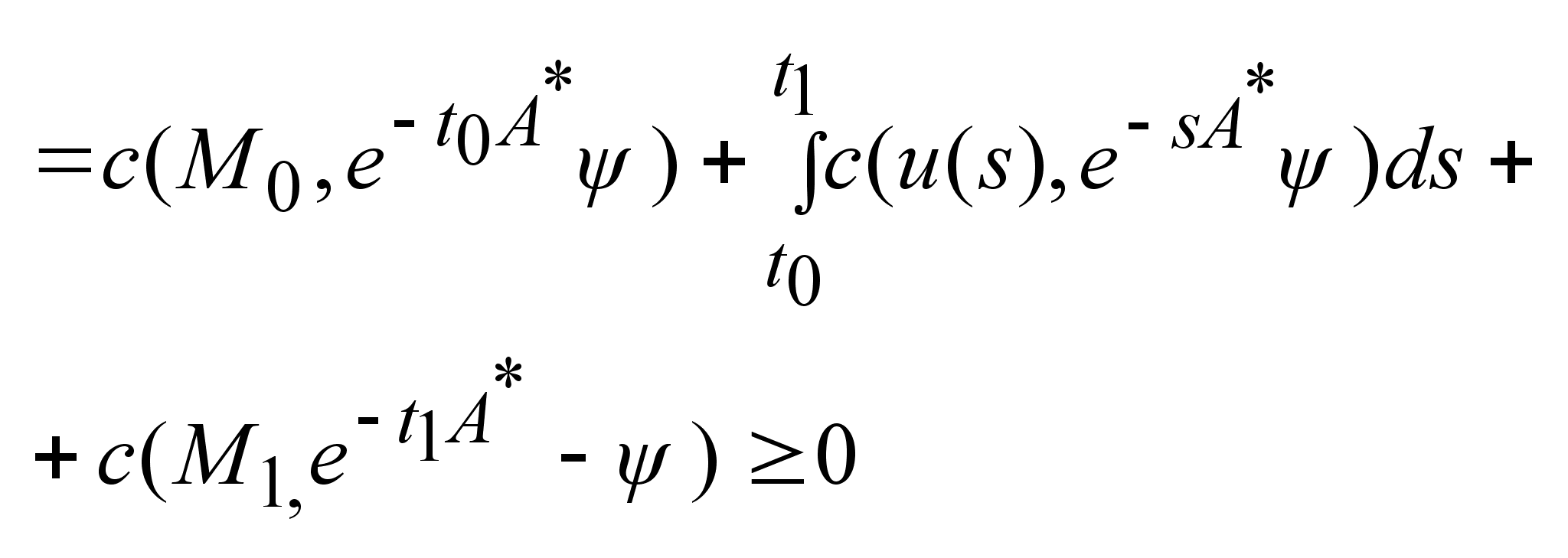
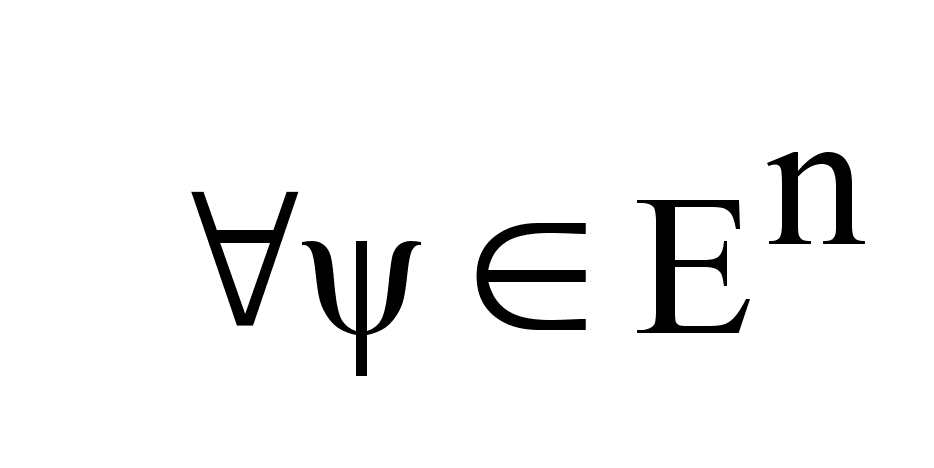 . .
В
силу положительной
опорной фун-ии
относительно
аргумента
 , получаем, что
это верно
, получаем, что
это верно
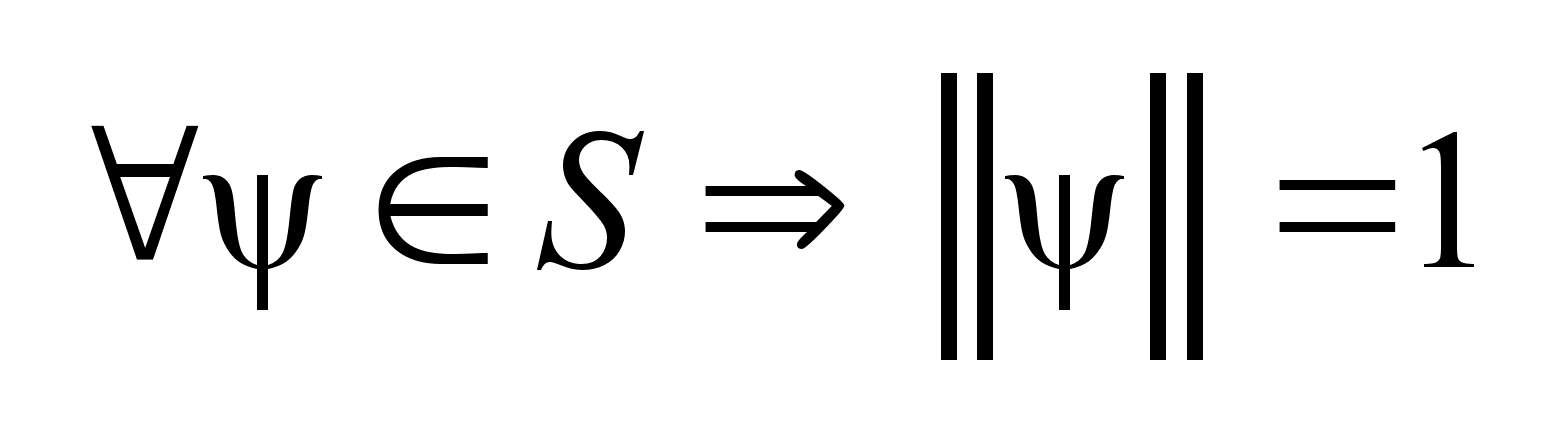 . .
Теорема
док-на, т.к. левая
часть неравенства
и есть
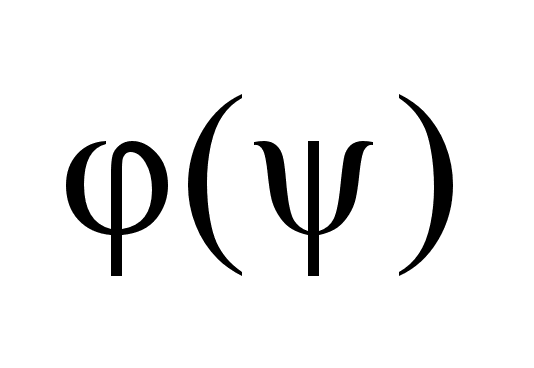 . .
17.Численное
решение задачи
управляемости.
Объект
управляем на
I=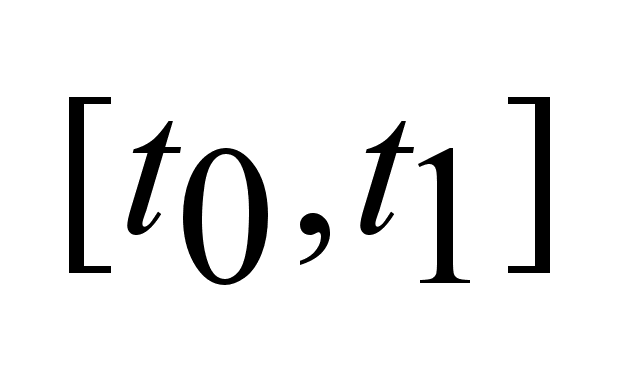 ,
если выполняется ,
если выполняется
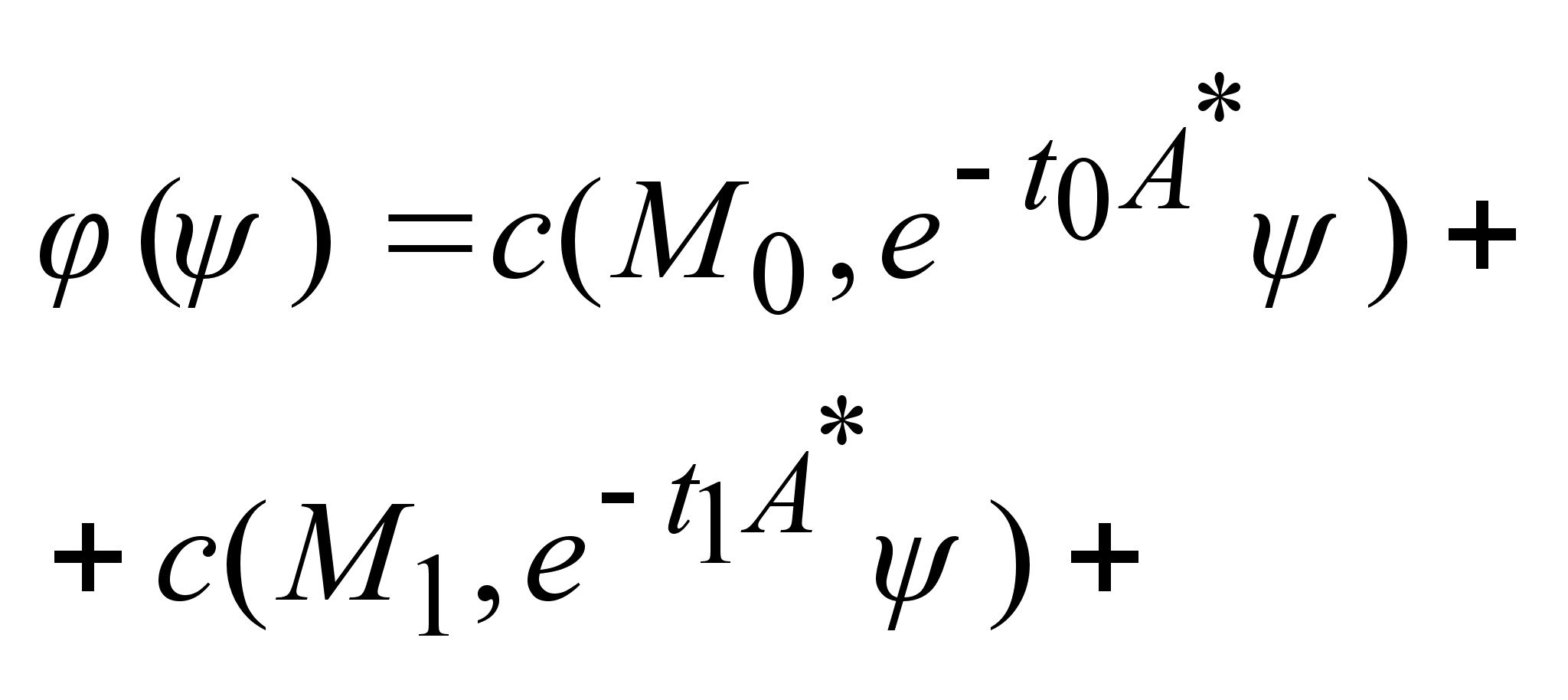 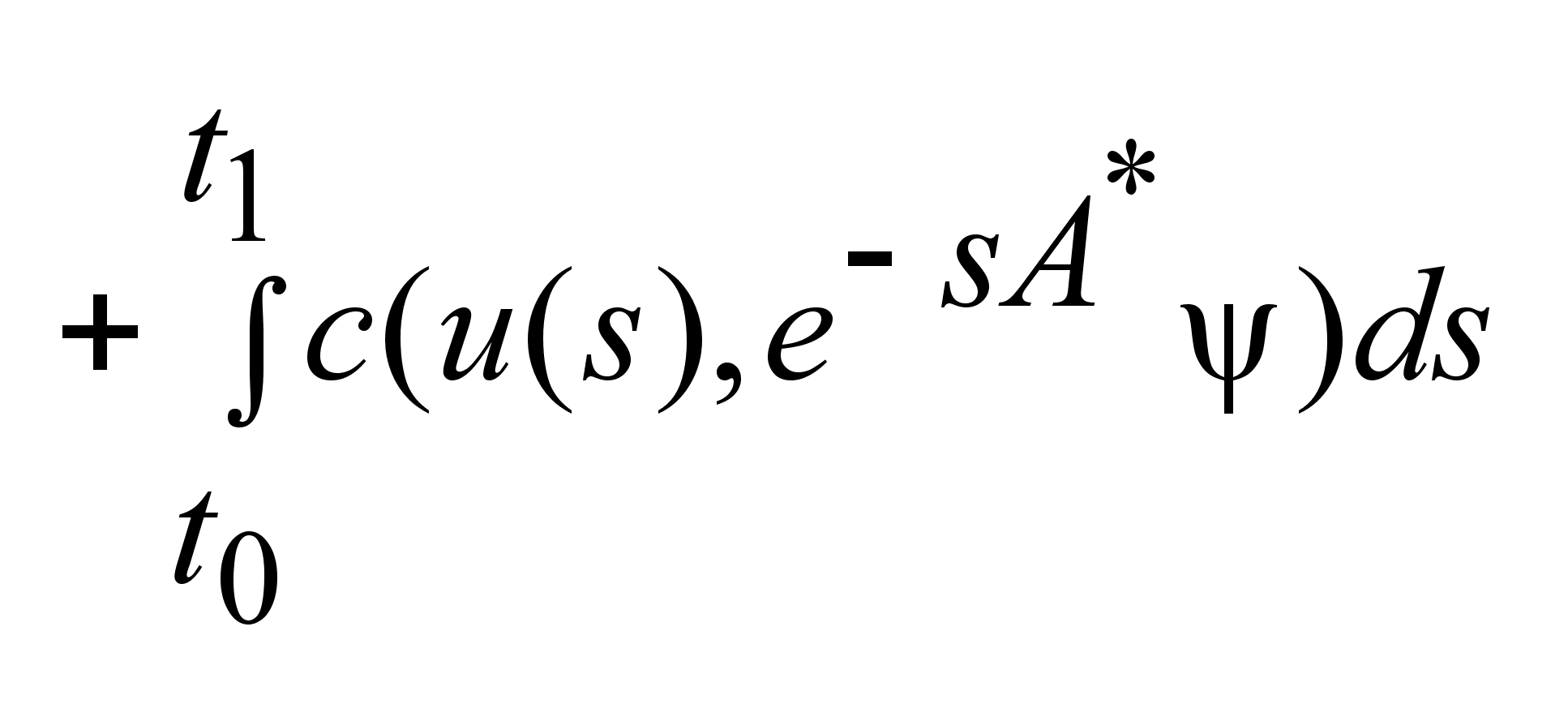
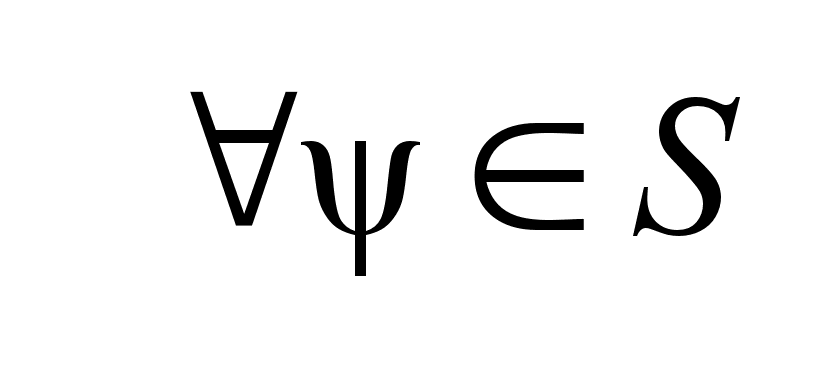 .
Если множнство .
Если множнство
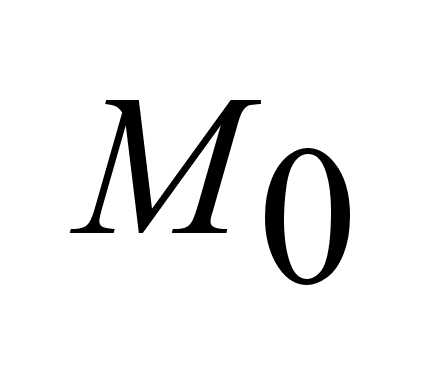 , ,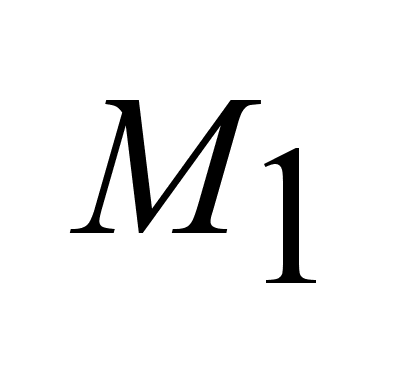 , ,
 таковы
что аналитически
невозможно
получить значение
опорной функции
u
таковы
что аналитически
невозможно
получить значение
опорной функции
u
Вычисление
матрицы
 и интеграл,
тогда задача
решается с
применением
ЭВМ. На ЭВМ решается
для конечного
числа
и интеграл,
тогда задача
решается с
применением
ЭВМ. На ЭВМ решается
для конечного
числа
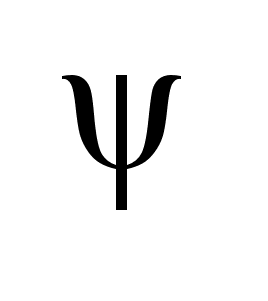 .
Для этого сфера
покрывается .
Для этого сфера
покрывается
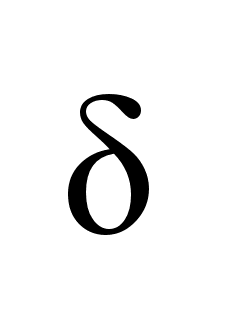 -сетью.
В двумерном
пространстве -сетью.
В двумерном
пространстве
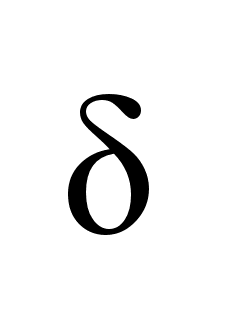 -сеть
определяется
углом -сеть
определяется
углом
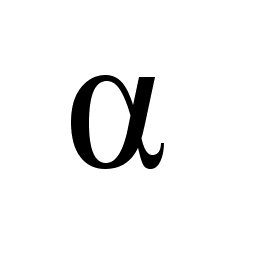 .
В трехмерном
пространстве .
В трехмерном
пространстве
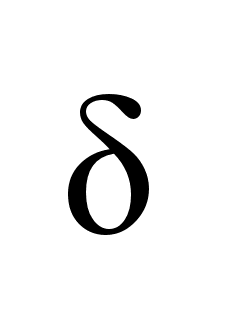 -сеть
определяется
двумя углами.
Пусть -сеть
определяется
двумя углами.
Пусть
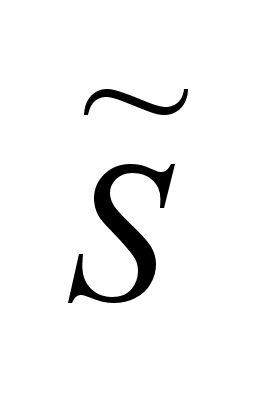 некоторая некоторая
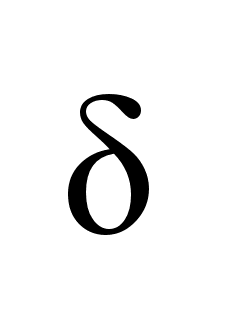 -сеть
некоторой
единичной сферы
S,
где -сеть
некоторой
единичной сферы
S,
где
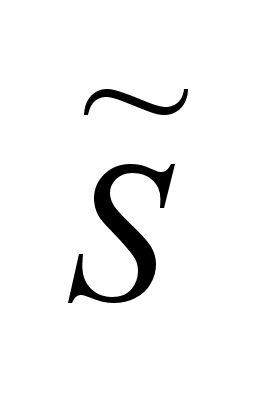 -конечное
множество.
Какой бы вектор -конечное
множество.
Какой бы вектор
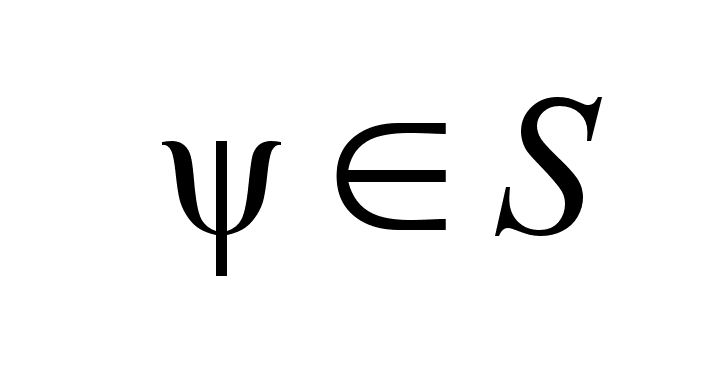 ,
найдется ,
найдется
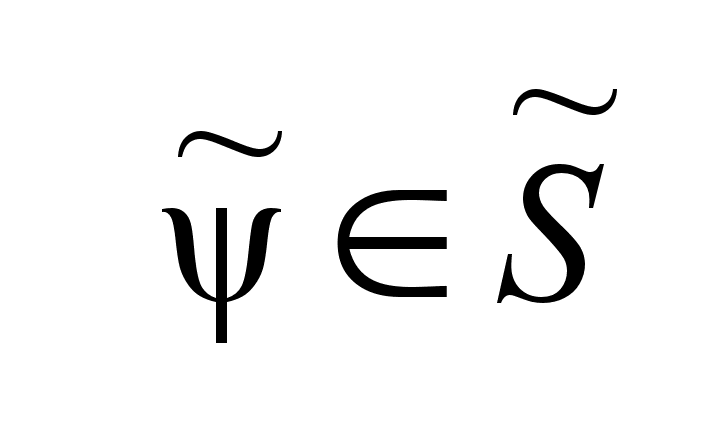 ,
такой что ,
такой что
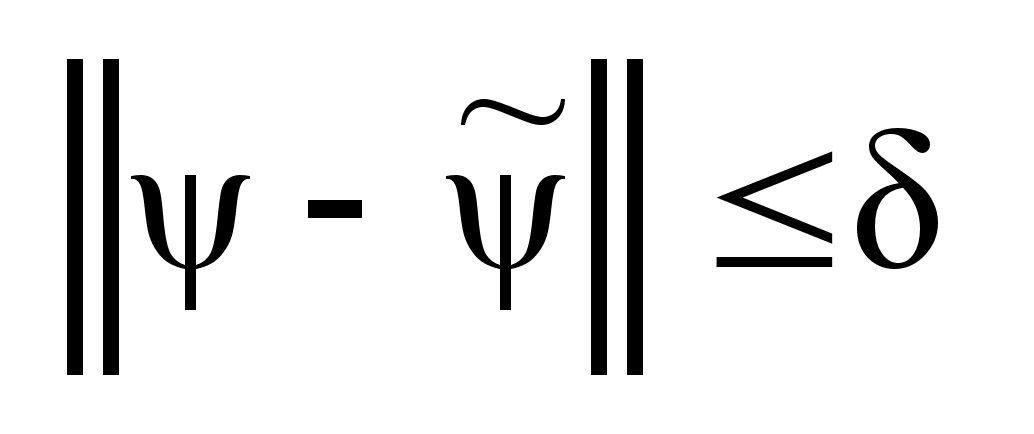 .
Пусть .
Пусть
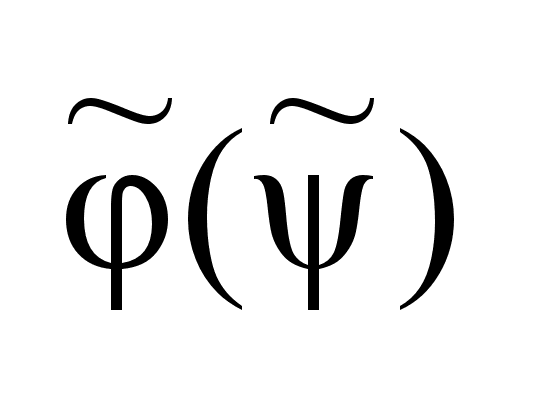 вычислимое
приближенное
значение вычислимое
приближенное
значение
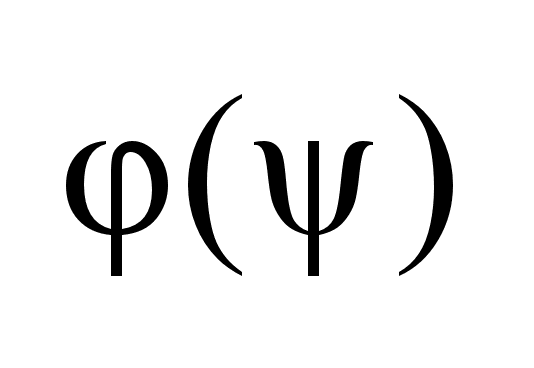 в точках
в точках
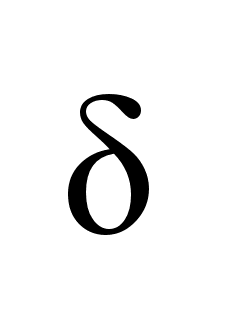 -сети. -сети.
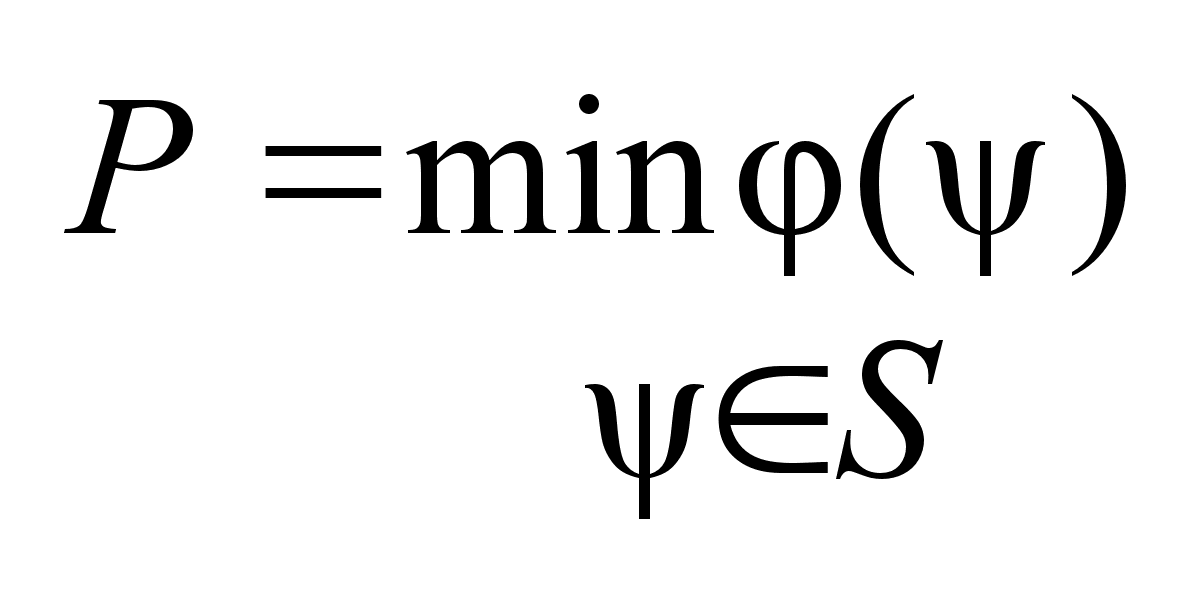 , ,
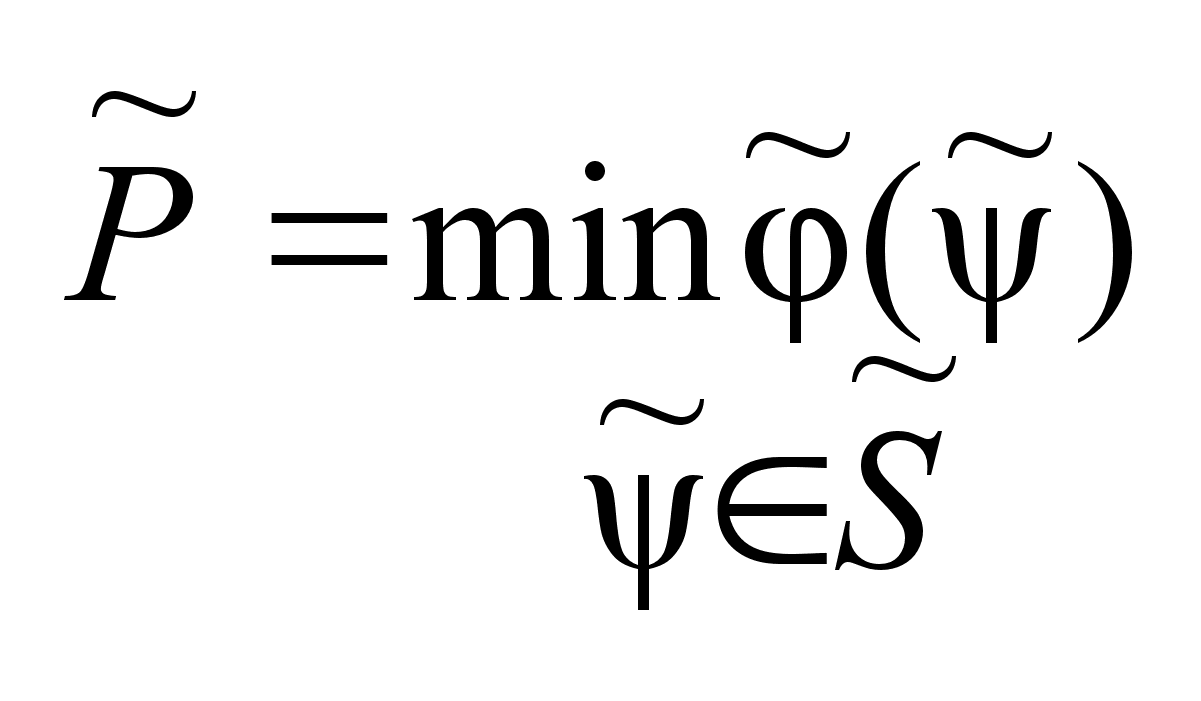 .
Необходимо,
чтобы .
Необходимо,
чтобы
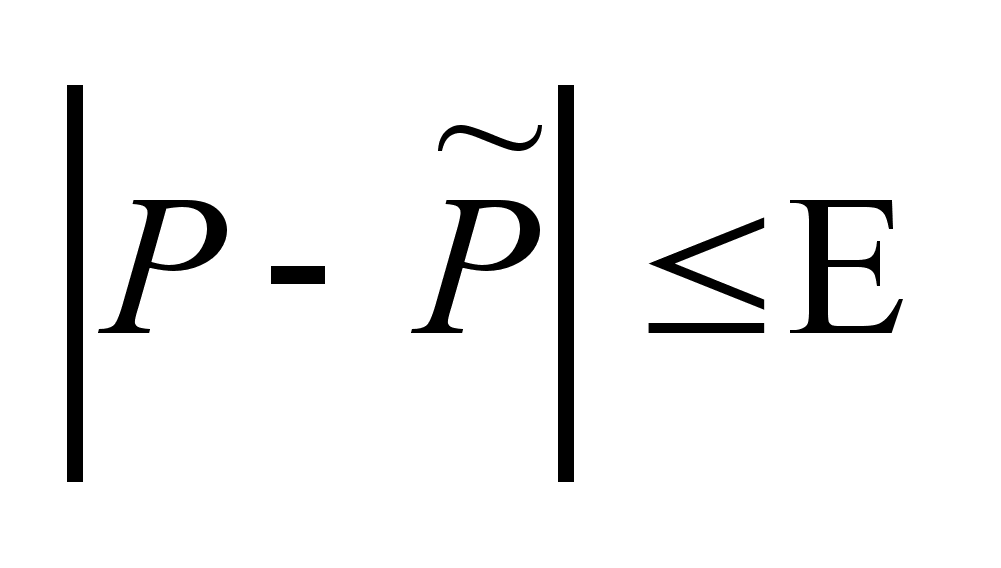 -
в этом случае
говорим, что
объект -
в этом случае
говорим, что
объект
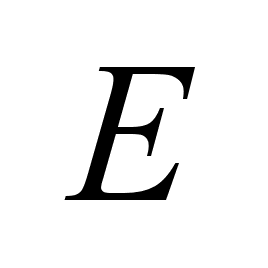 -управляем
и при этом -управляем
и при этом
 .
Отсюда имеем
следующее .
Отсюда имеем
следующее
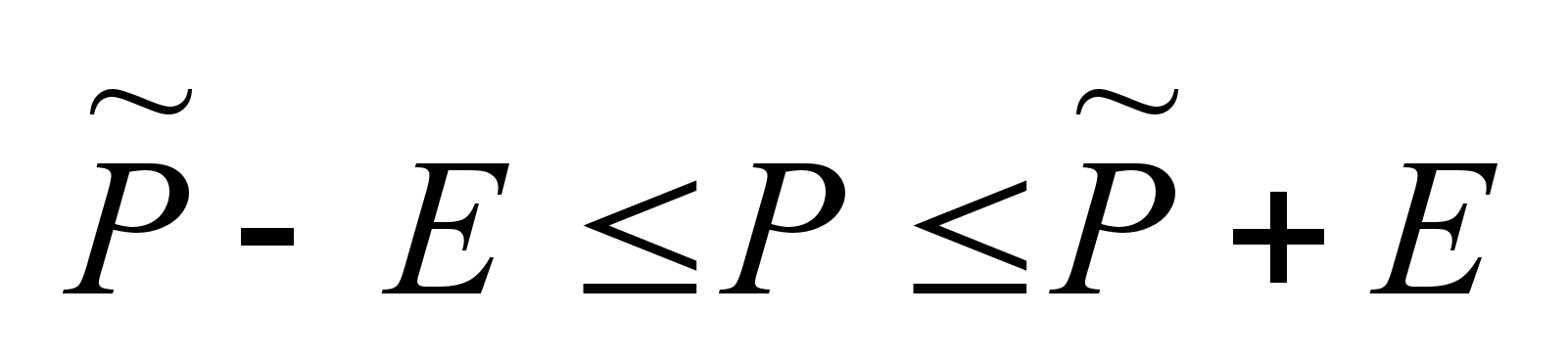 .
Если .
Если
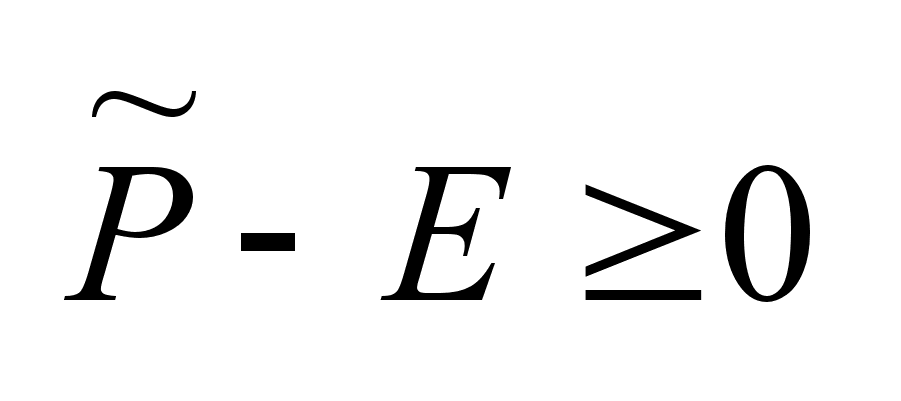 ,
то ,
то
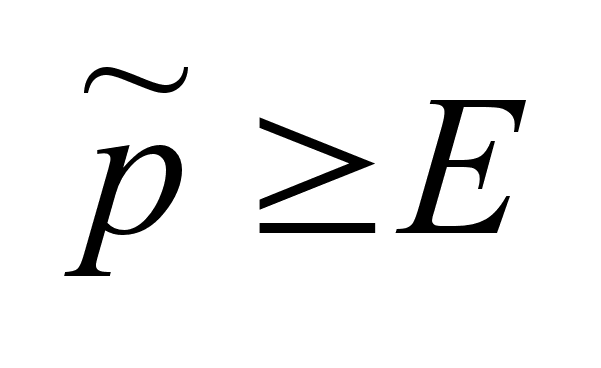 -объект
E-управляем.
Если -объект
E-управляем.
Если
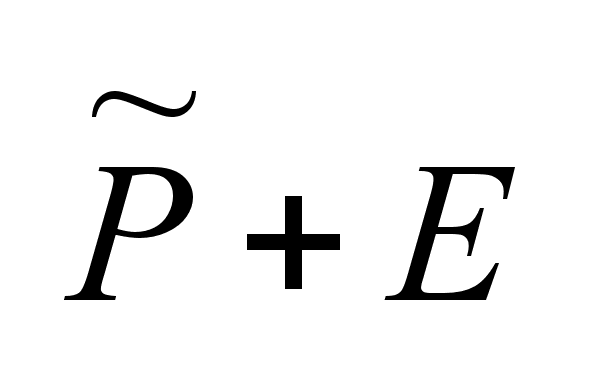  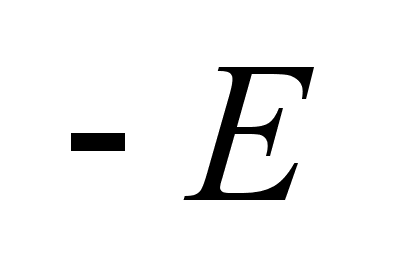 -объект
не управляем.
Если -объект
не управляем.
Если
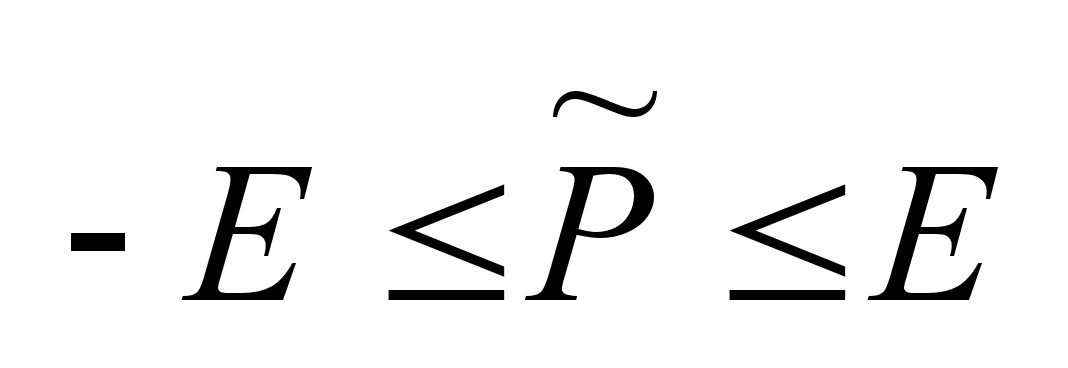 ,
то в этом случае
неопределенность.
Выясним вопрос
о погрешности. ,
то в этом случае
неопределенность.
Выясним вопрос
о погрешности.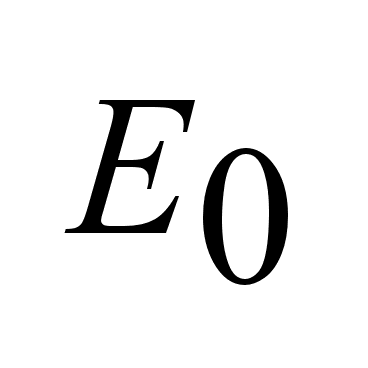 и и
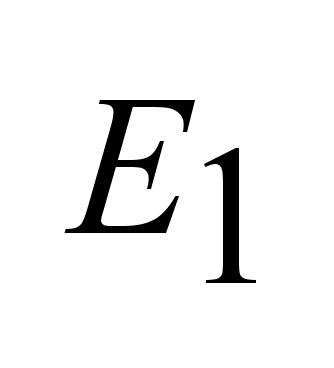 -погрешность
для вычисления
опорной функций -погрешность
для вычисления
опорной функций
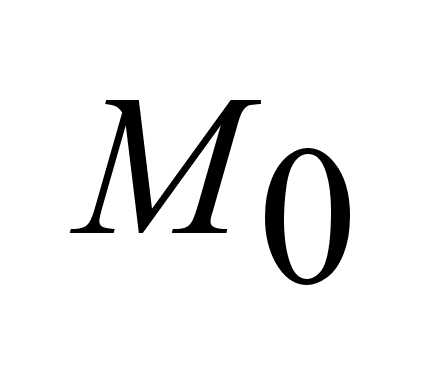 и и
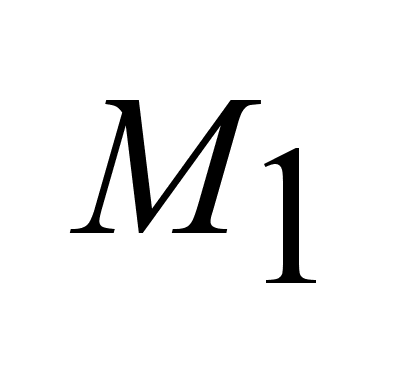 . .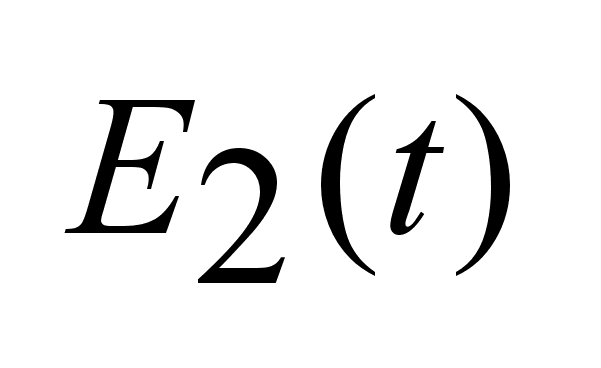 -
погрешность
для вычисления -
погрешность
для вычисления
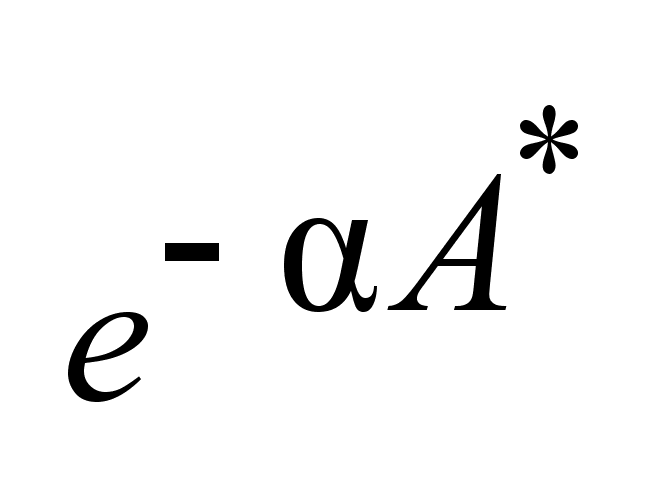 .
По условию
Липшица .
По условию
Липшица
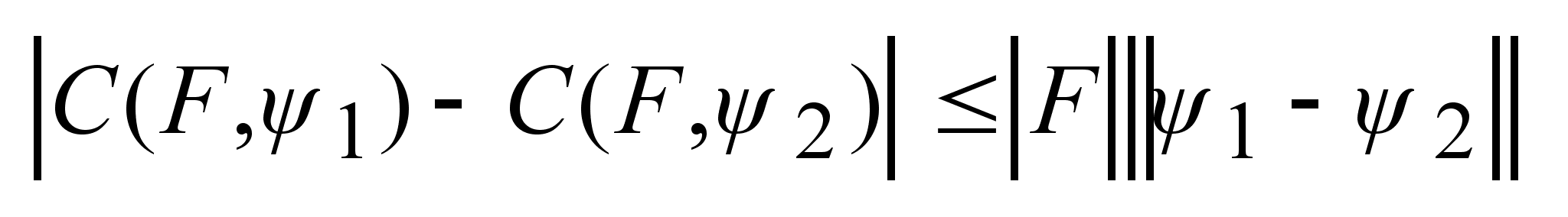 , ,
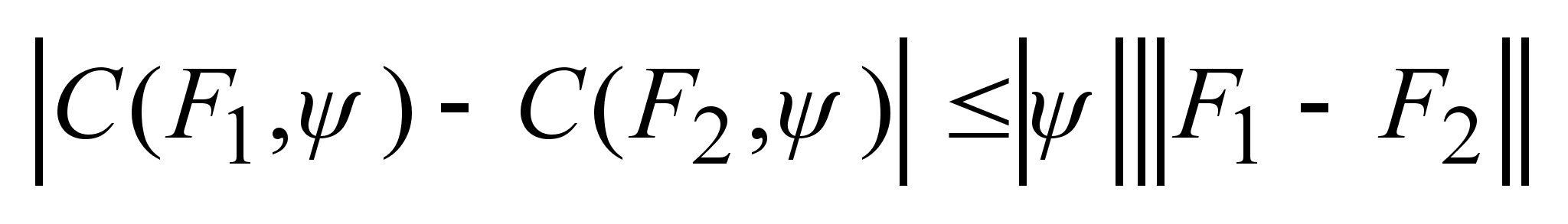 .
Используем
эти формулы
, получим следующие
погрешности: .
Используем
эти формулы
, получим следующие
погрешности:
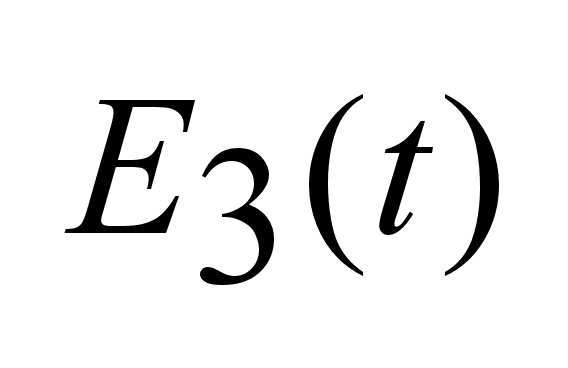 - погрешность
для вычисления
- погрешность
для вычисления
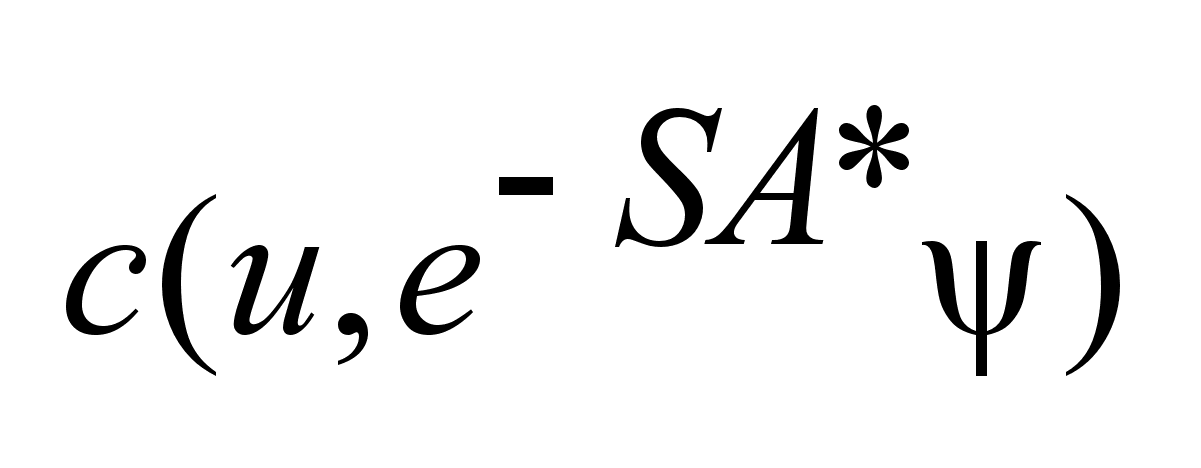 -предполагается,
что она интегрируема
по Лебегу. -предполагается,
что она интегрируема
по Лебегу.
 -это
вычисление
интеграла -это
вычисление
интеграла
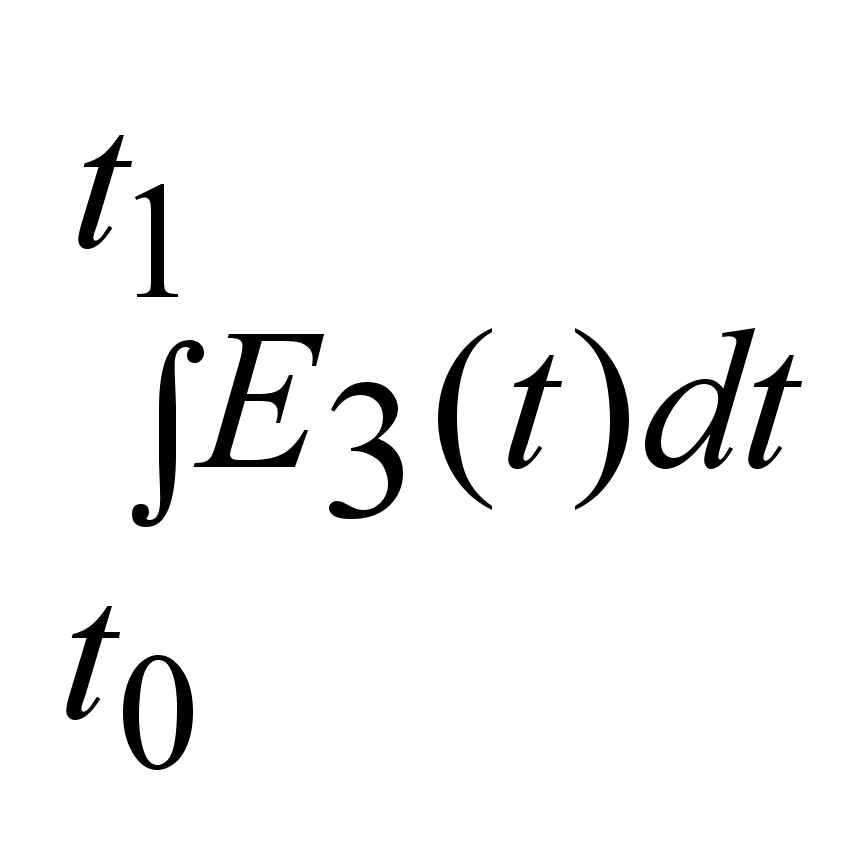 . .
 -
погрешность
для вычисления -
погрешность
для вычисления
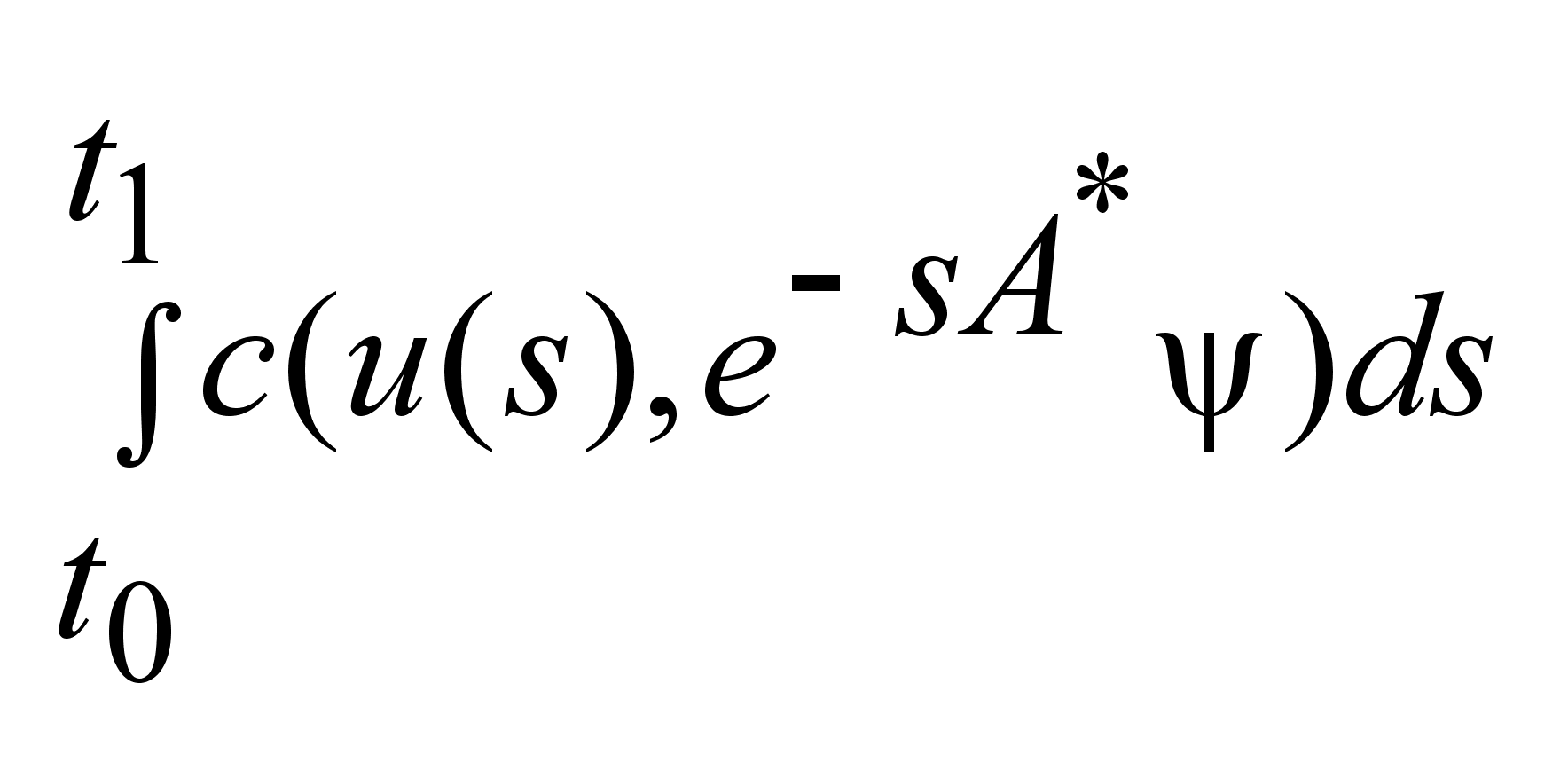 . .
 -погрешность
вычисления
минимума функций. -погрешность
вычисления
минимума функций.
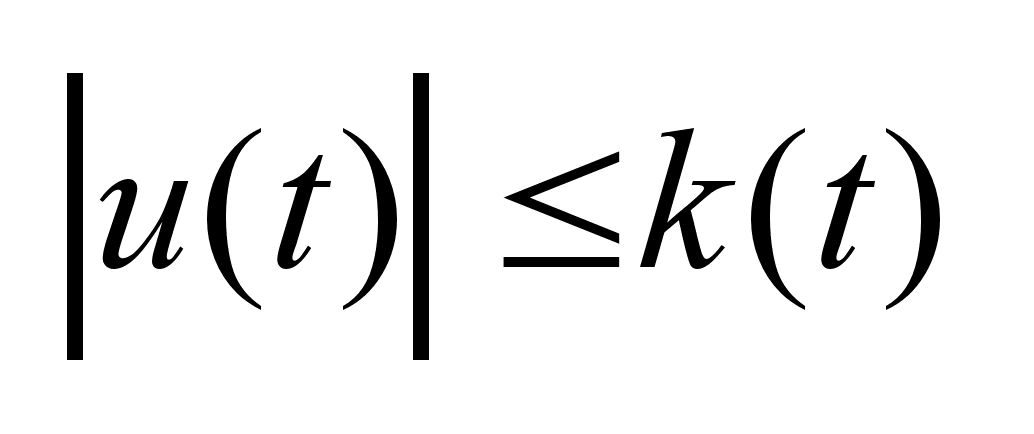 , ,
 . .
 + +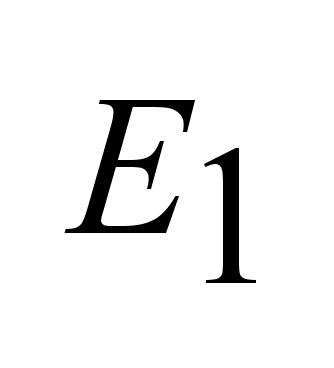 + + + + + +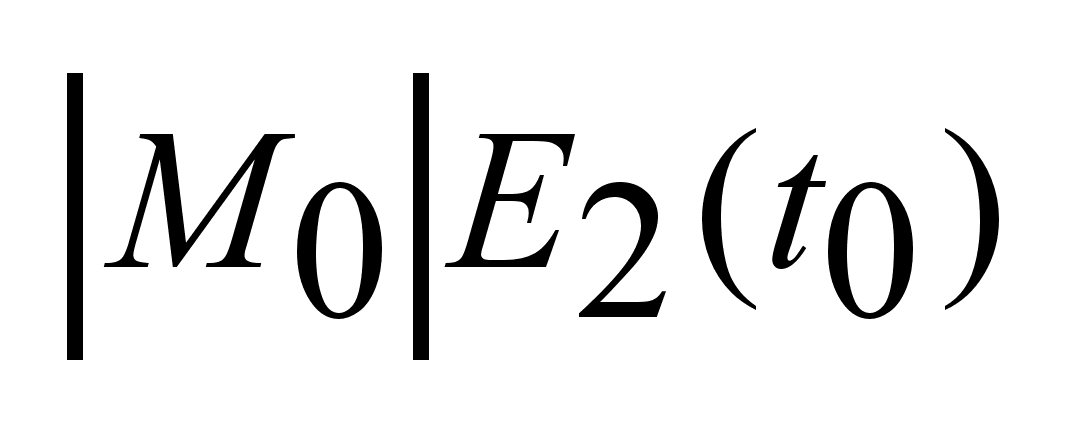 + +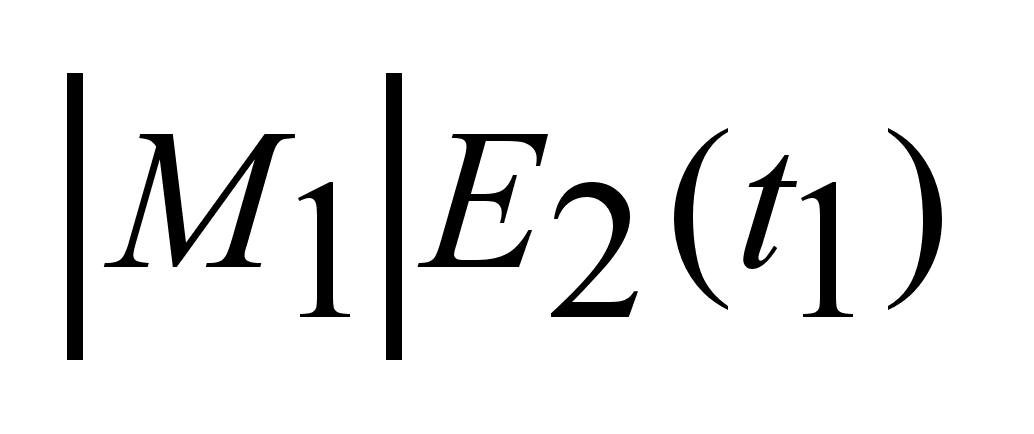 + +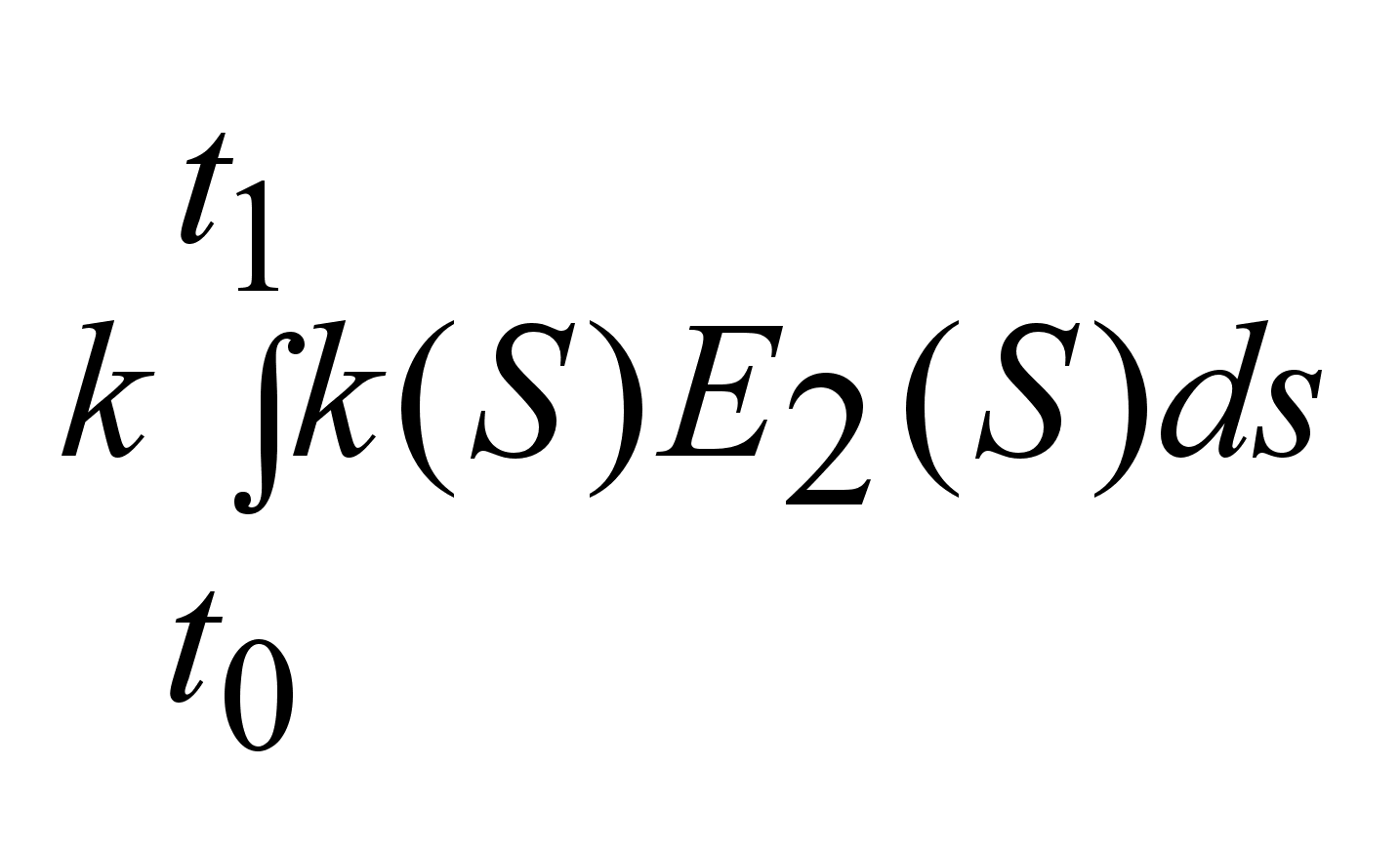 + +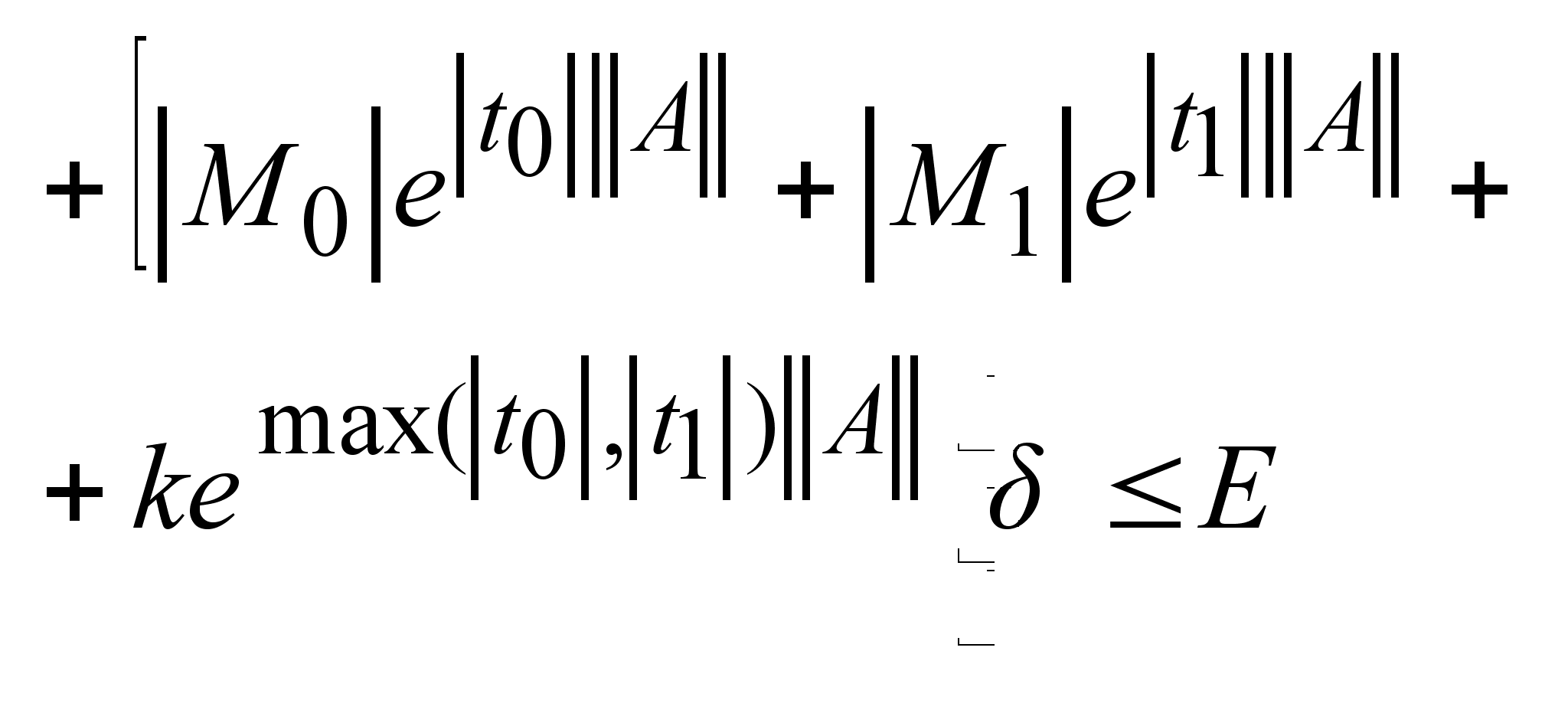
18.
Лемма
о внутренней
точке.
Пусть
А- квадратичная
матрица размера
nxn
, V-произвольный
вектор пр-ва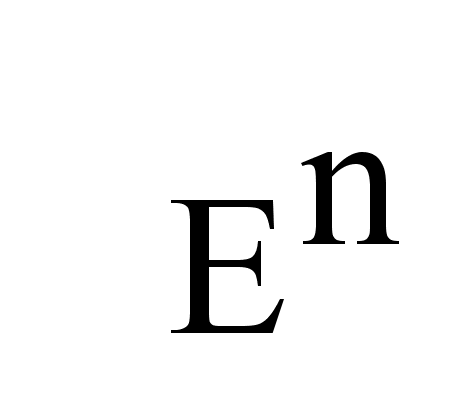 ,
отрезок I= ,
отрезок I=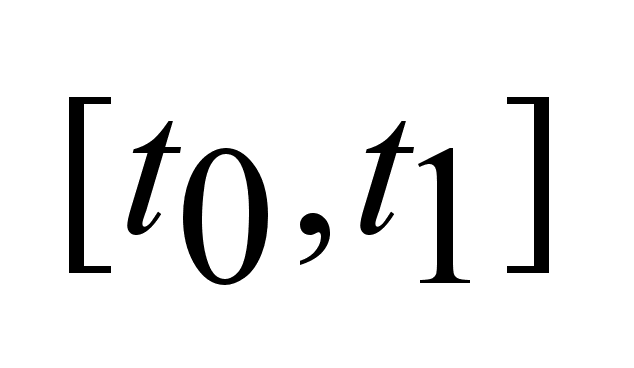 .
Тогда .
Тогда
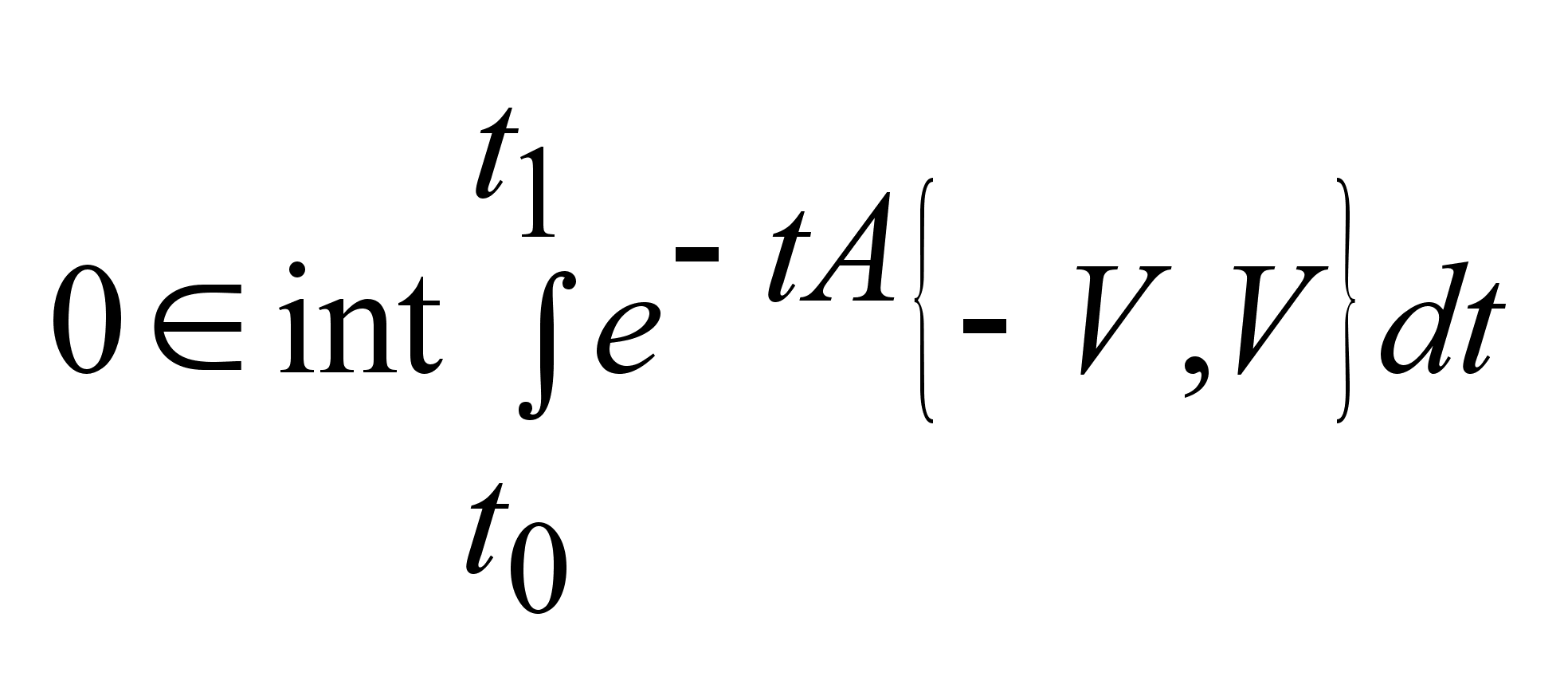 ,
тогда
и только тогда
, когда векторы ,
тогда
и только тогда
, когда векторы
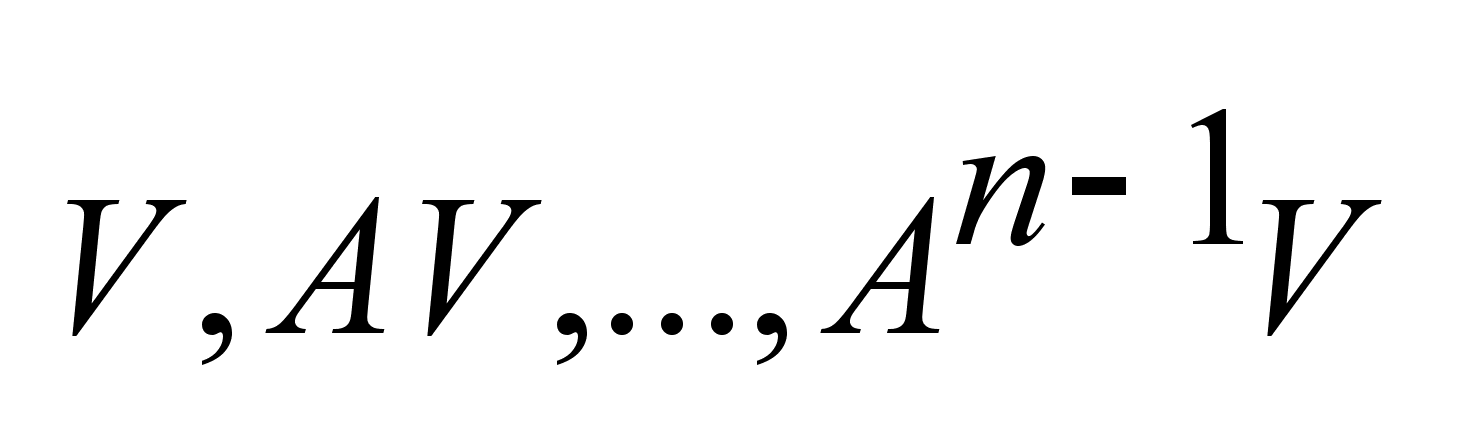 линейно
независимы. линейно
независимы.
Под
интегралом-
многозначное
отображения,
интеграл от
многозначного
отображения
– тоже многозначное
отображения.
Доказательство
:
Обозначим F=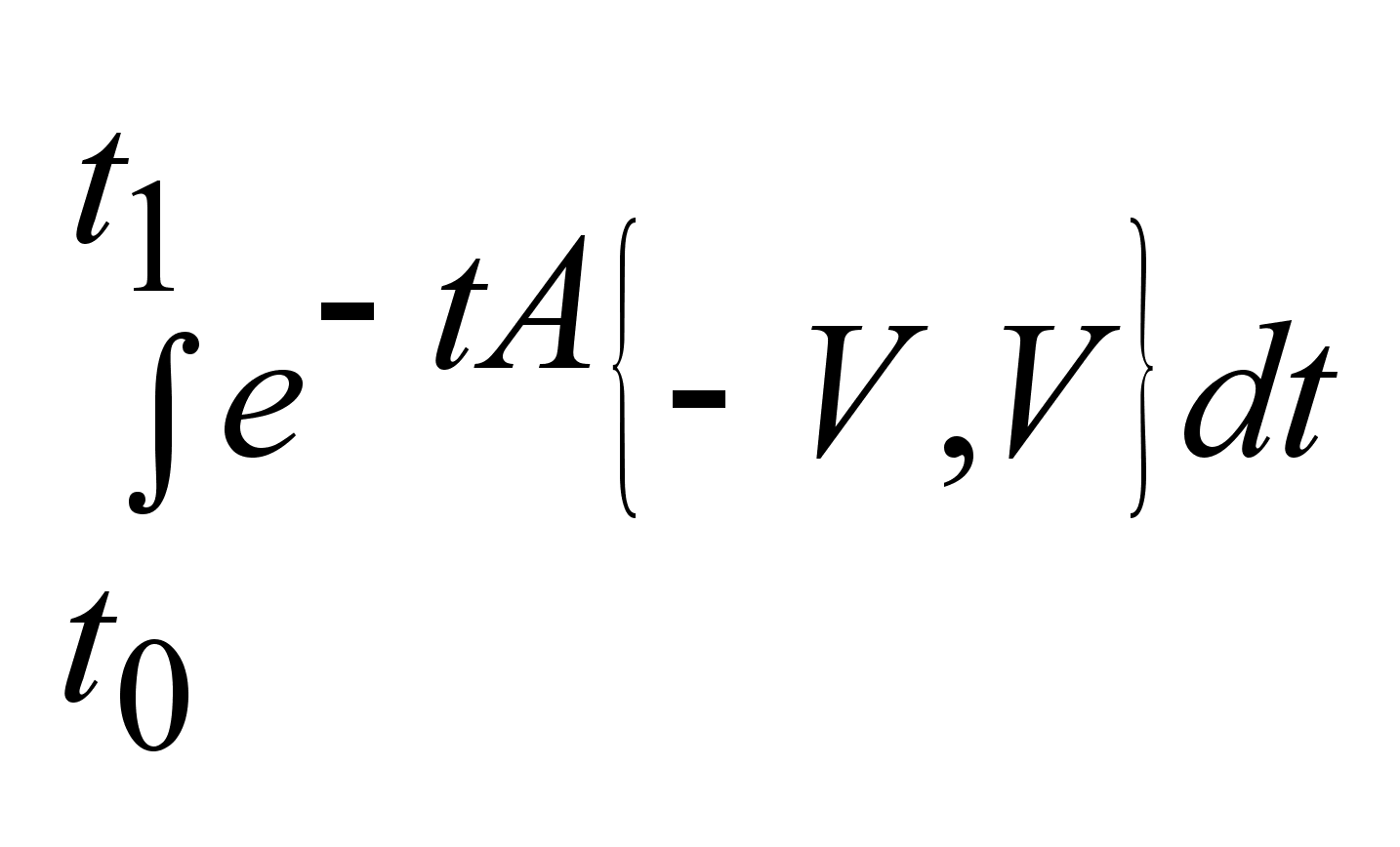 .
По свойствам
опорной функции
для того чтобы .
По свойствам
опорной функции
для того чтобы
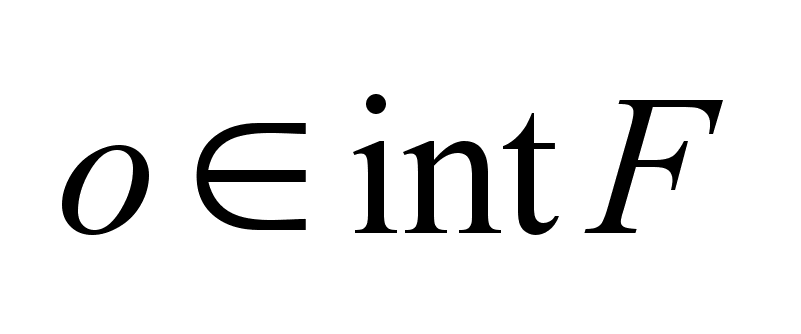 нужно,
чтобы выполнялось
условие нужно,
чтобы выполнялось
условие
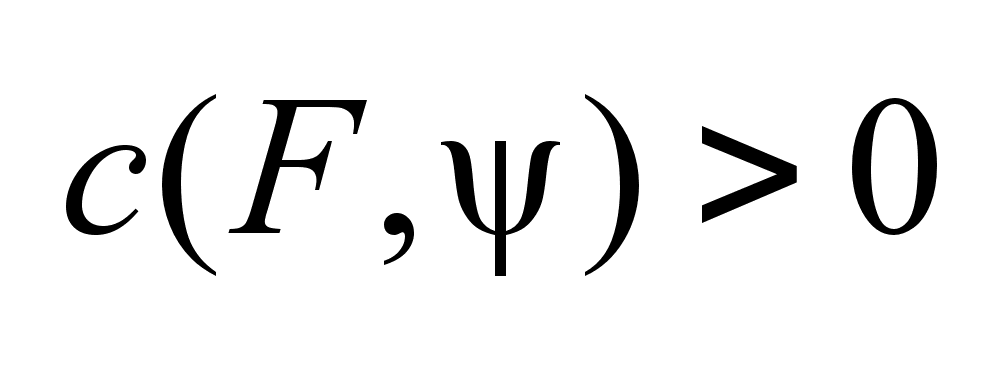 , ,
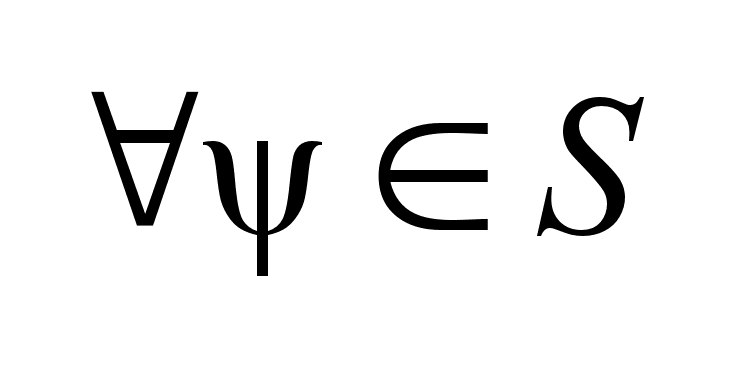 . .
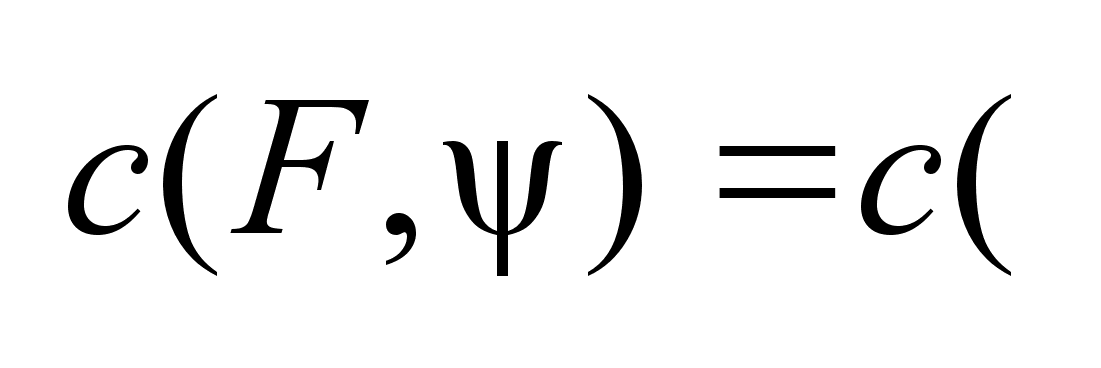 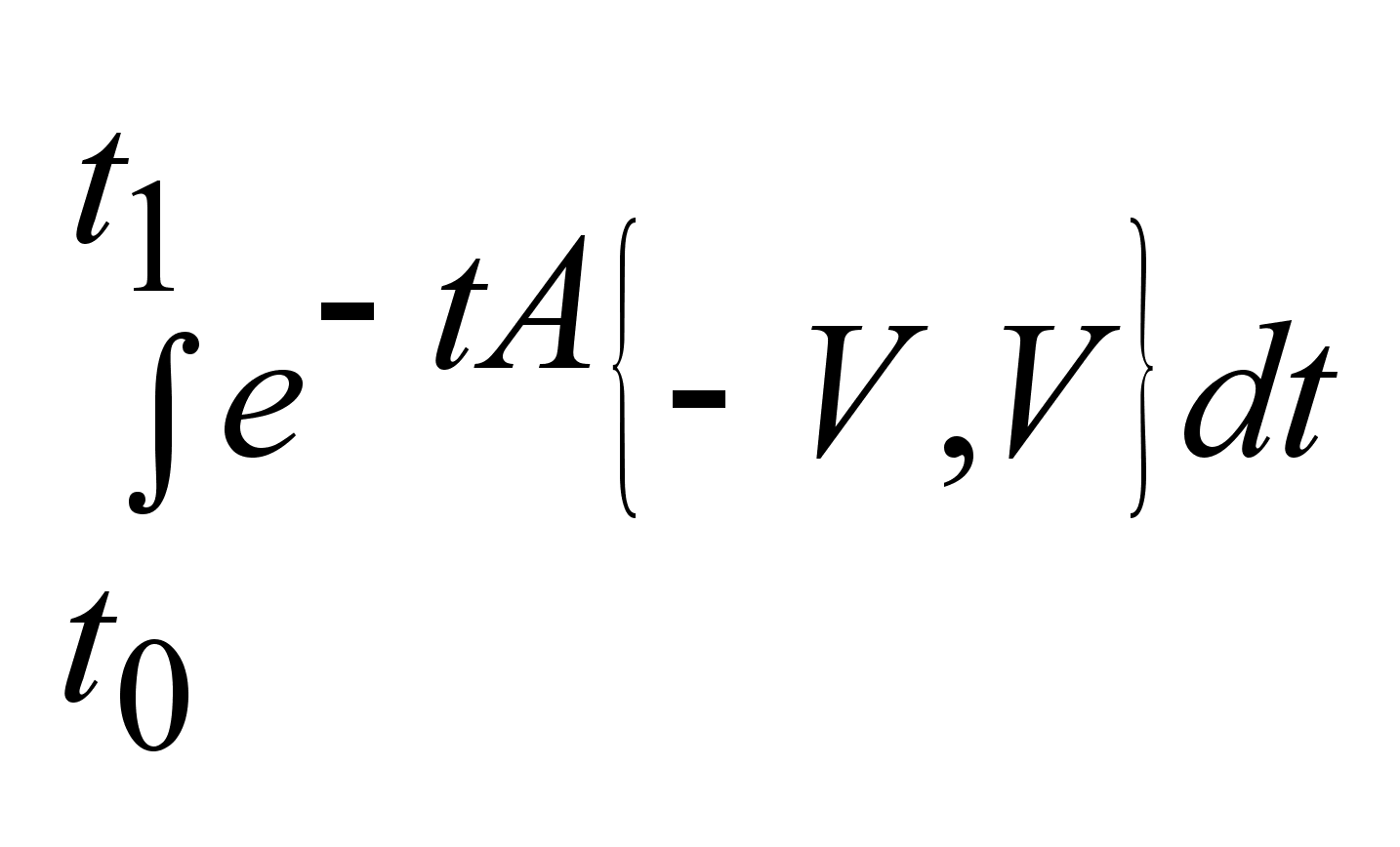 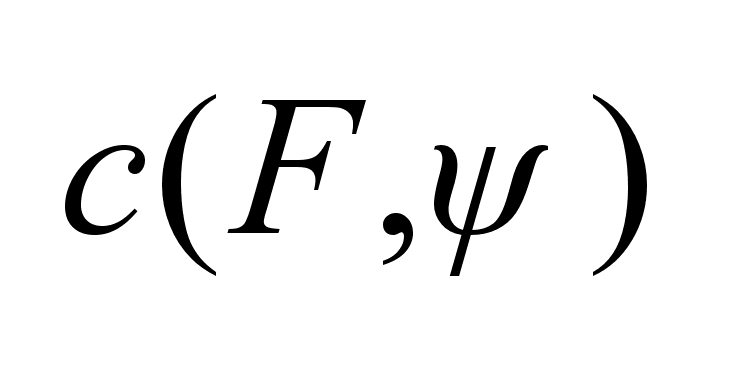 = =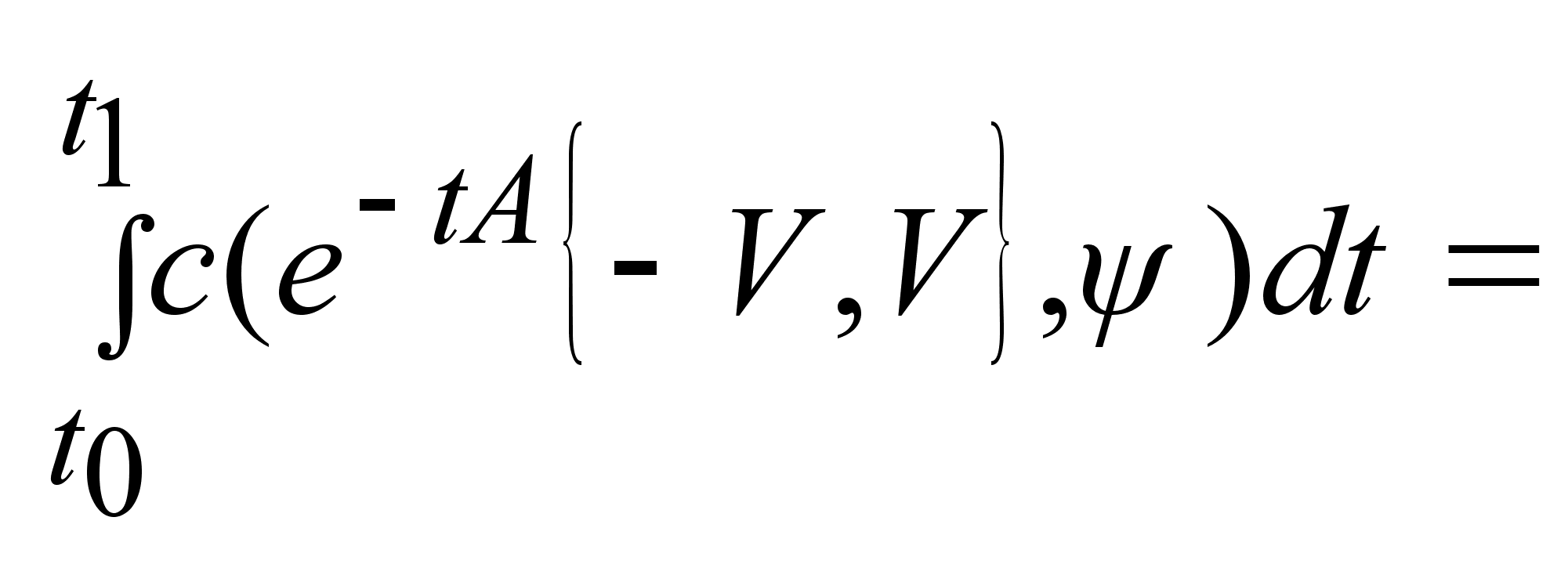
=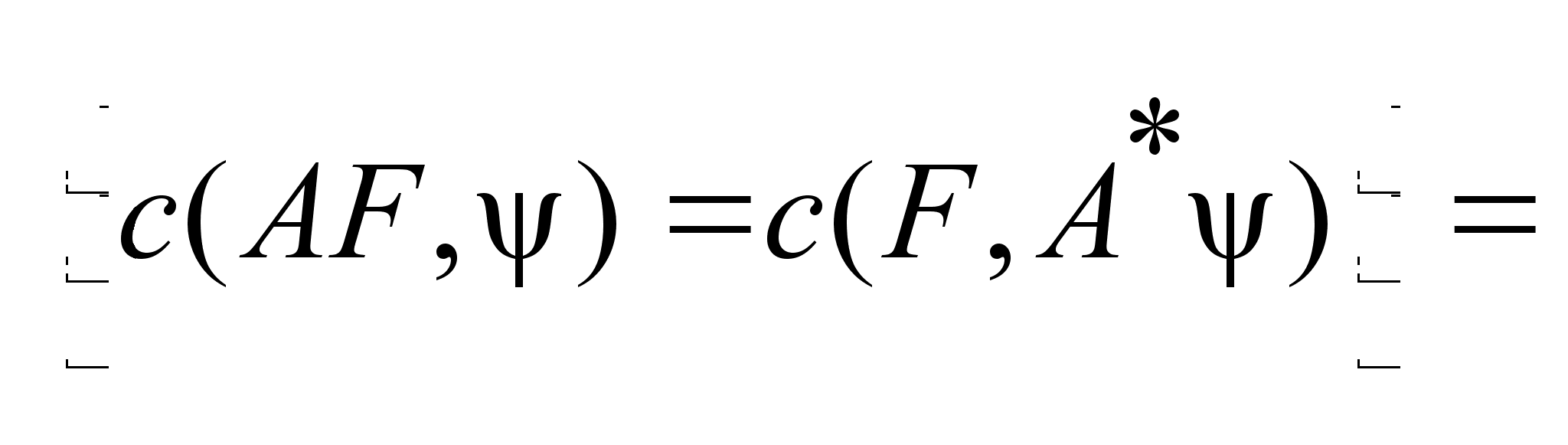 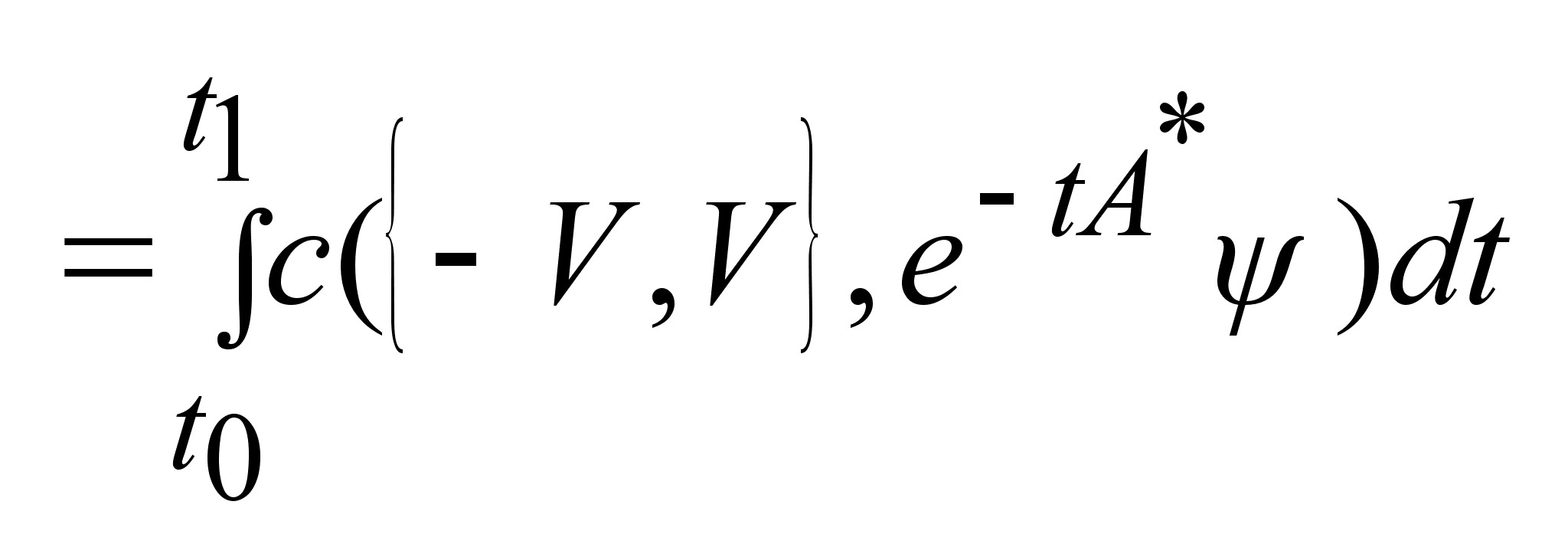 = =
=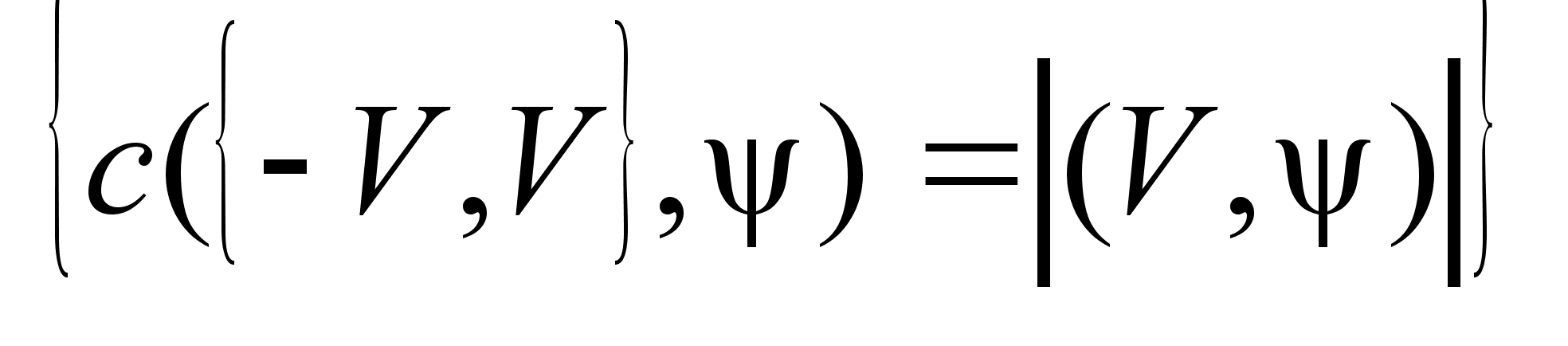 = =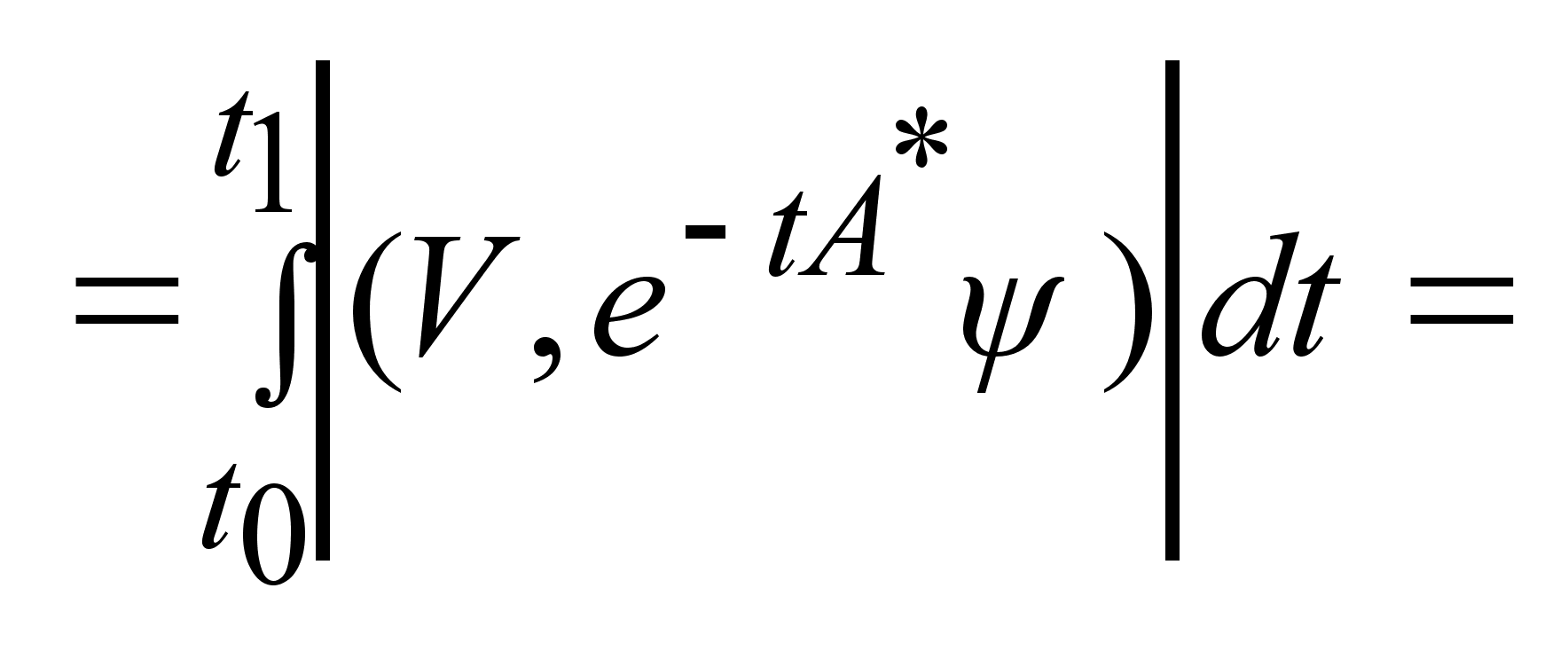 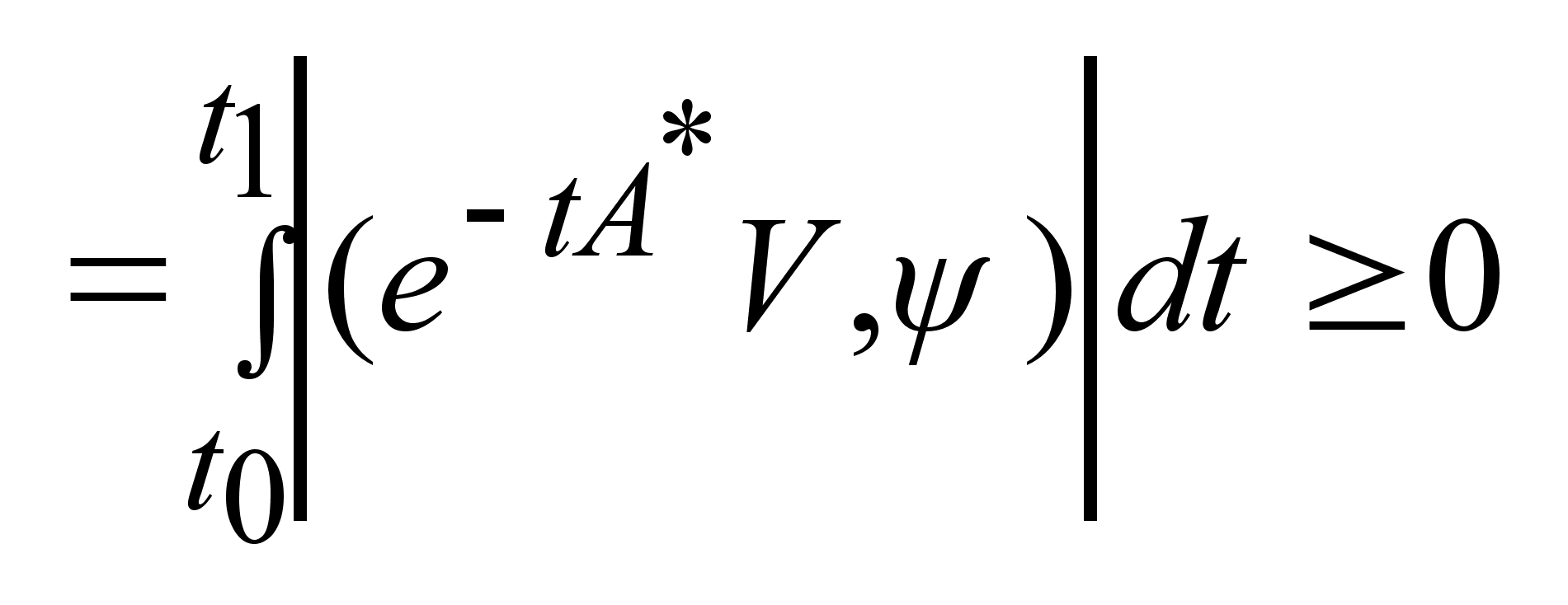 .Т.к.
подынтегральная
функция непрерывна
и неотрицательна,
то условие .Т.к.
подынтегральная
функция непрерывна
и неотрицательна,
то условие
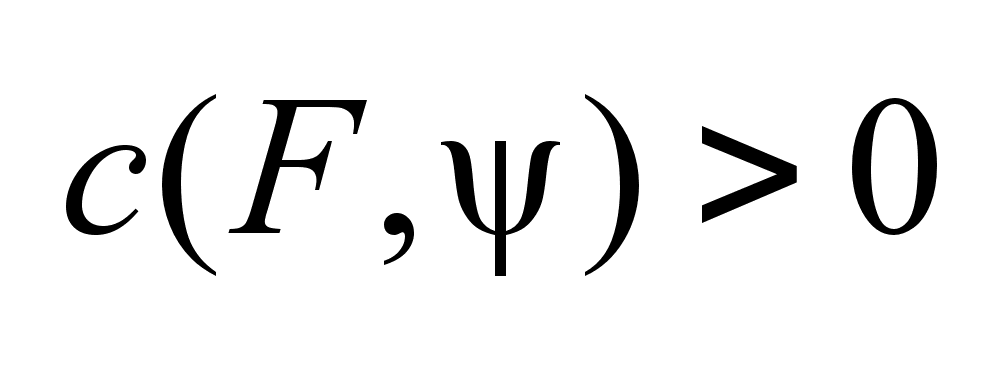 , ,
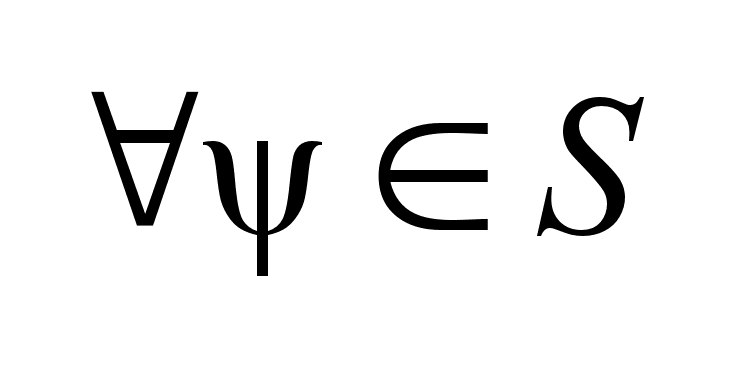 выполняется
тогда и только
тогда, когда
выполняется
тогда и только
тогда, когда
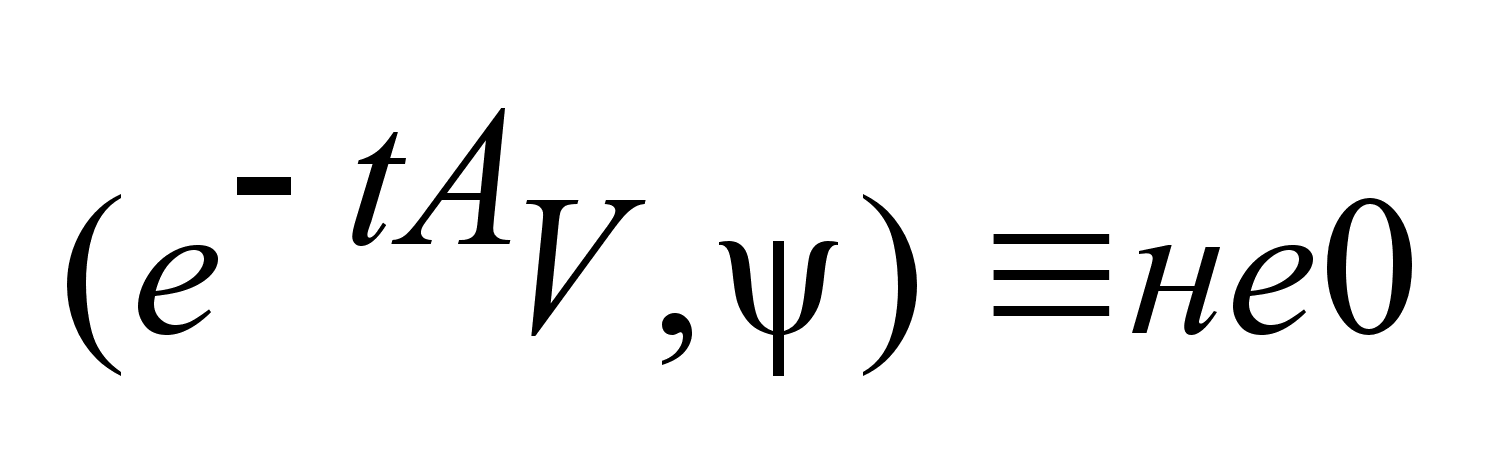 на
интервале I
. Покажем, что
для этого необходимо
и достаточно,
чтобы векторы
на
интервале I
. Покажем, что
для этого необходимо
и достаточно,
чтобы векторы
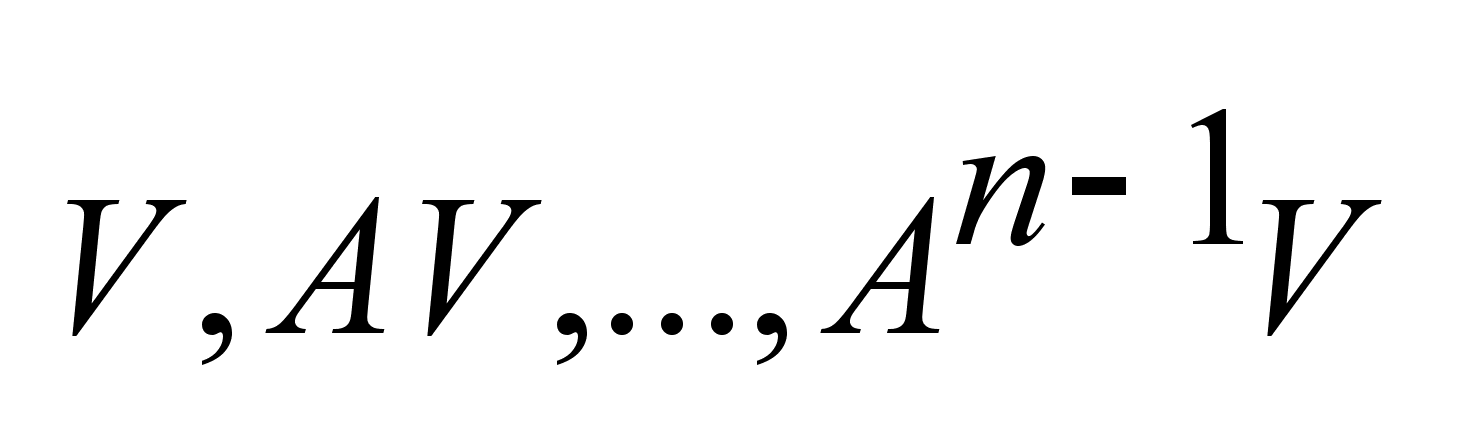 были
лин. независимы. были
лин. независимы.
Необходимость:
(доказательство
от противного)
 эквивалентно
эквивалентно
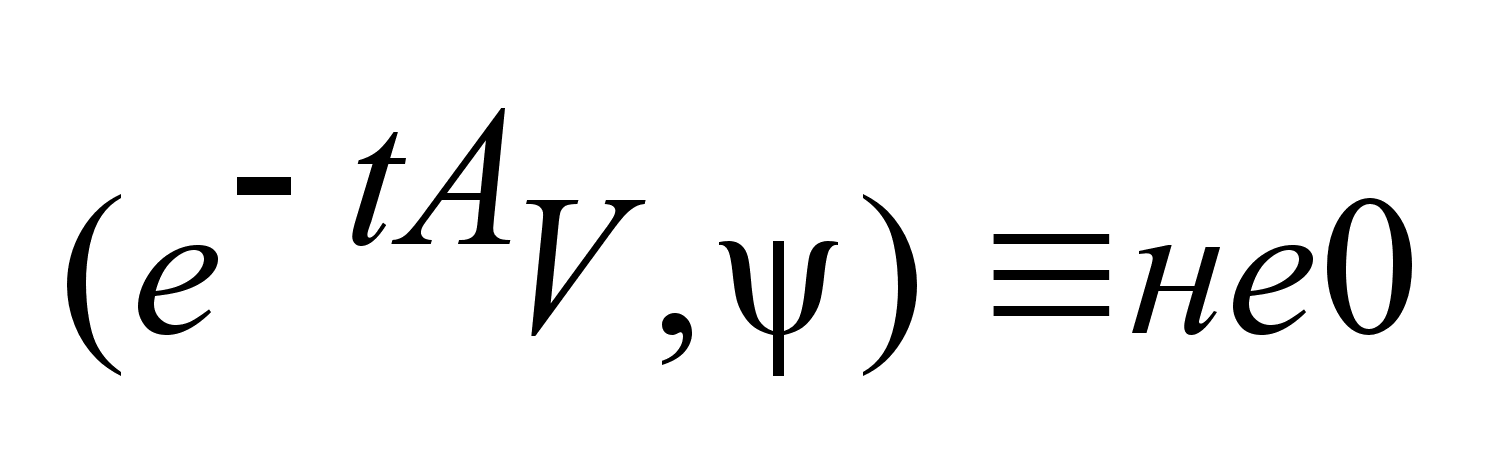 , ,
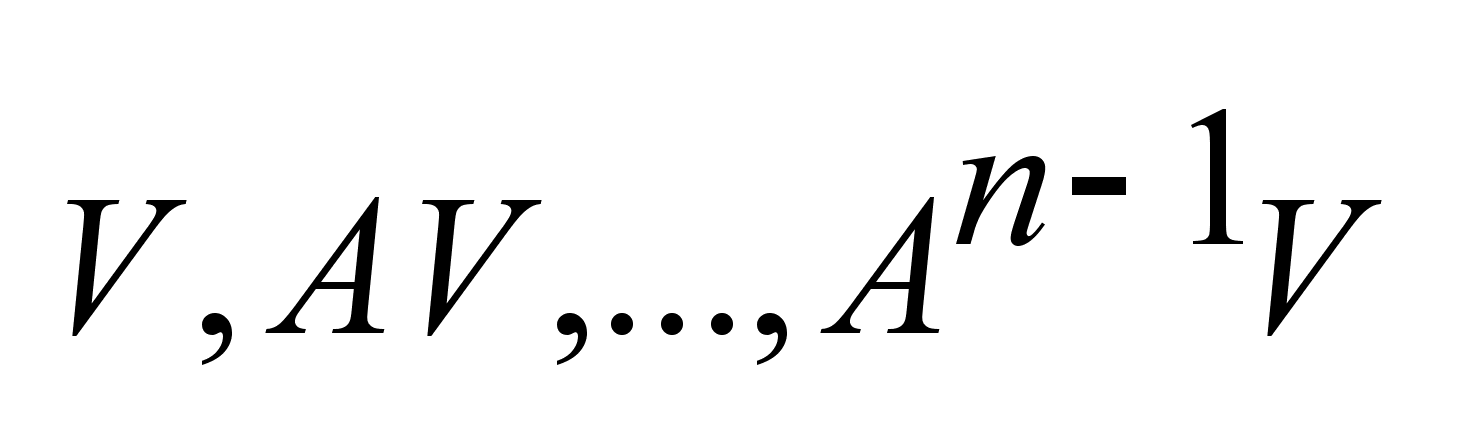 -лин.независимы
.Предположим,
что векторы -лин.независимы
.Предположим,
что векторы
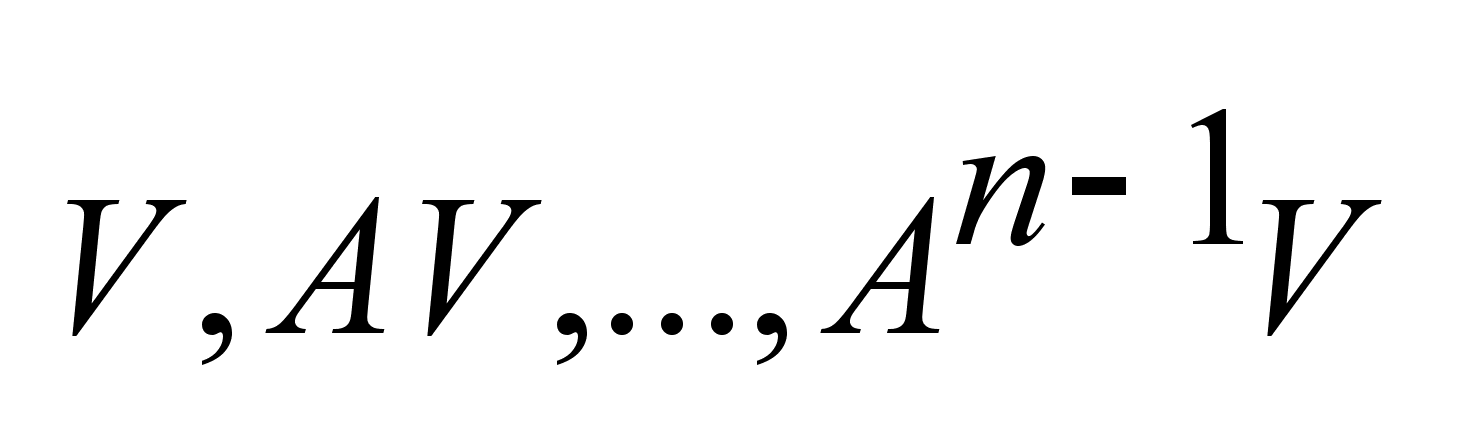 лин. зависимы.
Для 3-х векторов
:
лин. зависимы.
Для 3-х векторов
:
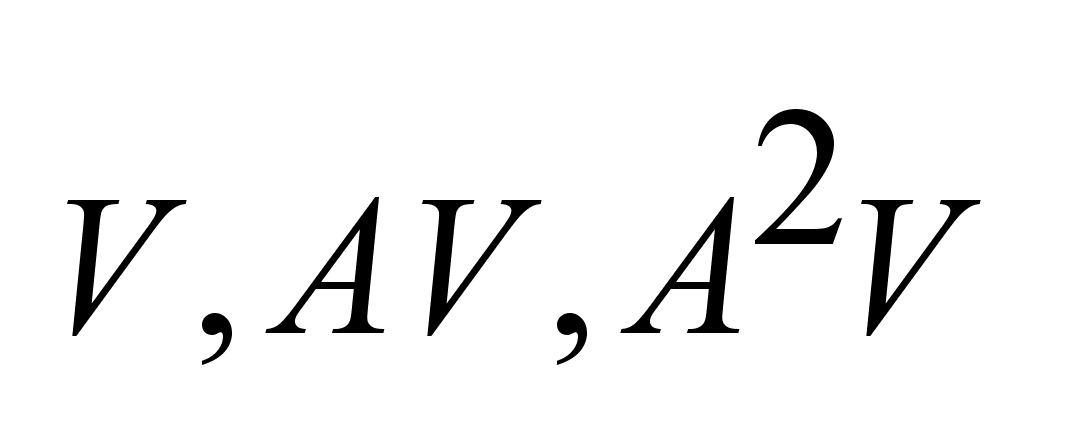 ; ;
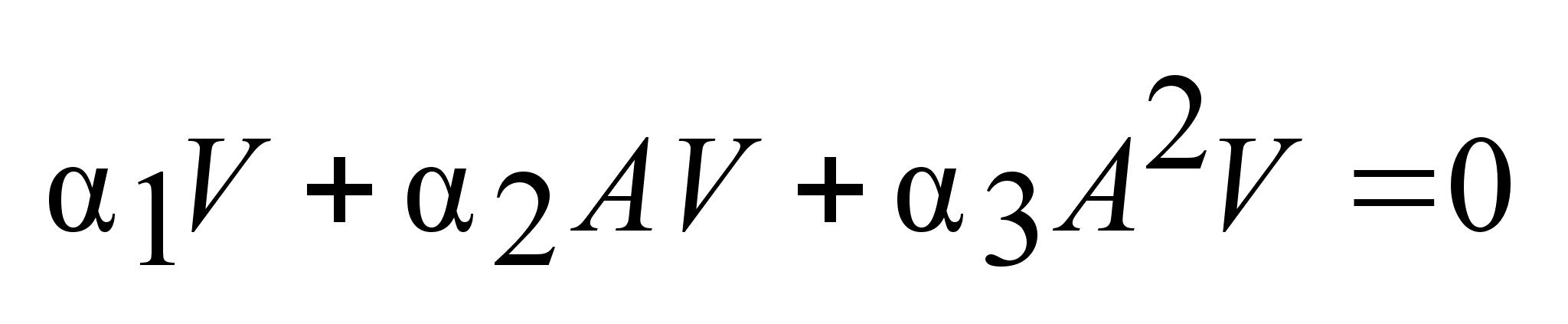 -
лежат в одной
плоскости, -
лежат в одной
плоскости,
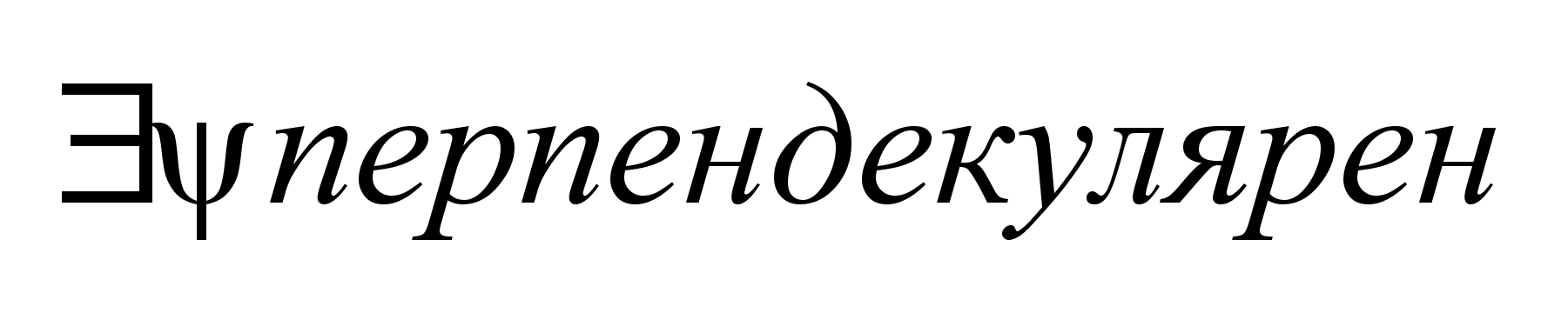 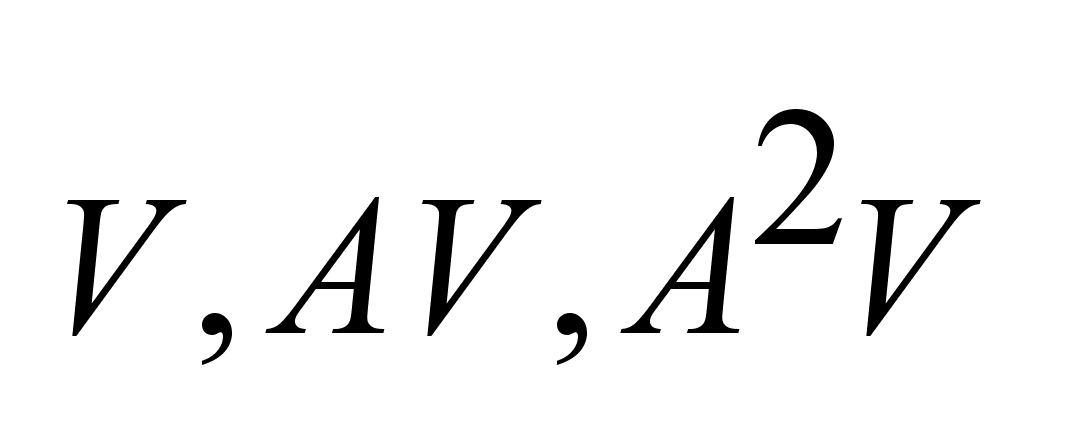 ; ;
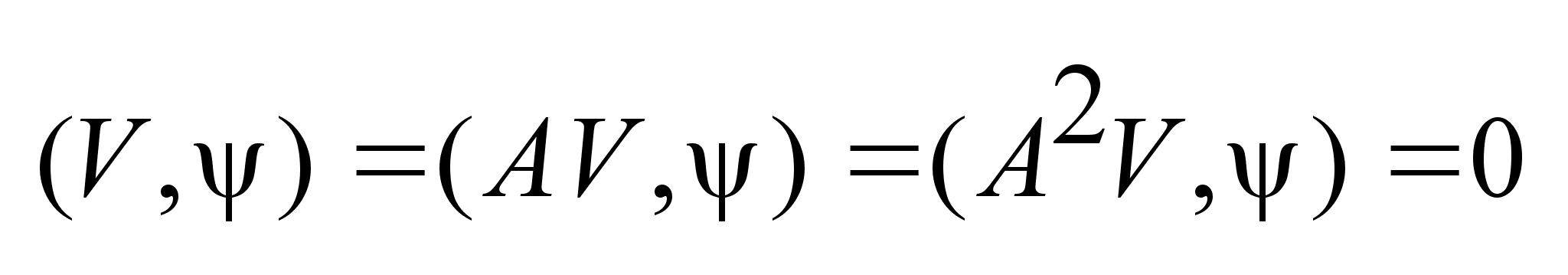 .
Тоже самое для
n-
векторов: .
Тоже самое для
n-
векторов:
 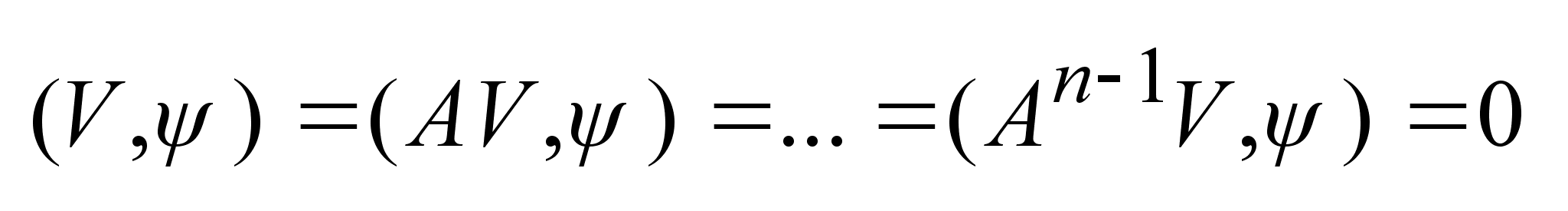 , ,
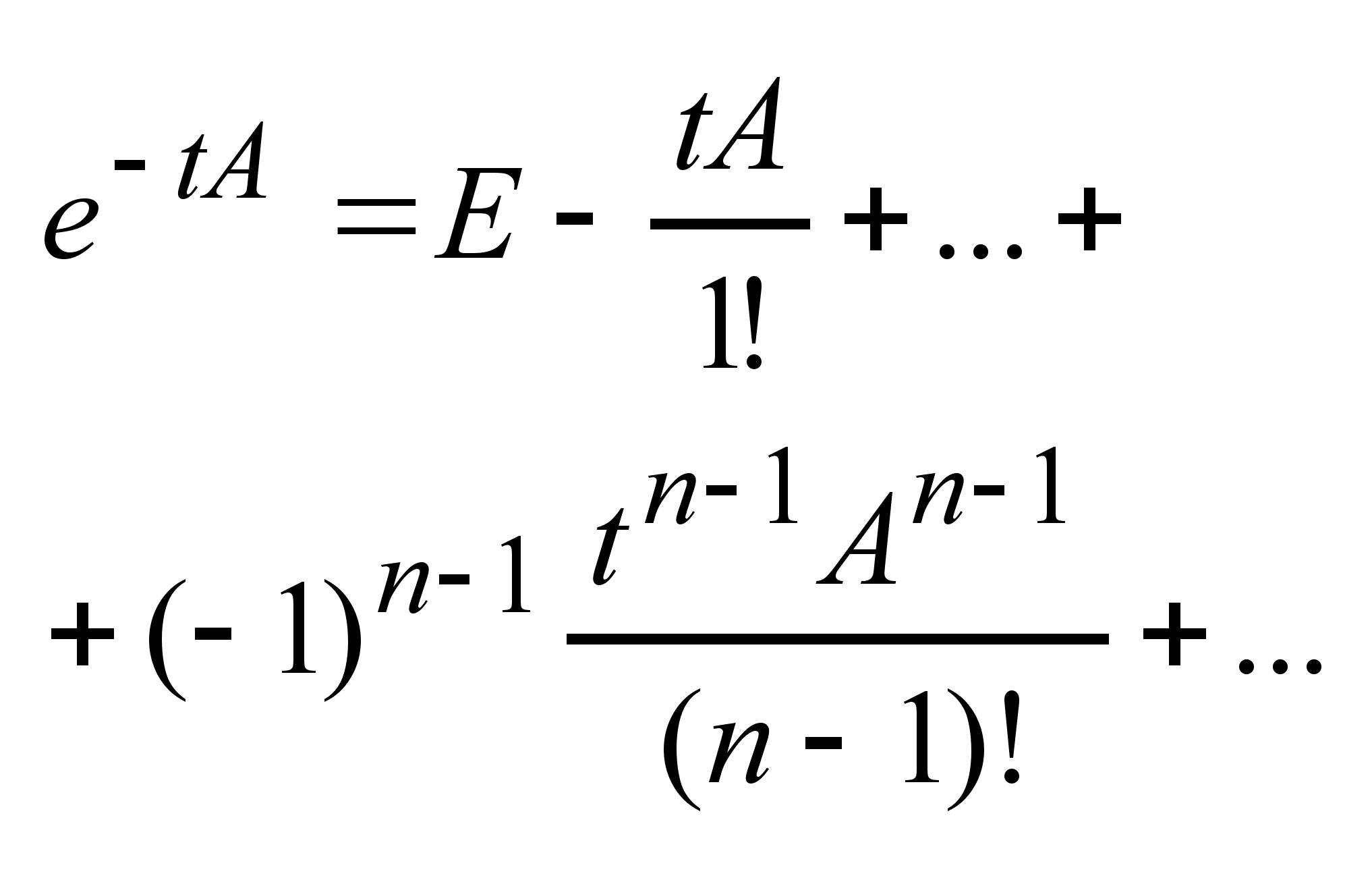 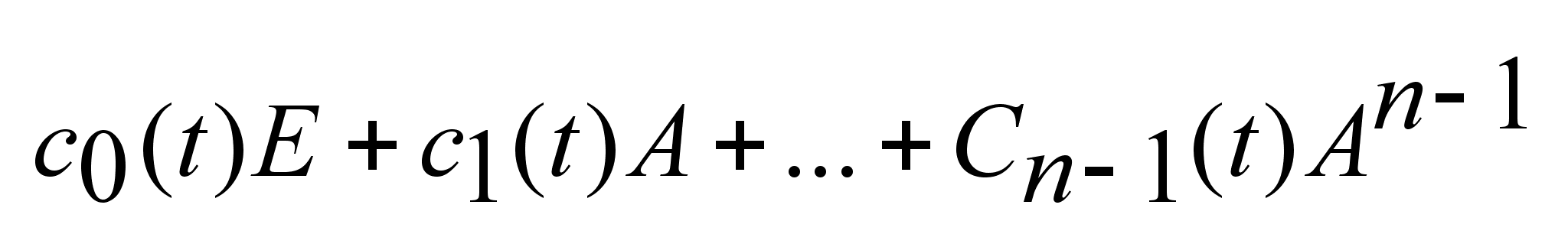 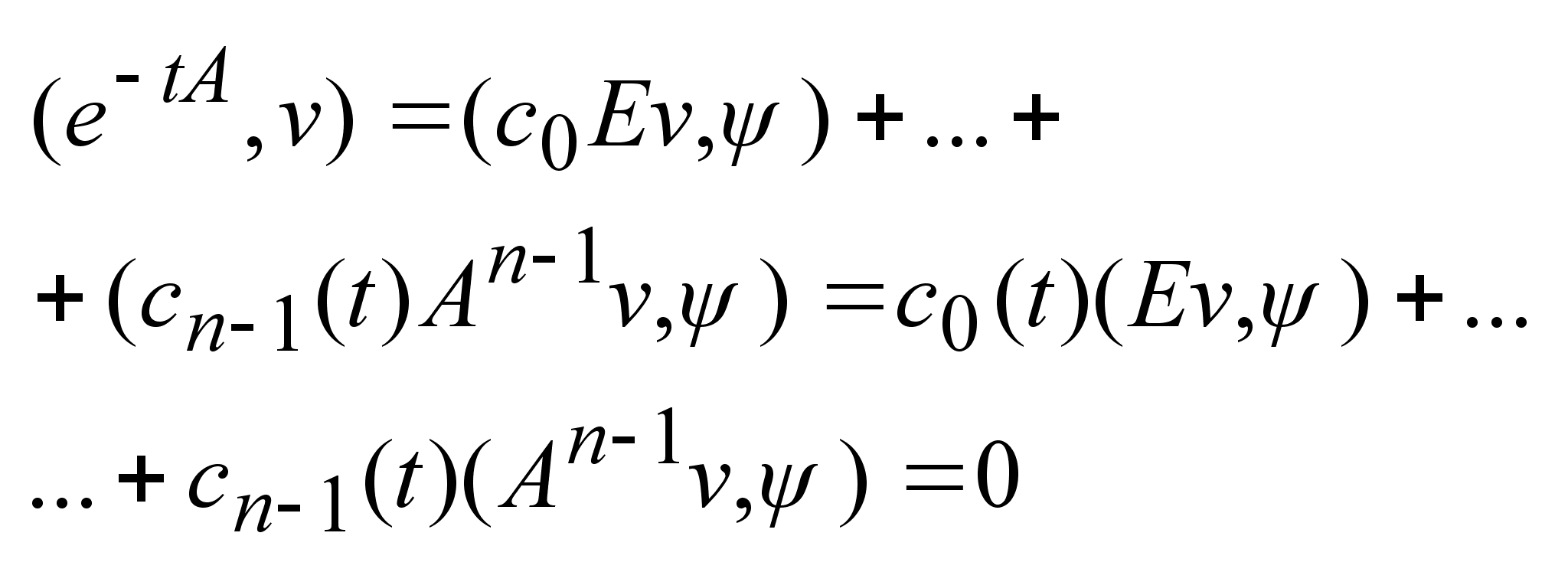 Пришли
к противоречию,
необходимость
доказана. Пришли
к противоречию,
необходимость
доказана.
Достаточность:
(от противного)
Если
векторы линейно
независимы,
то
 такой, что
такой, что
 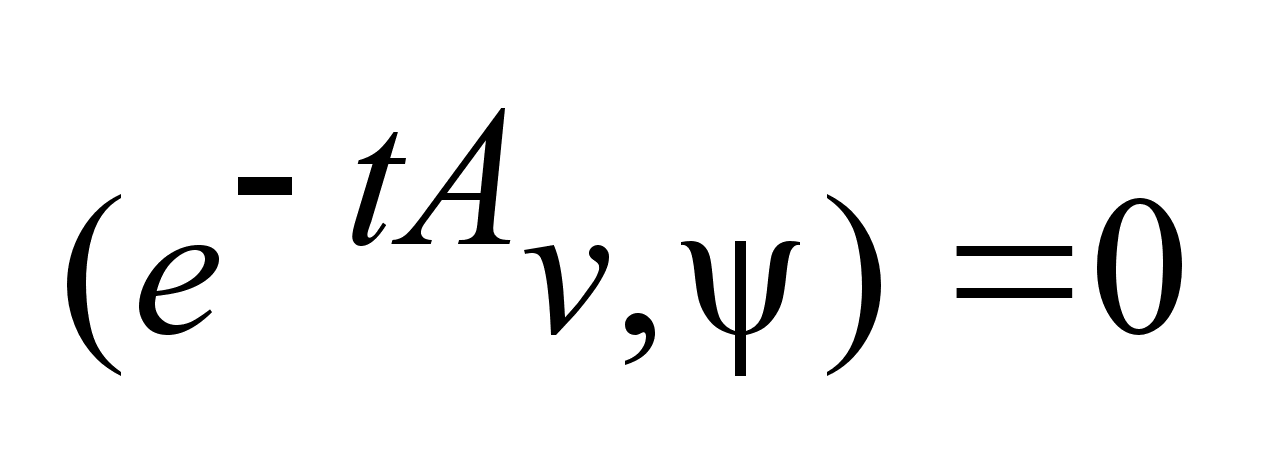 , ,
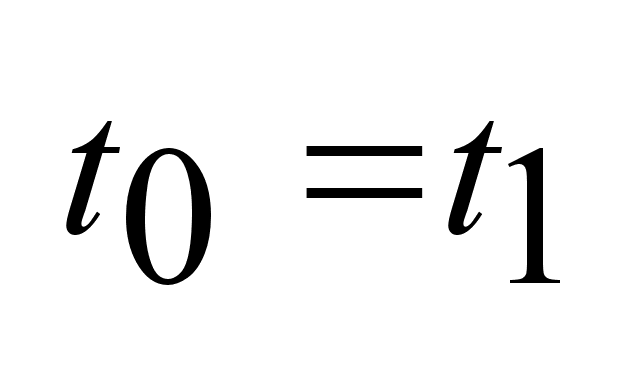 .
Продифференцируем .
Продифференцируем
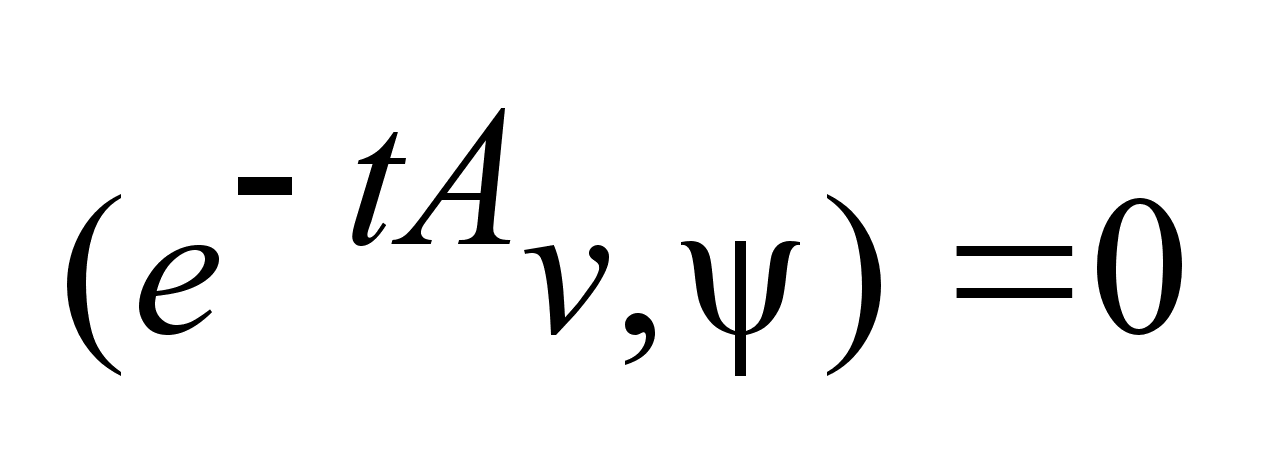 n-1
раз:0= n-1
раз:0=
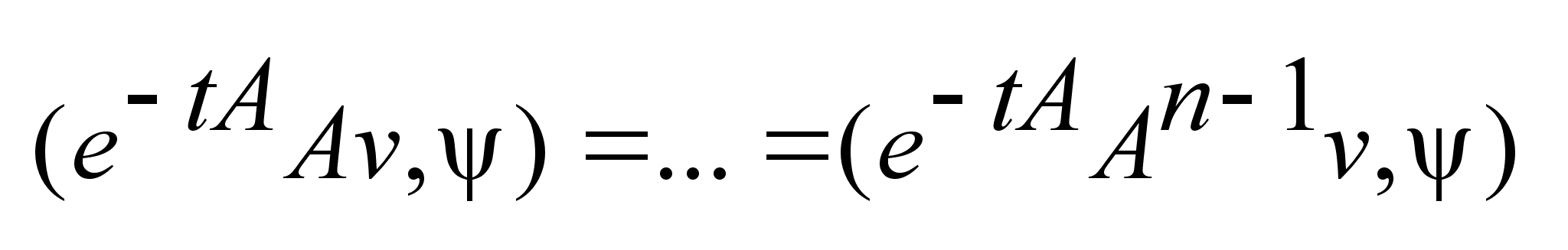 .Отсюда
следует: .Отсюда
следует:
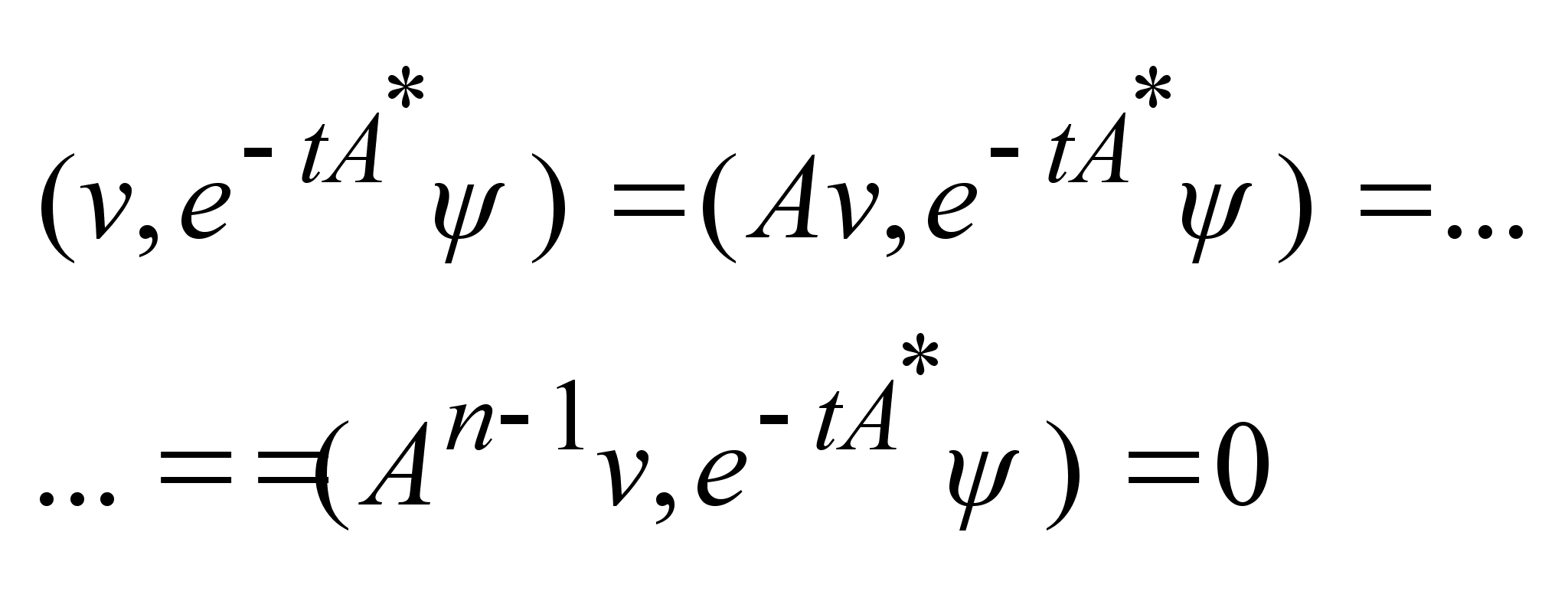 ,
где ,
где
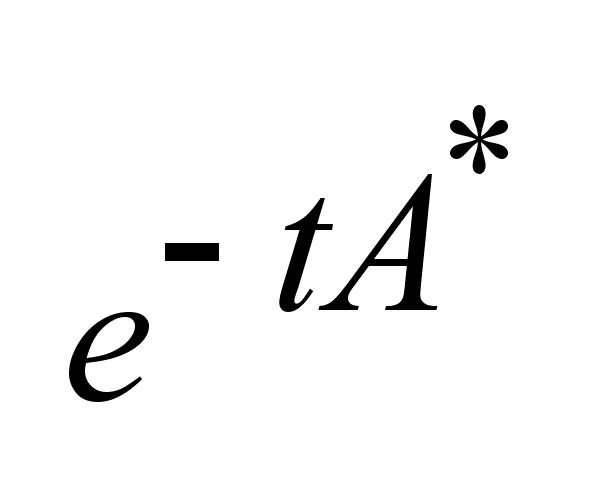 -
невырожденная
матрица, -
невырожденная
матрица,
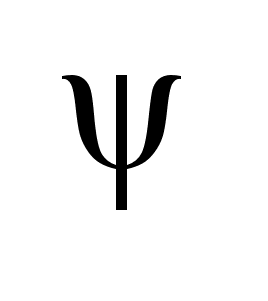 -не нулевой
вектор и
-не нулевой
вектор и
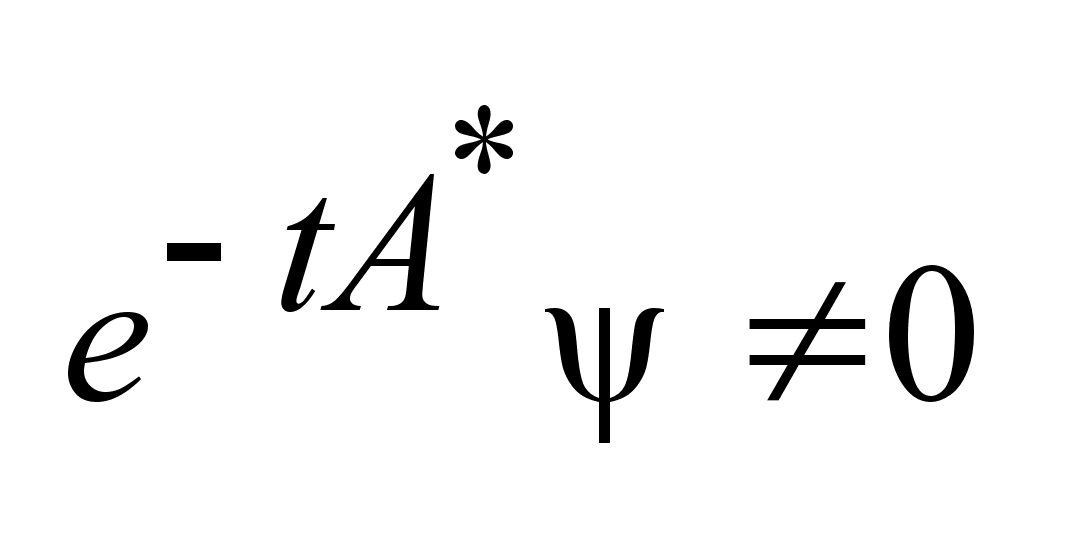 ,
а это означает,
что векторы ,
а это означает,
что векторы
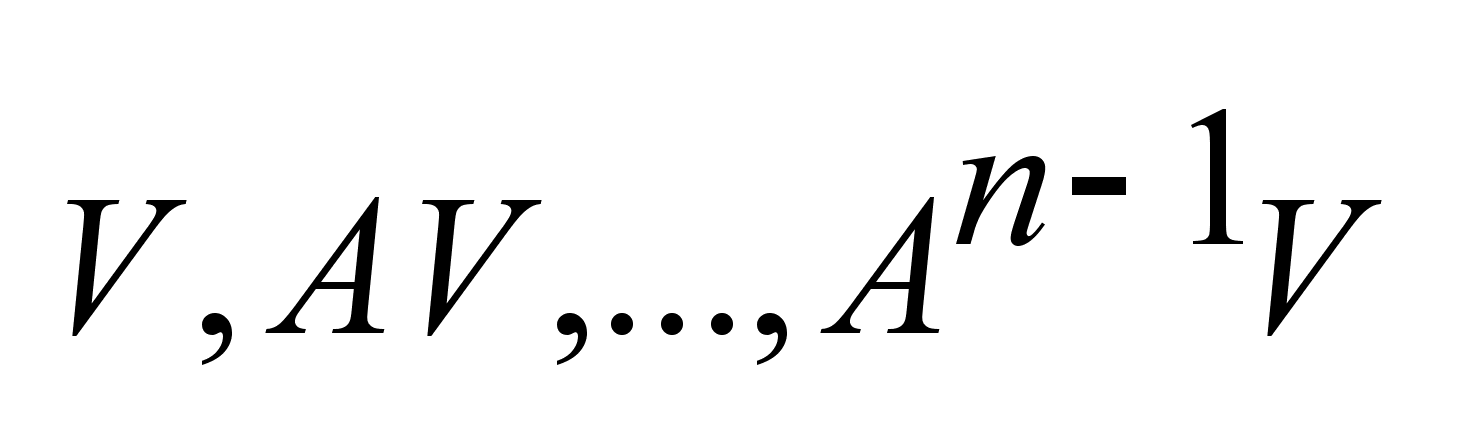 лин.зависимы
.Получили
противоречие.
лин.зависимы
.Получили
противоречие.
 перпендикуярен перпендикуярен
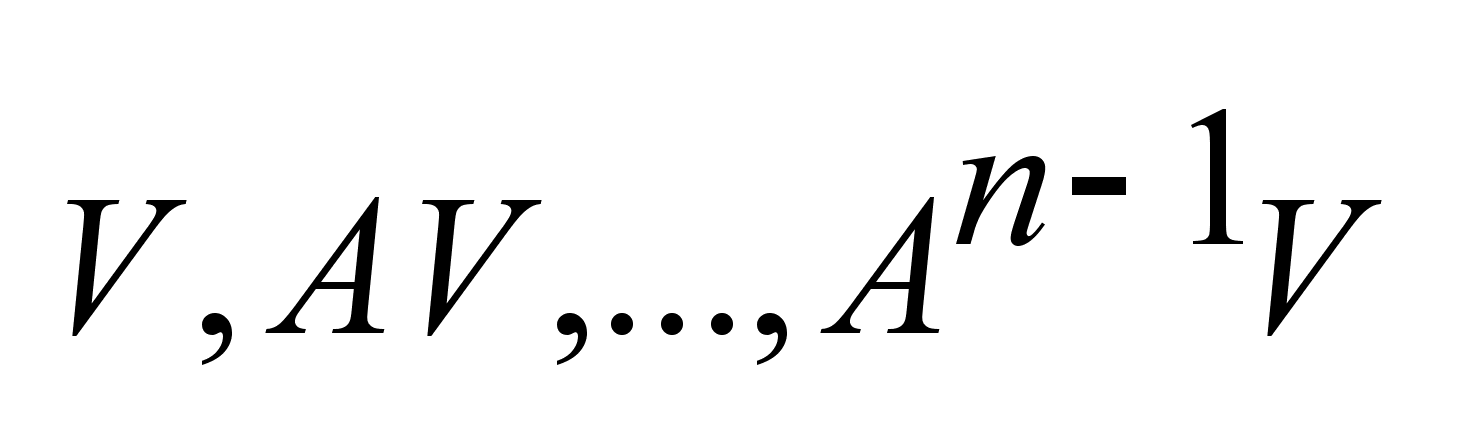 . .
19.
Локальная
управляемость.
Теорема о локальной
управляемости..
Рассматриваем
динамический
объект, поведение
которого описывается
системой (1)
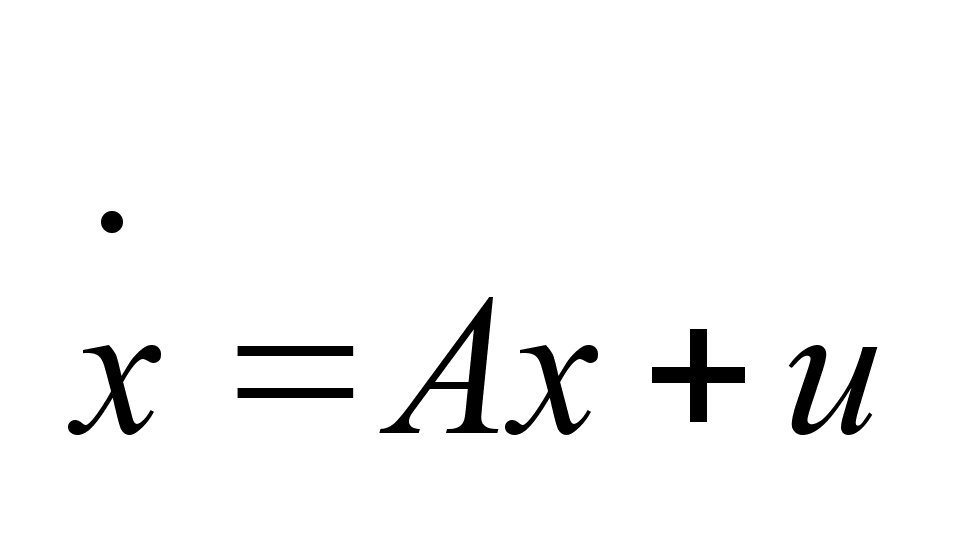 ,
x-
n-мерный
вектор, ,
x-
n-мерный
вектор,
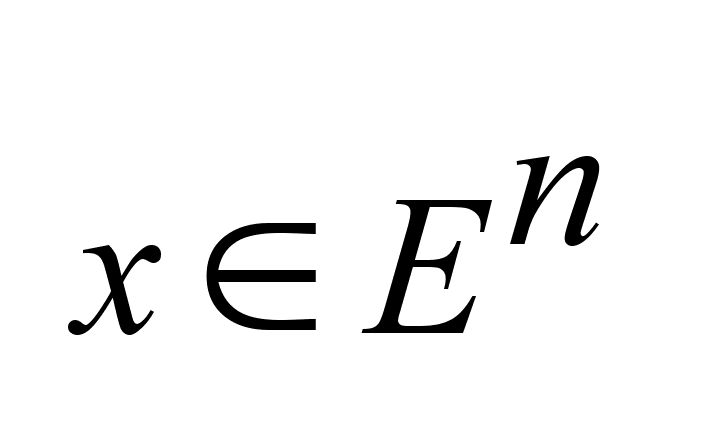 ,
A-матрица
nxn,
u
имеет ту же
размерность,
что
и ,
A-матрица
nxn,
u
имеет ту же
размерность,
что
и
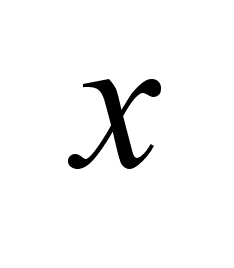 , ,
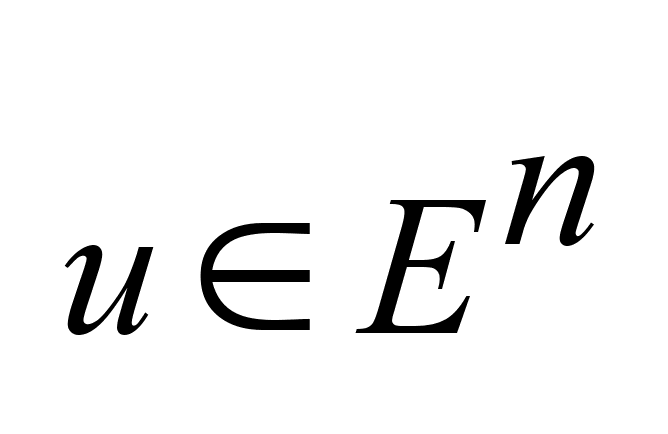 .Задано .Задано
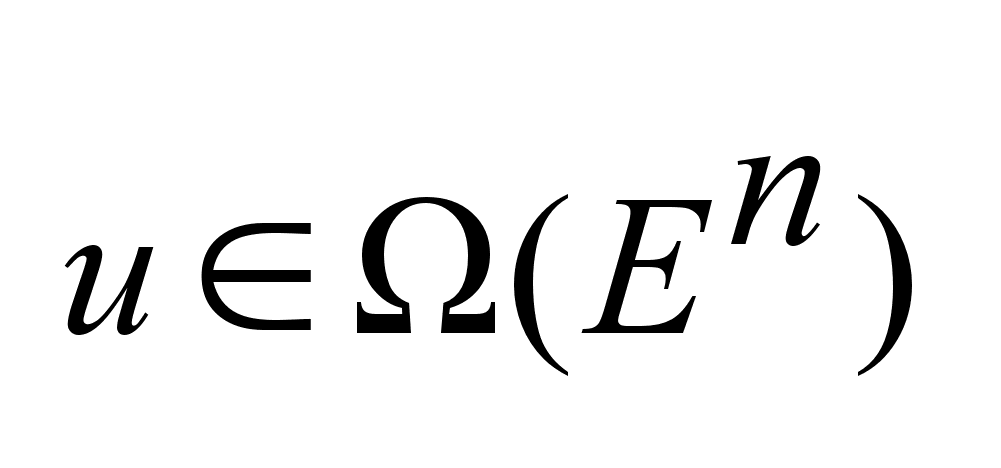 ,
u:
I ,
u:
I 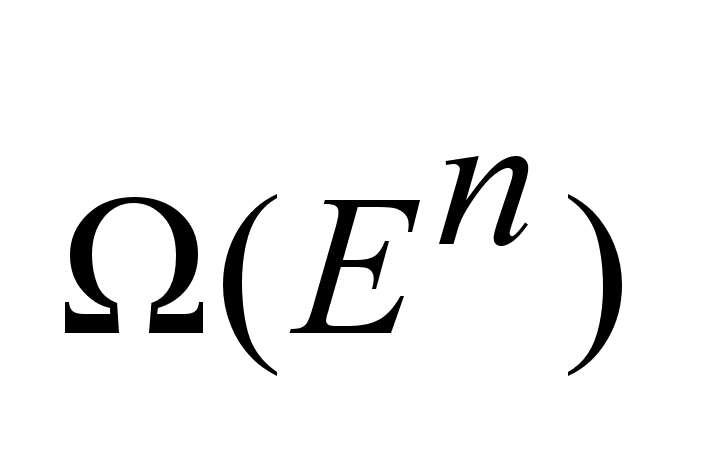 и полагается,
что u(t)
измеримо
и
и полагается,
что u(t)
измеримо
и
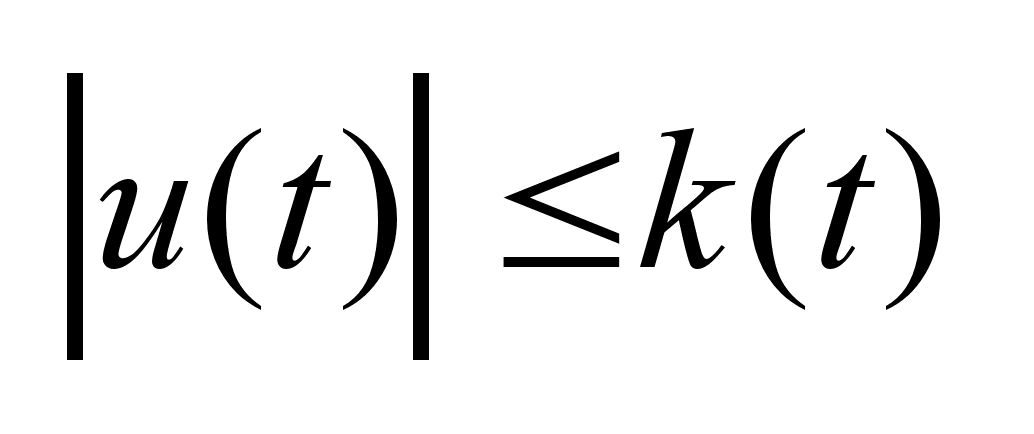 -
где
k(t)
скалярная
функция интегрируемая
по Лебегу на
отрезке I .Функция
u(t)-
называется
допустимым
управлением,
если измерима
и является
однозначной
ветвью из
многозначного
отображения
U
(2) u(t) -
где
k(t)
скалярная
функция интегрируемая
по Лебегу на
отрезке I .Функция
u(t)-
называется
допустимым
управлением,
если измерима
и является
однозначной
ветвью из
многозначного
отображения
U
(2) u(t)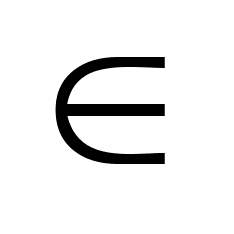 U(t)-
ограничения
на управления
. В фазовом
пространстве U(t)-
ограничения
на управления
. В фазовом
пространстве
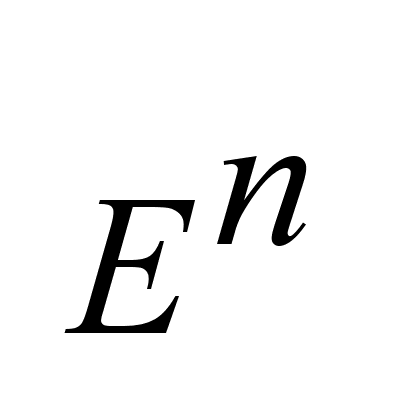 заданы
два не пустых
множества заданы
два не пустых
множества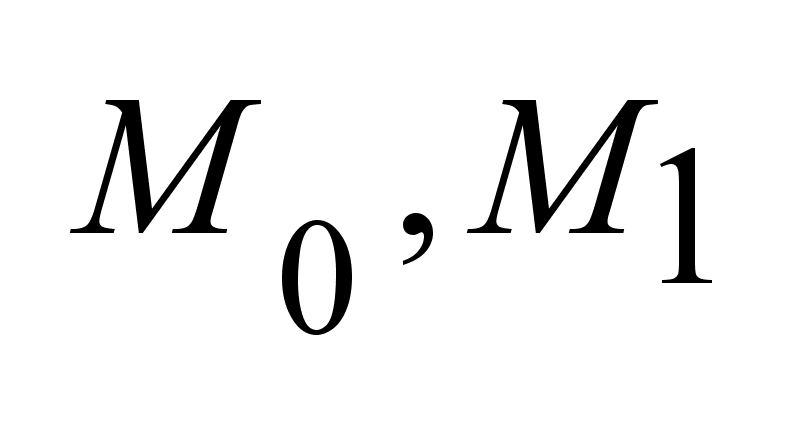 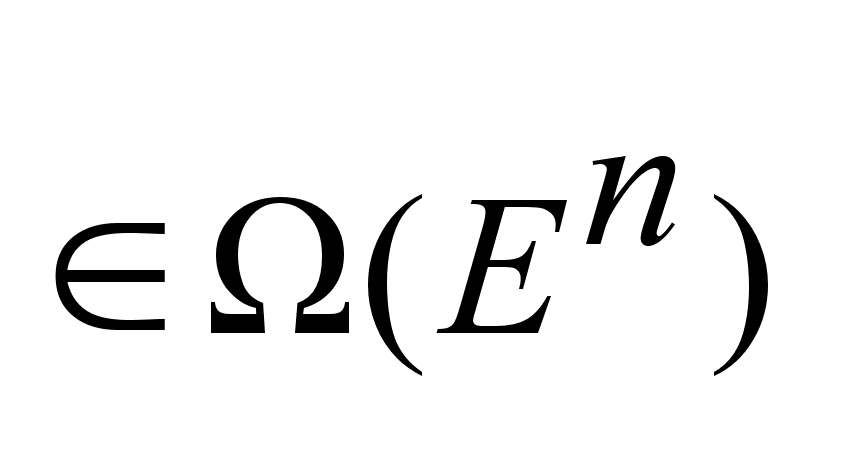 .
Допустимое
управление
u(t)
на отр.I
осуществляете
переход из
начального
мн-ва .
Допустимое
управление
u(t)
на отр.I
осуществляете
переход из
начального
мн-ва
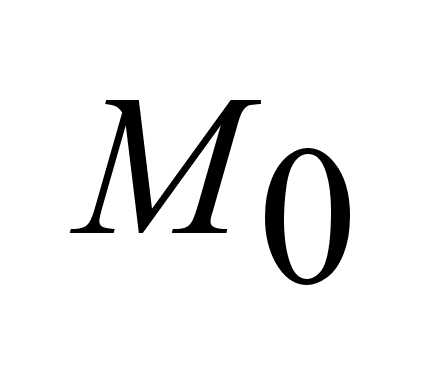 в конечное
множество
в конечное
множество
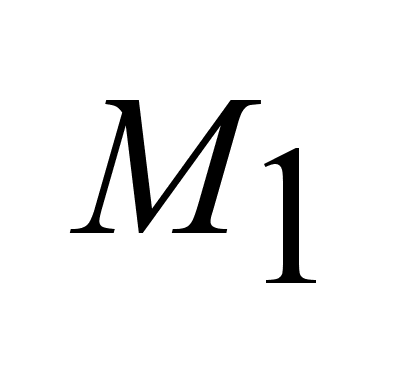 ,
если существует
решение уравнения
(1), удовлетворяющее
граничным
условиям (4) ,
если существует
решение уравнения
(1), удовлетворяющее
граничным
условиям (4)
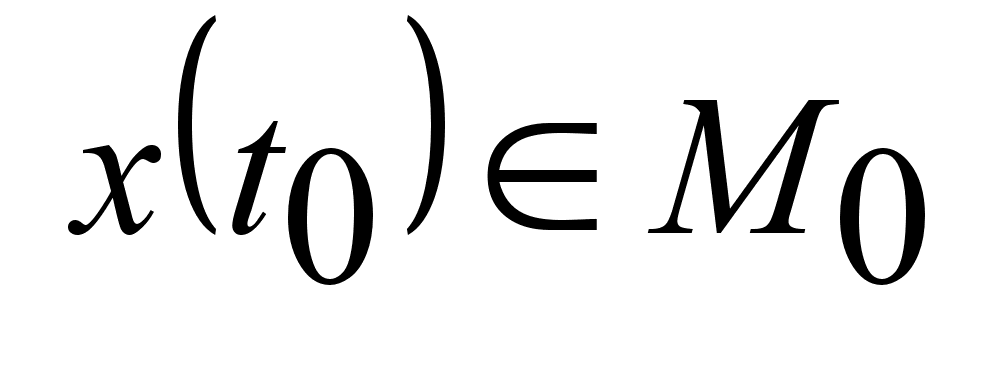 и и
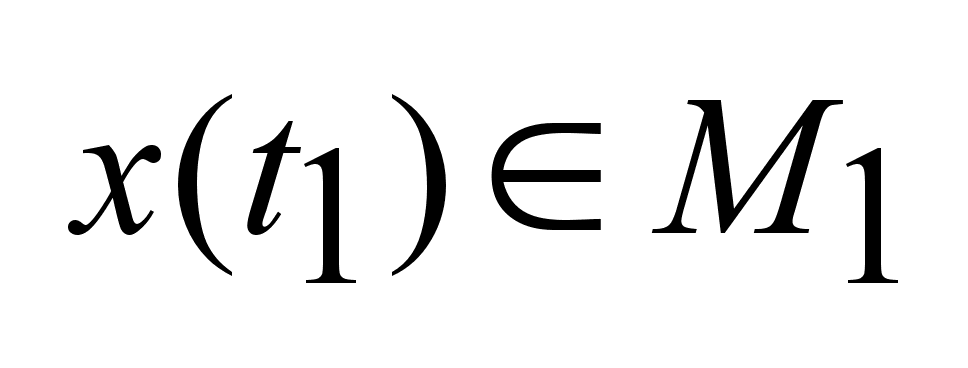 .
Цель управления-
перевод динамический
объекта из .
Цель управления-
перевод динамический
объекта из
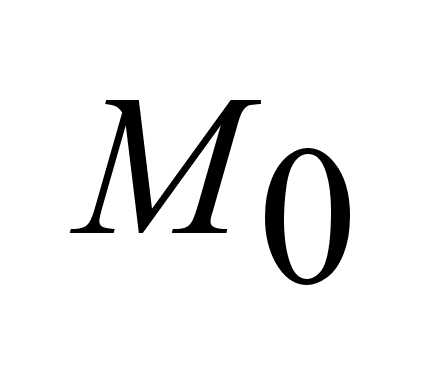 в в
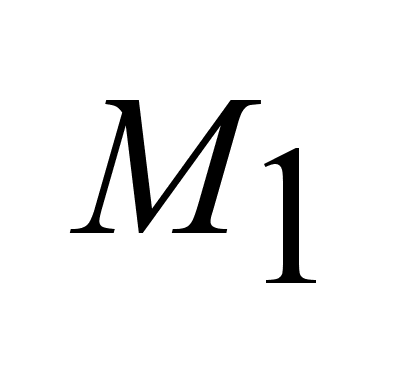 ,
а качество
определяет
функционал.
Таким функционалом
явл. время,
следовательно ,
а качество
определяет
функционал.
Таким функционалом
явл. время,
следовательно
задача
быстродействия
заключается
в нахождении
такого допустимого
управления,
которое осуществляет
переход из
множества
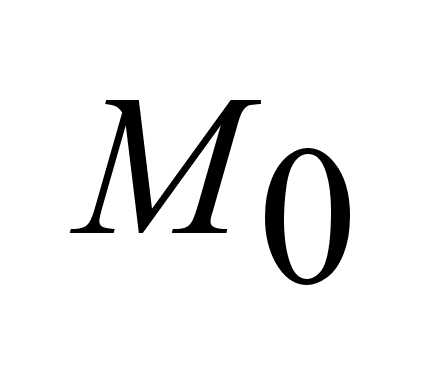 в в
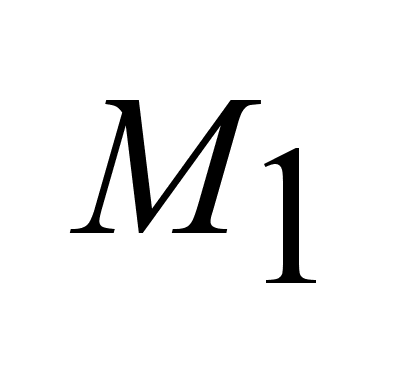 за
наименьшее
время. за
наименьшее
время.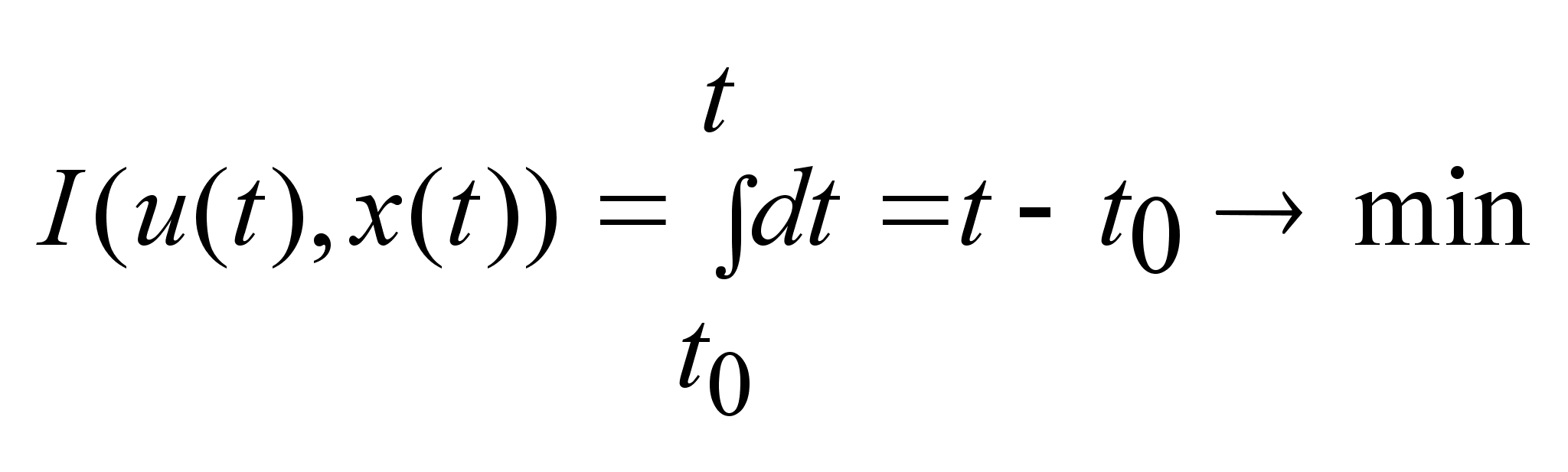 (4).
(4).
Предположим,
что
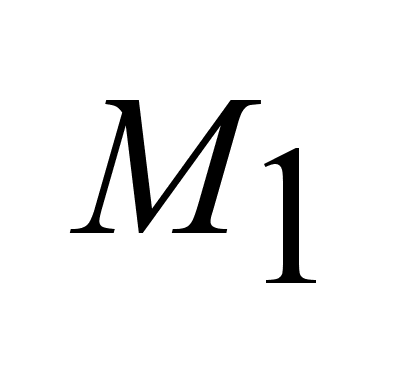 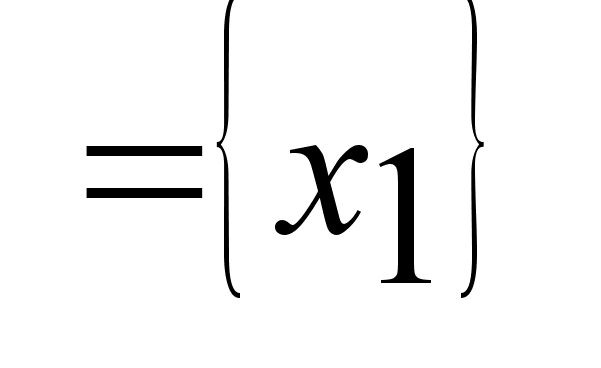 ,
а мн-во ,
а мн-во
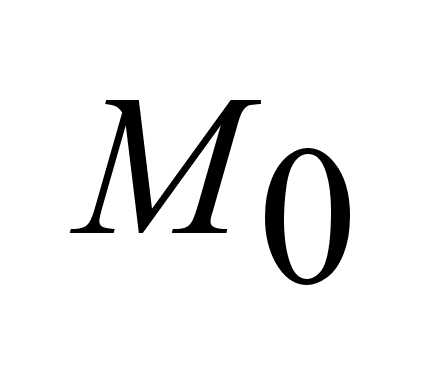 -произвольные
точки -произвольные
точки
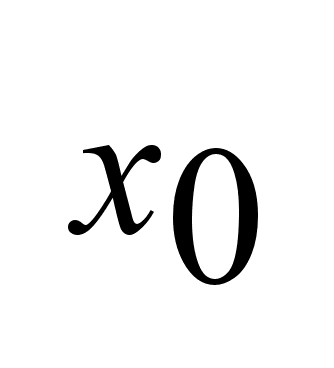 из
окрестности из
окрестности
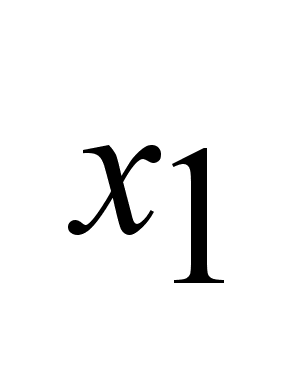 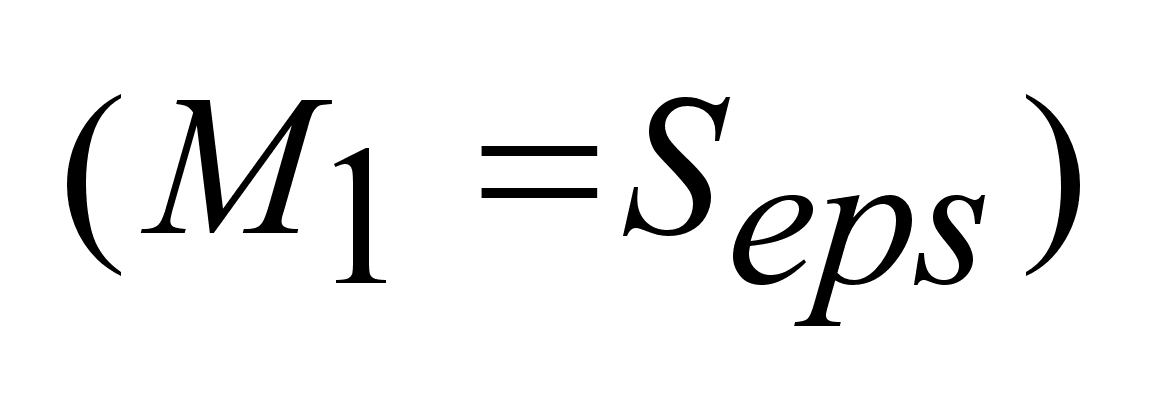 . .
Сделаем
линейную замену: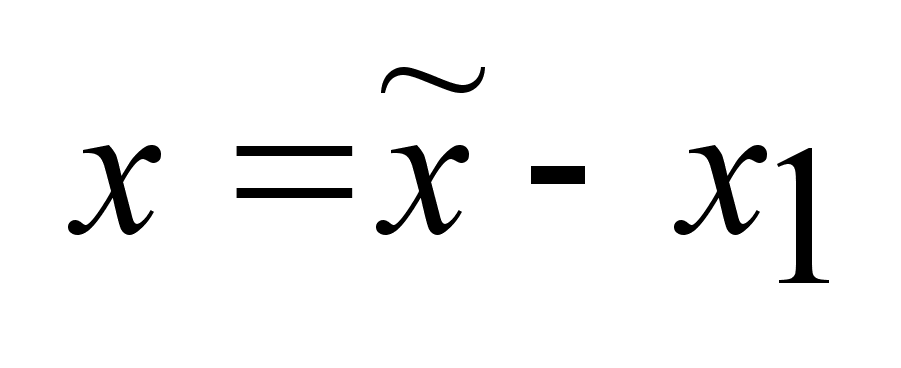 ,где ,где
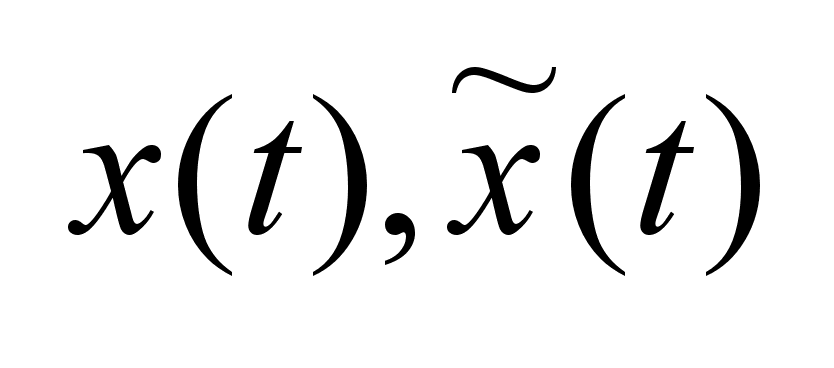 -функции,
получим -функции,
получим
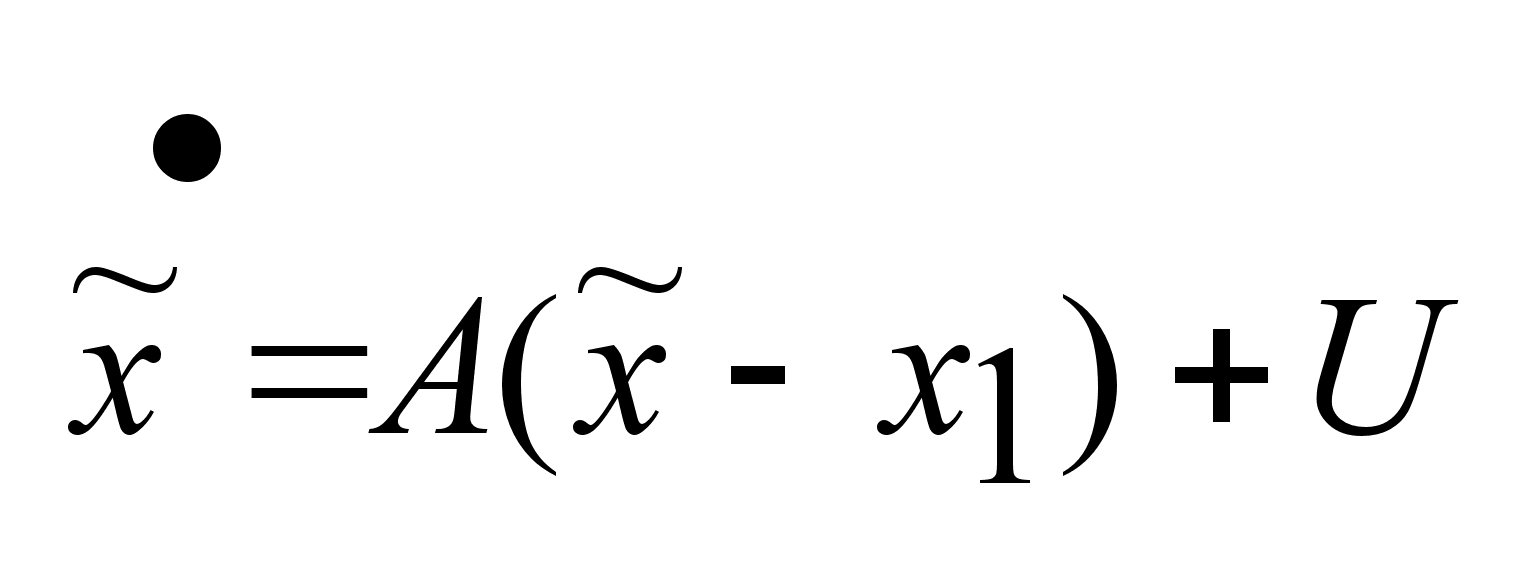 , ,
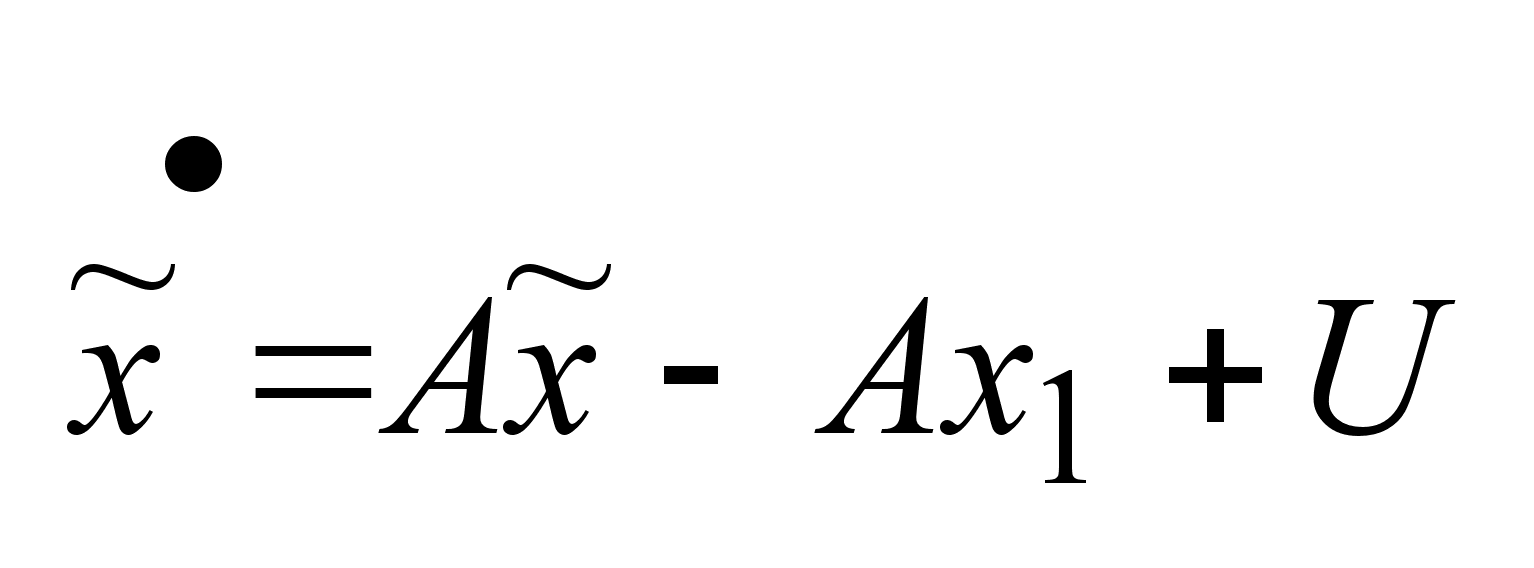 ,
где ,
где
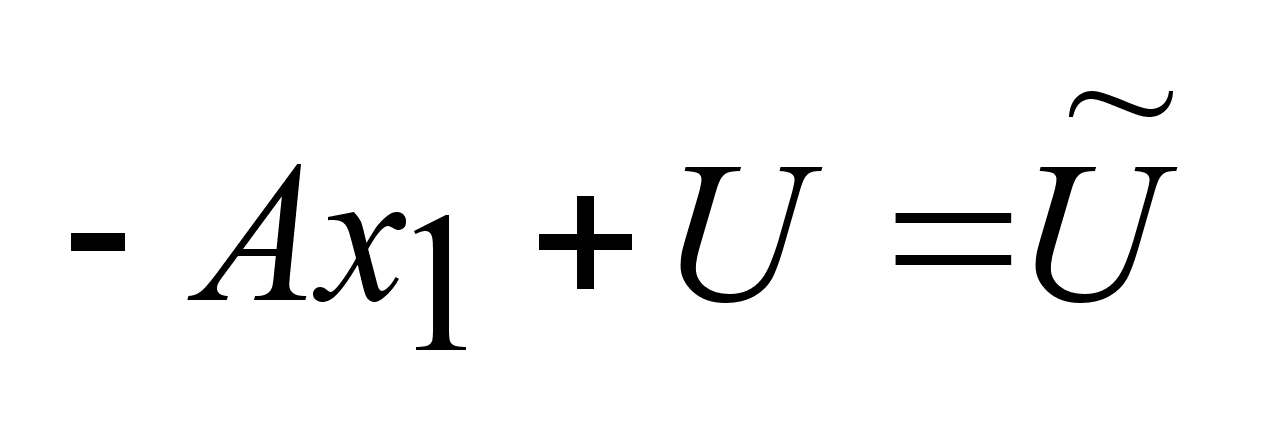 , ,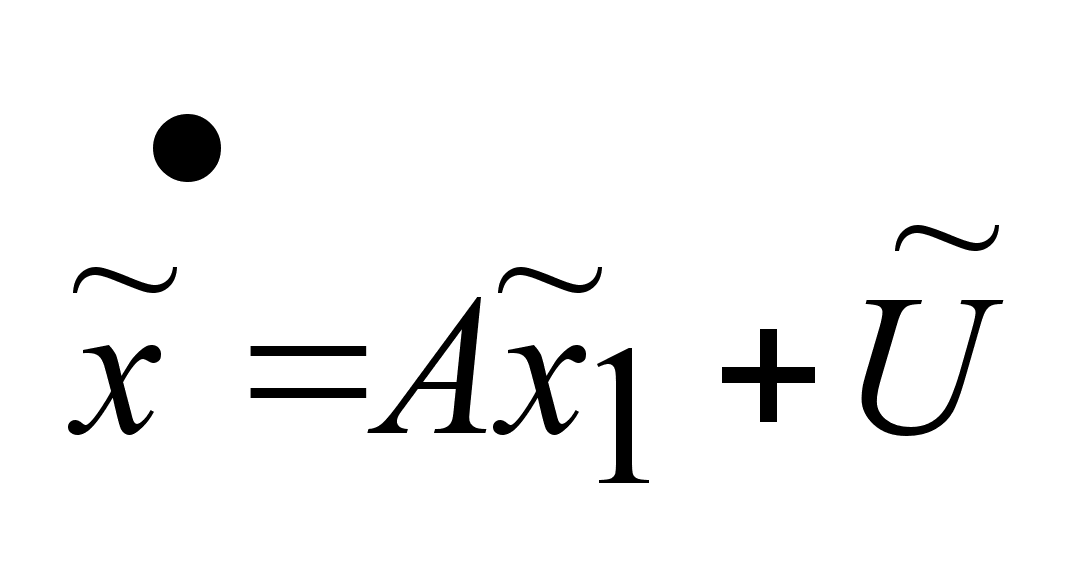 ,
поэтому вместо
точки ,
поэтому вместо
точки
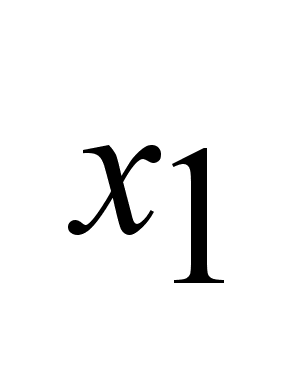 можно
рассматривать
т.0 и будем говорить
о локальной
управляемости
в т.0. Т.е. если
объект локально
управляем в
т.0, то он локально
управляем в
любой точки можно
рассматривать
т.0 и будем говорить
о локальной
управляемости
в т.0. Т.е. если
объект локально
управляем в
т.0, то он локально
управляем в
любой точки
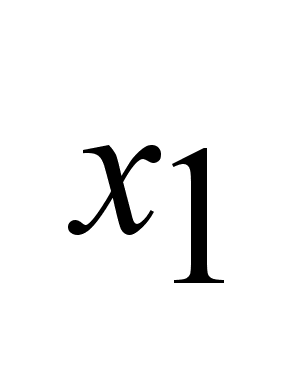 . .
Определение:
Объект
наз. локально
управляем в
т.
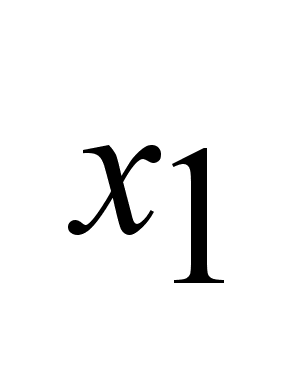 =0
на отр.I
, если =0
на отр.I
, если
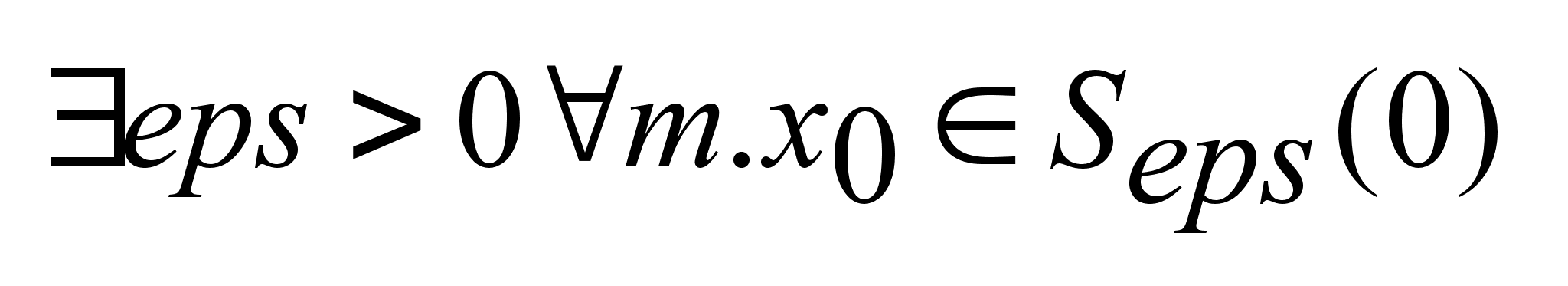 объект явл.
Управляемым
на отр.I
из т.
объект явл.
Управляемым
на отр.I
из т.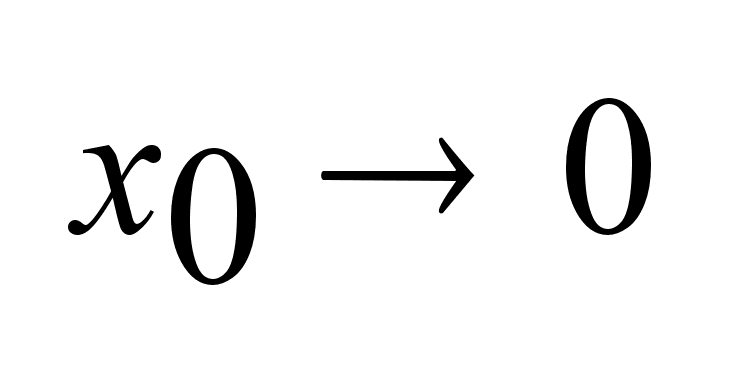 . .
Для
решения задачи
применим теорему
об управляемости,
но для конкретной
местности.
Исходя из теоремы
об управляемости,
объект явл.
управляемым
из
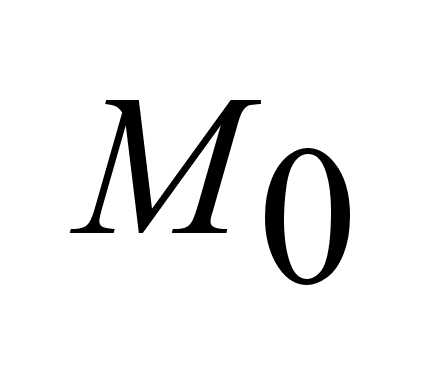 в в
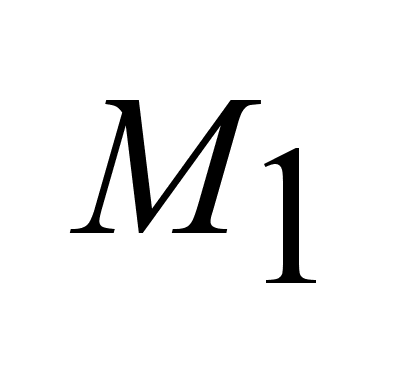 на I
, если
на I
, если
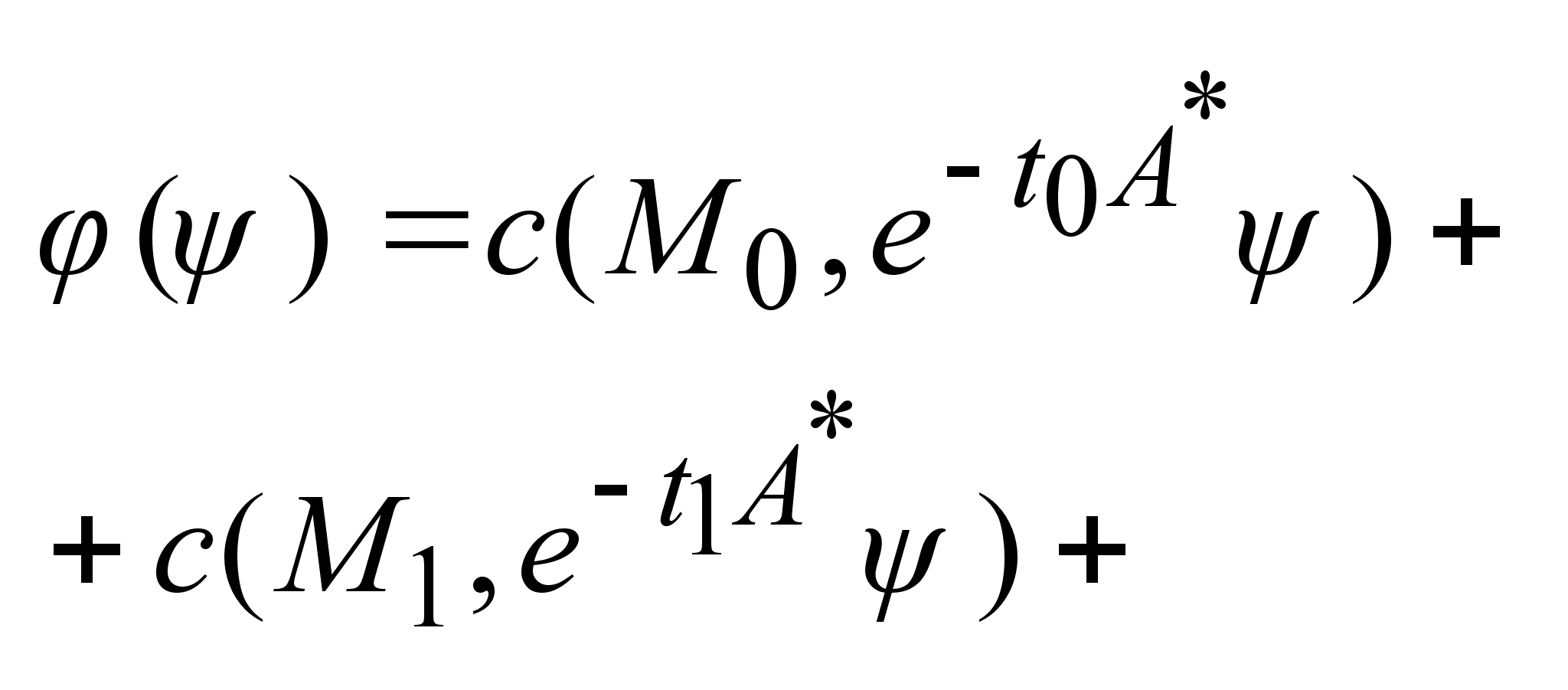 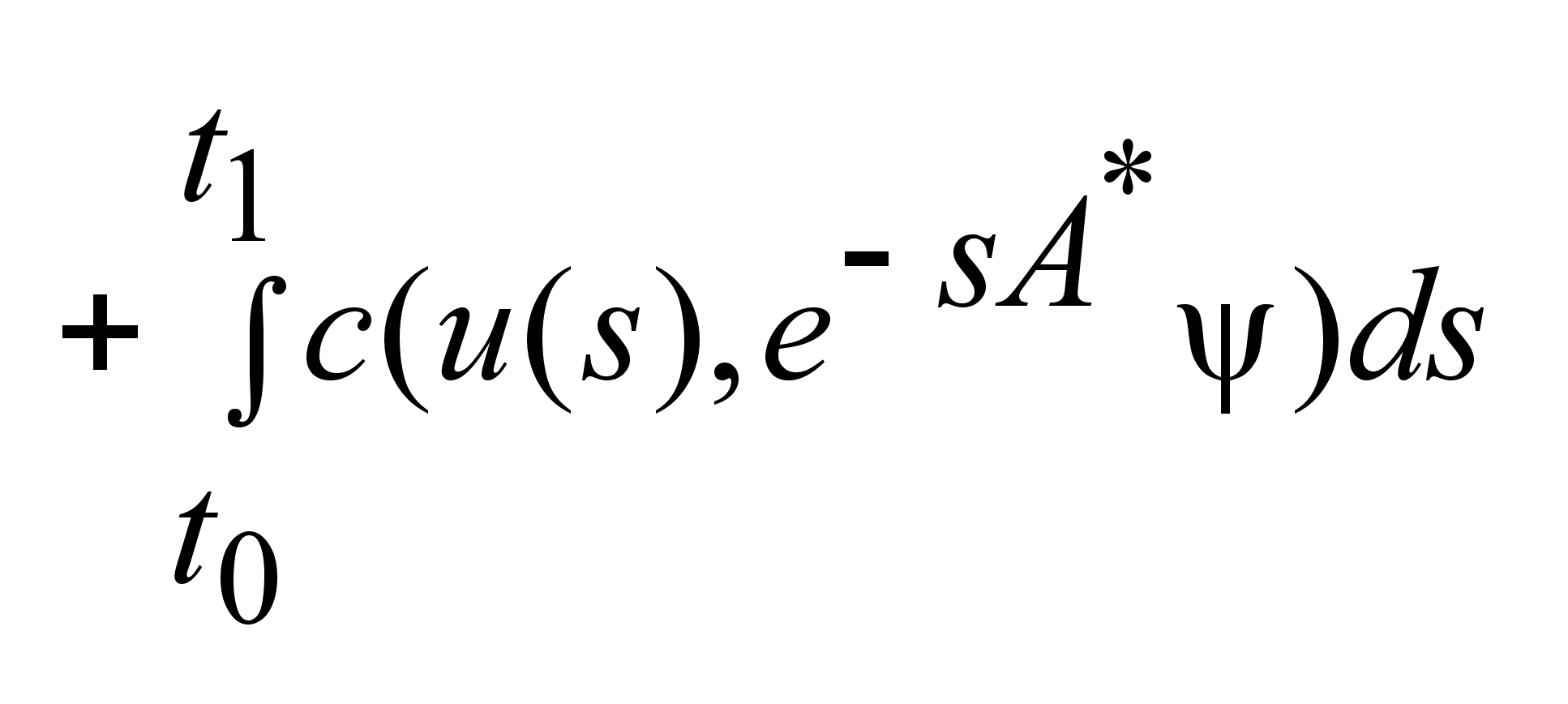 >=0. >=0.
20.
Теорема о локальной
управляемости.
(дает достаточное
условие локальной
управляемости)
Если
 вектор вектор
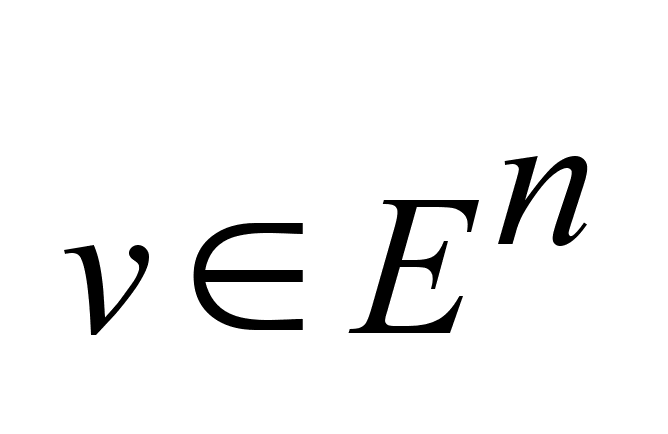 и выполняются
два условия:
и выполняются
два условия:
1)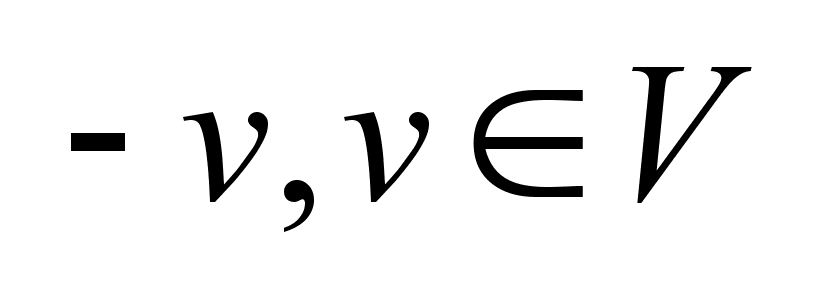 , ,
 ; ;
2)
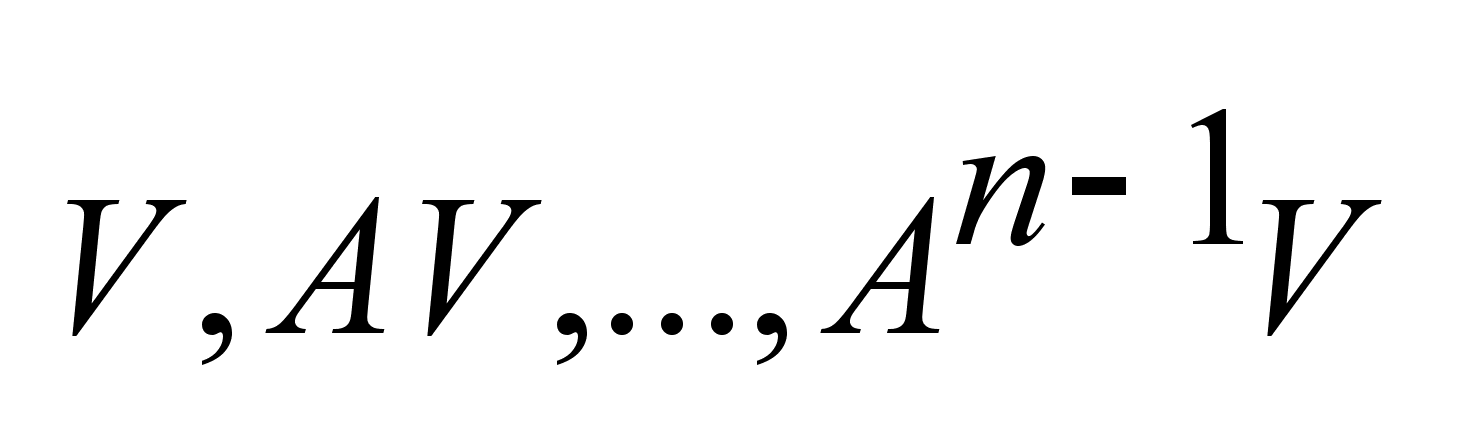 -лин.
независимы,
тогда объект
явл. локально
управляем в
точке x=0
на отр. I. -лин.
независимы,
тогда объект
явл. локально
управляем в
точке x=0
на отр. I.
Доказательство:
В силу определения
локальной
управляемости
выполняется
условие
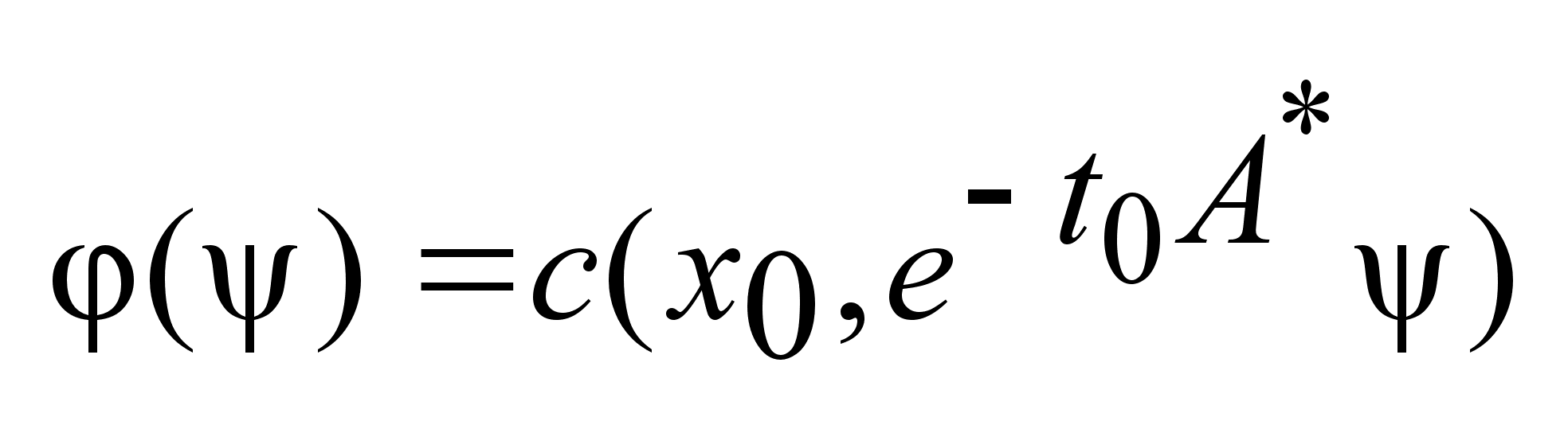 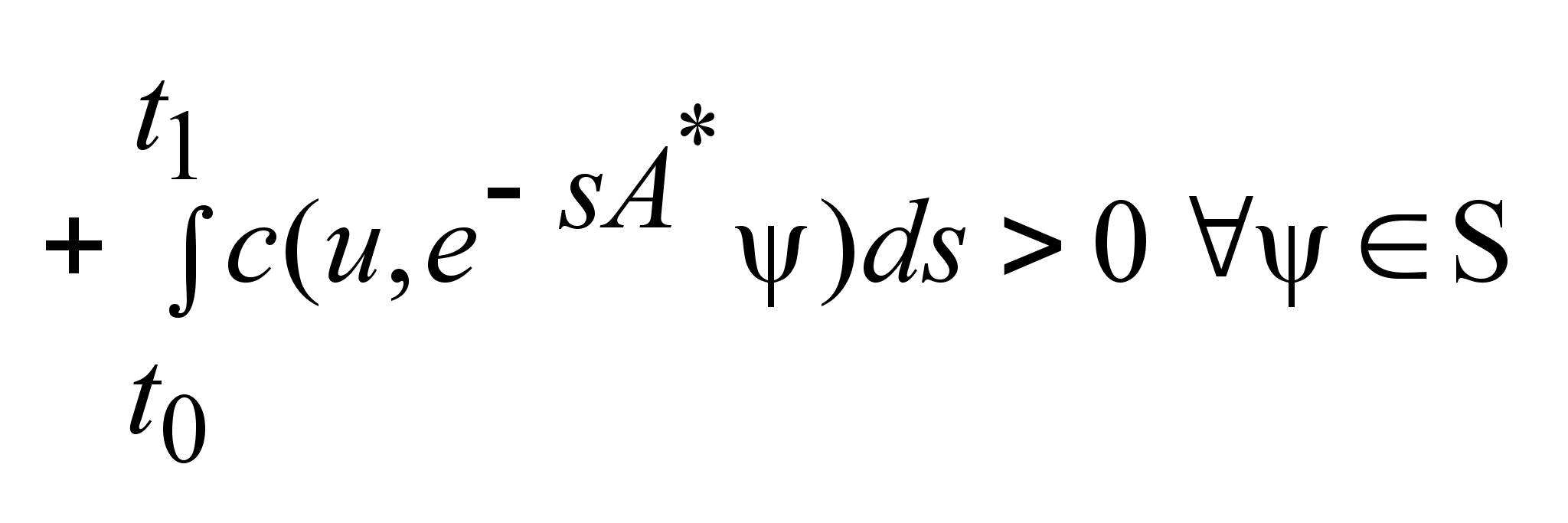 . .
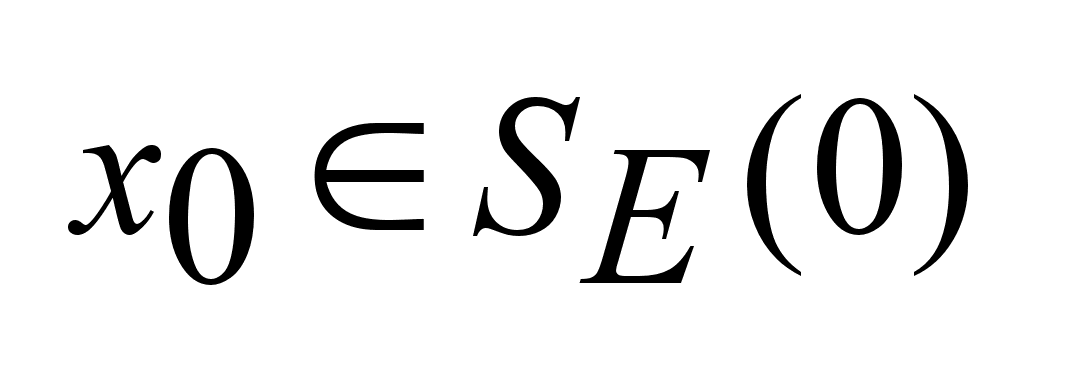 ,
получим (1) ,
получим (1)
 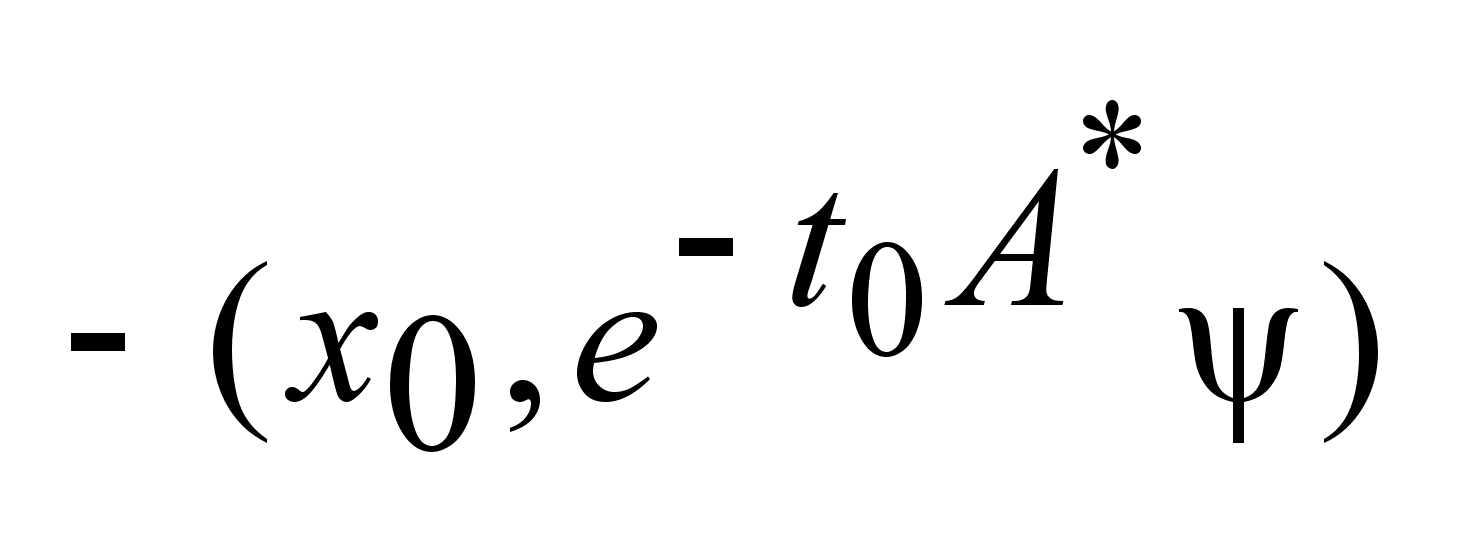 .
Покажем, что .
Покажем, что
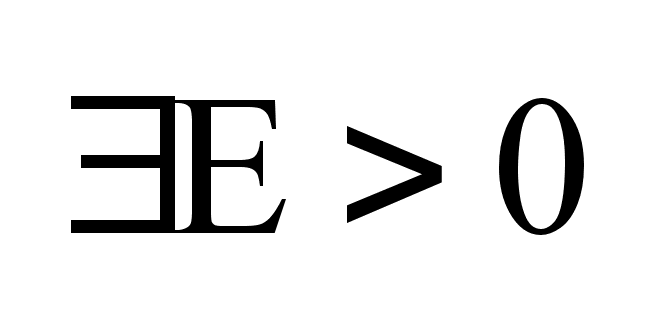 ,
такое , что
выполняется
(1) ,
такое , что
выполняется
(1)
 и и
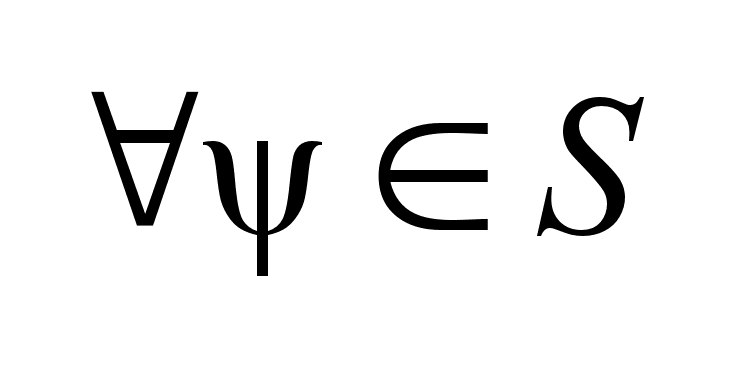 .
По предположению
теоремы 1) выполняется .
По предположению
теоремы 1) выполняется
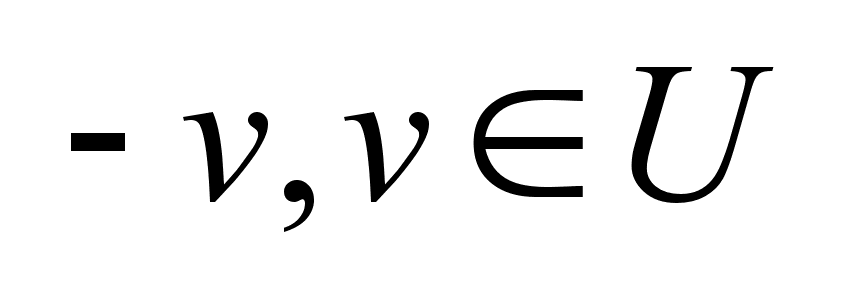 ,
получим ,
получим
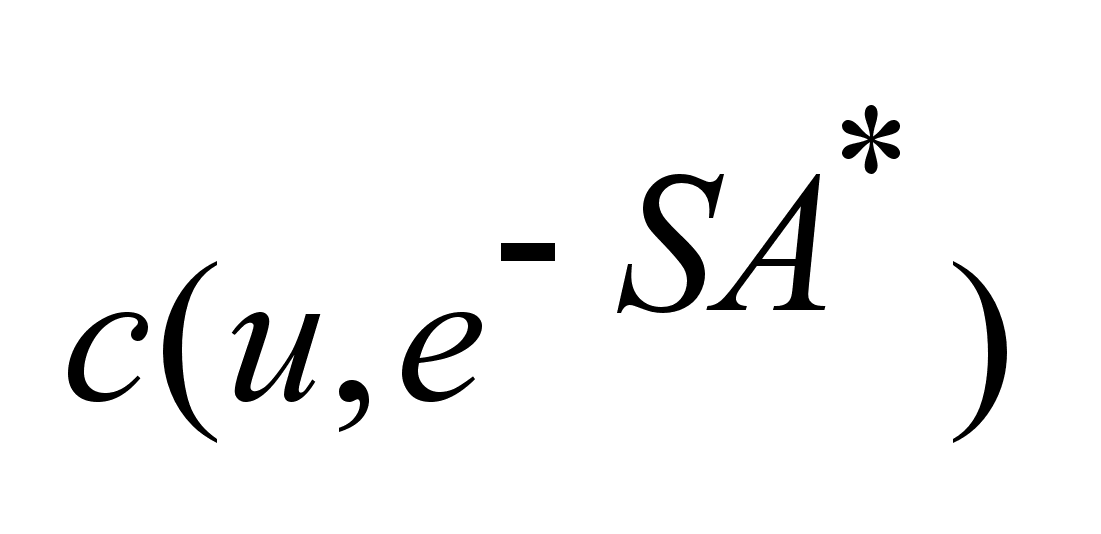 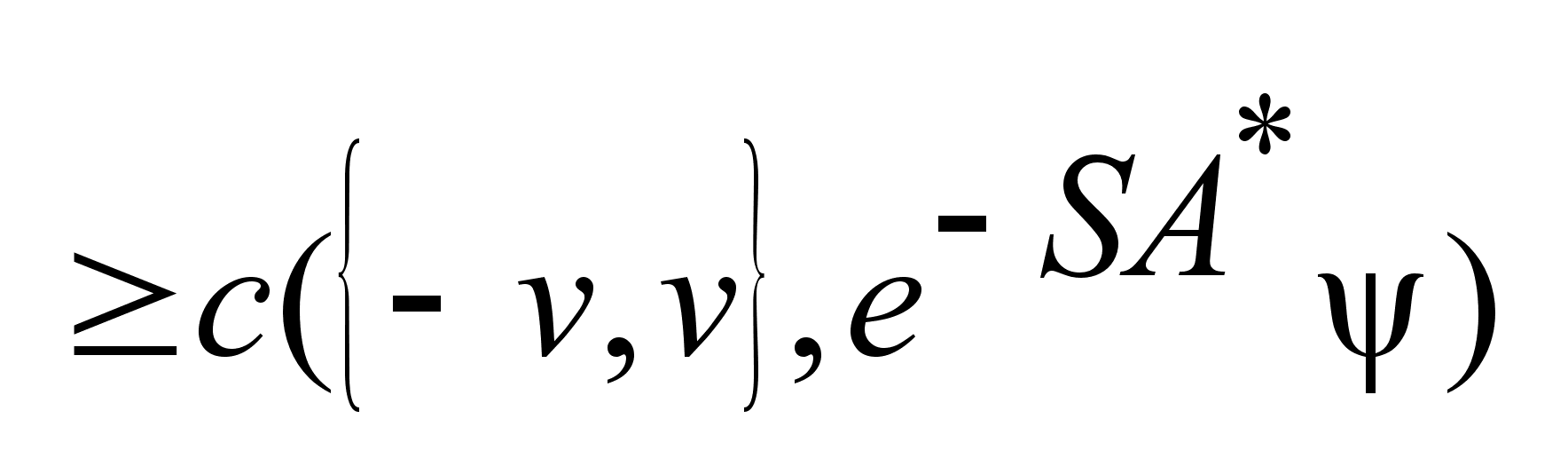 .
Сделаем оценку
для левой части
неравенства.
Оценим интеграл: .
Сделаем оценку
для левой части
неравенства.
Оценим интеграл:
 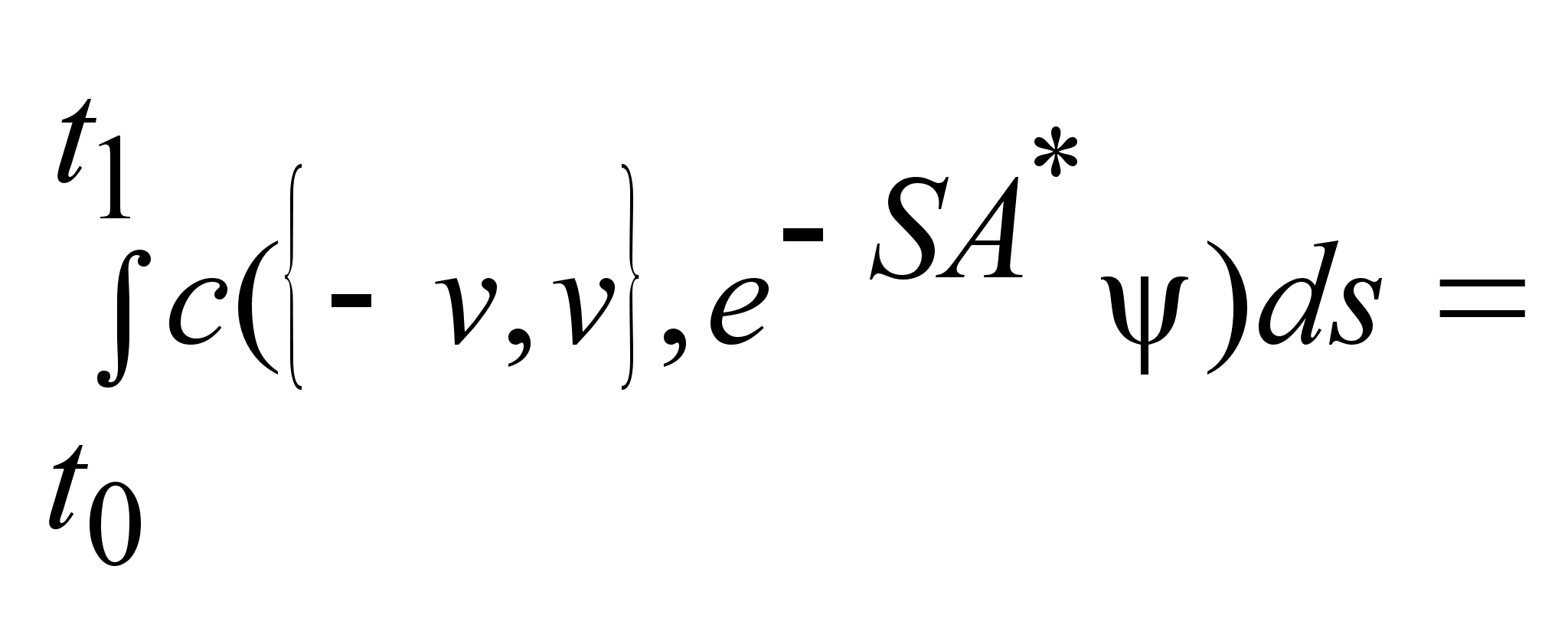 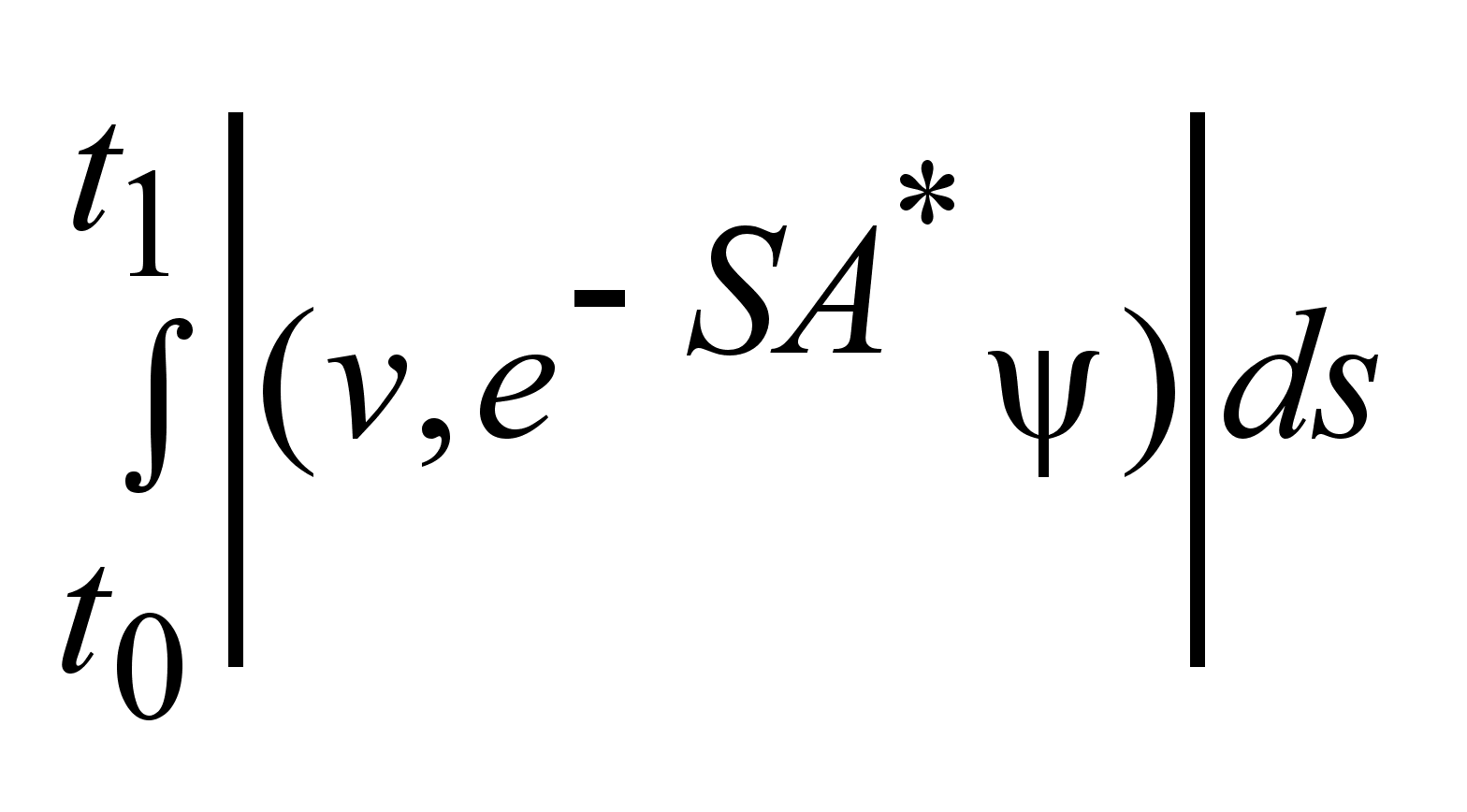 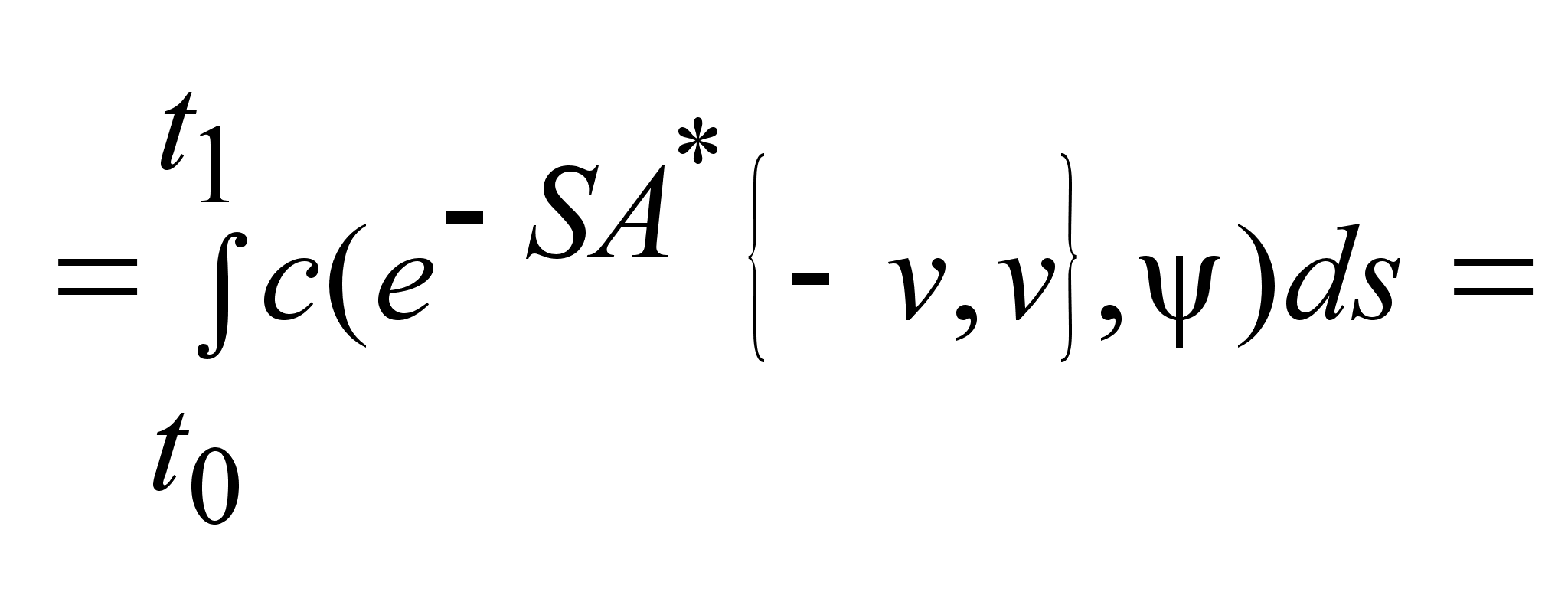 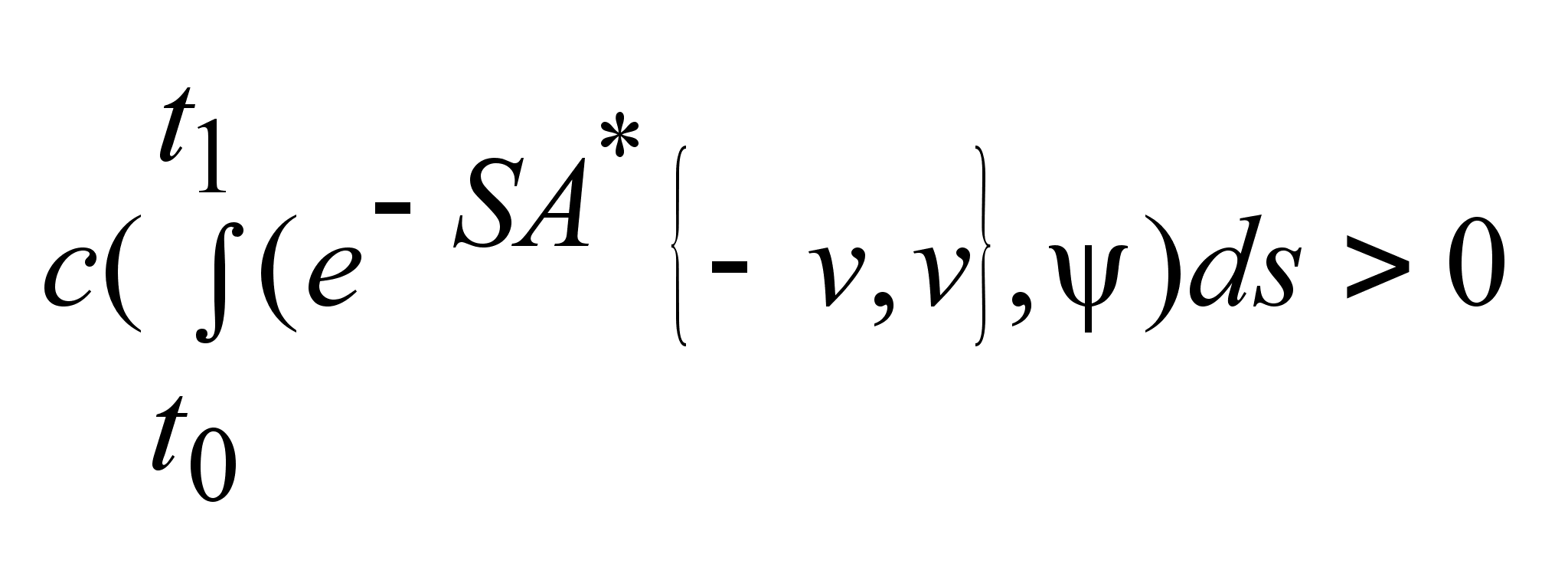 , ,
т.к.
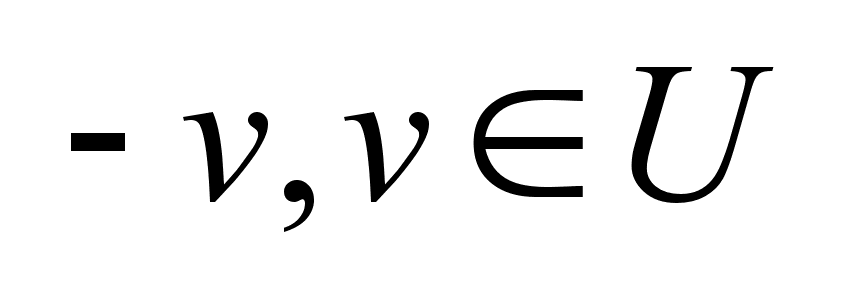 и выполняется
2) , то 0 явл. внутренней
точкой интеграла:
и выполняется
2) , то 0 явл. внутренней
точкой интеграла: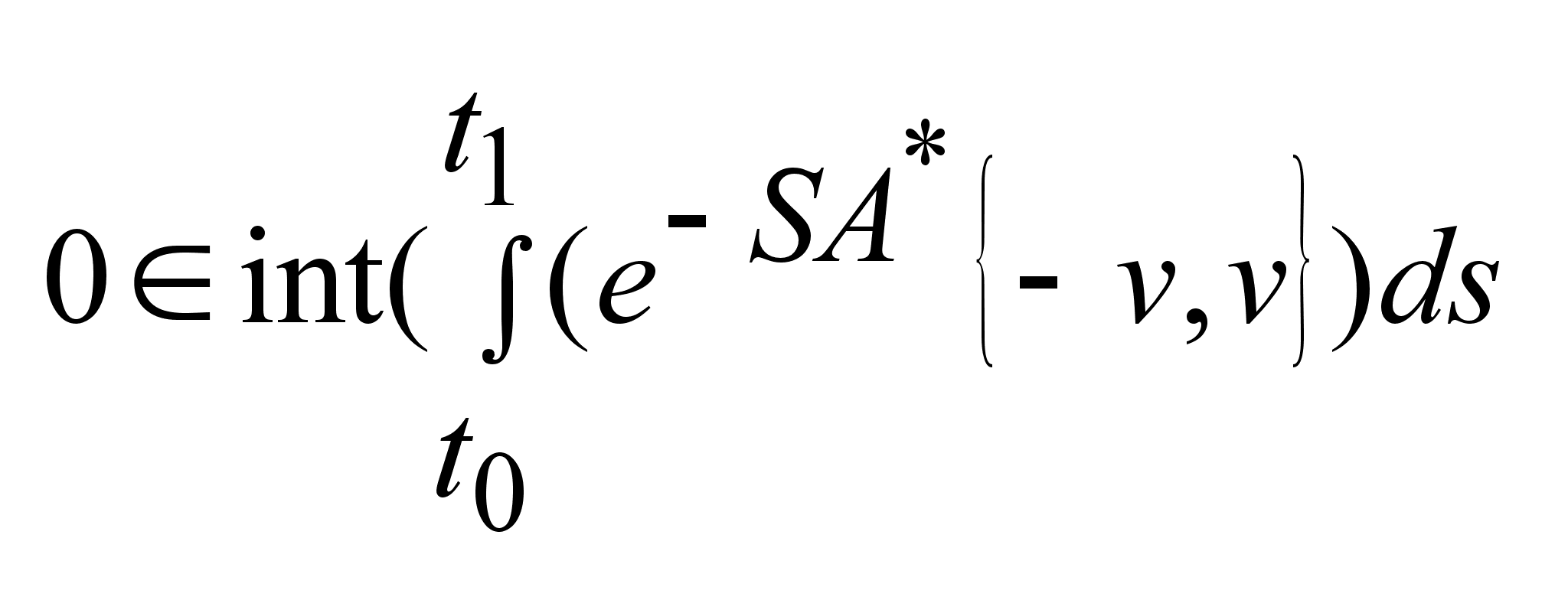 ,
а это означает,
что опорная
функция >0, ,
а это означает,
что опорная
функция >0,
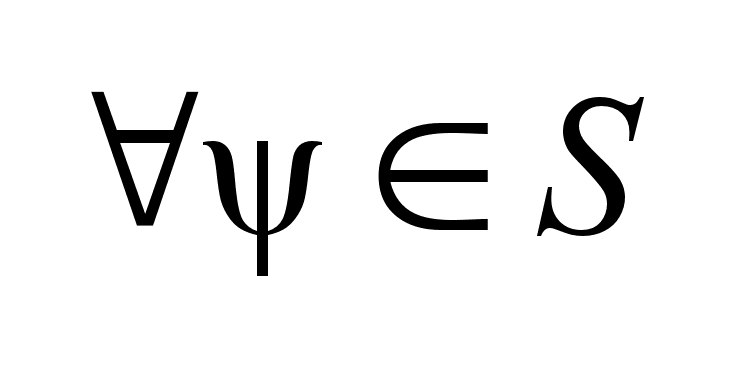 .
Из свойств
опорной функции
следует, что
опорная функция
непрерывна
по .
Из свойств
опорной функции
следует, что
опорная функция
непрерывна
по
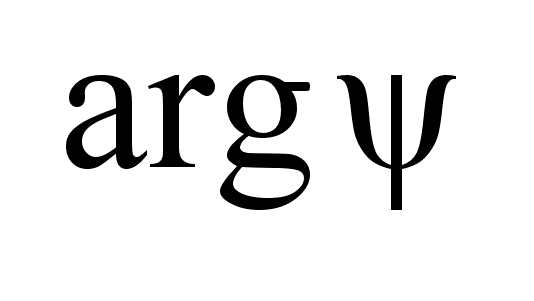 .
Если опорная
функция непрерывна,
>0,
и S
–компактное,
это означает,
что .
Если опорная
функция непрерывна,
>0,
и S
–компактное,
это означает,
что
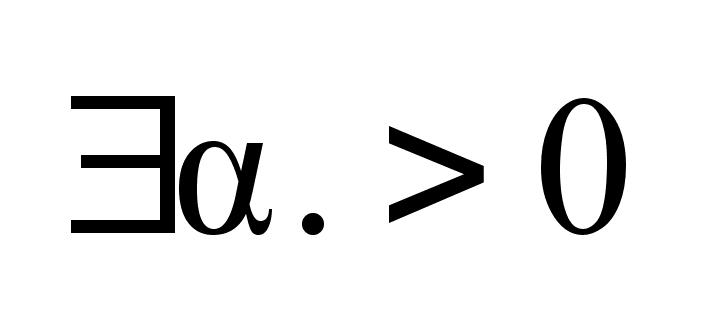 ,
такое что , ,
такое что ,
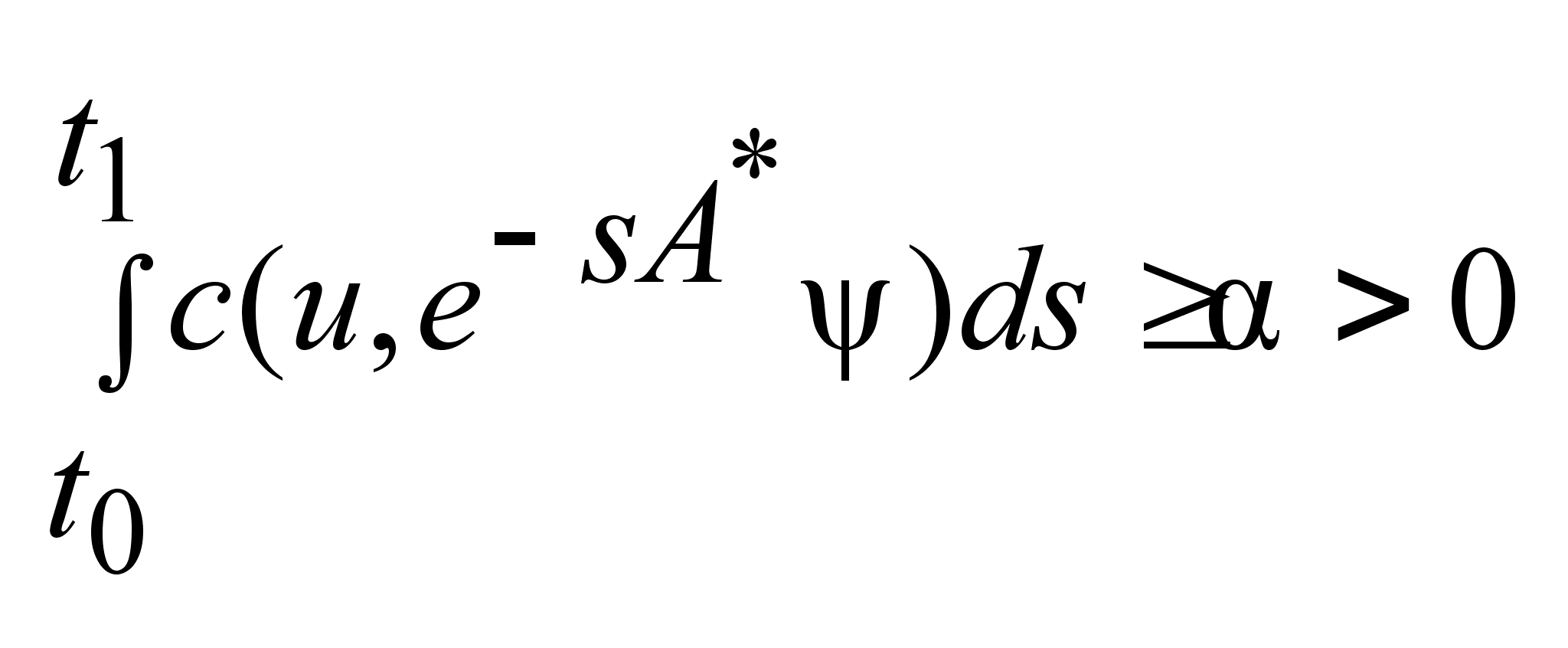 , ,
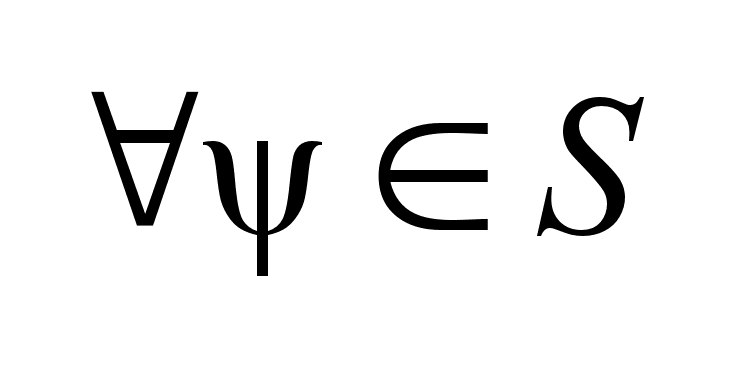 .
Т.о. оценили
левую часть
неравенства
(1), покажем , что
для правой
части , которая
зависит от .
Т.о. оценили
левую часть
неравенства
(1), покажем , что
для правой
части , которая
зависит от
 ,
по этому ,
по этому
 можно
найти можно
найти
 . .
Покажем
, что
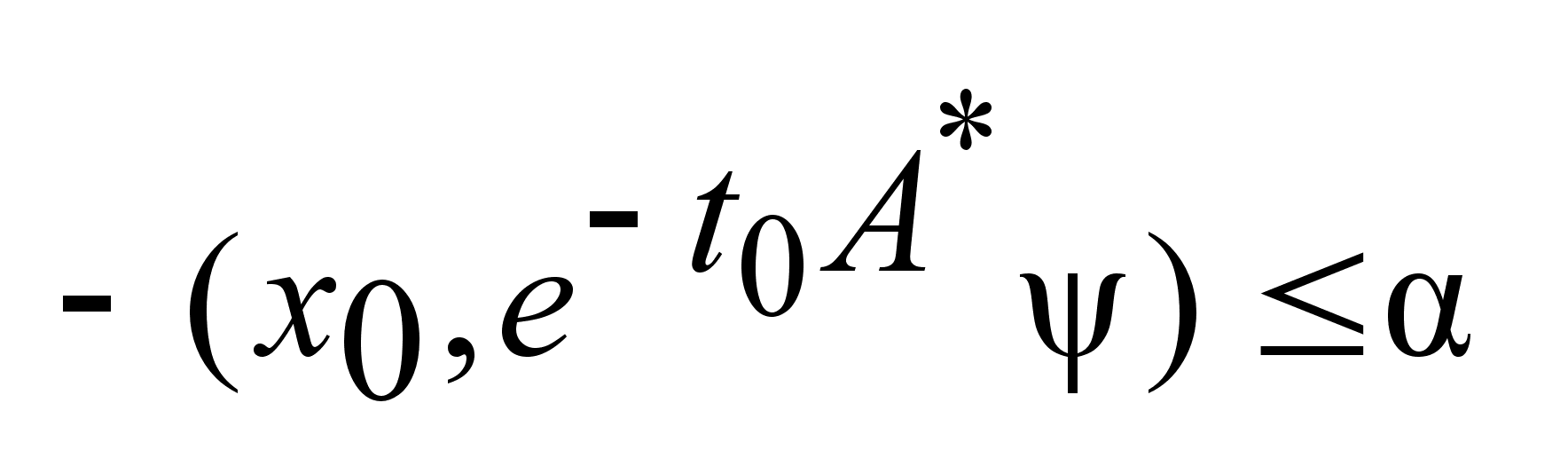 .
Оценим .
Оценим

,
отсюда имеем
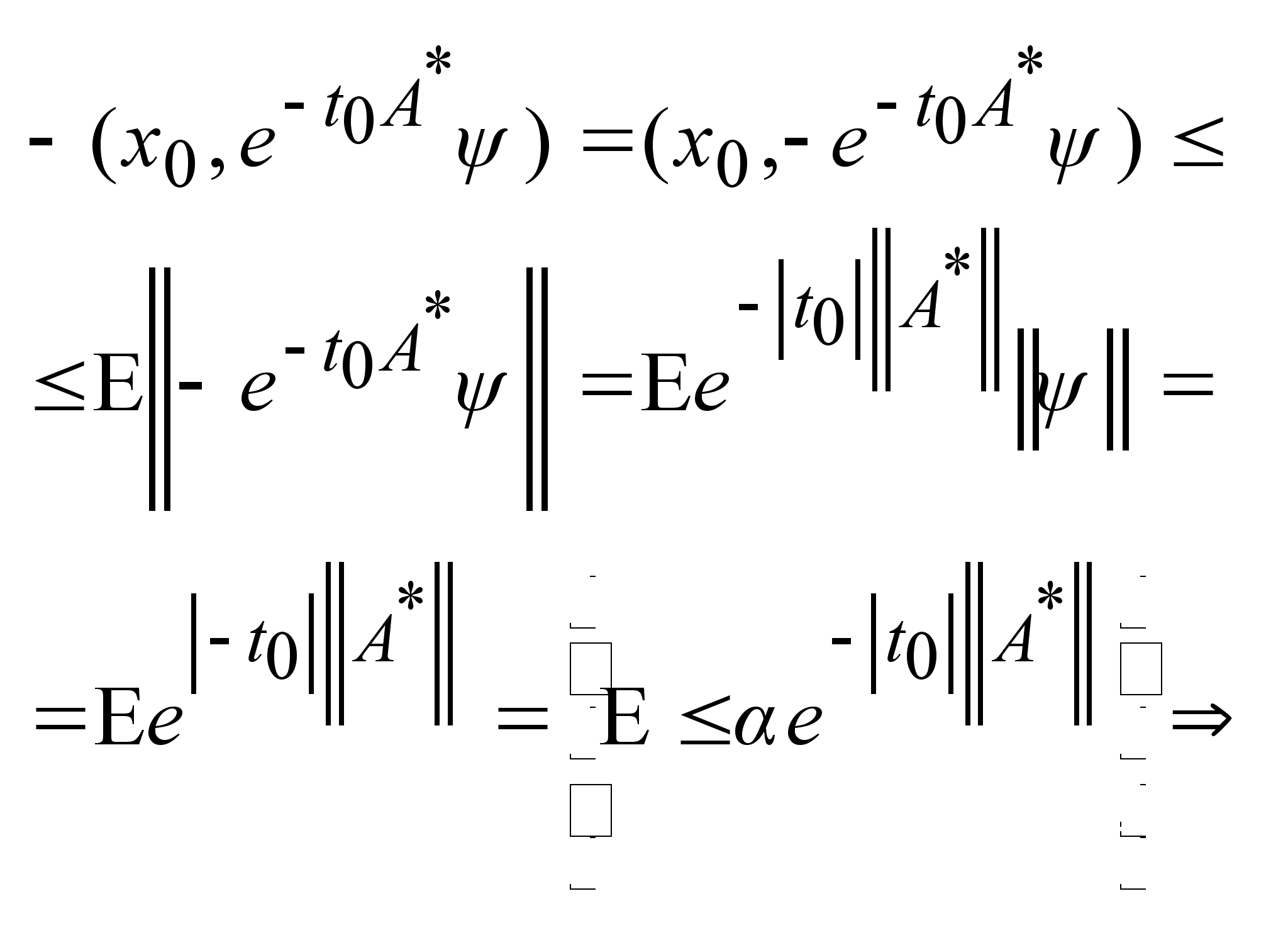 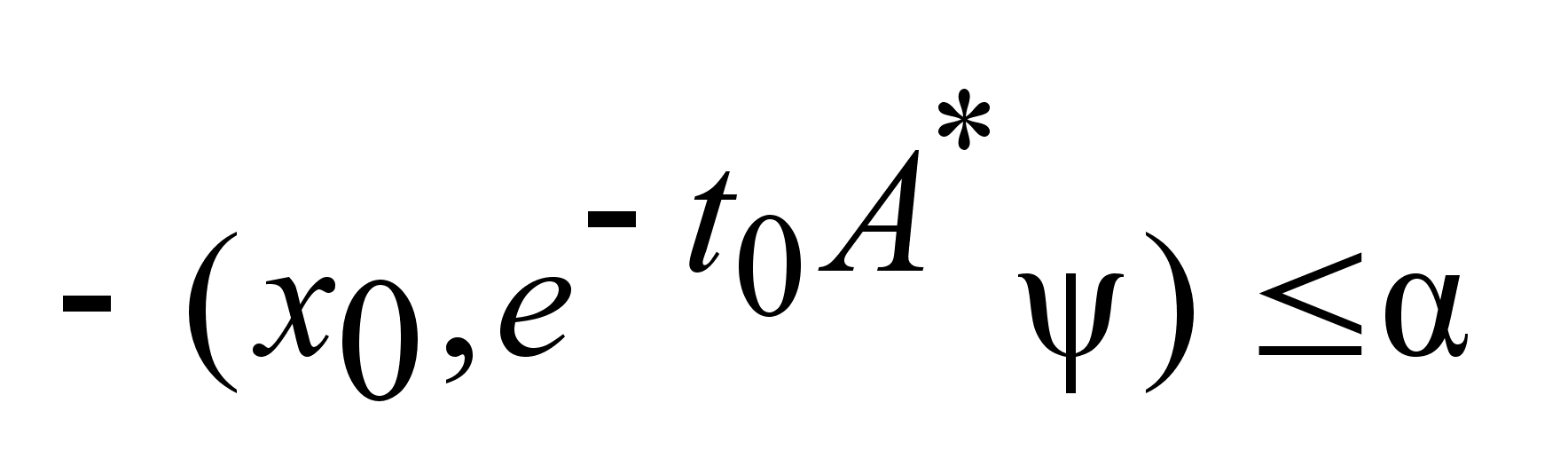 . .
  , ,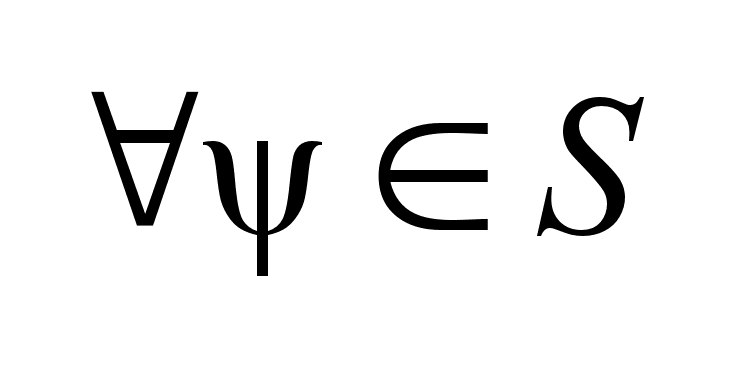 ,
а это значит
, ,
а это значит
,
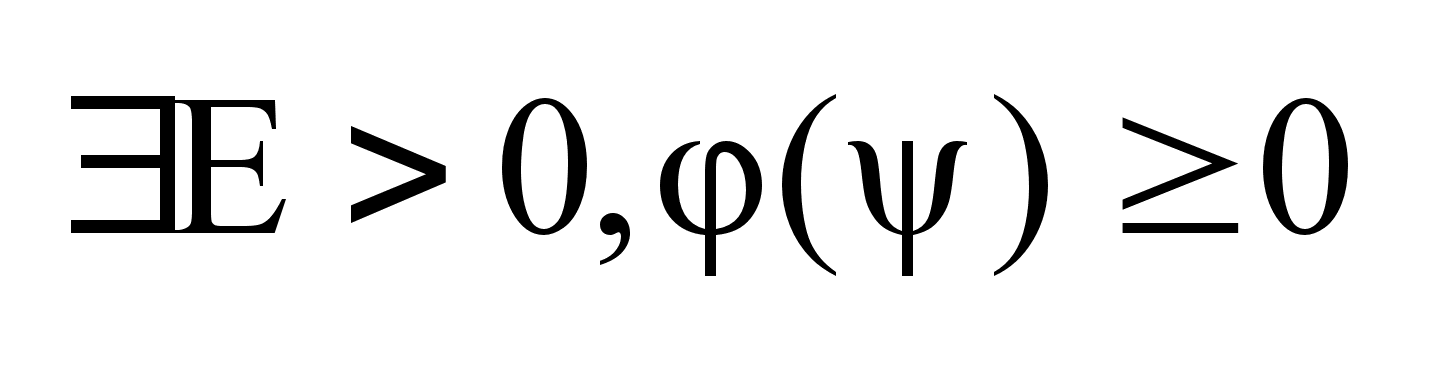 объект
локально управляем
в точке x=0. объект
локально управляем
в точке x=0.
21.
Теорема
о существовании
оптимального
управления.
Если
объект является
управляемым
из множества
 на отр.
на отр.
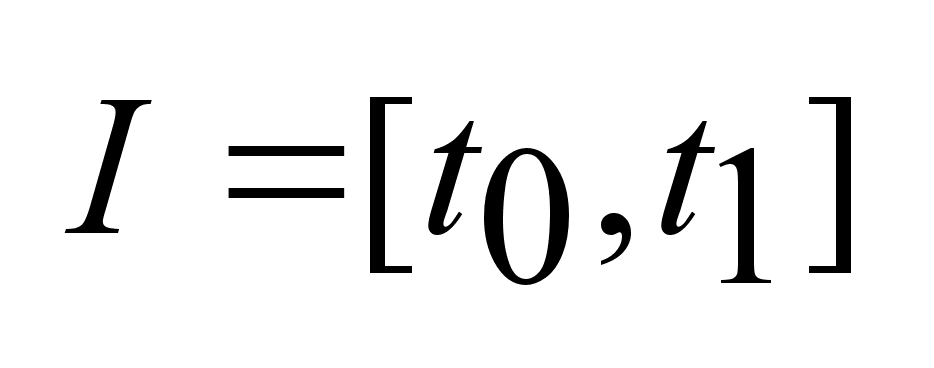 ,
то существует ,
то существует
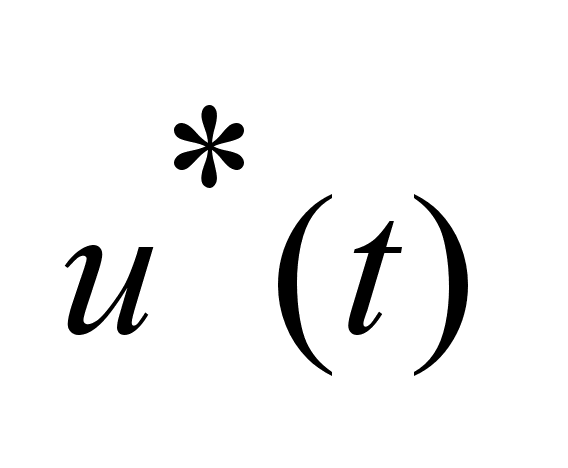  переводящее
объект из
переводящее
объект из
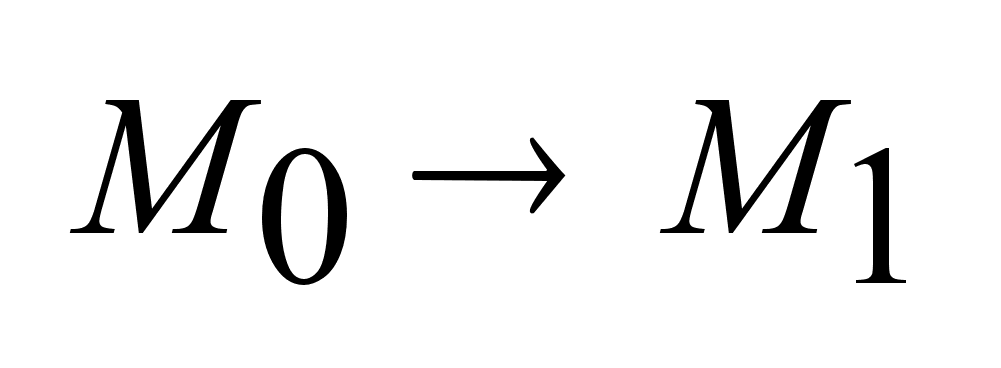 за время
за время
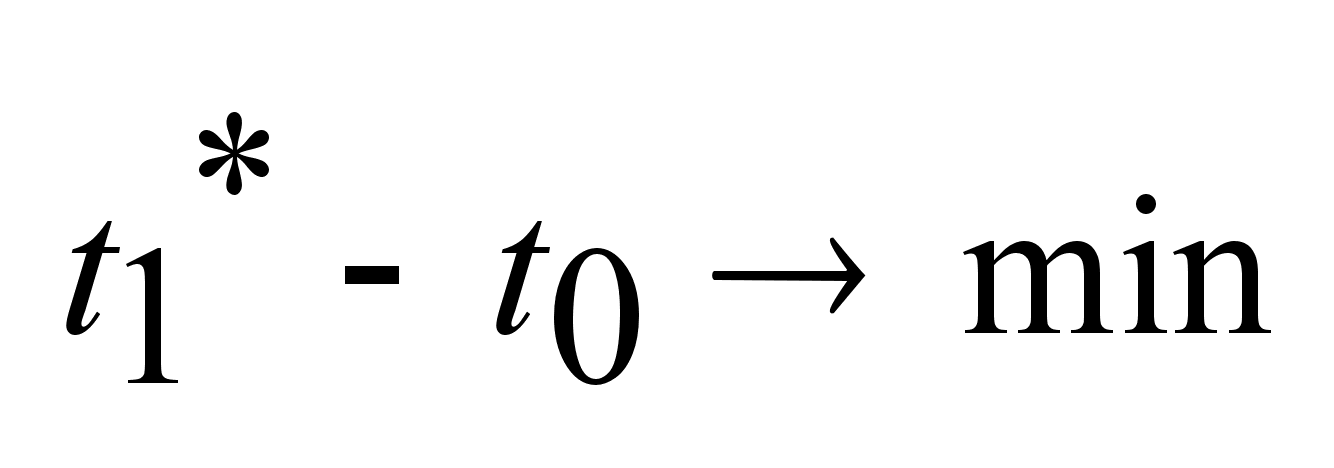 -
оптимально
управляем. -
оптимально
управляем.
Рассмотрим
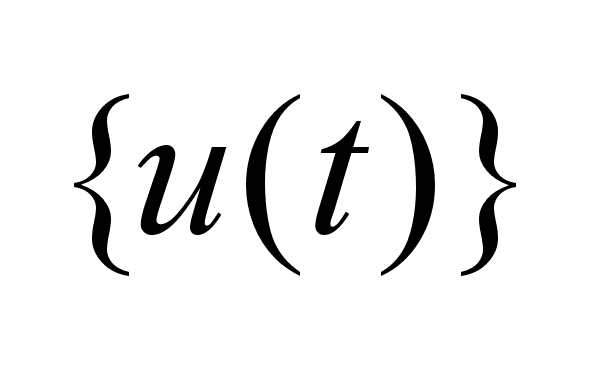 -множество всех
допустимых
управлений,
переводящих
объект из
-множество всех
допустимых
управлений,
переводящих
объект из
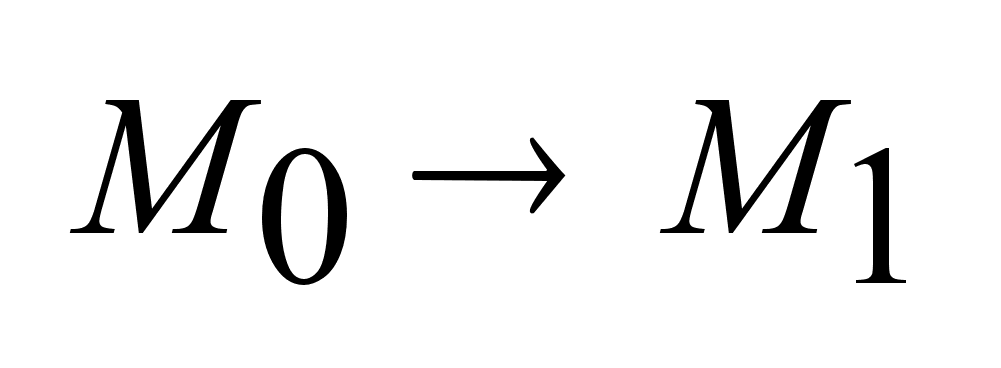 .
Т.к. объект является
управляемым
, то .
Т.к. объект является
управляемым
, то
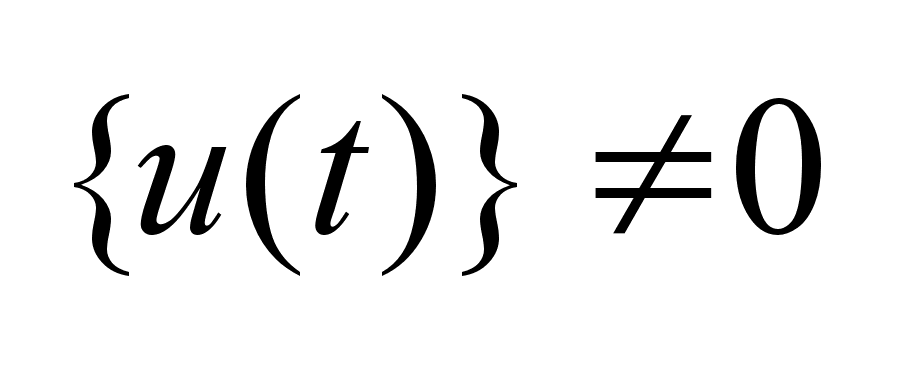 .
Обозначим через .
Обозначим через
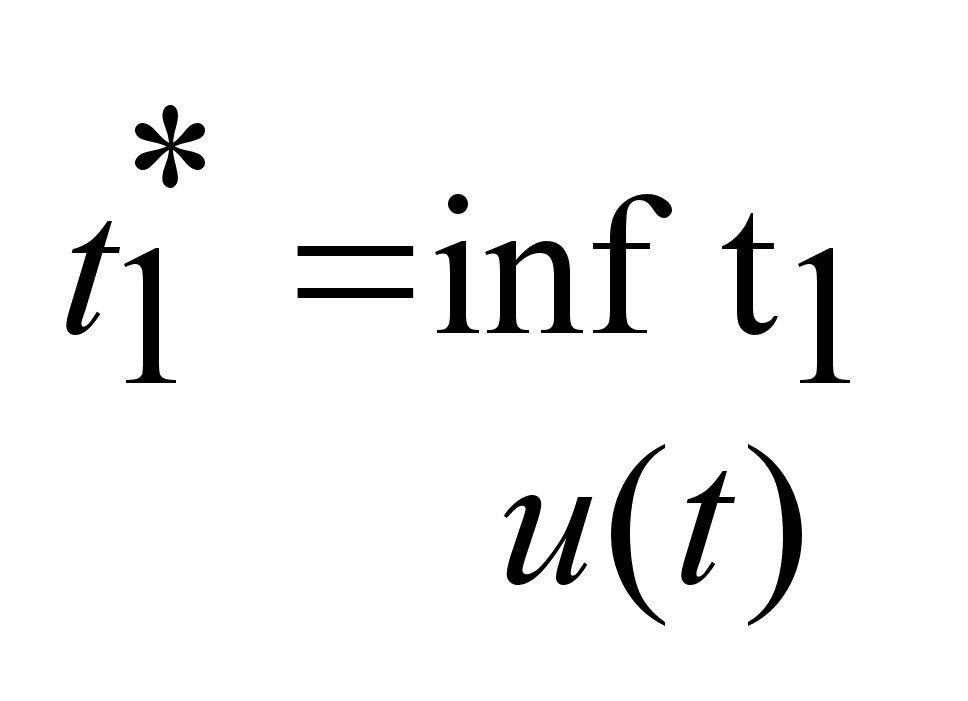 попадания
фазового вектора попадания
фазового вектора
 на
множестве на
множестве
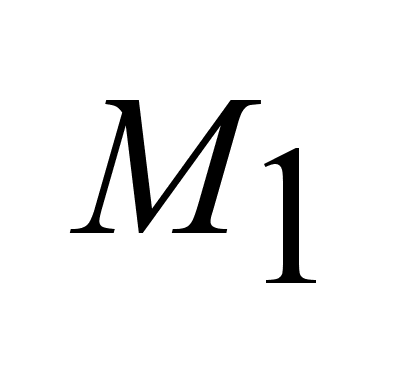 ,
т.е. ,
т.е.
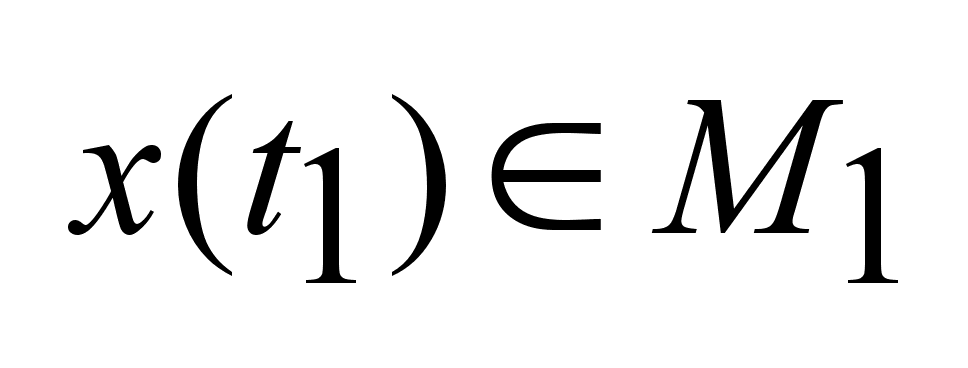 .
Следовательно
за меньшее .
Следовательно
за меньшее
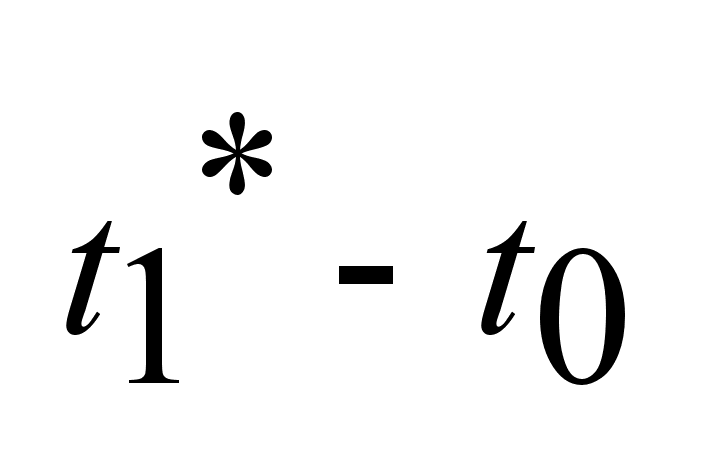 невозможно
перейти. невозможно
перейти.
Докажем,
что
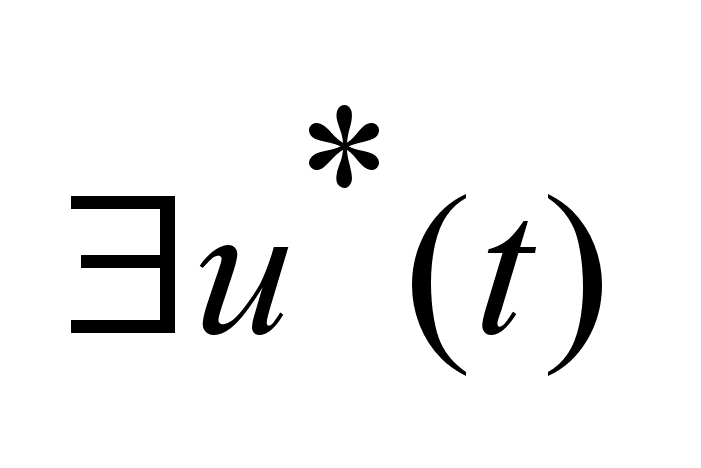 ,
переводящее
объект из ,
переводящее
объект из
 за за
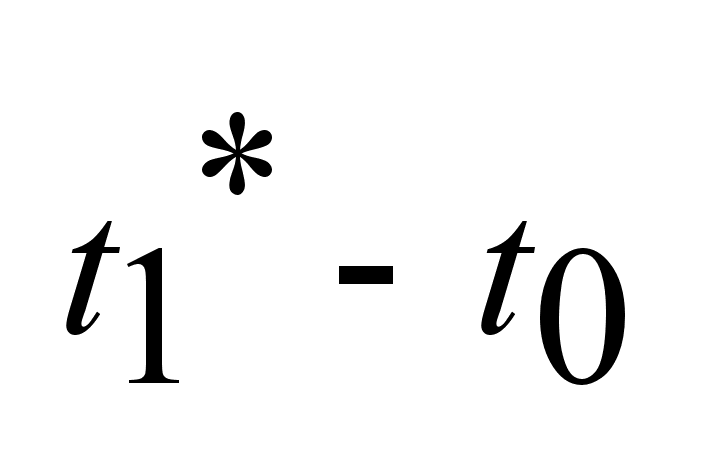 ,
при этом ,
при этом
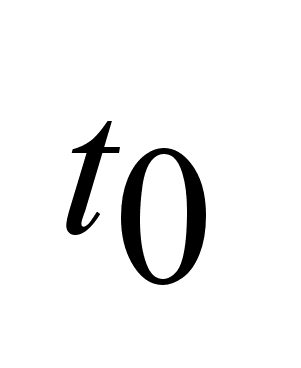 считается
фиксированым.
Т.к. считается
фиксированым.
Т.к.
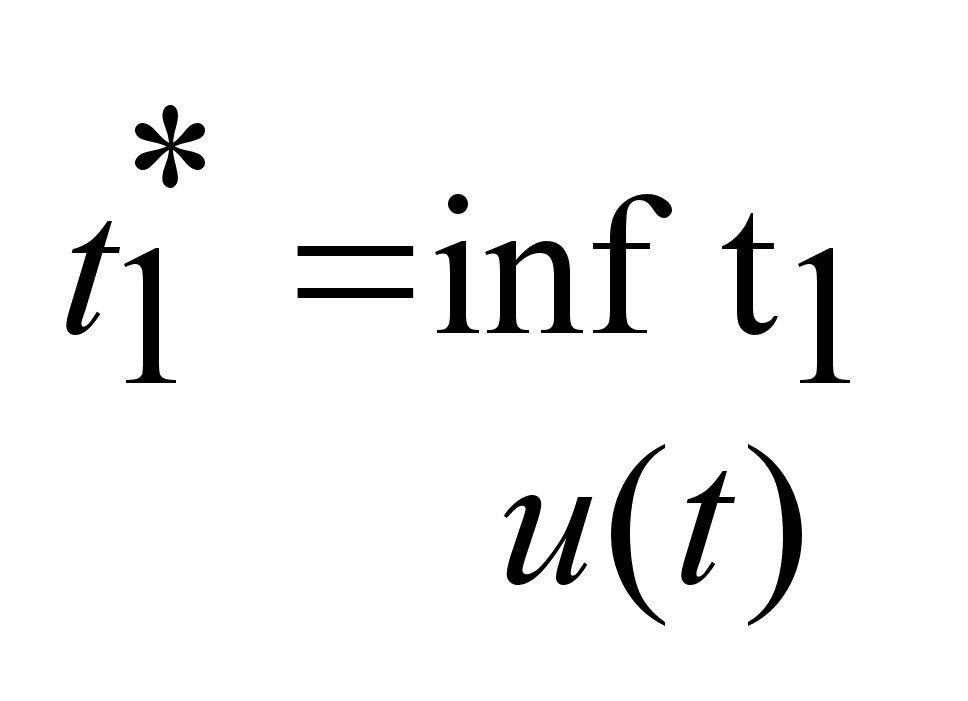 ,
то ,
то
 последовательность последовательность
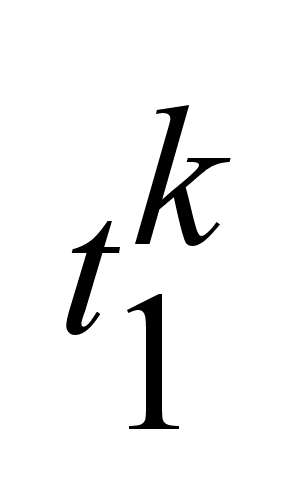 перехода,
сходящаяся
к перехода,
сходящаяся
к
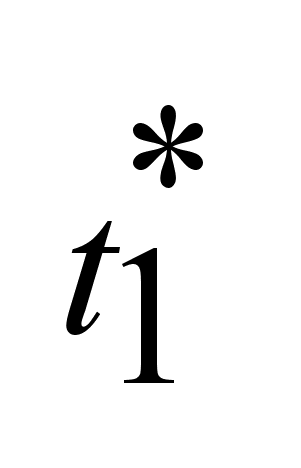 . .
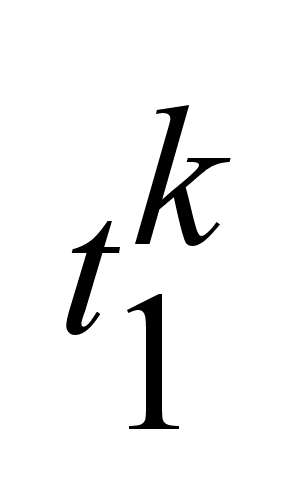 удовлетворяет
мн-во достижимости
удовлетворяет
мн-во достижимости
 (пустое
мн-во). Пусть
для (пустое
мн-во). Пусть
для
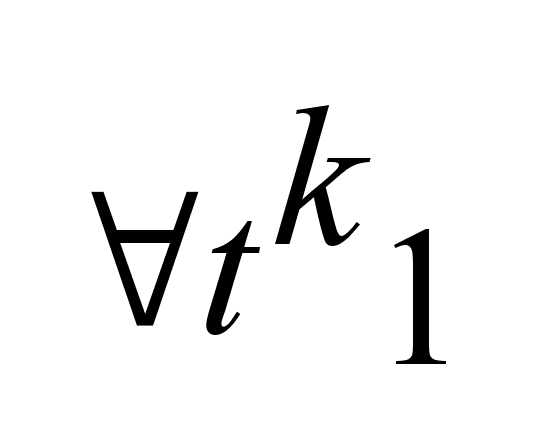 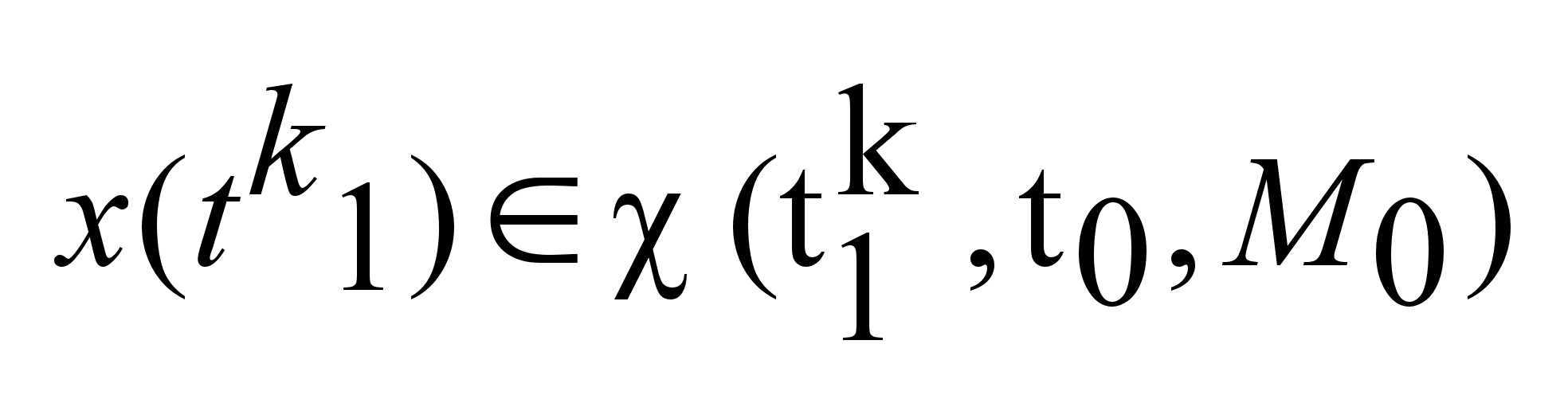 .
Т.к. множество .
Т.к. множество
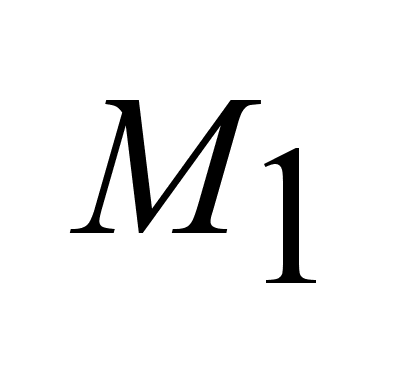 замкнуто
и ограничено,
то из замкнуто
и ограничено,
то из
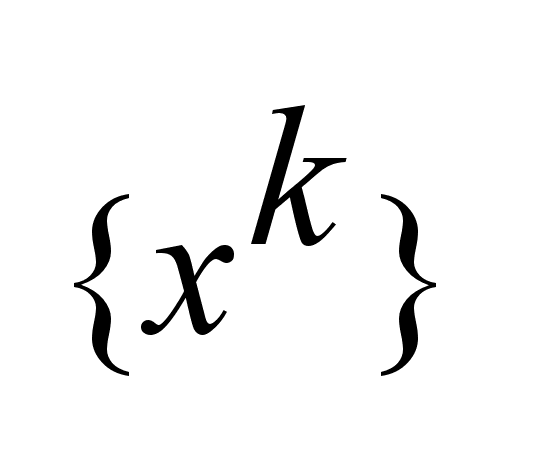 можно
выбрать
подпоследовательность можно
выбрать
подпоследовательность
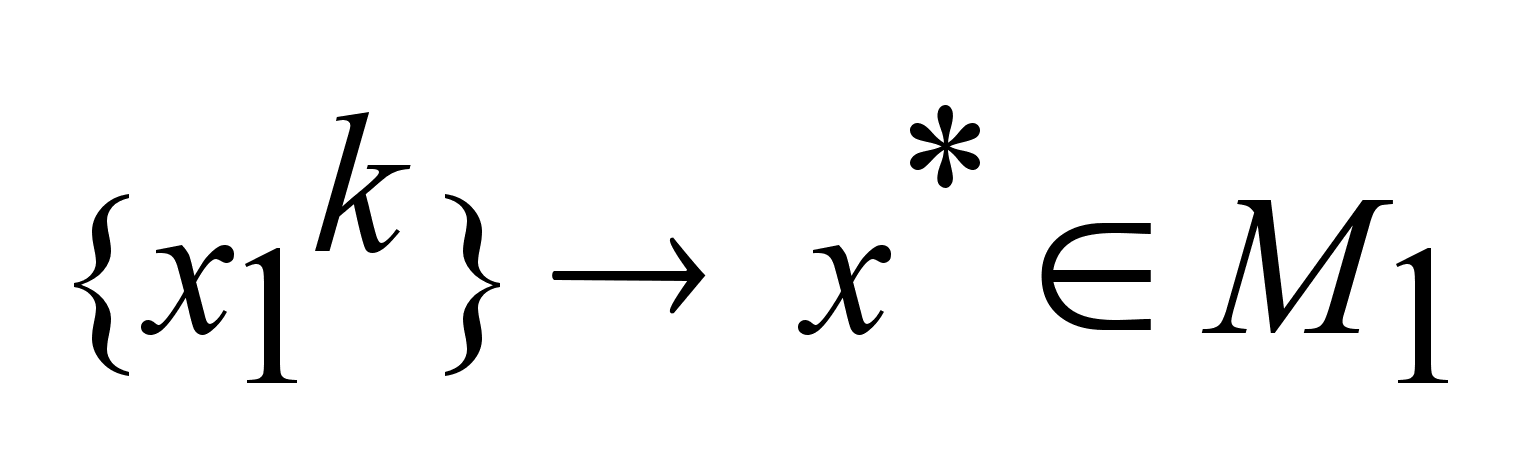 . .
Пусть
дано
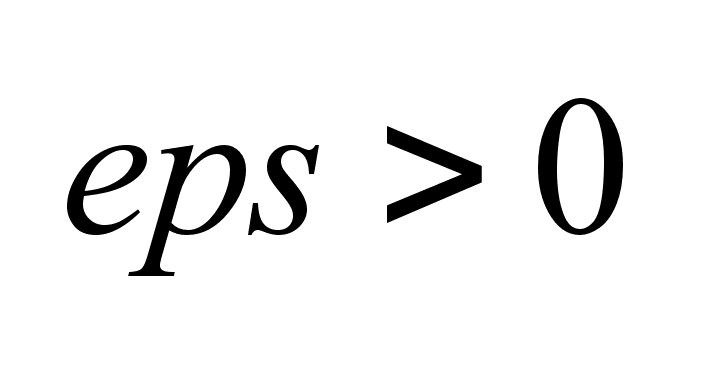 .
Т.к. .
Т.к.
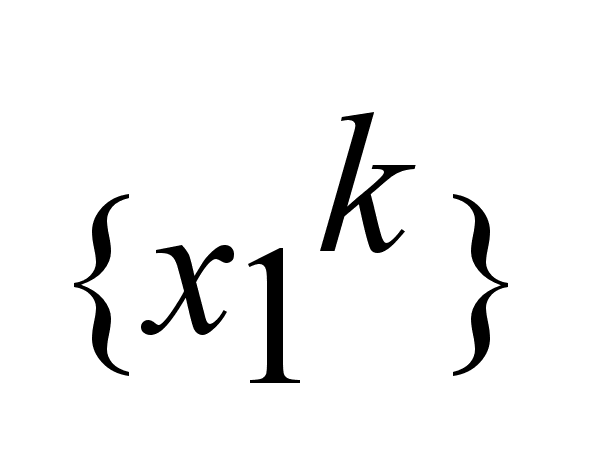 сходящаяся
к сходящаяся
к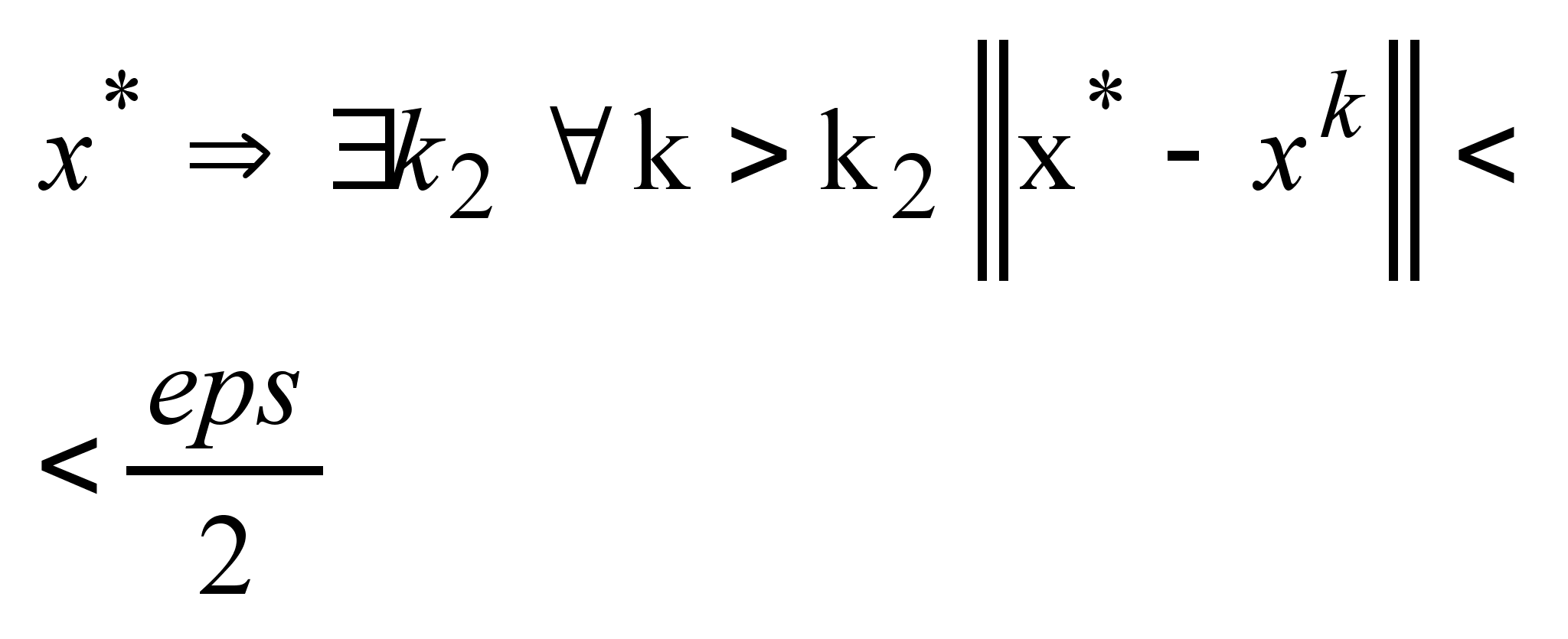 . .
Т.о.
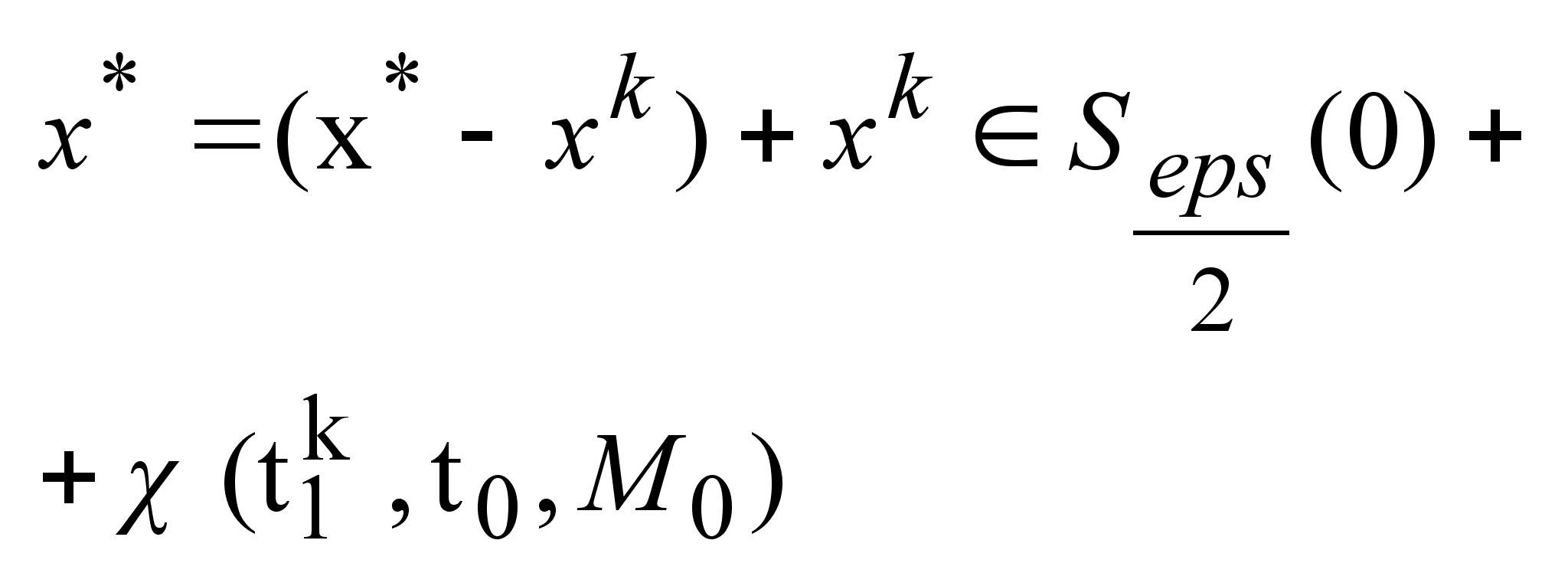 .
Множество .
Множество
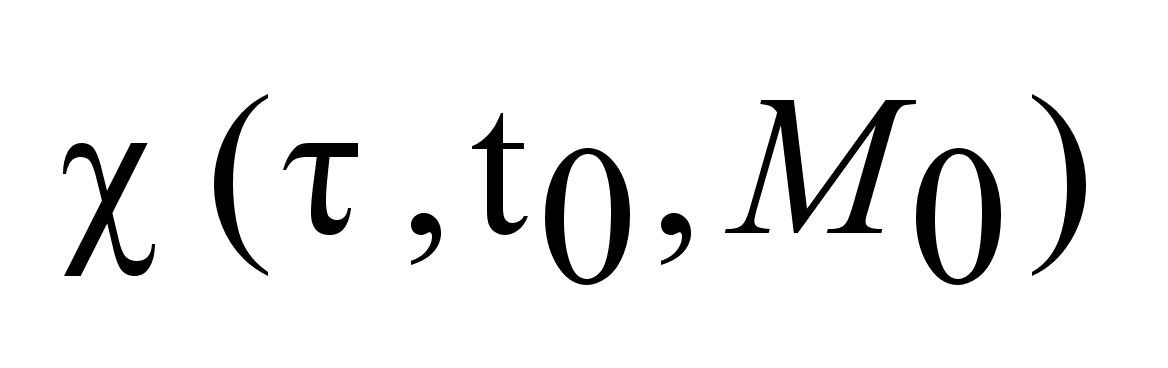 непрерывно
по аргументу непрерывно
по аргументу
 ,
т.е. начиная с
какого-то номера ,
т.е. начиная с
какого-то номера
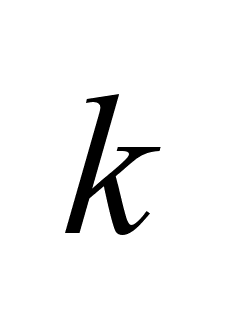
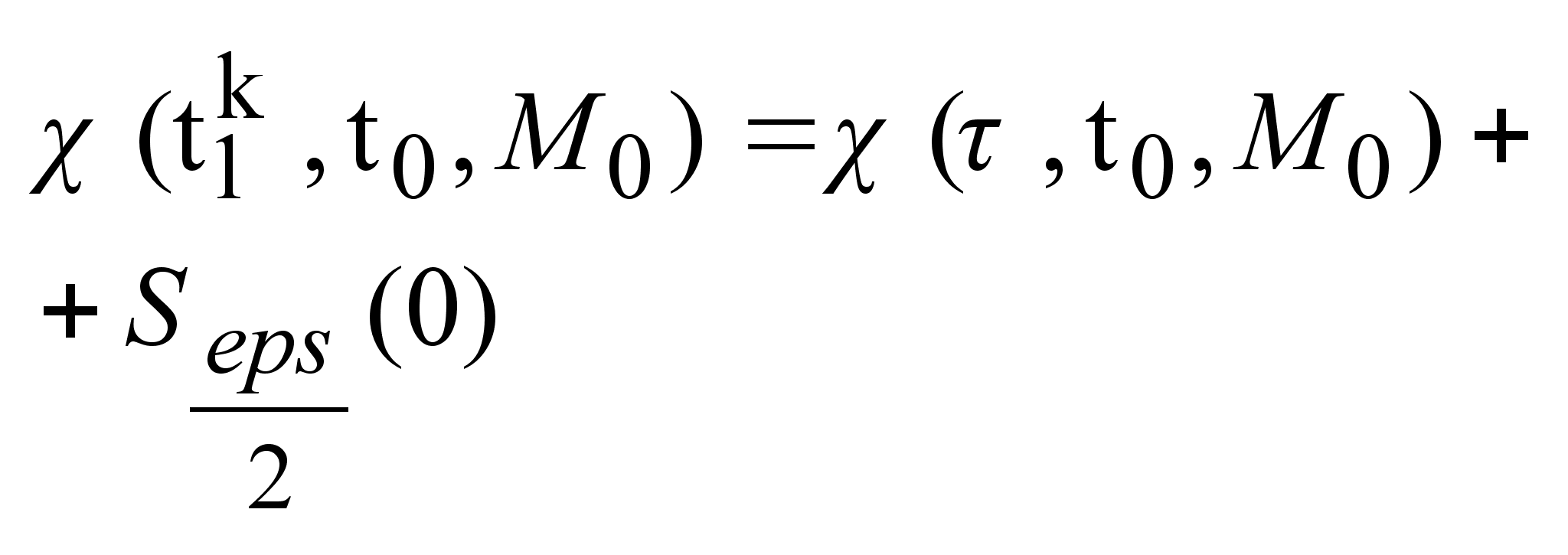 . .
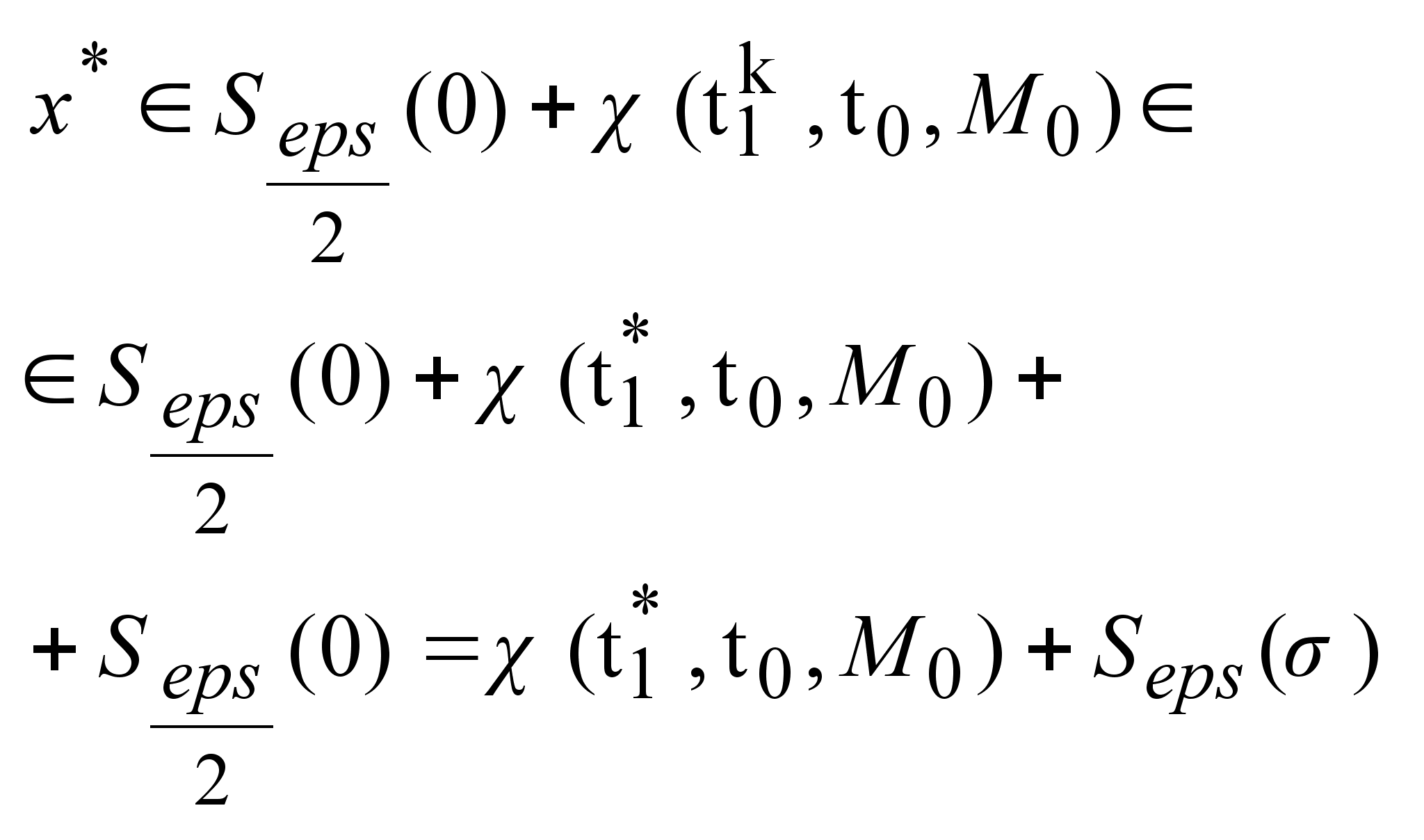 .
Т.к. .
Т.к.
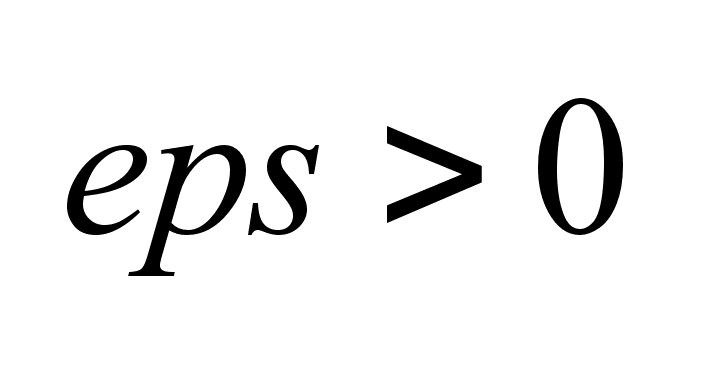 произвольная,
а мн-во
произвольная,
а мн-во
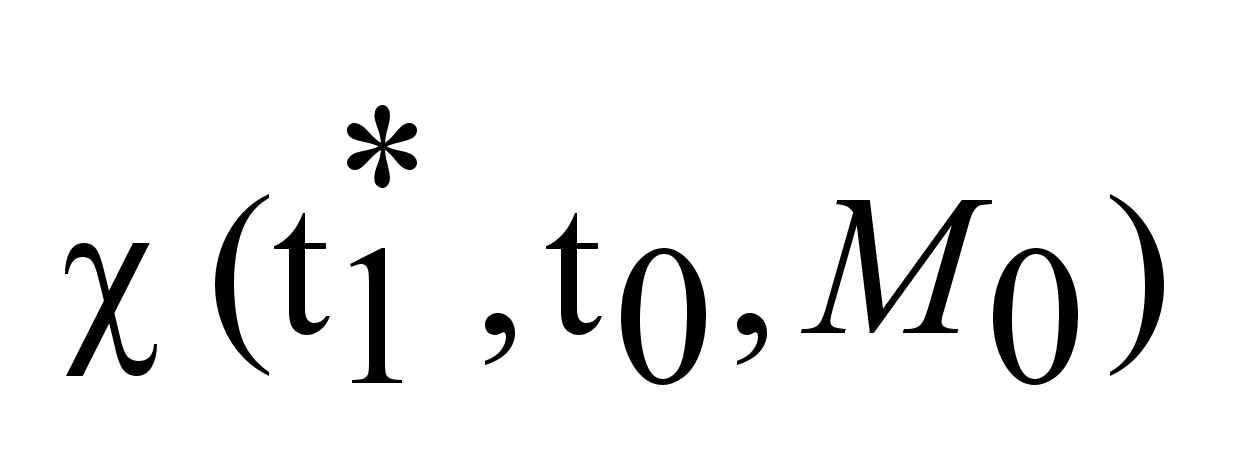 компактно,
то компактно,
то
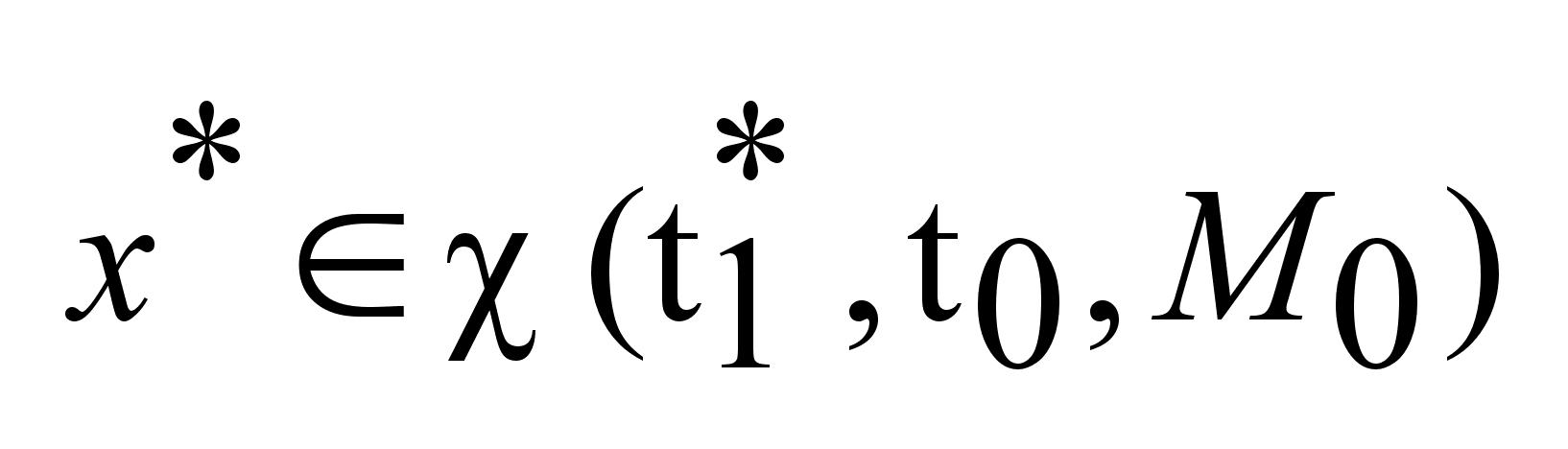 .
Т.к. .
Т.к.
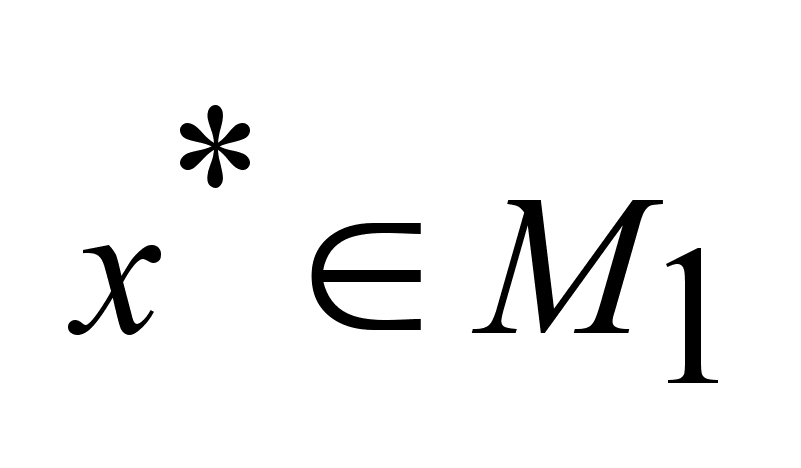 и и
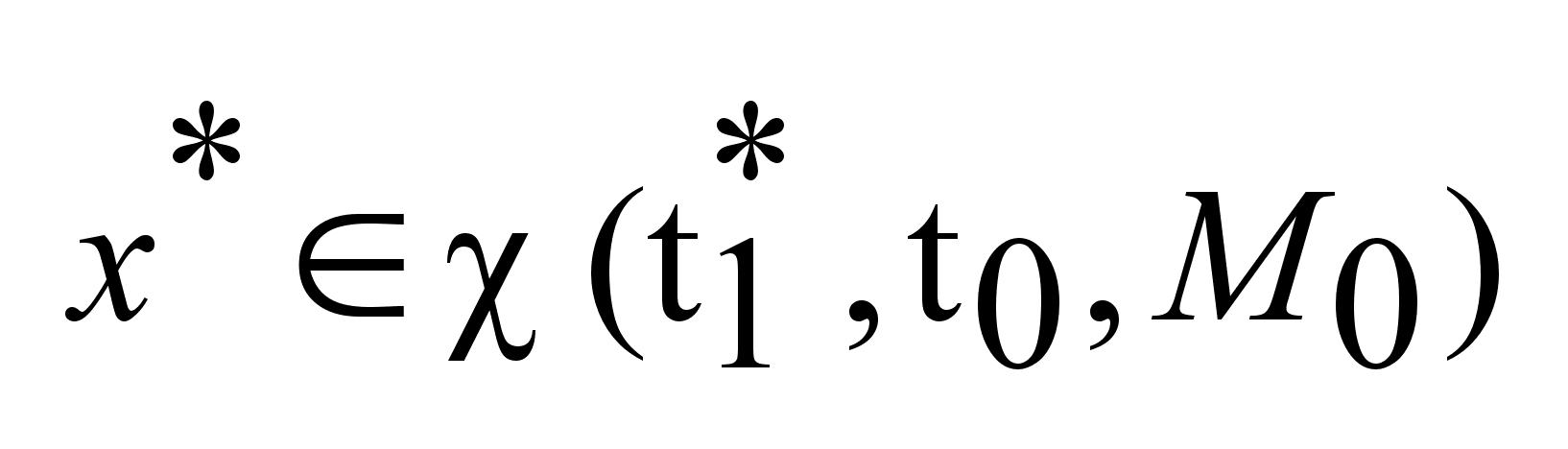 ,
то это обозначает,
что ,
то это обозначает,
что
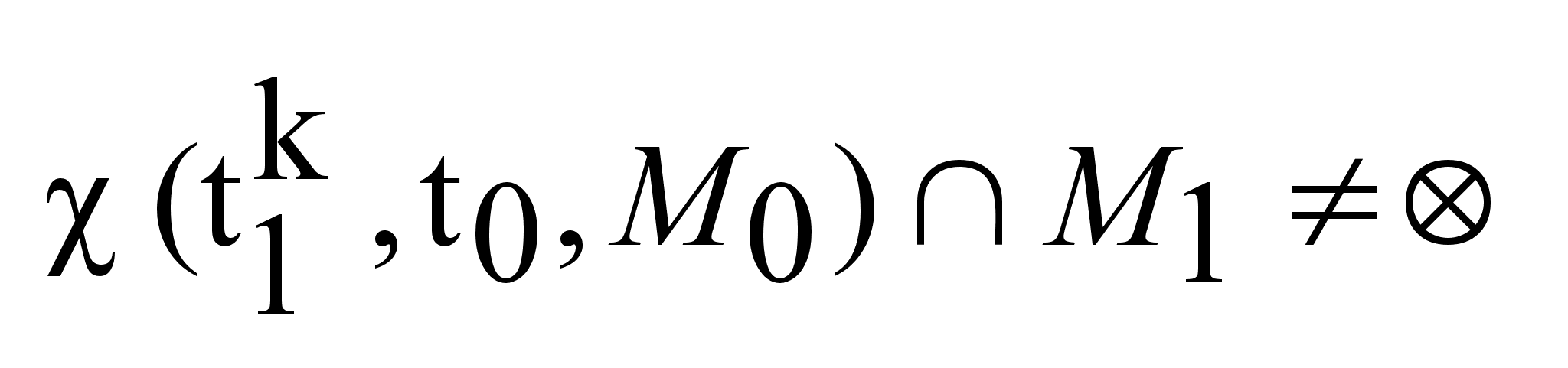 (пустое мн-во)
и это означает,
что
(пустое мн-во)
и это означает,
что
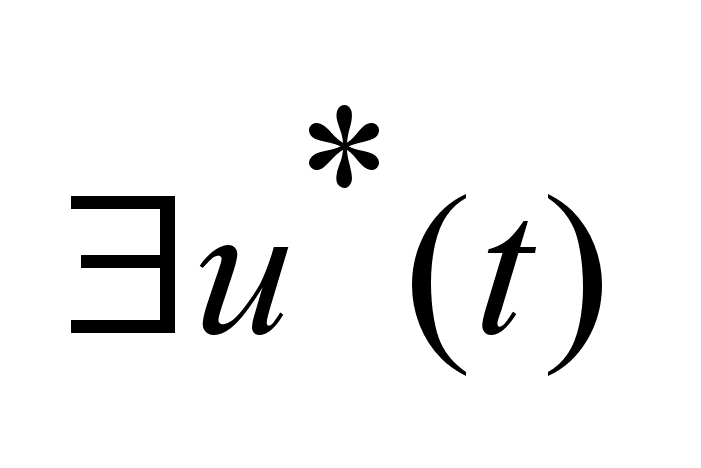 ,
переводящее
объект из ,
переводящее
объект из
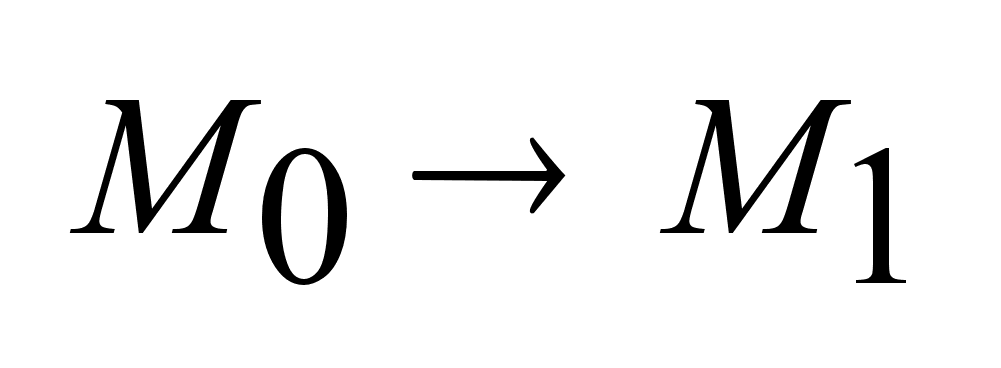 за за
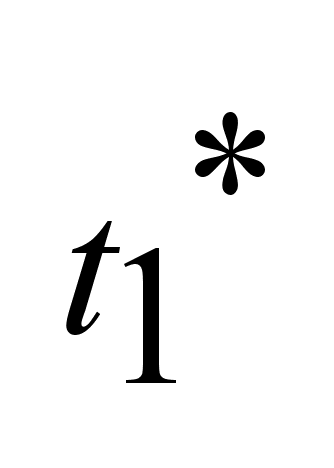 .
И т.к. .
И т.к.
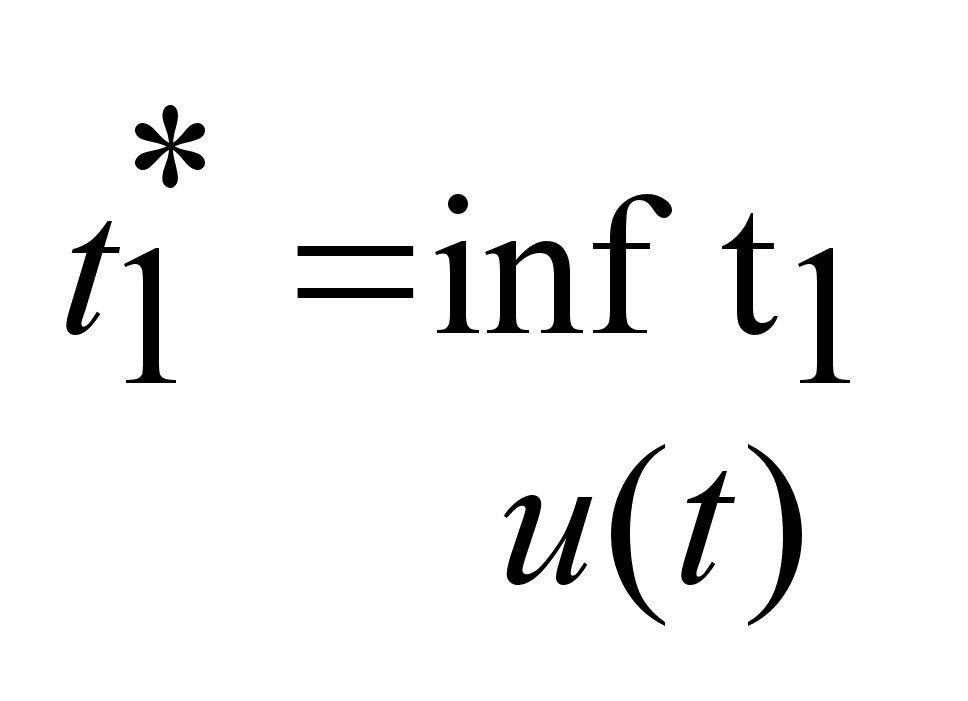 ,
то ,
то
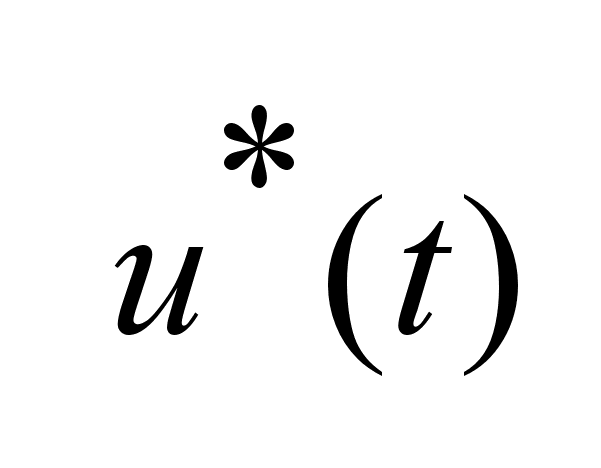 -
оптимальное
управление.
Теорема док-на. -
оптимальное
управление.
Теорема док-на.
22.
Принцип максимума
Понтрягина
на языке опорных
функций.
Рассматриваем
динамический
объект, поведение
которого описывается
системой (1)
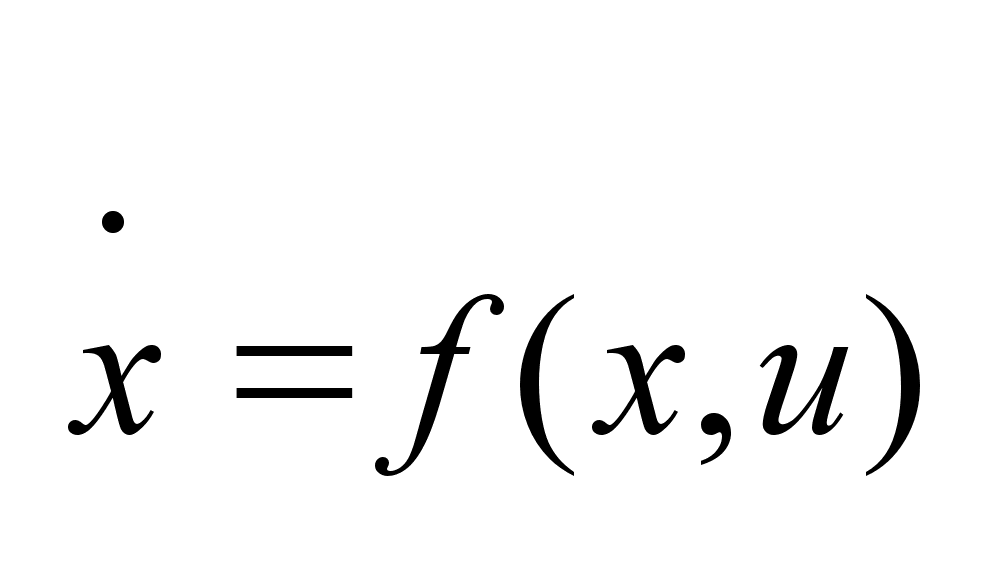 ,
x-
n-мерный
вектор, ,
x-
n-мерный
вектор,
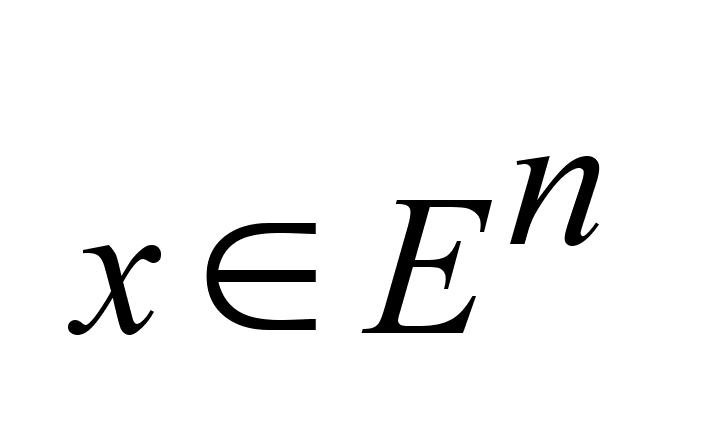 , ,
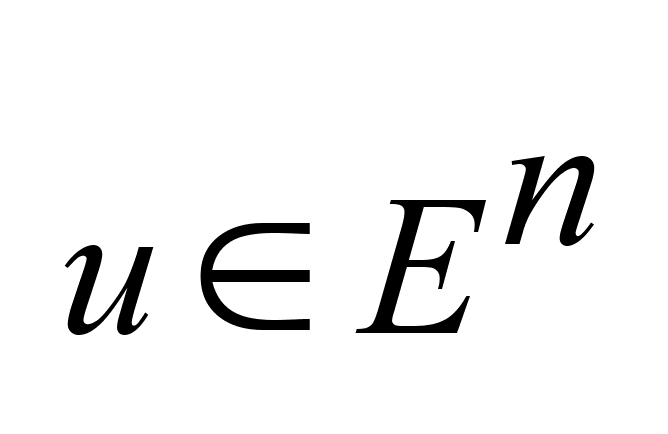 .Задано .Задано
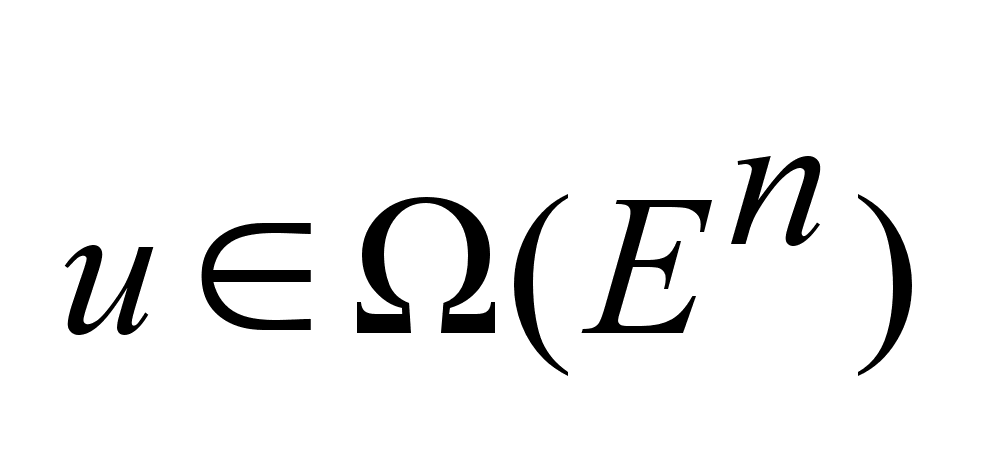 ,
u:
I ,
u:
I 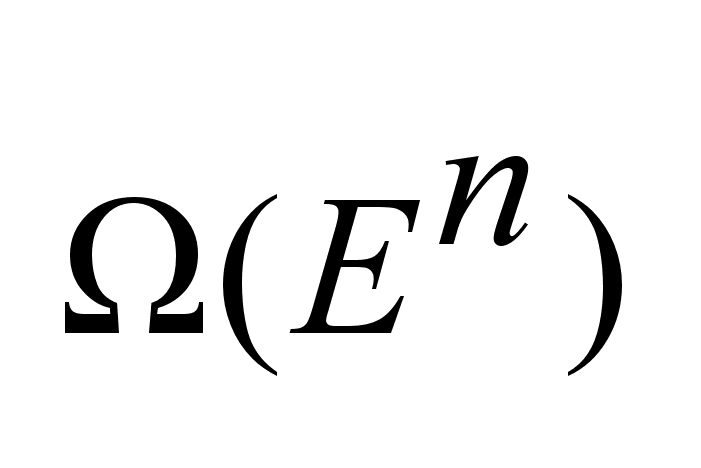 и полагается,
что u(t)
измеримо
и
и полагается,
что u(t)
измеримо
и
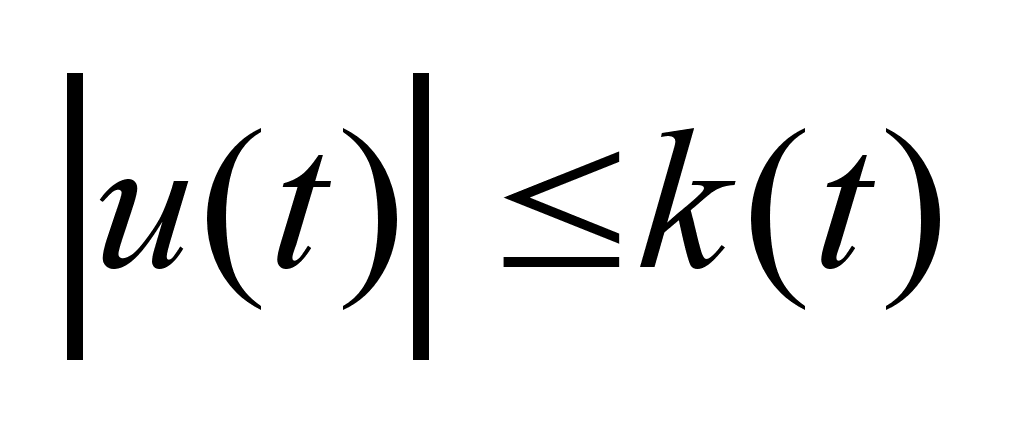 -
где
k(t)
скалярная
функция интегрируемая
по Лебегу на
отрезке I .
В фазовом
пространстве -
где
k(t)
скалярная
функция интегрируемая
по Лебегу на
отрезке I .
В фазовом
пространстве
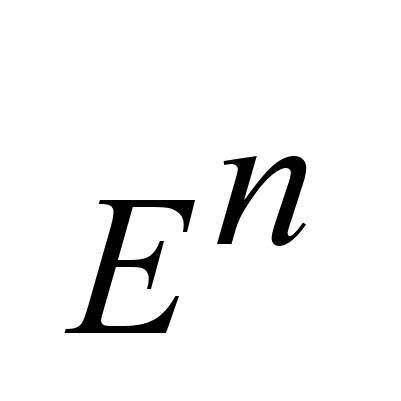 заданы
два не пустых
множества заданы
два не пустых
множества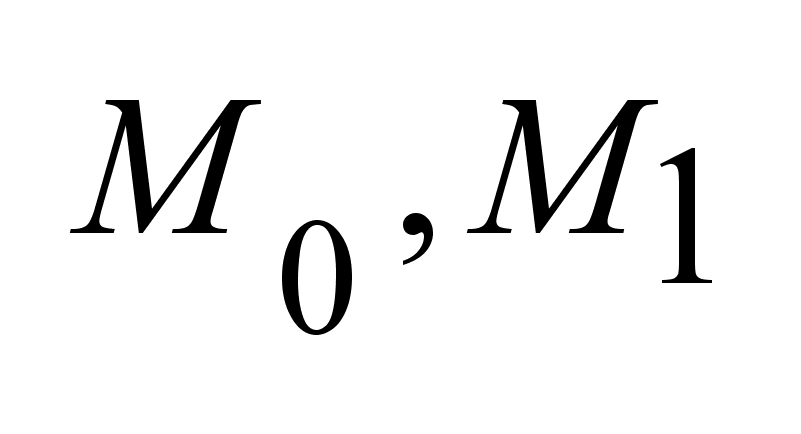 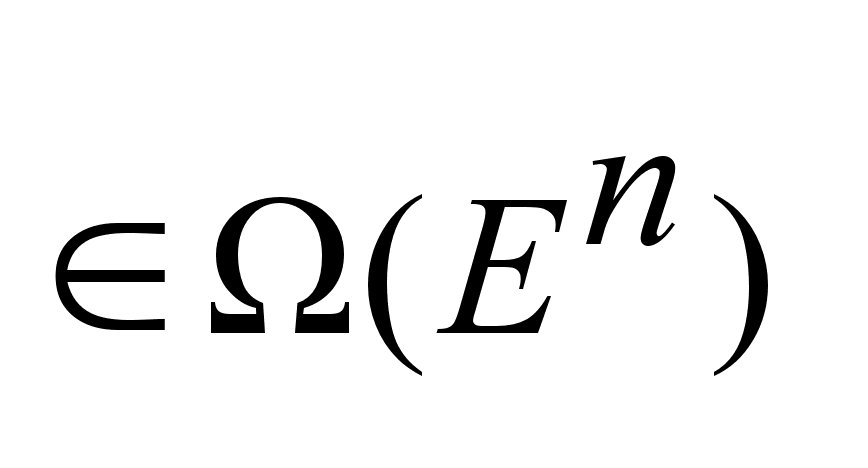 .
Допустимое
управление
u(t)
на отр.I
осуществляете
переход из
начального
мн-ва .
Допустимое
управление
u(t)
на отр.I
осуществляете
переход из
начального
мн-ва
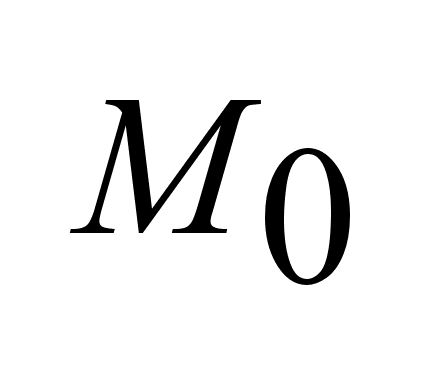 в конечное
множество
в конечное
множество
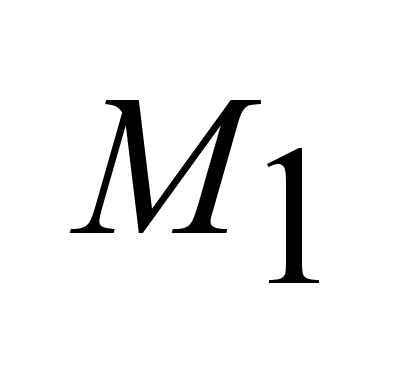 ,
если существует
решение уравнения
(1), удовлетворяющее
граничным
условиям ,
если существует
решение уравнения
(1), удовлетворяющее
граничным
условиям
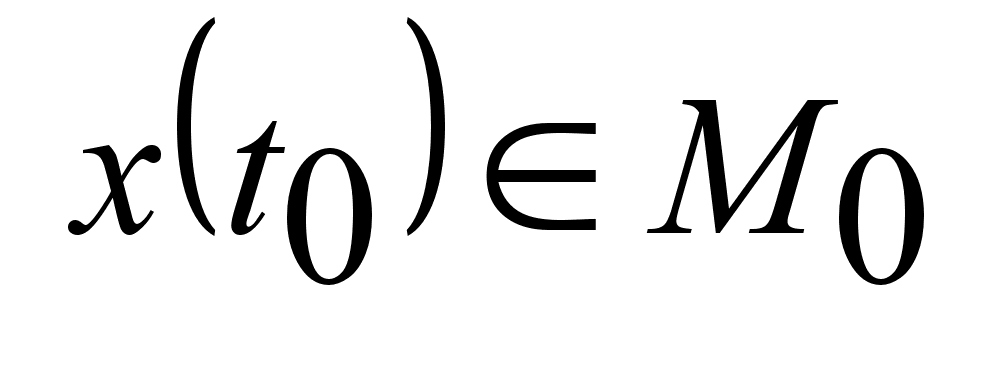 и и
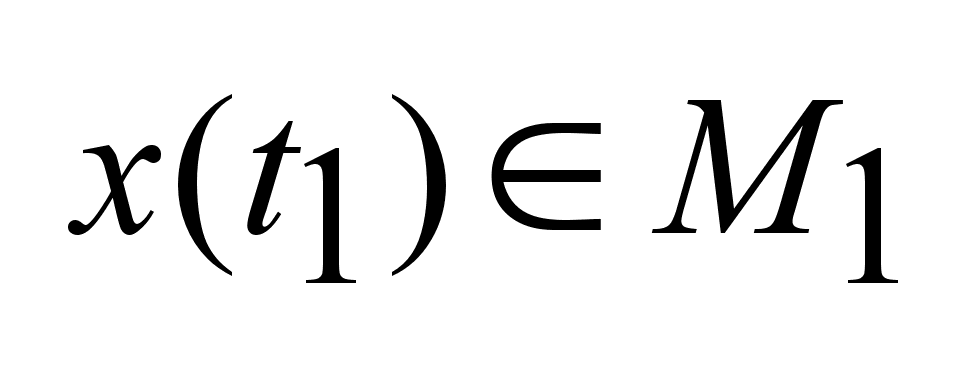 .
Цель управления-
перевод динамический
объекта из .
Цель управления-
перевод динамический
объекта из
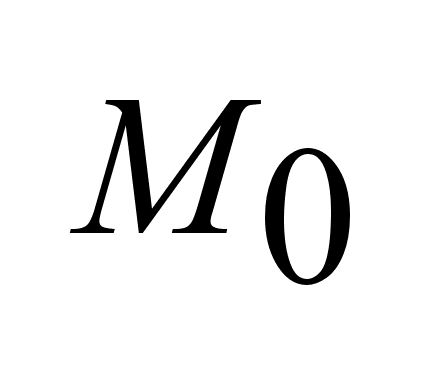 в в
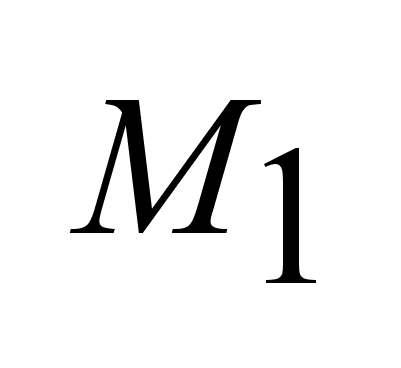 ,
а качество
определяет
функционал.
Таким функционалом
явл. время,
следовательно
задача быстродействия
заключается
в нахождении
такого допустимого
управления,
которое осуществляет
переход из
множества ,
а качество
определяет
функционал.
Таким функционалом
явл. время,
следовательно
задача быстродействия
заключается
в нахождении
такого допустимого
управления,
которое осуществляет
переход из
множества
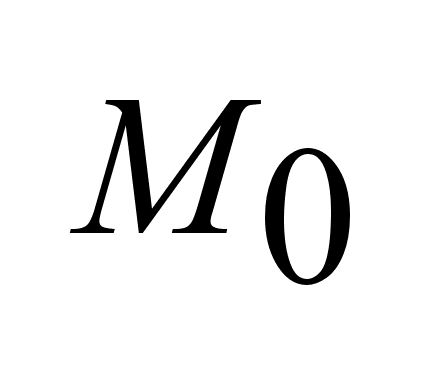 в в
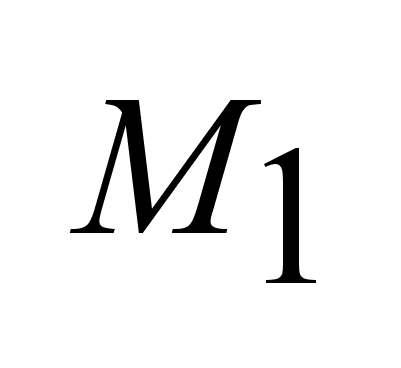 за
наименьшее
время. за
наименьшее
время.
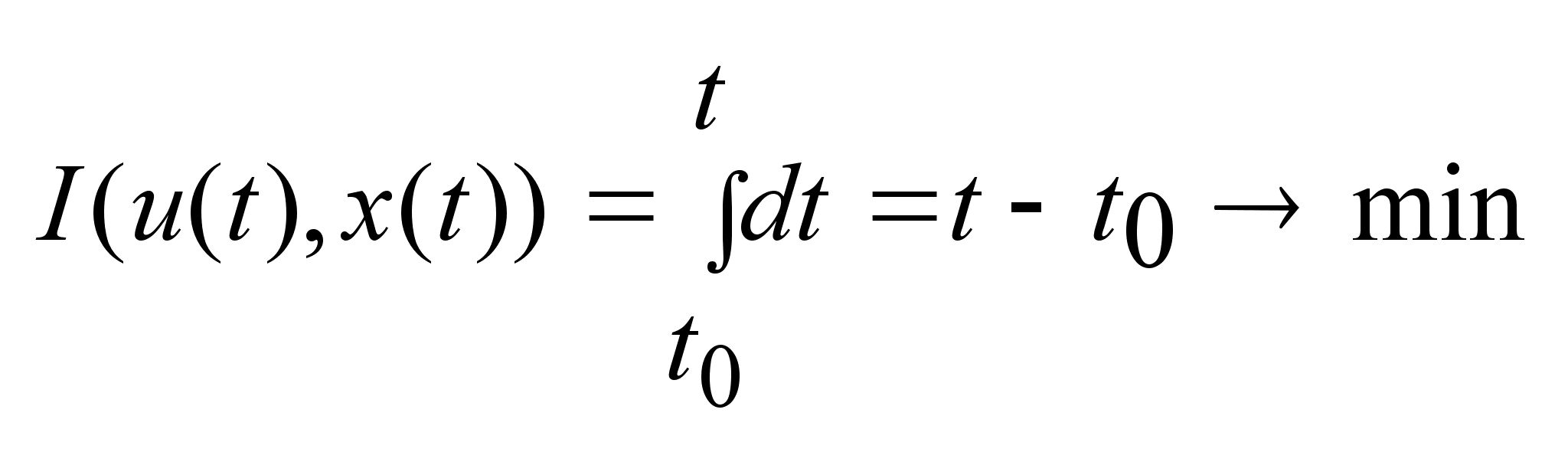 (4). (4).
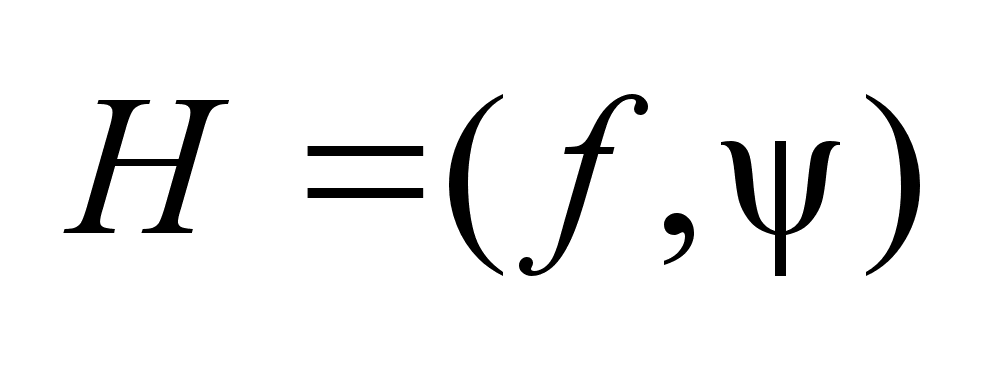 ,
где ,
где
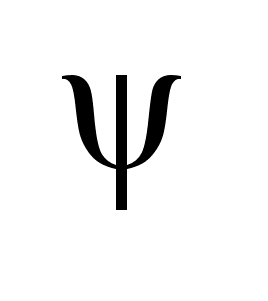 -ненулевая
вектор-функция. -ненулевая
вектор-функция.
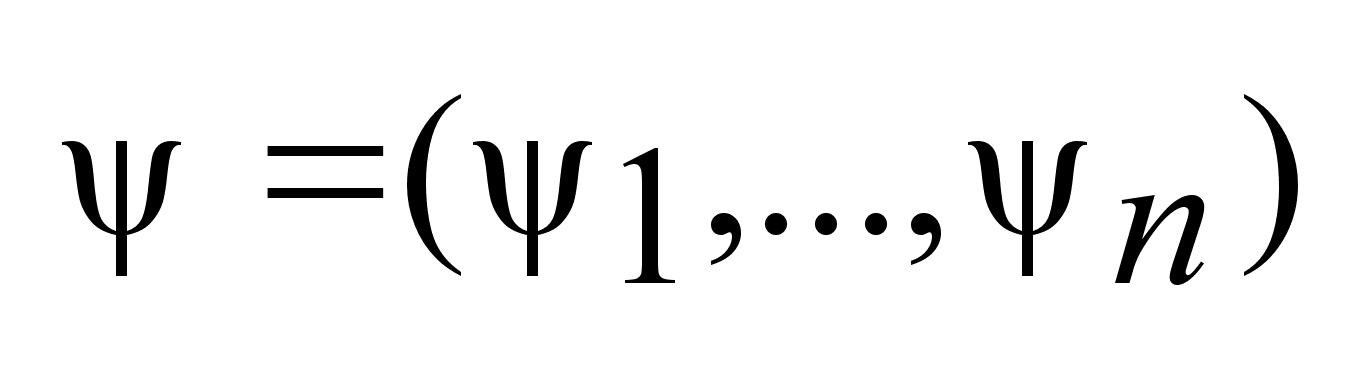 , ,
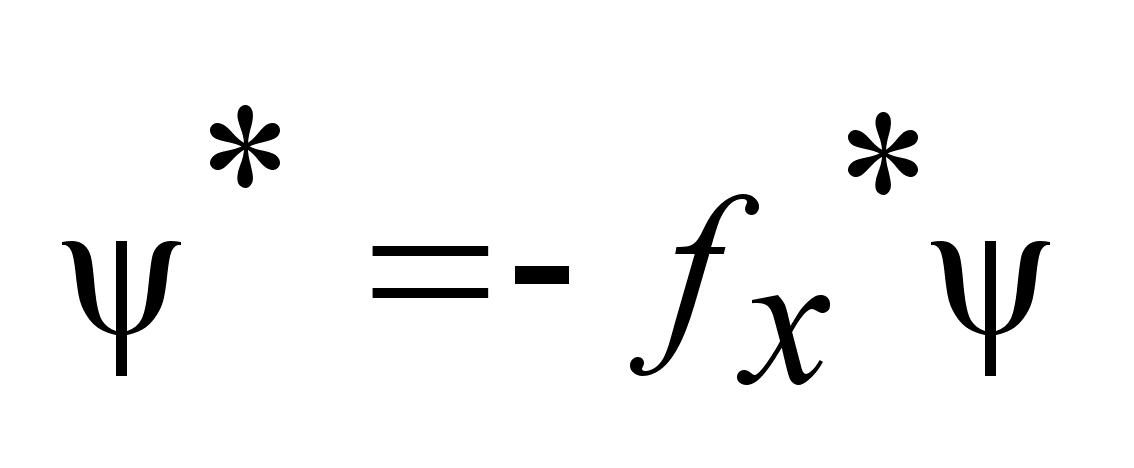 .
Если .
Если
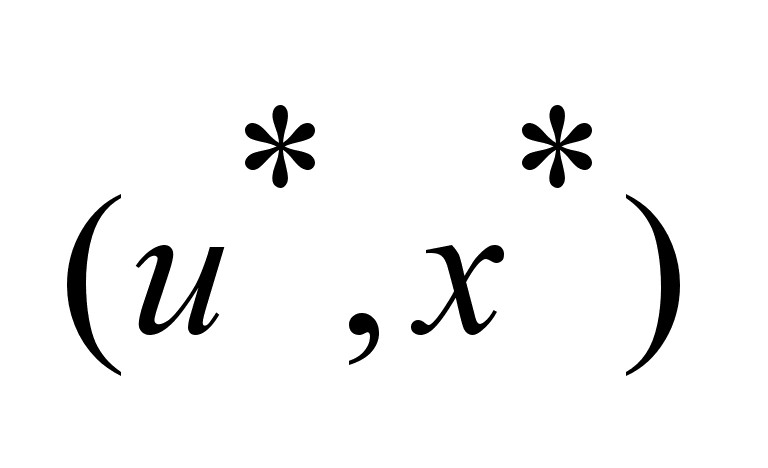 -оптимальное
управление,
переводящее -оптимальное
управление,
переводящее
 ,
то ,
то
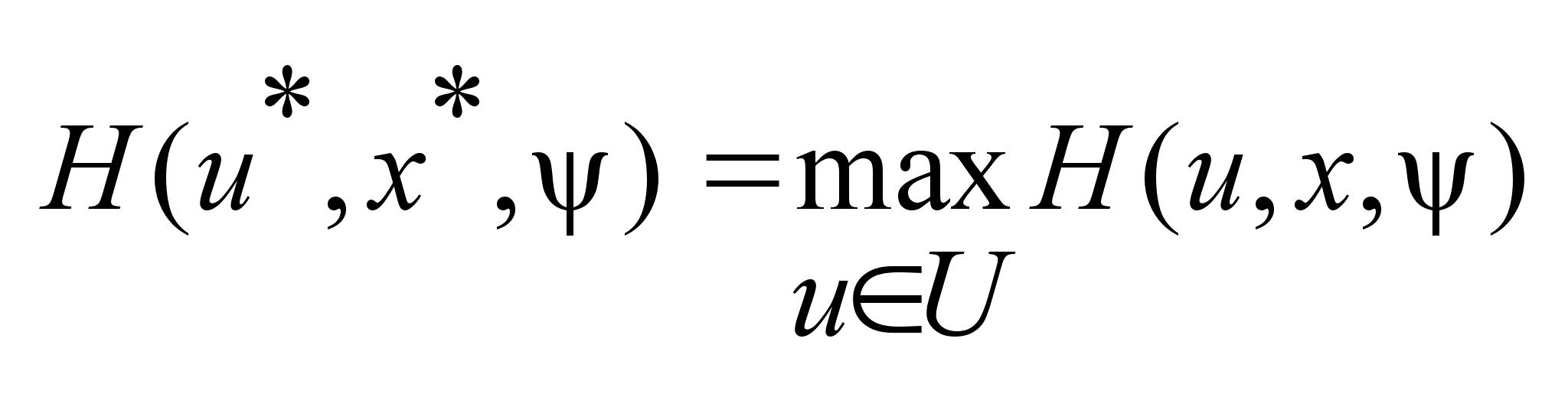 . .
Для
нашей задачи
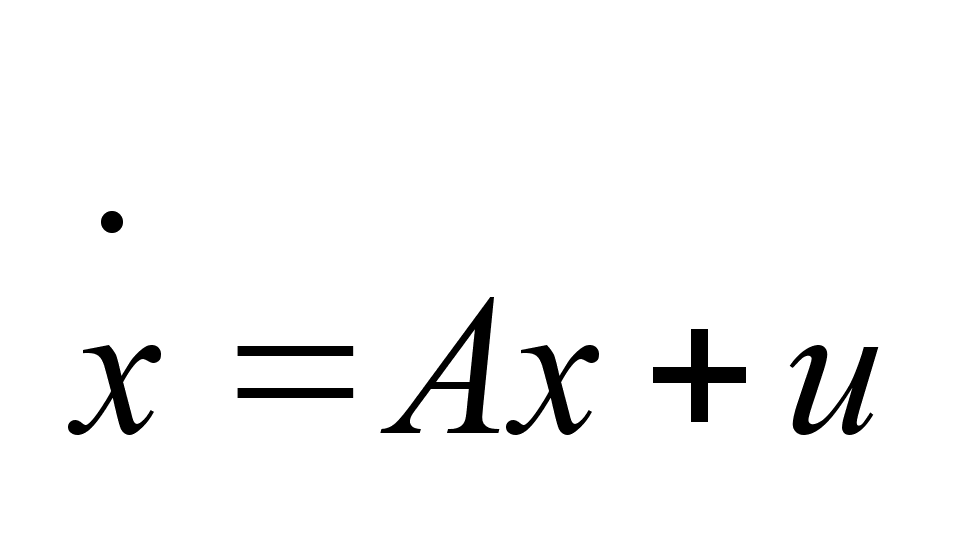 : :
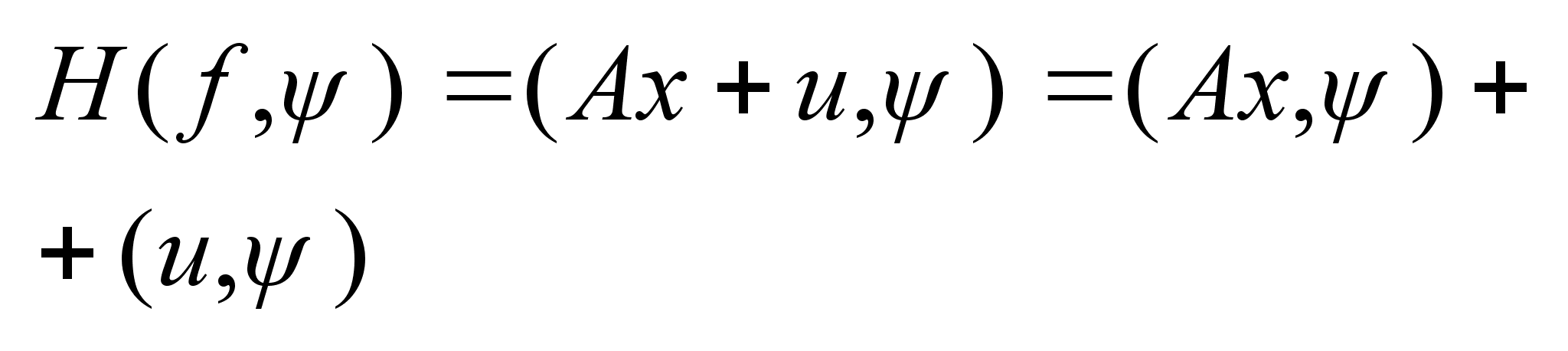 . .
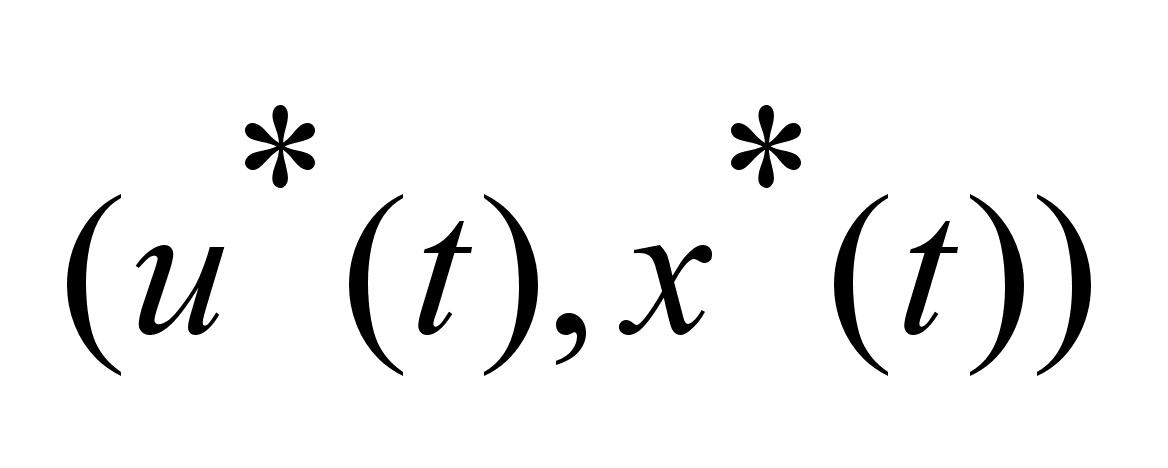 удовлетворяет
принципу максимума
Понтрягина
на удовлетворяет
принципу максимума
Понтрягина
на
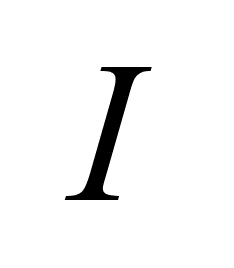 ,
если существует
не нулевая
вектор -функция. ,
если существует
не нулевая
вектор -функция.
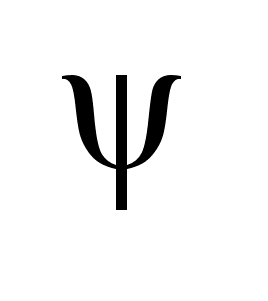 ,
удовлетворяющая
системе ,
удовлетворяющая
системе
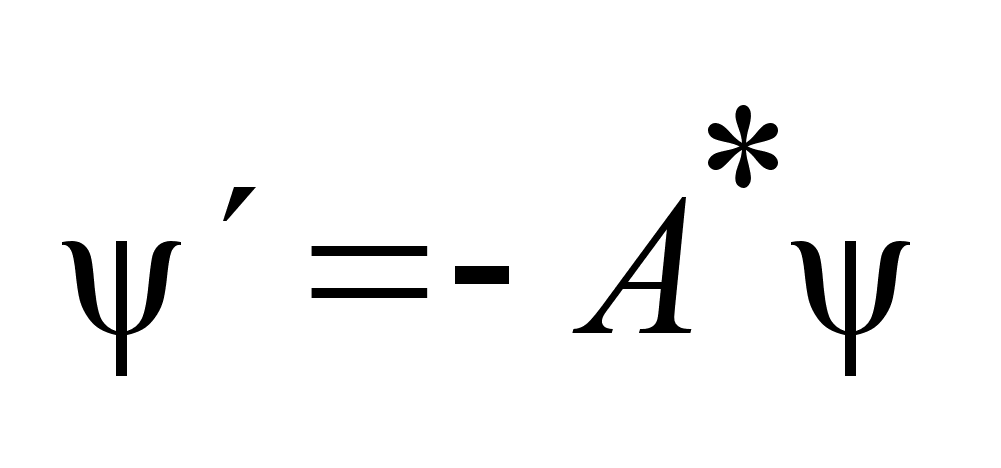 с
нач. условием с
нач. условием
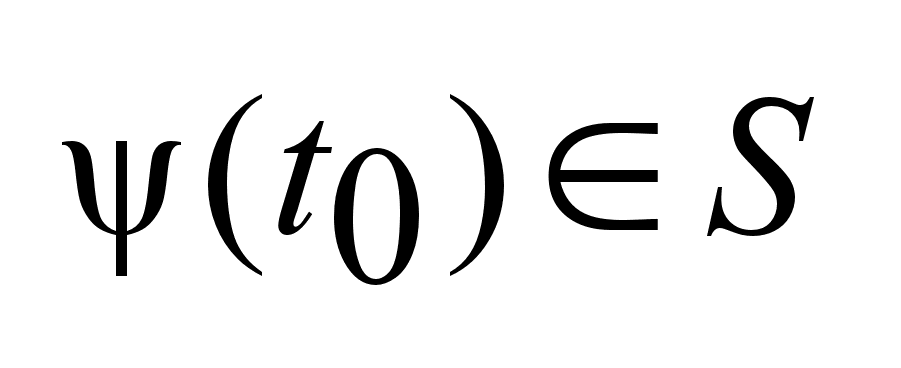 ,
такая что выполняется
условие: ,
такая что выполняется
условие:
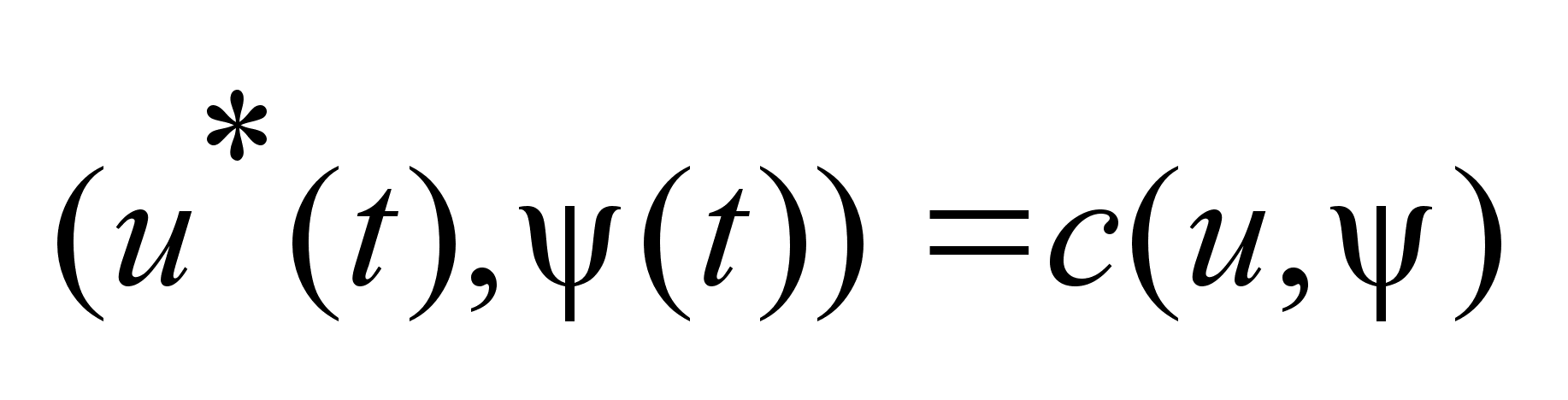 -здесь
достигается
максимум. -здесь
достигается
максимум.
2)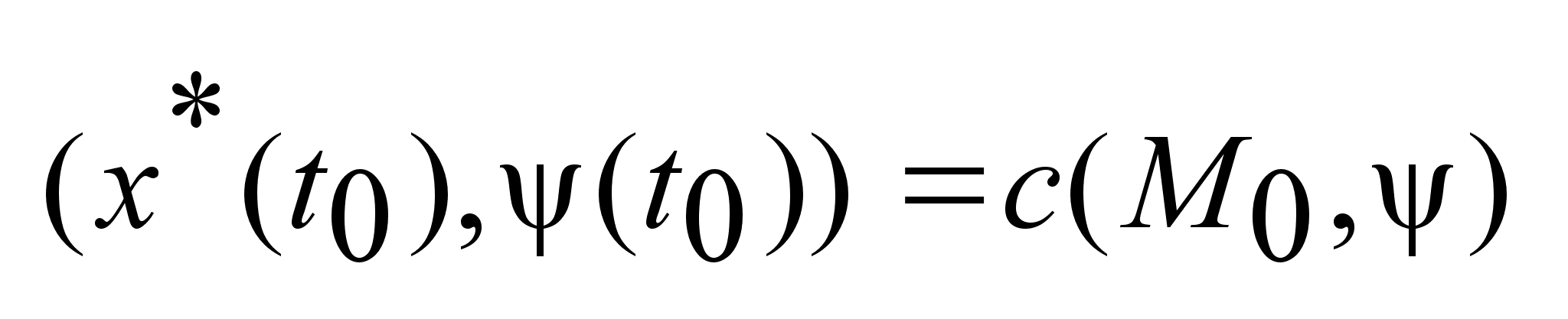 ; ;
3)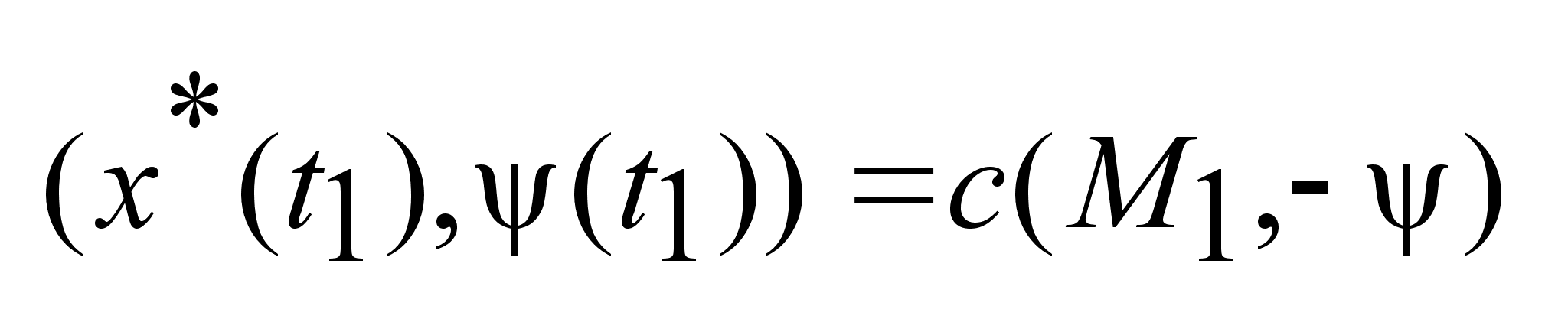 . .
Теорема
о необходимых
условиях
оптимальности.
Если в линейной
задаче быстродействия
мн-ва
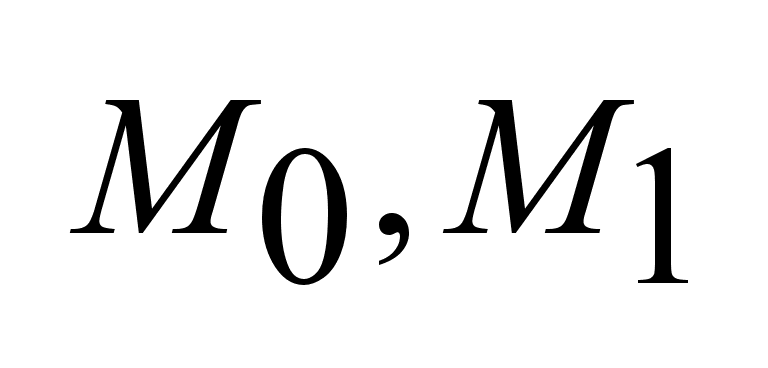 выпуклы, выпуклы,
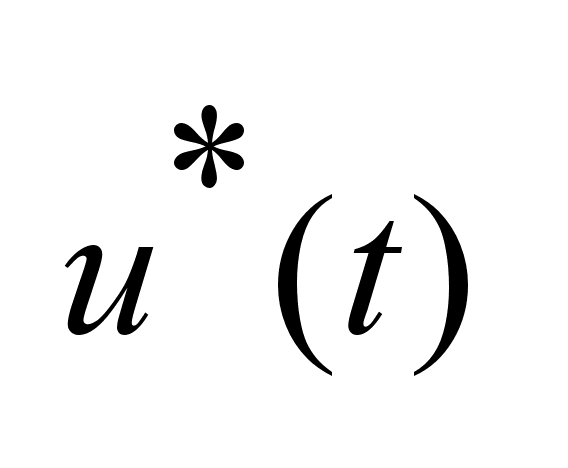 -оптимальное
управление,
переводящее -оптимальное
управление,
переводящее
 на
отр. на
отр.
 ,
а ,
а
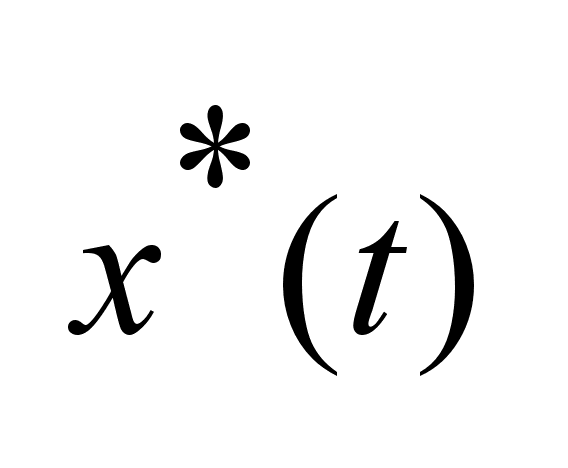 -соответствующая
траектория,
то пара -соответствующая
траектория,
то пара
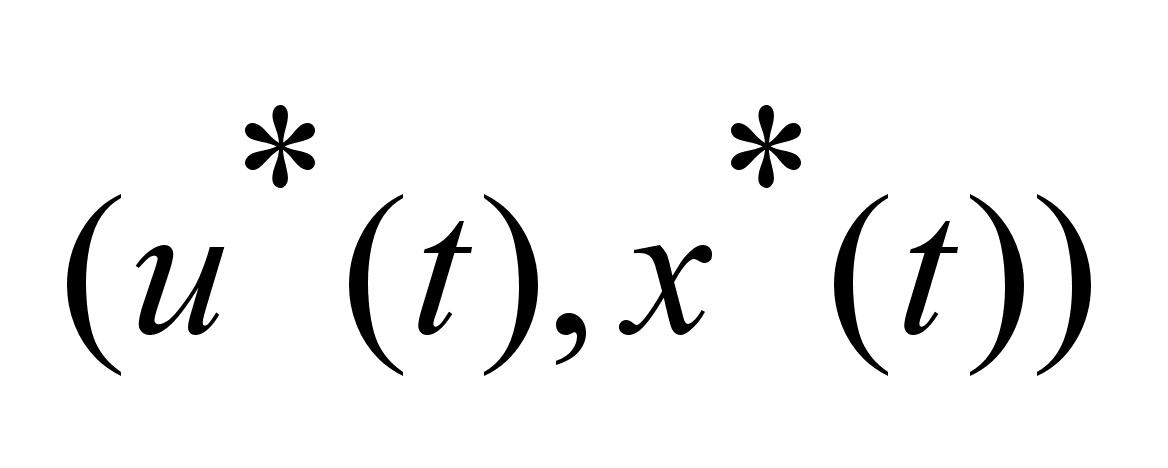 удовлетворяет
принципу максимума
Понтрягина. удовлетворяет
принципу максимума
Понтрягина.
23.
Применение
необходимых
условий
оптимальности(схема
и пояснения
к ней).
Рассматриваем
динамический
объект, поведение
которого описывается
системой (1)
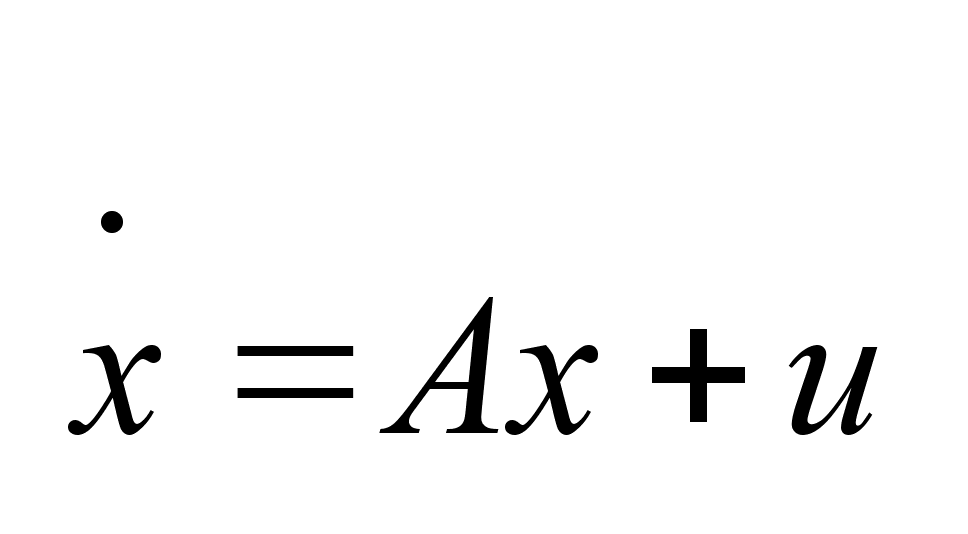 ,
x-
n-мерный
вектор, ,
x-
n-мерный
вектор,
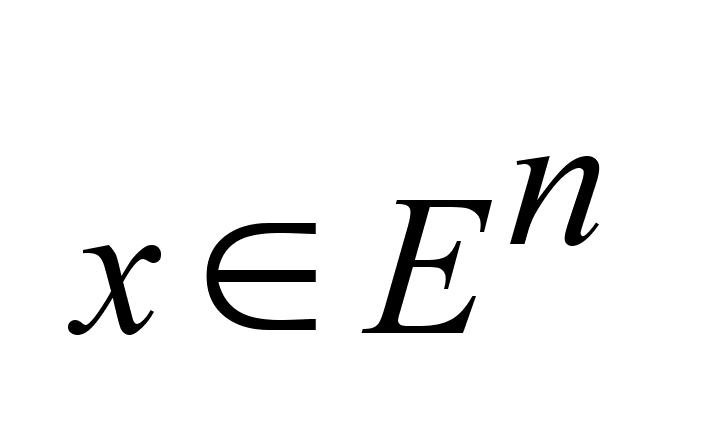 ,
A-матрица
nxn,
u
имеет ту же
размерность,
что
и ,
A-матрица
nxn,
u
имеет ту же
размерность,
что
и
 , ,
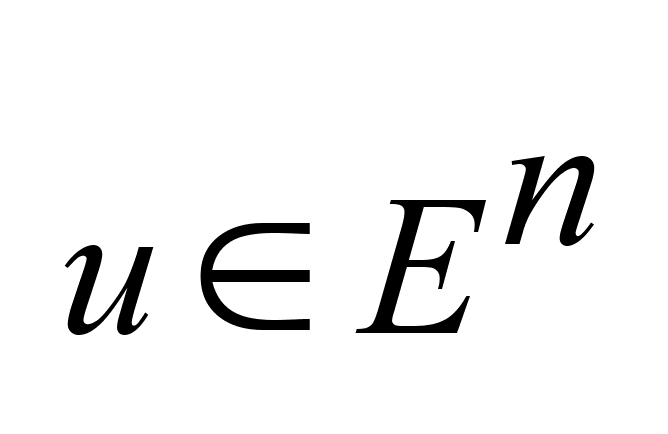 .Задано .Задано
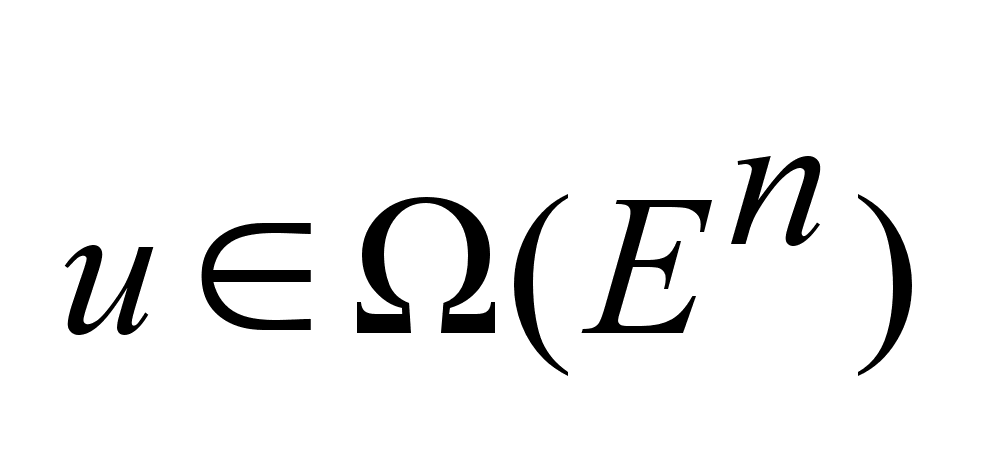 ,
u:
I ,
u:
I 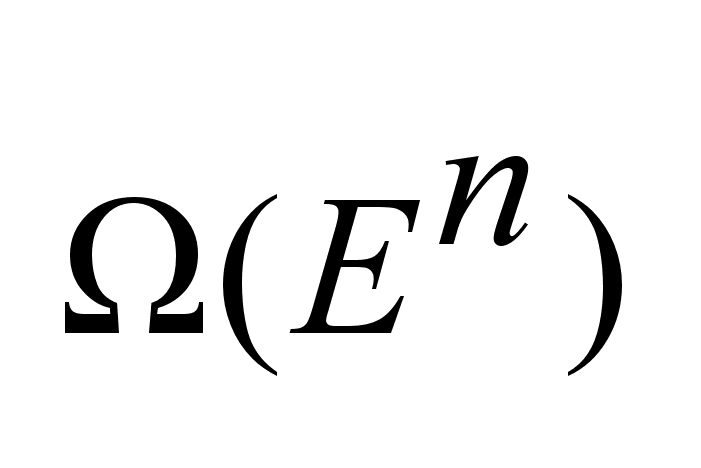 и полагается,
что u(t)
измеримо
и
и полагается,
что u(t)
измеримо
и
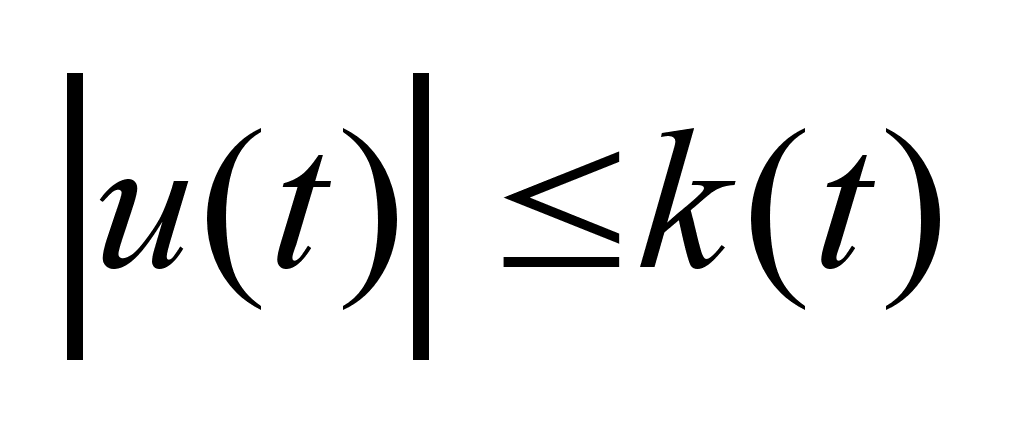 -
где
k(t)
скалярная
функция интегрируемая
по Лебегу на
отрезке I .Функция
u(t)-
называется
допустимым
управлением,
если измерима
и является
однозначной
ветвью из
многозначного
отображения
U
u(t) -
где
k(t)
скалярная
функция интегрируемая
по Лебегу на
отрезке I .Функция
u(t)-
называется
допустимым
управлением,
если измерима
и является
однозначной
ветвью из
многозначного
отображения
U
u(t)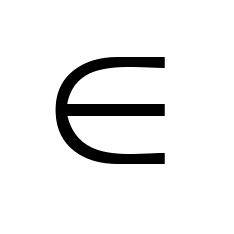 U(t)
-
ограничения
на управления
. В фазовом
пространстве U(t)
-
ограничения
на управления
. В фазовом
пространстве
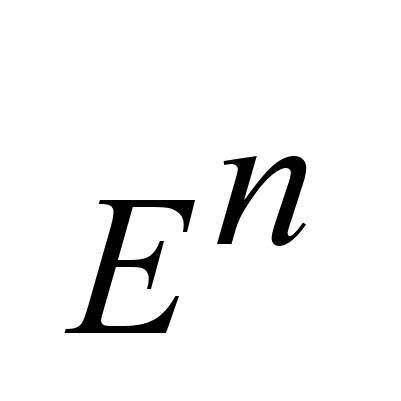 заданы
два не пустых
множества заданы
два не пустых
множества
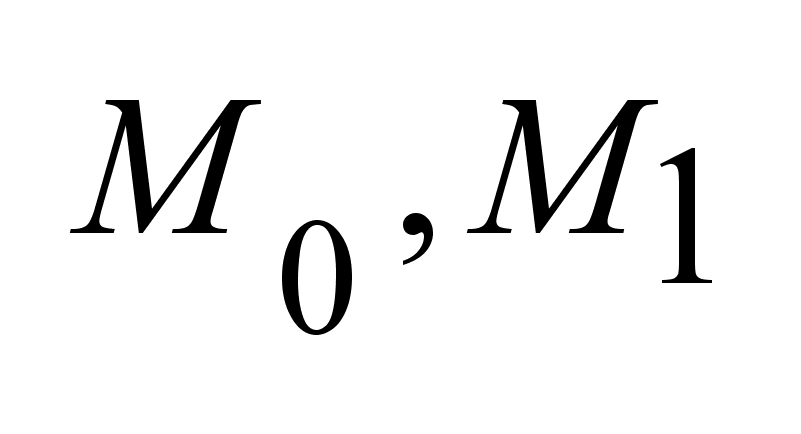 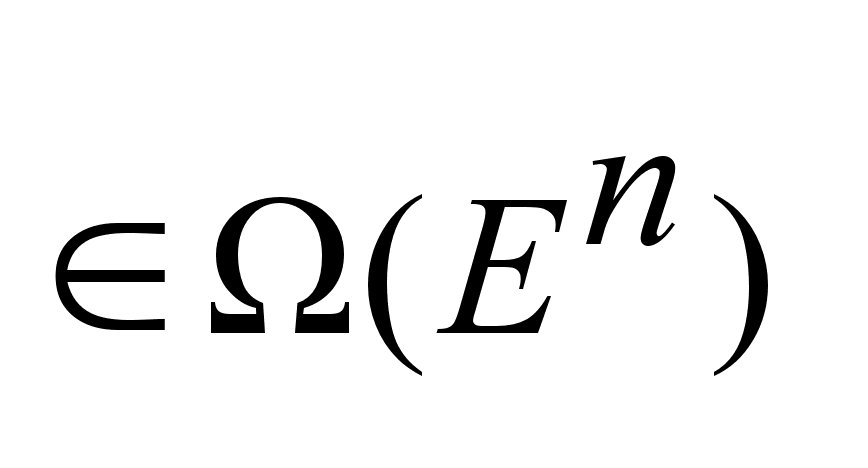 , ,
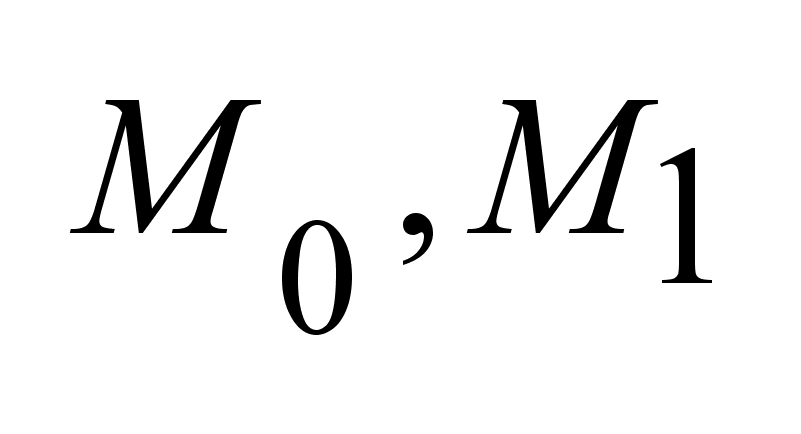 -выпуклы.
Допустимое
управление
u(t)
на отр.I
осуществляете
переход из
начального
мн-ва -выпуклы.
Допустимое
управление
u(t)
на отр.I
осуществляете
переход из
начального
мн-ва
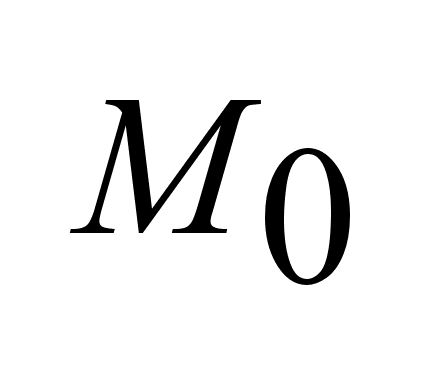 в конечное
множество
в конечное
множество
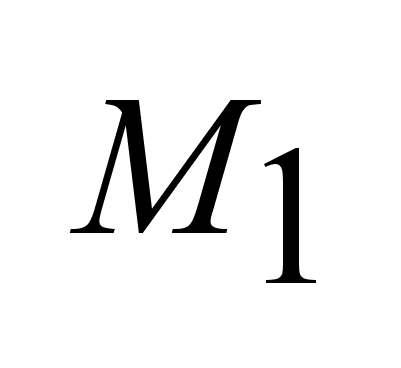 ,
если существует
решение уравнения
(1), удовлетворяющее
граничным
условиям ,
если существует
решение уравнения
(1), удовлетворяющее
граничным
условиям
 и и
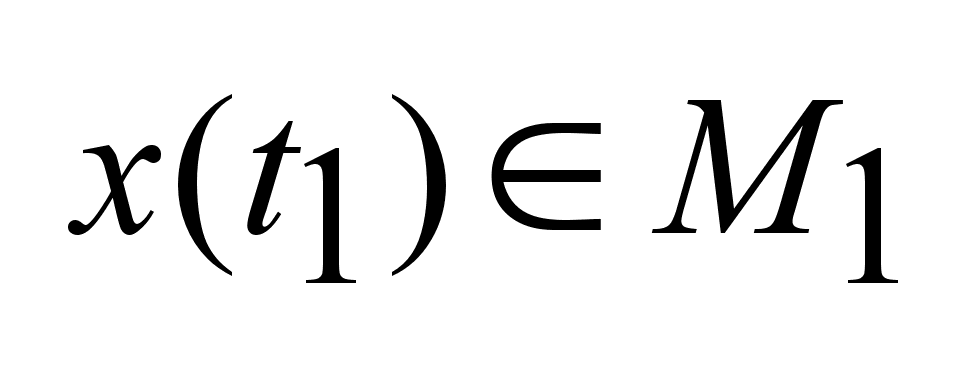 .
Цель управления-
перевод динамический
объекта из .
Цель управления-
перевод динамический
объекта из
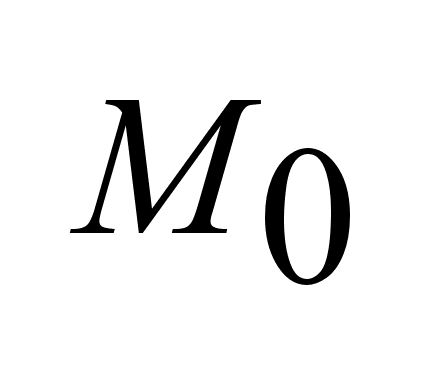 в в
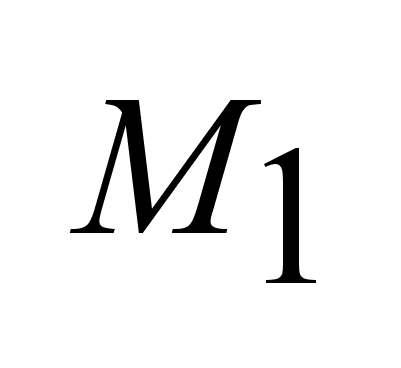 ,
а качество
определяет
функционал.
Таким функционалом
явл. время,
следовательно ,
а качество
определяет
функционал.
Таким функционалом
явл. время,
следовательно
задача
быстродействия
заключается
в нахождении
такого допустимого
управления,
которое осуществляет
переход из
множества
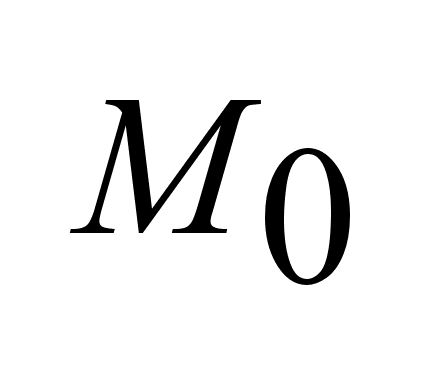 в в
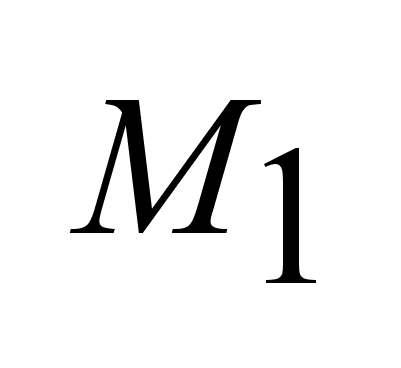 за
наименьшее
время. за
наименьшее
время.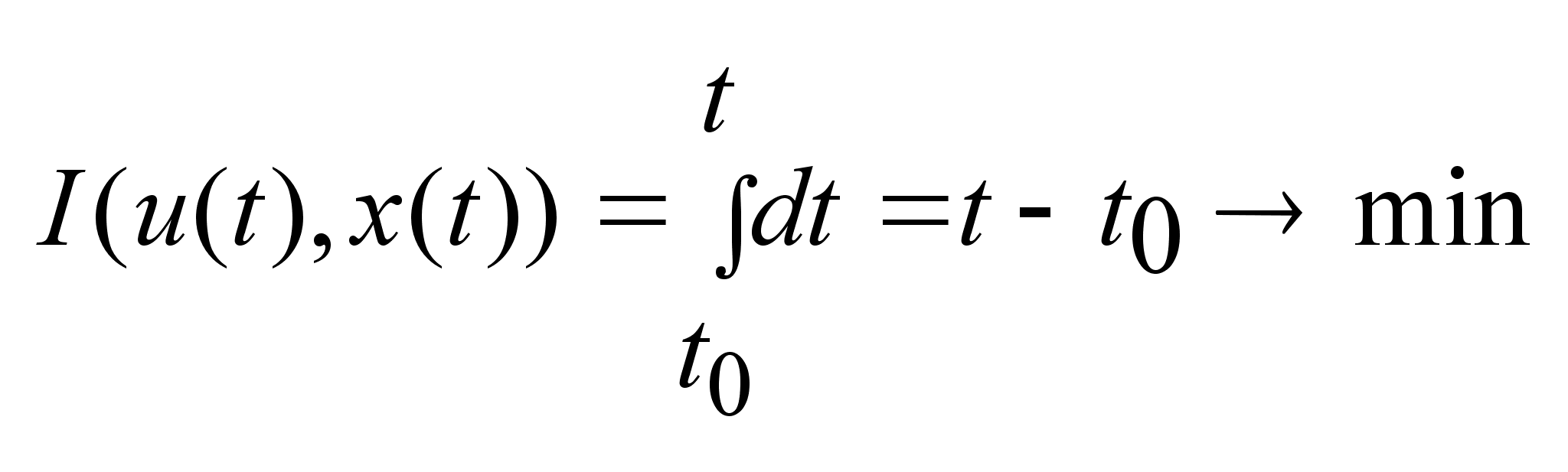 . .
Пусть
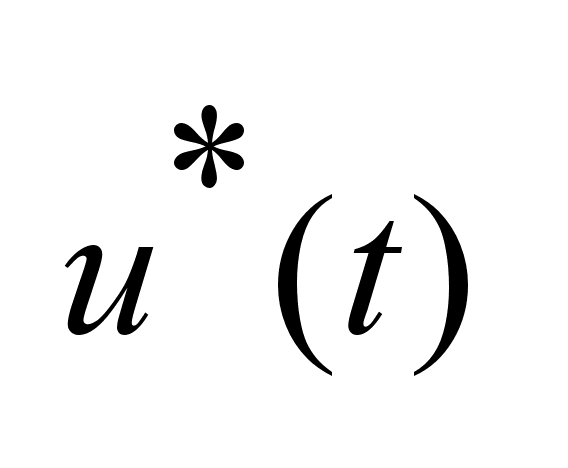 оптимальное
управление, оптимальное
управление,
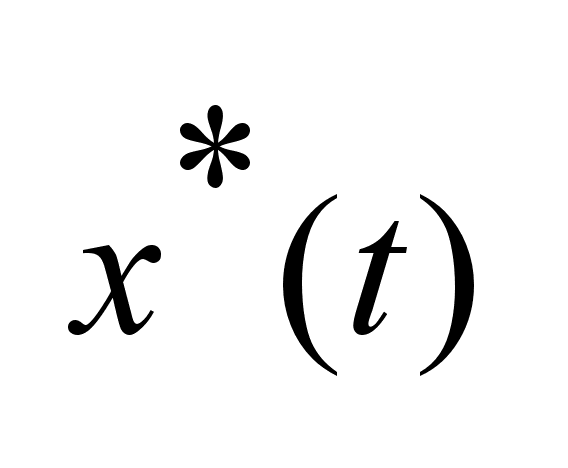 -соответствующая
траектория,
переводящая -соответствующая
траектория,
переводящая
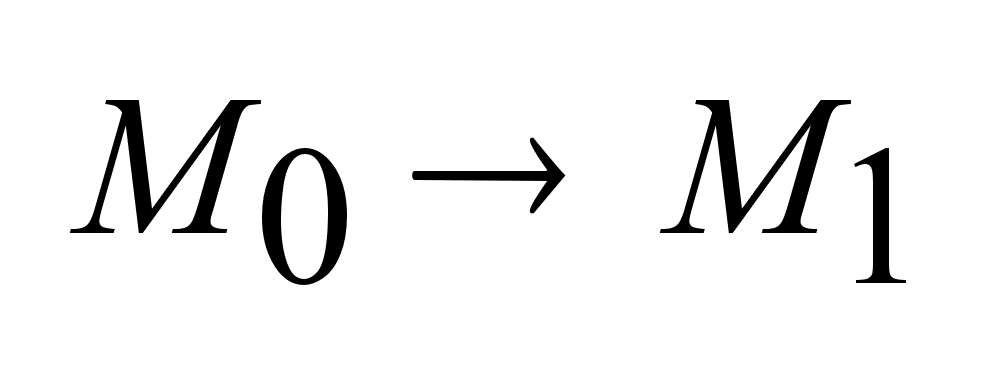 за
время I
. И за
время I
. И
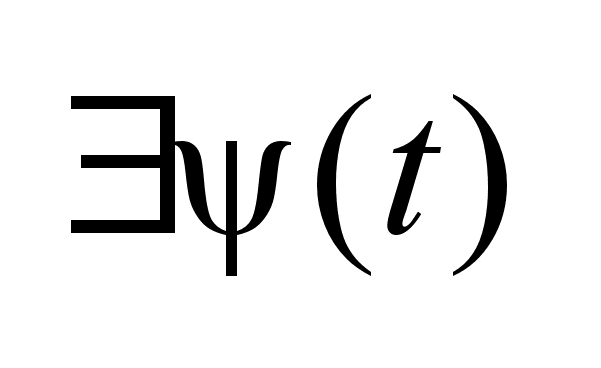 -
ненулевая
функция, такая
что -
ненулевая
функция, такая
что
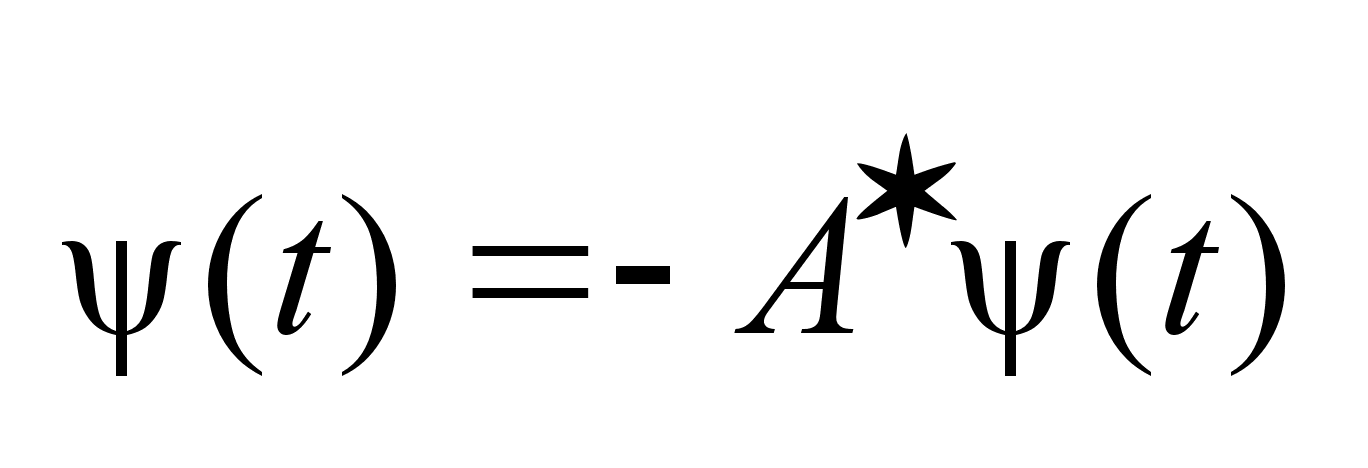 (2). (2).
1)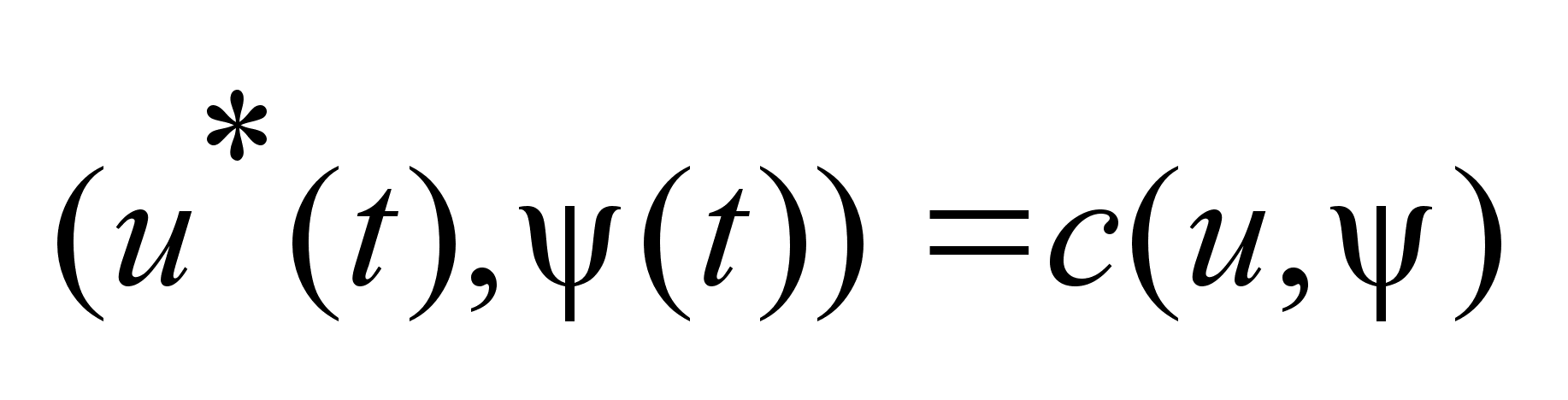 (3); (3);
2)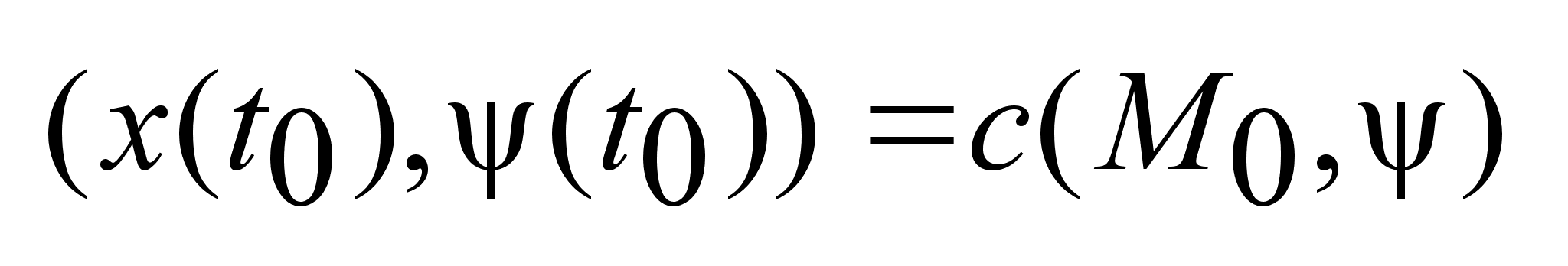 (4); (4);
3)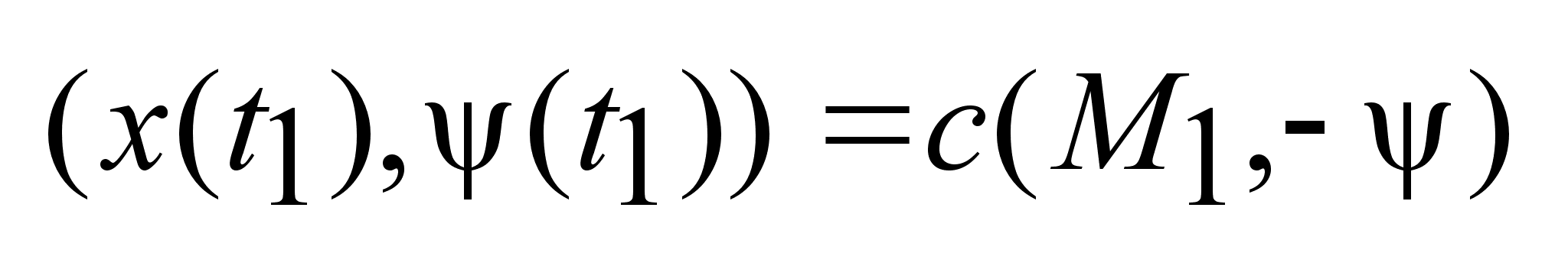 (5) (5)
Найти
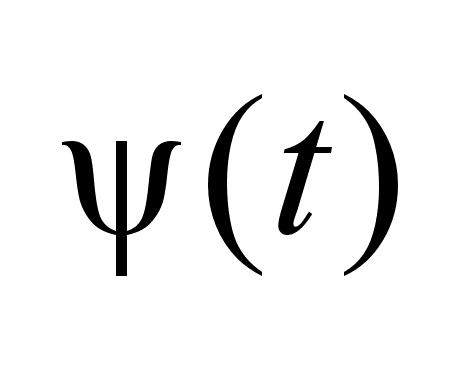 : :

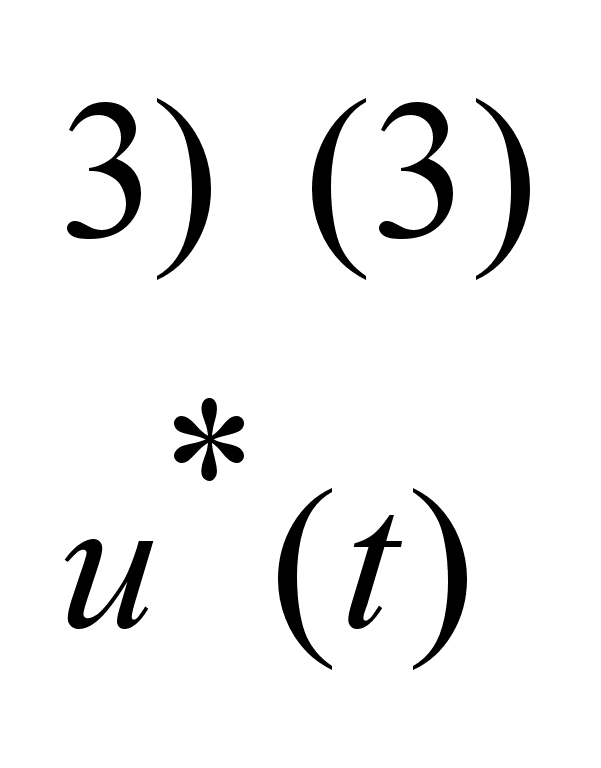
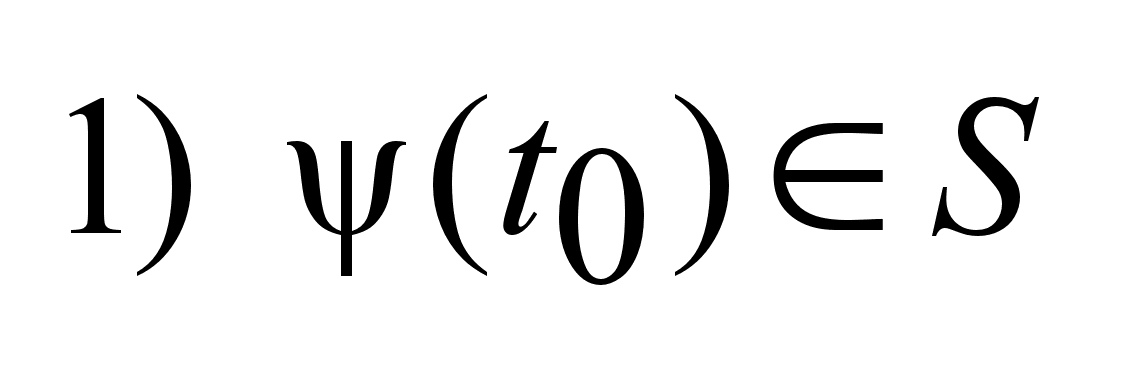
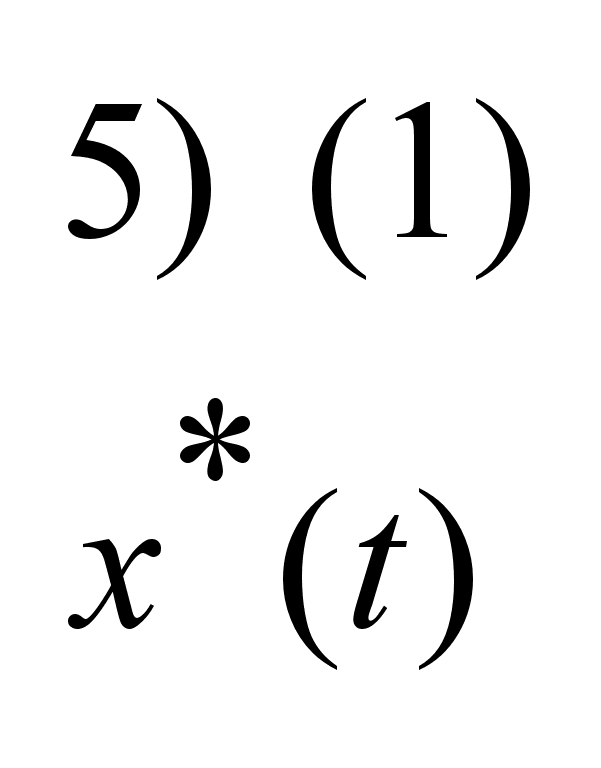
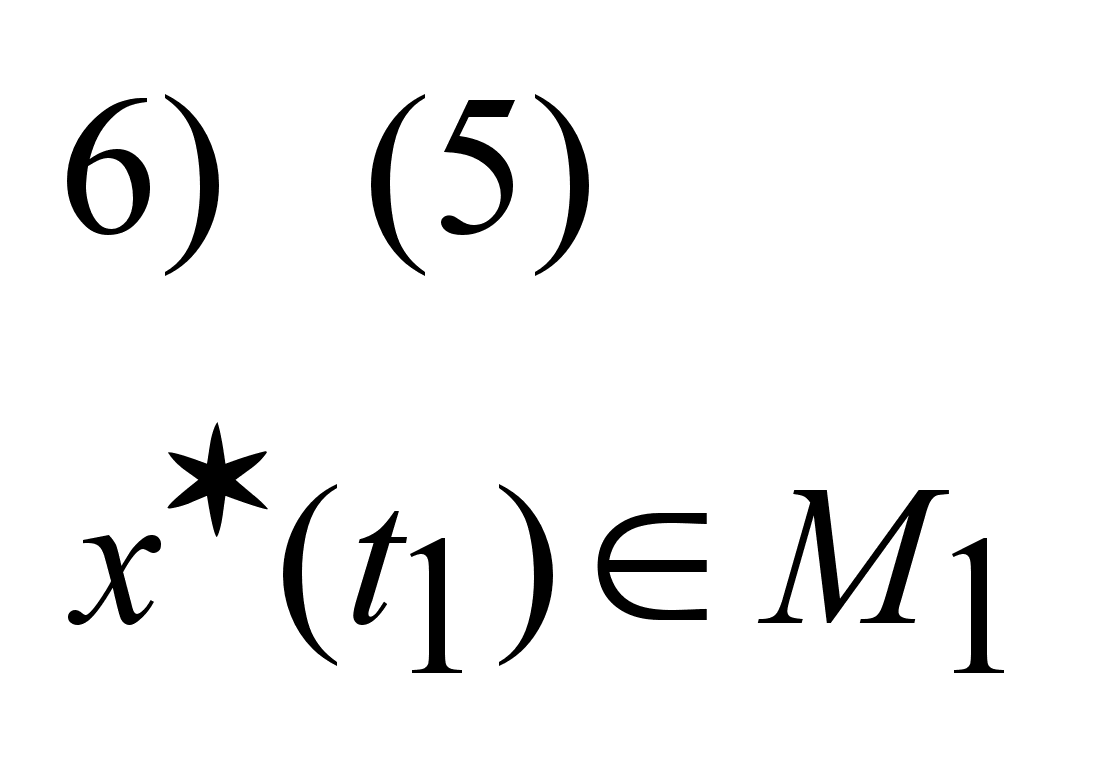
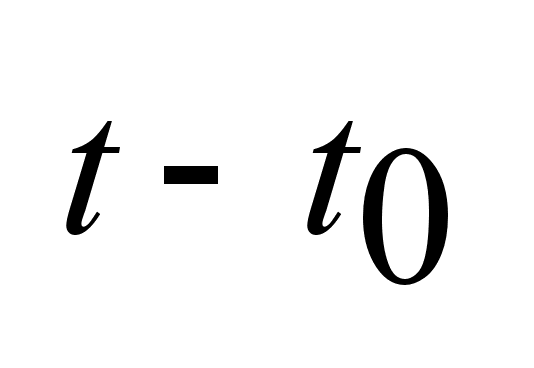
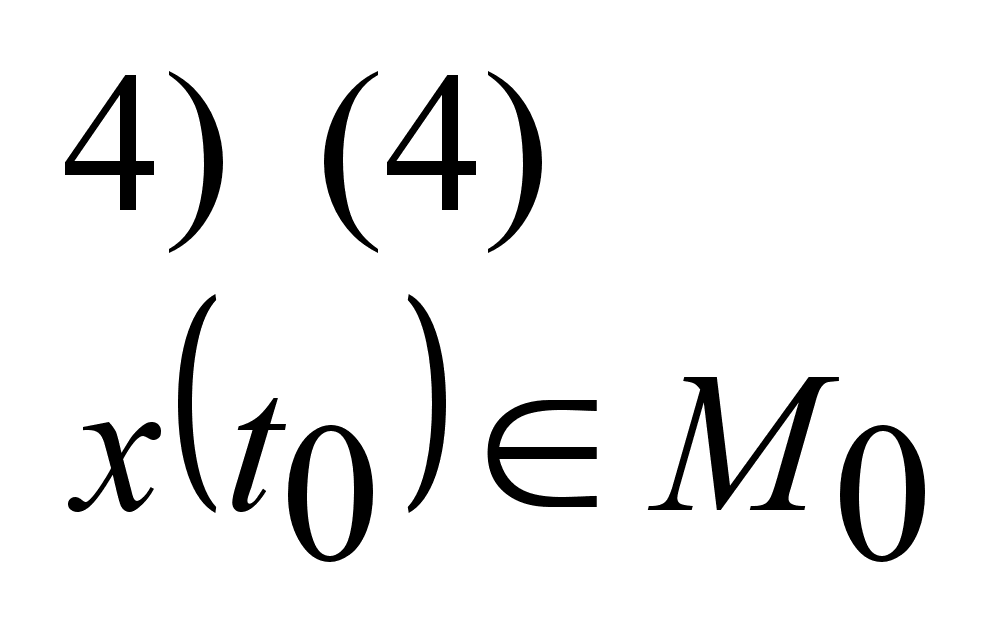
24.
Достаточное
условие оптимальности.
(
Вначале написать
вопрос «Применение
необходимых
условий оптимальности(схема
и пояснения
к ней»)
Для
линейной задачи
существует
дост. условие.
Для этого необходимо
выполнение
дополнительных
условий: усиление
условия трансверсальности
4) решение
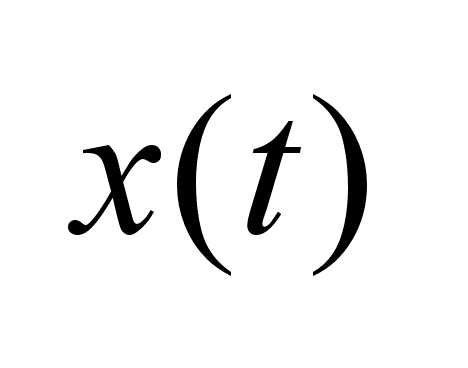 удовлетворяет
усиленному
условию трансверсальности
на удовлетворяет
усиленному
условию трансверсальности
на
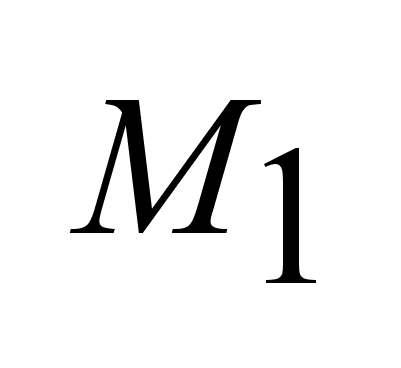 на
отр. на
отр.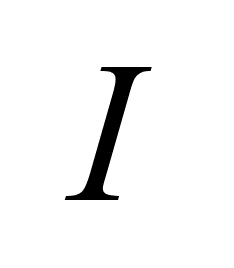 ,
если для ,
если для
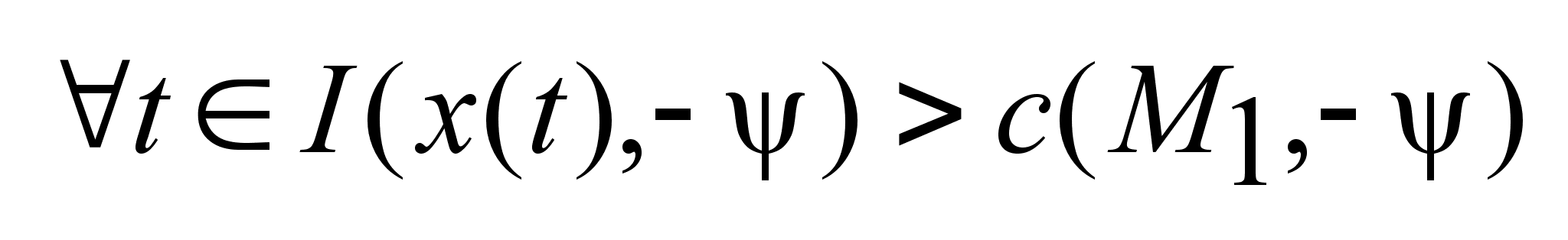 (6). (6).
Достаточное
условие: если
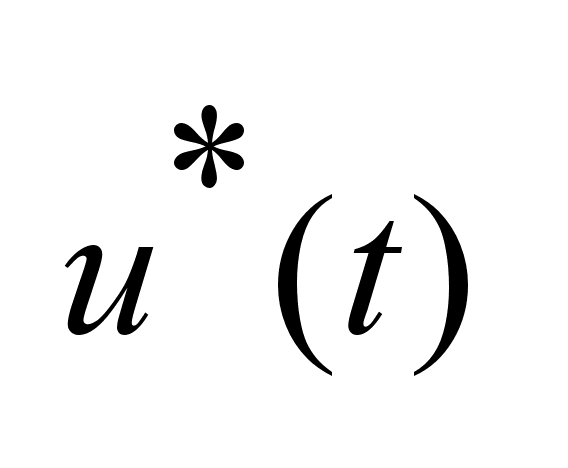 допустимое
управление, допустимое
управление,
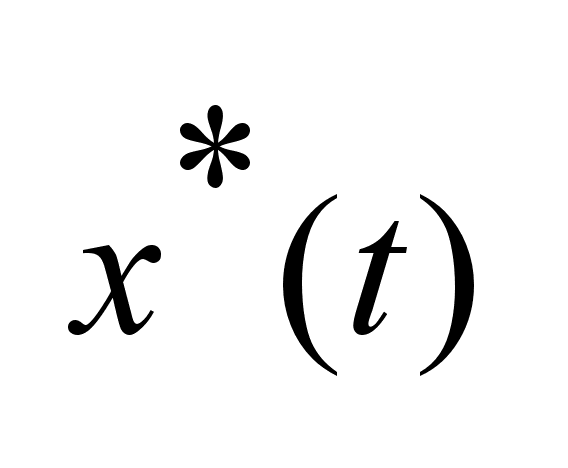 -соответствующая
траектория,
переводящая -соответствующая
траектория,
переводящая
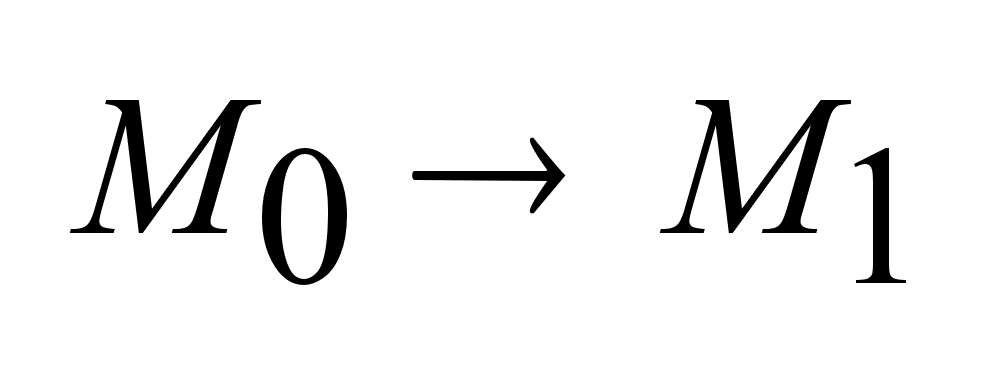 за
время I
и пара за
время I
и пара
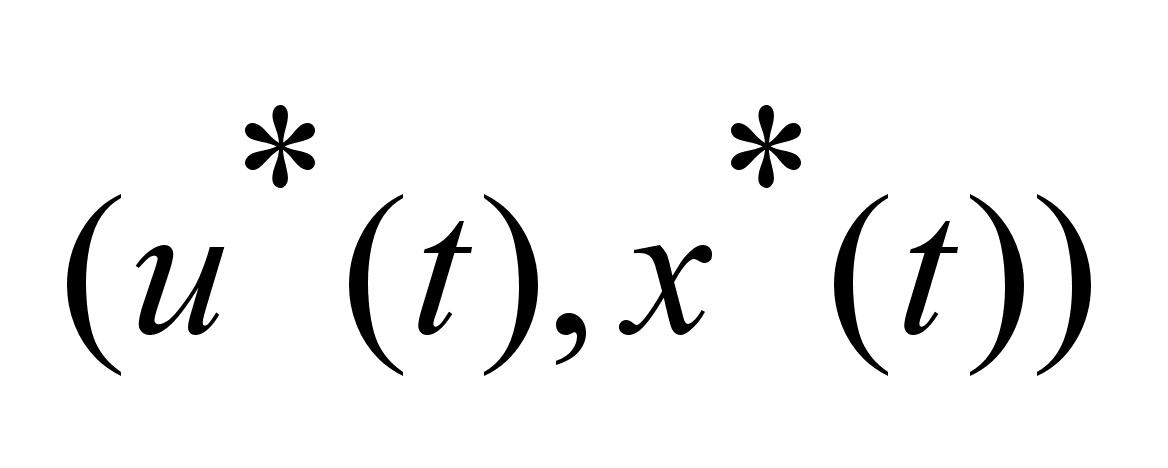 удовлетворяет
принципу максимума
Понтрягина
(2-5) и усиленному
условию трансверсальности
(6), то удовлетворяет
принципу максимума
Понтрягина
(2-5) и усиленному
условию трансверсальности
(6), то
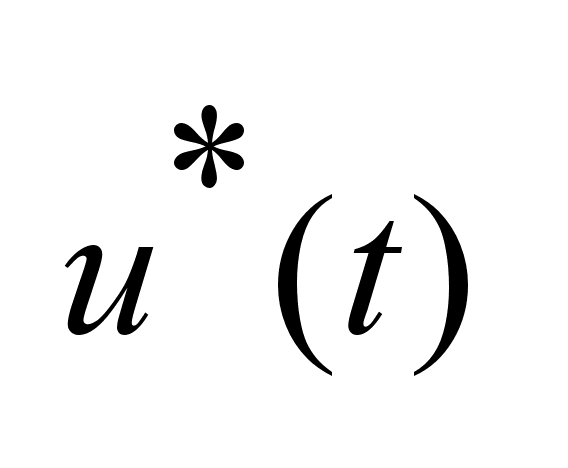 -
оптимальное
управление. -
оптимальное
управление.
Следствие
из теоремы
достаточного
условия трансверсальности.
Используем
локальную
управляемость:
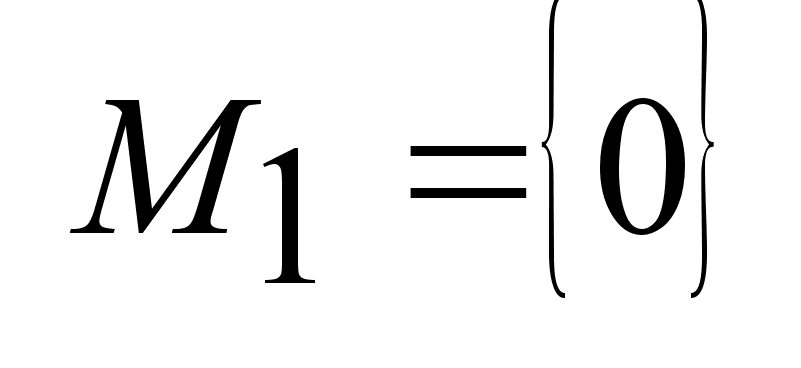 .Если .Если
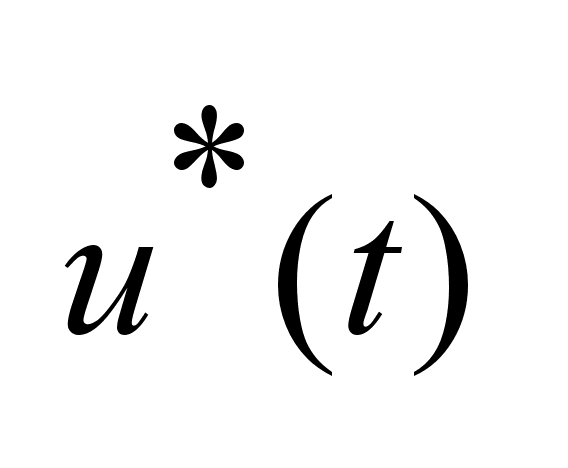 некоторое
допустимое
управление,
а некоторое
допустимое
управление,
а
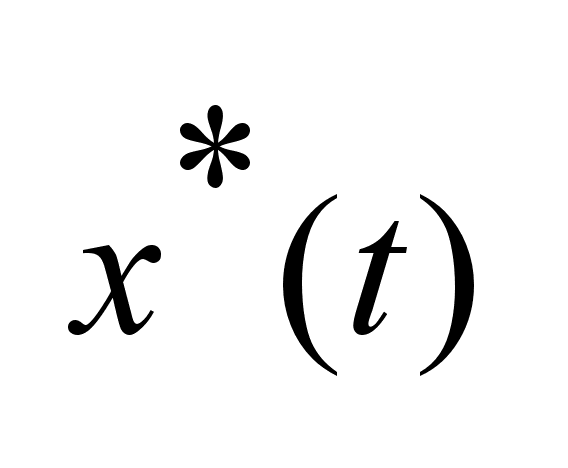 -
соответствующее
решение (1), переводящее -
соответствующее
решение (1), переводящее
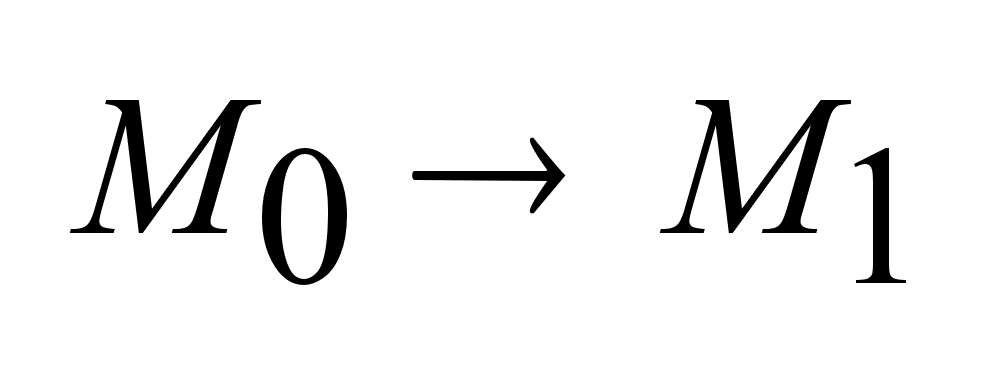 за время I,
удовлетворяет
принципу максимума
Понтрягина
и объект явл.
локально управляемым
в т.0 на любом
отр.
за время I,
удовлетворяет
принципу максимума
Понтрягина
и объект явл.
локально управляемым
в т.0 на любом
отр.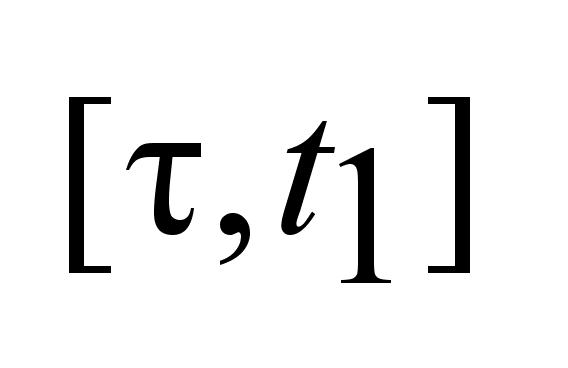 ,
то управление ,
то управление
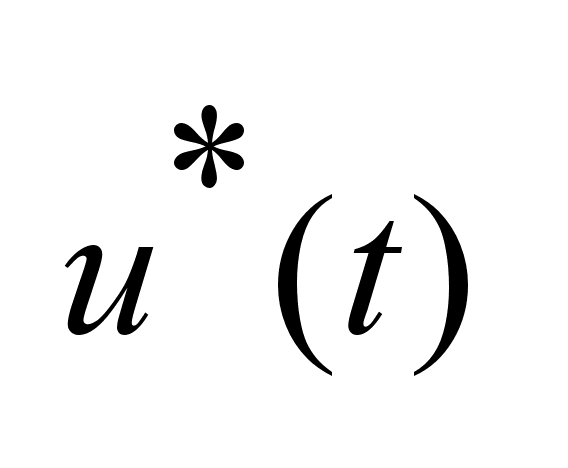 -
оптимально. -
оптимально.
25.
Единственность
оптимального
управления
для линейной
задачи.
(
В начале написать
вопрос «Применение
необходимых
условий оптимальности(схема
и пояснения
к ней)»)
При
решении с
использованием
принципа максимума
Понтрягина
в пунктах 3,4
нарушается
единственность.
При выборе
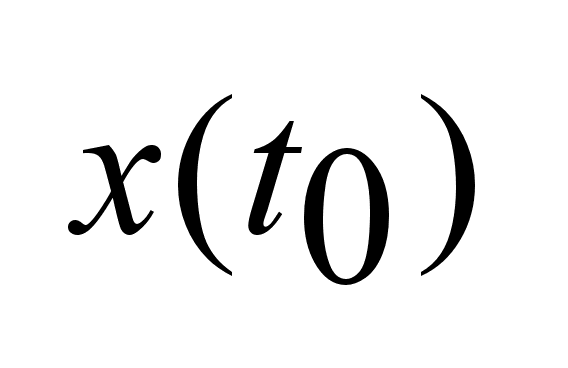 из
условия 4 и выборе из
условия 4 и выборе
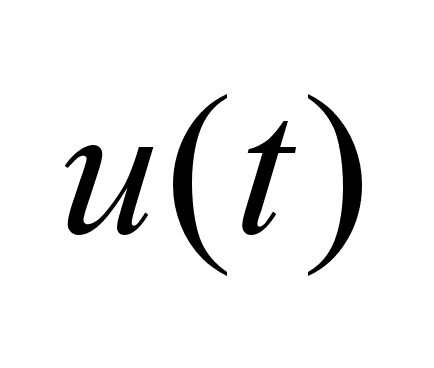 из условия (3).
Пусть задана
из условия (3).
Пусть задана
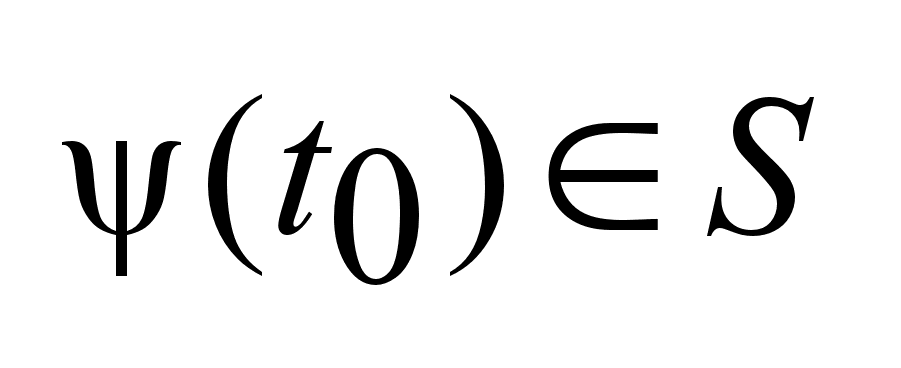 и
сопряженная
функция и
сопряженная
функция
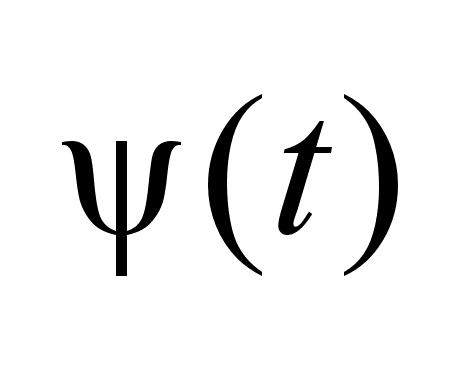 удовлетворяющая
системе (2), если
опорная функция удовлетворяющая
системе (2), если
опорная функция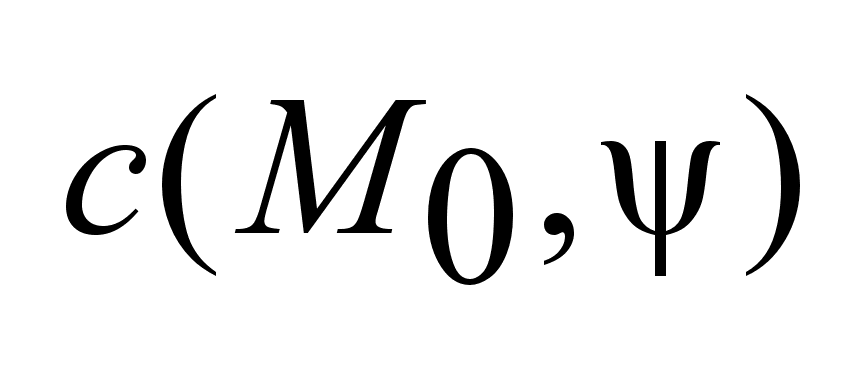 является
дифференцируемой
по является
дифференцируемой
по
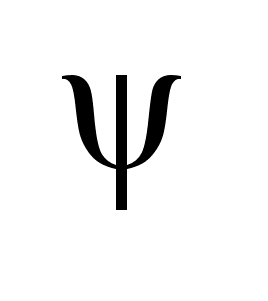 в точке
в точке
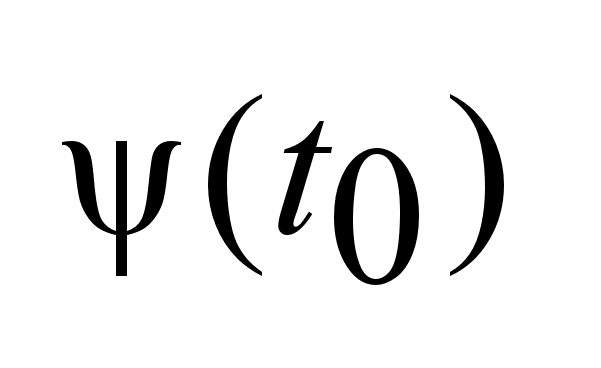 ,
т.е. в этой точке
существует
градиент функции ,
т.е. в этой точке
существует
градиент функции
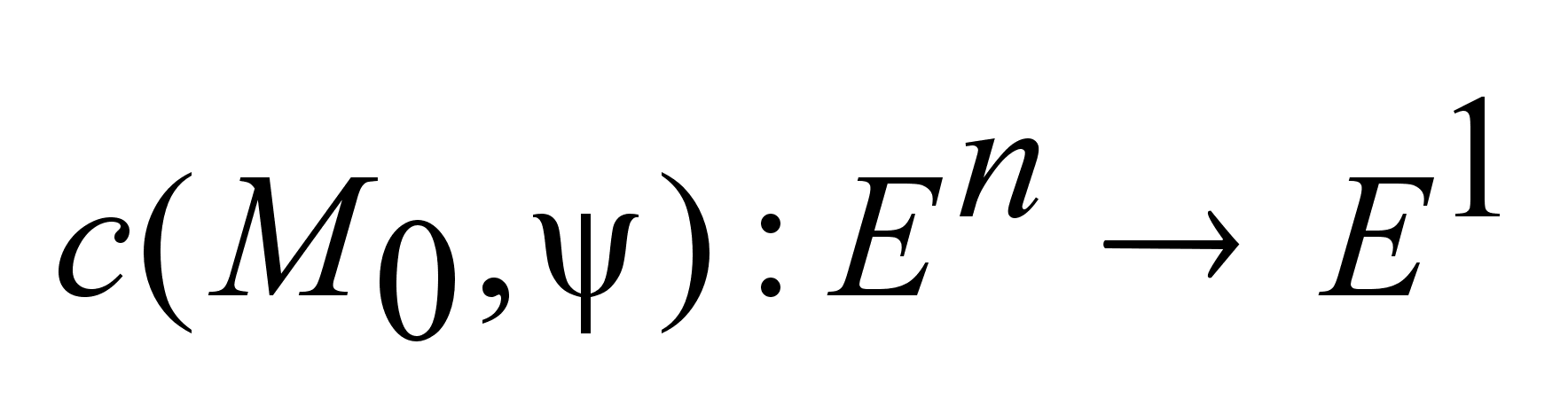 и
для почти всех и
для почти всех
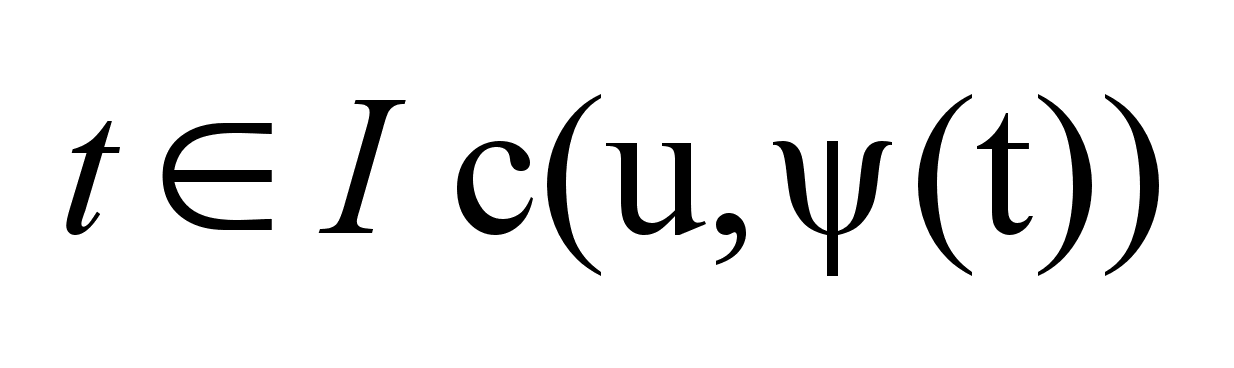 дифференцируемая
по
дифференцируемая
по
 ,
то соответствующая
пара ,
то соответствующая
пара
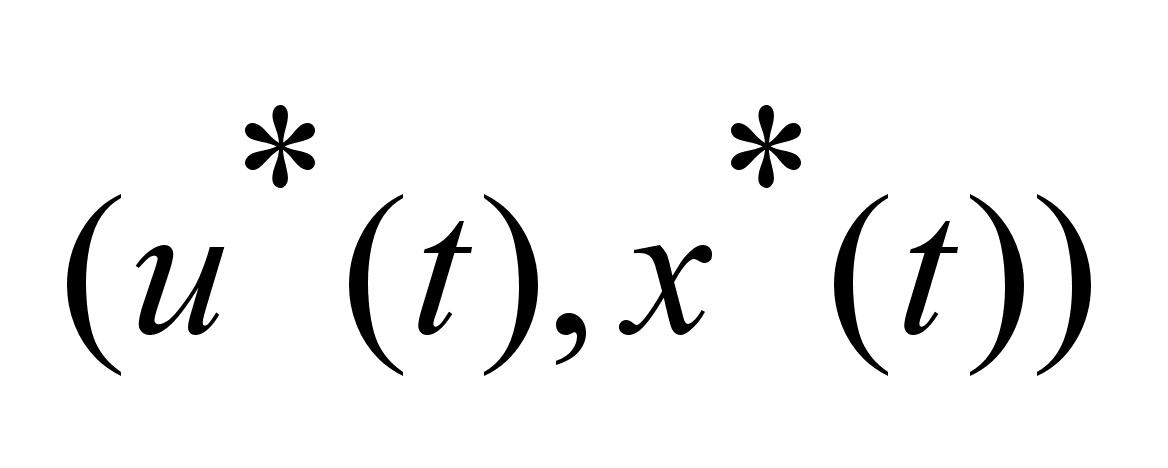 ,
удовлетворяющая
принципу максимума
Понтрягина,
является
единственной. ,
удовлетворяющая
принципу максимума
Понтрягина,
является
единственной.
Следствие:
Если мн-во
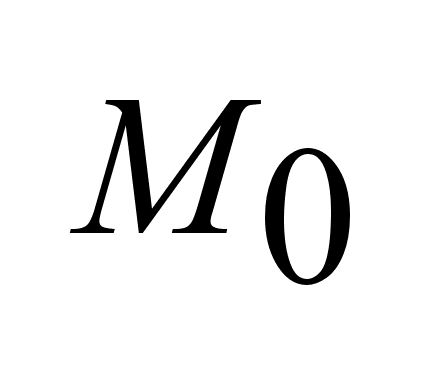 и и
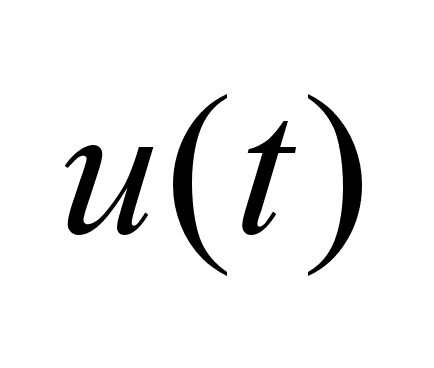 строго выпуклы
для почти всех
t
, принадлежащих
I,
тогда для любого
начального
значения
строго выпуклы
для почти всех
t
, принадлежащих
I,
тогда для любого
начального
значения
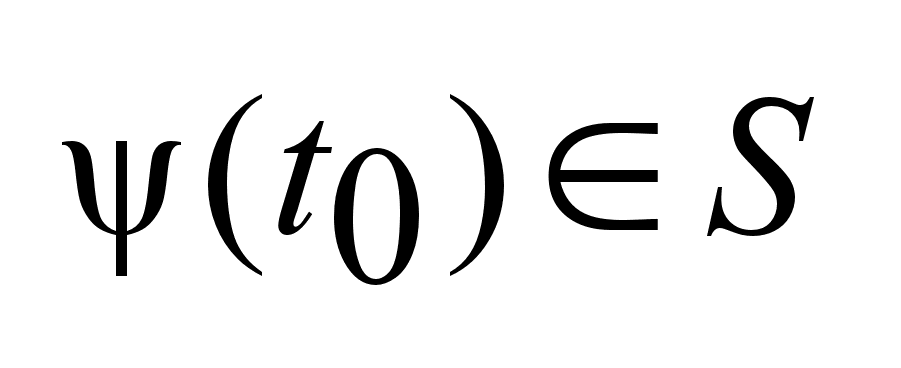 ,
соответствующая
пара ,
соответствующая
пара
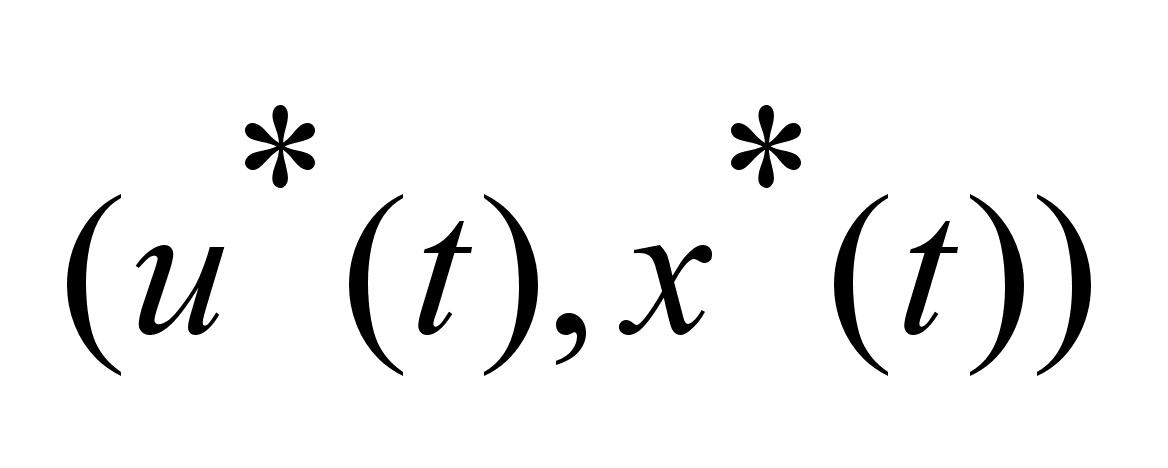 ,
удовлетворяющая
принципу максимума
Понтрягина,
является
единственной. ,
удовлетворяющая
принципу максимума
Понтрягина,
является
единственной.
|
1.
Общая
постановка
задачи управляемости.
2.
Основные
вопросы в теории
ОУ.
3.
Постановка
линейной задачи.
4.
Пространство
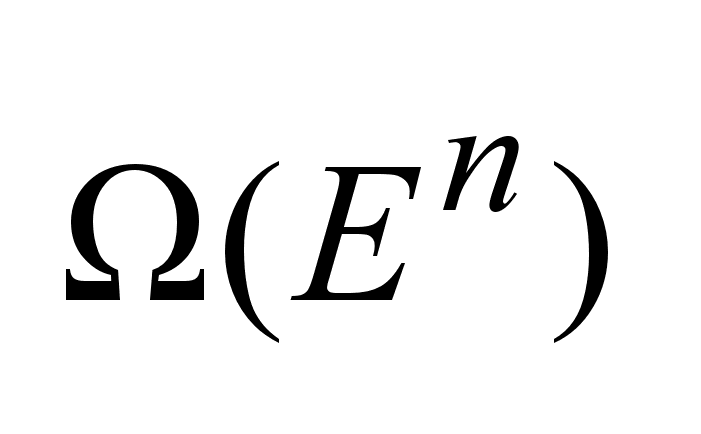 ,
алгебраическая
сумма ,
алгебраическая
сумма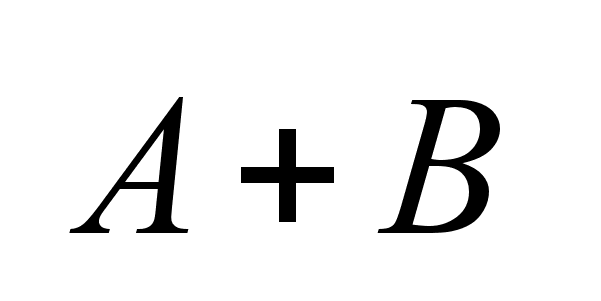 ,
произведение
множества на
число ,
произведение
множества на
число
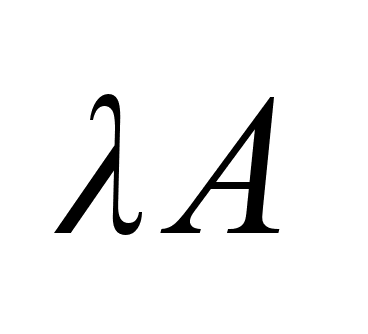 . .
5. ,
хаусдорффова
норма, лемма
про определенность
хаус. нормы. ,
хаусдорффова
норма, лемма
про определенность
хаус. нормы.
6.Опорные
функции.
7.Свойства
опорной функции.
8.
Непрерывные
функции. Условия
Липшица. Лемма
1,2 об условиях
Липшица для
опорных функций.
9.
Многозначные
отображения.
10.
Непрерывные
и равномерно
непрерывные
многозначные
отображения.
11.
Измеримые
многозначные
отображения.
Лемма о равномерной
непрерывности
многозначного
отображения.
12.
Интеграл
от многозначного
отображения.
Теорема о
непрерывности
от многозначного
отображения.
13.Теоремы
1, 2 о других видах
многозначных
отображений.
14.
Линейная задача
быстродействия.
Определение
абс. непрерывной
функции. Теорема
Каратеодори.
15.Множество
достижимости
и его свойства.
16.Общая
задача управляемости.
Теорема об
управляемости.
17.Численное
решение задачи
управляемости.
18.
Лемма
о внутренней
точке.
19.
Локальная
управляемость.
Теорема о
локальной
управляемости..
20.
Теорема
о локальной
управляемости.
(дает достаточное
условие локальной
управляемости)
21.
Теорема
о существовании
оптимального
управления.
22.
Принцип максимума
Понтрягина
на языке опорных
функций.
23.
Применение
необходимых
условий
оптимальности(схема
и пояснения
к ней).
24.
Достаточное
условие оптимальности.
25.
Единственность
оптимального
управления
для линейной
задачи.
|
|