Задача 1.
Генерация
случайных чисел
с заданным
законом распределения
с помощью случайных
чисел, равномерно
распределенных
на интервале
(0,1):
используя
центральную
предельную
теорему, с помощью
сумм 6 независимых
равномерно
распределенных
на интервале
(0,1) случайных
чисел получить
25 случайных
числа со стандартным
нормальным
законом распределения;
найти выборочное
среднее и выборочную
дисперсию;
получить 11
случайных
чисел с законом
распределения
Стьюдента с
10 степенями
свободы; найти
выборочное
среднее и выборочную
дисперсию.
Решение:
С помощью сумм
6 независимых
равномерно
распределенных
на интервале
(0,1) случайных
чисел получим
24 случайных
числа со стандартным
нормальным
законом распределения
по формуле
 ,
где zi -
равномерно
распределенные
на интервале
(0,1) случайные
числа. ,
где zi -
равномерно
распределенные
на интервале
(0,1) случайные
числа.
Получены следующие
числа:
|
-1.235
|
-0.904
|
-1.674
|
1.918
|
-0.335
|
|
1.082
|
-0.584
|
-0.565
|
0.149
|
0.528
|
|
1.076
|
1.011
|
0.671
|
-1.011
|
-1.502
|
|
0.627
|
-0.489
|
-0.486
|
1.022
|
-0.472
|
|
-0.844
|
0.92
|
-0.583
|
0.645
|
-0.495
|
Найдем выборочное
среднее по
формуле



Найдем выборочную
дисперсию по
формуле

Получим 11 случайных
чисел с законом
распределения
Стьюдента с
10 степенями
свободы:
С
лучайные
числа, распределенные
по закону «хи
квадрат» с 10
степенями
свободы:
, где xi
– нормальные
независимые
случайные
величины.
Случайные
числа, распределенные
по закону Стьюдента
с 10 степенями
свободы:
,
где x – нормальная
случайная
величина, а 2
– независимая
от x величина,
которая распределена
по закону «хи
квадрат» с 10
степенями
свободы.
Получены следующие
числа:
|
-0.58
|
-2.496
|
-0.06
|
-0.932
|
1.547
|
0.418
|
1.658
|
1.51
|
-0.171
|
-0.821
|
-1.728
|
Найдем выборочное
среднее по
формуле


Найдем выборочную
дисперсию по
формуле


Задача 2.
Проверка
статистической
гипотезы:
получить 100
случайных
чисел {x1,…,x100},
распределенных
по показательному
закону с параметром
= 1/6, найти
такое наименьшее
целое число
N, что N
xk для всех k =
1,…,100;
разделить
отрезок [0, N] на
10 равных отрезков;
получить
группированную
выборку {n1,…,n10},
где ni – число
чисел, попавших
в i-ый интервал;
построить
гистограмму
относительных
частот; по
группированной
выборке найти
оценку В
параметра ;
проверить с
помощью критерия
«хи квадрат»
гипотезу о
соответствии
группированной
выборки показательному
распределению
с параметром
В при
уровне значимости
0.05.
Решение:
Получим 100 случайных
чисел {x1,…,x100},
распределенных
по показательному
закону с параметром
= 1/6:
|
4,9713
|
3,2905
|
2,7849
|
4,1093
|
2,1764
|
9,9659
|
10,343
|
4,6924
|
13,966
|
14,161
|
|
0,4258
|
0,6683
|
8,8884
|
5,3392
|
2,7906
|
4,7696
|
3,0867
|
0,9414
|
2,8222
|
3,4177
|
|
10,148
|
3,5312
|
8,4915
|
3,0179
|
3,2209
|
4,2259
|
1,8006
|
2,8645
|
1,3051
|
3,3094
|
|
0,5557
|
1,9075
|
2,4227
|
6,9307
|
7,1085
|
13,322
|
0,9665
|
11,19
|
15,203
|
2,6685
|
|
3,6408
|
5,3646
|
4,5871
|
11,277
|
1,823
|
1,142
|
0,8126
|
7,2223
|
12,371
|
1,4527
|
|
2,9692
|
15,762
|
2,5493
|
13,533
|
8,8944
|
0,5005
|
2,4678
|
4,2491
|
4,1972
|
4,0488
|
|
2,2424
|
3,0025
|
30,785
|
13,778
|
0,8824
|
1,7475
|
5,8036
|
3,5565
|
0,2718
|
10,404
|
|
12,166
|
0,297
|
21,487
|
17,302
|
12,166
|
0,875
|
1,9573
|
25,326
|
2,0727
|
9,1516
|
|
10,669
|
6,4555
|
6,005
|
1,3209
|
3,8486
|
1,3525
|
11,593
|
5,4617
|
11,946
|
16,293
|
|
3,3376
|
3,6084
|
7,0011
|
1,279
|
7,5471
|
0,6641
|
1,776
|
6,1109
|
8,857
|
8,8327
|
Находим такое
наименьшее
целое число
N, что N
xk для всех k =
1,…,100:
N = 31
Разделяем
отрезок [0, 31]
на 10 равных отрезков
и получим
группированную
выборку {n1,…,n10},
где ni – число
чисел, попавших
в i-ый интервал:
|
xi
|
Xi+1
|
ni
|
ni/n
|
|
0
|
3,1
|
39
|
0,39
|
|
3,1
|
6,2
|
25
|
0,25
|
|
6,2
|
9,3
|
12
|
0,12
|
|
9,3
|
12,4
|
12
|
0,12
|
|
12,4
|
15,5
|
6
|
0,06
|
|
15,5
|
18,6
|
3
|
0,03
|
|
18,6
|
21,7
|
1
|
0,01
|
|
21,7
|
24,8
|
0
|
0
|
|
24,8
|
27,9
|
1
|
0,01
|
|
27,9
|
31
|
1
|
0,01
|
Гистограмма
относительных
частот:
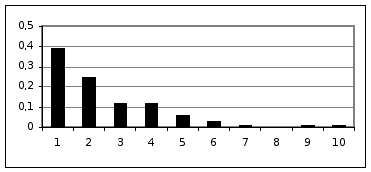
Находим выборочное
среднее по
формуле
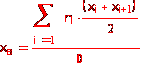

По группированной
выборке находим
оценку В
параметра
по формуле
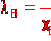

Проверяем с
помощью критерия
«хи квадрат»
гипотезу о
соответствии
группированной
выборки показательному
распределению
с параметром
В при
уровне значимости
0.05:
Находим вероятности
попадания X в
частичные
интервалы (xi,
xi+1) по формуле

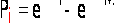
Вычисляем
теоретические
частоты по
формуле

|
xi
|
Xi+1
|
ni
|
Pi
|
fi
|
(ni
- fi)2
/ fi
|
|
0
|
3,1
|
39
|
0,3955
|
39,55
|
0,0076
|
|
3,1
|
6,2
|
25
|
0,2391
|
23,91
|
0,0499
|
|
6,2
|
9,3
|
12
|
0,1445
|
14,45
|
0,4162
|
|
9,3
|
12,4
|
12
|
0,0874
|
8,74
|
1,2188
|
|
12,4
|
15,5
|
6
|
0,0528
|
5,28
|
0,0977
|
|
15,5
|
18,6
|
3
|
0,0319
|
3,19
|
0,0116
|
|
18,6
|
21,7
|
1
|
0,0193
|
1,93
|
0,4482
|
|
21,7
|
24,8
|
0
|
0,0117
|
1,17
|
1,1668
|
|
24,8
|
27,9
|
1
|
0,0071
|
0,71
|
0,1231
|
|
27,9
|
31
|
1
|
0,0043
|
0,43
|
0,7717
|
Находим наблюдаемое
значение критерия
по формуле
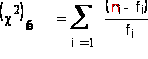
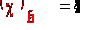
По таблице
критических
точек распределения
«хи квадрат»,
по заданному
уровню значимости
0.05 и числу
степеней свободы
8 находим критическую
точку
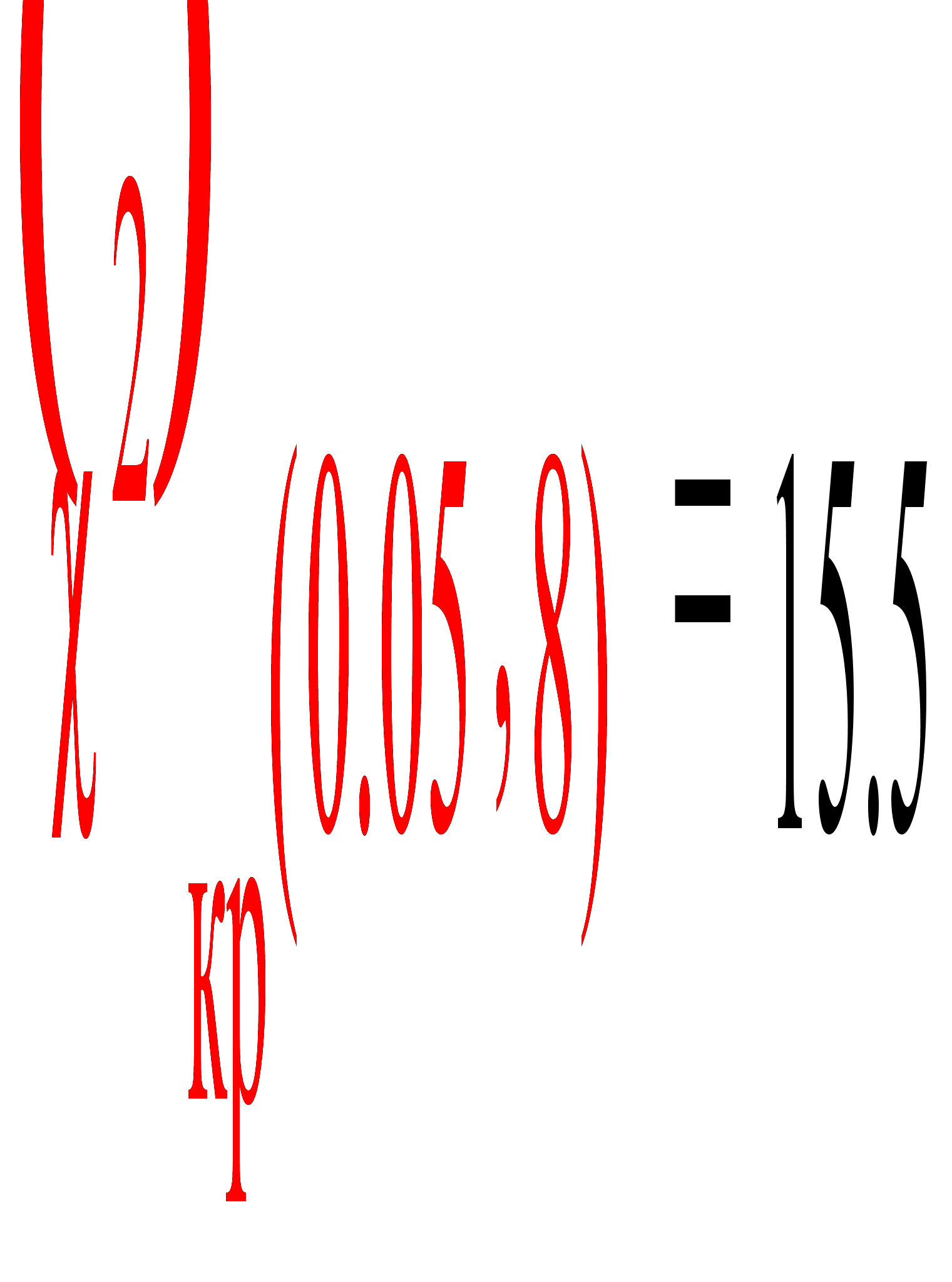
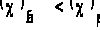
Гипотезу о
соответствии
группированной
выборки показательному
распределению
с параметром
В не
отвергаем.
Задача 3.
Проверка гипотезы
о равенстве
дисперсий:
получить 2 случайных
числа, распределенных
по стандартному
нормальному
закону с помощью
сумм 5 независимых
равномерно
распределенных
на интервале
(0, 1) случайных
чисел: аналогично,
получить 9 случайных
чисел, распределенных
по стандартному
нормальному
закону с помощью
сумм 9 независимых
равномерно
распределенных
на интервале
(0, 1) случайных
чисел;
проверить
гипотезу о
равенстве
генеральных
дисперсий
полученных
совокупностей
при уровне
значимости
0.1.
Решение:
Получим 2 случайных
числа, распределенных
по стандартному
нормальному
закону с помощью
сумм 5 независимых
равномерно
распределенных
на интервале
(0, 1) случайных
чисел по формуле
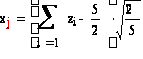 ,
где zi
- равномерно
распределенные
на интервале
(0, 1) случайные
числа. ,
где zi
- равномерно
распределенные
на интервале
(0, 1) случайные
числа.
Получены следующие
числа:
Получим 9 случайных
числа, распределенных
по стандартному
нормальному
закону с помощью
сумм 9 независимых
равномерно
распределенных
на интервале
(0, 1) случайных
чисел по формуле
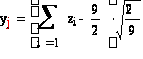 ,
где zi
- равномерно
распределенные
на интервале
(0, 1) случайные
числа. ,
где zi
- равномерно
распределенные
на интервале
(0, 1) случайные
числа.
Получены следующие
числа:
|
0.885
|
1.25
|
-0.365
|
-1.139
|
0.891
|
-1.176
|
0.237
|
1.807
|
-0.96
|
Проверим гипотезу
о равенстве
генеральных
дисперсий
полученных
совокупностей
при уровне
значимости
0.1:
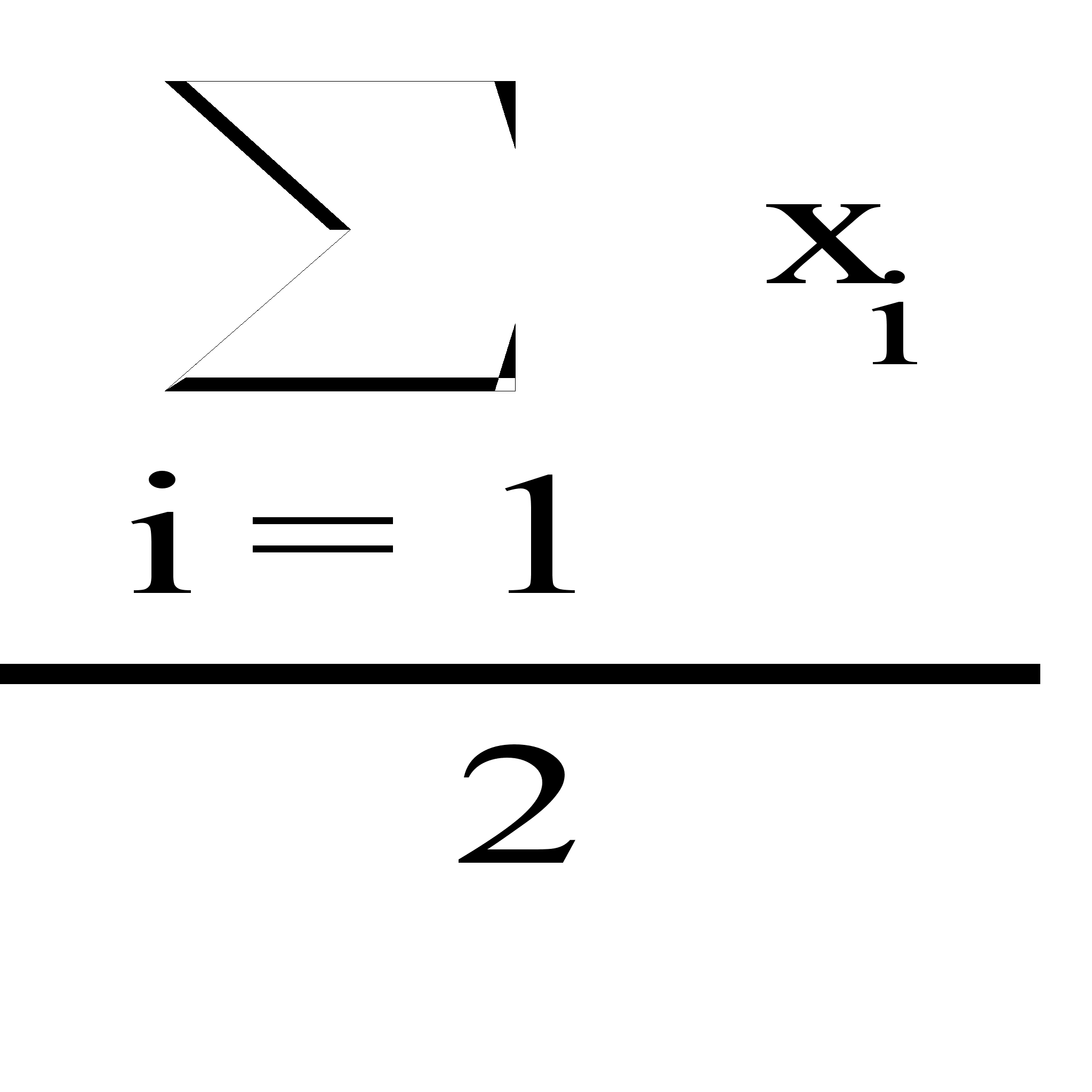
Найдем выборочное
среднее первой
совокупности
по формуле
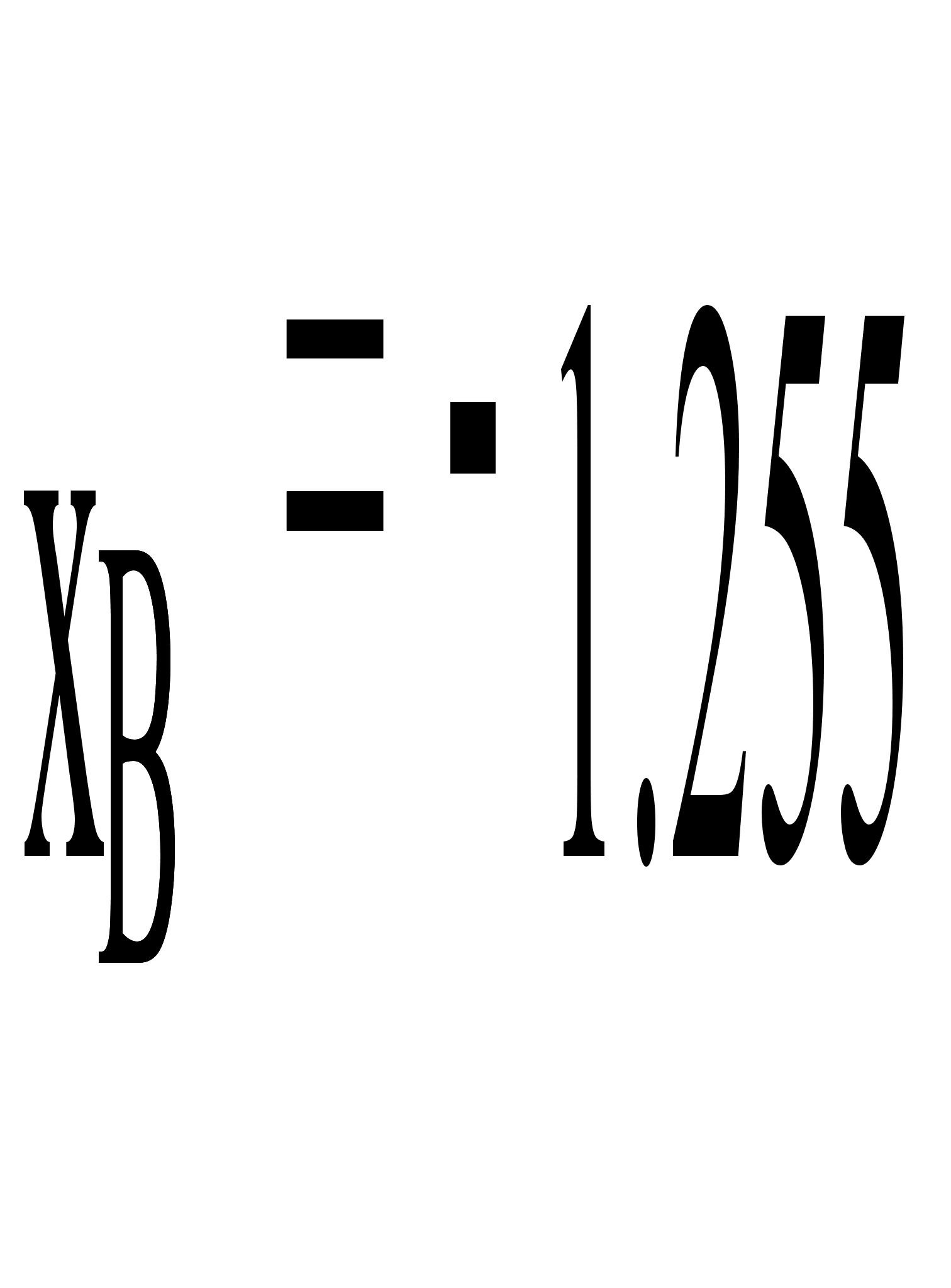 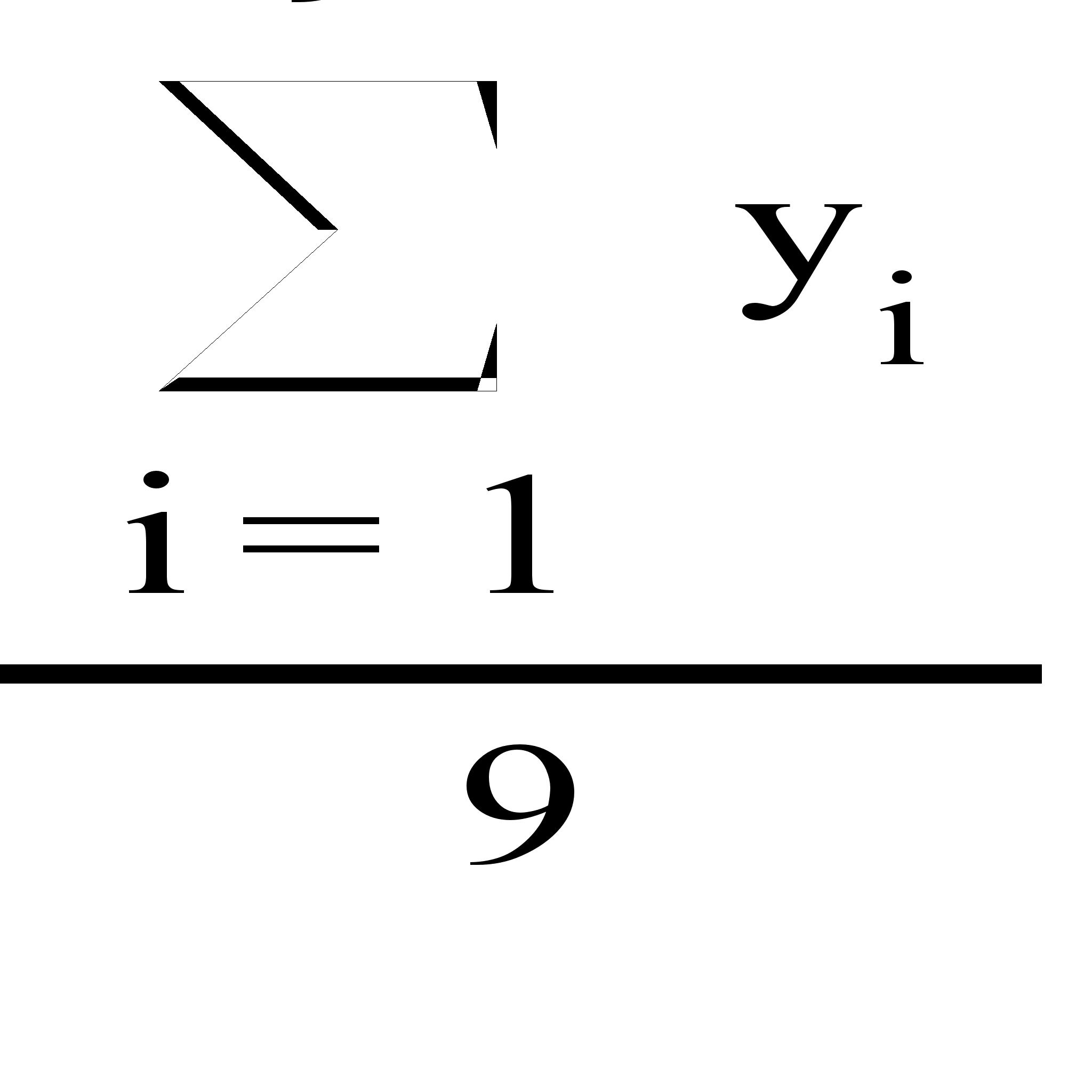
Найдем выборочное
среднее второй
совокупности
по формуле
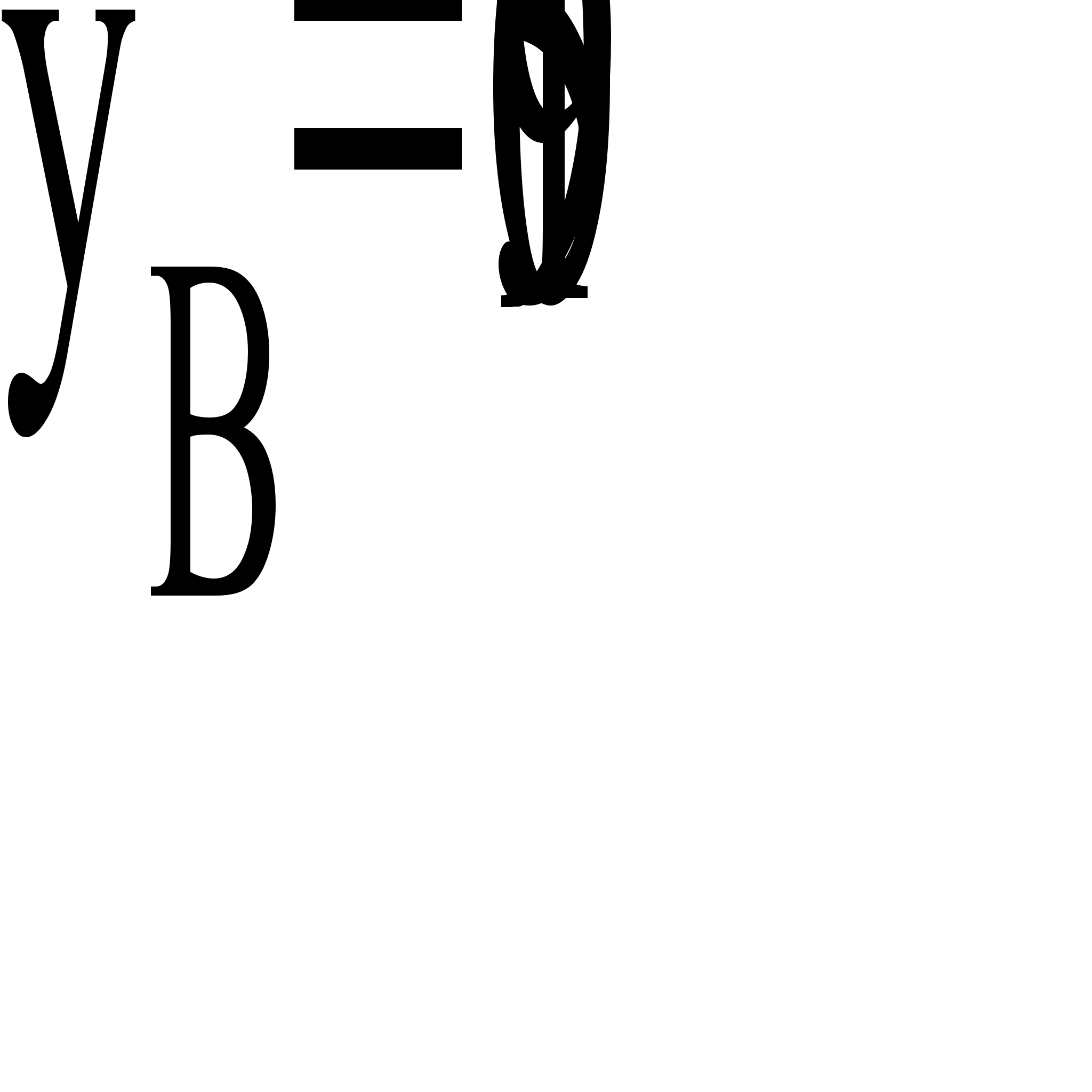
Найдем исправленную
дисперсию
первой совокупности
по формуле
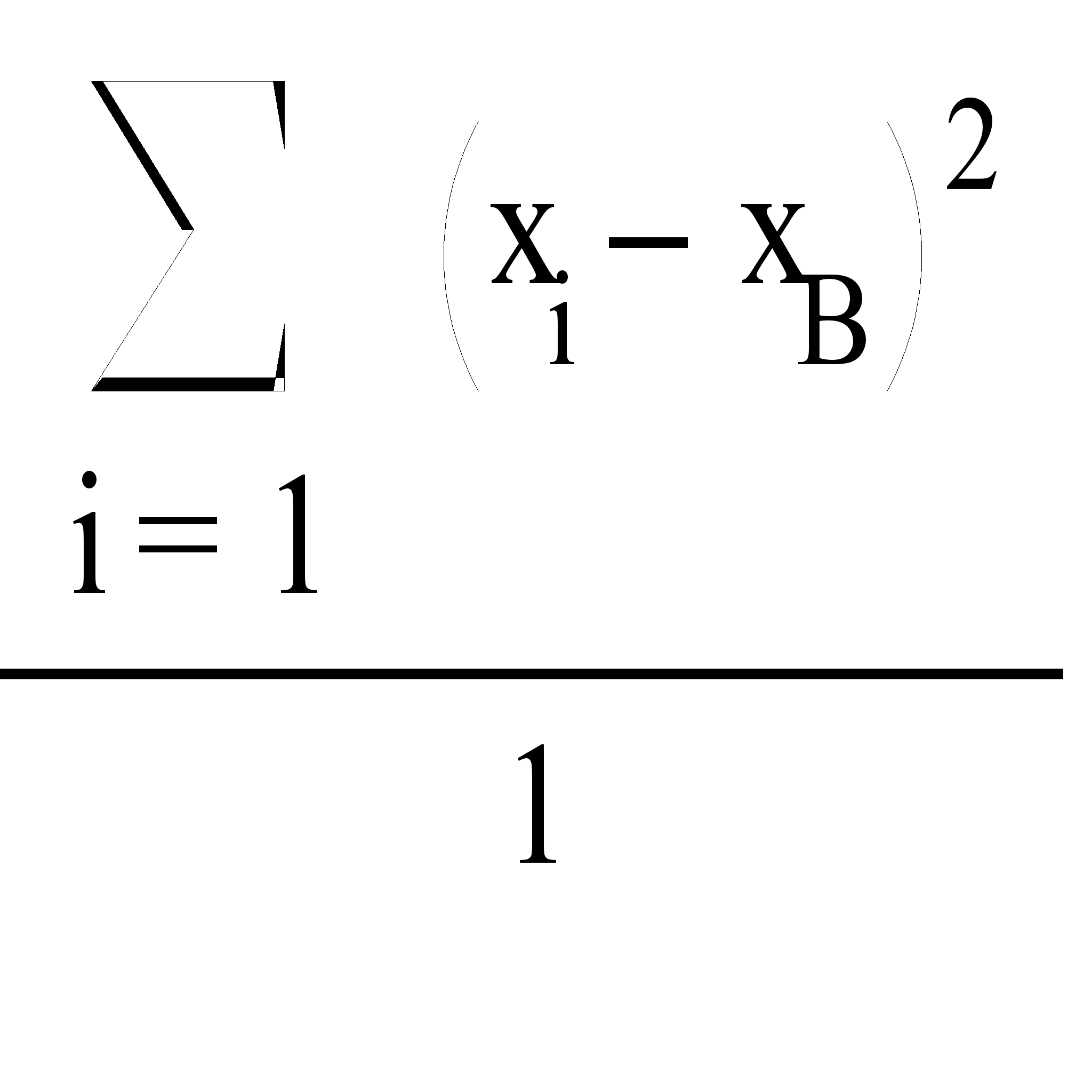
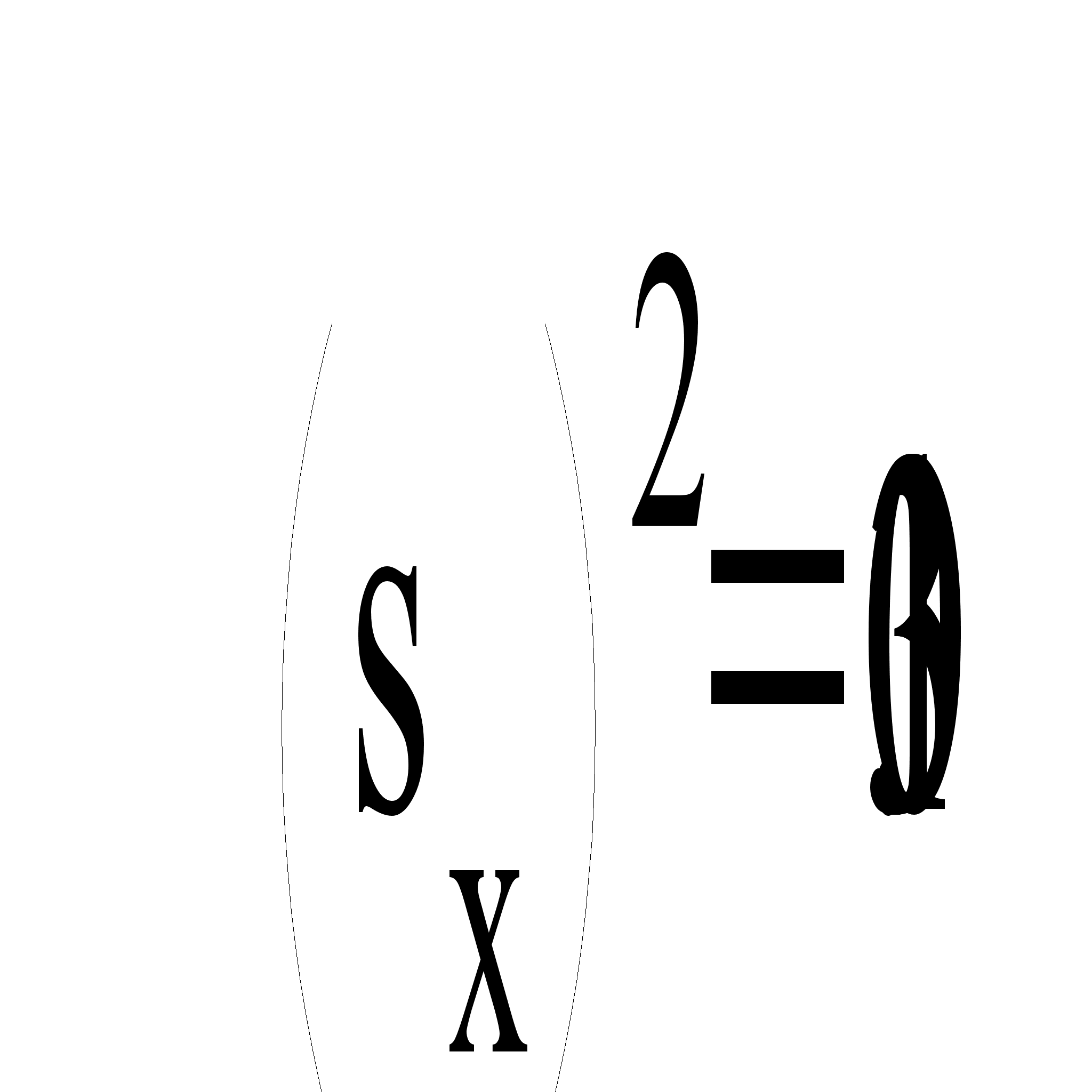
Найдем исправленную
дисперсию
второй совокупности
по формуле
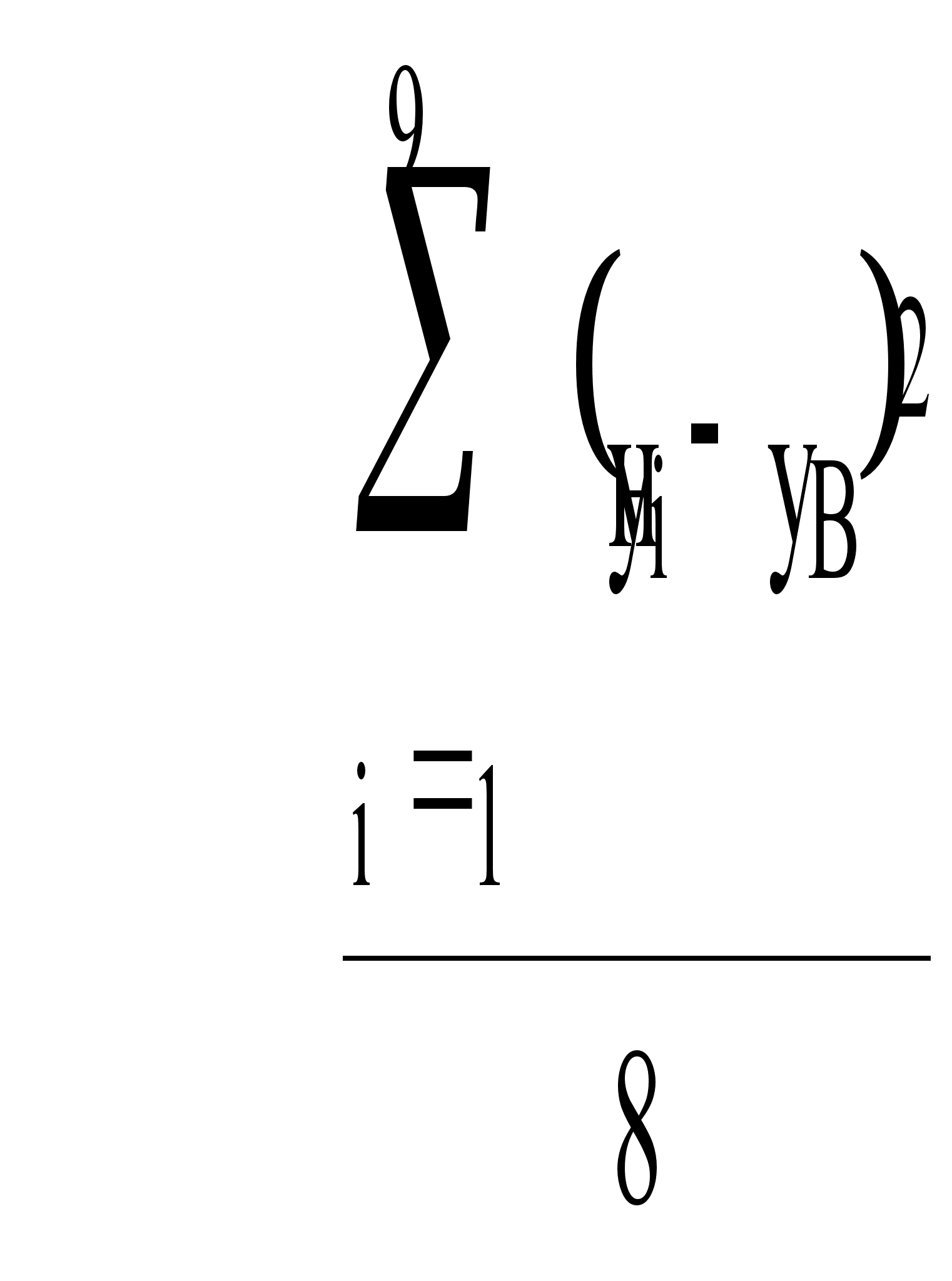

Вычислим наблюдаемое
значение критерия
(отношение
большей исправленной
дисперсии к
меньшей) по
формуле
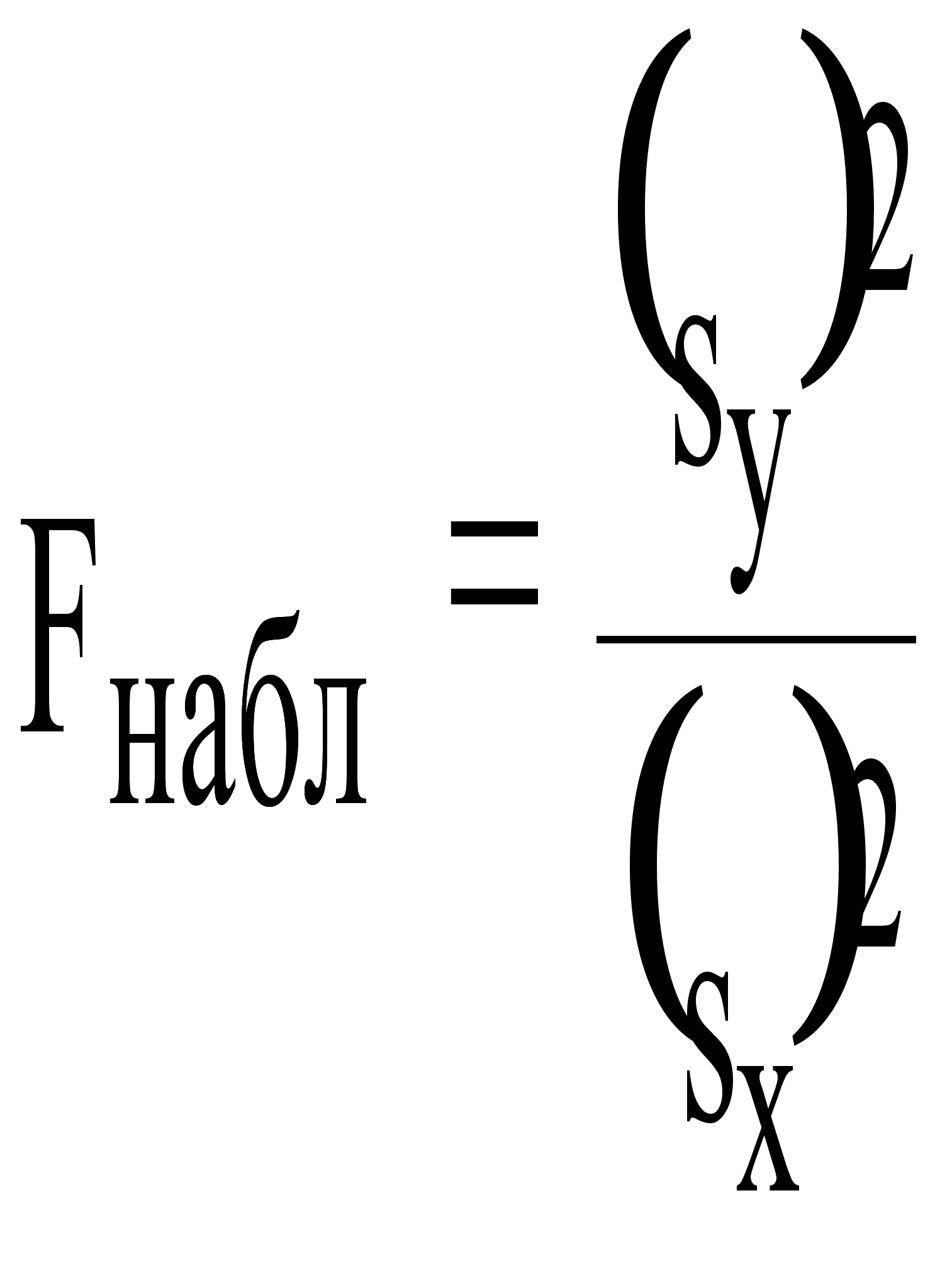 
По таблице
критических
точек распределения
Фишера-Снедекора,
по заданному
уровню значимости
0.1 и числам степеней
свободы 1 и 9 найдем
критическую
точку
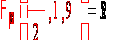

Гипотезу о
равенстве
генеральных
дисперсий
полученных
совокупностей
при уровне
значимости
0.1 не отвергается.
Задача 4.
Уравнение линии
регрессии:
получить 50
случайных
независимых
значений {x1,…,x50}
случайной
величины X,
равномерно
распределенной
на интервале
(0, 9); получить 50
случайных
независимых
значений {y1,…,y50}
случайной
величины Y следующим
образом: yi –
случайное
число, распределенное
по показательному
закону с параметром
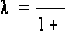
найти уравнение
прямой линии
регрессии Y на
X по этим данным;
проверить с
помощью критерия
«хи квадрат»
гипотезу о
нормальном
распределении
с нулевым
математическим
ожиданием
отклонений
имеющихся
данных от прямой
регрессии при
уровне значимости
0.05; при этом рассмотреть
группированную
выборку, разделив
отрезок [-max,
max] на
5 равных частей,
где max
– наибольшее
по абсолютной
величине отклонение
yi от линии
регрессии.
Решение:
Получим 50 случайных
независимых
значений {x1,…,x50}
случайной
величины X,
равномерно
распределенной
на интервале
(0, 9):
|
8.83174196071923
|
6.99053263384849
|
8.93890746776015
|
0.385410904884338
|
5.75393992289901
|
4.51090870331973
|
0.00656201597303152
|
7.97929550148547
|
6.6076143393293
|
4.54793028719723
|
|
1.40597840119153
|
2.18026433419436
|
5.0019520400092
|
5.61958408355713
|
0.148369995877147
|
4.25108801946044
|
4.77254802547395
|
1.53819094598293
|
6.14594876859337
|
0.812219920568168
|
|
6.2368449093774
|
1.69562757108361
|
0.777272606268525
|
2.94200689997524
|
7.07131071947515
|
2.973582518287
|
8.08092284202576
|
2.89726528152823
|
8.8169469544664
|
3.27939590346068
|
|
0.570096284151077
|
8.46246168483049
|
2.00763375777751
|
2.70446146745235
|
8.67470343410969
|
1.92118153441697
|
1.92350933980197
|
1.31150823365897
|
1.80795181263238
|
3.65427995938808
|
|
8.97048242390156
|
2.54362053237855
|
0.0568648930639029
|
6.36279229167849
|
1.68422971665859
|
4.25911642424762
|
2.50030734948814
|
4.91532963048667
|
7.35895295999944
|
4.39228433836252
|
Получим 50 случайных
независимых
значений {y1,…,y50}
случайной
величины Y следующим
образом: yi –
случайное
число, распределенное
по показательному
закону с параметром
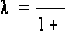 : :
|
24.9323592452182
|
15.7441606069719
|
15.5028112434691
|
2.87790855039727
|
4.16156795216443
|
0.190460347139702
|
0.252207251176988
|
5.55884492608762
|
11.5417165759534
|
11.8189116910915
|
|
9.57191092954621
|
6.48268208064067
|
10.6729845988228
|
11.9201379351172
|
0.0563900402236241
|
6.07239051882238
|
10.8341890845962
|
2.77373256888689
|
1.4735808529829
|
0.683544240471081
|
|
1.536352690789
|
0.100495382422226
|
6.48630115206778
|
1.01940005703768
|
6.79791391486788
|
2.34472037157293
|
2.06912254815368
|
3.42524848981833
|
9.45107565557296
|
3.18848770214796
|
|
1.69800713475763
|
2.42887690987151
|
6.18175839336735
|
4.85432860734921
|
3.12088295311468
|
0.14473630724364
|
0.312712437424258
|
1.16492882917332
|
2.95306149294792
|
6.38190212865322
|
|
0.293019110223049
|
0.664514453422601
|
3.47608211592645
|
20.3599120342622
|
1.45318365215952
|
9.23209976014301
|
0.965294785502523
|
6.29747102157127
|
6.46689933291391
|
3.14474865192493
|
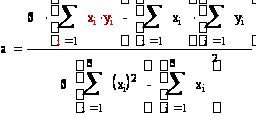
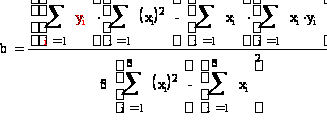
Найдем уравнение
прямой линии
регрессии Y на
X по этим данным
по формулам
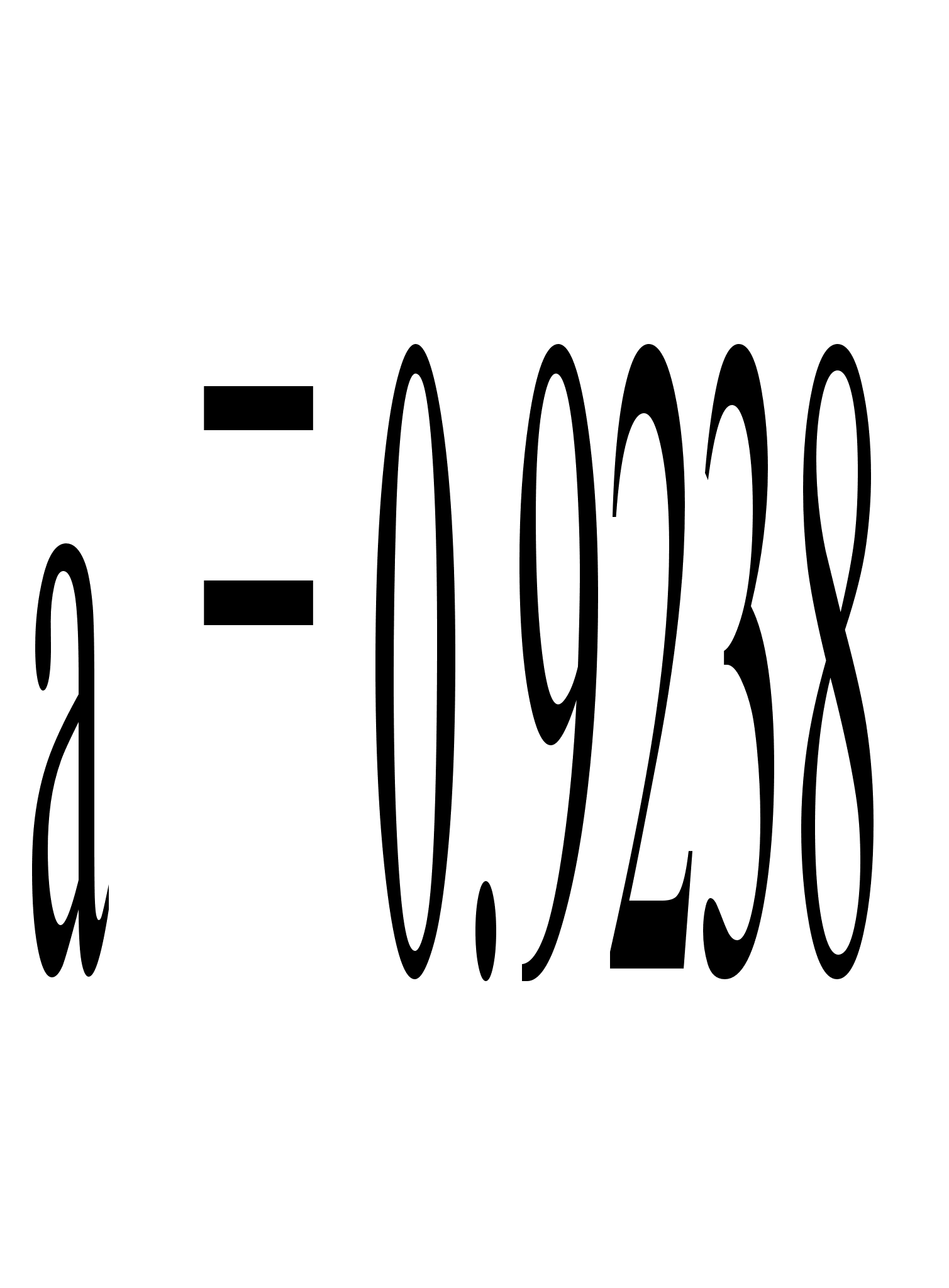
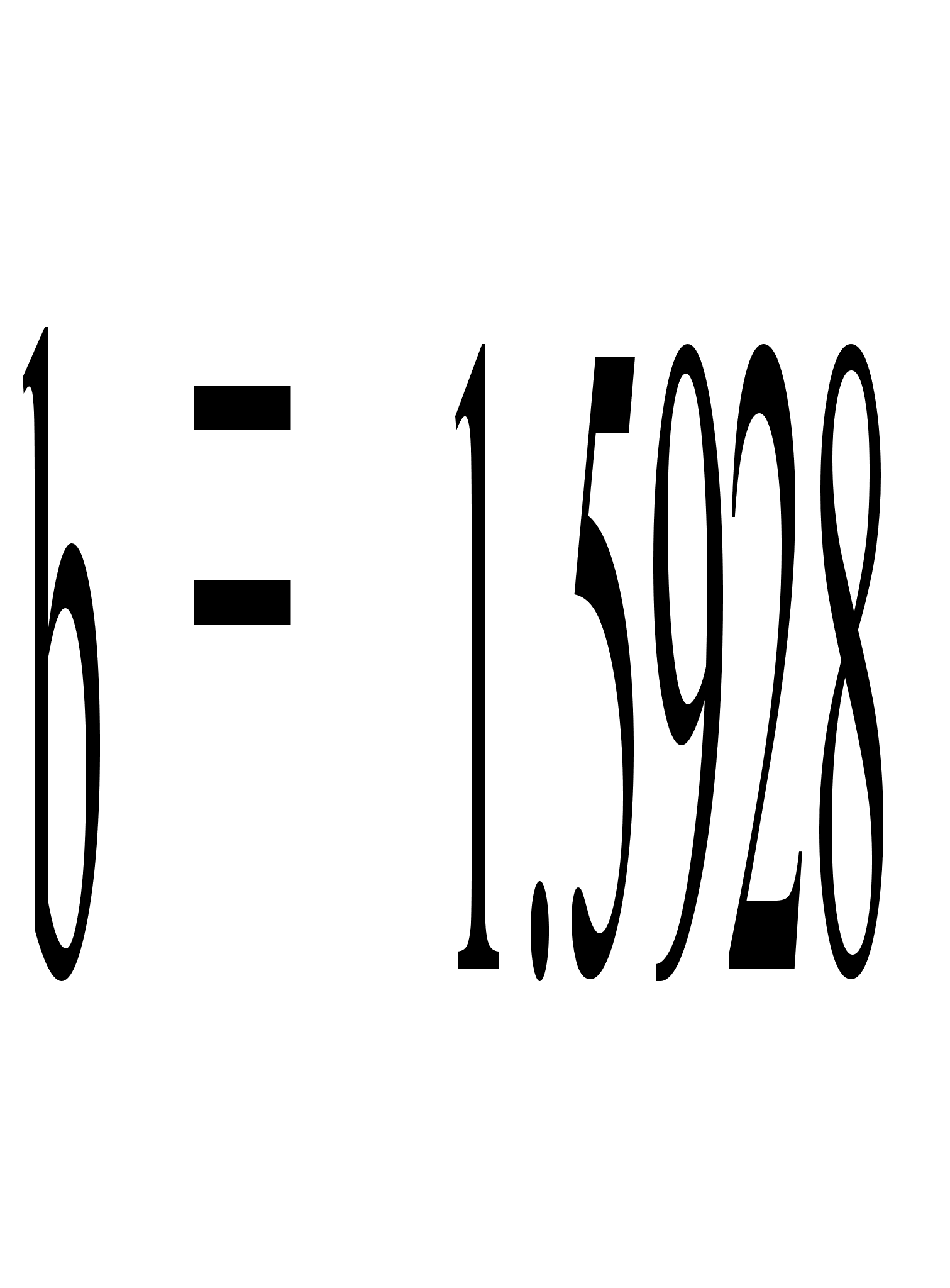
Уравнение
прямой линии
регрессии Y на
X:
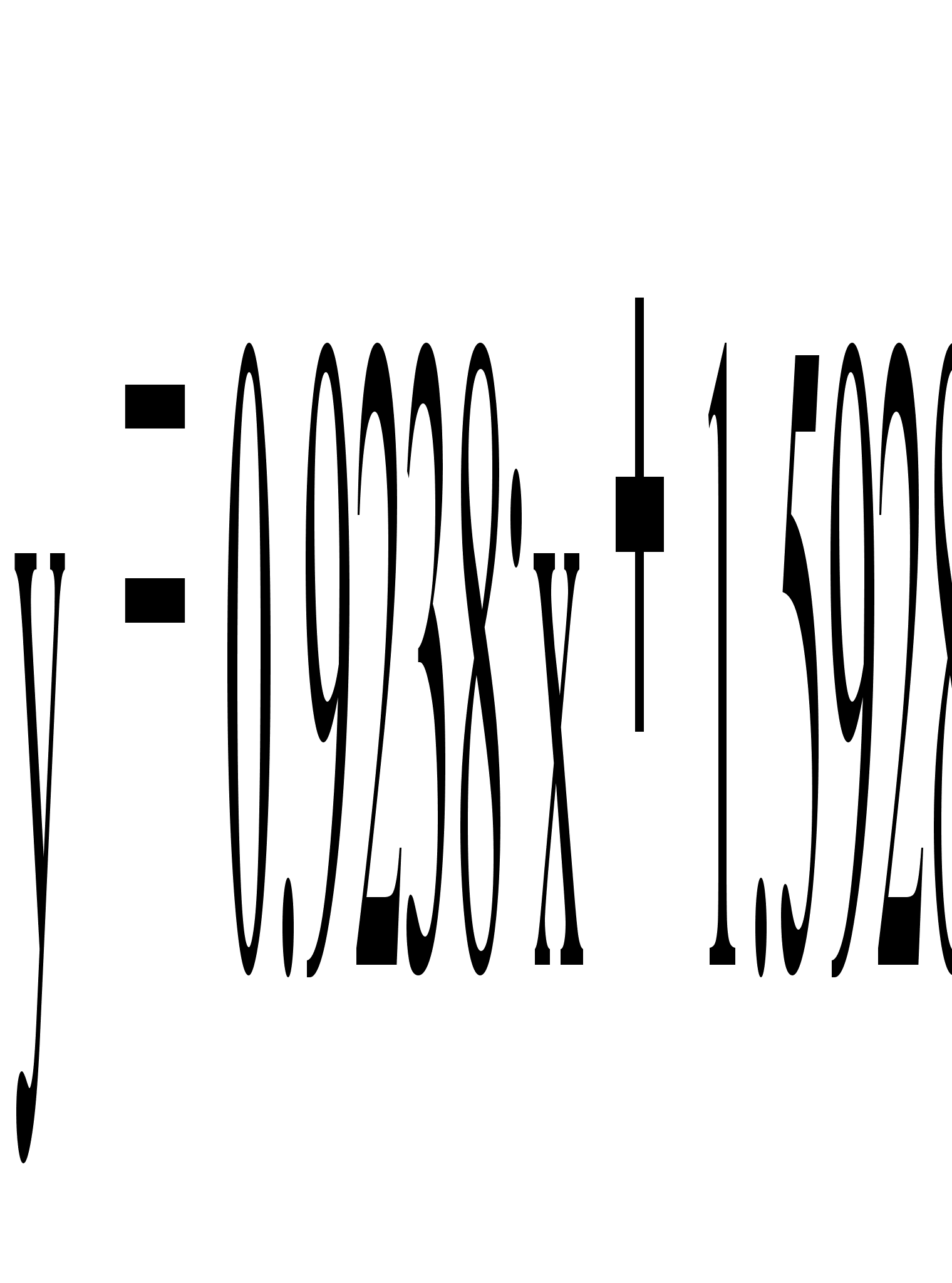
Получены следующие
значения отклонений
имеющихся
данных от прямой
регрессии:
|
15.1803992483777
|
7.69319511536507
|
5.65184678474214
|
0.929060620003659
|
-2.74697588437076
|
-5.56971364166513
|
-1.34664251825399
|
-3.40558552590376
|
3.84450875080244
|
6.024535447371
|
|
6.68021544884769
|
2.87566537149934
|
4.45916201865442
|
5.13571824955786
|
-1.67346851299683
|
0.55225091890577
|
4.83230056456327
|
-0.240106987952807
|
-5.79711892247662
|
-1.65960963866345
|
|
-5.81832115202078
|
-3.05879142493402
|
4.17543322148284
|
-3.29134973659658
|
-1.32767811582337
|
-1.99520044159931
|
-6.98919595084991
|
-0.844166923187427
|
-0.287216028830924
|
-1.43395768887411
|
|
-0.421461708068378
|
-6.98192485416478
|
2.73422581111747
|
0.763034293093572
|
-6.48599757504491
|
-3.22292770452086
|
-3.0571021088348
|
-1.63949073262982
|
-0.309995654309725
|
1.41312147312541
|
|
-9.58711575629829
|
-3.27818755099385
|
1.8307602174006
|
12.8888821627727
|
-1.69557328905632
|
3.70454314781532
|
-2.93739249325208
|
0.163674237751803
|
-1.9244299300759
|
-2.50583465100064
|
Проверим с
помощью критерия
«хи квадрат»
гипотезу о
нормальном
распределении
с нулевым
математическим
ожиданием
отклонений
имеющихся
данных от прямой
регрессии при
уровне значимости
0.05:
Найдем наибольшее
по абсолютной
величине отклонение
yi от линии
регрессии:
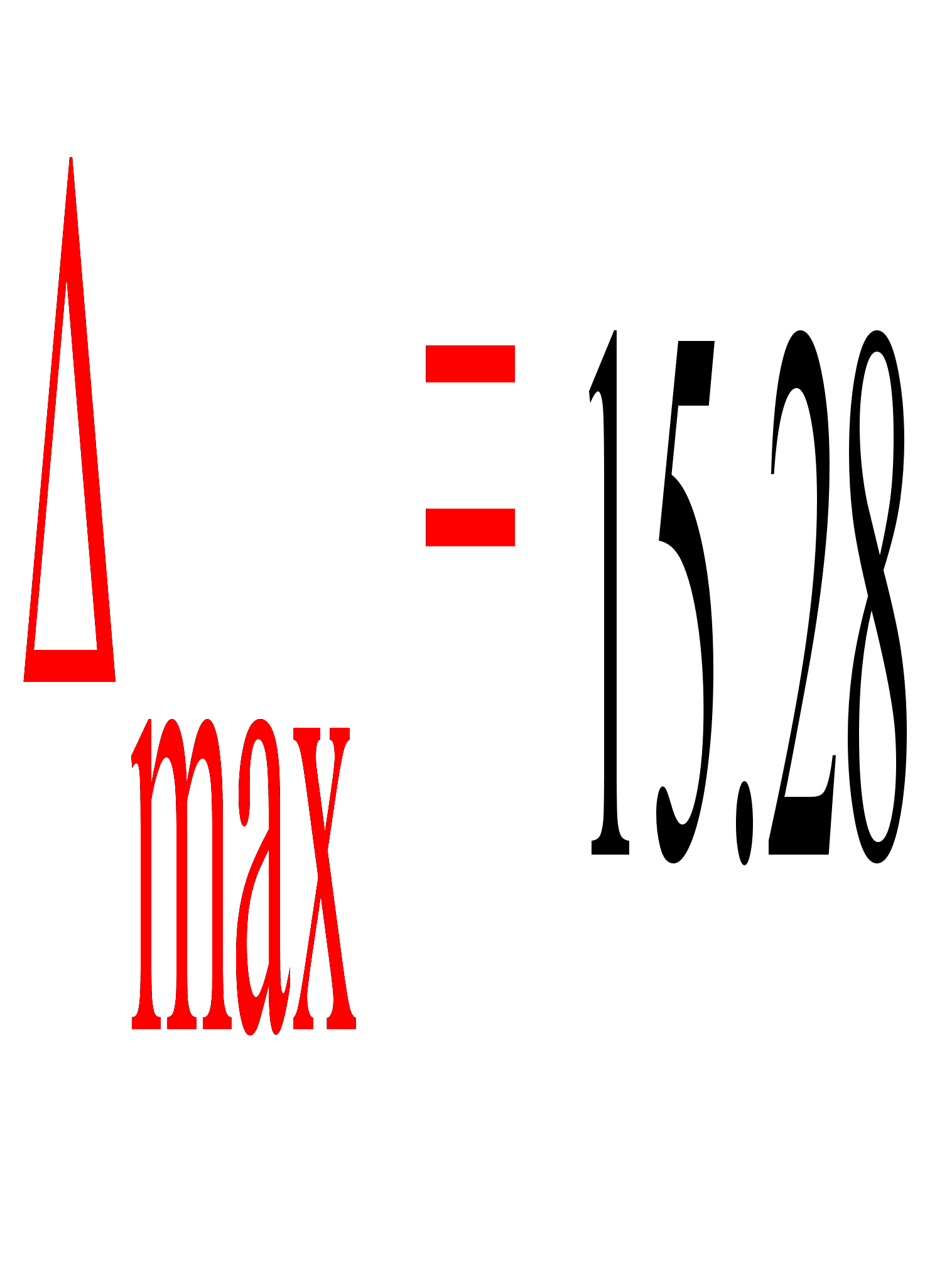
Рассмотрим
группированную
выборку, разделив
отрезок [-max,
max] на
5 равных частей:
|
zi
|
zi+1
|
ni
|
|
-15.1803992483777
|
-9.10823954902661
|
1 |
|
-9.10823954902661
|
-3.03607984967554
|
12 |
|
-3.03607984967554
|
3.03607984967554
|
25 |
|
3.03607984967554
|
9.10823954902662
|
10 |
|
9.10823954902662
|
15.1803992483777
|
2 |
Вычислим шаг:
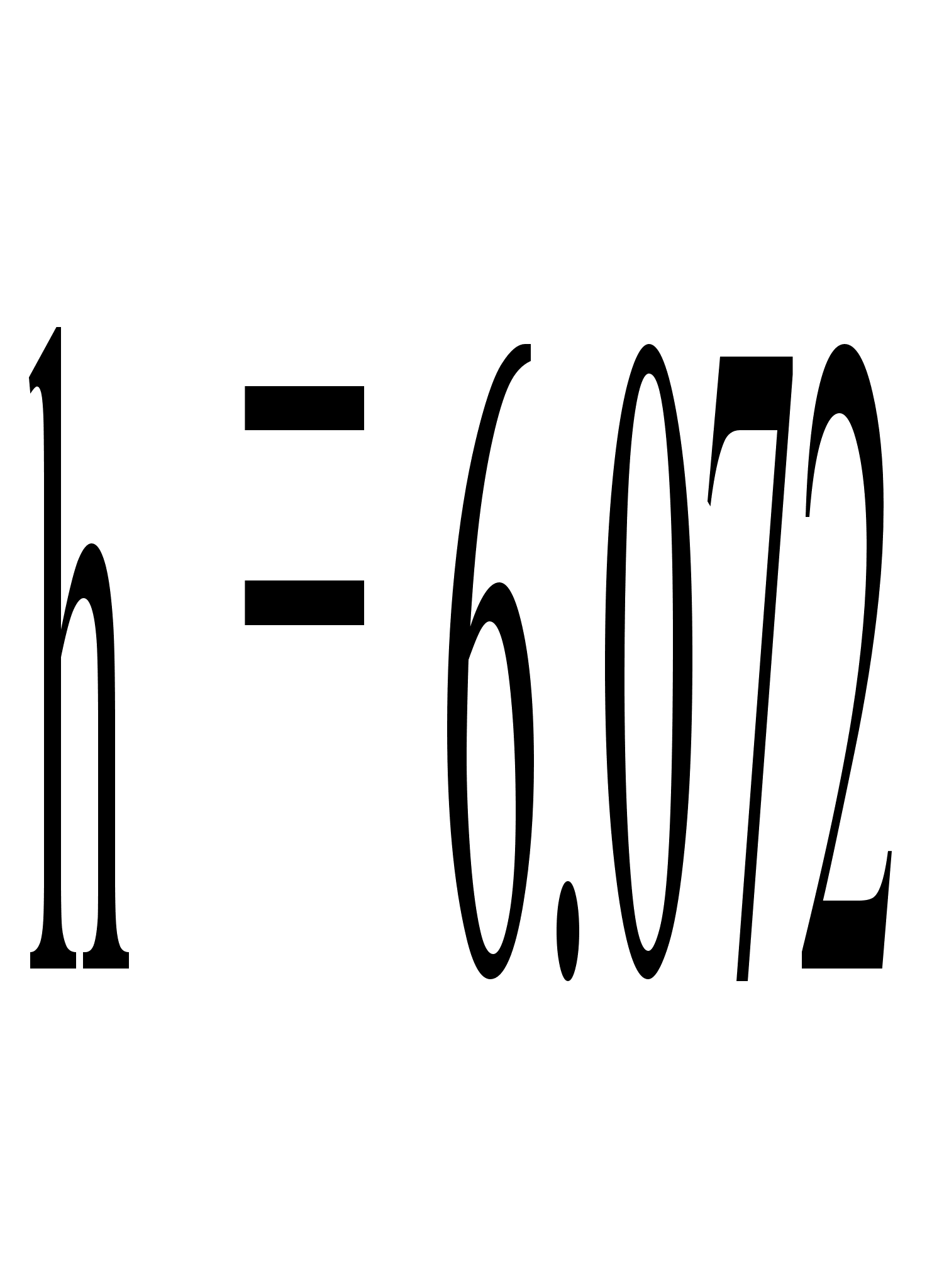
Вычислим выборочное
среднее по
формуле
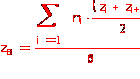
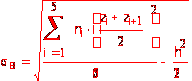
Вычислим выборочное
среднее квадратическое
отклонение
по формуле
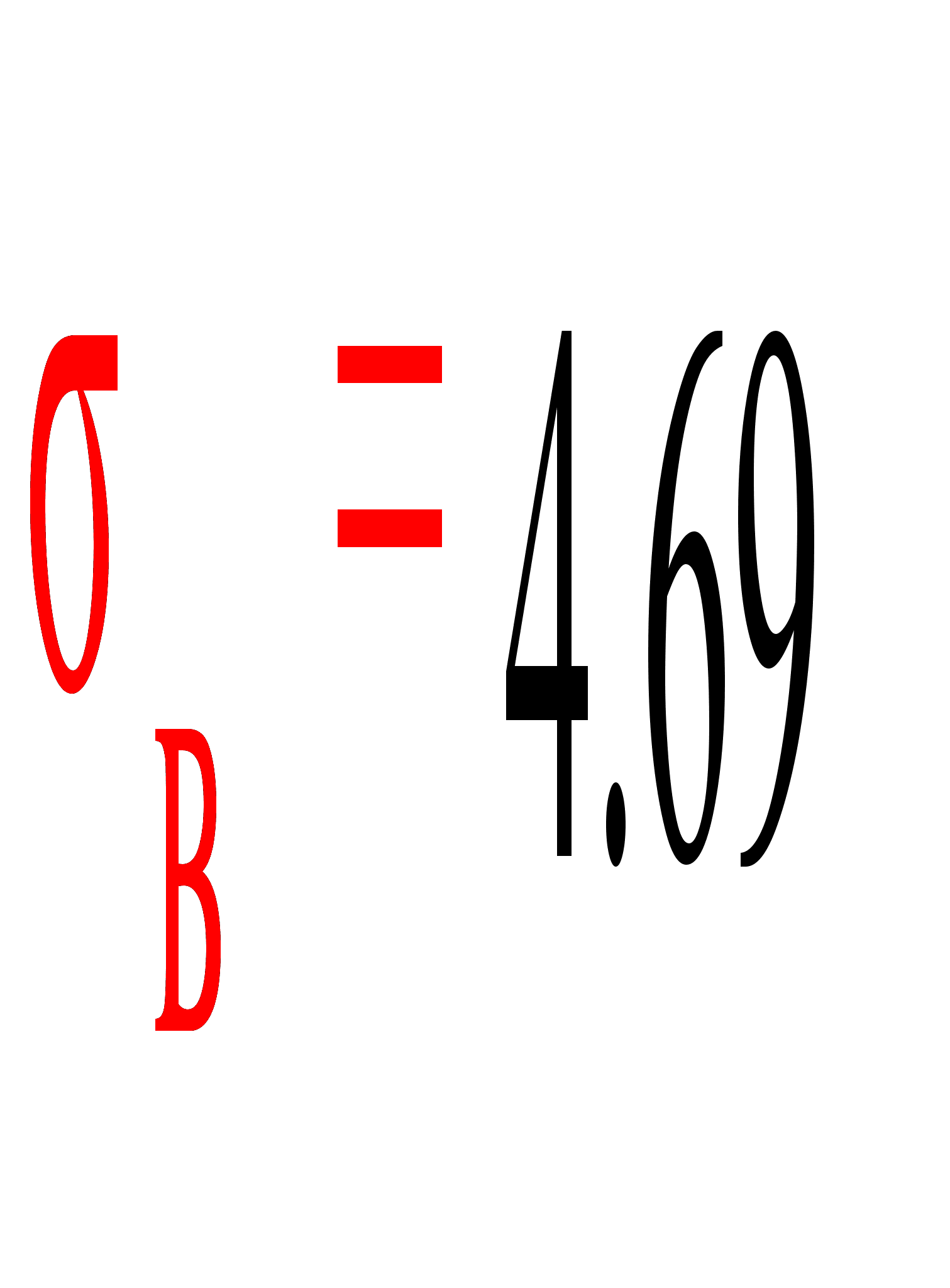
Вычислим
теоретические
вероятности
попадания в
интервалы (zi,
zi+1)
по формуле

Вычислим
теоретические
частоты по
формуле

|
zi
|
zi+1
|
ni
|
Pi
|
fi
|
(ni
- fi)2
/ fi
|
|
-15.1803992
|
-9.10823954
|
1
|
0.02546995
|
0.02546995
|
0.02546995
|
|
-9.10823954
|
-3.03607984
|
12
|
0.23264461
|
0.23264461
|
0.23264461
|
|
-3.03607984
|
3.036079849
|
25
|
0.48256076
|
0.48256076
|
0.48256076
|
|
3.036079849
|
9.108239549
|
10
|
0.23264461
|
0.23264461
|
0.23264461
|
|
9.108239549
|
15.18039924
|
2
|
0.02546995
|
0.02546995
|
0.02546995
|
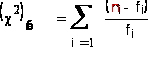
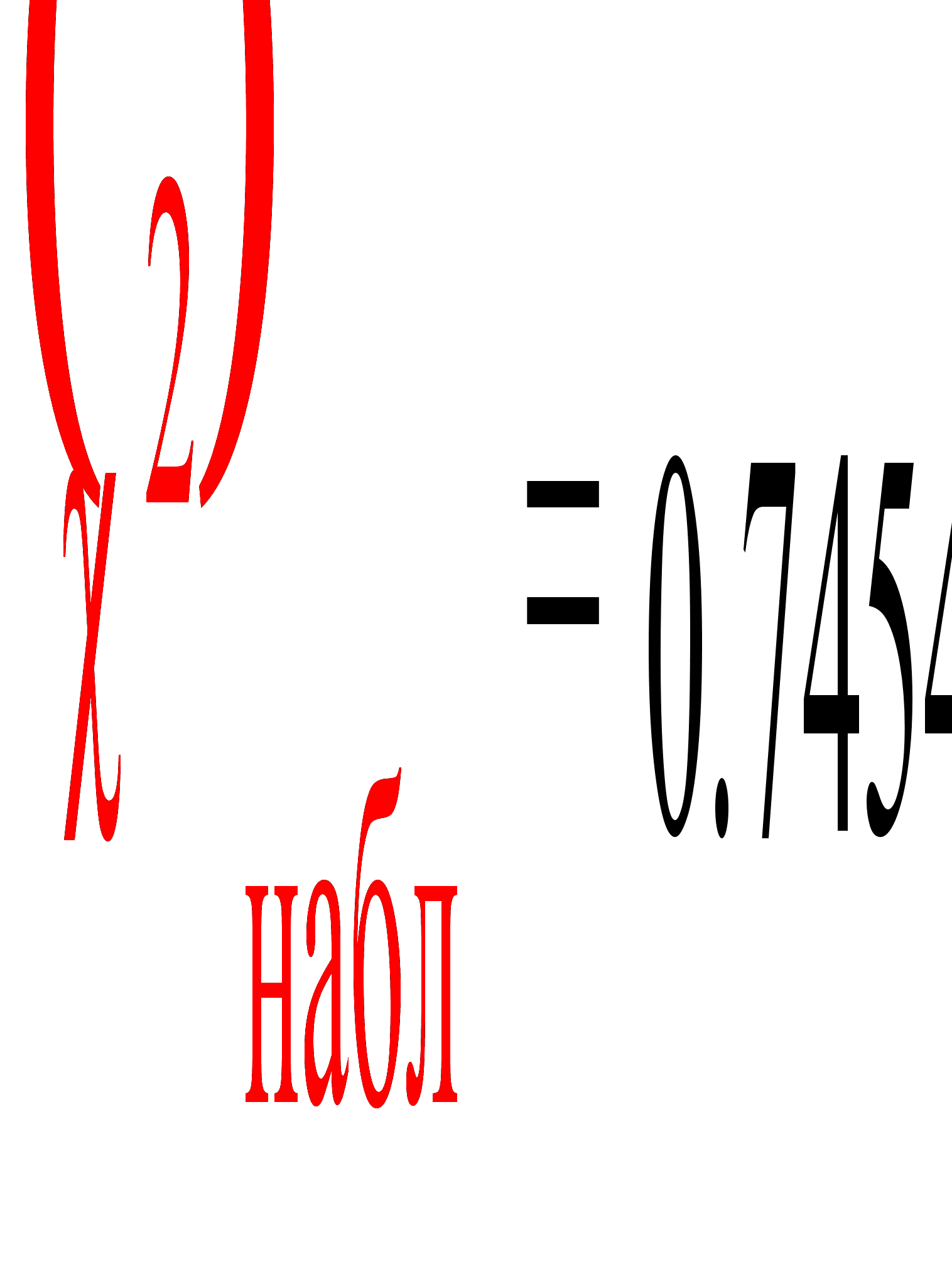
По таблице
критических
точек распределения
«хи квадрат»,
по заданному
уровню значимости
0.05 и числу степеней
свободы 3 находим
критическую
точку:

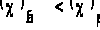
Гипотезу о
нормальном
распределении
с нулевым
математическим
ожиданием
отклонений
имеющихся
данных от прямой
регрессии при
уровне значимости
0.05 не отвергаем. |