Последовательность, у которой существует предел, называется сходящейся. Последовательность не являющаяся сходящейся называется расходящейся.
Определение: Последовательность {xn
} называется сходящейся, если существует такое число а, что последовательность {xn
-а} является бесконечно малой. При этом число а называется пределом последовательности {xn
}.
В соответствии с этим определением всякая бесконечно малая последовательность является сходящейся и имеет своим пределом число ноль.
Можно, также, дать еще одно определение сходящейся последовательности: Последовательность {xn
} называется сходящейся, если существует такое число а, что для любого положительного числа e можно указать номер N такой, что при n³N все элементы xn
этой последовательности удовлетворяют неравенству:
|xn
-a|<e.
Некоторые свойства сходящихся последовательностей:
ТЕОРЕМА: Сходящаяся последовательность имеет только один предел.
Доказательство: Пусть a и b – пределы сходящейся последовательности {xn
}. Тогда, используя специальное представление для элементов xn
сходящейся последовательности {xn
}, получим xn
=а+an
, xn
=b+bn
, где an
и bn
– элементы бесконечно малых последовательностей {an
} и {bn
}.
Вычитая данные соотношения, найдем an
-bn
=b-a. Так как все элементы бесконечно малой последовательности {an
-bn
} имеют одно и то же постоянное значение b-a, то (по теореме: Если все элементы бесконечно малой последовательности {an
} равны одному и тому же числу с, то с=0) b-a=0, т.е. b=a. Теорема доказана.
ТЕОРЕМА: Сходящаяся последовательность ограничена.
Доказательство: Пусть {xn
} - сходящаяся последовательность и а – ее предел. Представим ее в следующем виде:
xn
=а+an
,
где an
- элемент бесконечно малой последовательности. Так как бесконечно малая последовательность {an
} ограничена (по теореме: Бесконечно малая последовательность ограничена.), то найдется такое число А, что для всех номеров n справедливо неравенство |an
|£А. Поэтому | xn
| £ |a| + A для всех номеров n, что и означает ограниченность последовательности {xn
}. Теорема доказана.
Ограниченная последовательность может и не быть сходящейся. Например, последовательность 1, -1, 1, -1, … - ограничена , но не является сходящейся. В самом деле, если бы эта последовательность сходилась к некоторому числу а, то каждая из последовательностей {xn
-a} и {xn+1
-a} являлась бы бесконечно малой. Но тогда (по теореме: Разность бесконечно малых последовательностей есть бесконечно малая последовательность.) {(xn
-a) – (xn+1
-a)}={xn
– xn+1
} была бы бесконечно малой, что невозможно т.к. |xn
– xn+1
| = 2 для любого номера n.
Реклама

ТЕОРЕМА: Сумма сходящихся последовательностей {хn
} и {yn
} есть сходящаяся последовательность, предел которой равен сумме пределов последовательностей {хn
} и {yn
}.
Доказательство: Пусть а и b – соответственно пределы последовательностей {хn
} и {yn
}. Тогда:
xn
=а+an
, yn
=b+bn
,
где {an
} и {bn
) – бесконечно малые последовательности. Следовательно, (хn
+ yn
) - (а + b) =an
+bn
.
Таким образом, последовательность {(хn
+ yn
) - (а + b)} бесконечно малая, и поэтому последователдьность {хn
+ yn
} сходится и имеет своим пределом число а+b. Теорема доказана.
ТЕОРЕМА: Разность сходящихся последовательностей {хn
} и {yn
} есть сходящаяся последовательность, предел которой равен разности пределов последовательностей {хn
} и {yn
}.
Доказательство: Пусть а и b – соответственно пределы последовательностей {хn
} и {yn
}.Тогда:
xn
=а+an
, yn
=b+bn
,
где {an
} и {bn
) – бесконечно малые последовательности. Следовательно, (хn
- yn
) - (а - b) =an
-bn
.
Таким образом, последовательность {(хn
- yn
) - (а - b)} бесконечно малая, и поэтому последователдьность {хn
- yn
} сходится и имеет своим пределом число а-b. Теорема доказана.
ТЕОРЕМА: Произведение сходящихся последовательностей {хn
} и {yn
} есть сходящаяся последовательность, предел которой равен произведению пределов последовательностей {хn
} и {yn
}.
Доказательство: Пусть а и b – соответственно пределы последовательностей {хn
} и {yn
}, то xn
=а+an
, yn
=b+bn
и xn
×yn
=a×b+a×bn
+b×an
+an
×bn
. Следовательно,
xn
×yn
-а×b=a×bn
+b×an
+an
×bn
.
(в силу теоремы: Произведение ограниченной последовательности на бесконечно малую есть бесконечно малая последовательность.) последовательность {a×bn
+b×an
+an
×bn
} бесконечно малая, и поэтому последовательность {xn
×yn
-а×b} тоже бесконечно малая, а значит последовательность {xn
×yn
} сходится и имеет своим пределом число а×b. Теорема доказана.
Реклама

ЛЕММА: Если последовательность {yn
} сходится и имеет отличный от ноля предел b, то, начиная с некоторого номера, определена последовательность 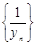 , которая является ограниченной. , которая является ограниченной.
Доказательство: Пусть 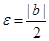 . Так как b¹0, то e>0. Пусть N – номер, соответствующий этому e, начиная с которого выполняется неравенство: . Так как b¹0, то e>0. Пусть N – номер, соответствующий этому e, начиная с которого выполняется неравенство:
|yn
-b|<e или |yn
-b|<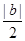
из этого неравенства следует, что при n³N выполняется неравенство |yn
|>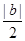 . Поэтому при n³N имеем . Поэтому при n³N имеем 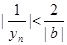 . Следовательно, начиная с этого номера N, мы можем рассматривать последовательность . Следовательно, начиная с этого номера N, мы можем рассматривать последовательность 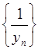 , и эта последовательность ограничена. Лемма доказана. , и эта последовательность ограничена. Лемма доказана.
ТЕОРЕМА: Частное двух сходящихся последовательностей {xn
} и {yn
} при условии, что предел {yn
} отличен от ноля, есть сходящаяся последовательность, предел которой равен частному пределов последовательностей {xn
} и {yn
}.
Доказательство: Из доказанной ранее леммы следует, что, начиная с некоторого номера N, элементы последовательности {yn
} отличны от ноля и последовательность 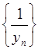 ограничена. Начиная с этого номера, мы и будем рассматривать последовательность ограничена. Начиная с этого номера, мы и будем рассматривать последовательность 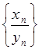 . Пусть а и b – пределы последовательностей {xn
} и {yn
}. Докажем, что последовательность . Пусть а и b – пределы последовательностей {xn
} и {yn
}. Докажем, что последовательность 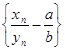 бесконечно малая. В самом деле, так как xn
=а+an
, yn
=b+bn
, то бесконечно малая. В самом деле, так как xn
=а+an
, yn
=b+bn
, то
 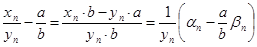 . .
Так как последовательность 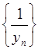 ограничена, а последовательность ограничена, а последовательность 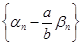 бесконечно мала, то последовательность бесконечно мала, то последовательность 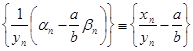 бесконечно малая. Теорема доказана. бесконечно малая. Теорема доказана.
Итак, теперь можно сказать, что арифметические операции над сходящимися последовательностями приводят к таким же арифметическим операциям над их пределами.
ТЕОРЕМА: Если элементы сходящейся последовательности {xn
}, начиная с некоторого номера, удовлетворяют неравентству xn
³b (xn
£b), то и предел а этой последовательности удовлетворяет неравенству а³b (a£b).
Доказательство: Пусть все элементы xn
, по крайней мере начиная с некоторого номера, удовлетворяют неравенству xn
³b. Предположим, что а<b. Поскольку а – предел последовательности {xn
}, то для положительного e=b-a можно указать номер N такой, что при n³N выполняется неравенство
|xn
-a|<b-a.
Это неравенство эквивалентно
-(b-a)<xn
-a<b-a
Используя правое из этих неравенств мы получим xn
<b, а это противоречит условию теоремы. Случай xn
£b рассматривается аналогично. Теорема доказана.
Элементы сходящейся последовательности {xn
} могут удовлетворять строгому неравенству xn
>b, однако при этом предел а может оказаться равным b. Например, если xn
=1/n, то xn
>0, однако 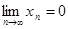 . .
Следствие 1: Если элементы xn
и уn
у сходящихся последовательностей {xn
} и {yn
}, начиная с некоторого номера, удовлетворяют неравенству xn
£ уn
, то их пределы удовлетворяют аналогичному неравенству
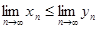 . .
Элементы последовательности {yn
-xn
} неотрицательны, а поэтому неотрицателен и ее предел 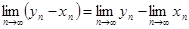 . Отсюда следует, что . Отсюда следует, что
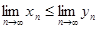 . .
Следствие 2: Если все элементы сходящейся последовательности {xn
} находятся на сегменте [a,b], то и ее предел с также находится на этом сегменте.
Это выполняется, так как а£xn
£b, то a£c£b.
ТЕОРЕМА: Пусть {xn
} и {zn
}- сходящиеся последовательности, имеющие общий предел а. Пусть, кроме того, начиная с некоторого номера, элементы последовательности {yn
}удовлетворяют неравенствам xn
£yn
£zn
. Тогда последовательность {yn
} сходится и имеет предел а.
Доказательство: достаточно доказать, что {yn
-a} является бесконечно малой. Обозначим через N’ номер, начиная с которого, выполняются неравенства, указанные в условии теоремы. Тогда, начиная с этого же номера, будут выполнятся также неравенства xn
-а £ yn
-а £ zn
-а. Отсюда следует, что при n³N’ элементы последовательности {yn
-a} удовлетворяют неравенству
|yn
-a| £ max {|xn
-a|, |zn
-a|}.
Так как 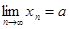 и и 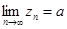 , то для любого e>0 можно указать номера N1
и N2
такие, что при n³N1
|xn
-a|<e, а при n³N2
|zn
-a|<e. Итак последовательность {yn
-a} бесконечно малая. Теорема доказана. , то для любого e>0 можно указать номера N1
и N2
такие, что при n³N1
|xn
-a|<e, а при n³N2
|zn
-a|<e. Итак последовательность {yn
-a} бесконечно малая. Теорема доказана.
Итак, мы показали неравенства, которым удовлетворяют элементы сходящихся последовательностей, в пределе переходят в соответствующие неравенства для пределов этих последовательностей.
ПРИМЕРЫ
1. Последовательность 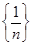 сходится и имеет своим пределом ноль. Ведь каково бы ни было e>0, по свойству Архимеда вещественных чисел существует такое натуральное число ne
, что ne
> сходится и имеет своим пределом ноль. Ведь каково бы ни было e>0, по свойству Архимеда вещественных чисел существует такое натуральное число ne
, что ne
>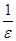 . Поэтому . Поэтому 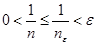 для всех n³ne
, а это означает, что для всех n³ne
, а это означает, что 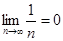 . .
2. Последовательность 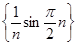 сходится и сходится и 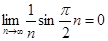 , что следует из того, что , что следует из того, что
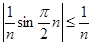 , и того, что , и того, что 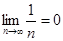 . .
ЗАДАЧИ
ЗАДАЧА № 1
Пусть числовая последовательность а1
, а2
, а3
, … удовлетворяет условию
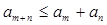 (m, n = 1, 2, 3, … ), (m, n = 1, 2, 3, … ),
тогда последовательность
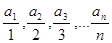 ,… ,…
должна либо расходиться к 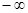 , причем предел этой последовательности будет равен ее нижней грани. , причем предел этой последовательности будет равен ее нижней грани.
РЕШЕНИЕ:
Видим частный случай теоремы у M. Fekete. Достаточно рассмотреть случай, когда нижняя грань a конечна. Пусть e>0 и 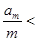 a+e. Всякое целое число n может быть представлено в форме n=qm+r, где r=0 или 1, или 2, …, или m-1. Полагая единообразие а0
=0, имеем: a+e. Всякое целое число n может быть представлено в форме n=qm+r, где r=0 или 1, или 2, …, или m-1. Полагая единообразие а0
=0, имеем:
an
=aqm+r
£am
+am
+…+am
+ar
=qam
+ar
,
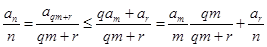 , ,
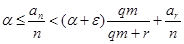
ЗАДАЧА № 2
Пусть числовая последовательность а1
, а2
, а3
, … удовлетворяет условию
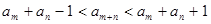
тогда существует конечный предел
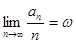 , ,
причем
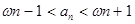 (n = 1, 2, 3, … ). (n = 1, 2, 3, … ).
РЕШЕНИЕ:
Из неравенств 2am
-1<a2m
<2am
+1 получаем:
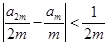 (*) (*)
Ряд
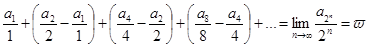
сходится, ибо в силу неравенства (*) он мажорируется сходящимся рядом:
|a1
|+2-1
+2-2
+2-3
+…
запишем целое число n по двоичной системе:
n=2m
+e1
2m-1
+e2
2m-2
+…+em
(e1
, e2
, …, em
= 0 или 1)
согласно предположению
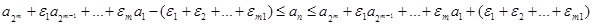
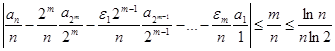 . .
Применяя теорему (1) для данных:
s0
=0, s1
=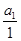 , sm-1
= , sm-1
=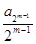 , sm
= , sm
=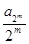 , …, pn0
=0, pn1
= , …, pn0
=0, pn1
=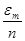 , …, pn, m-1
= , …, pn, m-1
=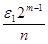 , ,
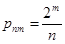 , pn, m+1
=0, …, , pn, m+1
=0, …,
заключаем, что 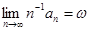 . Наконец, в силу (*) имеем: . Наконец, в силу (*) имеем:
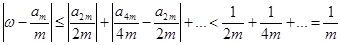 . .
ЗАДАЧА № 3
Если общий член ряда, не являющегося ни сходящимся, ни расходящимся в собственном смысле, стремится к нулю, то частичные суммы этого ряда расположены всюду плотно между их нижним и верхним пределами lim inf и lim sup.
РЕШЕНИЕ:
Нам достаточно рассмотреть случай, когда частичные суммы s1
, s2
, …, sn
, … ограничены. Пусть 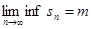 , , 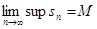 , l - целое положительное число, l>2 и , l - целое положительное число, l>2 и 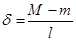 . .
Разобьем числовую прямую на l интервалов точками
-¥, m+d, m+2d, …, M-2d, M-d, +¥.
Выберем такое N, чтобы для n>N выполнялось неравенство |sn
-sn+1
|<d. Пусть, далее, sn1
(n1
>N) лежит в первом интервале и sn2
(n2
> n1
) – в последнем. Тогда числа конечной последовательности 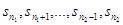 не смогут “перепрыгнуть” ни один из l-2 промежуточных интервалов длиной d. Аналогично рассуждаем и в том случае, когда последовательность будет не «медленно восходящей», а «медленно нисхожящей». не смогут “перепрыгнуть” ни один из l-2 промежуточных интервалов длиной d. Аналогично рассуждаем и в том случае, когда последовательность будет не «медленно восходящей», а «медленно нисхожящей».
ЗАДАЧА № 4
Пусть для последовательности t1
, t2
, … , tn
, … существует такая последовательность стремящихся к нулю положительных чисел 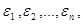 …, что для каждого n …, что для каждого n
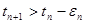 . .
Тогда числа t1
, t2
, … , tn
, …лежат всюду плотно между их нижним и верхним пределами.
РЕШЕНИЕ:
Существуют в сколь угодно большом удалении конечные последовательности 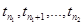 , произвольно медленно нисходящие от верхнего предела последовательности к ее нижнему пределу. , произвольно медленно нисходящие от верхнего предела последовательности к ее нижнему пределу.
ЗАДАЧА № 5
Пусть v1
, v2
, … , vn
, … - положительные числа, v1
£ v2
£ v3
… Совокупность предельных точек последовательности
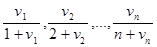 , … , …
заполняет замкнутый интервал (длина которого равна нулю, если эта последовательность стремится к пределу).
РЕШЕНИЕ:
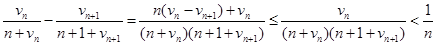
ЗАДАЧА № 6
Числовая последовательность, стремящаяся к 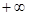 , имеет наименьший член. , имеет наименьший член.
РЕШЕНИЕ:
Какое бы число мы ни задали, слева от него будет находиться лишь конечное число членов последовательности, а среди конечного множества чисел существует одно или несколько наименьших.
ЗАДАЧА № 7
Сходящаяся последовательность имеет либо наибольший член, либо наименьший, либо и тот и другой.
РЕШЕНИЕ:
При совпадении верхней и нижней граней рассматриваемой последовательности теорема тривиальна. Пусть поэтому они различны. Тогда по крайней мере одна из них отличается от предела последовательности. Она и будет равна наибольшему, соответственно наименьшему, члену последовательности.
ЗАДАЧА № 8
Пусть l1
, l2
, l3
, … , lm
, … - последовательность положительных чисел и 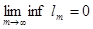 , тогда существует бесконечно много номеров n, для которых ln
меньше всех предшествующих ему членов последовательности l1
, l2
, l3
, … , ln-1
. , тогда существует бесконечно много номеров n, для которых ln
меньше всех предшествующих ему членов последовательности l1
, l2
, l3
, … , ln-1
.
РЕШЕНИЕ:
Пусть задано целое положительное число m и h – наименьшее из чисел l1
, l2
, l3
, … , lm
; h>0. Согласно предположению в рассматриваемой последовательности существуют члены, меньше чем h. Пусть n – наименьший номер, для которого ln
<h. Тогда:
n>m; ln
<l1
, ln
<l2
, …, ln
<ln-1
.
ЗАДАЧА № 9
Пусть l1
, l2
, l3
, … , lm
, … - последовательность положительных чисел и 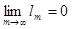 , тогда существует бесконечно много номеров n, для которых ln
превосходит все следующие за ним члены ln+1
, ln+2
, ln+3
,… , тогда существует бесконечно много номеров n, для которых ln
превосходит все следующие за ним члены ln+1
, ln+2
, ln+3
,…
ЗАДАЧА № 10
Пусть числовые последовательности
l1
, l2
, l3
, … , lm
, … (lm
>0),
s1
, s 2
, s 3
, … , s m
, … (s1
>0, sm+1
>sm
, m=1, 2, 3, …)
обладают тем свойством, что
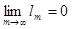 , , 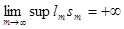 . .
Тогда существует бесконечно много номеров n, для которых одновременно выполняются неравенства
ln
>ln+1
, ln
>ln+2
, ln
>ln+3
, …
ln
sn
>ln-1
sn-1,
ln
sn
>ln-2
sn-2,
… ln
sn
>l1
s1,
РЕШЕНИЕ:
Будем называть lm
«выступающим» членом последовательности, если lm
больше всех последующих членов. Согласно предположению в первой последовательности содержится бесконечно много выступающих членов; пусть это будут:
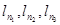 ,… ,… 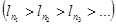
Каждый невыступающий член lv
заключается (для v>n1
) между двумя последовательными выступающими членами, скажем nr-1
<v<nr
. Имеем последовательно:
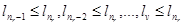 , ,
значит
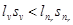 (*) (*)
отсюда заключаем, что
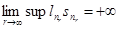
Действительно, в противном случае 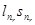 , значит, в силу (*) и вся последовательность , значит, в силу (*) и вся последовательность
l1
s1
, l2
s2
, … были бы ограничены, что противоречит предположению. Теперь пусть задано целое положительное число m и h – наименьшее из чисел 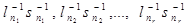 ,… ; h>0. Согласно предположению в рассматриваемой последовательности существуют члены, меньше чем h. Пусть k – наименьший номер, для которого ,… ; h>0. Согласно предположению в рассматриваемой последовательности существуют члены, меньше чем h. Пусть k – наименьший номер, для которого 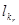 <h. Тогда: <h. Тогда:
k>m; 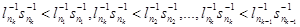 . .
ЗАДАЧА № 11
Если числовая последовательность 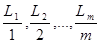 ,… стремится к ,… стремится к 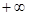 и А превышает ее наименьший член, то существует такой номер n (возможно несколько таких), n³1, что n отношений и А превышает ее наименьший член, то существует такой номер n (возможно несколько таких), n³1, что n отношений
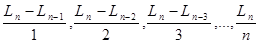
все не больше А, а бесконечное множество отношений
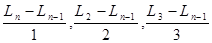 ,… ,…
все не меньше А.
РЕШЕНИЕ:
Имеем 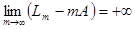 . Пусть минимум последовательности . Пусть минимум последовательности
L0
-0, L1
-A, L2
-2A, L3
-3A, …
Будет Ln
-nA; тогда
Ln-u
-(n-u)A³ Ln
-nA; Ln+v
-(n+v)A³ Ln
-nA,
u=1, 2, …, n; v=1, 2, 3, …; n=0 исключено в силу предложений относительно А.
ЗАДАЧА № 12
Пусть относительно числовой последовательности l1
, l2
, l3
, … , lm
, … предполагается лишь, что
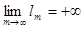 . .
Пусть, далее, А>l1
. Тогда существует такой номер n, n ³ 1, что одновременно выполняются все неравенства
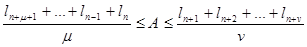
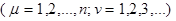 . .
Если А®¥, то также n®¥.
РЕШЕНИЕ:
Пусть
l1
+l2
+l3
+…+lm
=Lm
, m=1, 2, 3, …; L0
=0.
Так как L1
-A<0, то L0
-0 не является минимумом в предыдущем решении. ln+1
³A; поэтому ln+1,
а следовательно и n должны стремиться к бесконечности одновременно с А.
ЗАДАЧА № 13
Пусть числовая последовательность l1
, l2
, l3
, … , lm
, … удовлетворяет условиям
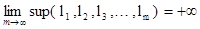 , , 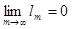
Пусть, далее, l1
>A>0. Тогда существует такой номер n, n ³ 1, что одновременно выполняются все неравенства
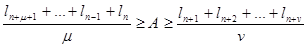
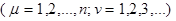 . .
Если А®0, то также n®0.
РЕШЕНИЕ:
Положим
l1
+l2
+l3
+…+lm
=Lm
, m=1, 2, 3, …; L0
=0.
Тогда 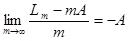 . Последовательность . Последовательность
L0
-0, L1
-A, L2
-2A, L3
-3A, …, Lm
-mA, …
стремится к -¥. Пусть ее наибольший член будет Ln
-nA. Тогда интересующие нас неравенства будут выполняться для этого номера n.
В последовательности L0
, L1
, …, Lm
, … содержится бесконечно много членов, превышающих все предыдущие. Пусть Ls
будет один из них. Тогда числа:
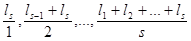
все положительны: коль скоро А меньше наименьшего из них, соответствующий А номер n больше или равен s. Точки (n, Ln
) должны быть обтянуты теперь бесконечным выпуклым сверху полигоном.
|