Вариант № 7
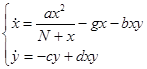
Задание:
1. Ввести новые переменные, максимально уменьшив число параметров системы.
2. Найти неподвижные точки системы и исследовать их характеристики в зависимости от параметров системы.
3. Исследовать поведение предельных циклов. Доказать их существование/несуществование.
4. Построить фазовые портреты системы при всех возможных параметрах системы.
5. Дать биологическую интерпретацию полученным результатам.
1. Вводим новые переменные x - Ax, y - By, t - Tt и переписываем систему:
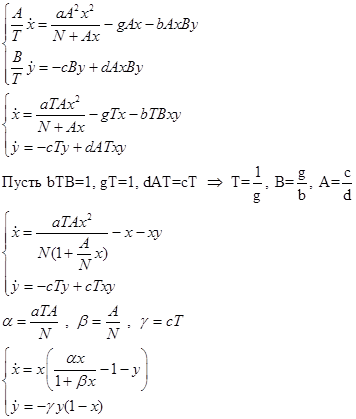
2. Нахождение неподвижных точек преобразованной системы
2.1 x=0,y=0 ==> O(0,0)
2.2 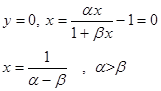
P
2.3 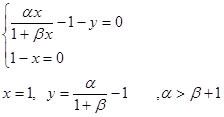
Q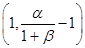
3. Характеристики неподвижных точек
Запишем Якобиан нашей системы
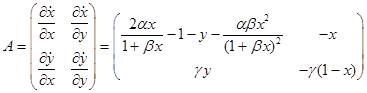
3.1 
3.2 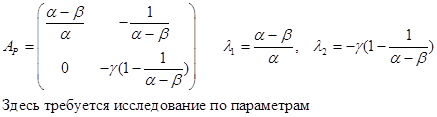
3.3 
Проведем дополнительное исследование, обозначив на параметрическом портрете возможные области значений  . .
а) точка О – сток, как было показано выше;
б) точка Р : :

Область 1: 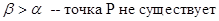
Область 2: 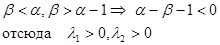
Точка Р – исток (неуст. узел)
Область 3: 
Точка Р – седло
в) точка Q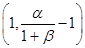 : :
Область 1: 
Область 2: 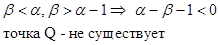
Область 3: 

Точка Q – исток ( неустойчивый узел)
Кроме того, при поиске собственных значений Якобиана возникает уравнение
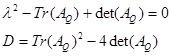
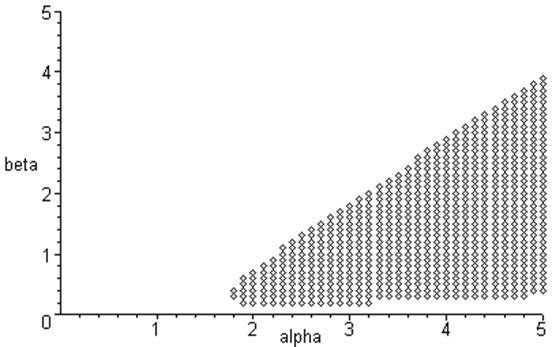
Решение уравнения D<0 производилось графически , поскольку аналитическое решение в этом случае представляется затруднительным. Для этого использовался математический пакет Maple 6. При фиксированном значении  были рассмотрены точки ( были рассмотрены точки ( )области 3, для которых проверялось неравенство D<0. Таким образом, как видно из рисунка, в 3-ей области появляется подобласть 3’. Неравенство D<0 выполняется в области 3 – 3’ , где вещественные части собственных значений будут положительны. В этой области точка Q превращается в неустойчивый фокус. )области 3, для которых проверялось неравенство D<0. Таким образом, как видно из рисунка, в 3-ей области появляется подобласть 3’. Неравенство D<0 выполняется в области 3 – 3’ , где вещественные части собственных значений будут положительны. В этой области точка Q превращается в неустойчивый фокус.
Запишем результаты исследования характеристик точек в таблицу:
\Область
Точка
|
1 |
2 |
3 |
3 – 3’ |
| O |
сток |
сток |
сток |
сток |
| P |
не сущ. |
исток |
седло |
седло |
| Q |
не сущ. |
не сущ. |
исток |
неуст. фокус |
4.1 Параметрические области системы
4.2 Область 1: 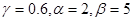

4.3 Область 2: 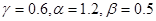
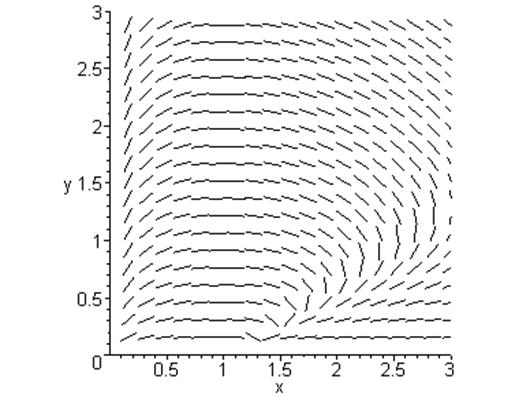
4.3 Область 3’ : 
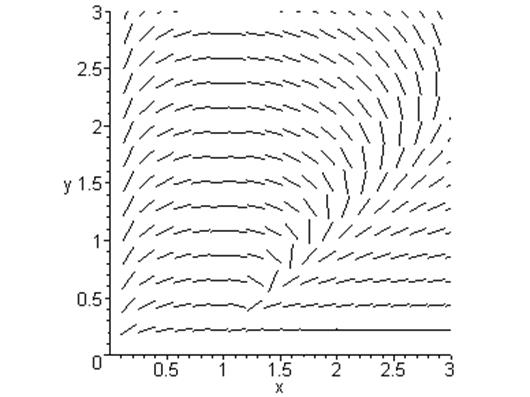
4.5 Область 3 – 3’ : 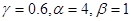
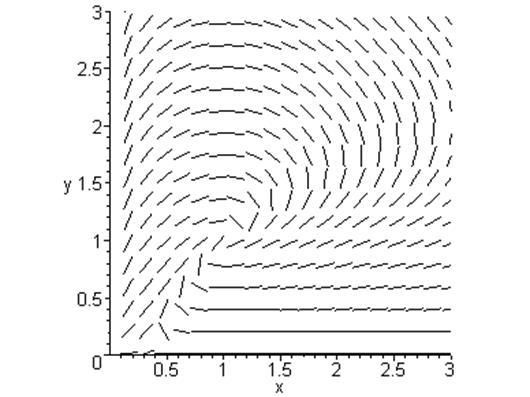
5. Биологическая интерпретация модели.
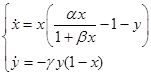
Данная система представляет собой модель взаимного влияния в природе двух животных видов – хищников и жертв. Как видно из рисунков, в этой системе оба вида вымирают. Предельных циклов в системе нет. X – жертвы, Y – хищники. Динамику взаимодействия двух видов описывают три функции: g(x) – функция динамики численности жертв, p(x) – трофическая функция жертв (характеризует число жертв убитых одним хищником), q(x) – трофическая функция хищников (характеризует влияние числа жертв, убиваемых одним хищником, на изменение численности популяции хищников).
Реклама


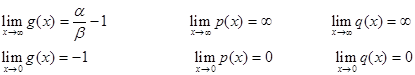
|