БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Механико-математический факультет
Кафедра теоретической механики и робототехники
Курсовая работа
Тема: Синтез оптимальных уравнений
Студента 3-го курса 13 группы
Павловского Сергея Александровича
Научный руководитель
Лютов Алексей Иванович
Минск 2001г.
ОГЛАВЛЕНИЕ
Г л а в а I. Введение
................................................................................................ 2
§ 1. Задача об оптимальном быстродействии.................................................... 2
1.Понятие об оптимальном быстродействии.................................................. 2
2.Задача управления........................................................................................ 3
3.Уравнения движения объекта....................................................................... 5
4.Допустимые управления............................................................................... 6
§ 2. Об основных направлениях в теории оптимальных процессов.................. 7
5.Метод динамического программирования.................................................. 7
6.Принцип максимума..................................................................................... 9
§ 3. Пример. Задача синтеза............................................................................... 12
7.Пример применения принципа максимума............................................... 12
8.Проблема синтеза оптимальных управлений............................................ 14
Г л а в а II. Линейные оптимальные быстродействия
..................................... 15
§ 4 Линейная задача оптимального управления............................................... 15
9.Формулировка задачи................................................................................ 15
10.Принцип максимума................................................................................. 16
11.Принцип максимума — необходимое и достаточное условие
оптимальности............................................................................................... 17
12.Основные теоремы о линейных оптимальных быстродействиях........... 18
§ 5. Решение задачи синтеза для линейных задач второго порядка................ 18
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
13.Упрощение уравнений линейного управляемого объекта...................... 18
Г л а в а III. Синтез оптимальных управлений для уравнения второго
порядка
.......................................................................................................... 20
§ 6. Решение задачи синтеза в случае комплексных собственных значений...... 20
14.Задача синтеза для малых колебаний маятника...................................... 20
Список используемой литературы....................................................................... 23
Г л а в а
I
ВВЕДЕНИЕ
Управляемые объекты прочно вошли в нашу повседневную жизнь и стали обиходными, обыденными явлениями. Мы видим их буквально на каждом шагу: автомобиль, самолёт, всевозможные электроприборы, снабжённые регуляторами (например, электрохолодильник), и т. п. Общим во всех этих случаях является то, что мы можем «управлять» объектом, можем в той или иной степени влиять на его поведение.
Обычно переход управляемого объекта из одного состояния в другое может быть осуществлён многими различными способами. Поэтому возникает вопрос о выборе такого пути, который с некоторой (но вполне определённой) точки зрения окажется наиболее выгодным. Это и есть (несколько расплывчато сформулированная) задача об оптимальном управлении.
§ 1. Задача об оптимальном быстродействии
1.
 Понятие об управляемых объектах.
Рассмотрим прямолинейное движение автомобиля. В каждый момент времени состояние автомобиля можно характеризовать двумя числами: пройденным расстоянием s и скоростью движения v.
Эти две величины меняются с течением времени, но не самопроизвольно, а сообразно воле водителя, который может по своему желанию управлять работой двигателя, увеличивая или уменьшая развиваемую этим двигателем силу F.
Таким образом, мы имеем три связанных между собой параметра: s
,v
,F
,показанных на схеме (рис. 1). Величины s
,v
,характеризующие состояние автомобиля, называют его фазовыми координатами
,а величину F
– управляющим параметром
. Понятие об управляемых объектах.
Рассмотрим прямолинейное движение автомобиля. В каждый момент времени состояние автомобиля можно характеризовать двумя числами: пройденным расстоянием s и скоростью движения v.
Эти две величины меняются с течением времени, но не самопроизвольно, а сообразно воле водителя, который может по своему желанию управлять работой двигателя, увеличивая или уменьшая развиваемую этим двигателем силу F.
Таким образом, мы имеем три связанных между собой параметра: s
,v
,F
,показанных на схеме (рис. 1). Величины s
,v
,характеризующие состояние автомобиля, называют его фазовыми координатами
,а величину F
– управляющим параметром
.
Если мы будем рассматривать движение автомобиля по плоскости (а не по прямой), то фазовых координат будет четыре (две «географические» координаты и две компоненты скорости), а управляющих параметров – два (например, сила тяги двигателя и угол поворота руля). У летящего самолёта можно рассматривать шесть фазовых координат (три пространственные координаты и три компоненты скорости) и несколько управляющих параметров (тяга двигателя, величины, характеризующие положение рулей высоты и направления, элеронов).
Сервис онлайн-записи на собственном Telegram-боте
Попробуйте сервис онлайн-записи VisitTime на основе вашего собственного Telegram-бота:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно.
Зарегистрироваться в сервисе
 Разумеется, в проводимом ниже математическом исследовании мы будем иметь дело не с самими реальными объектами, а с некоторой математической моделью. Сказанное выше делает естественным следующее математическое описание управляемого объекта. Состояние
объекта задаётся (в каждый момент времени) n
числами x
1
,
x
2
,…,
xn
,
которые называются фазовыми координатами
объекта. Движение
объекта заключается с математической точки зрения в том, что его состояние с течением времени изменяется, т. е. x
1
,
x
2
,…,
xn
являются переменными величинами (функциями времени). Движение объекта происходит не самопроизвольно. Им можно управлять; для этого объект снабжён «рулями», положение которых характеризуется (в каждый момент времени) r
числами u
1
,
u
2
,…,
ur
; эти числа называются управляющими параметрами
. Рулями можно «манипулировать», т. е. по своему желанию менять (конечно, в допустимых пределах) управляющие параметры u
1
,
u
2
,…,
ur
.
Иначе говоря, мы можем по желанию выбрать функции u
1
(
t),
u
2
(
t),…,
ur
(
t),
описывающие изменение управляющих параметров с течением времени. Мы будем предполагать (как это обычно и бывает), что, зная фазовое состояние объекта в начальный момент времени и выбрав управляющие функции u
1
(
t),
u
2
(
t),…,
ur
(
t)
(для t>
t
0
), мы можем точно и однозначно рассчитать поведение объекта для всех t>
t0
,т. е. можем найти функции x
1
(
t),
x
2
(
t),…,
xn
(
t),
характеризующие изменение фазовых координат с течением времени. Таким образом, изменение фазовых координат x
1
,
x
2
,…,
xn
уже не зависит непосредственно от нашего желания, но на движение объекта мы всё же можем в той или иной мере воздействовать, выбирая по своему желанию управляющие функции u
1
(
t),
u
2
(
t),…,
ur
(
t)
. Разумеется, в проводимом ниже математическом исследовании мы будем иметь дело не с самими реальными объектами, а с некоторой математической моделью. Сказанное выше делает естественным следующее математическое описание управляемого объекта. Состояние
объекта задаётся (в каждый момент времени) n
числами x
1
,
x
2
,…,
xn
,
которые называются фазовыми координатами
объекта. Движение
объекта заключается с математической точки зрения в том, что его состояние с течением времени изменяется, т. е. x
1
,
x
2
,…,
xn
являются переменными величинами (функциями времени). Движение объекта происходит не самопроизвольно. Им можно управлять; для этого объект снабжён «рулями», положение которых характеризуется (в каждый момент времени) r
числами u
1
,
u
2
,…,
ur
; эти числа называются управляющими параметрами
. Рулями можно «манипулировать», т. е. по своему желанию менять (конечно, в допустимых пределах) управляющие параметры u
1
,
u
2
,…,
ur
.
Иначе говоря, мы можем по желанию выбрать функции u
1
(
t),
u
2
(
t),…,
ur
(
t),
описывающие изменение управляющих параметров с течением времени. Мы будем предполагать (как это обычно и бывает), что, зная фазовое состояние объекта в начальный момент времени и выбрав управляющие функции u
1
(
t),
u
2
(
t),…,
ur
(
t)
(для t>
t
0
), мы можем точно и однозначно рассчитать поведение объекта для всех t>
t0
,т. е. можем найти функции x
1
(
t),
x
2
(
t),…,
xn
(
t),
характеризующие изменение фазовых координат с течением времени. Таким образом, изменение фазовых координат x
1
,
x
2
,…,
xn
уже не зависит непосредственно от нашего желания, но на движение объекта мы всё же можем в той или иной мере воздействовать, выбирая по своему желанию управляющие функции u
1
(
t),
u
2
(
t),…,
ur
(
t)
.
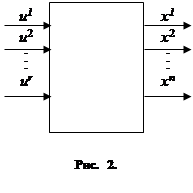
Управляемый объект, о котором только что шла речь, в теории автоматического управления принято изображать так, как это показано на рис. 2. Величины u
1
,
u
2
,…,
ur
(управляющие параметры) часто называют также «входными переменными», а величины x
1
,
x
2
,…,
xn
(фазовые координаты) – «выходными переменными». Говорят ещё, что «на вход» объекта поданы величины u
1
,
u
2
,…,
ur
, а «на выходе» мы получаем величины x
1
,
x
2
,…,
xn
. Разумеется, на рис. 2 показано лишь условное обозначение
управляемого объекта и никак не отражено его «внутреннее устройство», знание которого необходимо, чтобы выяснить, каким образом,
зная управляющие функции u
1
(
t),
u
2
(
t),…,
ur
(
t)
, можно вычислить изменение фазовых координат x
1
(
t),
x
2
(
t),…,
xn
(
t)
.
Величины u
1
,
u
2
,…,
ur
удобно считать координатами некоторого вектора
u=
(u
1
,
u
2
,…,
ur
), также называемого управляющим параметром
(векторным). Точно так же величины x
1
,
x
2
,…,
xn
удобно рассматривать как координаты некоторого вектора (или точки) x=
(x
1
,
x
2
,…,
xn
) в n –
мерном пространстве с координатами x
1
,
x
2
,…,
xn
.
Эту точку называют фазовым состоянием
объекта, а n –
мерное пространство, в котором в виде точек изображаются фазовые состояния, называется фазовым пространством
рассматриваемого объекта. Если объект таков, что его фазовое состояние характеризуется только двумя фазовыми координатами x
1
,
x
2
(см. рис. 1), то мы будем говорить о фазовой плоскости
. В этом случае фазовые состояния объекта изображаются особенно наглядно.
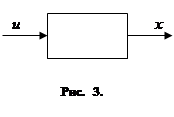 Итак, в векторных обозначениях рассматриваемый управляемый объект можно изобразить так, как показано на рис. 3. Входящая величина u=
(u
1
,
u
2
,…,
ur
) представляет собой управляющий параметр, а выходная величина x=
(x
1
,
x
2
,…,
xn
) представляет собой точку фазового пространства (или, иначе, фазовое состояние объекта). Итак, в векторных обозначениях рассматриваемый управляемый объект можно изобразить так, как показано на рис. 3. Входящая величина u=
(u
1
,
u
2
,…,
ur
) представляет собой управляющий параметр, а выходная величина x=
(x
1
,
x
2
,…,
xn
) представляет собой точку фазового пространства (или, иначе, фазовое состояние объекта).
 Как сказано выше, чтобы полностью задать движение объекта, надо задать его фазовое состояние x0
=
(x
0
1
,
x
0
2
,…,
x
0
n
) в начальный момент времени t0
и выбрать управляющие функции u
1
(
t),
u
2
(
t),…,
ur
(
t)
(для t
>t
0
), т. е. выбрать векторную функцию u(
t)=
u
1
(
t),
u
2
(
t),…,
ur
(
t)
). Эту функцию u(
t)
мы будем называть управлением
. Задание начального фазового состояния x0
и управления u(
t)
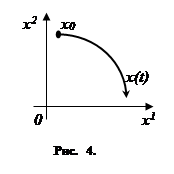
однозначно определяет дальнейшее движение объекта. Это движение заключается в том, что фазовая точка x
(t)=
(x
1
(
t),
x
2
(
t),…,
xn
(
t)
), изображающая состояние объекта, с течением времени перемещается, описывая в фазовом пространстве некоторую линию, называемую фазовой траекторией
рассматриваемого движение объекта (случай n=
2 изображён на рис. 4). Очевидно, что эта линия исходит из точки x
0
, поскольку x
(t
0
)=x
0
. Как сказано выше, чтобы полностью задать движение объекта, надо задать его фазовое состояние x0
=
(x
0
1
,
x
0
2
,…,
x
0
n
) в начальный момент времени t0
и выбрать управляющие функции u
1
(
t),
u
2
(
t),…,
ur
(
t)
(для t
>t
0
), т. е. выбрать векторную функцию u(
t)=
u
1
(
t),
u
2
(
t),…,
ur
(
t)
). Эту функцию u(
t)
мы будем называть управлением
. Задание начального фазового состояния x0
и управления u(
t)
однозначно определяет дальнейшее движение объекта. Это движение заключается в том, что фазовая точка x
(t)=
(x
1
(
t),
x
2
(
t),…,
xn
(
t)
), изображающая состояние объекта, с течением времени перемещается, описывая в фазовом пространстве некоторую линию, называемую фазовой траекторией
рассматриваемого движение объекта (случай n=
2 изображён на рис. 4). Очевидно, что эта линия исходит из точки x
0
, поскольку x
(t
0
)=x
0
.
Пару векторных функций (u(
t),
x(
t)
), т. е. управление u(
t)
и соответствующую фазовую траекторию x(
t)
, мы будем называть в дальнейшем процессом управления
или просто процессом
.
 Итак, резюмируем. Состояние управляемого объекта
в каждый момент времени характеризуется фазовой точкой
x=
(x
1
,
x
2
,…,
xn
). На движение объекта можно воздействовать при помощи управляющего параметра
u=
(u
1
,
u
2
,…,
ur
). Изменение величин u,
x
с течением времени мы называем процессом
; процесс (u(
t),
x(
t)
) составляется из управления
u(
t)
и фазовой траектории
x(
t)
. Процесс полностью определяется, если задано управление u(
t)
(при t
>t
0
) и начальное фазовое состояние x
0
=
x(
t
0
)
. Итак, резюмируем. Состояние управляемого объекта
в каждый момент времени характеризуется фазовой точкой
x=
(x
1
,
x
2
,…,
xn
). На движение объекта можно воздействовать при помощи управляющего параметра
u=
(u
1
,
u
2
,…,
ur
). Изменение величин u,
x
с течением времени мы называем процессом
; процесс (u(
t),
x(
t)
) составляется из управления
u(
t)
и фазовой траектории
x(
t)
. Процесс полностью определяется, если задано управление u(
t)
(при t
>t
0
) и начальное фазовое состояние x
0
=
x(
t
0
)
.
2.
Задача управления.
Часто встречается следующая задача, связанная с управляемыми объектами. В начальный момент времени t
0
объект находится в фазовом состоянии x
0
; требуется выбрать такое управление u(
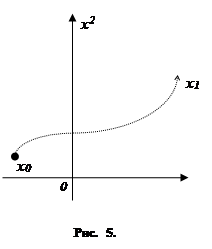
t)
, которое переведёт объект в заранее заданное конечное фазовое состояние x
1
(отличное от x
0
; рис. 5). При этом нередко бывает, что начальное состояние x
0
заранее не известно. Рассмотрим один из наиболее типичных примеров. Объект должен устойчиво работать в некотором режиме (т. е. находиться в некотором фазовом состоянии x
1
). В результате тех или иных причин (например, под воздействием неожиданного толчка) объект может выйти из рабочего состояния x
1
и оказаться в некотором другом состоянии x
0
. При этом точка x
0
, в которую может попасть объект, заранее не известна, и мы должны уметь так управлять объектом, чтобы из любой точки x
0
(или хотя бы из точек x
0
достаточно близких к x
1
) вернуть его в рабочее состояние x
1
(рис. 6).
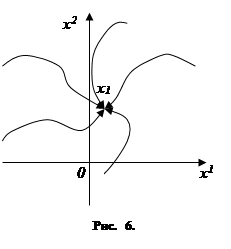 Такое управление часто осуществляется человеком (оператором), который следит за приборами и старается выбирать управление, поддерживающее объект в требуемом рабочем режиме. Такое управление часто осуществляется человеком (оператором), который следит за приборами и старается выбирать управление, поддерживающее объект в требуемом рабочем режиме.
Однако в современных условиях высокого развития техники оператор зачастую не может успешно справиться с этой задачей ввиду сложности поведения объекта, большой быстроты протекания процессов и т. п. Поэтому чрезвычайно важно создать такие приборы, которые сами, без участия человека, управляли бы работой объекта (например, в случае выхода объекта из рабочего состояния возвращали бы его в это рабочее состояние). Такие приборы («регуляторы», «автоматические управляющие устройства» и т. п.) сейчас очень распространены в технике, их изучением занимается теория автоматического управления.
Первым устройством этого рода был центробежный регулятор Уатта, сконструированный для управления работой паровой машины (см. рис. 9). Схема этого регулятора показана на рис. 7. В общем случае (рис. 8) на вход регулятора подаются фазовые координаты объекта.
Обычно требуется, чтобы переходный процесс
(т. е. процесс перехода из начального фазового состояния x
0
в предписанное состояние x
1
, рис. 5) был в определённом смысле «наилучшим», например, чтобы время перехода было наименьшим или чтобы энергия, затраченная в течение переходного процесса, была минимальной и т. п. Такой «наилучший» переходный процесс называется оптимальным процессом
. Термин «оптимальный процесс» требует уточнения, т. к. необходимо разъяснить, в каком смысле
понимается оптимальность. Если речь идёт о наименьшем времени перехода, то такие процессы называются оптимальными в смысле быстродействия
. Иначе говоря, процесс, в результате которого объект переходит из точки x
0
в точку x
1
(рис. 5), называется оптимальным в смысле быстродействия, если не существует процесса, переводящего объект из x
0
в x
1
за меньшее время (здесь и далее предполагается, что x
1
≠x
0
). Разумеется, желательно, чтобы регулятор не просто возвращал объект в рабочее состояние, а делал это наилучшим образом, например, в смысле быстродействия (т. е. возвращал объект в рабочее состояние за кратчайшее время). В связи с этим в теории автоматического управления рассматриваются весьма различные регуляторы. Рассмотрение регуляторов приводит к тому, что уменьшение времени переходного процесса связано с усложнением конструкции регулятора; поэтому, усложняя конструкцию регулятора, можно лишь приближаться к «идеальному», «оптимальному» регулятору, который во всех случаях осуществляет переходный процесс за кратчайшее время. В точности же «оптимального» регулятора, по-видимому, осуществить нельзя. Однако такой вывод является ошибочным, т. к. сейчас уже создали математический аппарат, рассчитывающий такие регуляторы. Можно предполагать, что оптимальные регуляторы будут играть важную роль в технике будущего.3.
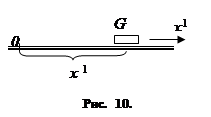 Уравнения движения объекта.
Начнём с рассмотрения одного простого примера. Пусть G
– тело, которое может совершать прямолинейное движение (рис. 10). Массу этого тела будем предполагать постоянной и равной m
, а его размерами будем пренебрегать (т. е. будем считать G
материальной точкой.) Координату тела G
(отсчитываемую от некоторой точки O
той прямой, по которой оно движется) будем обозначать через x
1
.
При движении тела G
его координата x
1
меняется с течением времени. Производная Уравнения движения объекта.
Начнём с рассмотрения одного простого примера. Пусть G
– тело, которое может совершать прямолинейное движение (рис. 10). Массу этого тела будем предполагать постоянной и равной m
, а его размерами будем пренебрегать (т. е. будем считать G
материальной точкой.) Координату тела G
(отсчитываемую от некоторой точки O
той прямой, по которой оно движется) будем обозначать через x
1
.
При движении тела G
его координата x
1
меняется с течением времени. Производная 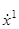 представляет собой скорость движения тела G
. Будем предполагать, что на тело G
действуют две внешние силы: сила трения ─ представляет собой скорость движения тела G
. Будем предполагать, что на тело G
действуют две внешние силы: сила трения ─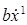 и упругая сила ─ kx
1
и что, кроме того, тело G
снабжено двигателем. Развиваемую двигателем силу воздействия на тело G
обозначим через u
. Таким образом, по второму закону Ньютона движение телаG
с течением времени будет описываться дифференциальным уравнением и упругая сила ─ kx
1
и что, кроме того, тело G
снабжено двигателем. Развиваемую двигателем силу воздействия на тело G
обозначим через u
. Таким образом, по второму закону Ньютона движение телаG
с течением времени будет описываться дифференциальным уравнением
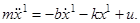
Обозначив скорость движения через x2
(т. е. положив 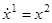 ), мы сможем записать этот закон движения в виде следующей системы дифференциальных уравнений: ), мы сможем записать этот закон движения в виде следующей системы дифференциальных уравнений:
 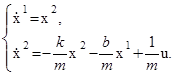 (1.1) (1.1)
Здесь величины x
1
,
x
2
являются фазовыми координатами тела G
, а величина u
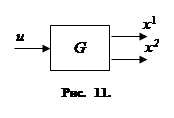
– управляющим параметром, т. е. мы имеем объект, схематически изображённый на рис. 11.
Уравнения (1.1) представляют собой закон изменения фазовых координат с течением времени (с учётом воздействия управляющего параметра), т. е. представляют собой закон движения фазовой точки в фазовой плоскости.
Мы рассмотрели лишь один частный случай, но можно было бы указать целый ряд других примеров, в которых закон движения объекта описывается дифференциальными уравнениями. Чаще всего (см.(1.1)) эти уравнения дают выражения производных от фазовых координат через сами фазовые координаты и управляющие параметры, т. е. имеют вид
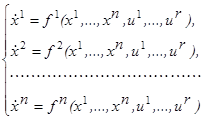 (1.2) (1.2)
где f
1
, f
2
,…, fn
–
некоторые функции, определяемые внутренним устройством объекта.
В дальнейшем мы сосредоточим своё внимание именно на таких объектах (рис. 2), закон движения которых описывается системой дифференциальных уравнений вида (1.2). В векторной форме систему (1.2) можно записать в виде
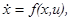 (1.3) (1.3)
где x
─ вектор с координатами x
1
,…, xn
, u
– вектор с координатами u
1
,…, ur
и, наконец, f
(x, u
) – вектор, координатами которого служат правые части системы (1.2).
Разумеется, невозможно решить систему дифференциальных уравнений (1.2) (т. е. найти закон движения объекта), не зная каким образом будут меняться с течением времени управляющие параметры u
1
, u
2
,…, ur
. Напротив, зная поведение величин u
1
, u
2
,…,ur
, т. е. зная управляющие функции u
1
(t), u
2
(t),…, ur
(t)
для t
>t
0
мы сможем из системы уравнений
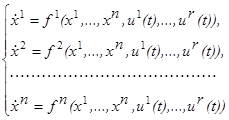 (1.4) (1.4)
или, что то же самое, из векторного уравнения
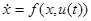 (1.5)
(1.5)
однозначно определить движение объекта (при t
>t
0
), если нам известно начальное фазовое состояние объекта (в момент t=t
0
). Иначе говоря, задание управления u(t)
и начального фазового состояния x
0
однозначно определяет фазовую траекторию x(t)
при t
>t
0
, что согласуется со сделанными ранее (стр. 1) предположениями о свойствах объекта.
Тот факт, что задание начального фазового состояния (в момент t=t
0
) позволяет из системы (1.4) однозначно определить фазовую траекторию x(t), t
>t
0
,
вытекает из теоремы о существовании и единственности решений системы дифференциальных уравнений.
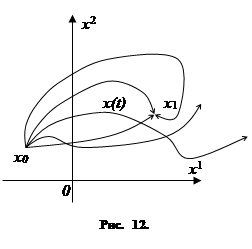 Предположим, что, зная начальное фазовое состояние x
0
и управление u(t)=(u
1
(t),…, ur
(t)),
мы определили фазовую траекторию x(t)
(с помощью системы (1.4)). Если мы изменим управление u(t)
(сохранив то же начальное состояние x
0
), то получим некоторую другую траекторию, исходящую из той же точки x
0
; вновь изменим управлениеu(
t)
– получим ещё одну траекторию и т. д. Таким образом, рассматривая различные управления u(
t)
, мы получим много траекторий, исходящих из точки x
0
(рис. 12). (Разумеется, это не противоречит теореме единственности в теории дифференциальных уравнений, так как, заменяя функции u
1
(
t),…,
ur
(
t)
другими функциями, мы переходим от системы дифференциальных уравнений относительно фазовых координат x
1
,…,
xn
.
) Предположим, что, зная начальное фазовое состояние x
0
и управление u(t)=(u
1
(t),…, ur
(t)),
мы определили фазовую траекторию x(t)
(с помощью системы (1.4)). Если мы изменим управление u(t)
(сохранив то же начальное состояние x
0
), то получим некоторую другую траекторию, исходящую из той же точки x
0
; вновь изменим управлениеu(
t)
– получим ещё одну траекторию и т. д. Таким образом, рассматривая различные управления u(
t)
, мы получим много траекторий, исходящих из точки x
0
(рис. 12). (Разумеется, это не противоречит теореме единственности в теории дифференциальных уравнений, так как, заменяя функции u
1
(
t),…,
ur
(
t)
другими функциями, мы переходим от системы дифференциальных уравнений относительно фазовых координат x
1
,…,
xn
.
)
Напомним, что задача оптимального быстродействия
заключается в отыскании такого управления u(
t)
, для которого фазовая траектория x(
t)
, соответствующая этому управлению в силу уравнения (1.5), проходит через точку x
1
и переход из x
0
вx
1
осуществляется за кратчайшее время. Такое управление u(
t)
будем называть оптимальным управлением (в смысле быстродействия)
; точно так же соответствующую траекторию x(
t)
буде называть оптимальной траекторией
.
4.
Допустимые управления.
Обычно управляющие параметры u
1
,…,
ur
не могут принимать совершенно произвольные значения, а подчинены некоторым ограничениям. Так, например, в случае объекта, описанного на стр. 4, естественно предположить, что сила u
, развиваемая двигателем, не может быть как угодно большой по величине, а подчинена ограничениям α
≤u
≤β
, где α
и β
– некоторые постоянные, характеризующие двигатель. В частности, при α=
─1, β=
1 мы получаем ограничение ─1≤u
≤1, которое означает, что двигатель может развивать силу, направленную вдоль оси x
1
как в положительном, так и в отрицательном направлении, но не превосходящую единицы по абсолютной величине.
Для объектов, содержащих r
управляющих параметров u
1
,…,
ur
, в приложениях часто встречается случай, когда эти параметры могут произвольно меняться в следующих пределах:
α
1
≤u
1
≤ β
1
, α
2
≤u
2
≤β
2
,…, α
r
≤ur
≤βr
.
Иначе говоря, каждая из величин u
1
,
u
2
,…,
u
r
в уравнениях (1.2) представляет собой отдельный управляющий параметр, область изменения которого не зависит от значений остальных
управляющих параметров и задаётся неравенствами
α
i
≤ui
≤β
i
, i=
1,…,r.
(1.6)
Заметим, что при r
=2 точки u=
(u
1
,
u
2
), координаты которых подчинены неравенствам (1.6), заполняют прямоугольник; при r=
3 неравенства (1.6) определяют в пространстве переменных u
1
,
u
2
,
u
3
прямоугольный параллелепипед; в случае произвольного r
говорят, что неравенства (1.6) определяют r-мерный параллелепипед.
В общем случае будем считать, что в соответствии с конструкцией объекта и условиями его эксплуатации задано в пространстве переменных u
1
,…,
ur
некоторое множество U
и управляющие параметры u
1
,
u
2
,…,
ur
должны в каждый момент времени принимать лишь такие значения, чтобы точка u=
(u
1
,
u
2
,…,
ur
) принадлежала множеству U
. Иначе говоря, разрешается рассматривать лишь такие управления u(
t)
, что u(
t)
 U
для любого t
. Множество U
в дальнейшем будем называть областью управления
. Область управления U
не всегда будет параллелепипедом; она может иметь геометрически более или менее сложный характер, так как в силу конструкции объекта между управляющими параметрами u
1
,
u
2
,…,
ur
могут существовать связи, выражаемые, например, уравнениями вида φ(u
1
,
u
2
,…,
ur
)=0 или неравенствами ψ(u
1
,
u
2
,…,
ur
)≤0. Так, если параметры u
1
,
u
2
характеризуют векторную величину на плоскости, модуль которой не превосходит единицы, а направление произвольно, то эти параметры подчинены только одному условию U
для любого t
. Множество U
в дальнейшем будем называть областью управления
. Область управления U
не всегда будет параллелепипедом; она может иметь геометрически более или менее сложный характер, так как в силу конструкции объекта между управляющими параметрами u
1
,
u
2
,…,
ur
могут существовать связи, выражаемые, например, уравнениями вида φ(u
1
,
u
2
,…,
ur
)=0 или неравенствами ψ(u
1
,
u
2
,…,
ur
)≤0. Так, если параметры u
1
,
u
2
характеризуют векторную величину на плоскости, модуль которой не превосходит единицы, а направление произвольно, то эти параметры подчинены только одному условию
(u
1
)2
+(u
2
)2
─1≤0 (1.7)
и область управления U
представляет собой круг. В дальнейшем будем предполагать, что указание области управления входит в математическое определение объекта, т. е. что для математического задания управляемого объекта надо указать закон его движения
(1.2) и область управления
U
.
Наконец, сделаем ещё одно, весьма существенное предположение о характере управлений. Именно, будем предполагать, что «рули», положения которых характеризуются управляющими параметрами u
1
,
u
2
,…,
ur
, безынерционны,
так что мы можем, если нужно, мгновенно
переключать эти «рули» из одного положения в другое, т. е. менять скачком значения управляющих параметров u
1
,
u
2
,…,
ur
. В соответствии с этим будем рассматривать не только непрерывные, но и кусочно-непрерывные
управления u(
t)
. Кроме того, будем предполагать, что каждое рассматриваемое управление u(
t)
непрерывно на концах отрезка t
0
≤t
≤t
1
, на котором оно задано, т. е. что все точки разрыва, если они есть, расположены на интервале t
0
<t
<t
1
. Для удобства условимся называть допустимым управлением
всякую кусочно-непрерывную функцию u
(t
), t
0
≤t
≤t
1
, со значениями в области управления U
, непрерывную справа в точках разрыва (для определённости нам так удобно предполагать) и непрерывную в концах отрезка [t
0
; t
1
], на котором она задана.
Задача об оптимальных быстродействиях уточняется теперь следующим образом:
Среди всех допустимых управлений
u=
u(
t), под воздействием которых управляемый объект
(1.3) переходит из заданного начального фазового состояния
x
0
в предписанное конечное состояние
x
1
, найти такое, для которого этот переход осуществляется за кратчайшее время
§ 2. Об основных направлениях в теории оптимальных процессов
5.
Метод динамического программирования.
Для управляемого объекта, описанного в предыдущем параграфе, мы рассмотрим задачу об оптимальном переходе ─ в смысле быстродействия ─ из фазового состояния x
в фазовое состояние x
1
. При этом конечную фазовую точку x
1
будем считать фиксированной, а в качестве начальной точки x
будем рассматривать различные точки фазового пространства. Мы будем предполагать в этом пункте, что для рассматриваемого управляемого объекта выполняется следующая гипотеза:
Г и п о т е з а 1. Какова бы ни была отличная от
x
1
точка x фазового пространства, существует оптимальный (в смысле быстродействия) процесс перехода из точки
x
0
в точку
x
1
(рис. 6).
Время, в течение которого осуществляется оптимальный переход из точки x
0
в точку x
1
, обозначим через T(
x
). В дальнейших рассуждениях будет удобно вместо T(
x
) ввести функцию ω
(x
), отличающуюся от неё знаком
ω
(x
)= ─T(x
). (1.8)
Так как каждая точка x
фазового пространства имеет координаты x
1
,…,
xn
, то ω
(x
)= ─T(
x
) является функцией от
n переменных,
т. е. ω
(x
)= ω
(x
1
,…,
xn
). Поэтому имеет смысл говорить о непрерывности этой функции (по совокупности переменных x
1
,…,
xn
) и о дифференцируемости этой функции по каждой из переменных x
1
,…,
xn
.
А также будем предполагать, что для рассматриваемого управляемого объекта выполняется следующая гипотеза:
Г и п о т е з а 2. Функция
ω
(x
) непрерывна и всюду, кроме точки
x
1
, имеет непрерывные частные производные 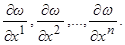
Пусть теперь x
0
─ произвольная отличная от x
1
точка фазового пространства, а u
0
─ произвольная точка области U
. Предположим, что объект находится в момент t
0
в фазовом состоянии x
0
и движется в течение некоторого времени под воздействием постоянного управления u=
u
0
. Фазовую траекторию объекта при этом движении обозначим через y
(t)=(y
1
(
t),…,
yn
(
t
)). Таким образом, фазовая траектория y(
t
) при t>
t
0
удовлетворяет уравнениям
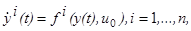 (1.9) (1.9)
(см. (1.2), (1.3)) и начальному условию
y
(t
0
)=x
0
. (1.10)
Если мы будем двигаться из точки x
0
до точки y(
t
) (по рассматриваемой фазовой траектории), то затратим на это движение время t
─ t
0
. Двигаясь затем из точки y(
t
) оптимально, мы затратим на движение от точки y
(t
) до точки x
1
время T(
y(
t
)). В результате мы совершим переход из точки x
0
в точку x
1
, затратив на этот переход время (t
─t
0
)+T
(y
(t)). Но так как оптимальное время движения от точки x
0
до точки x
1
равно T
(x
0
), т. е. равно T
(y
(t
0
)), то T
(y(t
0
))≤(t
─t
0
)+T
(y
(t
)). Заменяя функцию T
через ω
(см. (1.8)) и разделив обе части неравенства на положительную величину t
─t
0
, получаем отсюда 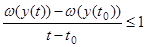 и поэтому, переходя к пределу при t→
t
0
, находим и поэтому, переходя к пределу при t→
t
0
, находим
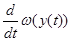 │при │при
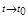 ≤1. (1.11)
≤1. (1.11)
Но производная, указанная в левой части этого неравенства, вычисляется по формуле полной производной 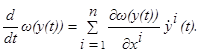 Поэтому согласно (1.9) и (1.10) неравенство (1.11) принимает вид Поэтому согласно (1.9) и (1.10) неравенство (1.11) принимает вид 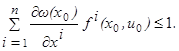 Точки x
0
, u
0
здесь были произвольными. Таким образом, для любой (отличной от
x
1
) точки
x фазового пространства и любой точки
u области управления
U выполнено соотношение Точки x
0
, u
0
здесь были произвольными. Таким образом, для любой (отличной от
x
1
) точки
x фазового пространства и любой точки
u области управления
U выполнено соотношение
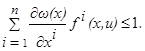 (1.12) (1.12)
Пусть теперь (u
(t
), x
(t
)) ─ оптимальный процесс, переводящий объект из фазового состояния x
0
в состояние x
1
, и t
0
≤t
≤t
1
─ отрезок времени, в течение которого это оптимальное движение происходит, так что x
(t
0
)=x
0
, x
(t
1
)=x
1
и t
1
=t
0
+ T
(x
0
). Движение по рассматриваемой оптимальной траектории от точки x
0
до точки x
(t
) осуществляется в течение времени t
─t
0
, а движение от точки x
(t
) до точкиx
1
─ в течение времени T
(x
0
) ─ (t
─t
0
). Быстрее, чем за время T
(x
0
) ─ (t
─t
0
), из точки x
(t
) попасть в точку x
1
невозможно. Итак, T
(x
0
) ─ (t
─t
0
) есть время оптимального движения из точки x
(t
) в точку x
1
, т. е. T
(x
(t
))=T
(x
0
) ─ (t
─t
0
). Заменив здесь T
через ω
, т. е. ω
(x
(t
))=ω
(x
0
) + t
─t
0
) и взяв производную по t
, получаем
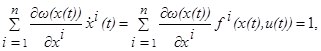 t
0
≤t
≤t
1
. (1.13) t
0
≤t
≤t
1
. (1.13)
Таким образом, для каждого оптимального процесса в течение всего движения выполняется равенство
(1.13).
Если мы теперь введём в рассмотрение функцию
B
(x, u
(t
))=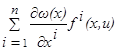 , (1.14) , (1.14)
То соотношения (1.12) и (1.13) могут быть записаны следующим образом:
B
(x,
u
)≤1 для всех точек x
≠x
1
и u
; (1.15)
B
(x,
u
)≡1 для любого оптимального процесса (u
(t
), x
(t
)). (1.16)
Итак, справедлива следующая
Т е о р е м а 1.1. Если для управляемого объекта, описываемого уравнением
(1.5) и предписанного конечного состояния
x
1
выполнены гипотезы
1 и
2, то имеют место соотношения
(1.15) и
(1.16) (оптимальность понимается в смысле быстродействия).
Эта теорема и составляет сущность метода динамического
программирования
для рассматриваемой задачи. Эту теорему можно сформулировать и несколько иначе. Написав соотношение (1.16)
Для t
=t
0
, получим
B
(x
0
, u
(t
0
))=1, т. е. для любой точки
x
0
(отличной от x
1
) найдётся в
U такая точка
u
(а именно
u=
u
(t
0
)), что
B
(x
0
, u
)=1. В сопоставлении с неравенством (1.15) получаем соотношение
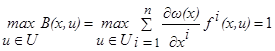 для любой точки x
≠x
1
. (1.16*
) для любой точки x
≠x
1
. (1.16*
)
Метод динамического программирования (1.15), (1.16) (или, что то же самое, (1.16*
), (1.16)) содержит некоторую информацию об оптимальных процессах и потому может быть использован для их разыскания. Однако он имеет ряд неудобств. Во-первых, применение этого метода требует нахождения не только оптимальных управлений, но и функции ω
(x
), так как эта функция входит в соотношения (1.15) ─ (1.16*
). Во-вторых, уравнение Беллмана (1.16*
) (или соотношения (1.15), (1.16)) представляет собой уравнение в частных производных относительно функции ω
, осложнённое к тому же знаком максимума. Указанные обстоятельства сильно затрудняют возможность пользования методом динамического программирования для отыскания оптимальных процессов в конкретных примерах. Но самым главным недостатком этого метода является предположение о выполнении гипотез 1 и 2. Ведь оптимальные управления и функция ω
нам заранее не известны, так что гипотезы 1 и 2 содержат предположение о неизвестной функции, и проверить выполнение этих гипотез по уравнениям движения объекта невозможно. Этот недостаток можно было бы считать не особенно существенным, если бы после решения оптимальной задачи этим методом оказалось, что функция ω
(x
) действительно является непрерывно дифференцируемой. Но дело заключается в том, что даже в простейших, линейных задачах оптимального управления функция ω
(x
) не является, как правило, всюду дифференцируемой. Тем не менее, методом динамического программирования можно нередко пользоваться как ценным эвристическим средством.
6.
Принцип максимума.
Продолжим теперь рассуждения предыдущего пункта, предположив функцию ω
(x
) уже дважды непрерывно дифференцируемой (всюду, кроме точки x
1
). Итак, будем предполагать, что выполнена следующая
Г и п о т е з а 3. функция
ω
(x
) имеет при
x≠
x
1
вторые непрерывные производные 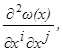 i,
j=
1,2,…,n
, а функции
fi
(x,
u
) ─ первые непрерывные производные
i,
j=
1,2,…,n
, а функции
fi
(x,
u
) ─ первые непрерывные производные 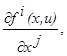 где
i,
j=
1,2,…,n. где
i,
j=
1,2,…,n.
Пусть (u(
t),
x(
t)
), t
0
≤t
≤t
1
, ─ оптимальный процесс, переводящий объект (1.2) (или (1.3)) из фазового состояния x
0
в состояние x
1
. Фиксируем некоторый момент времени t
, t
0
≤t
≤t
1
, и рассмотрим функцию B
(x,
u
(t
))=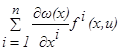 переменного x.
В силу гипотезы 3 вытекает, что функция B
(x,
u
(t
)) всюду, кроме точки x
1
, имеет непрерывные производные по переменным x
1
,x
2
,…,xn
: переменного x.
В силу гипотезы 3 вытекает, что функция B
(x,
u
(t
)) всюду, кроме точки x
1
, имеет непрерывные производные по переменным x
1
,x
2
,…,xn
:
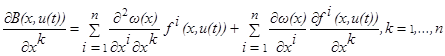 (1.17) (1.17)
В частности, так как x
(t
)≠x
1
(поскольку t
<t
1
), то функция B
(x,
u
(t
)) имеет вблизи точки x
=x
(t
) непрерывные производные по переменным x
1
,x
2
,…,xn
. Далее, мы имеем в силу (1.15), (1.16) B
(x,
u
(t
))≤1 для любого x≠
x
1
; B
(x,
u
(t
))=1 при x=
x
(t
).
Эти два соотношения означают, что функция B
(x,
u
(t
)) достигает в точке x
=x
(t
) максимума, и потому её частные производные по x
1
,…,
xn
обращаются в нуль в этой точке:
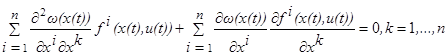 (1.18) (1.18)
Кроме того, дифференцируя функцию 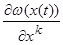 по t,
находим по t,
находим
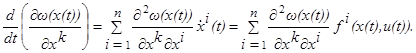
Поэтому соотношение (1.18) может быть переписано в следующем виде:
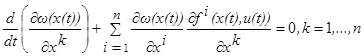 (1.19) (1.19)
Заметим теперь, что в формулы (1.15), (1.16), (1.17) и (1.19) сама функция ω
не входит, а входят только её частные производные 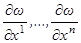 . Поэтому мы введём для удобства следующие обозначения: . Поэтому мы введём для удобства следующие обозначения:
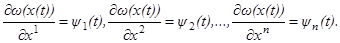 (1.20) (1.20)
Тогда функция B
(см. (1.14)) записывается таким образом:
B
(x
(t
), u
(t
))=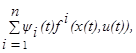
и соотношение (1.16) принимает вид
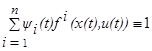 , для оптимального процесса (x
(t
), u
(t
)), t
0
≤t
<t
1
. (1.21) , для оптимального процесса (x
(t
), u
(t
)), t
0
≤t
<t
1
. (1.21)
Кроме того, согласно (1.15)
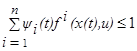 для любой точки u для любой точки u U
и всех t
0
≤t
<t
1
. (1.22) U
и всех t
0
≤t
<t
1
. (1.22)
Наконец, соотношения (1.19) записываются следующим образом:
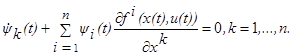 (1.23) (1.23)
Итак, если
(u
(t
), x
(t
)), t
0
≤t
<t
1
, ─ оптимальный процесс, то существуют такие функции ψ
1
(t
), ψ
2
(t
),…, ψ
n
(t
) (они определяются равенствами
(1.20)), что имеют место соотношения
(1.21), (1.22), (1.23).
Рассмотрение левых частей соотношений (1.21), (1.22) подсказывает нам, что целесообразно ввести в рассмотрение следующую функцию:
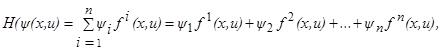 (1.24) (1.24)
зависящую от 2n+
r
аргументов ψ
1
, ψ
2
,…, ψ
n
, x
1
,…, xn
, u
1
,…, ur
. С помощью этой функции соотношения (1.21), (1.22) записываются в следующем виде:
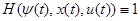 для оптимального процесса (u
(t
), x
(t
)), t
0
≤t
<t
1
, (1.25) для оптимального процесса (u
(t
), x
(t
)), t
0
≤t
<t
1
, (1.25)
где ψ
(t
)=(ψ
1
(t
),…,ψ
n
(t
)) определяются равенствами (1.20);
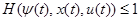 для любой точки u для любой точки u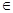 U
и всех t
0
≤t
<t
1
. (1.26) U
и всех t
0
≤t
<t
1
. (1.26)
Вместо неравенства (1.26) мы можем в силу (1.25) написать следующее соотношение:
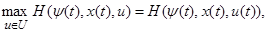 t
0
≤t
<t
1
. (1.27) t
0
≤t
<t
1
. (1.27)
Наконец, соотношения (1.23) можно, очевидно, переписать так:
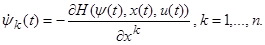 (1.28) (1.28)
Итак, если
(u
(t
), x
(t
)), t
0
≤t
<t
1
, ─ оптимальный процесс
, то существует такая функция ψ
(t
)=(ψ
1
(t
),…, ψ
n
(t
)), что выполняются соотношения
(1.25), (1.27), (1.28), где функция
H определяется соотношением
(1.24).
Так как в соотношениях (1.24), (1.25), (1.27), (1.28) нигде не участвует явно функция ω
(x
), то равенства (1.20), выражающие функции ψ
1
(t
),…, ψ
n
(t
) через ω
, никаких добавочных сведений не дают, и о них можно забыть, ограничившись утверждением, что какие-то функции ψ
1
(t
),…, ψ
n
(t
), удовлетворяющие перечисленным соотношениям (1.25), (1.27), (1.28), существуют. Соотношения (1.28) представляют собой систему уравнений, которым эти функции удовлетворяют. Заметим, что функции ψ
1
(t
),…, ψ
n
(t
) составляют нетривиальное решение этой системы (т. е. ни в какой момент времени t
все эти функции одновременно в нуль не обращаются); действительно, если бы при некотором t
было ψ
1
(t
)= ψ
2
(t
)=…=ψ
n
(t
)=0, то в силу (1.24) мы получили бы H
(ψ
(t
), x
(t
), u
(t
))=0, что противоречит равенству (1.25). Таким образом, мы получаем следующую теорему, которая носит название принципа максимума.
Т е о р е м а 1.2. Предположим, что для рассматриваемого управляемого объекта, описываемого уравнением
(в векторной форме
)
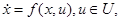 (A)
(A)
и предписанного конечного состояния
x
1
выполнены гипотезы
1, 2 и
3. Пусть
(u
(t
), x
(t
)), t
0
≤t
≤t
1
, ─ некоторый процесс, переводящий объект из начального состояния
x
0
в состояние
x
1
. Введём в рассмотрение функцию
H, зависящую от переменных
x
1
(t
),…, xn
(t
),
u
1
,…,
ur
и некоторых вспомогательных переменных ψ
1
(t
),…, ψ
n
(t
) (см. (1.24)):
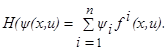 (B) (B)
С помощью этой функции
H запишем следующую систему дифференциальных уравнений для вспомогательных переменных:
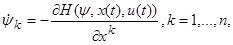 (C) (C)
где
(u
(t
), x
(t
)) ─ рассматриваемый процесс
(см. (1.28)). Тогда, если процесс
(u
(t
), x
(t
)), t
0
≤t
<t
1
, является оптимальным, то существует такое нетривиальное решение ψ
(t
)=(ψ
1
(t
),…, ψ
n
(t
)),
t
0
≤t
<t
1
, системы
(C), что для любого момента
t,
t
0
≤t
<t
1
, выполнено условие максимума
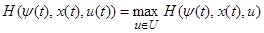 (D) (D)
(см. (1.27)) и условие
(1.25) H
(ψ
(t
),x
(t
),u
(t
))=1.
Однако в приведённой здесь форме принцип максимума страдает одним недостатком: он выведен в предположение дифференцируемости (и даже двукратной) функции ω
(x
), а эта функция в действительности не является (в обычно встречающихся случаях) всюду дифференцируемой.
Из-за предположения о выполнении сформулированных гипотез (о функции ω
(x
)) принцип максимума в том виде, в каком он сформулирован выше, не является удобным условием оптимальности. По форме он выведен как необходимое условие оптимальности: если процесс оптимален, то выполнено соотношение (1.16*
) и соответственно (D), т. е. выполнение этого условия необходимо для оптимальности. Однако это условие выведено лишь в предположении выполнения гипотез 1, 2, 3, а их выполнение отнюдь не необходимо для оптимальности. Вот почему сформулированные выше теоремы не могут считаться необходимыми условиями оптимальности.
Замечательным, однако, является тот факт, что если в теореме
1.2 решение ψ
(t
) и условие максимума
(D) рассматривать на всём отрезке
t
0
≤t
≤t
1
(а не только при
t
0
≤t
<t
1
), а заключительное условие
H
(ψ
(t
1
), x
(t
1
), u
(t
1
))≥0, (E)
то в этой форме принцип максимума будет справедлив без каких бы то ни было предположений о функции ω, т. е. принцип максимума станет весьма удобным и широко применимым необходимым условием оптимальности.
§ 3. Пример. Задача синтеза
7.
Пример применения принципа максимума.
В этом пункте мы разберём один пример вычисления оптимальных процессов. Именно, рассмотрим управляемый объект, упомянутый в п. 3 (см. уравнения (1.1)), при условии, что сила трения и упругая сила отсутствуют (т. е. b
=0, k
=0), масса m
равна единице (m
=1), а управляющий параметр подчинён ограничениям |u
|≤1. Иначе говоря, мы рассматриваем материальную точку G
массы m=
1 (см. рис. 10), свободно и без трения движущуюся по горизонтальной прямой и снабжённую двигателем, развивающим силу u
, где |u
|≤1. Согласно (1.1) уравнения движения этого объекта имеют вид:
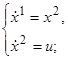 (1.29)
(1.29)
─1≤u
≤1. (1.30)
Для этого объекта рассмотрим задачу о быстрейшем попадании в начало координат (0, 0) из заданного начального состояния x
0
=(x
0
1
, x
0
2
). Иначе говоря, будем рассматривать задачу об оптимальном быстродействии в случае, когда конечным положением служит точка x
1
=(0, 0). Механически это означает, что материальную точку, имеющую заданное положение x
0
1
и заданную начальную скорость x
0
2
, мы хотим за кратчайшее время привести в начало отсчёта с нулевой скоростью (т. е. добиться того, чтобы точка пришла в начало отсчёта и остановилась там).
Функция H
в рассматриваемом случае имеет вид
H
=ψ
1
x
2
+ψ
2
u
(1.31)
(см. (1.29) и (B)). Далее, для вспомогательных переменных ψ
1
, ψ
2
мы получаем систему уравнений 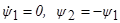 . Из этой системы уравнений находим: ψ
1
=d
1
; ψ
2
= ─d
1
t+
d
2
, где d
1, d2
─ постоянные интегрирования. Далее, в силу соотношения максимума (D) мы находим, учитывая (1.31) и (1.30): . Из этой системы уравнений находим: ψ
1
=d
1
; ψ
2
= ─d
1
t+
d
2
, где d
1, d2
─ постоянные интегрирования. Далее, в силу соотношения максимума (D) мы находим, учитывая (1.31) и (1.30):
u
(t
)= +1, если ψ
2
(t
)>0; u
(t
)= ─1, если ψ
2
(t
)<0.
Иначе говоря, u
(t
)=signψ
2
(t
)=sign (─ d
1
t
+ d
2
). Отсюда следует, что каждое оптимальное управление
u
(t
), t
0
≤t
≤t
1
, является кусочно-постоянной функцией, принимающей значения 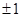 и имеющей не более двух интервалов постоянства
(ибо линейная функция ─d
1
t +
d
2
не более одного раза меняет знак на отрезке t
0
≤t
≤t
1
).
и имеющей не более двух интервалов постоянства
(ибо линейная функция ─d
1
t +
d
2
не более одного раза меняет знак на отрезке t
0
≤t
≤t
1
).
Для отрезка времени, на котором u 1, мы имеем (в силу системы (1.29)) 1, мы имеем (в силу системы (1.29)) 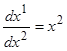 , откуда находим , откуда находим
x
1
=1/2(x
2
)2
+c
. (1.32)
  Таким образом, кусок фазовой траектории, для которого u Таким образом, кусок фазовой траектории, для которого u 1, представляет собой дугу параболы (1.32). Семейство парабол (1.32) показано на рис. 13 (они получаются друг из друга сдвигом в направлении осиx
1
). По этим параболам фазовые точки движутся снизу вверх (ибо 1, представляет собой дугу параболы (1.32). Семейство парабол (1.32) показано на рис. 13 (они получаются друг из друга сдвигом в направлении осиx
1
). По этим параболам фазовые точки движутся снизу вверх (ибо 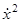 = u = u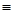 1, т. е.
1, т. е. 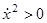 ). ).Аналогично для отрезка времени, на котором u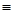 ─1, мы имеем, откуда находим ─1, мы имеем, откуда находим
x
1
= ─1/2(x
2
)2
+ c
’. (1.33)
Семейство парабол (1.33) (также получающихся друг из друга сдвигом в направлении оси x
1
) показано на рис. 14. По параболам (1.33) фазовые точки движутся сверху вниз (ибо  ) )
Как было указано выше, каждое оптимальное управление u
(t
) является кусочно-постоянной функцией, принимающей значения 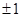 и имеющей не более двух интервалов постоянства. Если управление u
(t
) сначала, в течение некоторого времени, равно +1, а затем равно ─1, то фазовая траектория состоит из двух кусков парабол (рис. 15), примыкающих друг к другу, причём второй из этих кусков лежит на той из парабол (1.33), которая проходит через начало координат (ибо искомая траектория должна вести в начало координат). Если же, наоборот, сначала u=
─1, а затем u= +
1, то мы получаем фазовую траекторию, изображённую на рис. 16. На рис. 15, 16 надписаны на дугах парабол соответствующие значения управляющего параметра u
. и имеющей не более двух интервалов постоянства. Если управление u
(t
) сначала, в течение некоторого времени, равно +1, а затем равно ─1, то фазовая траектория состоит из двух кусков парабол (рис. 15), примыкающих друг к другу, причём второй из этих кусков лежит на той из парабол (1.33), которая проходит через начало координат (ибо искомая траектория должна вести в начало координат). Если же, наоборот, сначала u=
─1, а затем u= +
1, то мы получаем фазовую траекторию, изображённую на рис. 16. На рис. 15, 16 надписаны на дугах парабол соответствующие значения управляющего параметра u
.На рис. 17 изображено всё семейство полученных таким образом фазовых траекторий (здесь AO
─ дуга параболы x
1
=1/2(x
2
)2
, расположенная в нижней полуплоскости; BO
─ дуга параболы x
1
= ─1/2(x
2
)2
, расположенная в верхней полуплоскости).
Итак, согласно принципу максимума только изображённые на рис.
17 траектории могут быть оптимальными,
причём видно, что из каждой точки фазовой плоскости исходит только одна траектория, ведущая в начало координат, которая может быть оптимальной (т. е. задание начальной точки x
0
однозначно определяет соответствующую траекторию).8.
Проблема синтеза оптимальных управлений.
Посмотрим на разобранный в предыдущих пунктах пример с несколько иной точки зрения. Найденное выше решение оптимальной задачи можно истолковать следующим образом. Обозначим через v
(x
)= +1 ниже линии AOB
и на дуге AO
, v
(x
)= ─1 выше линии AOB
и на дугеBO
. Тогда (см. 17) на каждой оптимальной траектории значение u
(t
) управляющего параметра (в произвольный момент времени t
) равно v
(x
(t
)), т. е. равно значению функции v
в той точке, в которой в момент t
находится движущаяся фазовая точка, пробегающая оптимальную траекторию u
(t
)=v
(x
(t
)). Это означает, что, заменив в системе (1.29) величину u
функцией v
(x
), мы получим систему
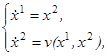 (1.34)
(1.34)
решение которой (при произвольном начальном состоянииx
0
) даёт оптимальную фазовую траекторию, ведущую в начало координат. Иначе говоря, система (1.34) представляет собой систему дифференциальных уравнений (с разрывной правой частью) для нахождения оптимальных траекторий, ведущих в начало координат.
Рассмотренный пример показывает, что решение задачи об оптимальных управлениях естественно ожидать в следующей форме. Будем решать оптимальную задачу в общей постановке:
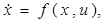 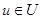
(см. п. 3), рассматривая всевозможные начальные состояния и каждый раз предписывая в качестве конечного состояния начало координат O
фазового пространства. Тогда (насколько можно судить по разобранному выше примеру) существует такая функция
v
(x
), заданная в фазовом пространстве
V принимающая значения в области управления
U, что уравнение
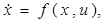 (1.35) (1.35)
определяет все оптимальные траектории, ведущие в начало координат.
Иначе говоря, оптимальное управление оказывается естественным искать не в форме u=
u
(t
), а в форме u=
v
(x
), т. е. искомое оптимальное управление в каждый момент зависит лишь от того, в какой точке пространства находится в данный момент фазовая точка
.
Функцию v
(x
), дающую уравнение оптимальных траекторий в форме (1.35), называют синтезирующей функцией,
а задачу нахождения синтезирующей функции ─ задачей синтеза
оптимальных управлений. В разобранном примере синтезирующая функция была кусочно-непрерывной (даже кусочно-постоянной).
Г л а в а
II
ЛИНЕЙНЫЕ ОПТИМАЛЬНЫЕ БЫСТРОДЕЙСТВИЯ
§ 4. Линейная задача оптимального управления
9.
Формулировка задачи.
Ниже будут подробно изучены управляемые объекты, движение которых описывается линейными дифференциальными уравнениями относительно величин x
1
,…,xn
, u
1
,…,ur
, т. е. уравнениями вида
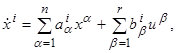 i
=1,2,…,n
, (2.1) i
=1,2,…,n
, (2.1)
где ai
α
и bi
β
─ некоторые постоянные коэффициенты.
Одним из наиболее важных для приложений является случай, когда каждая из величин u
1
,
u
2
,…,
ur
в уравнениях (2.1) представляет собой отдельный управляющий параметр, область изменения которого не зависит от значений остальных управляющих параметров и задаётся неравенствами
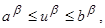 β
=1,…,r
. (2.2) β
=1,…,r
. (2.2)
Как было указано выше (см. п. 4), эти неравенства определяют r
-мерный параллелепипед
.
В дальнейшем при рассмотрении объектов вида (2.1) будет предполагаться, что управляющий параметр u=
(u
1
,u
2
,…, ur
) может меняться в замкнутой области управления U
, представляющей собой выпуклый многогранник
(лежащий в пространстве переменных u
1
,u
2
,…, ur
).
Для того чтобы записать уравнения (2.1) в векторной форме, мы введём в рассмотрение матрицы
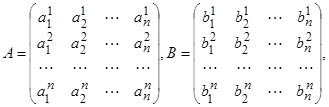 (2.3) (2.3)
элементами которых являются коэффициенты ai
α
, bi
β
, входящие в уравнения (2.1). Как обычно, результат применения матрицы A
к векторуx
=(x
1
, x
2
,…, xn
) мы будем обозначать символом Ax
, т. е. y
=Ax
есть n-
мерный вектор, координаты которого определяются формулами
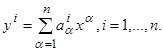 (2.4) (2.4)
Аналогично для любого r-
мерного вектора u=
(u
1
, u
2
,…, ur
) через Bu
обозначается вектор, i-
я координата которого равна 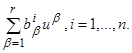 Таким образом, матрица A
определяет линейное отображение координатного n-
мерного пространства снова в n-
мерное пространство, а матрица B
определяет отображение r-
мерного пространства в n-
мерное. Таким образом, матрица A
определяет линейное отображение координатного n-
мерного пространства снова в n-
мерное пространство, а матрица B
определяет отображение r-
мерного пространства в n-
мерное.
Пользуясь матрицами A
и B
, мы можем теперь записать уравнения (2.1) в векторной форме:
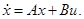 (2.5) (2.5)
Пусть u
(t
)=(u
1
, u
2
,…, ur
) ─ произвольное допустимое (в смысле п. 4) управление, заданное на некотором отрезке t
0
≤t
≤t
1
, и x
0
=(x
1
0
,…, xn
0
) ─ некоторая точка фазового пространства. Обозначим θ
1
, θ
2
,…, θ
k
все точки, в которых хотя бы одна из функций u
1
(t
), u
2
(t
),…, ur
(t
) терпит разрыв, причём занумеруем эти точки таким образом, что t
0
<θ
1
<θ
2
<…<θ
k
<t
1
. Подставив функции u
1
(t
), u
2
(t
),…, ur
(t
) в правые части системы (2.1),мы придём к системе уравнений
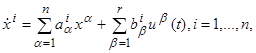 (2.6) (2.6)
или в векторной форме,
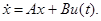 (2.7) (2.7)
Систему (2.7) мы рассмотрим сначала для значений t
, удовлетворяющих неравенствам t
0
≤t
≤θ
1
. На этом отрезке изменения аргумента существуют такие функции x
1
(t
),…, xn
(t
), определённые и непрерывные на всём отрезке t
0
≤t
≤θ
1
, которые, рассматриваемые на интервале t
0
<t
<θ
1
, являются решениями системы (2.6) и, кроме того, удовлетворяют начальным условиям x
1
(t
0
)=x
1
0
, x
2
(t
0
)=x
2
0
,…, xn
(t
0
)=xn
0
(согласно сведениям из дифференциальных уравнений (см. книгу Л.С. Понтрягина «Обыкновенные дифференциальные уравнения», «Наука», М., 1965 (стр. 23, 24 и 168-172))).
Теперь мы можем рассмотреть систему (2.6) на отрезке θ
1
≤t
≤θ
2
, воспользовавшись точкой γ
1
=(x
1
(θ
1
),…, xn
(θ
1
), θ
1
) в качестве начального значения. На отрезке θ
1
≤t
≤θ
2
снова существует решение с начальным значением γ
1
. Это решение мы снова обозначим через x
(t
)=(x
1
(t
),…, xn
(t
)). Теперь функция x
(t
) построена на отрезке t
0
≤t
≤θ
2
и непрерывна на всём этом отрезке (и, в частности, в «точке сопряжения» θ
1
;). Воспользовавшись, далее, новым начальным значением γ
2
=(x
1
(θ
2
),…, xn
(θ
2
), θ
2
), мы продолжим эту функцию x
(t
) на отрезок θ
2
≤t
≤θ
3
и т. д. В конце концов мы определим x
(t
) на всём отрезке t
0
≤t
≤t
1
.
Полученная функция x
(t
)=(x
1
(t
),…, xn
(t
)) непрерывна на всём отрезке t
0
≤t
≤t
1
и является на нём кусочно-дифференцируемой
; именно, во всех точках интервала t
0
<t
<t
1
, кроме θ
1
, θ
2
,…, θ
k
, функция x
(t
) непрерывно дифференцируема (и удовлетворяет системе (2.6)). Построенную функцию мы будем называть решением
системы (2.6) (или уравнения (2.7)), соответствующим
управлению u
(t
), при начальном условии x
1
(t
0
)=x
1
0
, x
2
(t
0
)=x
2
0
,…, xn
(t
0
)=xn
0
. Наконец, мы будем говорить, что допустимое управление u
(t
), t
0
≤t
≤t
1
, переводит
фазовую точку из состояния x
0
в состояние x
1
(в силу закона движения (2.1) или (2.5)), если соответствующее ему решение x
(t
) системы (2.1), удовлетворяющее начальному условию x
(t
0
)=x
0
, приходит в момент t
1
в точку x
1
, т. е. удовлетворяет также «конечному» условию x
(t
1
)=x
1
.
Теперь можно уточнить постановку задачи.
Линейной задачей оптимального управления
мы будем называть задачу об отыскании оптимальных быстродействий в случае, когда выполнены следующие три условия:
1 ) уравнения движения объекта линейны (см. (2.1) или (2.5));
2 ) предписанное конечное состояние x
1
совпадает с началом координат (0, 0,…, 0) n
-мерного фазового пространства переменных x
1
, x
2
,…,xn
;
3 ) область управления U
является r
-мерным выпуклым многогранником в r
-мерном пространстве (u
1
, u
2
,…, ur
), причём начало координат этого пространства принадлежит многограннику U
, но не является его вершиной.
Заметим, что начало координат xi
=0, i
=1,…,n
, является положением равновесия системы
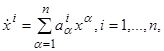 (2.8) (2.8)
получающейся из системы (2.1) отбрасыванием управлений (т. е. получающейся из (2.1) при u
1
=
u
2
=…=ur
=0). Таким образом, условие 2) означает, что ищется управление, переводящее объект из заданного начального состояния x
0
в положение равновесия.
10.
Принцип максимума.
В пункте 6 мы сформулировали необходимое условие оптимальности, называемое принципом максимума
. Данный пункт посвящён принципу максимума в случае линейной задачи оптимального управления. Вначале укажем те упрощения в формулировке принципа максимума, которые возникают в этом частном случае (т. е. в случае линейной задачи оптимального управления).
Заметим, прежде всего, что функция H
(см. формулу (B) на стр. 10) принимает вид
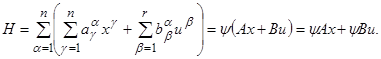 (2.9) (2.9)
(Здесь в правой части записаны скалярные произведения; например, ψ
Ax
есть скалярное произведение векторов ψ
и Ax
.)
Далее, рассмотрим систему дифференциальных уравнений для вспомогательных переменных ψ
1
, ψ
2
,…, ψ
n
(см. формулу (C) на стр. 10). Мы имеем
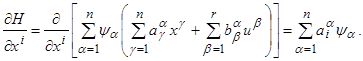
Следовательно, система уравнений для вспомогательных переменных принимает вид
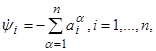 (2.10) (2.10)
т. е. представляет собой так называемую сопряжённую систему (по отношению к линейной системе (2.8)). В векторной форме система (2.10) записывается в виде
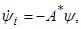 (2.11) (2.11)
где
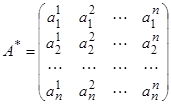
─ матрица, получающаяся из матрицы A
транспонированием
(т. е. заменой строк столбцами).
Так как в правой части соотношения (2.9) первое слагаемое совсем не зависит от u
, то при написании соотношения (D) (см. стр. 11) достаточно рассмотреть лишь второе слагаемое. Таким образом, соотношение (D) принимает в рассматриваемом случае вид
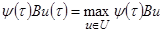 (2.12) (2.12)
для любого момента τ
, t
0
≤τ≤
t
1
.
Наконец, соотношение (E) (стр. 11) становится просто ненужным, так как в рассматриваемом случае оно всегда выполняется. Действительно, так как x
(t
1
)=(0, 0,…, 0) (условие 2) на стр. 15), то в H
(ψ
(t
1
), x
(t
1
), u
(t
1
)) первое слагаемое обращается в нуль (см. (2.9)). Второе же слагаемое, в силу (2.12), заведомо неотрицательно, ибо при u
1
=…=ur
=0 (эта точка, в силу условия 3) на стр.15, принадлежит многограннику U
) мы имеем ψ
(τ
)Bu
=0, а потому максимальное значение выражения ψ
(τ
)Bu
неотрицатнльно. Итак, соотношение H
(ψ
(t
1
), x
(t
1
), u
(t
1
))³0 для линейной оптимальной задачи всегда выполнено.
Сказанное можно резюмировать следующим образом. Пусть u
(t
), t
0
£t
£t
1
, - допустимое управление, переводящее объект (2.5) из заданного начального состояния x
0
в положение равновесия (0, 0,…, 0). Будем говорить, что управление u
(t
) удовлетворяет принципу максимума
, если существует такое нетривиальное решение y(t
) уравнения (2.11), для которого выполняется условие максимума (2.12) (в каждый момент времени t, t
0
£t£t
1
). Для оптимальности управления
u
(t
) необходимо, чтобы оно удовлетворяло принципу максимума
. Это и есть та упрощённая формулировка принципа максимума, к которой мы приходим в случае линейной задачи оптимального управления.
11.
Принцип максимума — необходимое и достаточное условие оптимальности.
Замечательным фактом является то, что в случае линейной задачи оптимального управления принцип максимума представляет собой не только необходимое, но и достаточное условие оптимальности. Однако факт этот имеет место не для произвольной линейной задачи — имеются малосущественные исключения. Поэтому мы наложим на линейную задачу некоторое ограничение, называемое условием общности положения
. Сформулируем это условие:
Условие общности положения
: если
w — вектор, параллельный произвольному ребру многогранника
U, то вектор
B
w не принадлежит никакому собственному инвариантному подпространству относительно преобразования
A
. Невыполнение условия общности положения означает, что хотя бы для одного ребра многогранника U
векторы B
w
, AB
w
, A
2
B
w
,…, An
-1
B
w
линейно зависимы, т. е. определитель n-
го порядка, составленный из координат этих векторов, обращается в нуль. Однако всюду в дальнейшем условие общности положения предполагается
(если не оговорено противное
) выполненным
.
Теперь перейдём к теореме, упоминавшейся в начале этого пункта.
Т е о р е м а 2.1. Пусть
u
(t
), t
0
£t
£t
1
, — допустимое управление, переводящее объект из заданного начального состояния
x
0
в положение равновесия
(0, 0,…, 0). Для оптимальности управления
u
(t
) необходимо и достаточно, чтобы оно удовлетворяло принципу максимума
.
12.
Основные теоремы о линейных оптимальных быстродействиях.
Т е о р е м а 2.2. Для каждого нетривиального решения
y
(t
) уравнения
(2.11) соотношение
(2.12) однозначно определяет допустимое управление
u
(t
); при этом оказывается, что функция
u
(t
) кусочно-постоянна и её значениями являются лишь вершины многогранника
U
.
Каждую точку разрыва оптимального управления мы будем называть точкой переключения
.
Т е о р е м а 2.3. Предположим, что многогранник
U является
r-мерным параллелепипедом
(2.2) и что все собственные значения матрицы
A=
(ai
j
), составленной из коэффициентов уравнений
(2.1), действительны. Тогда в оптимальном управлении
u
(t
)=(u
1
(t
),…, ur
(t
)) каждая из функций
u
b
(t
), b=1,…,r
, кусочно-постоянна, принимает только значения
a
b
и
b
b
(см. (2.2)) и имеет не более
n-
1 переключений
(т. е.
не более
n интервалов постоянства
), где
n — порядок системы
(2.1).
Т е о р е м а 2.4 (т е о р е м а е д и н с т в е н н о с т и). Пусть
u
1
(t
) и
u
2
(t
) — два оптимальных управления, заданных соответственно на отрезках
t
0
£t
£t
1
и
t
0
£t
£t
2
и переводящих точку
x
0
в начало координат
. Тогда эти управления совпадают
, т. е.
t
1
=t
2
и
u
1
(t
)ºu
2
(t
) на отрезке
t
0
£t
£t
1
.
Областью управляемости
для объекта (2.5)мы будем называть множество всех точек x
0
фазового пространства X
, из которых возможно при помощи какого-либо допустимого управления попасть в начало координат. Само начало координат мы также будем причислять к области управляемости. Ясно, что вопрос о нахождении оптимальных процессов разумно ставить лишь в случае, если начальное фазовое состояние x
0
принадлежит области управляемости (ведь из точек, не принадлежащих области управляемости, вообще нельзя попасть в начало координат).
Т е о р е м а 2.5 (т е о р е м а с у щ е с т в о в а н и я). Область управляемости является выпуклым открытым множеством фазового пространства
X
; для любой точки
x
0
, принадлежащей области управляемости
, существует оптимальное управление
, переводящее точку
x
0
в начало координат
.
Т е о р е м а 2.6. Если в линейной задаче оптимального управления матрица
A
(см. (2.3)) устойчива
, т. е. все её собственные значения имеют отрицательные действительные части, то область управляемости совпадает со всем фазовым пространством
X
. Следовательно
, для любой точки
x
0
Î
X существует оптимальное управление
, переводящее фазовую точку
x
0
в начало координат
.
§ 5. Решение задачи синтеза для линейных задач второго порядка
13.
Упрощение уравнений линейного управляемого объекта.
Нередко бывает, что в линейной задаче общая запись уравнений движения объекта в виде (2.1) неудобна и целесообразно воспользоваться некоторыми упрощениями. Мы здесь отметим стандартные упрощения, которые можно осуществить с помощью замены координат.
- Прежде всего, рассмотрим вопрос о замене координат в фазовом пространстве X
рассматриваемого управляемого объекта. Предположим, что в пространстве X
вместо координат x
1
,…, xn
введены новые координаты y
1
,…, yn
, связанные с прежними координатами соотношениями
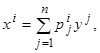 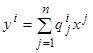 (2.13) (2.13)
(где матрицы P
=(pi
j
) и Q=(qi
j
) взаимно обратны). Ясно, что при такой замене линейная система (2.1) превращается в новую линейную систему
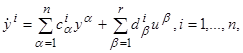
коэффициенты которой легко вычисляются:
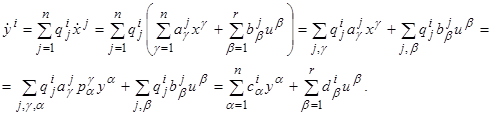
Таким образом, 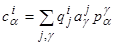 , , 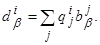
Переходя к векторным обозначениям, можно сказать, что указанная замена координат переводит уравнение (2.5) в уравнение 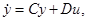 где матрицы C
и D
выражаются через матрицы A,
B,
P,
Q
по формулам C
=QAP
, D
=QB
. где матрицы C
и D
выражаются через матрицы A,
B,
P,
Q
по формулам C
=QAP
, D
=QB
.
Очевидно, при такой замене условия 1), 2), указанные на стр. 15, сохраняются и для уравнения 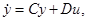 получаемого после замены. Далее, каждый процесс (u
(t
), x
(t
)), удовлетворяющий уравнению получаемого после замены. Далее, каждый процесс (u
(t
), x
(t
)), удовлетворяющий уравнению 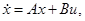 переходит в процесс (u
(t
), y(t
)), удовлетворяющий уравнению переходит в процесс (u
(t
), y(t
)), удовлетворяющий уравнению 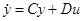 (и обратно). Так как при этом время t
не меняется, то указанная замена переводит оптимальные процессы для уравнения (и обратно). Так как при этом время t
не меняется, то указанная замена переводит оптимальные процессы для уравнения 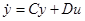 (и наоборот). В частности, синтез оптимальных управлений для уравнения (и наоборот). В частности, синтез оптимальных управлений для уравнения 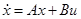 переводится с помощью преобразования координат (2.13) в синтез оптимальных управлений для уравнения переводится с помощью преобразования координат (2.13) в синтез оптимальных управлений для уравнения 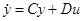 . .
Таким образом, если уравнение 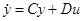 окажется проще и для него синтез оптимальных управлений можно будет построить, то из этого синтеза можно (с помощью афинного преобразования (2.13)) получит синтез и для первоначального уравнения окажется проще и для него синтез оптимальных управлений можно будет построить, то из этого синтеза можно (с помощью афинного преобразования (2.13)) получит синтез и для первоначального уравнения 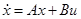 . В этом и заключается смысл замены координат (2.13): она позволяет заменить матрицу A
трансформированной матрицей C
=QAP,
в то же время вызывая лишь афинное искажение картины синтеза оптимальных управлений. Таким образом, преобразованием (2.13) можно воспользоваться для упрощения матрицы A
, составленной из коэффициентов при фазовых координатах. . В этом и заключается смысл замены координат (2.13): она позволяет заменить матрицу A
трансформированной матрицей C
=QAP,
в то же время вызывая лишь афинное искажение картины синтеза оптимальных управлений. Таким образом, преобразованием (2.13) можно воспользоваться для упрощения матрицы A
, составленной из коэффициентов при фазовых координатах.
- Предположим, что в уравнении 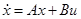 матрица A
уже приведена к простейшему виду (с помощью описанного выше приёма). Укажем теперь, каким образом может быть упрощена матрица B
, составленная из коэффициентов при управляющих параметрах. матрица A
уже приведена к простейшему виду (с помощью описанного выше приёма). Укажем теперь, каким образом может быть упрощена матрица B
, составленная из коэффициентов при управляющих параметрах.
С этой целью положим
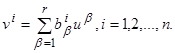 (2.14) (2.14)
Это означает, что вместо r
управляющих параметров u
1
,…,ur
вводятся n
других управляющих параметров v
1
,…, vn
, благодаря чему система (2.1) заменяется следующей:
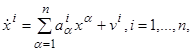
или в векторной форме, 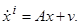
Нужно только выяснить, в каких пределах может изменяться точка v
=(v
1
, v
2
,…, vn
). Удобно считать, что эта точка v
=(v
1
, v
2
,…, vn
) расположена в том же пространстве X
, что и точка x
=(x
1
,…, xn
).
Соотношения (2.14) определяют линейное отображение r-
мерного пространства переменных u
1
,…,ur
в фазовое пространство X
. Образом многогранника U
при отображении (2.14) является некоторый выпуклый многогранник в пространстве X
, который мы обозначим через V
.
Таким образом, получаем два линейных уравнения:
 (2.15) (2.15)
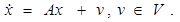 (2.16) (2.16)
Г л а в а
III
СИНТЕЗ ОПТИМАЛЬНЫХ УПРАВЛЕНИЙ ДЛЯ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
§ 6. Решение задачи синтеза в случае комплексных собственных значений
14.
Задача синтеза для малых колебаний маятника.
Здесь будет дано полное решение задачи синтеза оптимальных управлений для линейных объектов, описываемых уравнениями второго порядка. Фазовое пространство X
в этом случае представляет собой плоскость.
Рассмотрим колебание плоского маятника. Как известно колебание маятника, подвешенного к точке опоры, описывается дифференциальным уравнением второго порядка:
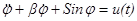 (в нашем случае положим β
=1) (в нашем случае положим β
=1)
при малых колебаниях маятника Sinφ≈φ тогда уравнение движения маятника запишется в виде:
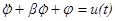 (3.1) (3.1)
Управляющий параметр u
(скалярный) будем предполагать изменяющимся в пределах -1£u
£1.
Пусть 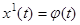 — угол отклонения, а — угол отклонения, а 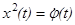 — скорость маятника. Тогда уравнение (3.1) перепишется в виде следующей нормальной системы: — скорость маятника. Тогда уравнение (3.1) перепишется в виде следующей нормальной системы:
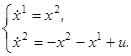 (3.2) (3.2)
На плоскости x
1
, x
2
«многогранник» U
будет представляться отрезком [-1, 1], расположенным на оси x
2
. Легко видеть, что ось x
2
не является собственным инвариантным подпространством матрицы A
, которая для системы (3.2) имеет вид:
A
=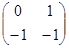 , ,
и потому условие общности положения всегда выполнено.
Найдём собственные значения матрицы A
. Для этого составим характеристическое уравнение |λE─
A
|=0, т. е. λ
2
+λ
+1=0. Откуда находим, что собственные значения матрицы A такие:
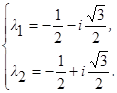
т. е. собственные значения матрицы A
комплексные. Введём обозначения 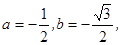 где b
≠0. где b
≠0.
Тогда матрица A преобразуется к виду:
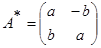 = =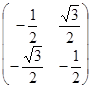 . .
Будем рассматривать систему, соответствующую матрице 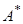 , т. е. систему вида: , т. е. систему вида:
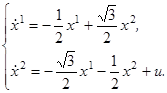 (3.3) (3.3)
Вначале рассмотрим соответствующую однородную систему:
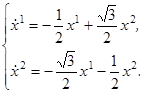 (3.4) (3.4)
Общее решение этой системы имеет вид:
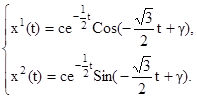
где c,
γ
– произвольные постоянные интегрирования.
Запишем функцию H
и применим принцип максимума.
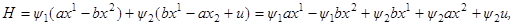
где ψ1
, ψ2
определяются системой, сопряжённой к системе (3.3), т. е. системой вида:
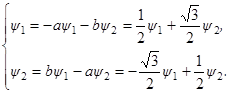 (3.5) (3.5)
Общее решение этой системы имеет вид:
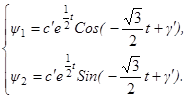
где c’,
γ’
– произвольные постоянные интегрирования. Т. е. функция H
имеет вид:
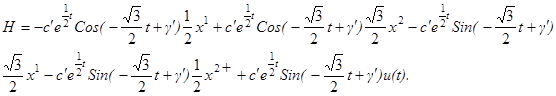
Подставим в функцию H
представление решений x
1
, x
2
:
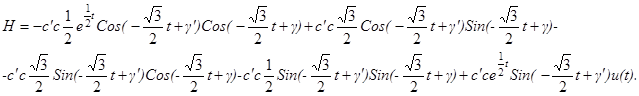
Т. к. собственный вектор матрицы A
, соответствующий собственному значению l
имеет вид q
1
─iq
2
, где q
1
=(1;─1/2); q
2
=(0;─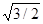 ). ).
Пусть q
1
и q
2
– базисные векторы новой косоугольной системы координат y
1
, y
2
. Тогда переход от системы y
1
, y
2
к системе x
1
, x
2
выражается формулами:
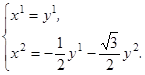
Тогда в новых координатах система уравнений (3.2) запишется в виде
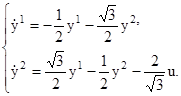
или, иначе, в виде
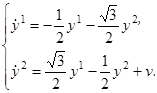
где v
=(v
1
, v
2
) ─ управляющая точка, которая может меняться в пределах многогранника V
, представляющего собой отрезок [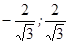 ] оси y
2
. ] оси y
2
.
     Согласно теории вершинам e
1
=(0, Согласно теории вершинам e
1
=(0, 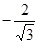 ), e
2
=(0, ), e
2
=(0, 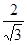 ) многогранника V
соответствуют точки h
1
=(1, - ) многогранника V
соответствуют точки h
1
=(1, -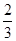 ), h
2
=(-1, ), h
2
=(-1, 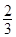 ) (координаты указаны в системе y
1
, y
2
), а каждый из углов a
1
, a
2
, соответствующих этим вершинам, равен p. ) (координаты указаны в системе y
1
, y
2
), а каждый из углов a
1
, a
2
, соответствующих этим вершинам, равен p.
Теперь уже нетрудно построить синтез оптимальных управлений в плоскости y
1
, y
2
. Кусками фазовых траекторий будут дуги логарифмических спиралей, т. к. у нас b=1, т. е. b>0 (рис. 18).
При переходе от координат y
1
, y
2
к координатам x
1
, x
2
картина синтеза афинно искажается.
Список используемой литературы:
1.
В.Г. Болтянский. «Математические методы оптимального управления», М.: «Наука», 1968г.
2.
Л.С. Понтрягин, В.Г. Болтянский, Р.В. Гамкрелидзе, Е.Ф. Мищенко. «Математическая теория оптимальных процессов», 4-е издательство. М.: «Наука», 1983г.
3.
Р. Габасов, Ф.М. Кириллова. «Методы оптимизации», Минск, издательство БГУ, 1981г.
|