Абстрактная
теория групп
- Понятие абстрактной
группы.
1.Понятие
алгебраической
операции.
Говорят, что
на множестве
X определена
алгебраическая
операция
(*), если
каждой упорядоченной
паре элементов
 поставлен в
соответствие
некоторый
элемент
поставлен в
соответствие
некоторый
элемент
 называемый
их произведением.
называемый
их произведением.
Примеры.
Композиция
перемещений
на множествах
 является
алгебраической
операцией.
является
алгебраической
операцией.
Композиция
подстановок
является
алгебраической
операцией на
множестве
 всех подстановок
степени n.
всех подстановок
степени n.
Алгебраическими
операциями
будут и обычные
операции сложения,
вычитания и
умножения на
множествах
 соответственно
целых, вещественных
и комплексных
чисел. Операция
деления не
будет алгебраической
операцией на
этих множествах,
поскольку
частное
соответственно
целых, вещественных
и комплексных
чисел. Операция
деления не
будет алгебраической
операцией на
этих множествах,
поскольку
частное
 не определено
при
не определено
при
 .
Однако на множествах .
Однако на множествах
 , ,
 это будет
алгебраическая
операция.
это будет
алгебраическая
операция.
Сложение
векторов является
алгебраической
операцией на
множестве
 . .
Векторное
произведение
будет алгебраической
операцией на
множестве
 . .
Умножение
матриц будет
алгебраической
операцией на
множестве всех
квадратных
матриц данного
порядка.
2.Свойства
алгебраических
операций.
Операция
(*) называется
ассоциативной,
если
 . .
Это
свойство выполняется
во всех приведенных
выше примерах,
за исключением
операций вычитания
( и деления) и
операции векторного
умножения
векторов. Наличие
свойства
ассоциативности
позволяет
определить
произведение
любого конечного
множества
элементов.
Например, если
 , ,
 .
В частности
можно определить
степени с натуральным
показателем: .
В частности
можно определить
степени с натуральным
показателем:
 .
При этом имеют
место обычные
законы: .
При этом имеют
место обычные
законы:
 , ,
 . .
2.
Операция (*)
называется
коммутативной,
если

В
приведенных
выше примерах
операция коммутативна
в примерах 3 и
4 и не коммутативна
в остальных
случаях. Отметим,
что для коммутативной
операции

Элемент
 называется
нейтральным
для алгебраической
операции (*)
на множестве
X,
если
называется
нейтральным
для алгебраической
операции (*)
на множестве
X,
если
 .
В примерах 1-6
нейтральными
элементами
будут соответственно
тождественное
перемещение,
тождественная
перестановка,
числа 0 и 1 для
сложения и
умножения
соответственно
(для вычитания
нейтральный
элемент отсутствует
!),
нулевой вектор,
единичная
матрица. Для
векторного
произведения
нейтральный
элемент отсутствует.
Отметим,
что нейтральный
элемент (если
он существует)
определен
однозначно.
В самом деле,
если .
В примерах 1-6
нейтральными
элементами
будут соответственно
тождественное
перемещение,
тождественная
перестановка,
числа 0 и 1 для
сложения и
умножения
соответственно
(для вычитания
нейтральный
элемент отсутствует
!),
нулевой вектор,
единичная
матрица. Для
векторного
произведения
нейтральный
элемент отсутствует.
Отметим,
что нейтральный
элемент (если
он существует)
определен
однозначно.
В самом деле,
если
 - нейтральные
элементы, то
- нейтральные
элементы, то
 .
Наличие нейтрального
элемента позволяет
определить
степень с нулевым
показателем: .
Наличие нейтрального
элемента позволяет
определить
степень с нулевым
показателем:
 . .
Допустим,
что для операции
(*) на
X существует
нейтральный
элемент. Элемент
 называется
обратным для
элемента
называется
обратным для
элемента
 ,
если ,
если
 .
Отметим, что
по определению .
Отметим, что
по определению
 .
Все перемещения
обратимы также
как и все подстановки.
Относительно
операции сложения
все числа обратимы,
а относительно
умножения
обратимы все
числа, кроме
нуля. Обратимые
матрицы - это
в точности все
матрицы с ненулевым
определителем.
Если элемент
x обратим,
то определены
степени с
отрицательным
показателем: .
Все перемещения
обратимы также
как и все подстановки.
Относительно
операции сложения
все числа обратимы,
а относительно
умножения
обратимы все
числа, кроме
нуля. Обратимые
матрицы - это
в точности все
матрицы с ненулевым
определителем.
Если элемент
x обратим,
то определены
степени с
отрицательным
показателем:
 .
Наконец, отметим,
что если x
и
y обратимы,
то элемент .
Наконец, отметим,
что если x
и
y обратимы,
то элемент
 также обратим
и
также обратим
и
 .
(Сначала мы
одеваем рубашку,
а потом куртку;
раздеваемся
же в обратном
порядке!). .
(Сначала мы
одеваем рубашку,
а потом куртку;
раздеваемся
же в обратном
порядке!).
Определение
(абстрактной)
группы.
Пусть на множестве
G определена
алгебраическая
операция (*).
(G ,*)
называется
группой, если
Операция
(*)
ассоциативна
на G.
Для
этой операции
существует
нейтральный
элемент e
(единица
группы).
Каждый
элемент из G
обратим.
Примеры
групп.
Любая
группа преобразований.
(Z,
+), (R,
+), (C, +).

Матричные
группы:
 -
невырожденные
квадратные
матрицы порядка
n,
ортогональные
матрицы того
же порядка,
ортогональные
матрицы с
определителем
1. -
невырожденные
квадратные
матрицы порядка
n,
ортогональные
матрицы того
же порядка,
ортогональные
матрицы с
определителем
1.
Простейшие
свойства групп.
В
любой группе
выполняется
закон сокращения:
 (левый
закон сокращения;
аналогично,
имеет место
и правый закон).
Доказательство.
Домножим
равенство
слева на (левый
закон сокращения;
аналогично,
имеет место
и правый закон).
Доказательство.
Домножим
равенство
слева на
 и воспользуемся
свойством
ассоциативности:
и воспользуемся
свойством
ассоциативности:


 . .
Признак
нейтрального
элемента:

Доказательство
Применим
к равенству
 закон сокращения.
закон сокращения.
Признак
обратного
элемента:
 Доказательство
Применим
закон сокращения
к равенству
Доказательство
Применим
закон сокращения
к равенству
 . .
Единственность
обратного
элемента. Обратный
элемент определен
однозначно.
Следует
из п.3.
Существование
обратной операции.
Для любых двух
элементов
 произвольной
группы G
уравнение произвольной
группы G
уравнение
 имеет и притом
единственное
решение.
Доказательство
Непосредственно
проверяется,
что
имеет и притом
единственное
решение.
Доказательство
Непосредственно
проверяется,
что
 (левое
частное элементов (левое
частное элементов
 )
является решением
указанного
уравнения.
Единственность
вытекает из
закона сокращения,
примененного
к равенству )
является решением
указанного
уравнения.
Единственность
вытекает из
закона сокращения,
примененного
к равенству
 .
Аналогично
устанавливается
существование
и единственность
правого частного. .
Аналогично
устанавливается
существование
и единственность
правого частного.
Изоморфизм
групп.
Определение.
Отображение
 двух групп G
и K
называется
изоморфизмом
, если
двух групп G
и K
называется
изоморфизмом
, если
1.Отображение
j взаимно
однозначно.
2.Отображение
j сохраняет
операцию:
 . .
Поскольку
отображение
обратное к j
также является
изоморфизмом,
введенное
понятие симметрично
относительно
групп G
и
K , которые
называются
изоморфными.
Примеры.
1.Группы
поворотов
плоскости
 и
и
 вокруг
точек вокруг
точек
 и
и
 изоморфны
между собой.
Аналогично,
изоморфными
будут и группы,
состоящие из
поворотов
пространства
относительно
любых двух
осей. изоморфны
между собой.
Аналогично,
изоморфными
будут и группы,
состоящие из
поворотов
пространства
относительно
любых двух
осей.
2.Группа диэдра
 и соответствующая
пространственная
группа
и соответствующая
пространственная
группа
 изоморфны.
изоморфны.
Группа
тетраэдра T
изоморфна
группе
 состоящей из
четных подстановок
четвертой
степени. Для
построения
изоморфизма
достаточно
занумеровать
вершины тетраэдра
цифрами 1,2,3,4 и
заметить, что
каждый поворот,
совмещающий
тетраэдр с
собой некоторым
образом переставляет
его вершины
и, следовательно,
задает некоторую
подстановку
множества{1,2,
3, 4} Повороты
вокруг оси,
проходящей
через некоторую
вершину (например
1), оставляет
символ 1 на месте
и циклически
переставляет
символы 1, 2, 3. Все
такие перестановки
- четные. Поворот
вокруг оси,
соединяющей
середины ребер
(например, 12 и
34 ) переставляет
символы 1 и 2 , а
также 3 и 4. Такие
перестановки
также являются
четными.
состоящей из
четных подстановок
четвертой
степени. Для
построения
изоморфизма
достаточно
занумеровать
вершины тетраэдра
цифрами 1,2,3,4 и
заметить, что
каждый поворот,
совмещающий
тетраэдр с
собой некоторым
образом переставляет
его вершины
и, следовательно,
задает некоторую
подстановку
множества{1,2,
3, 4} Повороты
вокруг оси,
проходящей
через некоторую
вершину (например
1), оставляет
символ 1 на месте
и циклически
переставляет
символы 1, 2, 3. Все
такие перестановки
- четные. Поворот
вокруг оси,
соединяющей
середины ребер
(например, 12 и
34 ) переставляет
символы 1 и 2 , а
также 3 и 4. Такие
перестановки
также являются
четными.
Формула
 определяет
взаимно однозначное
соответствие
между множеством
R
вещественных
чисел и множеством определяет
взаимно однозначное
соответствие
между множеством
R
вещественных
чисел и множеством
 положительных
чисел. При этом
положительных
чисел. При этом
 .
Это означает,
что .
Это означает,
что
 является
изоморфизмом.
является
изоморфизмом.
Замечание.
В абстрактной
алгебре изоморфные
группы принято
считать одинаковыми.
По существу
это означает,
что игнорируются
индивидуальные
свойства элементов
группы и происхождение
алгебраической
операции.
- Понятие
подгруппы.
Непустое подмножество
 называется
подгруппой,
если
называется
подгруппой,
если
 само
является группой.
Более подробно
это означает,
что само
является группой.
Более подробно
это означает,
что
 , ,
 и
и
 . .
Признак
подгруппы.
Непустое
подмножество
 будет подгруппой
тогда и только
тогда, когда
будет подгруппой
тогда и только
тогда, когда
 . .
Доказательство.
В
одну сторону
это утверждение
очевидно. Пусть
теперь
 -
любой элемент.
Возьмем -
любой элемент.
Возьмем
 в признаке
подгруппы.
Тогда получим
в признаке
подгруппы.
Тогда получим
 .
Теперь возьмем .
Теперь возьмем
 .
Тогда получим .
Тогда получим
 . .
Примеры
подгрупп.
Для
групп преобразований
новое и старое
понятие подгруппы
равносильны
между собой.
 -
подгруппа
четных подстановок. -
подгруппа
четных подстановок.

 и т.д.
и т.д.
Пусть
G -
любая группа
и
 - любой фиксированный
элемент. Рассмотрим
множество
- любой фиксированный
элемент. Рассмотрим
множество
 всевозможных
степеней этого
элемента. Поскольку всевозможных
степеней этого
элемента. Поскольку
 ,
рассматриваемое
множество
является подгруппой.
Она называется
циклической
подгруппой
с образующим
элементом g
. ,
рассматриваемое
множество
является подгруппой.
Она называется
циклической
подгруппой
с образующим
элементом g
.
Пусть
 любая подгруппа
Рассмотрим
множество
любая подгруппа
Рассмотрим
множество
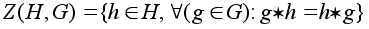 -
централизатор
подгруппы H
в группе G.
Из определения
вытекает, что
если -
централизатор
подгруппы H
в группе G.
Из определения
вытекает, что
если
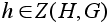 ,
то ,
то
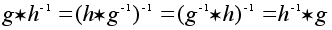 ,
то есть ,
то есть
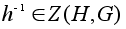 .
Теперь ясно,
что если .
Теперь ясно,
что если
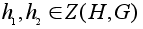 ,
то и ,
то и
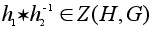 и значит централизатор
является подгруппой.
Если группа
G
коммутативна,
то
и значит централизатор
является подгруппой.
Если группа
G
коммутативна,
то
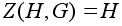 .
Если G=H,
то централизатор
состоит из тех
элементов,
которые перестановочны
со всеми элементами
группы;
в этом случае
он называется
центром группы
G
и обозначается
Z(G). .
Если G=H,
то централизатор
состоит из тех
элементов,
которые перестановочны
со всеми элементами
группы;
в этом случае
он называется
центром группы
G
и обозначается
Z(G).
Замечание
об аддитивной
форме записи
группы.
Иногда,
особенно когда
операция в
группе коммутативна,
она обозначается
(+) и называется
сложением. В
этом случае
нейтральный
элемент называется
нулем и удовлетворяет
условию:
g+0=g. Обратный
элемент в этом
случае называется
противоположным
и обозначается
(-g).
Степени
элемента g
имеют вид
g+g+...+g ,
называются
кратными элемента
g и
обозначаются
ng.
Абстрактная
теория групп
(продолжение)
- Реализация
абстрактной
группы как
группы преобразований.
Существует
несколько
способов связать
с данной абстрактной
группой некоторую
группу преобразований.
В дальнейшем,
если не оговорено
противное, знак
алгебраической
операции в
абстрактной
группе будет
опускаться.
Пусть
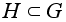 некоторая
подгруппа.
некоторая
подгруппа.
А)
Для каждого
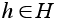 определим
отображение
определим
отображение
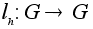 (левый
сдвиг на элемент
h)
формулой (левый
сдвиг на элемент
h)
формулой
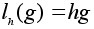 . .
Теорема
1
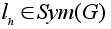
Множество
L(H,G)=
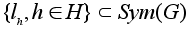 является
группой преобразований
множества G. является
группой преобразований
множества G.
Соответствие:
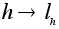 является
изоморфизмом
групп H
и L(H,G).
является
изоморфизмом
групп H
и L(H,G).
Доказательство.
Надо
проверить, что
отображение
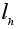 взаимно однозначно
для всякого
взаимно однозначно
для всякого
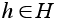 .
Если .
Если
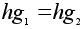 ,
то ,
то
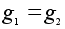 по закону
сокращения.
Значит
по закону
сокращения.
Значит
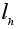 инъективно.
Если
инъективно.
Если
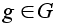 любой
элемент, то любой
элемент, то
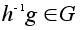 и
и
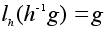 так что
так что
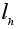 к тому же и
сюръективно.
к тому же и
сюръективно.
Обозначим
через ·
операцию композиции
в группе Sym(G)
взаимно
однозначных
отображений
 .
Надо проверить,
что .
Надо проверить,
что
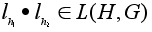 и
и
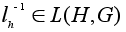 .
Пусть .
Пусть
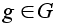 любой элемент.
Имеем:
любой элемент.
Имеем:
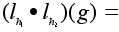 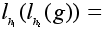 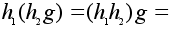 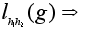 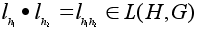 ; ;
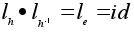 и значит,
и значит,
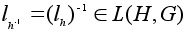 . .
Пусть
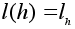 .
Надо проверить,
что l
взаимно
однозначно
и сохраняет
операцию. По
построению
l
сюръективно.
Инъективность
вытекает из
закона правого
сокращения: .
Надо проверить,
что l
взаимно
однозначно
и сохраняет
операцию. По
построению
l
сюръективно.
Инъективность
вытекает из
закона правого
сокращения:
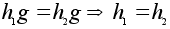 .
Сохранение
операции фактически
уже было установлено
выше: .
Сохранение
операции фактически
уже было установлено
выше:
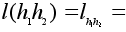
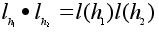 . .
Следствие.
Любая
абстрактная
группа изоморфна
группе преобразований
некоторого
множества
(Достаточно
взять G=H
и рассмотреть
левые сдвиги).
Для
случая конечных
групп получается
теорема Кэли:
Любая
группа из n
элементов
изоморфна
подгруппе
группы
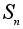 подстановок
степени n. подстановок
степени n.
Для
каждого
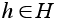 определим
отображение
определим
отображение
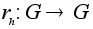 (правый
сдвиг на элемент
h)
формулой (правый
сдвиг на элемент
h)
формулой
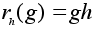 . .
Теорема
B.
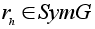 . .
Множество
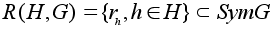 является группой
преобразований
множества G.
является группой
преобразований
множества G.
Соответствие
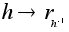 является
изоморфизмом
групп H
и R(H,G). является
изоморфизмом
групп H
и R(H,G).
Доказательство
теоремы B
вполне аналогично
доказательству
теоремы A.
Отметим только,
что
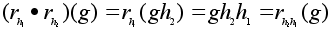 .
Именно поэтому
в пункте 3 теоремы
В появляется
не .
Именно поэтому
в пункте 3 теоремы
В появляется
не
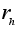 ,
а ,
а
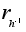 . .
С)
Для каждого
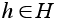 определим
определим
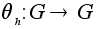 (сопряжение
или трансформация
элементом h
) формулой (сопряжение
или трансформация
элементом h
) формулой
 . .
Теорема
С.
Каждое
отображение
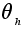 является
изоморфизмом
группы G
с собой
(автоморфизмом
группы G).
является
изоморфизмом
группы G
с собой
(автоморфизмом
группы G).
Множество
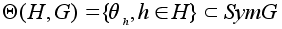 является группой
преобразований
множества G.
является группой
преобразований
множества G.
Отображение
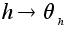 сюръективно
и сохраняет
операцию.
сюръективно
и сохраняет
операцию.
Доказательство.
Поскольку
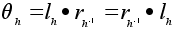 ,
отображение ,
отображение
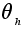 взаимно однозначно
как композиция
двух отображений
такого типа.
Имеем:
взаимно однозначно
как композиция
двух отображений
такого типа.
Имеем:
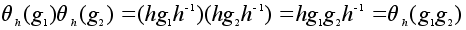 и потому
и потому
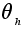 сохраняет
операцию.
сохраняет
операцию.
Надо
проверить, что
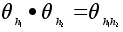 и
и
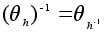 .
Оба равенства
проверяются
без труда. .
Оба равенства
проверяются
без труда.
Сюръективность
отображения
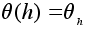 имеет место
по определению.
Сохранение
операции уже
было проверено
в пункте 2.
имеет место
по определению.
Сохранение
операции уже
было проверено
в пункте 2.
Замечание
об инъективности
отображения
q.
В
общем случае
отображение
q не является
инъективным.
Например, если
группа H
коммутативна,
все преобразования
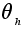 будут тождественными
и группа
будут тождественными
и группа
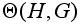 тривиальна.
Равенство тривиальна.
Равенство
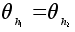 означает,
что означает,
что
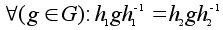 или
или
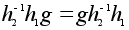 (1) В связи
с этим удобно
ввести следующее
определение:
множество
(1) В связи
с этим удобно
ввести следующее
определение:
множество
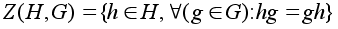 называется
централизатором
подгруппы
называется
централизатором
подгруппы
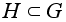 .
Легко проверить,
что централизатор
является подгруппой
H.
Равенство (1)
означает, что .
Легко проверить,
что централизатор
является подгруппой
H.
Равенство (1)
означает, что
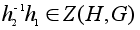 .
Отсюда вытекает,
что если централизатор
подгруппы H
в G
тривиален,
отображение
q является
изоморфизмом. .
Отсюда вытекает,
что если централизатор
подгруппы H
в G
тривиален,
отображение
q является
изоморфизмом.
Смежные
классы;
классы
сопряженных
элементов.
Пусть, как и
выше,
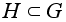 некоторая
подгруппа.
Реализуем H
как группу
L(H,G) левых
сдвигов на
группе G.
Орбита
некоторая
подгруппа.
Реализуем H
как группу
L(H,G) левых
сдвигов на
группе G.
Орбита
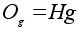 называется
левым смежным
классом группы
G по
подгруппе H.
Аналогично,
рассматривая
правые сдвиги,
приходим к
правым смежным
классам
называется
левым смежным
классом группы
G по
подгруппе H.
Аналогично,
рассматривая
правые сдвиги,
приходим к
правым смежным
классам
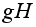 .Заметим,
что .Заметим,
что
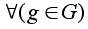 стабилизатор
St(g, L(H,G)) (как и St(g,
R(H,G)) ) тривиален
поскольку
состоит из
таких элементов
стабилизатор
St(g, L(H,G)) (как и St(g,
R(H,G)) ) тривиален
поскольку
состоит из
таких элементов
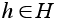 ,
что hg=g ,
что hg=g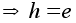 .
Поэтому, если
группа H
конечна, то
все левые и
все правые
смежные классы
состоят из
одинакового
числа элементов,
равного .
Поэтому, если
группа H
конечна, то
все левые и
все правые
смежные классы
состоят из
одинакового
числа элементов,
равного
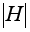 . .
Орбиты
группы
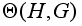 называются
классами
сопряженных
элементов
группы G
относительно
подгруппы H
и обозначаются
называются
классами
сопряженных
элементов
группы G
относительно
подгруппы H
и обозначаются
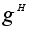 Если G=H,
говорят просто
о классах сопряженных
элементов
группы G.
Классы сопряженных
элементов могут
состоять из
разного числа
элементов . Это
число равно
Если G=H,
говорят просто
о классах сопряженных
элементов
группы G.
Классы сопряженных
элементов могут
состоять из
разного числа
элементов . Это
число равно
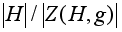 ,
где Z(H,g)
подгруппа
H ,
состоящая из
всех элементов
h
перестановочных
с g. ,
где Z(H,g)
подгруппа
H ,
состоящая из
всех элементов
h
перестановочных
с g.
Пример.
Пусть
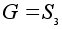 -
группа подстановок
степени 3. Занумеруем
ее элементы: -
группа подстановок
степени 3. Занумеруем
ее элементы:
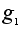 =(1,2,3); =(1,2,3);
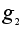 =(1,3,2); =(1,3,2);
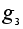 =(2,1,3); =(2,1,3);
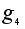 =(2,3,1); =(2,3,1);
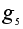 =(3,1,2); =(3,1,2);
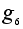 =(3,2,1).
Пусть =(3,2,1).
Пусть
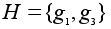 .
Легко проверить,
что левые смежные
классы суть: .
Легко проверить,
что левые смежные
классы суть:
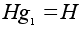 , ,
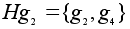 , ,
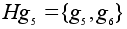 . .
Правые
смежные классы:
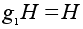 , ,
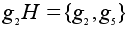 , ,
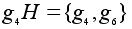 . .
Все
эти классы
состоят из 2
элементов.
Классы
сопряженных
элементов G
относительно
подгруппы H:
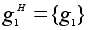 , ,
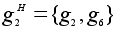 , ,
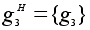 , ,
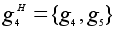 . .
В то
же время,
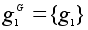 , ,
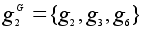 , ,
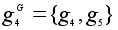 . .
Теорема
Лагранжа.
Пусть
H подгруппа
конечной группы
G.
Тогда порядок
H является
делителем
порядка
G.
Доказательство.
По
свойству орбит
G
представляется
в виде объединения
непересекающихся
смежных классов:
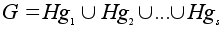 .
Поскольку все
смежные классы
состоят из
одинакового
числа элементов, .
Поскольку все
смежные классы
состоят из
одинакового
числа элементов,
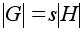 ,
откуда и вытекает
теорема. ,
откуда и вытекает
теорема.
Замечание.
Число s
левых (или
правых) смежных
классов называется
индексом подгруппы
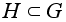 . .
Следствие.
Две
конечные подгруппы
группы G
порядки
которых взаимно
просты пересекаются
только по
нейтральному
элементу.
В
самом деле,
если
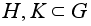 эти подгруппы,
то
эти подгруппы,
то
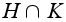 их общая подгруппа
и по теореме
Лагранжа
их общая подгруппа
и по теореме
Лагранжа
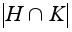 - общий делитель
порядков H
и K
то есть 1.
- общий делитель
порядков H
и K
то есть 1.
- Нормальные
подгруппы.
Факторгруппы.
Пусть
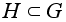 любая подгруппа
и
любая подгруппа
и
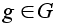 -любой
элемент. Тогда -любой
элемент. Тогда
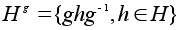 также
является подгруппой
G
притом изоморфной
H,
поскольку
отображение
сопряжения также
является подгруппой
G
притом изоморфной
H,
поскольку
отображение
сопряжения
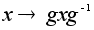 является
изоморфизмом.
Подгруппа
является
изоморфизмом.
Подгруппа
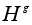 называется
сопряженной
по отношению
к подгруппе
H.
называется
сопряженной
по отношению
к подгруппе
H.
Определение.
Подгруппа
H называется
инвариантной
или нормальной
в группе G,
если все сопряженные
подгруппы
совпадают с
ней самой:
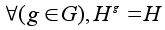 . .
Равенство
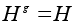 можно
записать в виде
Hg = gH и
таким образом,
подгруппа
инвариантна
в том и только
в том случае,
когда левые
и правые смежные
классы по этой
подгруппе
совпадают. можно
записать в виде
Hg = gH и
таким образом,
подгруппа
инвариантна
в том и только
в том случае,
когда левые
и правые смежные
классы по этой
подгруппе
совпадают.
Примеры.
В
коммутативной
группе все
подгруппы
нормальны, так
как отображение
сопряжения
в такой группе
тождественно.
В
любой группе
G нормальными
будут , во первых,
тривиальная
подгруппа
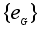 и, во вторых,
вся группа G.
Если других
нормальных
подгрупп нет,
то G
называется
простой.
и, во вторых,
вся группа G.
Если других
нормальных
подгрупп нет,
то G
называется
простой.
В
рассмотренной
выше группе
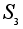 подгруппа
подгруппа
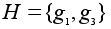 не
является нормальной
так как левые
и правые смежные
классы не совпадают.
Сопряженными
с H
будут подгруппы не
является нормальной
так как левые
и правые смежные
классы не совпадают.
Сопряженными
с H
будут подгруппы
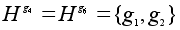 и
и
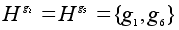 . .
Если
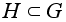 -
любая подгруппа,
то ее централизатор
Z = Z(H,G) -
нормальная
подгруппа в
G ,
так как для
всех ее элементов
z -
любая подгруппа,
то ее централизатор
Z = Z(H,G) -
нормальная
подгруппа в
G ,
так как для
всех ее элементов
z
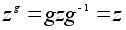 .
В частности,
центр Z(G)
любой группы
G -нормальная
подгруппа. .
В частности,
центр Z(G)
любой группы
G -нормальная
подгруппа.
Подгруппа
H индекса
2 нормальна. В
самом деле,
имеем 2 смежных
класса :
H и Hg
= G-H = gH.
Теорема
(свойство смежных
классов по
нормальной
подгруппе).
Если
подгруппа H
нормальна
в G,
то множество
всевозможных
произведений
элементов из
двух каких либо
смежных классов
по этой подгруппе
снова будет
одним из смежных
классов, то
есть
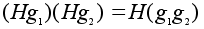 . .
Доказательство.
Очевидно,
что для любой
подгруппы H
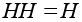 .Но
тогда .Но
тогда
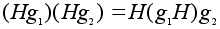 = =
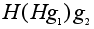 = =
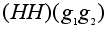 = =
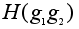 . .
Таким образом,
в случае нормальной
подгруппы H
определена
алгебраическая
операция на
множестве
смежных классов.
Эта операция
ассоциативна
поскольку
происходит
из ассоциативного
умножения в
группе G.
Нейтральным
элементом для
этой операции
является смежный
класс
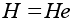 .
Поскольку .
Поскольку
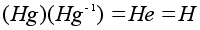 ,
всякий смежный
класс имеет
обратный. Все
это означает,
что относительно
этой операции
множество всех
(левых или правых)
смежных классов
по нормальной
подгруппе
является группой.
Она называется
факторгруппой
группы G
по H
и обозначается
G/H.
Ее порядок
равен индексу
подгруппы H
в G. ,
всякий смежный
класс имеет
обратный. Все
это означает,
что относительно
этой операции
множество всех
(левых или правых)
смежных классов
по нормальной
подгруппе
является группой.
Она называется
факторгруппой
группы G
по H
и обозначается
G/H.
Ее порядок
равен индексу
подгруппы H
в G.
Абстрактная
теория групп
(продолжение)
9
Гомоморфизм.
Гомоморфизм
групп - это
естественное
обобщение
понятия изоморфизма.
Определение.
Отображение
групп
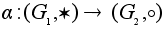 называется
гомоморфизмом,
если оно сохраняет
алгебраическую
операцию, то
есть называется
гомоморфизмом,
если оно сохраняет
алгебраическую
операцию, то
есть
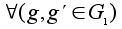 : :
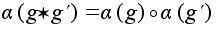 . .
Таким
образом, обобщение
состоит в том,
что вместо
взаимно однозначных
отображений,
которые участвуют
в определении
изоморфизма,
здесь допускаются
любые отображения.
Примеры.
Разумеется,
всякий изоморфизм
является
гомоморфизмом.
Тривиальное
отображение
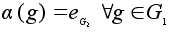 является
гомоморфизмом.
является
гомоморфизмом.
Если
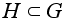 -
любая подгруппа,
то отображение
вложения -
любая подгруппа,
то отображение
вложения
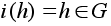 будет инъективным
гомоморфизмом.
будет инъективным
гомоморфизмом.
Пусть
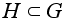 -
нормальная
подгруппа.
Отображение -
нормальная
подгруппа.
Отображение
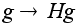 группы G
на факторгруппу
G/H будет
гомоморфизмом
поскольку
группы G
на факторгруппу
G/H будет
гомоморфизмом
поскольку
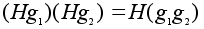 .
Этот сюръективный
гомоморфизм
называется
естественным. .
Этот сюръективный
гомоморфизм
называется
естественным.
По
теореме С
предыдущего
раздела отображение
сопряжения
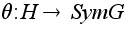 сохраняет
операцию и,
следовательно
является
гомоморфизмом.
сохраняет
операцию и,
следовательно
является
гомоморфизмом.
Отображение
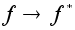 ,
которое каждому
перемещению ,
которое каждому
перемещению
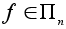 n-
мерного пространства
ставит в соответствие
ортогональный
оператор
n-
мерного пространства
ставит в соответствие
ортогональный
оператор
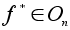 (см.
лекцию №3) является
гомоморфизмом
поскольку по
теореме 4 той
же лекции (см.
лекцию №3) является
гомоморфизмом
поскольку по
теореме 4 той
же лекции
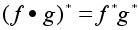 . .
Теорема
(свойства
гомоморфизма)
Пусть
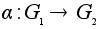 -
гомоморфизм
групп, -
гомоморфизм
групп,
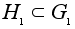 и
и
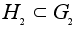 -
подгруппы.
Тогда: -
подгруппы.
Тогда:
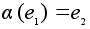 , ,
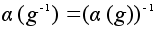 . .
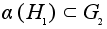 -
подгруппа. -
подгруппа.
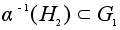 -подгруппа,
причем нормальная,
если таковой
была -подгруппа,
причем нормальная,
если таковой
была
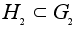 . .
Доказательство.
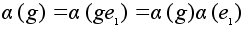 и по признаку
нейтрального
элемента
и по признаку
нейтрального
элемента
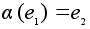 .
Теперь имеем: .
Теперь имеем:
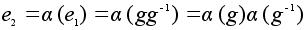 . .
Пусть
p = a(h)
, q = a(k)
. Тогда
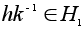 и
и
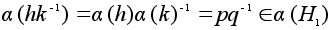 .
По признаку
подгруппы
получаем 2. .
По признаку
подгруппы
получаем 2.
Пусть
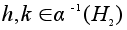 то есть элементы
p = a(h)
, q = a(k)
входят в
то есть элементы
p = a(h)
, q = a(k)
входят в
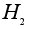 .
Тогда .
Тогда
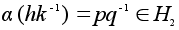 то есть
то есть
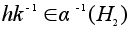 .
Пусть теперь
подгруппа .
Пусть теперь
подгруппа
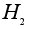 нормальна
и нормальна
и
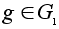 -
любой элемент. -
любой элемент.
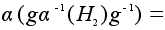
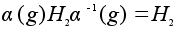 и потому
и потому
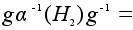 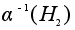 . .
Определение.
Нормальная
подгруппа
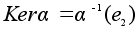 называется
ядром гомоморфизма
называется
ядром гомоморфизма
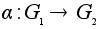 .Образ
этого гомоморфизма
обозначается .Образ
этого гомоморфизма
обозначается
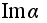 . .
Теорема.
Гомоморфизм
a инъективен
тогда и только
тогда, когда
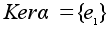
Доказательство.
Поскольку
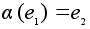 ,
указанное
условие необходимо.
С другой стороны,
если ,
указанное
условие необходимо.
С другой стороны,
если
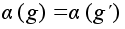 ,
то ,
то
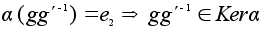 и если ядро
тривиально,
и если ядро
тривиально,
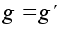 и отображение
инъективно.
и отображение
инъективно.
Понятие гомоморфизма
тесно связано
с понятием
факторгруппы.
Теорема
о гомоморфизме.
Любой
гомоморфизм
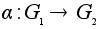 можно представить
как композицию
естественного
(сюръективного)
гомоморфизма
можно представить
как композицию
естественного
(сюръективного)
гомоморфизма
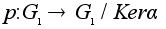 ,
изоморфизма ,
изоморфизма
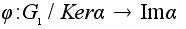 и (инъективного)
гомоморфизма
и (инъективного)
гомоморфизма
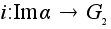 (вложения подгруппы
в группу):
(вложения подгруппы
в группу):
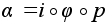 . .
Доказательство.
Гомоморфизмы
p и
i описаны
выше (см. примеры)
Построим изоморфизм
j. Пусть
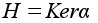 .
Элементами
факторгруппы .
Элементами
факторгруппы
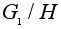 являются смежные
классы Hg
. Все элементы
являются смежные
классы Hg
. Все элементы
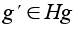 имеют одинаковые
образы при
отображении
a :
имеют одинаковые
образы при
отображении
a :
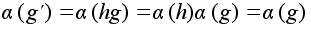 .
Поэтому формула .
Поэтому формула
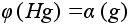 определяет
однозначное
отображение
определяет
однозначное
отображение
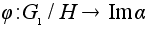 .
Проверим сохранение
операции .
Проверим сохранение
операции
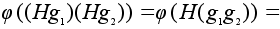
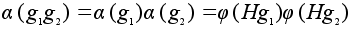 .Поскольку
отображение
j очевидно
сюръективно,
остается проверить
его инъективность.
Если .Поскольку
отображение
j очевидно
сюръективно,
остается проверить
его инъективность.
Если
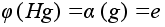 ,
то ,
то
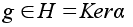 и потому
и потому
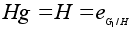 .
Следовательно, .
Следовательно,
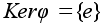 и по предыдущей
теореме j
инъективно.
и по предыдущей
теореме j
инъективно.
Пусть
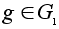 - любой элемент.
Имеем :
- любой элемент.
Имеем :
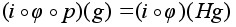
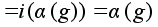 .
Следовательно, .
Следовательно,
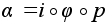 . .
10
Циклические
группы.
Пусть G
произвольная
группа и
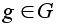 -
любой ее элемент.
Если некоторая
подгруппа -
любой ее элемент.
Если некоторая
подгруппа
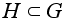 содержит g
, то она содержит
и все степени
содержит g
, то она содержит
и все степени
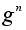 .
С другой стороны,
множество .
С другой стороны,
множество
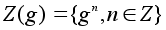 очевидно
является подгруппой
G . очевидно
является подгруппой
G .
Определение.
Подгруппа
Z(g)
называется
циклической
подгруппой
G с
образующим
элементом g.
Если G
= Z(g) , то и вся
группа G
называется
циклической.
Таким
образом, циклическая
подгруппа с
образующим
элементом g
является
наименьшей
подгруппой
G,
содержащей
элемент g.
Примеры
Группа
Z целых
чисел с операцией
сложения является
циклической
группой с образующим
элементом 1.
Группа
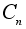 поворотов
плоскости на
углы кратные
2p¤n
является
циклической
с образующим
элементом
поворотов
плоскости на
углы кратные
2p¤n
является
циклической
с образующим
элементом
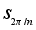 -
поворотом на
угол 2p¤n.
Здесь n
= 1, 2, ... -
поворотом на
угол 2p¤n.
Здесь n
= 1, 2, ...
Теорема
о структуре
циклических
групп.
Всякая
бесконечная
циклическая
группа изоморфна
Z.
Циклическая
группа порядка
n изоморфна
Z / nZ .
Доказательство.
Пусть
G = Z(g) -
циклическая
группа. По
определению,
отображение
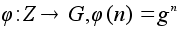 -
сюръективно.
По свойству
степеней -
сюръективно.
По свойству
степеней
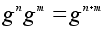 и потому j
- гомоморфизм.
По теореме о
гомоморфизме
и потому j
- гомоморфизм.
По теореме о
гомоморфизме
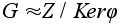 .
H = KerjМZ.
Если H
- тривиальная
подгруппа, то .
H = KerjМZ.
Если H
- тривиальная
подгруппа, то
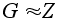 .
Если H
нетривиальна,
то она содержит
положительные
числа. Пусть
n -
наименьшее
положительное
число входящее
в H.
Тогда nZМH.
Предположим,
что в H
есть и другие
элементы то
есть целые
числа не делящееся
на n
нацело и k
одно из них.
Разделим k
на n
с остатком:
k = qn +r , где 0
< r < n. Тогда r
= k - qn О
H , что противоречит
выбору n.
Следовательно,
nZ = H и
теорема доказана. .
Если H
нетривиальна,
то она содержит
положительные
числа. Пусть
n -
наименьшее
положительное
число входящее
в H.
Тогда nZМH.
Предположим,
что в H
есть и другие
элементы то
есть целые
числа не делящееся
на n
нацело и k
одно из них.
Разделим k
на n
с остатком:
k = qn +r , где 0
< r < n. Тогда r
= k - qn О
H , что противоречит
выбору n.
Следовательно,
nZ = H и
теорема доказана.
Отметим,
что
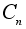 »
Z / nZ . »
Z / nZ .
Замечание.
В
процессе
доказательства
было установлено,
что каждая
подгруппа
группы Z
имеет вид
nZ ,
где n
= 0 ,1 , 2 ,...
Определение.
Порядком
элемента
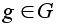 называется
порядок соответствующей
циклической
подгруппы Z(
g ) .
называется
порядок соответствующей
циклической
подгруппы Z(
g ) .
Таким
образом, если
порядок g
бесконечен,
то все степени
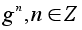 - различные
элементы группы
G.
Если же этот
порядок равен
n,
то элементы
- различные
элементы группы
G.
Если же этот
порядок равен
n,
то элементы
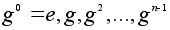 различны и
исчерпывают
все элементы
из Z(
g ), а
различны и
исчерпывают
все элементы
из Z(
g ), а
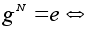 N
кратно n
. Из теоремы
Лагранжа вытекает,
что порядок
элемента является
делителем
порядка группы.
Отсюда следует,
что для всякого
элемента g
конечной
группы G
порядка n
имеет место
равенство N
кратно n
. Из теоремы
Лагранжа вытекает,
что порядок
элемента является
делителем
порядка группы.
Отсюда следует,
что для всякого
элемента g
конечной
группы G
порядка n
имеет место
равенство
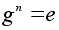 . .
Следствие.
Если
G - группа
простого порядка
p,
то
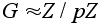 -
циклическая
группа. -
циклическая
группа.
В
самом деле,
пусть
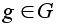 - любой элемент
отличный от
нейтрального.
Тогда его порядок
больше 1 и является
делителем p,
следовательно
он равен p.
Но в таком случае
G = Z( g )»
- любой элемент
отличный от
нейтрального.
Тогда его порядок
больше 1 и является
делителем p,
следовательно
он равен p.
Но в таком случае
G = Z( g )»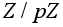 . .
Теорема
о подгруппах
конечной циклической
группы.
Пусть
G -
циклическая
группа порядка
n и
m - некоторый
делитель n.
Существует
и притом только
одна подгруппа
HМG
порядка m.
Эта подгруппа
циклична.
Доказательство.
По
предыдущей
теореме G»Z
/ nZ. Естественный
гомоморфизм
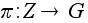 устанавливает
взаимно однозначное
соответствие
между подгруппами
HМG
и теми подгруппами
KМZ
, которые
содержат Kerp
= nZ . Но, как отмечалось
выше, всякая
подгруппа K
группы Z
имеет вид
kZ Если
kZЙnZ
, то k
- делитель
n и
p(k)
- образующая
циклической
группы H
порядка m
= n /k. Отсюда и
следует утверждение
теоремы.
устанавливает
взаимно однозначное
соответствие
между подгруппами
HМG
и теми подгруппами
KМZ
, которые
содержат Kerp
= nZ . Но, как отмечалось
выше, всякая
подгруппа K
группы Z
имеет вид
kZ Если
kZЙnZ
, то k
- делитель
n и
p(k)
- образующая
циклической
группы H
порядка m
= n /k. Отсюда и
следует утверждение
теоремы.
Верна
и обратная
теорема:
если конечная
группа G
порядка
n
обладает
тем свойством,
что для всякого
делителя m
числа n
существует
и притом ровно
одна подгруппа
H
порядка
m, то G
- циклическая
группа.
Доказательство.
Будем
говорить, что
конечная группа
G порядка
N обладает
свойством (Z),
если для всякого
делителя m
числа N
существует
и притом только
одна подгруппа
HМG
порядка m.
Нам надо доказать,
что всякая
группа, обладающая
свойством (Z)
циклическая.
Установим
прежде всего
некоторые
свойства таких
групп.
Лемма.
Если
G обладает
свойством (Z),
то
Любая
подгруппа G
нормальна.
Если
x и
y
два элемента
такой группы
и их порядки
взаимно просты,
то xy
= yx.
Если
H подгруппа
порядка m
такой группы
G порядка
N
и числа m
и N/m
взаимно просты,
то H
обладает
свойством (Z).
Доказательство
леммы.
1. Пусть
HМG
. Для любого
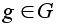 подгруппа
подгруппа
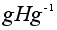 имеет тот же
порядок, что
и H.
По свойству
(Z)
имеет тот же
порядок, что
и H.
По свойству
(Z)
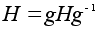 то есть подгруппа
H нормальна.
то есть подгруппа
H нормальна.
2. Пусть
порядок x
равен p,
а порядок
y равен
q.
По пункту 1)
подгруппы Z(x)
и Z(y)
нормальны.
Значит, Z(x)y
= yZ(x) и xZ(y)
= Z(y)x и потому
для некоторых
a и b
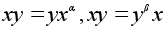 .
Следовательно, .
Следовательно,
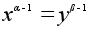 .
Но, поскольку
порядки подгрупп
Z(x) и
Z(y)
взаимно просты,
то .
Но, поскольку
порядки подгрупп
Z(x) и
Z(y)
взаимно просты,
то
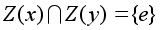 .
Следовательно, .
Следовательно,
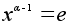
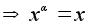 и потому xy
= yx.
и потому xy
= yx.
Используя
свойство (Z)
, выберем в
G подгруппу
K порядка
N/m.
По 1) эта подгруппа
нормальна, а
поскольку
порядки H
и K
взаимно просты,
эти подгруппы
пересекаются
лишь по нейтральному
элементу. Кроме
того по 2) элементы
этих подгрупп
перестановочны
между собой.
Всевозможные
произведения
hk
=kh,
где hОH,
kОK
попарно различны,
так как
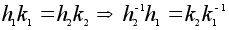 =e
поскольку это
единственный
общий элемент
этих подгрупп.
Количество
таких произведений
равно m
N/m = =e
поскольку это
единственный
общий элемент
этих подгрупп.
Количество
таких произведений
равно m
N/m =
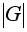 и, следовательно,
они исчерпывают
все элементы
G.
Сюръективное
отображение
и, следовательно,
они исчерпывают
все элементы
G.
Сюръективное
отображение
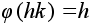 является
гомоморфизмом
является
гомоморфизмом
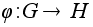 с ядром K.
Пусть теперь
число s
является
делителем m.
Выберем в G
подгруппу
S порядка
s.
Поскольку s
и N/m
взаимно
просты,
с ядром K.
Пусть теперь
число s
является
делителем m.
Выберем в G
подгруппу
S порядка
s.
Поскольку s
и N/m
взаимно
просты,
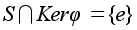 и потому
и потому
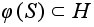 - подгруппа
порядка s.
Если бы подгрупп
порядка s
в H
было несколько,
то поскольку
все они были
бы и подгруппами
G условие
(Z) для
G было
бы нарушено.
Тем самым мы
проверили
выполнение
условия (S)
для подгруппы
H.
- подгруппа
порядка s.
Если бы подгрупп
порядка s
в H
было несколько,
то поскольку
все они были
бы и подгруппами
G условие
(Z) для
G было
бы нарушено.
Тем самым мы
проверили
выполнение
условия (S)
для подгруппы
H.
Доказательство
теоремы.
Пусть
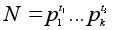 - разложение
числа N
в произведение
простых чисел.
Проведем индукцию
по k.
Пусть сначала
k = 1,
то есть
- разложение
числа N
в произведение
простых чисел.
Проведем индукцию
по k.
Пусть сначала
k = 1,
то есть
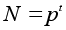 .
Выберем в G
элемент x
максимального
порядка .
Выберем в G
элемент x
максимального
порядка
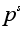 .
Пусть y
любой другой
элемент этой
группы. Его
порядок равен .
Пусть y
любой другой
элемент этой
группы. Его
порядок равен
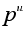 ,
где u
Ј
s. Группы ,
где u
Ј
s. Группы
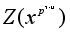 и
и
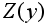 имеют одинаковые
порядки и по
свойству (Z)
они совпадают.
Поэтому
имеют одинаковые
порядки и по
свойству (Z)
они совпадают.
Поэтому
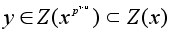 и мы доказали,
что x
- образующий
элемент циклической
группы G.
Пусть теорема
уже доказана
для всех меньших
значений k.
Представим
N в
виде произведения
двух взаимно
простых множителей
N = pq
(например,
и мы доказали,
что x
- образующий
элемент циклической
группы G.
Пусть теорема
уже доказана
для всех меньших
значений k.
Представим
N в
виде произведения
двух взаимно
простых множителей
N = pq
(например,
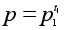 )
. Пусть H
и K
подгруппы G
порядка p
и q.
Использую 3) и
предположение
индукции , мы
можем считать,
что H
= Z(x), K = Z(y), причем
xy = yx .
Элемент xy
имеет порядок
pq = N и,
следовательно,
является образующим
элементом
циклической
группы G. )
. Пусть H
и K
подгруппы G
порядка p
и q.
Использую 3) и
предположение
индукции , мы
можем считать,
что H
= Z(x), K = Z(y), причем
xy = yx .
Элемент xy
имеет порядок
pq = N и,
следовательно,
является образующим
элементом
циклической
группы G.
11.
Некоторые
теоремы о подгруппах
конечных групп.
Теорема
Коши.
Если
порядок конечной
группы делится
на простое
число p,
то в ней имеется
элемент порядка
p.
Прежде
чем переходить
к доказательству
этой теоремы,
отметим, что
если g№e
и
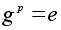 ,
где p
- простое
число, то порядок
g равен
p.
В самом деле,
если m
- порядок g,
то p
делится на
m,
откуда m=1
или m=p.
Первое из этих
равенств невозможно
по условиям
выбора g. ,
где p
- простое
число, то порядок
g равен
p.
В самом деле,
если m
- порядок g,
то p
делится на
m,
откуда m=1
или m=p.
Первое из этих
равенств невозможно
по условиям
выбора g.
Индукция
, с помощью которой
проводится
доказательство
теоремы, основана
на следующей
лемме
Лемма.
Если
некоторая
факторгруппа
G/H конечной
группы G
имеет элемент
порядка p,
то тем же свойством
обладает и сама
группа G.
Доказательство
леммы.
Пусть
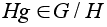 - элемент порядка
p.
Обозначим через
m порядок
элемента
- элемент порядка
p.
Обозначим через
m порядок
элемента
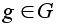 .
Тогда .
Тогда
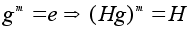 и значит m
делится на
p.
Но тогда
и значит m
делится на
p.
Но тогда
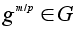 - элемент порядка
p.
- элемент порядка
p.
Доказательство
теоремы Коши.
Зафиксируем
простое число
p и
будем проводить
индукцию по
порядку n
группы G.
Если n=p,
то G»Z/pZ
и теорема
верна. Пусть
теорема уже
доказана для
всех групп
порядка меньше
n и
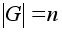 ,
причем n
делится на
p. ,
причем n
делится на
p.
Рассмотрим
последовательно
несколько
случаев
G
содержит
собственную
( то есть не
совпадающую
со всей группой
и нетривиальную)
подгруппу H
, порядок
которой делится
на p.
В этом случае
порядок H
меньше n
и по предположению
индукции имеется
элемент
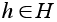 порядка p.
Поскольку
порядка p.
Поскольку
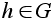 в этом случае
теорема доказана.
в этом случае
теорема доказана.
G
содержит
собственную
нормальную
подгруппу.
Если ее порядок
делится на p,
то по 1 теорема
доказана. В
противном
случае на p
делится
порядок факторгруппы
G/H и
теорема в этом
случае следует
из доказанной
выше леммы.
Если
G -
коммутативна,
то возьмем
любой
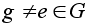 .
Если порядок
g делится
на p,
то теорема
доказана по
1, поскольку
Z(g)МG.
Если это не
так, то , поскольку
в коммутативной
группе все
подгруппы
нормальны,
теорема доказана
по 2. .
Если порядок
g делится
на p,
то теорема
доказана по
1, поскольку
Z(g)МG.
Если это не
так, то , поскольку
в коммутативной
группе все
подгруппы
нормальны,
теорема доказана
по 2.
Остается
рассмотреть
случай, когда
порядки всех
собственных
подгрупп G
не делятся
на p,
группа G
проста ( то
есть не имеет
собственных
нормальных
подгрупп ) и
не коммутативна.
Покажем, что
этого быть не
может. Поскольку
центр группы
G
является нормальной
подгруппой
и не может совпадать
со всей группой,
он тривиален.
Поэтому G
можно рассматривать
как группу
преобразований
сопряжения
на множестве
G.
Рассмотрим
разбиение
множества G
на классы
сопряженных
элементов:
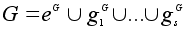 .
Здесь отдельно
выделен класс .
Здесь отдельно
выделен класс
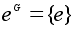 и классы неединичных
элементов.
Стабилизатор
St(g)
элемента
g№
e представляет
собой подгруппу
группы G,
не совпадающую
со всей группой.
В самом деле,
если St(g)
= G, то g
коммутирует
со всеми элементами
из G
и потому
gОZ(g)
= {e}. Значит,
порядок этой
подгруппы не
делится на p,
а потому
и классы неединичных
элементов.
Стабилизатор
St(g)
элемента
g№
e представляет
собой подгруппу
группы G,
не совпадающую
со всей группой.
В самом деле,
если St(g)
= G, то g
коммутирует
со всеми элементами
из G
и потому
gОZ(g)
= {e}. Значит,
порядок этой
подгруппы не
делится на p,
а потому
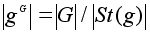 делится на p:
делится на p:
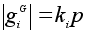 .
Но тогда .
Но тогда
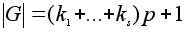 - не делится
на p,
что не соответствует
условию.
- не делится
на p,
что не соответствует
условию.
Замечание.
Если
число p
не является
простым, то
теорема неверна
даже для коммутативных
групп. Например,
группа
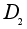 порядка 4 коммутативна,
но не является
циклической,
а потому не
имеет элементов
порядка 4.
порядка 4 коммутативна,
но не является
циклической,
а потому не
имеет элементов
порядка 4.
Теорема
о подгруппах
коммутативной
группы.
Для
конечной
коммутативной
группы G
справедлива
теорема обратная
к теореме Лагранжа
:
если m
- делитель
порядка группы,
то в G
имеется подгруппа
порядка m.
Доказательство.
Проведем
индукцию по
порядку n
группы G.
Для n
= 2 теорема
очевидна. Пусть
для всех коммутативных
групп порядка
< n теорема
доказана. Пусть
простое p
делит m
. По теореме
Коши в G
имеется
циклическая
подгруппа S
порядка p.
Так как G
коммутативна,
S - нормальная
подгруппа. В
факторгруппе
G/S
используя
предположение
индукции выберем
подгруппу K
порядка m/p
.Если
 естественный
гомоморфизм,
то
естественный
гомоморфизм,
то
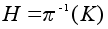 - подгруппа
G порядка
m
.
- подгруппа
G порядка
m
.
Замечание.
Для
некоммутативных
групп данная
теорема неверна.
Так, например,
в группе
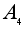 четных перестановок
степени 4, которая
имеет порядок
12, нет подгрупп
шестого порядка.
четных перестановок
степени 4, которая
имеет порядок
12, нет подгрупп
шестого порядка.
|