xO(x0)O(x0)
Теорема:(о
непрерывности
сложной функции)
Пусть y=f(x)
непрерывна
в точки х0,
а z=g(y)
непрерывна
в точки y0=f(x0),
тогда сложная
функция имеет
вид z=g(f(x0))
– непрерывна
в точки х0.
Доказательство:
Зададим
ε>0
в силу непрерывности
z=g(y)
в точки у0
б>0x:
y-y0|<б
g(y)-g(x0)<ε
По
найденному
б>0 в силу непрерывности
функции f(x)
в точки х0
>0
x:
x-x0<
f(x)-f(x0)<б
ε>0
>0
x:x-x0<
y-y0<б
g(y)-g(y0)<ε
g(f(x))-g(f(x0))
то есть lim
g(f(x))=g(f(x0))
xx
Замечание:
можно переходить
к пределу под
знаком непрерывной
функции limf(x)=limg(y)
limf(x)=f(x0)=y0
xx
xx
xx
Непрерывность
некоторых
функций.
1) y=c
(постоянная)
непрерывна
в х0
R
lim
c=c.
Зададим ε>0
рассмотрим
разность
f(x)-f(x0)=c-c=0<ε
xx
x:
x-x0<
(>0)!
2) y=x
непрерывна
в
x0R,
то есть lim
x=x0.
Зададим
ε>0
рассмотрим
разность
f(x)-f(x0)=x-x0<ε
xx
x:
x-x0<
(>0)!
=ε!
Следствие.
Многочлен
p(x)=anxn+
an-1xn-1+…+a1x+a0
(an,an-1…a1,a0
– зададим
число)
n=0,1,2,3….
непрерывен
в любой точки
х0 оси
как сумма
произведения
непрерывной
функции. Рациональная
функция:
R(x)=p(x)/q(x).
Частная двух
многочленов
непрерывна
в любой точки
х0 в
которой q(x)0
Лекция
№9
Ведущая:
Голубева Зоя
Николаевна
Дата:
среда, 11 октября
2000 г.
Тема:
«Точки разрыва»
1)
Доказать, что
lim
[((1+x)p-1)/px]=1
x0
 y=(1+x)p-1
y=(1+x)p-1
lim
[((1+x)p-1)/px]=
x0
y0
=lim ([ln(1+x)]/x)([(1+x)p-1]/[pln(1+x)]=lim
([ln(1+x)]/x)
x0
(1+x)p=y+1
x0
x0
p[ln(1+x)]=ln(y+1)
lim([(1+x)p-1]/[pln(1+x)]=lim
y/[ln(y+1)]=1
что и требовалось
доказать
(1+x)p-1~px
при x0
x0
y0
(1+x)p=1+px+o(x)
при х0
2)
Доказать, что
lim
(ex-1)/x=1
x0
 y=ex-1
y=ex-1
lim
(ex-1)/x=
x0
y0
=lim
y/[ln(y+1)]=1
что и требовалось
доказать
x0
ex=y+1
y0
x=ln(y+1)
ex-1~x
при x0
ex=1+x+o(x)
при х0
Классификация
точек разрыва
функции.
Определение:
Пусть y=f(x)
определена
в О(х0),
а в самой точке
х0 может
быть как и
определена,
так и неопределенна.
1) Точка
х0
называется
точкой разрыва
1ого
рода функции,
если
а)
Существует
lim
f(x)’=lim
f(x)’’
, но либо функция
неопределенна
в точки х0
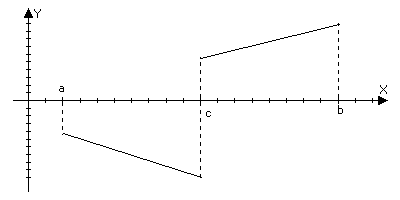
либо f(x0)b.
Тогда точка
х0
xx+0
xx-0
точка
устранимого
разрыва. 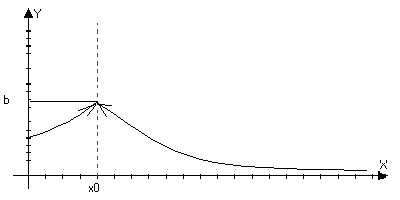
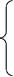
 1,x=1
1,x=1
Y=(x-1)/(x-1)=
Не ,
x=1
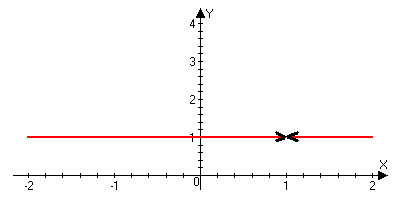
б)
f(x)=cb
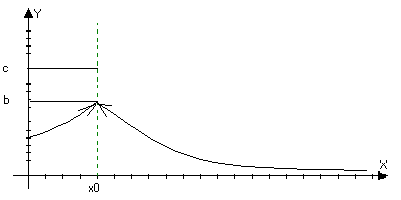
Можно
доопределить
или переопределить
в точке х0,
так что она
станет непрерывной.
lim
f(x)=b; lim f(x)=c, но
bc
xx+0
xx-0
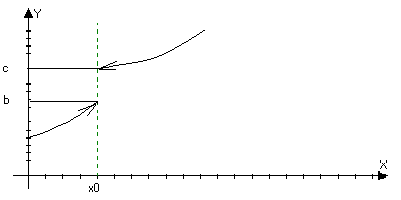
Может
быть и определена
f(x0)=b
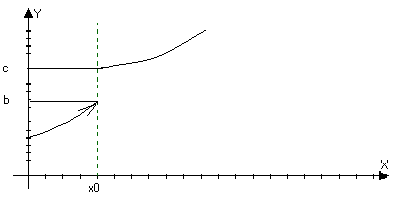
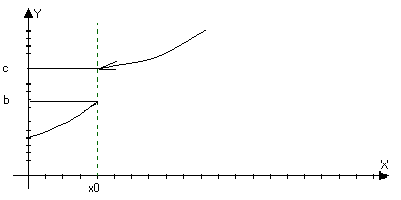
Или
f(x0)=d
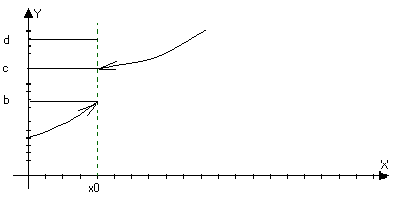
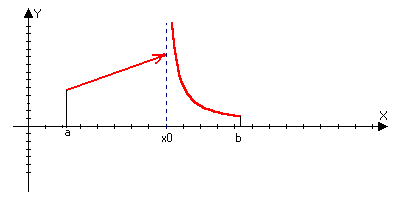
2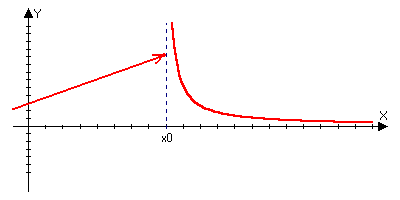 )Точка
х0
называется
точкой разрыва
2ого
рода функции
если она не
является точкой
разрыва 1ого
порядка, то
есть если хотя
бы один из
односторонних
пределов не
существует
или равен
бесконечности.
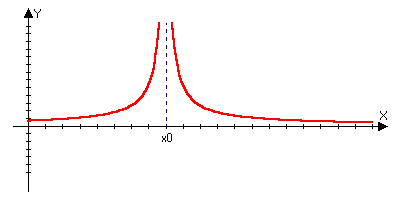
)Точка
х0
называется
точкой разрыва
2ого
рода функции
если она не
является точкой
разрыва 1ого
порядка, то
есть если хотя
бы один из
односторонних
пределов не
существует
или равен
бесконечности.
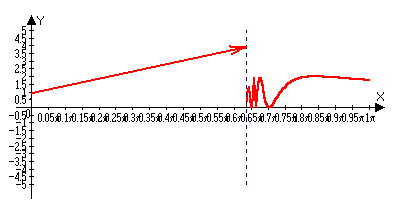
y=sin(1/x)
Основные
теоремы о непрерывных
функциях.
Теорема:
Все основные
элементы функции
непрерывны
в любой точки
своей области
определения.
Определение:
(функции непрерывной
на отрезке)
y=f(x)
– называется
непрерывной
на отрезке
[a,b],
если она непрерывна
в любой точке
х(a,b).
В точке х=а функция
непрерывна
справа, то есть
lim
f(x)=f(a),
а в точке х=b
функция непрерывна
слева lim
f(x)=f(b).
xx+0
xx-0
Функция
непрерывна
на множестве
D
если она непрерывна
в этой точке.
Теорема:
(о сохранение
знака непрерывной
функции)
Пусть
y=f(x)
непрерывна
в точке х0
и f(x0)>0
(f(x0)<0),
тогда f(x)>0
f(x)<0
непрерывна
в некоторой
точки О(х0)
Доказательство:
lim
f(x)=f(x0)
ε>0
>0
x:
x-x0<
f(x)-f(x0)|<ε.
xx
Пусть
f(x0)>0,
выберем ε=f(x0)
f(x)-f(x0)0)
xO(x0)
(>0!)
-f(x0)0)0);
f(x)>0
xO(x0),
если f(x0)<0,
то ε=-f(x0)
Теорема
Коши:
( о нуле непрерывной
функции)
Пусть
f(x)
непрерывна
на [a,b]
и на концах его
принимает
значение разных
знаков f(a)
f(b)
<0, тогда
x0(a,b):
f(x0)=0
Доказательство:
f(b)>0
f(a)<0
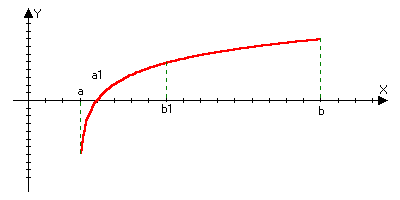
Разделим
отрезок [a,b]
пополам. Если
в середине
отрезка f(x)=0,
то всё доказано,
если нет, то
выберем ту
половину отрезка,
на концах которой
функция принимает
значение разных
знаков. Выбранной
отрезок поделим
пополам. Если
в середине
нового отрезка
f(x)=0,
то всё доказано,
если нет, то
выберем ту
половину от
той половины,
на концах которой
функция принимает
значение разных
знаков и т.д.
[a,b][a1,b1][a2,b2]
Последовательность
левых концов
удовлетворяет
отношению
a12<…n<…
bb1b2…bn…>a
{ an}-ограниченная
не убывающая
lim
an=b f(a)<0
f(an)<0
n
an}-ограниченная
не убывающая
lim
an=b f(a)<0
f(an)<0
n
x+
[anbn]=(b-a)/2n
0
при
n
{bn}-ограниченная
не возрастающая
lim
bn= f(b)>0
f(bn)>0
n
x+
В
силу непрерывности
функции lim
f(an)=f
(lim
bn)=f()0
lim
(bn-an)=-=
lim
(b-a)/2n=0=
 x+
x+
x+
x+
x+
x+
x+
x+
f()0
f()=0
x0=
f()=f()0
Условие
непрерывности
функции нельзя
отбросить:
f(b)>0;
f(a)<0
Теоремы
Вейштрасса.
1) Теорема:
Пусть функция
y=f(x)
непрерывна
на отрезке
[a,b].
Тогда она ограниченна
на нём.
 Замечание:
а) Условие
непрерывности
нельзя отбросить
Замечание:
а) Условие
непрерывности
нельзя отбросить
Неограниченна
сверху
неограниченна
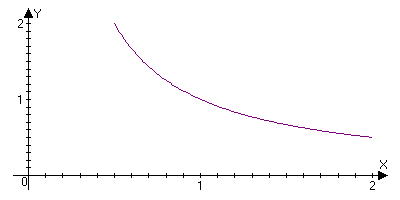
б)
Нельзя заменить
отрезок на
интервал или
полуинтервал.
Непрерывна
на (0;1]
2) Теорема:
Пусть функция
y=f(x)
непрерывна
на отрезке
[a,b].
Среди её значений
есть наибольшее
и наименьшее.
Замечание:
а) Множество
[0;1] наибольшее
значение 1М
наименьшее
значение 0
М
 б) Множество
(0;1]=М наибольшее
значение 1М
б) Множество
(0;1]=М наибольшее
значение 1М
нет
наименьшего
в) Множество
[0;1)=M
нет наибольшего
наименьшее
значение 0
М
г)
Множество
(0;1)=М нет ни того
не другого.
Условие
отрезка нельзя
заменить на
интервал или
полуинтервал.
x(0;1]
непрерывна
на (0;1] нет наибольшего
значения
Л
По всем
вопросам и по
дальнейшему
пополнению
лекций обращаться
на ящик
van_mo_mail@mtu-net.ru
или на сотовый:
8-901-7271056 спросить
Ваню
екция №10
Ведущая:
Голубева Зоя
Николаевна
Дата:
вторник, 17 октября
2000 г.
Тема:
«Коши, производные»
Теорема:
(Коши о промежуточных
значениях)
Пусть
функция y=f(x)
непрерывна
на отрезке
[a,b]
и на концах
принимает
значение разные
значения.
f(a)=A
f(b)=B
AB.
Тогда С
лежащею между
А и В,
х0(a,b):
f(x0)=C.
Другими словами
нет точек которые
не являются
значением
отрезка.
Д оказательство:
AC(A,B)
(x)=f(x)-C.
оказательство:
AC(A,B)
(x)=f(x)-C.
Эта
функция непрерывна
на отрезке
[a,b]
(a)=f(a)-c=A-C<0
по теореме
Коши №1
x0(a,b):(x0),
то естьf(x0)-C=0
f(x0)=c
(b)=f(b)-c=B-C>0
Замечание:
Условие непрерывности
нельзя отбросить
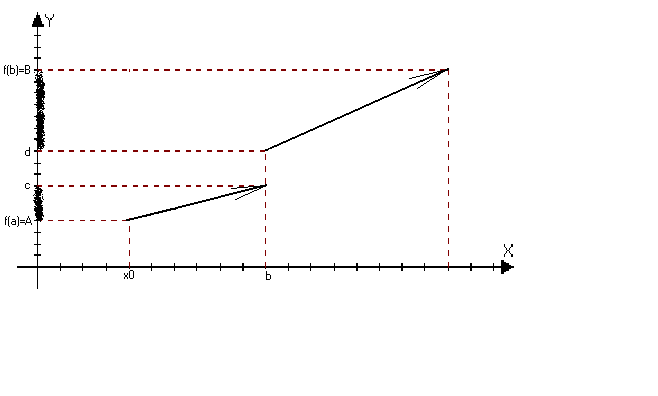
[c,d][A,B]
[c,d)E(f)
Теорема:
(о существование
и непрерывности
обратной функции)
«Без доказательства»
П усть
на множестве
D
задана непрерывная
возрастающая
или убывающая
функция y=f(x).
Тогда на множестве
её значений
Е определена
обратная ей
функция x=g(y),
которая непрерывна
и возрастает
или убывает
на множестве
Е.
усть
на множестве
D
задана непрерывная
возрастающая
или убывающая
функция y=f(x).
Тогда на множестве
её значений
Е определена
обратная ей
функция x=g(y),
которая непрерывна
и возрастает
или убывает
на множестве
Е.
 Производная
функции.
∆Х
Производная
функции.
∆Х
П
 усть
y=f(x)
определена
в O(x0)
усть
y=f(x)
определена
в O(x0)
∆
 x=x-x0
– называется
приращением
аргумента в
т х0
Х
x=x-x0
– называется
приращением
аргумента в
т х0
Х
Х Х
Разность
значений функций.
∆y=∆f(x0)=f(x)-f(x0)=f(x0+∆x)-f(x0)
– называется
приращением
функции в точки
х0. Через
эти обозначения
можно определить
непрерывность
функций:
f(x)
– неопределенна
в точки х0,
если она определена
в O(x0)
и lim
∆y=0
∆
x0
lim[f(x)-f(x0)]=lim[f(x)-f(x0)]0
lim[f(x)]=f(x0)]
x-x0
xx
xx
Определение
непрерывной
функции в точки
приращения:
f(x)
– неопределенна
в точки х0,
если она определена
в O(x0)
и lim
∆y=0
∆
x0
Определение:
(производной
функции)
Пусть
y=f(x)
определена
в О(х0)
и
lim[∆y/∆x]<,
тогда этот
предел называется
производной
функции f(x)
в
∆х0
точке
х0.
Обозначения:
f’(x0),
y’(x0),
dy/dx,
df(x0)/dx=df(x)/d(x)
То
есть f’(x0)
по определению
=
lim[f(x)-f(x0)]/(x-x0)lim∆y/∆xdy/dx
∆x0
∆x0
Физический
смысл производной.
Рассмотрим
прямолинейное
движение материальной
точки:

 S
S
x
x0
x
t0
t
s(t)x(t);
∆s=∆x(t)=x(t)-x(t0)
∆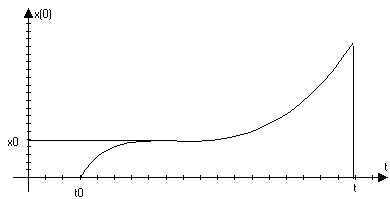 s/∆t=[x(t)-x(t0)]/[t-t0]=vcp.
Если ∆t0
s/∆t=[x(t)-x(t0)]/[t-t0]=vcp.
Если ∆t0
тогда
vcpvмнг
lim
∆s/∆t=lim[x(t)-x(t0)]/[t-t0]=vмнг
∆t0
tt
Геометрический
смысл производной.
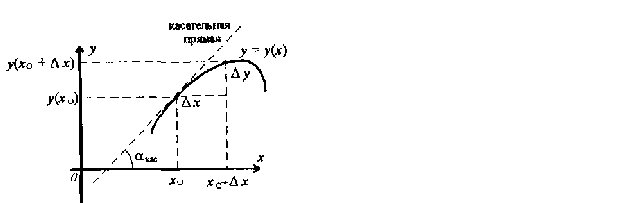 y’(x0)=lim∆y/∆x
– производная
функции у(х) и
в точке х0.
y’(x0)=lim∆y/∆x
– производная
функции у(х) и
в точке х0.
∆х0
∆y=y(x0+∆x)-y(x0)
y’(x0)=tgкас
где кас
– угол наклона
в точке (х0;y(x0))
к оси
Основные
теоремы о
производной.
Теорема:
Пусть
f’(x)
и g’(x),
тогда
[f(x)+g(x)]’=
f’(x)+g’(x)
Доказательство:
следует непосредственно
из определения
производной
и свойств предела
суммы.
Теорема:
(связи между
непрерывностью
функции и
существование
производной)
Пусть
f’(x)
функция f(x)
– непрерывна.
Доказательство:
Пусть f(x)
определена
в О(х0)
и lim[f(x)-f(x0)]/(x-x0)=f’(x0)<
[f(x)-f(x0)]/(x-x0)=f(x0)+(x-x0)
∆xx
[f(x)-f(x0)]=f’(x0)(x-x0)+(x-x0)(x-x0)
при хх0
lin[f(x)-f(x0)]=limf’(x0)(x-x0)+lim(x-x0)(x-x0)=0+0=0linf(x)=f(x0)
то есть f(x)
непрерывна
в точки х0
xx
xx
xx
xx
Замечание:
обратное
утверждение
неверно, из-за
непрерывности
функции в точке
х0 не
следует существование
функции в этой
точки.
y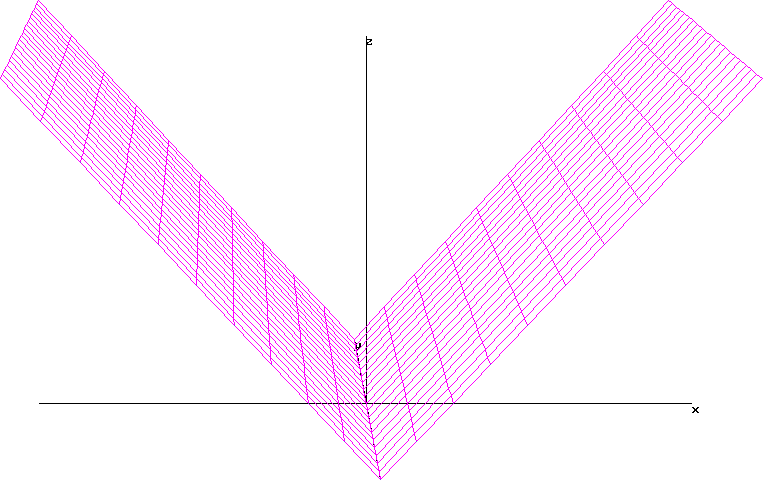 =х
=х
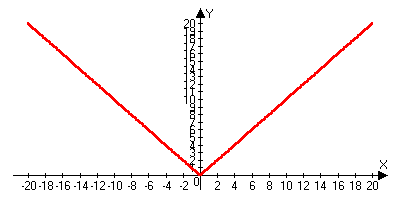
Н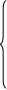 епрерывна
в точки х0=0
епрерывна
в точки х0=0
limx,
x0
x+0
lim|x|= =0
lim(-x),
x<0
x-0
y(0)=0
limy(x)=limy(x)=y(0)=0
limy(x)=y(0)=0
функция
непрерывна
x+0 x-0
x0
lim∆y/∆x-не
существует,
действительно
х+0y(x)=x
x0
lim[y(x)-y(0)]/x=lim(x-0)/x=1
x+0 x+0
x-0y(x)=-x
lim[y(0)-y(x)]/x=lim(0-x)/x=-1
то есть lim∆y/∆x
– не существует
x-0 x-0
х0
Теорема:
Пусть
u’(x)
и v’(x),
тогда (uv)’=u’v+v’u
Доказательство:
Зададим приращение
∆х
в точки х.
Рассмотрим:
lim[∆(uv)]/∆x=
∆x0
lim[1/∆x][u(x+∆x)v(x+∆x)-u(x)v(x)]=lim[1/∆x][
u(x+∆x)v(x+∆x)-u(x)v(x+∆x)+u(x)v(x+∆x)-u(x)v(x)=
∆x0
∆x0
lim[(v(x+∆x))(u(x+∆x)-u(x))]/∆x+lim[(u(x))(v(x+∆x)-v(x))]/∆x=v(x)u’(x)+u(x)v’(x)
∆x0 ∆x0
Теорема:
(о произведение
частного)
Пусть
u’(x)
и v’(x),
v’(x)0
в О(х), тогда
(u/v)’=[u’v-v’u]/v2
Доказательство:
(u/v)’=[u(1/v)]’=[u’(1/v)]+[(1/v)’u].
Функция u(x)
и v(x)
–непрерывны
в точки х0.
lim[∆(1/v)/∆x]=lim[1/∆x][1/(v(x+∆x))-1/v(x)]=lim[[v(x)-v(x-∆x)]/[∆xv(x)x(x+∆x)]]-[v’(x)/v2(x)]
∆x0
∆x0
∆x0
(u/v)’=u’(1/v)-(uv)’/v2=[u’v-uv’]/v2
что и требовалось
доказать
Таблица
производных
y=sinx
(sinx)’=lim[sin(x+∆x)-sinx]/∆x=lim[2sin(∆x/2)cos((2x+∆x)/2)]/∆x=lim[2(∆x/2)cos(x+(∆x/2))]/∆x=cosx
∆x0 ∆x0
(sinx)’=cosx
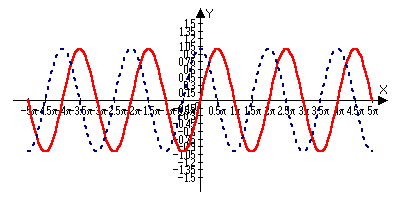
г де sin(x)
де sin(x)
 (sin(x))’=cos(x)
(sin(x))’=cos(x)
y=cos(x)
(cos(x))’=lim[cos(x+∆x)-cos(x)]/∆x=lim[-2sin(∆x/2)sin((2x+∆x)/2)]/∆x=lim[-2(∆x/2)sin(x+(∆x/2))]/∆x=-sinx
∆x0
∆x0
∆x0
(cos(x))’=-sinx
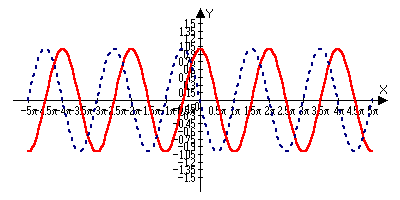
г де cosx
де cosx
 (cos(x))’=-sin(x)
(cos(x))’=-sin(x)
y=tg(x)
(tg(x))’=(sin(x)/cos(x))’=[(sin(x))’cos(x)-(cos(x))’sin(x)]/cos2x=[cos2x+sin2x]/cos2x=1/cos2x
(tg(x))’=1/cos2x
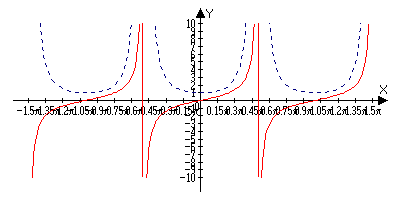
г де tg(x)
де tg(x)
 (tg(x))’=1/cos2x
(tg(x))’=1/cos2x
Лекция
№11
Ведущая:
Голубева Зоя
Николаевна
Дата:
вторник, 24 октября
2000 г.
Тема:
«Производные,
дифференциал»
y=xn
y’(x)=lim[(x+∆x)n-xn]/∆x==lim[xn(1+(∆x/x))-1]/∆x=/∆x/x0,∆x0\=lim[xn(∆x/x)n]/∆x=nxn-1
∆x0
∆x0
∆x0
(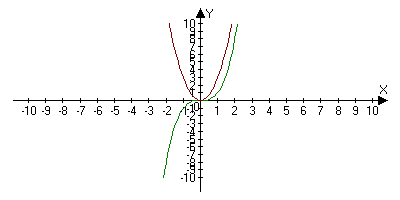 xn)’=nxn-1
xn)’=nxn-1
 y=x^3
y=x^3
 y’=3x^2
y’=3x^2
Рассмотрим
когда х=0
y’(0)=lim(∆x)n/∆x=lim(∆x)n-1=/n>1\=0
если
n=1/0,n>1;1,n=1\
∆x0 ∆x0
Дифференциал
функции.
Определение:
Пусть y=f(x)
определена
в некоторой
О(х0)
– она называется
дифференцируемой
в точке х0,
если её приращение
в этой точки
представимо
в виде:
∆y=∆f(x0)=A∆x+(∆x)∆x)
(0)=0
A=const
Определение:
линейная
∆х
часть приращение
дифференцируемой
функции называется
дифференциалом
функции в точке
х0:
dy=df(x0)A∆x
Теорема:
Если функция
дифференцируема
в точке х0
то A=f’(x0),
то она имеет
производную
в этой точке,
то A=f’(x0);
наоборот если
функция имеет
производную
в этой точке,
то она дифференцируема
в этой точке
– называется
дифференциалом.
Доказательство:
Пусть y=f(x)
дифференцируема
в точке х0,
то есть в некоторой
О(х0)
справедливо
равенство
∆f(x0)=A∆x+(∆x)∆x1;
(0)=0.
Поделим обе
части этого
равенства на
∆х
и приведём к
пределу при
∆х0:
lim(∆f(x0))/∆x=lim(A+(x))=A.
Этот предел
существует,
меньше ,
тогда по определению
этот предел
есть
∆x0
∆x0
производная.
Доказательство:
(в обратную
сторону) Пусть
в точке х0
f’(x0)(<)
– это означает,
что f(x)
определена
в некоторой
О(х0)
и
lim(∆f(x0))/∆x=f’(x0)
по определению
предела следует,
что в некоторой
О(х0)
∆x0
(∆f(x0))/∆x=(∆х)+f’(x0)
при ∆х0
∆f(x0)=f’(x0)+(∆x)∆x,
так как lim(∆x)=0,
то в точке х0
y
(∆x)
может
∆х0
быть лишь
устранимым
разрывом . Устраним
его, определим
и доопределим:
(0)=0,
тогда ∆f(x0)=f’(x0)∆x+(∆x)∆x
A=f’(x0)
из установленного
соответствия
получим выражения
для дифференцируемой
функции df(x0)=f’(x0)∆x
Следствие:
по определению
полагают дифференциал
независимой
переменной
равной её приращению
dx=∆x
(х - независимая
переменная)
df(x)=f’(x)dx
f(x)=x
– вычислим
дифференциал
f’(x)=1 df(x)=dx=f(x)∆x=1∆x
Замечание:
дифференциал
функции зависит
от двух переменных
– от самой точки
х и от ей приращения
y=cosx
x0=/2
∆x=/180
y’=-sinx
y’(/2)=-sin(/2)=-1
dy(/2)=-1∆x=-1/180=-/180
Теорема:
Пусть y=f(x)
дифференцируема
в точке х0,
а z=g(y)
дифференцируема
в точке у0=f(x0),
тогда сложная
функция z=g(f(x)
- дифференцируема
в точке х0
и z’(x0)=g’(f)f’(x)
Доказательство:
(1) ∆z=g’(y0)∆y+(∆y)∆y
(2)
∆y=f(x0)∆x+(∆x)∆x
(0)=0
(0)=0
Подставим
в первое равенство
второе:
∆z=g’(y0)f(x0)∆x+g’(y0)(∆x)∆x+[f’(x0)+(∆x)∆x][f’(x0)∆x+(∆x0∆x]
lim∆z/∆x=limg’(x0)f’(x0)+limg’(x0)(∆x)+lim
(f’(x0)+(∆x)∆x)[f’(x0)+∆x]
z’(x0)=g’(y0)f’(x0)
что и требовалось
∆x0
∆x0 ∆x0
∆x0
доказать.
Теорема:
Пусть
функция y=f(x)
возрастает
(убывает) в О(х0)
и дифференцируема
в точке х0.
Тогда обратная
у ней функция
x=g(y)
дифференцируема
в точки y0=f(x0),
причём g’(y0)=1/f(x0)
Д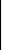
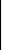 оказательство:
из дифференцируемой
функции f(x)
в точке х0
и из монотонности
следует существование
обратной функции
в точке х0
и её непрерывность
lim[∆y(y0)]/∆y=
∆y0,
то ∆у0
в силу строгой
оказательство:
из дифференцируемой
функции f(x)
в точке х0
и из монотонности
следует существование
обратной функции
в точке х0
и её непрерывность
lim[∆y(y0)]/∆y=
∆y0,
то ∆у0
в силу строгой
∆у0 монотонности
функции и обратной
=
к
ней следует
∆х0
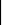
 =lim∆x/∆y=lim1 /(∆y/∆x)=
в силу непрерывности
следует
=1/[lim∆y/∆x]=1/[lim∆f(x0)/∆x]=1/f(x0)
f(x0)0
=lim∆x/∆y=lim1 /(∆y/∆x)=
в силу непрерывности
следует
=1/[lim∆y/∆x]=1/[lim∆f(x0)/∆x]=1/f(x0)
f(x0)0
∆y0
∆y0
∆у0,
то ∆х0
и наоборот
∆x0
∆x0
y=ax
y’(x)=lim[ax+∆x-ax]/∆x=lim[ax(a∆x-1)]/∆x=lim[ax(e∆xlna-1)]/∆x=/∆x0,
то ∆xlna0\=lim[ax∆xlna]/∆x=axlna
∆x0
∆x0
∆x0
∆x0
y ’=axlna,
частный случай
y=ex
(ex)’=ex
’=axlna,
частный случай
y=ex
(ex)’=ex
 y=x^2
y=x^2
 y’=x^2
lnx
y’=x^2
lnx
y=lnx
y’=lim[ln(x+∆x)-lnx]/∆x=lim[ln((x+∆x)/x)]/∆x=lim[ln(1+∆x/x)]/∆x=/∆x/x0
при
∆x0\=lim(∆x/x)/∆x=1/x
∆x0 ∆x0
∆x0
∆x0
( lnx)’=1/x
lnx)’=1/x
 y=lnx
y=lnx
 y’=1/x
y’=1/x
y =logax=lnx/lna
(logax)’=1/xlna
=logax=lnx/lna
(logax)’=1/xlna
 y=lgx
y=lgx
 y’=1/xln10
y’=1/xln10
y=arcsinx
обратная функция
x=siny
x[-1;1]
y[-/2;/2]
(arcsinx)’x=x0=1/(siny)’y0=y=1/cosyy0=y=
y[-/2;/2],
cosy0
cosy>0,
если y[-/2;/2]
то есть x1
=1/(1-sin2y)y=y0=1/(1-(sinarccosx)2)x=x0=1/(1-x02)
(arcsinx)’=1/(1-x2)
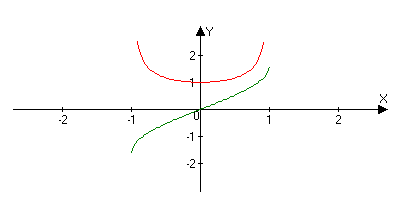
 y=arcsinx
y=arcsinx
 y’=1/(1-x^2)
y’=1/(1-x^2)
y=acrcosx,
обратная
x=cosy x[-1;1]
y[0;]
(arcosx)’=1/(cosy)’y=y0=1/-sinyy=y0=-1/(1-cos2y)y=y0=-1/(1-(cosarccosy)2)x=x0=-1/(1-x02)
(arcosx)’=-1/(1-x2)
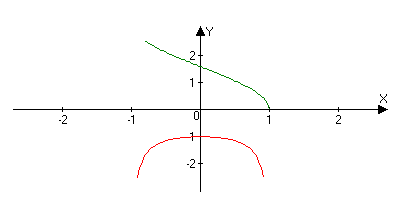
 y=arccosx
y=arccosx
 y’=--1/(1-x^2)
y’=--1/(1-x^2)
y=arctgx
обратная функция
x=tgy
y(-/2;/2)
(arctgy)’=1/(tgy)’=cos2y=
/ 1+tg2y=1/cos2y
\ =1/(1+x2)
(arctgy)’=1/(1+x2)
(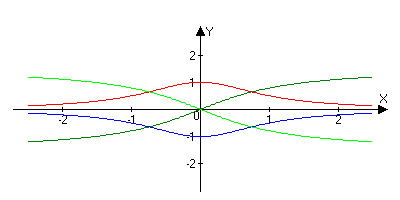 arcctgy)’=-1/(1+x2)
arcctgy)’=-1/(1+x2)
 y=arctgsx
y=arctgsx
 y’=-1/
(1+x^2)
y’=-1/
(1+x^2)
 y=arcctgx
y=arcctgx
 y’=--1/
(1+x^2)
y’=--1/
(1+x^2)
Гиперболические
функции.
chx=(ex+e-x)/2
shx=(ex-e-x)/2
chx2-shx2=1
chx2+shx2=ch2x
ch(-x)=chx
sh(-x)=-shx
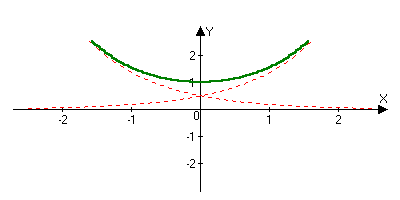
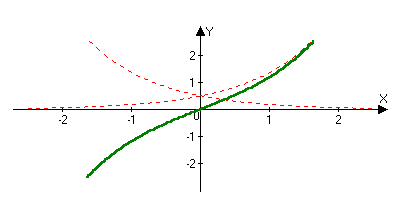
chx shx
c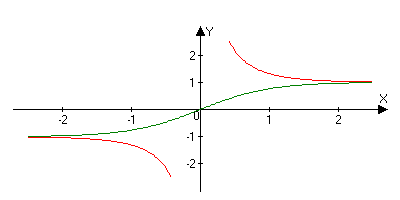
 thx=chx/shx
thx=chx/shx
t hx=shx/chx
hx=shx/chx
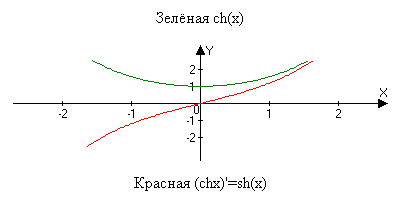
(chx)’=sh(x)
(shx)’=ch(x)
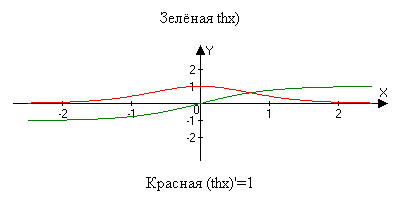
(thx)=1
Лекция
№12
Ведущая:
Голубева Зоя
Николаевна
Дата:
среда, 25 октября
2000 г.
Тема:
«Линеаризация»
Геометрический
смысл дифференциала
функции и уравнение
касательной.
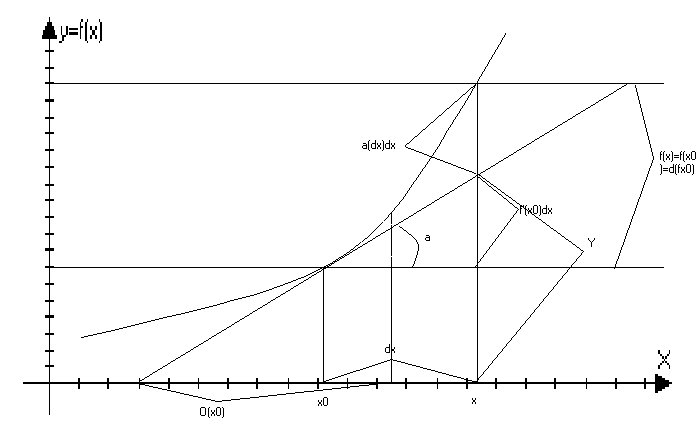
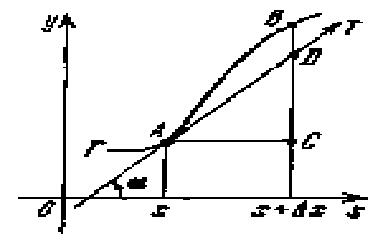
f’(x0)=tg
уравнение
прямой : Y=kx+b
y0=f(x0)=kx0+b
k-угловой
коэффициент
прямой
k=tg=f’(x0)
Y=f(x0)+f(x0)-f’(x0)x0
b=f(x0)-kx0
Y=f(x)+f’(x0)(x-x0)
∆f(x0)=f’(x0)∆x+(∆x)∆x
при ∆х0
в некоторой
O(x0)
f(x0)=f’(x0)+f’(x0)∆x+(∆x)∆x
при ∆х0
Y=f(x0)+f’(x0)(x-x0)=f’(x0)+f’(x0)∆x
df(x0)=f’(x0)∆x
Геометрический
смысл дифференциала:
df(x0)
– это приращение
ординаты при
движение по
касательной
проведённой
к графику функции
в точки (х0;f(x0).
Замечание:
Часто
говорят о касательной
проведённой
в точке х0.
Линеаризация
функции.
Определение:
Замена
функции в окрестности
данной точки
линейной функции
называется
линеаризацией
функции, точнее
в О(х0)
заменяется
отрезком касательной
в точке х0.
( *)
f(x)-Y=(∆x)∆x-o(∆x)
*)
f(x)-Y=(∆x)∆x-o(∆x)
Если
в равенстве
(*) отбросить
правую часть,
то мы
получим
приближённое
равенство:
f(x)f(x0)+f’(x0)(x-x0),
xx0
Y=f(x0)+f’(x0)(x-x0)
– уравнение
касательной
в точке х0
Формула
получена из
определения
дифференциала
в точке х0
функции
f(x)=f(x0)+f(x0)∆x+o∆x
при ∆х0
– называется
критерием
дифференциальности
функции в точке
х0.
Приближенные
вычисления
и оценка погрешности
вычисления.
Можно
приближенно
вычислять
значение функции
в точках близких
к заданной
точки.
38,001=1
х0=8
х=8,000
f(x)=3x
f(x0)=f(8)=2
Проведём
линеаризацию
выбранного
корня.
f’(x)х=8=(3x)’x=8=1/3x-2/3x=8=1/12
3x2+1/12(x-8),
x8
3x2+0,001/12
Yкас=2+1/12(x-8)
3x=2+1/12(x-8)+o(x-8)
при х8
Погрешности
вычисления.
f(x)-f(x0)=df(x0)+o(x-x0)
при хх0
∆f(x0)df(x0),
xx0
∆=∆f(x0)df(x0)
f(x)=10x
в точке х0=4,
если ∆х=0,001
х=40,001
104∆=10423
f’(x)=10xln10;
f’(4)=104ln10=23000;
ln102,2
∆230000,001=23
Изучение
поведения
функции при
помощи первой
производной.
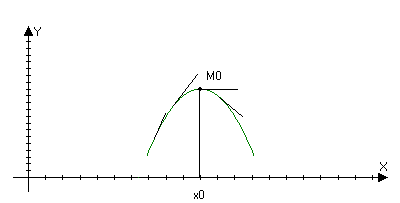
Слева
от М0
tg
>0;
Справа от М0
tg
<0
tg
f’(x)>0
слева от М0
tg
f’(x)<0
справа от М0
Теорема:
Пусть y=f(x)
дифференцируема
x(a,b)
и f’(x)>0
(f’(x)<0),
тогда f(x)
возрастает
(убывает) на
(а,b)
 a(
|x1
|x2
)b
a(
|x1
|x2
)b
x1,x2(a,b)
x12
Надо
доказать: f(x1)2)
Применим
теорему Лангранджа
на отрезке
(х1,x2)еорема.
f(x2)-f(x1)=f’(c)(x2-x1)
где c(x1,x2)
f(x2)-f(x1)>0
f(x2)>f(x1)
Экстремумы
функции.
М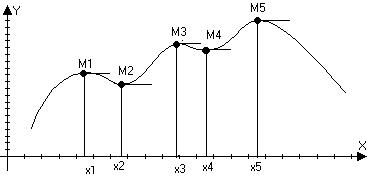 ожно
указать О(х1)
в которой все
значения функции
ожно
указать О(х1)
в которой все
значения функции
f(x)1)
b и О1(х1)
анологично
для точки х2
f(x)>f(x1)
b и О2(х1).
Значенгие
функции в точке
М1, М3
и М5 –
max;
M2
и М4
– min –
такие точки
назавыются
точкками
экстремума
или точками
локального
max и min.
Определение:
(точки экстремума)
Пусть
функия f(x)
определена
в некоторой
О(х0)
и f(x)>f(x0)
в
О(х0)
или f(x)0)
в этом случае
точка х0
– называется
точкой локального
max
(min).
З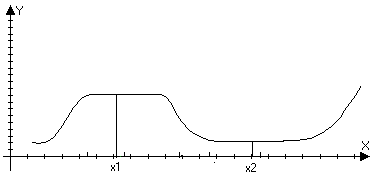 амечание:
амечание:
f(x)f(x1)
в О1(х1)
f(x)f(x2)
в О2(х2)
говорят,
что точки х1
и х2 точки
не строгого
локального
экстремума.
Теорема:
(Ферма) (о необходимости
условия экстремума
дифференцируемой
функции)
Пусть
y=f(x)
дифференцируема
в точки х0
и точка х0
– точка экстремума,
тогда f(x0)=0
Доказательсто:
Заметим, что
х0
точка экстремума,
то в её окрестности
f(x)
– f(x0)
сохраняет знак.
Запишем условие
∆f(x0)=f(x)-f(x0)(x-x0)+o(x-x0)
f(x)-f(x0)=(x-x0)[f(x0)+(x-x0)]
то при х – достаточно
близких к х0
знак выражения
стоящего в
квадратных
скобках совпадает
со знаком f’(x0)0
(x-x0)
– меняет знак
при переходе
черех точку
х0
f’(x0)=0
Лекция
№13
Ведущая:
Голубева Зоя
Николаевна
Дата:
вторник, 31 октября
2000 г.
Тема:
«Экстремумы»
Замечание:
О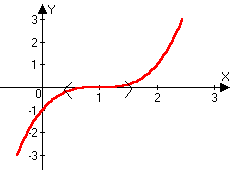 братное
утверждение
неверно. Из-за
того, что произведение
в данной точки
равно нулю, не
следует, что
это экстремум.
братное
утверждение
неверно. Из-за
того, что произведение
в данной точки
равно нулю, не
следует, что
это экстремум.
y=(x-1)3
y’=3(x-1)2
y’(1)=0
x0=1
xO-(1)f(x)<0
xO+(1)f(x)<0
x=1 –
не точка экстремума.
Теорема
(Ролля):
Пусть
функция y=f(x)
непрерывна
на отрезке
[a,b]
и дифференцируема
на (a,b).
Кроме того на
концах интервала
она принемает
равные значения
f(a)=f(b),
тогда
с(a,b):
f(c)=0
Доказательство:
Така как функция
непрерывна
на отрезке
[a,b],
то по второй
теореме Вейштрасса
есть наибольшее
и наименьшее
значение (m,M), если
m=M,
то f(x)const
(x[a,b])
(const)’=0.
Пусть
mf(a):
c(a,b):f(c)=M,
то есть точка
с точка экстремума
максимума
следовательно
по теореме
Ферма f’(c)=0
Замечание:
условие
дифференцируемсти
нельзя отбросить.
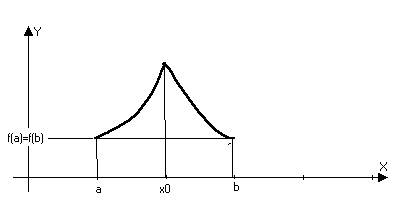
непрерывна
на отрезке
[a,b]
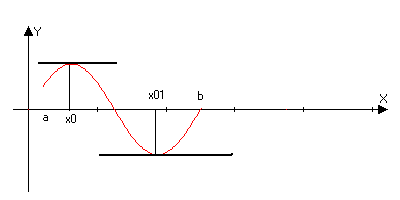
Геометрический
смысл.
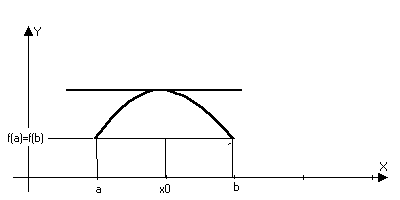
f’(x)=0,
то касательная
оси х. Теорема
не утверждает,
что это единственная
точка.
Теорема
Лангранджа:
Пусть
функция y=f(x)
непрерывна
на отрезке
[a,b] и
дифференцируема
на отрезке
(а,b), то
с(a,b):
f(b)-f(a)=f(c)(b-a)
Доказательство:
F(x)=f(x)+x
где -
пока неизвестное
число.
F(x)
– непрерывна
на отрезке
[a,b] как
сумма непрерывной
функции
f(x)
– дифференцируема
на отрезке
[a,b] как
сумма дифференцируемой
функции.
Выберем
число ,
так чтобы на
отрезке [a,b]
F(x) принимало
равное значение.
F(a)=f(a)+a
F(b)=f(b)+b
F(a)=F(b)
f(a)-f(b)=(a-b)
=[f(b)-f(a)]/[b-a]
F(x)
– удовлетворяет
условию теоремы
Роллера на
отрезке [a,b]
c(a,b):F’(c)=0,
то есть F’(x)=f’(x)+
0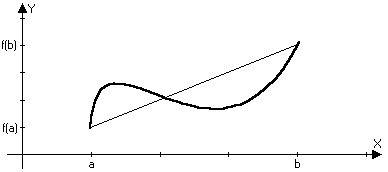 =f’(c)+
f’(c)=-=[f(b)-f(a)]/[b-a]
=f’(c)+
f’(c)=-=[f(b)-f(a)]/[b-a]
То есть
на кривой которая
наклонена
к оси х
под таким же
углом как и
секущая
[f(b)-f(a)]/[b-a]=tg=f(x)
c(a,b)
Замечание:
Часто
точку с можно
представить
в
нужном
виде:
с=х0+∆х
0<(c-x0)/(x-x0)=
<1
c-x0=(x-x0)
c=x0+(x-x0)
f(x)-f(x0)=f’(x0+∆x)(x-x0)
0<<1
∆f(x0)=f’(x0+∆x)∆x
Теорема:
(о необходимых
и достаточных
условиях экстремума
по первой
производной)
Пусть
y=f(x)
непрерывна
на отрезке
[a,b] и
дифференцируема
в О(х0).
Если f’(x)
меняет знак
при переходе
через точку
х0, то точка
х0 – точка
экстремума.
Если меняет
знак:
с + на – то
это точка максимума
с – на + то
это точка минимума
Доказательство:
х1
О-(х0)
на [x1,x0];
c1(x1,x0)
f(x0)-f(x1)=f’(c1)(x0-x1)
f(x0)>f(x1)
x1O-(x0)
х2
О+(х0)
на [x0,x2];
c2(x0,x2)
f(x2)-f(x0)=f’(c2)(x2-x0)
f(x2)0)
x2O+(x0)
f(x0)>f(x)
xO(x0)
точка х точка
максимума.
Если в
точке х0 существует
производная
то она обязательно
равна 0 в силе
теоремы Ферма.
Но могут быть
точки в которых
f(x) существует,
а f’(x)
не существует.
Принцип
решения подобных
задач:
Условие:
найти наибольшее
и наименьшее
значение функции
не отрезке
[a,b].
Ход решения:
Находим
точки в которых
производная
либо равна 0
либо не существует
f’(x)=0
или f’(x)
x1,
xn
Вычисляем
знак функции
на концах отрезка
и в этих точках
f(a), f(b),
f(x1)….f(xn)
Выбираем
наибольшее
и наименьшее
mf(x)
Определение:
точки в которых
функция определена,
а производная
либо равняется
нулю, либо не
существует
называют критическими
точками.
Производная
функции высшего
порядка.
Существует
f’(x)
x(a,b),
тогда эта производная
сама является
функцией х
(х)=f’(x)
и можно ставить
о дифференцируемости
этой функции.
Существует
’(x)
x(a,b),
то мы называем
её второй производной
’(x)f’’(x)
Лекция
№14
Ведущая:
Голубева Зоя
Николаевна
Дата:
среда, 8 ноября
2000 г.
Тема:
Производная
функции высшего
порядка.
f(n)=def=(f(n-1)(x))’
’’’ –
[dnf(x)]/dxn=(d/dx)([dn-1f(x)]/dxn)
Теорема:
(Коши – обобщение
теоремы Лангранджа)
Пусть
функция f(x)
и g(x)
непрерывны
на отрезке
[a,b],
дифференцируема
на интервале
(a,b) и
g’(x)0,
x(a,b),
тогда
с (a,b)
такая, что
[f(b)-f(a)]/[g(b)-g(a)]=f’’(c)/g’(c)
Доказательство:
Отметим прежде
всего, что g(b)g(a),
так как по теореме
Лангранджа1
для функции
g(x)
g(b)-g(a)=g’(c1)I
(b-a)II0
(c1(a,b))
Рассмотрим
вспомогательную
функцию
F(x)=f(x)-g(X)
где
-неизвестное
число
F(x)
– непрерывна
на отрезке
[a,b] и
дифференцируема
на интервале
(a,b)
Потребуем
F(a)=f(b)
F(b)=f(b)-g(b)
---
F(a)=f(a)-g(a)
___________________
0=f(b)-f(a)-(g(b)-g(a))
=[f(b)-f(a)]/[g(b)-g(a)].
Получим, что
F(x)
удовлетворяет
условию теоремы
Ролля
с(a,b):F’(c)=0,
то есть F’(c)=f’(c)-g’(c)
=f’(c)/g’(c)=[f(b)-f(a)]/[g(b)-g(a)],
что и требовалось
доказать.
Правила
Лопиталя.
Это правило
в случае дифференцируемости
функции позволяет
избавляться
от неопределённостей
типа 0/0 или /
при вычисление
пределов.
Теорема:
Пусть функции
f(x) и g(x)
дифференцируемы
в О(х0), g’(x0)0
в О(х0),
f(x0)=g(x0)=0
и
lim
f’(x)/g’(x)=k
(конечный или
бесконечный
предел), тогда
lim
f(x)/g(x)=lim
f’(x)/g’(x)=k
xx
xx
xx
Доказательство:
lim f(x)/g(x)=lim
[f(x)-f(x0)]/g(x)-g(x0)=lim
f’(c(x))/g’(c(x))=
c=c(x)
лежащая между
х их0 если
xx
xx
xx
хх0
то сх0=lim
f’(x)/g’(x)=k
xx
Замечание(1):
f(x0)=g(x0)=0
требование
можно заменить
требованием
lim f(x)=0,
lim g(x)=0,
то есть в т х0
f(x) и
xx
xx
g(x)
могут иметь
устранимый
разрыв, действительно
достаточно
переопределить
или доопределить
f(x) и g(x)
по непрерывности,
так чтобы
f(x0)=g(x0)=0
Замечание(2):
Если
f’(x0)
и g’(x0),
g’(x0)0,
то утверждение
теоремы будет:
lim
f(x)/g(x)=lim
f’(x)/g’(x)=lim
[(x-x0)(f’(x0)+(x-x0))]/
[(x-x0)(g’(x0)+
(x-x0))]=f’(x0)/g’(x0)
xx
xx
xx
Теорема:
(/)
Пусть функции
f(x) и g(x)
непрерывны
в О(х0),
g'(x)0 и О(х0),
дифференцируемы
в О(х0)
и
lim
f(x)=lim
g(x)=;
lim
f’(x)/g’(x)=k.
Тогда lim
f(x)/g(x)=lim
f’(x)/g’(x)=k
xx
xx
xx
xx
xx
Без
доказательства!
Замечание:
Если функции
f’(x) и
g’(x) сами
удовлетворяют
условия теоремы
то правило
Лопиталя можно
применить
повторно:
f(x)=ex
g(x)=xn
x
lim ex/xn=
lim ex/1!=
nN
lim ex/xn=
lim ex/nxn-1=
lim ex/[n(n-1)xn-2]=lim
ex/n!=+
x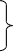 +
x+
x+
x+
x+
x+
+
x+
x+
x+
x+
x+
f(x)=lnx
x+
g(x)=xn
lim lnx/xn=
lim (1/x)/nxn-1=
lim 1/nxn=0
x+
x+
x+
Формулы
Тейлора.
Определение:
(многочлена
Тейлора) Пусть
функция y=f(x)
– n – раз
дифференцируема
в точке х0
многочлен
(полином) вида
Tn(х)=f(x0)+[f’(x0)(x-x0)]/1!+
[f’’(x0)(x-x0)2]/2!+
[fn(x0)(x-x0)]/n!
называется
многочлен
Тейлора с центром
в точке х0 или
многочленом
по степеням
(х-х0)
Свойства
многочлена
Тейлора.
Теорема:
(основное свойство
многочлена
Тейлора) Пусть
функция y=f(x)
– n – раз
дифференцируема
в точке х0
f(x)=Tn(x0);
f’(x0)=Tn’(x0),…,f(n)(x0)=Tn(n)(x0)
Доказательство;
(подстановкой)
Tn(х)=f(x0)+[f’(x0)(x-x0)]/1!+
[f’’(x0)(x-x0)2]/2!+
[fn(x0)(x-x0)]/n!
, подставим х0
получим Tn(x0)=f(x0).
Продифференцируем
многочлен
Тейлора
Tn’(x)=f’(x0)/1!+[f’’(x0)2(x-x0)]/2!+
[f’’’(x0)3(x-x0)2]/3!+
[fn(x0)n(x-x0)n-1]/n!,
подставим
вместо х х0
Tn(x0)=f(x0)
Tn’’(x)=f’’(x0)/1!+[f’’’(x0)32(x-x0)]/3!+…+
[f(n)(x0)n(n-1)(x-x0)n-2]/n!
Tn’’(x)=f’’(x0)
Формула
Тейлора с остаточным
членом пеано.
Теорема:
Пусть функция
y=f(x)
– n – раз
дифференцируема
в точке х0,
тогда в О(х0)
f(x)=Tn(x)+o((x-x0)n),
xx0
f(x)=
f(x0)+[f’(x0)(x-x0)]/1!+
[f’’(x0)(x-x0)2]/2!+
[fn(x0)(x-x0)n]/n!+0((x-x0)n)(x-x0)
lim[f(x)-Tn(x)]/(x-x0)n=(0/0)=lim
[f’(x)-Tn’(x)]/n(x-x0)n-1=(0/0)=….=lim
[f(n)(x)-Tn(n)(x)]/n!=0
функция
xx
xx
xx
[f(x)-Tn(x)]/(x-x0)n=(х-х0)i
f(x)-Tn(x)=(x-x0)n(x-x0)=0((x-x0)n)
при хх0
что и требовалось
доказать.
Замечание:
в случае если
х0=0 формула
Тейлора называется
Маклорена
f(x)=f(0)+[f’(0)x]/1!+
[f’’(0)x2]/2!+
[fn(0)xn]/n!+0xn
при х0
Л
По всем
вопросам и по
дальнейшему
пополнению
лекций обращаться
на ящик
van_mo_mail@mtu-net.ru
или на сотовый:
8-901-7271056 спросить
Ваню
екция №15