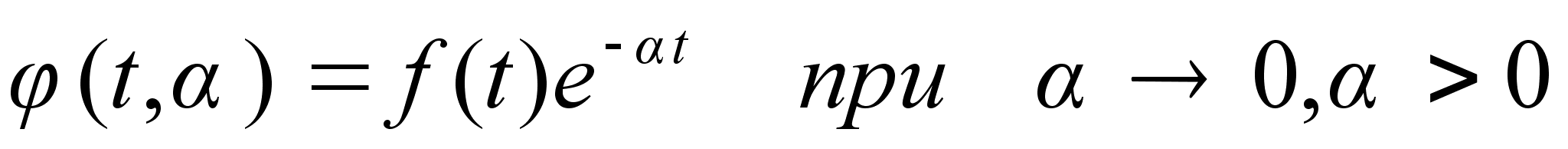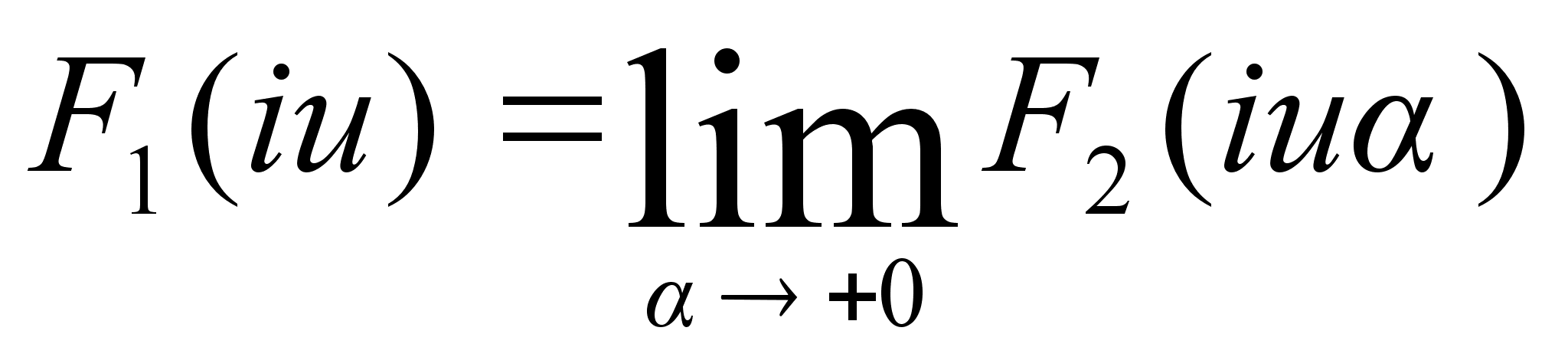Функция
f (z), которая
может быть
представлена
в виде ряда (2)
является
аналитической
функцией.
Неаналитическая
функция в ряд
Тейлора не
раскладывается.
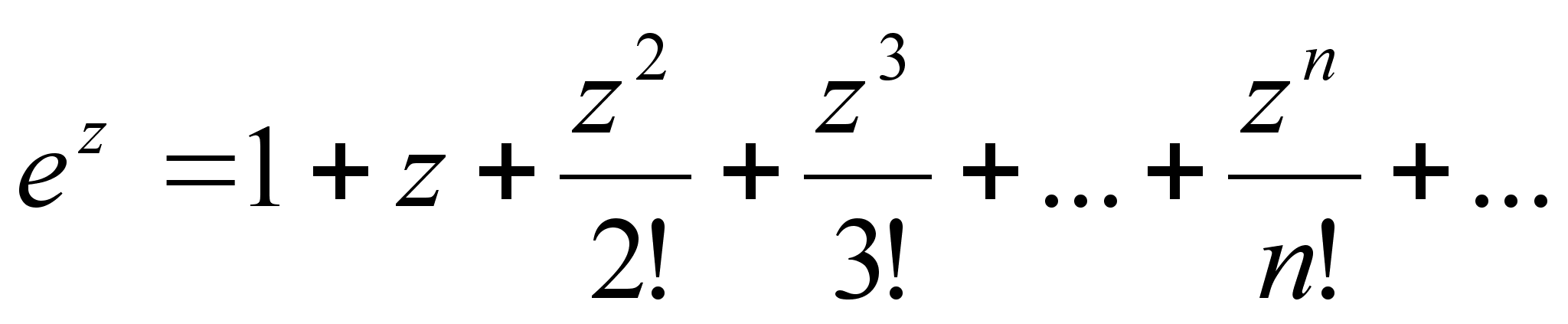 (3)
(3)
 (4)
(4)
 (5)
(5)
Причем
| Z | < R, R
.
Формулы ЭЙЛЕРА.
Применим
разложение
(3) положив, что
Z = ix
и Z= - ix;
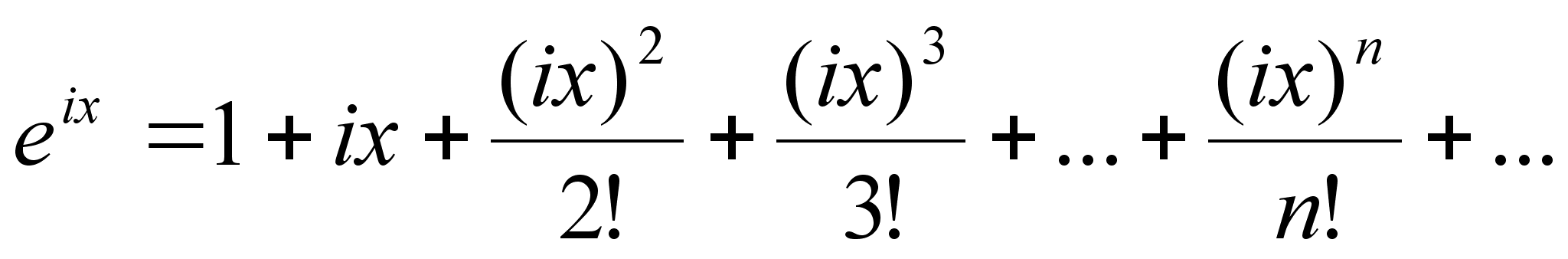

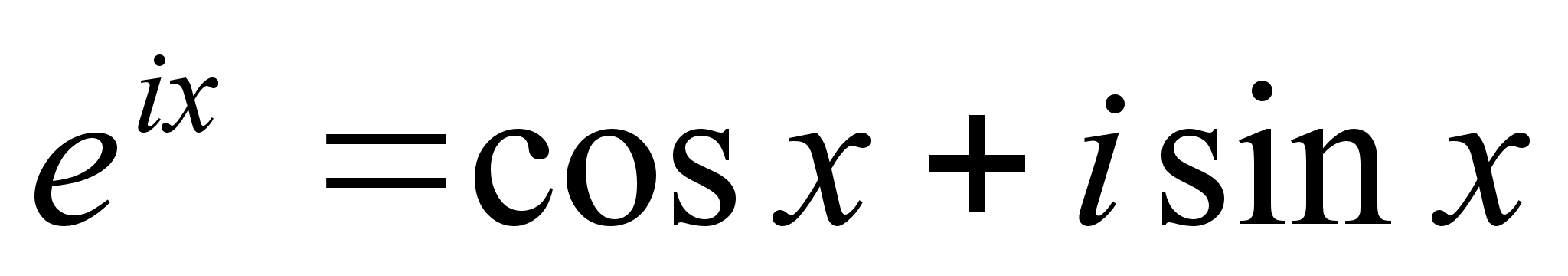 (6)
(6)
Аналогично
взяв Z = - ix
получим :
 (7)
(7)
Из
(6) и (7) можно выразить
т.н. формулы
Эйлера :
 (8)
(8)
В
общем случае
:
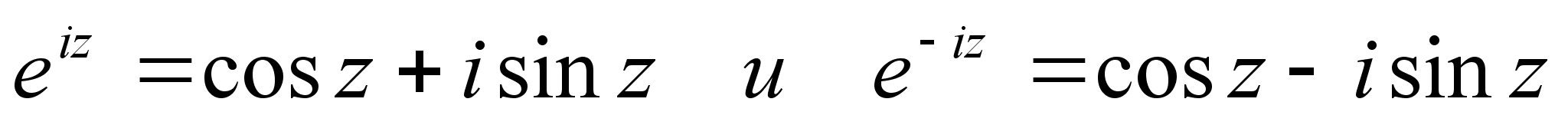 (9)
(9)
Известно,
что :
 (10)
(10)
Тогда
из (9) и (10) вытекает
связь между
тригонометрическими
и гиперболическими
косинусами
и синусами:
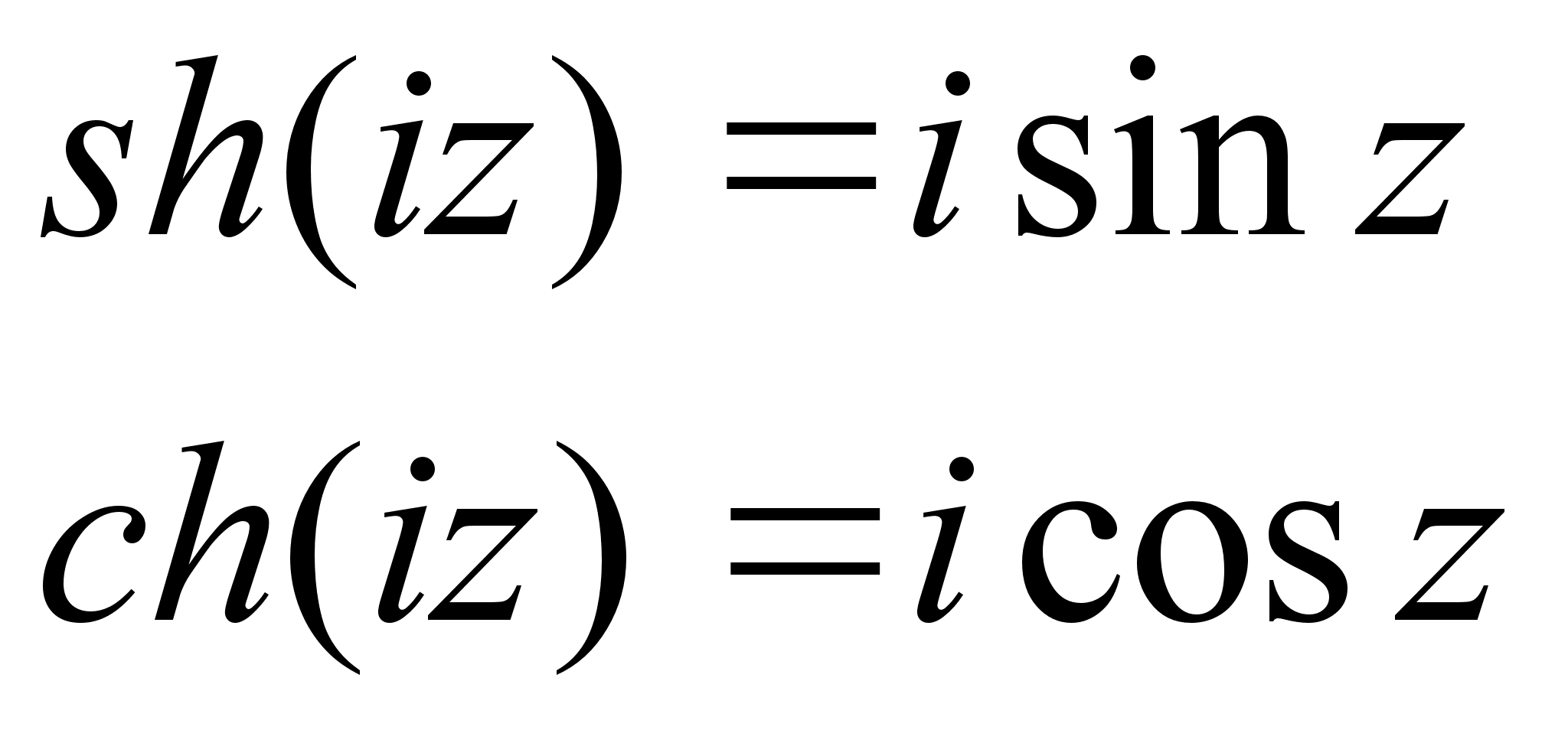
Ряд ЛОРАНА.
Пусть
функция f(z) является
аналитической
функцией в
некотором круге
радиусом R, тогда
ее можно разложить
в ряд Тейлора
(2). Получим тот
же ряд другим
путем.
ТЕОРЕМА
1.

Однозначная
функция f(Z) аналитическая
в круге радиусом
|Z-Z0| < R раскладывается
в сходящийся
к ней степенной
ряд по степеням
Z-Z0.
Опишем
в круге радиусом
R окружность
r, принадлежащую
кругу с радиусом
R.
Возьмем
в круге радиуса
r точку Z,
а на границе
области точку
,
тогда f(z) будет
аналитична
внутри круга
с радиусом r
и на его границе.
Выполняется
условие для
существования
интеграла Коши
:
 (13)
(13)
 (11)
(11)
Поскольку
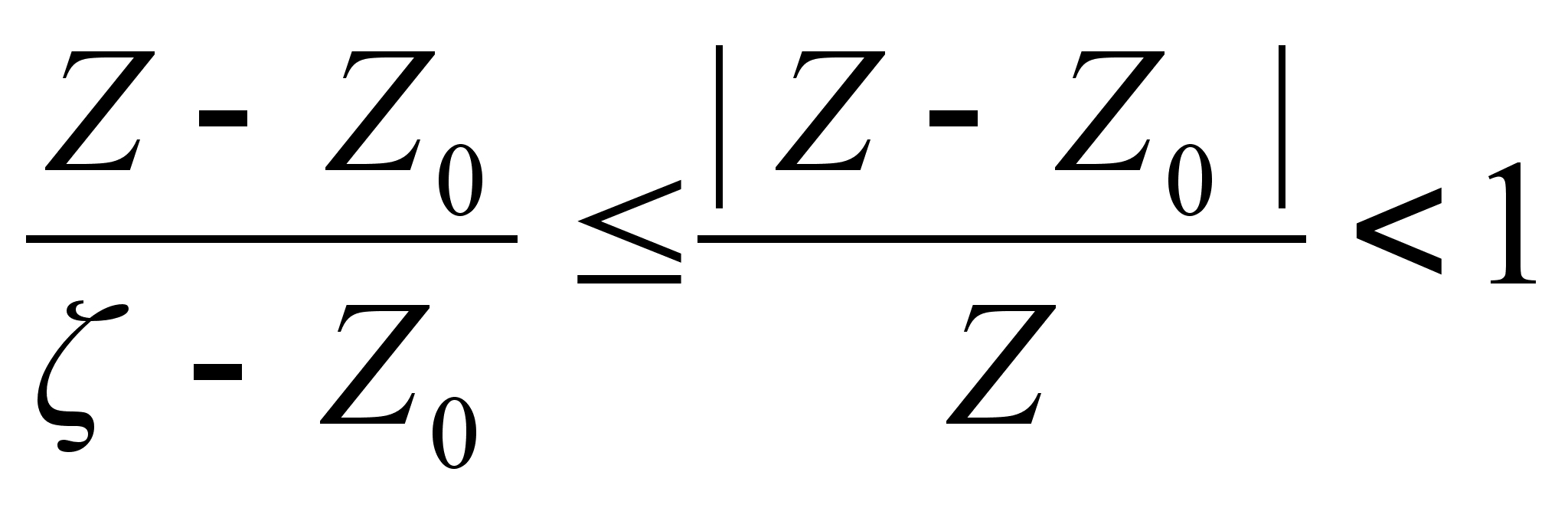 ,
то выражение
,
то выражение
 можно представить
как сумму бесконечно
убывающей
геометрической
прогрессии
со знаменателем
можно представить
как сумму бесконечно
убывающей
геометрической
прогрессии
со знаменателем
 ,
т.е. :
,
т.е. :
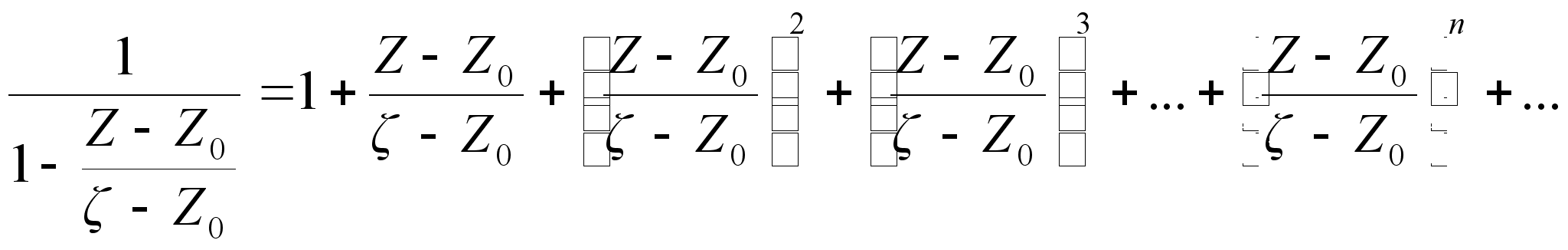

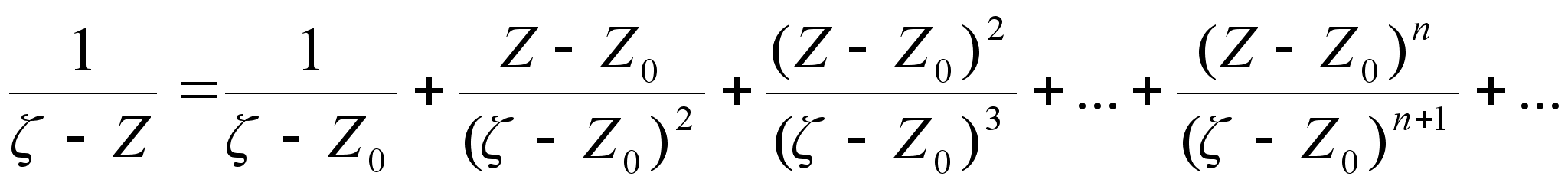 (12)
(12)
Представим
равномерно
сходящимся
рядом в круге
радиуса r,
умножая (12) на
1/(2i)
и интегрируя
по L при
фиксированном
Z, получим
: слева интеграл
(13) который равен
f (Z), а справа
будет сумма
интегралов
:

Обозначая
 ,
получим :
,
получим :
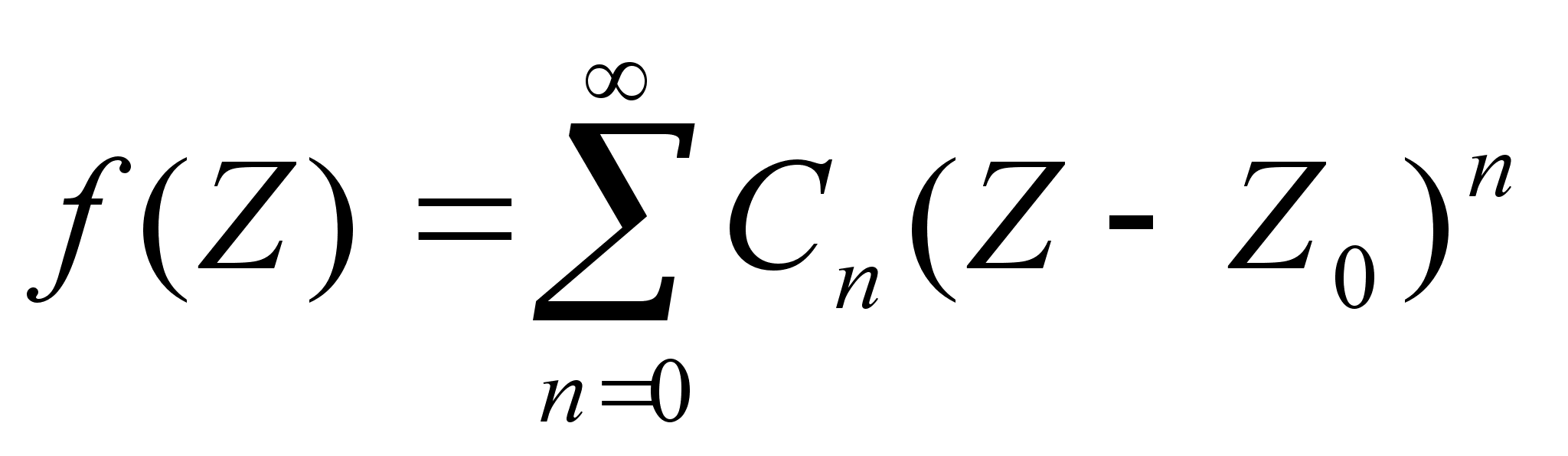 (14)
(14)
Это
разложение
функции f
(Z) в круге R в ряд
Тейлора. Сравнивая
(14) с рядом (2) находим,
что
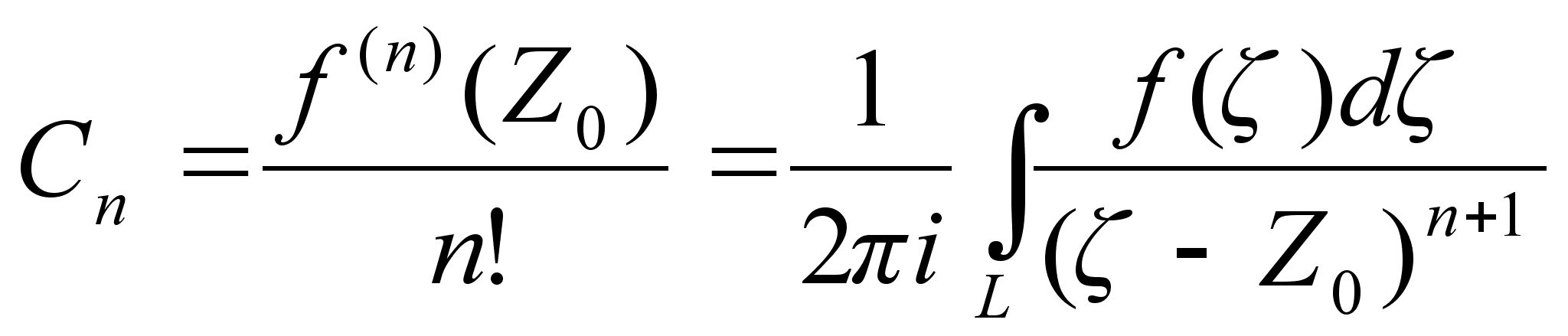 (15)
(15)
ТЕОРЕМА
2.
Если
однозначная
функция f(Z)
аналитична
вне круга с
радиусом r с
центром в точке
Z0 для всех Z
выполняется
неравенство
r < |Z-Z0 |, то она
представляется
рядом :
 (16)
(16)
где
h - ориентированная
против часовой
стрелки
окружность
радиуса r
(сколь угодно
большое число).
Если обозначить
 (17) , получим :
(17) , получим :
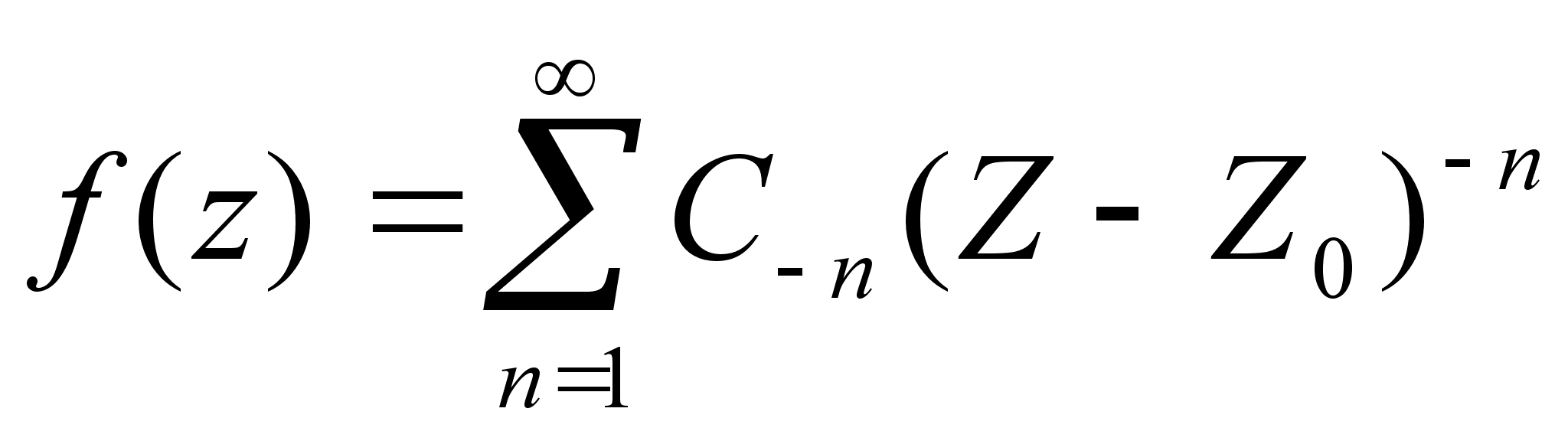 (18)
(18)
ТЕОРЕМА
3.
Если
однозначная
функция f(Z)
аналитическая
в кольце Z< |Z-Z0
|
Z
, то она раскладывается
в сходящийся
степенной ряд
:
 (19)
(19)
f1
и f2
можно представить
в виде двух
рядов :
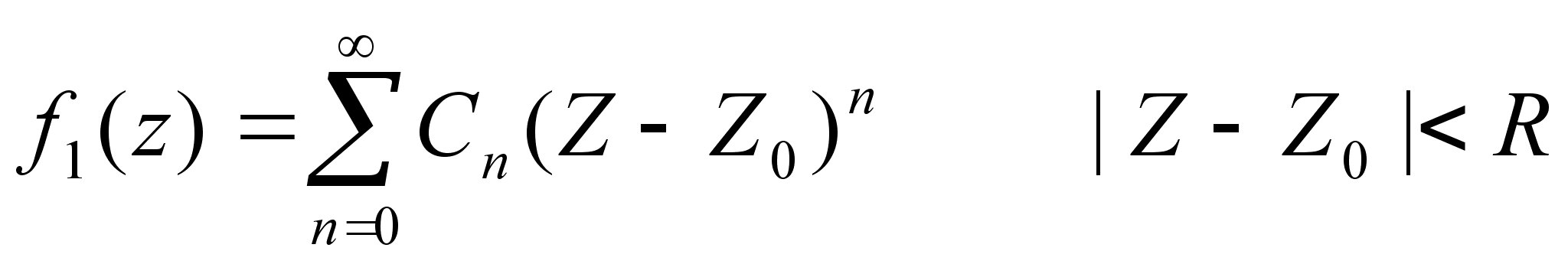 (20)
(20)
 (21)
(21)
Ряд
(19) – ряд Лорана,
при этом ряд
(20) сходится в
круге радиуса
R, ряд (21) сходится
вне круга радиуса
R функции
f2(Z). Общая область
сходимости
ряда – кольцо
между r и R.
f1(Z)
– правильная
часть.
f2(Z)
– главная часть
ряда Лорана.
Ряд
Тейлора – частный
случай ряда
Лорана при
отсутствии
главной его
части.
Классификация
изолированных
особых точек.
Вычеты.
Определение
1. Особой точкой
функции f(Z) определенной
в области (замкнутой)
G, ограниченной
Жордановой
кривой, называется
точка Z=Z0
G в которой
аналитичность
функции f1(Z) нарушается.
Рабочая точка
Z=Z0 функции
f(Z), ограниченной
в круге |Z-Z0|0.
В зависимости
от поведения
функции f(Z)
в окрестности
изолированных
особых точек
последние
классифицируются
на :
Устранимые
особые точки.
Ими называются
особые точки,
для которых
существует
 ,
где А – конечное
число.
,
где А – конечное
число.
Если
для особой
точки существует
предел
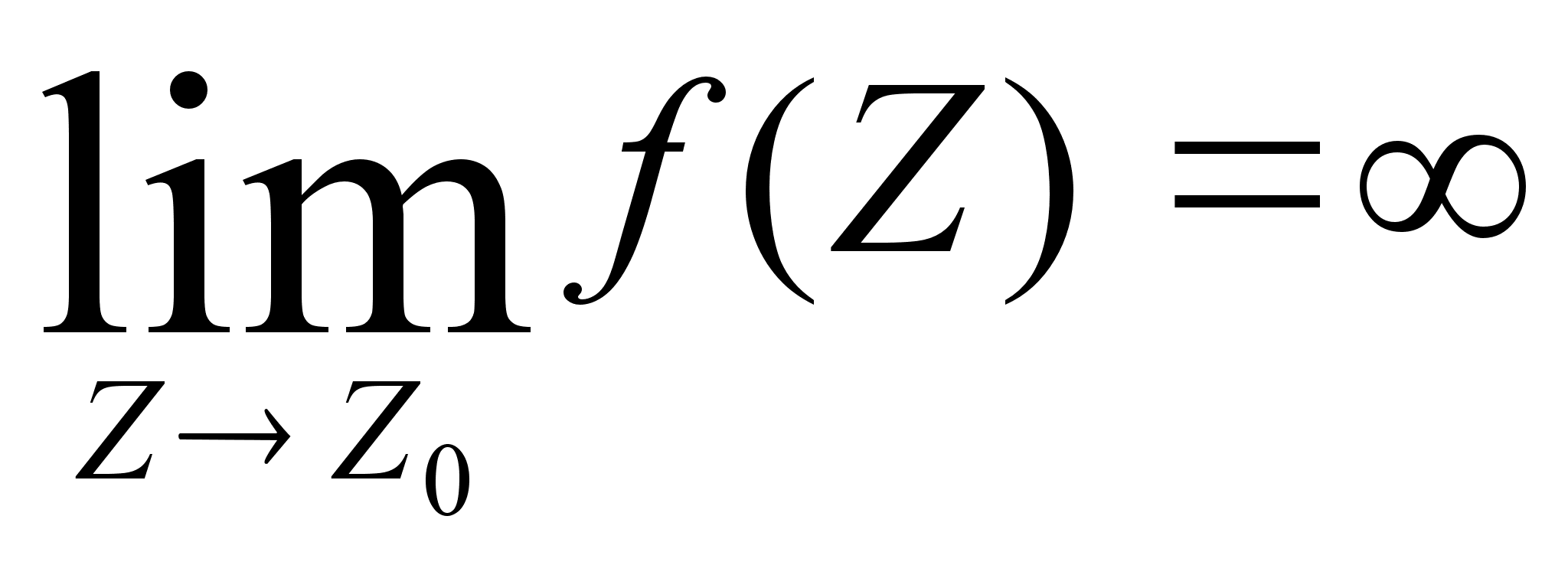 ,
то такая особая
точка называется
полюсом.
,
то такая особая
точка называется
полюсом.
Если
 не существует,
то точка Z=Z0
называется
существенной
особой точкой.
не существует,
то точка Z=Z0
называется
существенной
особой точкой.
Если
С-n=0,
то особая
точка есть
устранимая
особая точка.
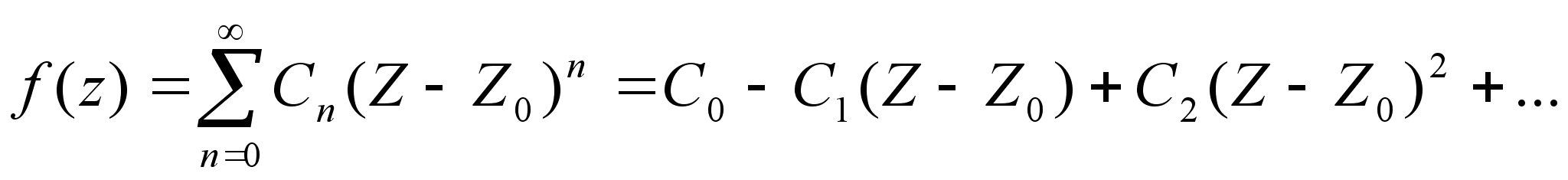
Пусть
f(Z0)=C0
и C-n для
всех n=1,2,3,..,m отличного
от 0, а для всех
n m+1
C-n=0, тогда
Z=Z0 будет
являться полюсом
порядка m.
При
m>1 такой полюс
будет называться
простым.
 ,
если m
, то в этом случае
в точке Z=Z0
имеем существенную
особенность.
,
если m
, то в этом случае
в точке Z=Z0
имеем существенную
особенность.
Определение
2. Вычетом функции
f(Z) в круге
|Z-Z0|
, где L – ориентированный
против часовой
стрелки контур
целиком расположенный
в круге радиуса
R, содержащем
Z0.
Вычет существует
только для
изолированных
особых точек.
Очевидно, что
вычет функции
f(z) при Z=Z0
равен первому
коэффициенту
ряда главной
части Лорана
:

Если
полюс имеет
кратность m
1, то для
определения
вычетов используется
формула :
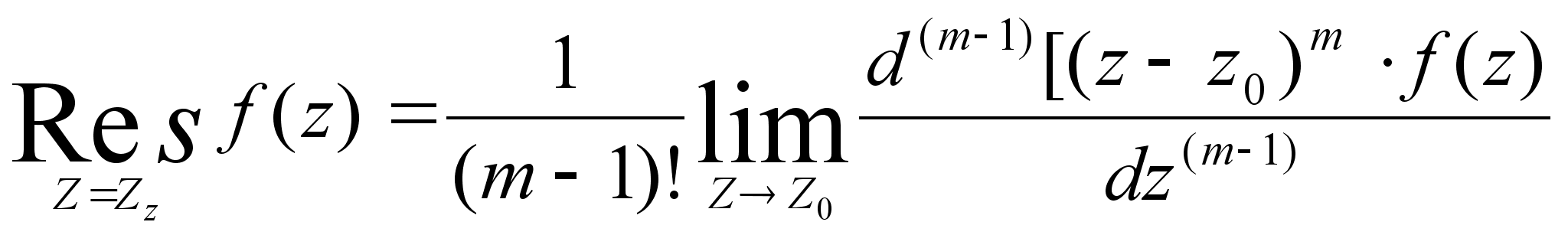 (3)
(3)
при
m=1 :
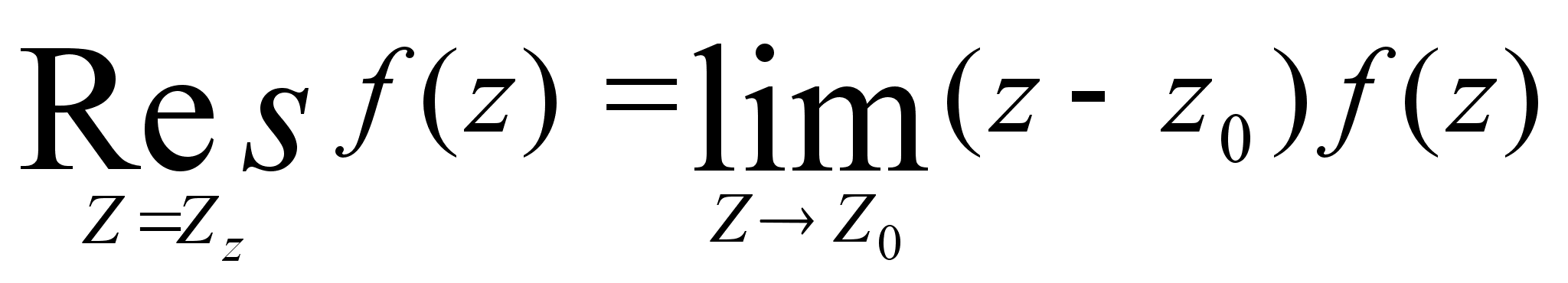
Основная
теорема о вычетах.
Пусть
f(z) аналитическая
в области G
кроме конечного
числа полюсов
Z = a1,
a2,
…, ak.
–произвольный,
кусочно-гладкий
замкнутый
контур содержащий
внутри себя
эти точки и
целиком лежащий
внутри области
G. В этом
случае интеграл
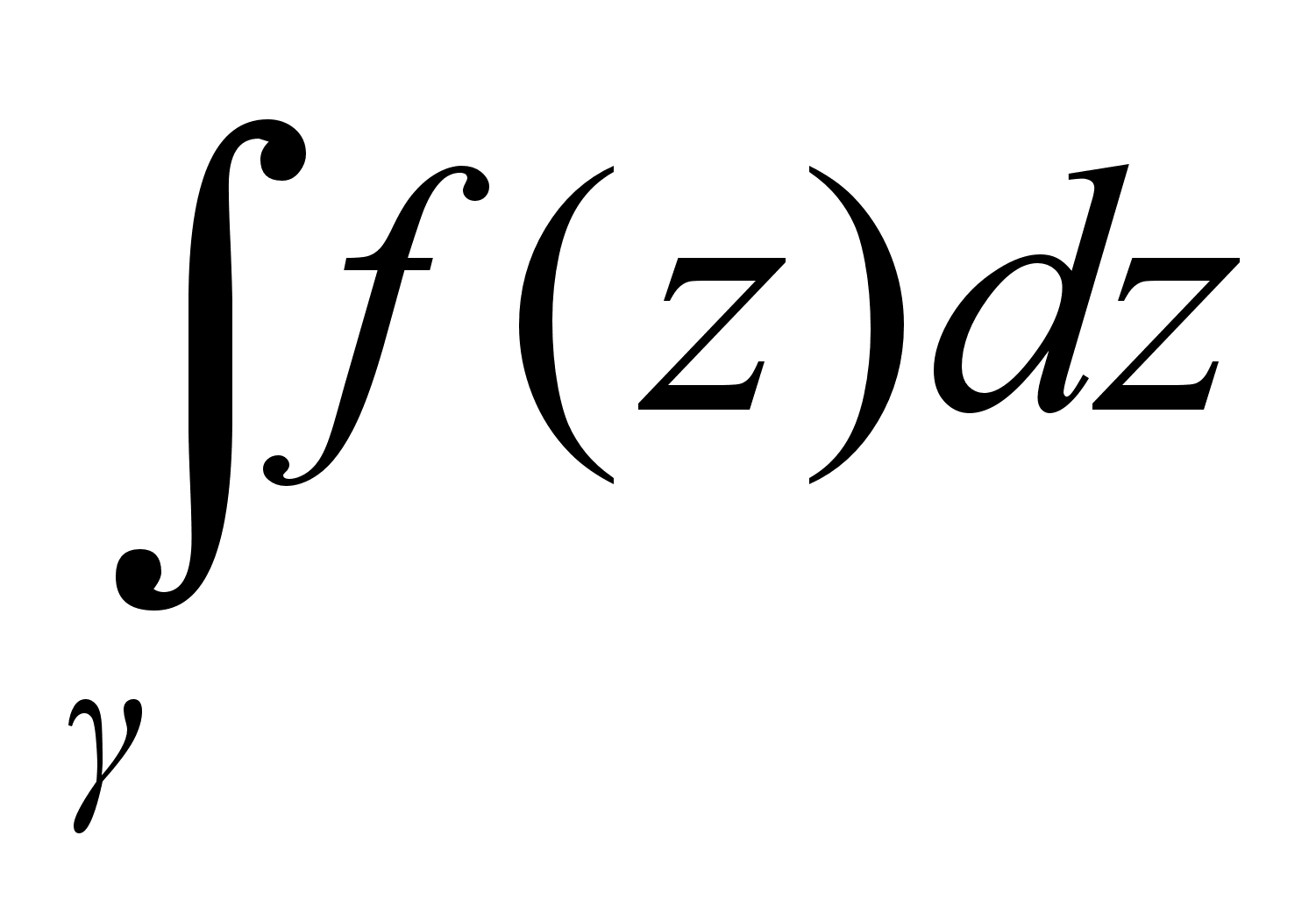 равен
сумме вычетов
относительно
a1,
a2,
…, ak
и т.д. умноженный
на 2i
:
равен
сумме вычетов
относительно
a1,
a2,
…, ak
и т.д. умноженный
на 2i
:
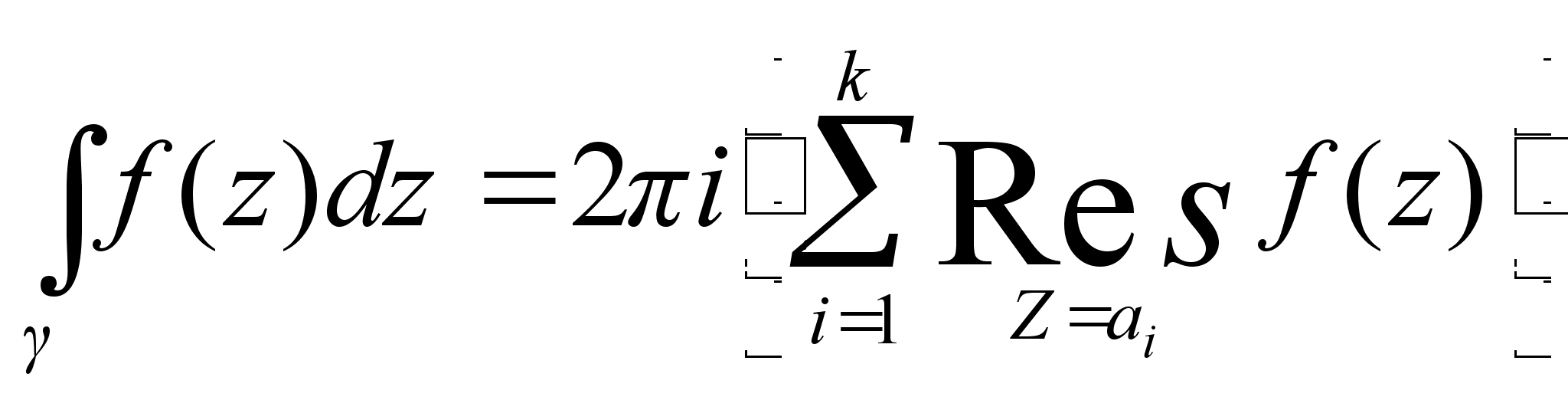 (5)
(5)
Пример
:
Найти
вычет
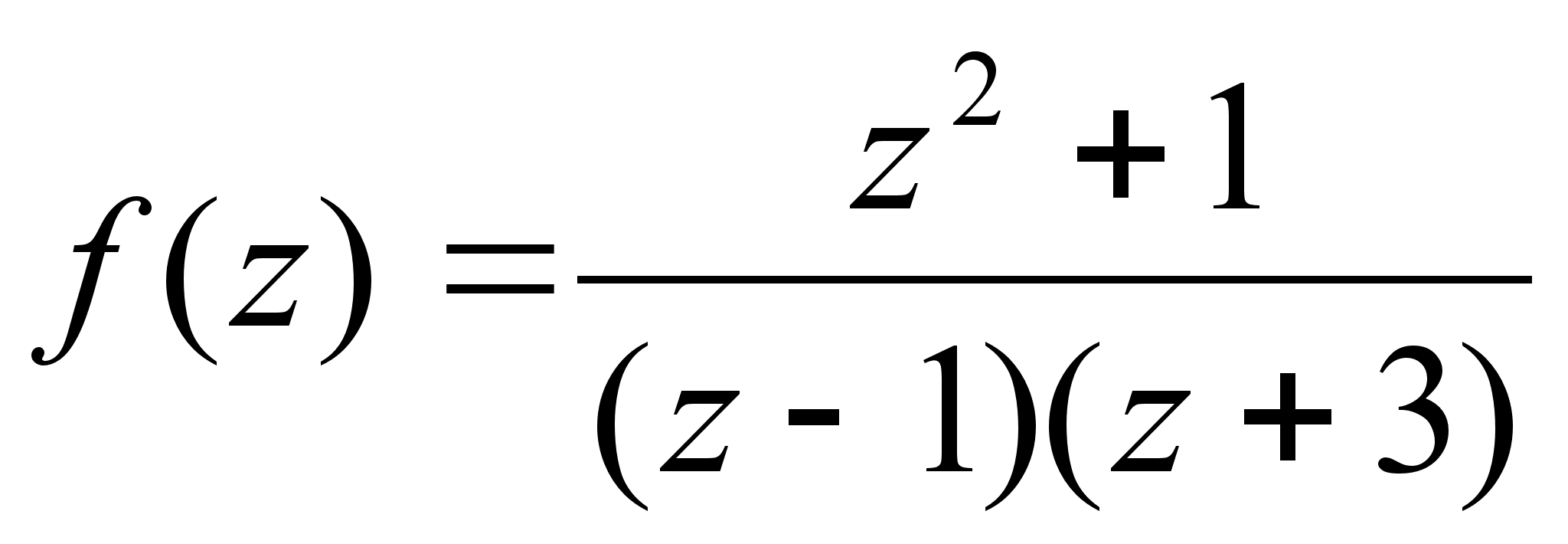
Особые
точки : Z1=1,
Z2=
- 3.
Определим
порядок полюсов
– все полюсы
первого порядка.
Используем
формулу (3) :
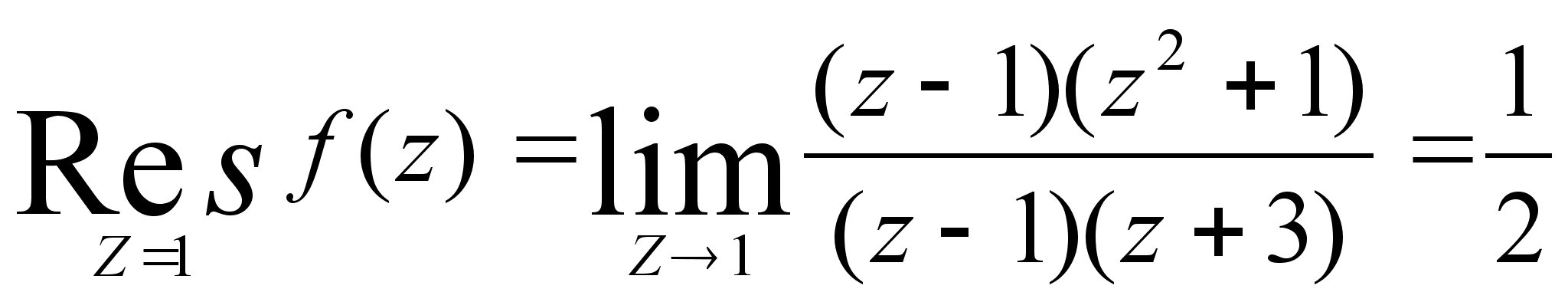
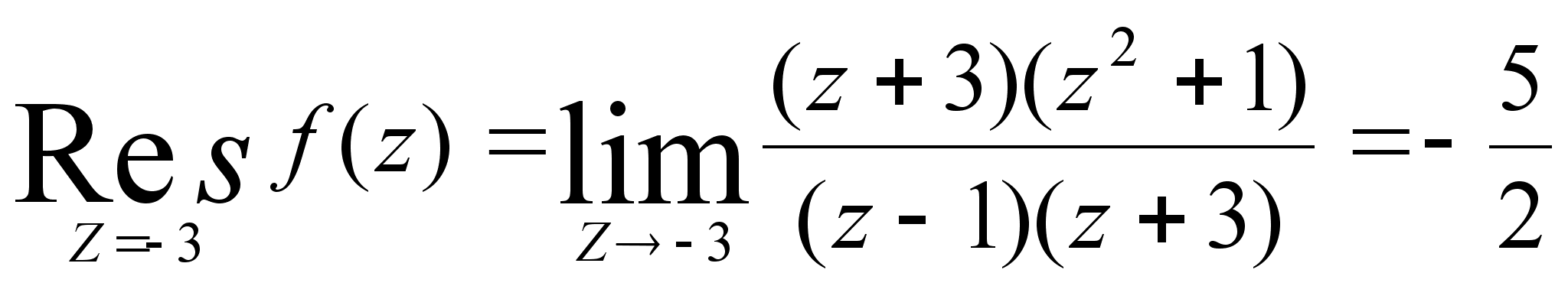
Интегральные
преобразования.
Операционное
исчисление
и некоторые
его приложения.
Пусть задана
функция действительного
переменного
t, которая
удовлетворяет
условиям :

Функция f(t)
кусочно-непрерывная
(имеет конечное
число точек
разрыва первого
рода).
Для любого
значения параметра
t>0 существует
M>0 и S00
такие, что
выполняется
условие : |f(t)|S0t
Рассмотрим
функцию f(t)e-pt
, где р – комплексное
число р = ( а +
i b).
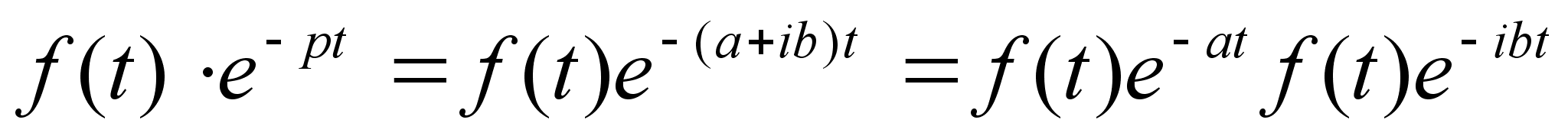 (1)
(1)
Применим к
этому соотношению
формулу Эйлера
:

Проинтегрировав
это равенство
получим :
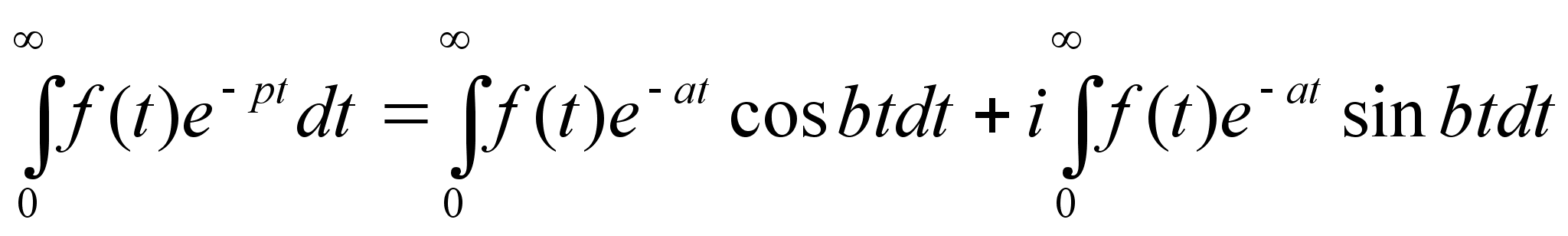 (2)
(2)
Оценим левую
часть равенства
(2) :

А согласно
свойству (3) |f(t)|
< Me S0t
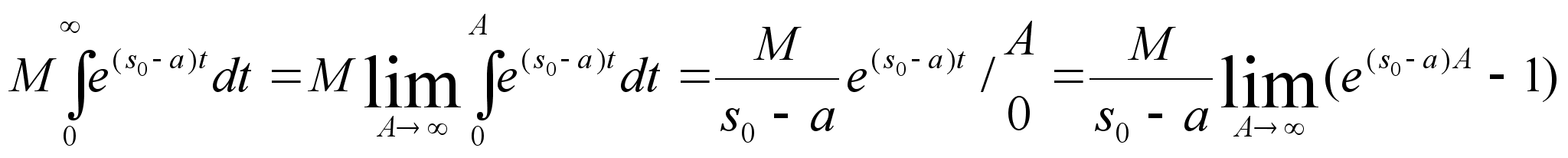
В случае если
a>S0
имеем :

Аналогично
можно доказать,
что существует
и сходится
второй интеграл
в равенстве
(2).
Таким образом
при a>S0
интеграл, стоящий
в левой части
равенства (2)
также существует
и сходится.
Этот интеграл
определяет
собой функцию
от комплексного
параметра р
:
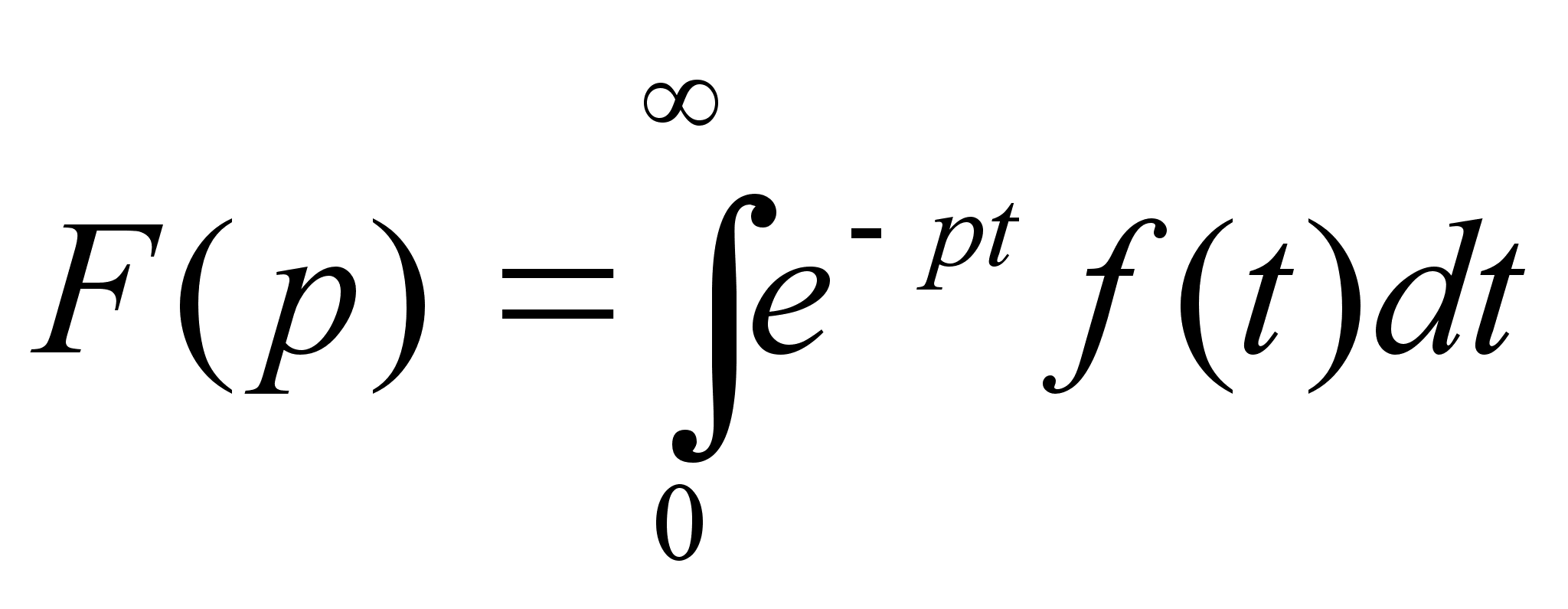 (3)
(3)
Функция F(p)
называется
изображением
функции f(t)
по Лапласу,
а функция f(t)
по отношению
к F(p) называется
оригиналом.
f(t)
F(p), где F(p) – изображение
функции f(t)
по Лапласу.
 - это оператор
Лапласа.
- это оператор
Лапласа.
Смысл
введения интегральных
преобразований.
Этот смысл
состоит в следующем
: с помощью перехода
в область изображения
удается упростить
решение многих
задач, в частности
свести задачу
решения многих
задач дифференциального,
интегрального
и интегро-дифференциального
уравнения к
решению алгебраических
уравнений.
Теорема единственности:
если две функции
tиt
имеют одно и
то же изображение
F(p), то эти
функции тождественно
равны.
Смысл теоремы
: если при решении
задачи мы определим
изображение
искомой функции,
а затем по
изображению
нашли оригинал,
то на основании
теоремы единственности
можно утверждать,
что найденная
функция является
решением в
области оригинала
и причем единственным.
Изображение
функций 0(t),
sin (t), cos (t).
Определение:
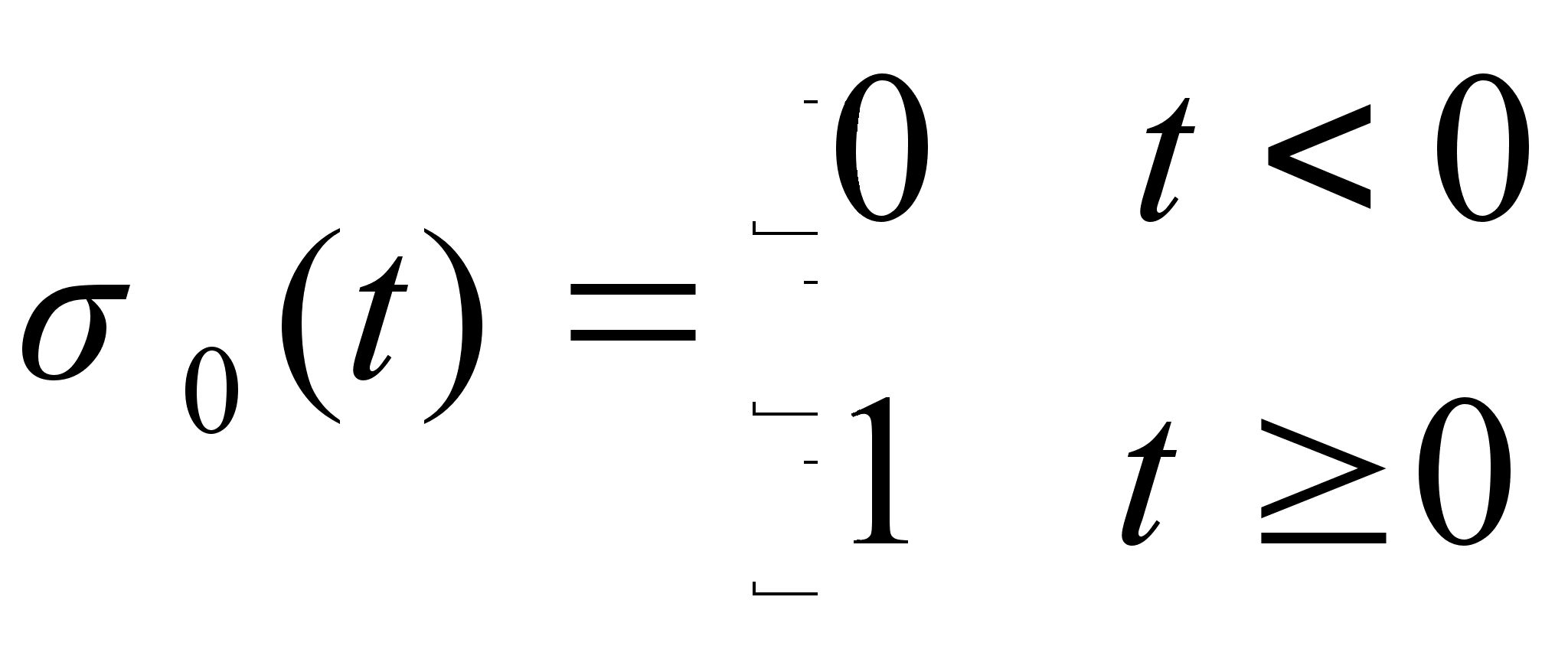 называется
единичной
функцией.
называется
единичной
функцией.
Единичная
функция удовлетворяет
требованиям,
которые должны
быть наложены
на функцию для
существования
изображения
по Лапласу.
Найдем это
изображение
:

Изображение
единичной
функции
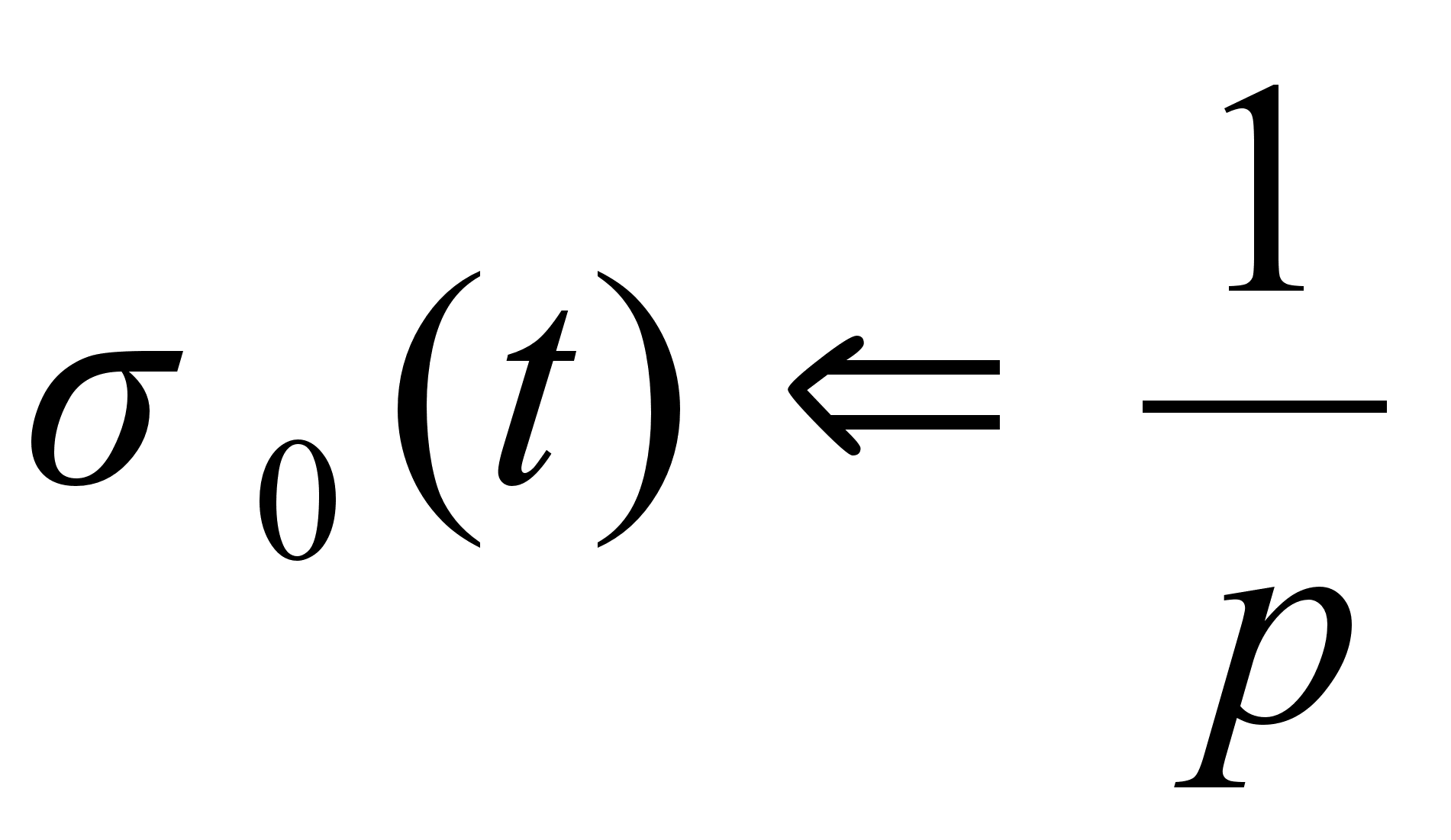
Рассуждая
аналогичным
образом получим
изображение
для функции
sin(t) :

интегрируя
по частям получим
:
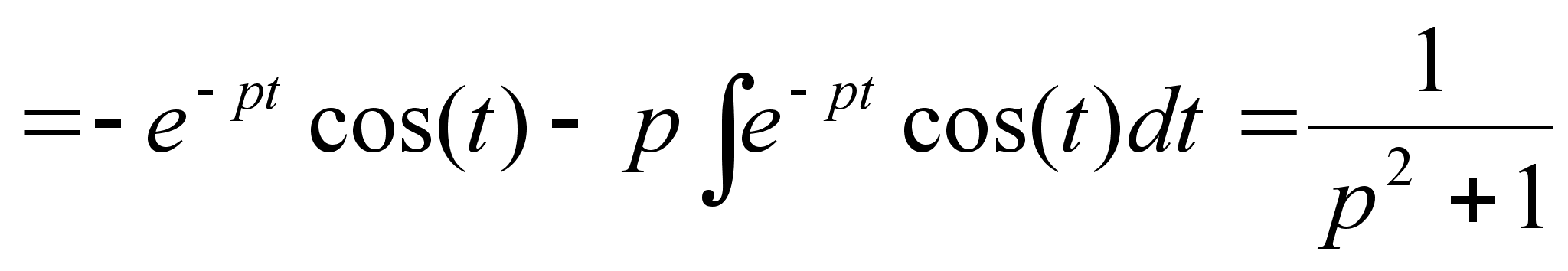 т.е.
т.е.
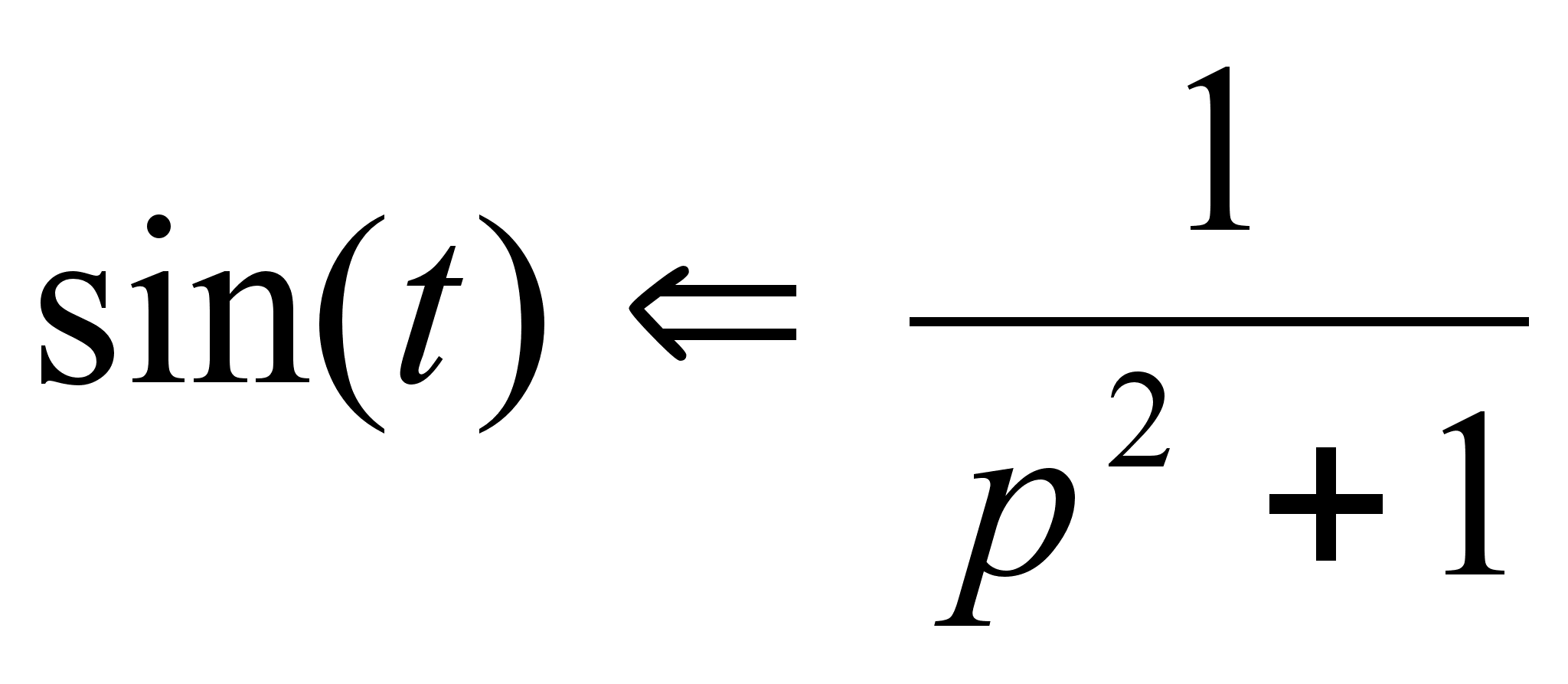
Аналогично
можно доказать,
что cos (t) переходит
в функцию
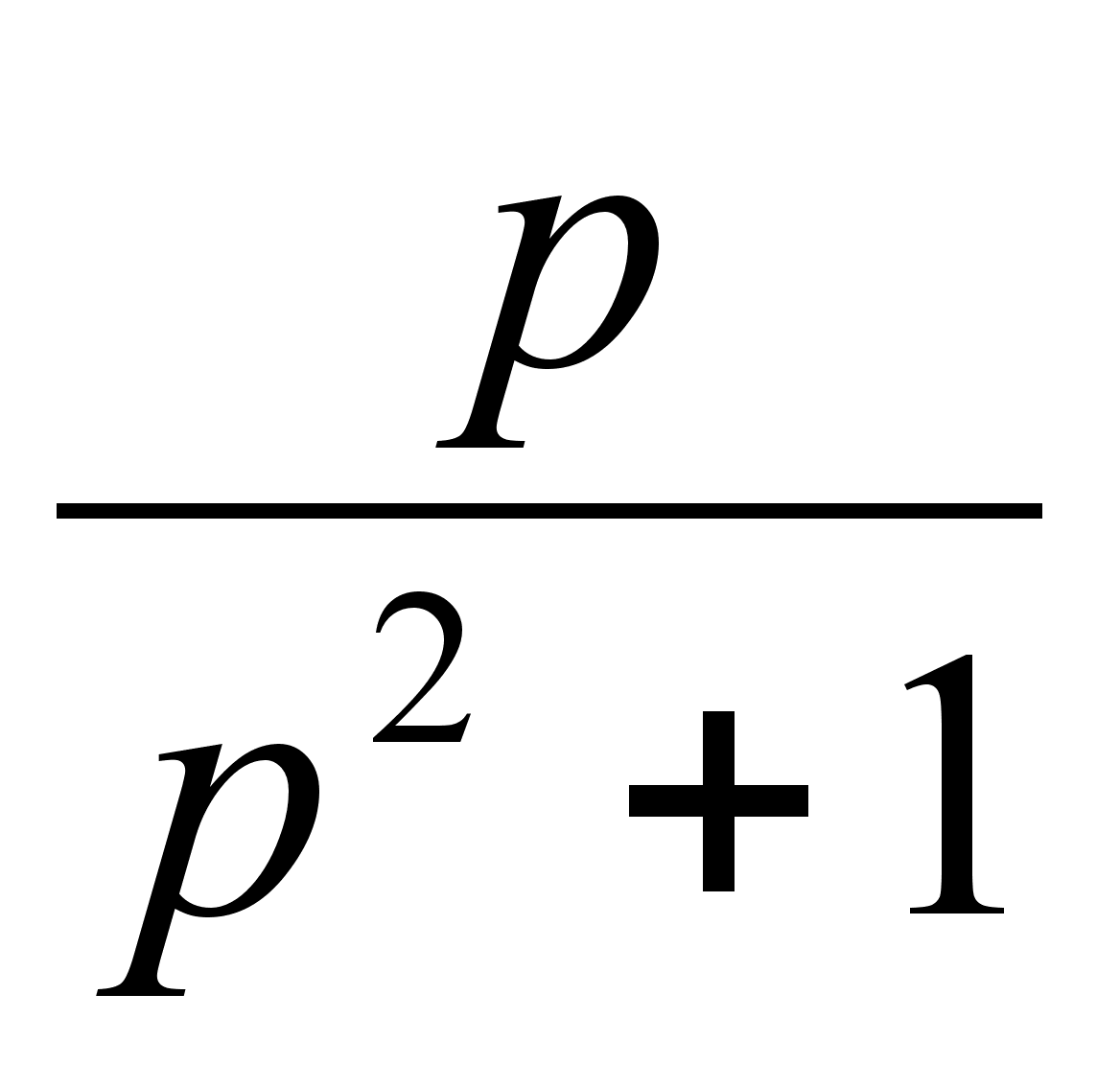 в
области преобразований.
Откуда :
в
области преобразований.
Откуда :

Изображение
функции с измененным
масштабом
независимого
переменного.
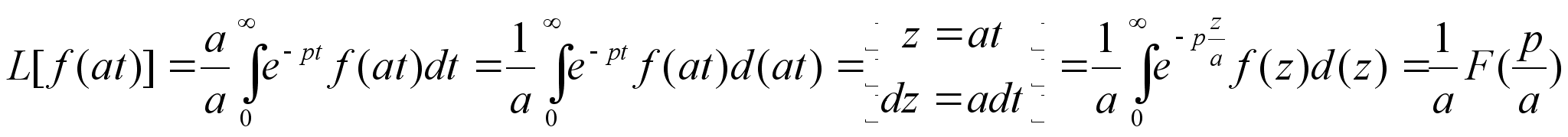 где
а – константа.
где
а – константа.
Таким образом
:

 и
и

Свойства
линейности
изображения.
Теорема :
изображение
суммы нескольких
функций умноженное
на постоянные
равны сумме
изображений
этих функций
умноженных
на те же постоянные.

Если
 ,
то
,
то
 ,
где
,
где
Теорема смещения
: если функция
F(p) это изображение
f(t), то F(+p)
является
изображением
функции e-t
f(t) (4)
Доказательство
:
Применим оператор
Лапласа к левой
части равенства
(4)
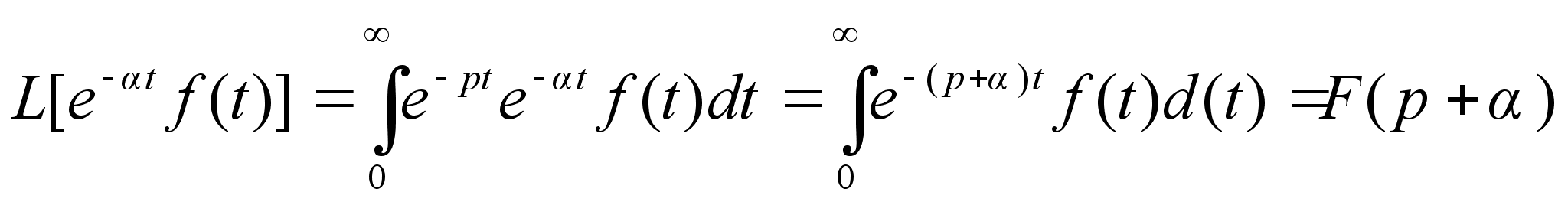
Что и требовалось
доказать.
Таблица
основных изображений:
Изображение
производных.
Теорема. Если
 ,
то справедливо
выражение :
,
то справедливо
выражение :
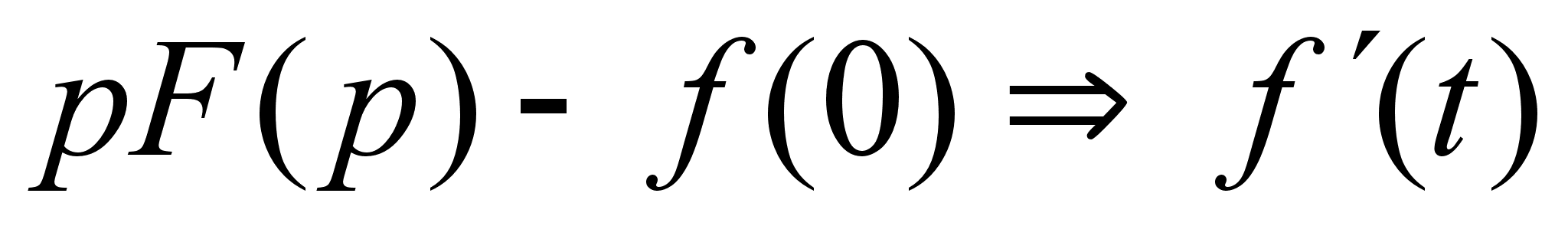 (1)
(1)
Доказательство
:

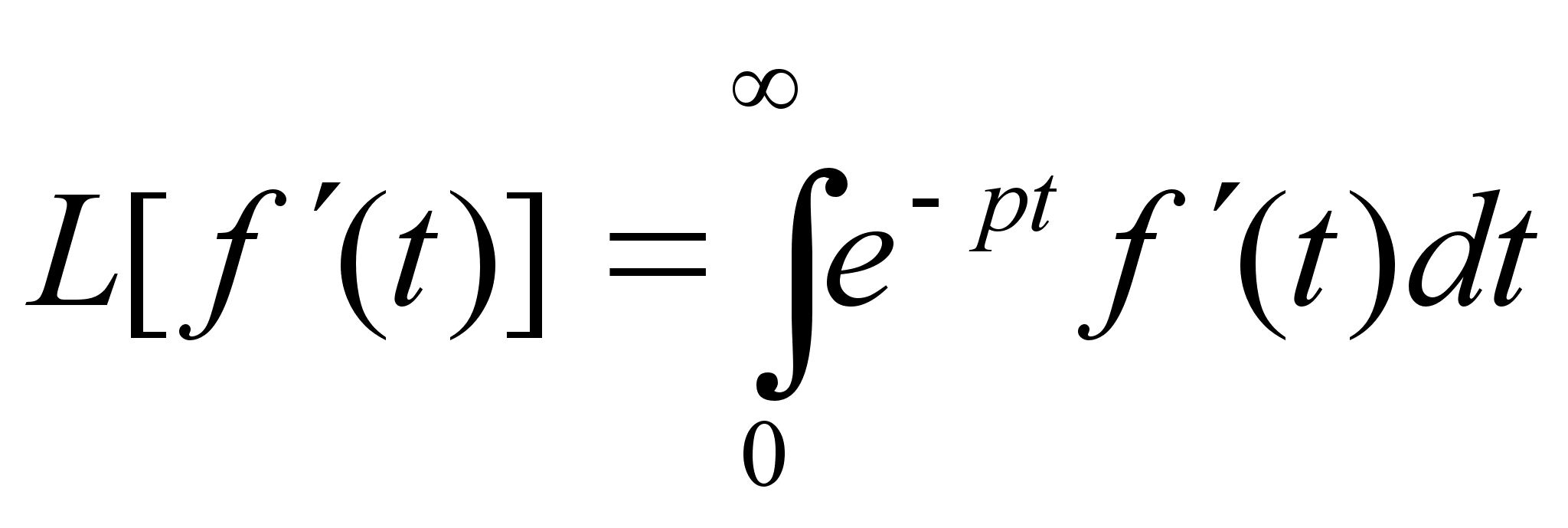
 (2)
(2)
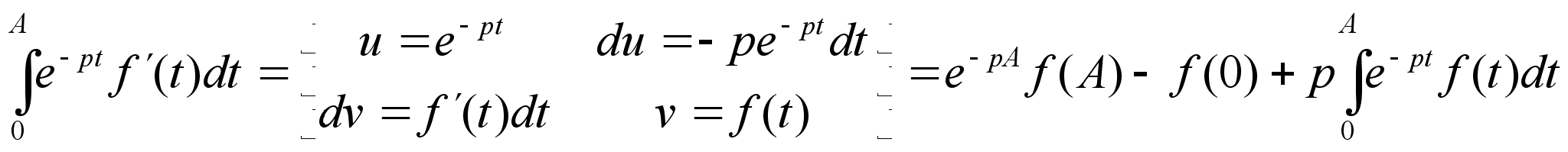 (3)
(3)
Подставляя
(3) в (2) и учитывая
третье условие
существования
функции Лапласа
имеем :
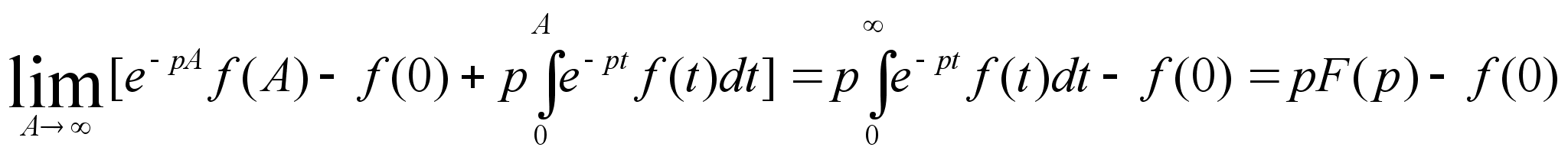
Что и требовалось
доказать.
Пример: Решить
дифференциальное
уравнение :
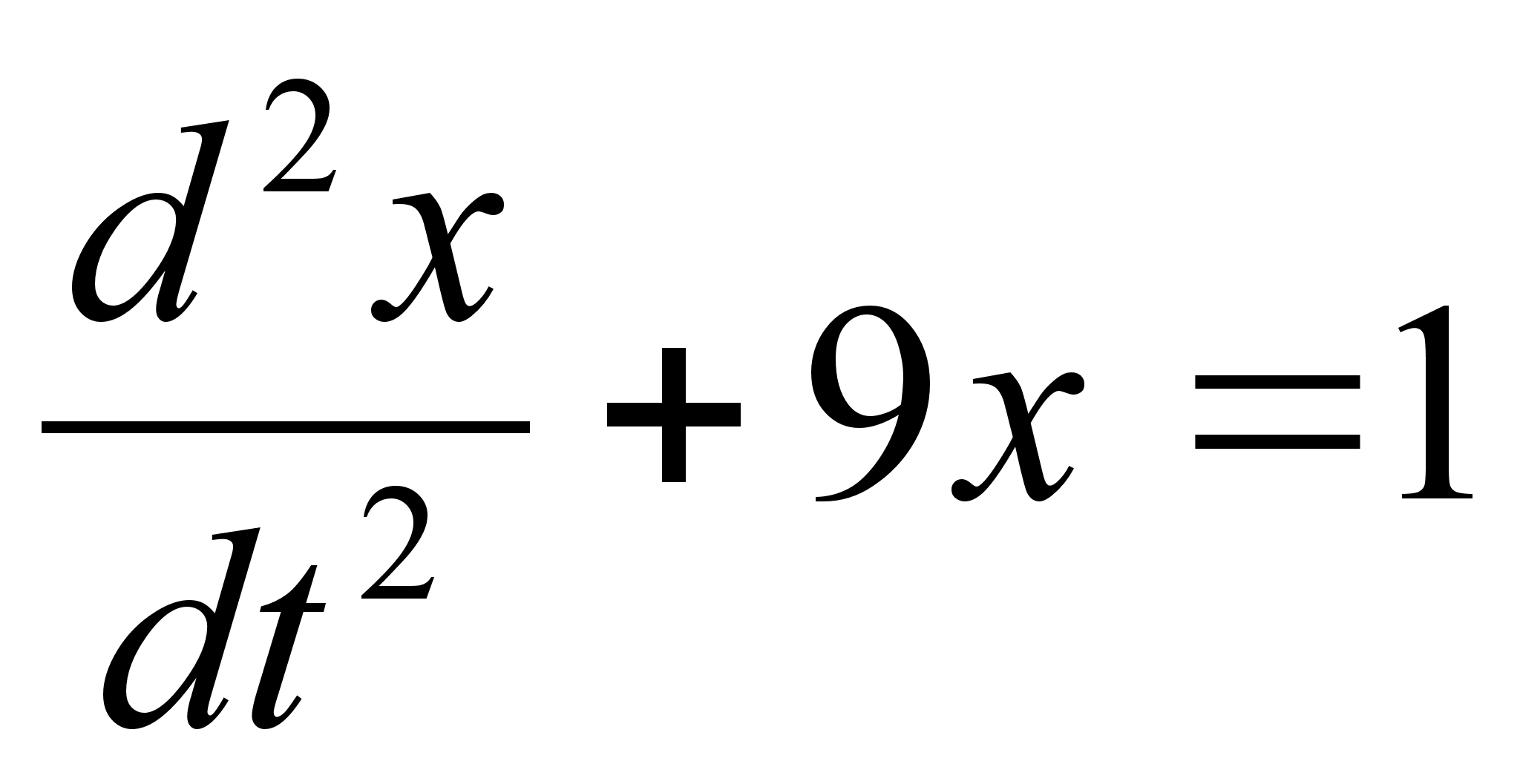 Если x(0)=0
и x’(0)=0
Если x(0)=0
и x’(0)=0
Предположим,
что x(t)
– решение в
области оригиналов
и
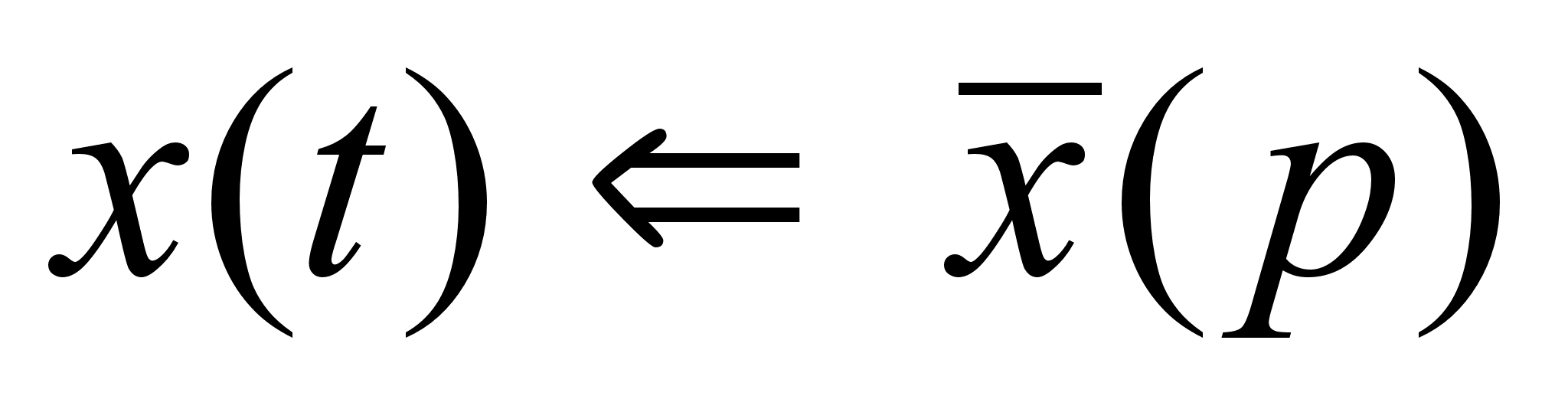 ,
где
,
где
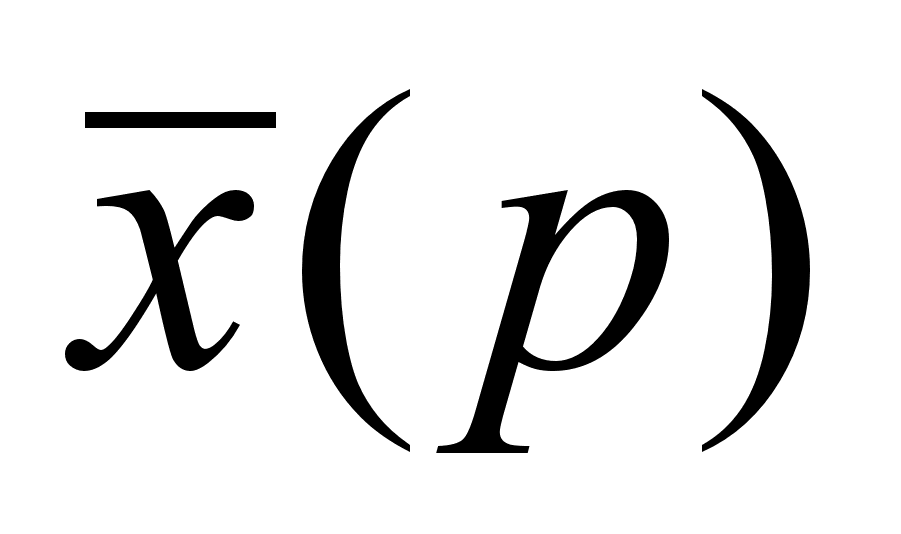 -
решение в области
изображений.
-
решение в области
изображений.

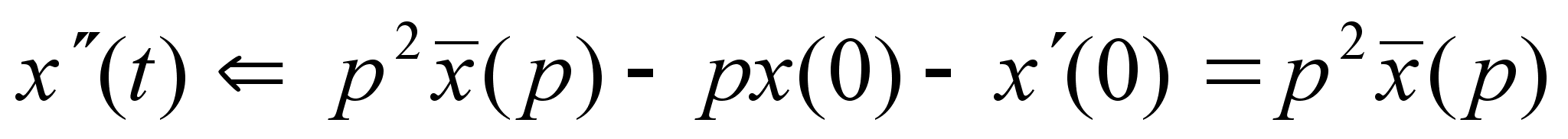

Изображающее
уравнение :

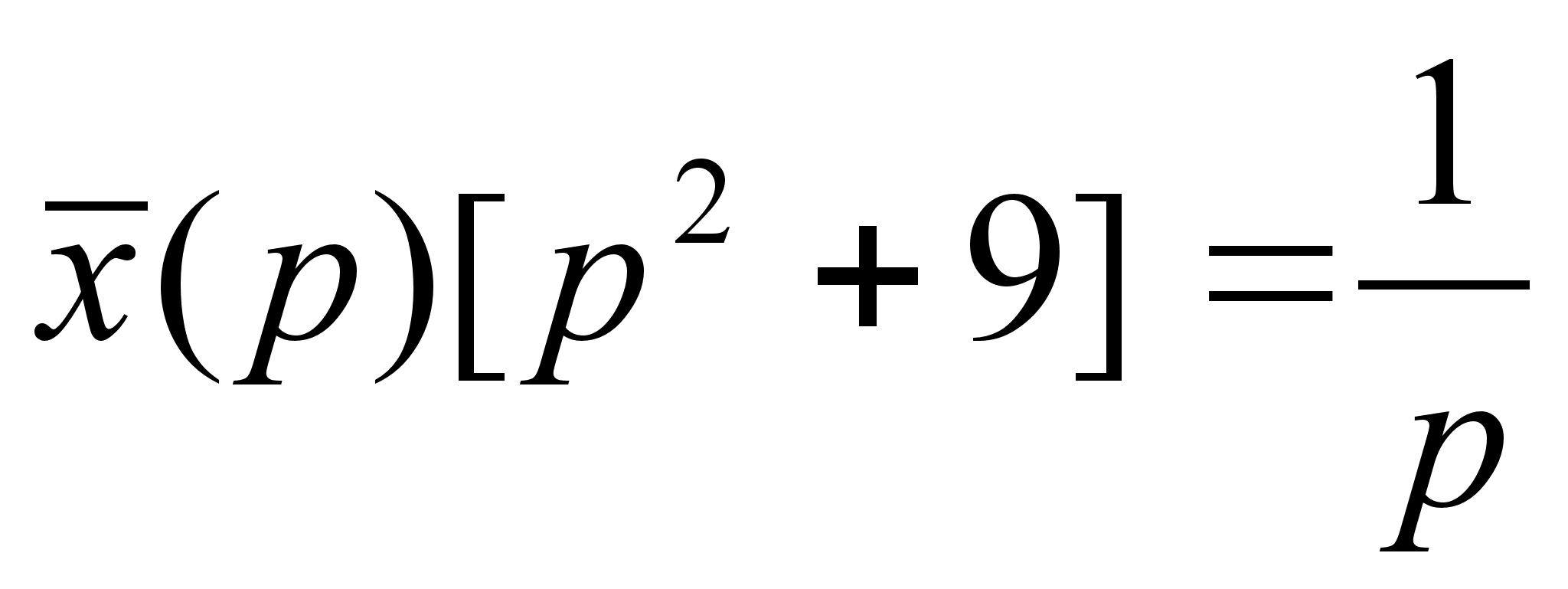

Теорема о
интегрировании
оригинала.
Пусть
 находится в
области оригиналов,
находится в
области оригиналов,
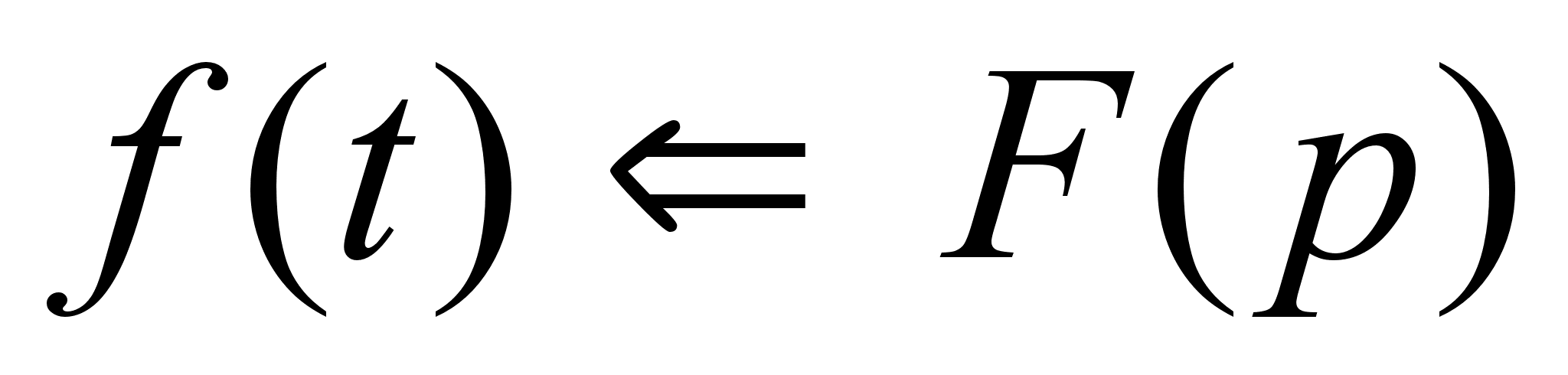 ,
тогда
,
тогда
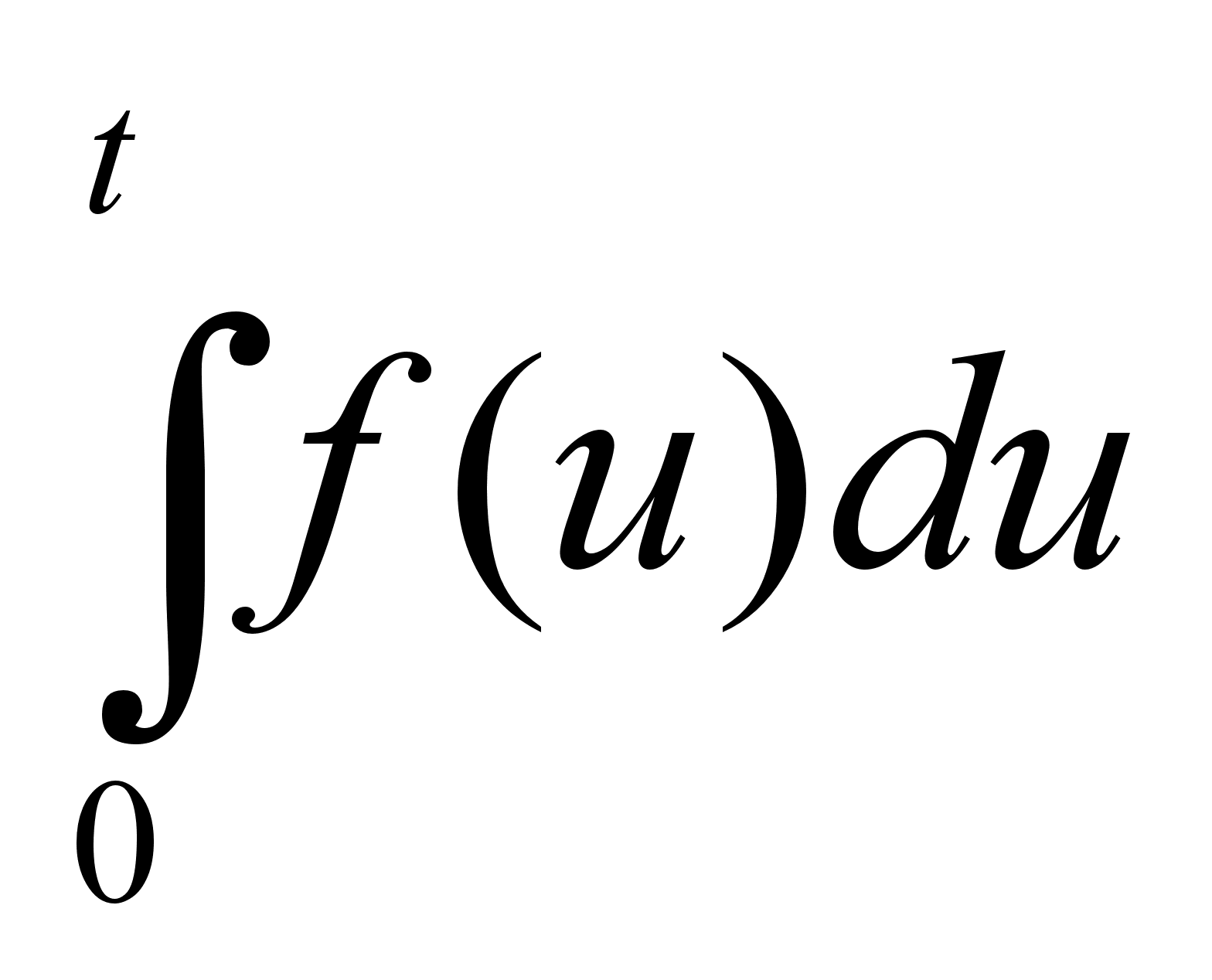 также
оригинал, а его
изображение
также
оригинал, а его
изображение
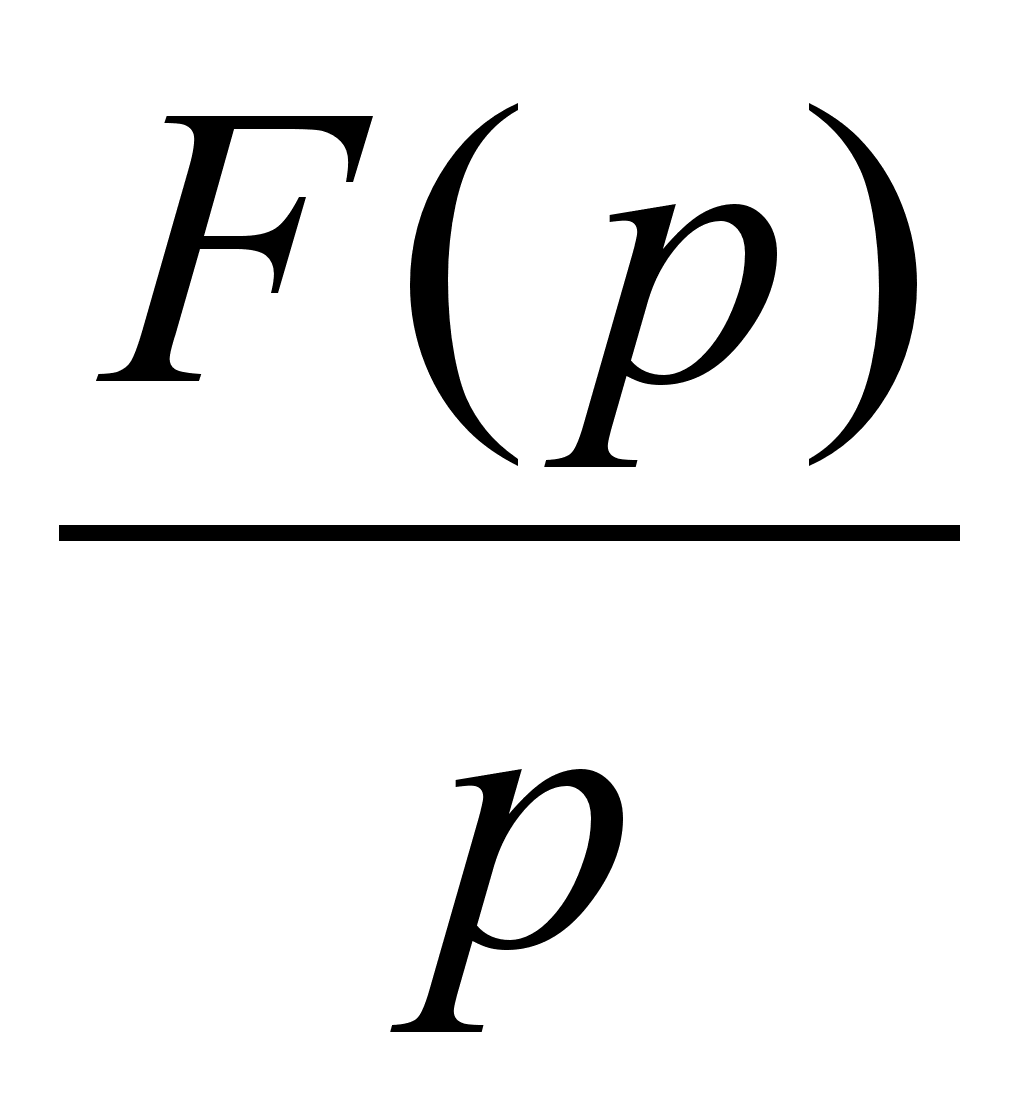 .
.
Таким образом
операции
интегрирования
в области оригиналов
соответствует
операция деления
в области
изображений.
Теорема о
интегрировании
изображений
: Пусть
 – функция
оригинал, которая
имеет изображение
– функция
оригинал, которая
имеет изображение
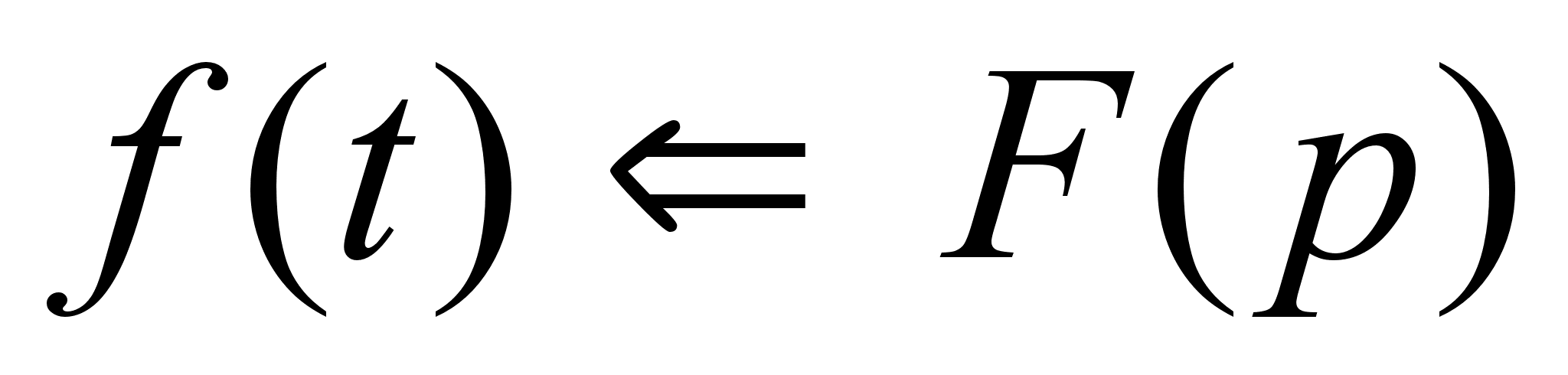 и
и
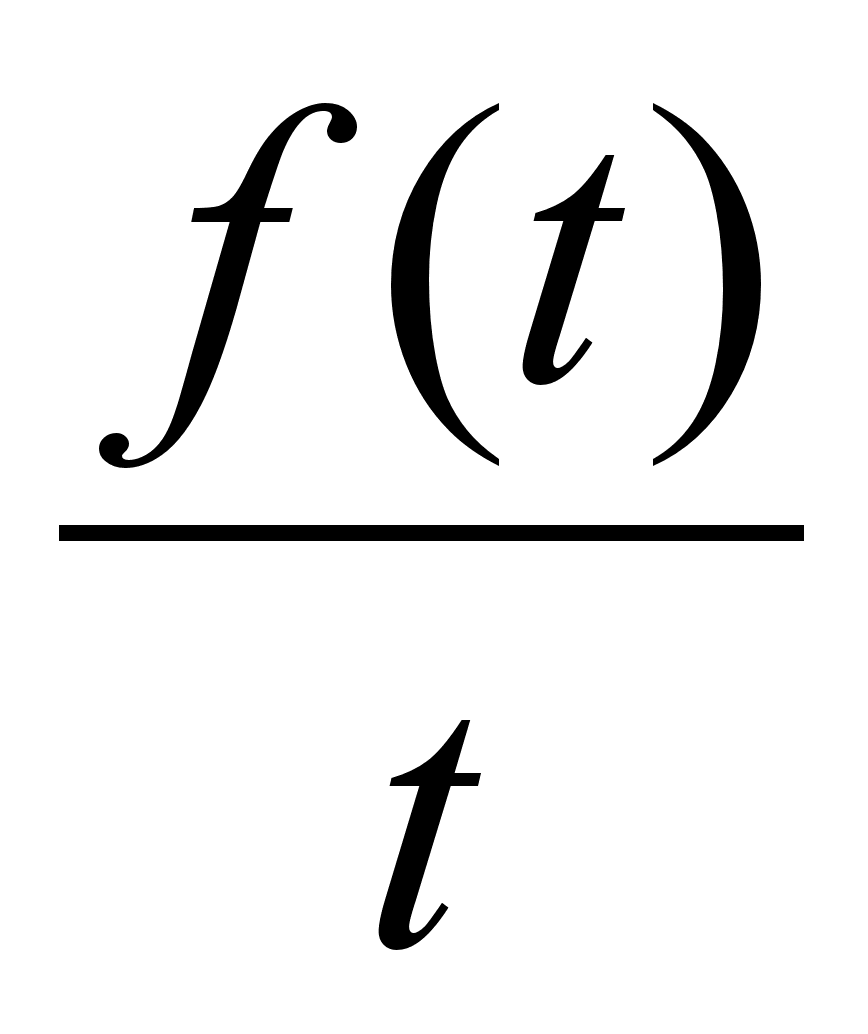 также оригинал,
а
также оригинал,
а
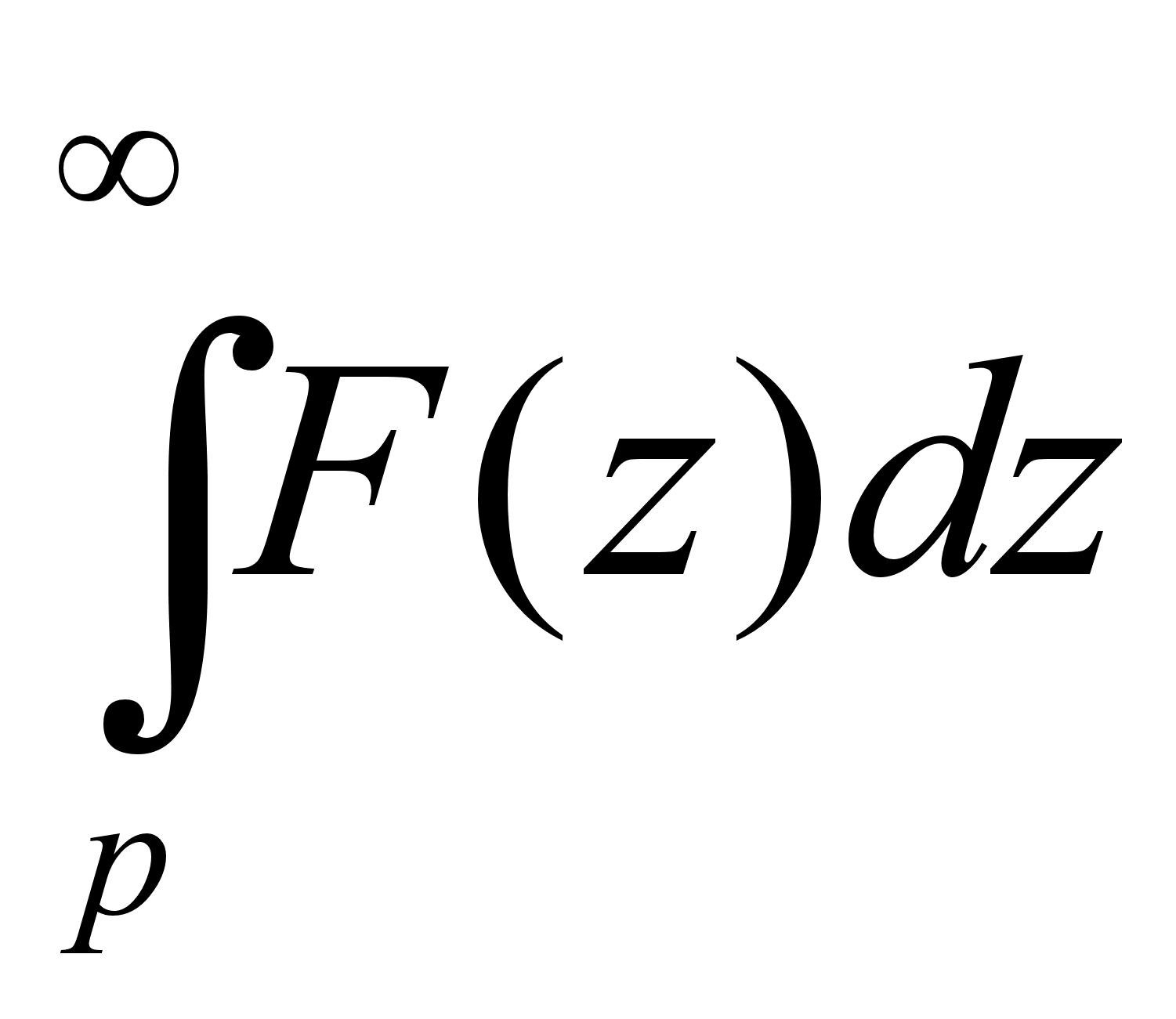 -
является сходящимся
интегралом,
тогда
-
является сходящимся
интегралом,
тогда
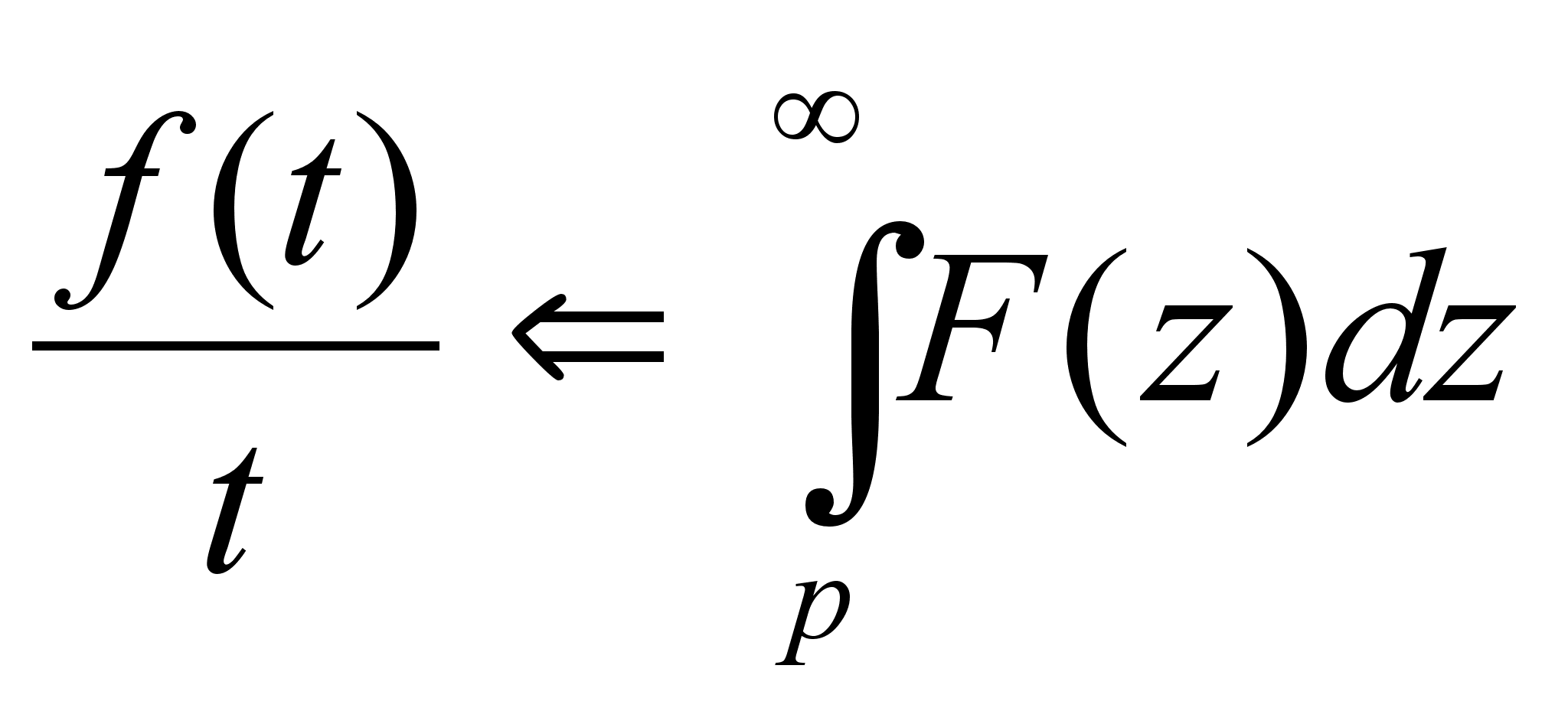 .
.
Толкование
теоремы : операция
деления на
аргумент в
области оригиналов
соответствует
операции
интегрирования
в пределах от
р до
в области
изображений.
Понятие
о свертке функций.
Теорема о свертке.
Пусть заданы
две функции
a(t) и b(t),
удовлетворяющие
условиям
существования
изображения
по Лапласу,
тогда сверткой
таких функций
называется
следующая
функция :
 (1)
(1)
Свертка обозначается
следующим
образом :
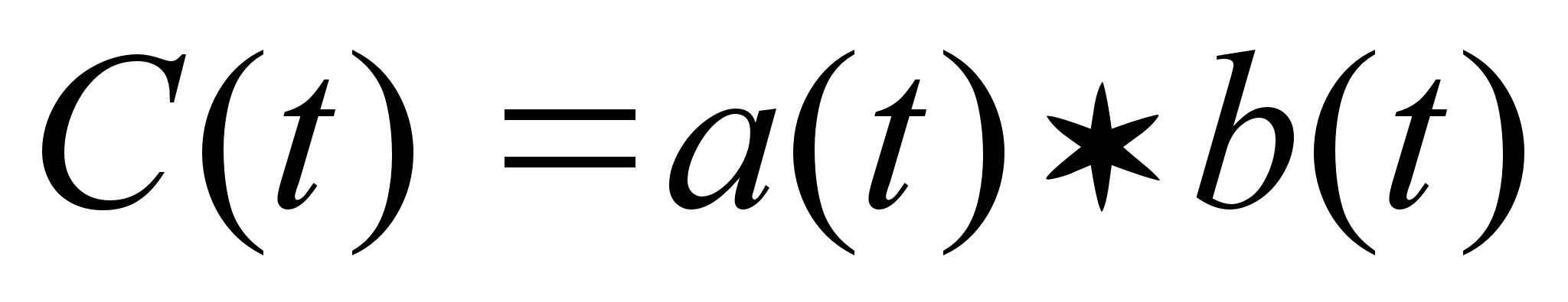 (1’)
(1’)
Равенства (1) и
(1’) идентичны.
Свертка функции
подчиняется
переместительному
закону.
Доказательство:
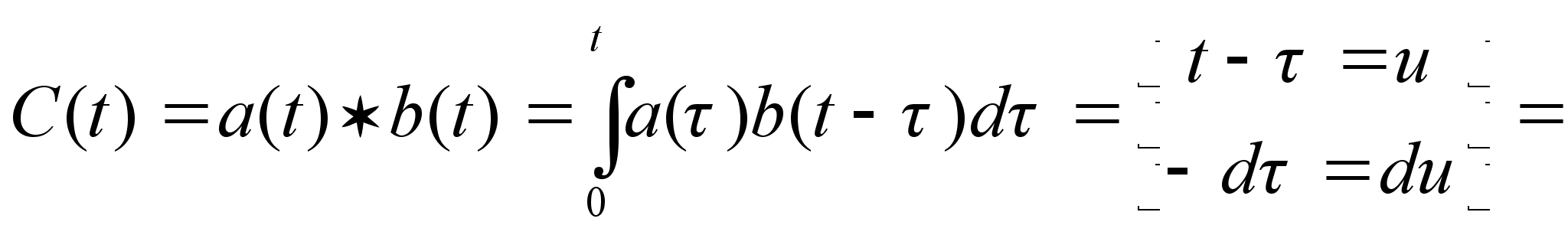
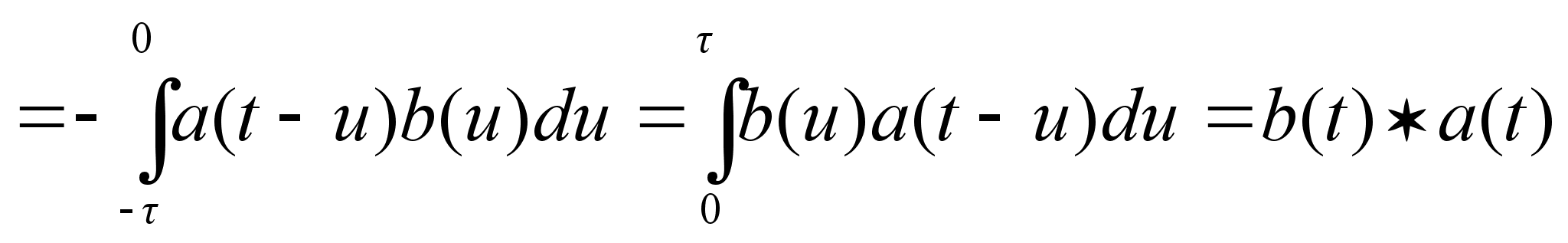
Теорема о
умножении
изображений.
Пусть
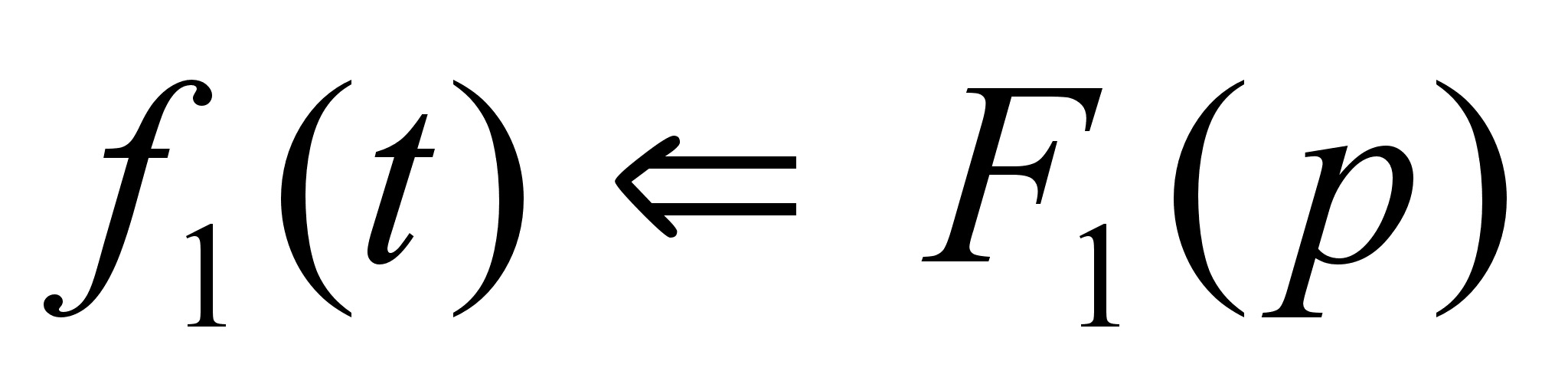 и
и
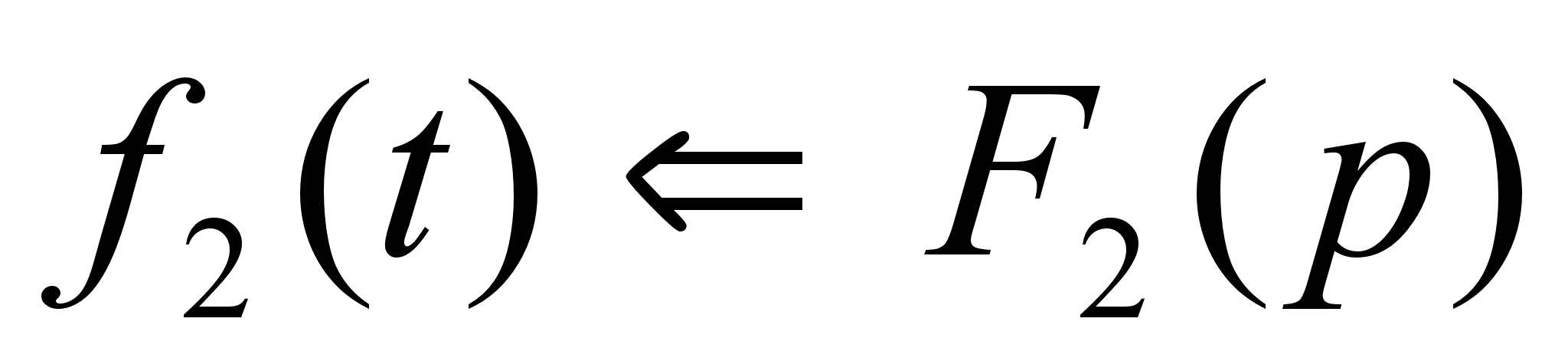 ,
тогда произведение
изображений
,
тогда произведение
изображений
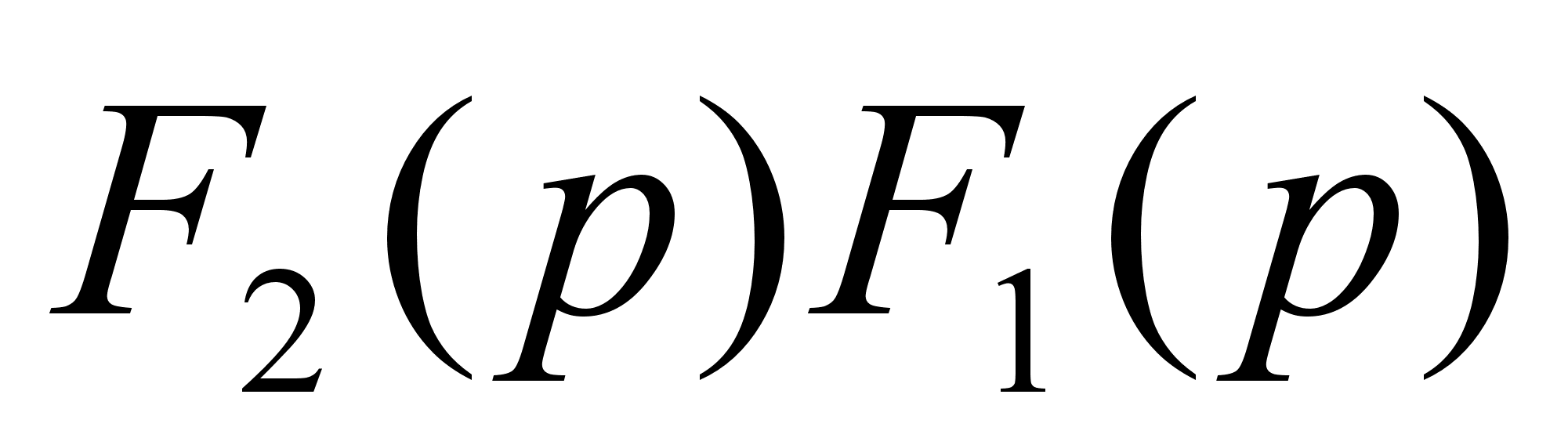 представляется
сверткой оригиналов
представляется
сверткой оригиналов
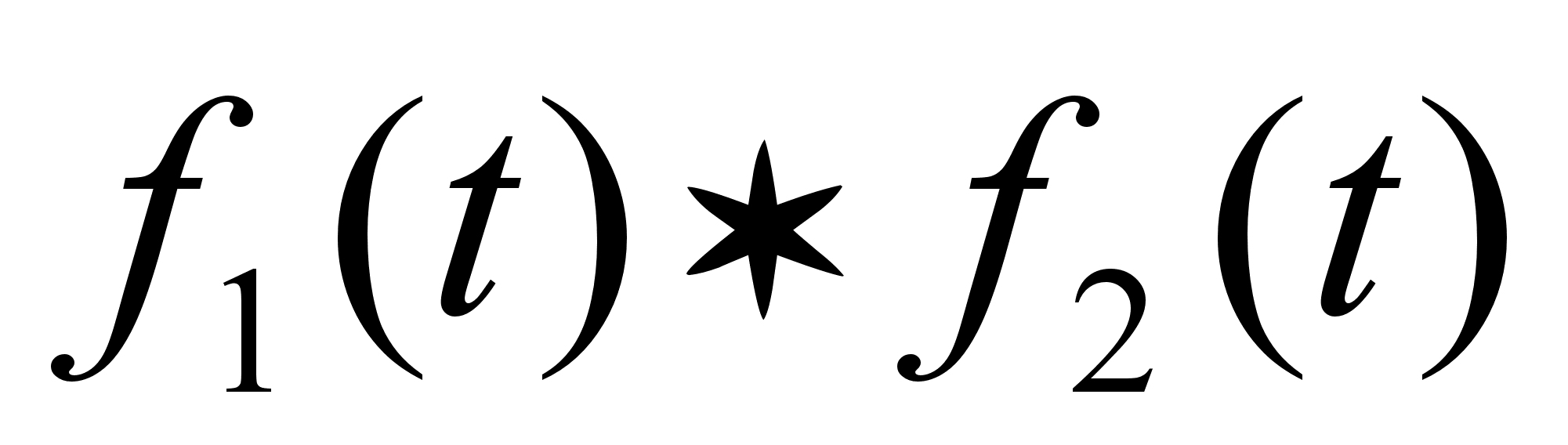 .
.
Доказательство
:
Пусть изображение
свертки
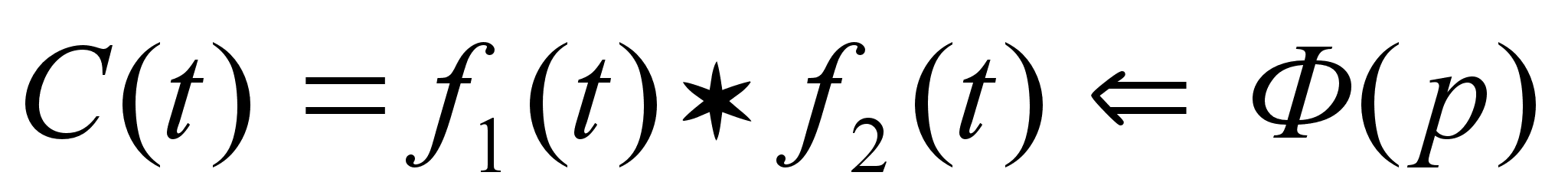
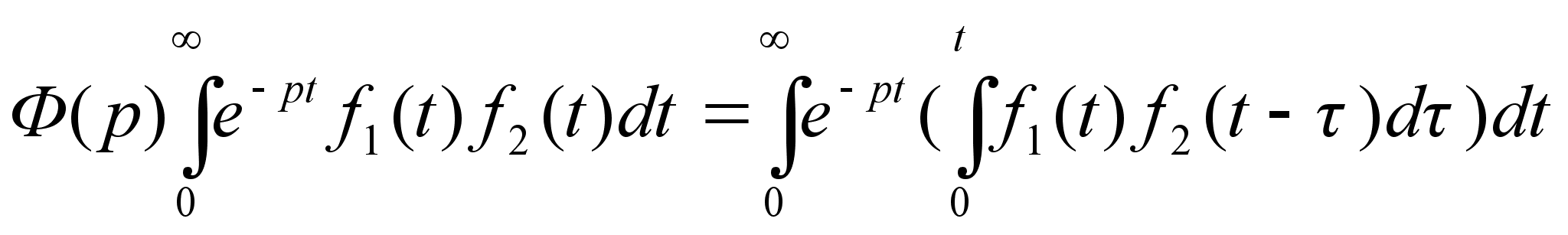 (1)
(1)
Интеграл (1)
представляет
собой повторный
интеграл относительно
переменных
t и
. Изменим порядок
интегрирования.
Переменные
t и
входят в выражение
симметрично.
Замена переменной
производится
эквивалентно.
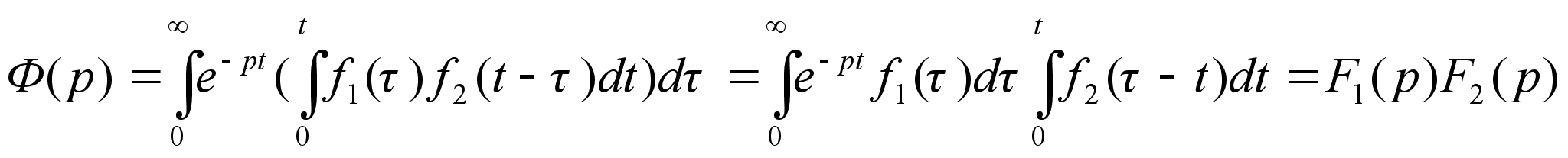
Если в последнем
интеграле
сделать замену
переменной,
то после преобразований
последний
интеграл
преобразуется
в функцию F2(p).
Операция умножения
двух функций
в пространстве
изображений
соответствует
операции свертки
их оригиналов
в области оригиналов.
Обобщением
теоремы о свертке
есть теорема
Эфроса.
Теорема Эфроса.
Пусть функция
 находится в
области оригиналов,
находится в
области оригиналов,
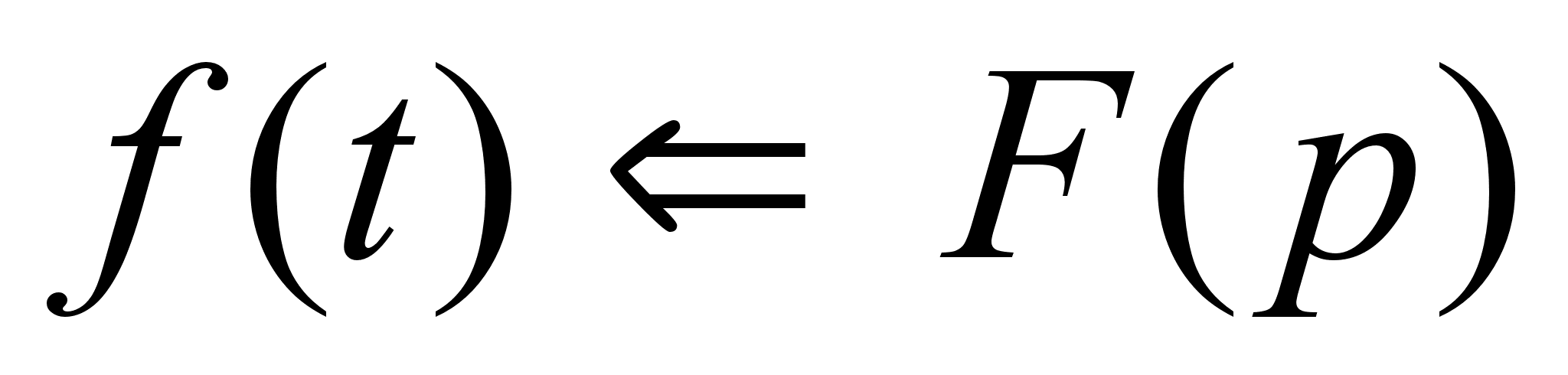 ,
а Ф(р) и q(р)
– аналитические
функции в области
изображений,
такие, что
,
а Ф(р) и q(р)
– аналитические
функции в области
изображений,
такие, что
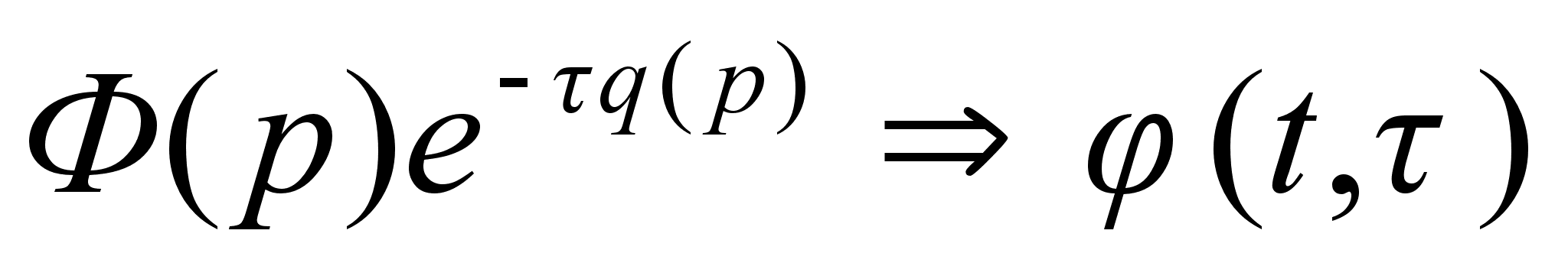 ,
тогда
,
тогда
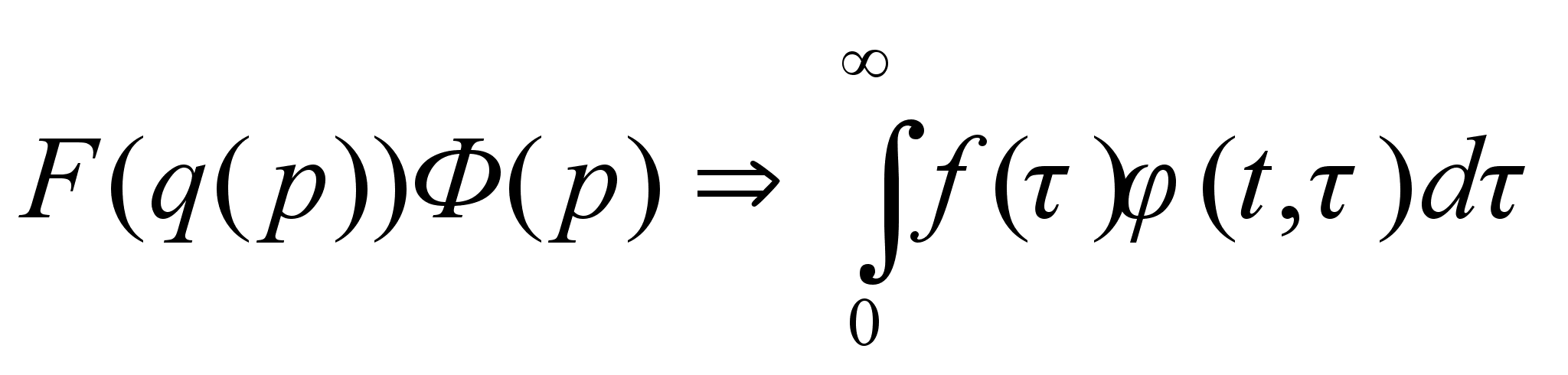 .
.
В практических
вычислениях
важную роль
играет следствие
из теоремы о
свертке, наз.
интеграл Дюамеля.
Пусть все условия
теоремы выполняются,
тогда
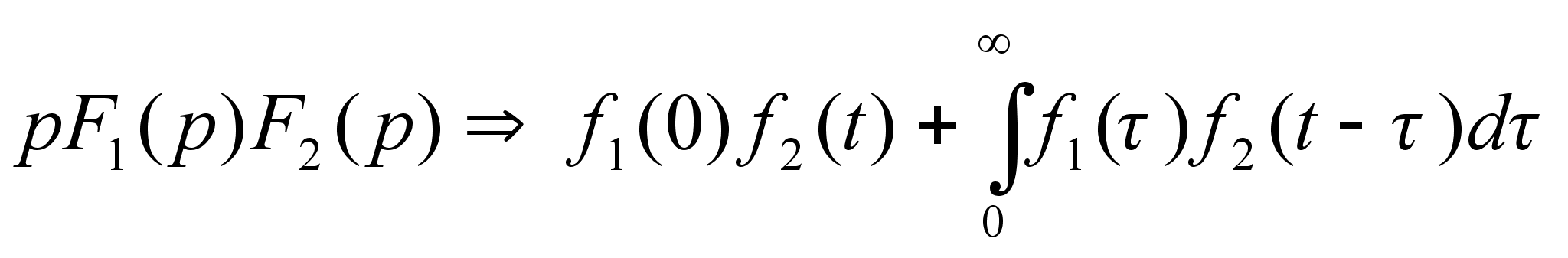 (2)
(2)
Соотношение
(2) применяется
при решении
дифференциальных
уравнений.
Обратное
преобразование
Лапласа.
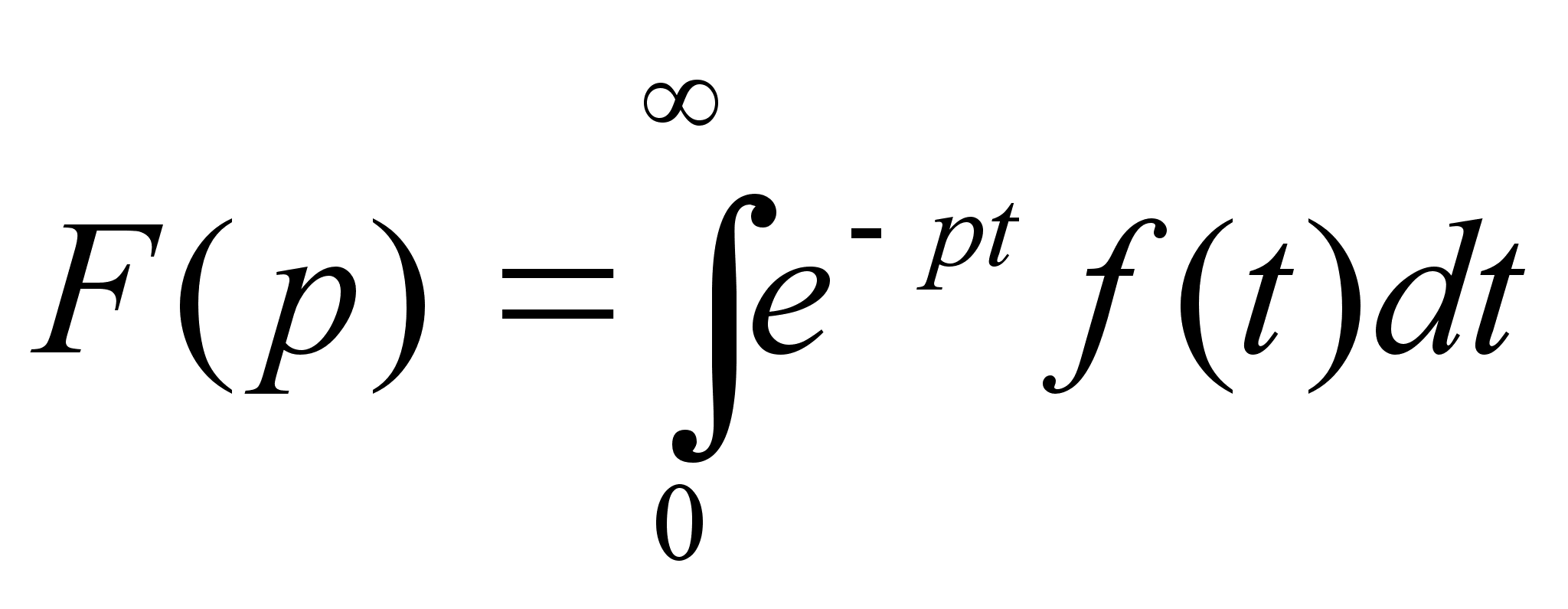 - Это прямое
преобразование
Лапласа.
- Это прямое
преобразование
Лапласа.
Обратное
преобразование
есть возможность
получить
функцию-оригинал
через известную
функцию-изображение
:
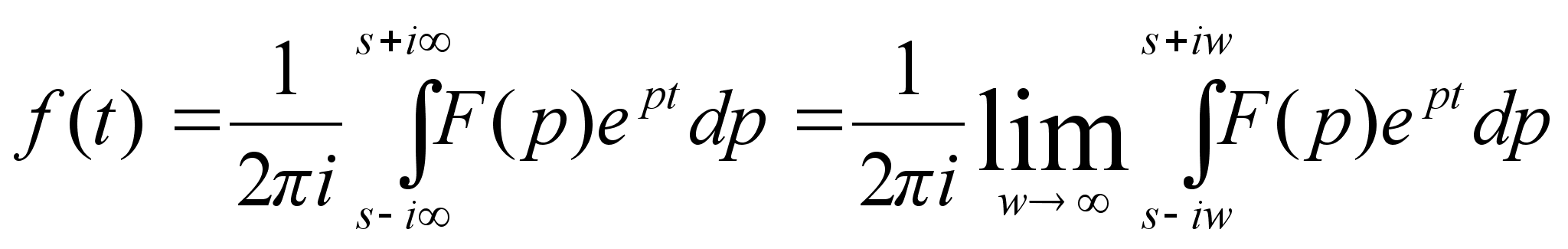 ,
где s
– некоторая
константа.
,
где s
– некоторая
константа.
Пользоваться
формулой для
обратного
преобразования
можно при
определенном
виде функции
F(p), либо для
численного
нахождения
функции-оригинала
по известному
изображению.
Теоремы
разложения.
Известная
методика разложения
дробно-рациональных
функций на
сумму элементарных
дробей (1)-(4) может
быть представлена
в виде двух
теорем разложения.
Первая теорема
разложения.
Пусть F(p) –
изображение
некоторой
функции, тогда
эта функция
представляется
в виде
 ,
k – постоянная,
может быть
сколь угодно
большим числом,
,
k – постоянная,
может быть
сколь угодно
большим числом,
 ,
то возможен
почленный
переход в
пространство
оригиналов
с помощью формулы
:
,
то возможен
почленный
переход в
пространство
оригиналов
с помощью формулы
:
 .
.
Вторая теорема
разложения.
Если изображение
представляется
дробно-рациональной
функцией
 .
Степень числа
s меньше
степени знаменателя
n, знаменатель
имеет корни
1,
2,
…,
n
соответствующий
кратности k1,
k2, …,
kn ,
при этом k1+
k2 +…+
kn =
n. В этом случае
оригинал функции
определяется
по формуле :
.
Степень числа
s меньше
степени знаменателя
n, знаменатель
имеет корни
1,
2,
…,
n
соответствующий
кратности k1,
k2, …,
kn ,
при этом k1+
k2 +…+
kn =
n. В этом случае
оригинал функции
определяется
по формуле :
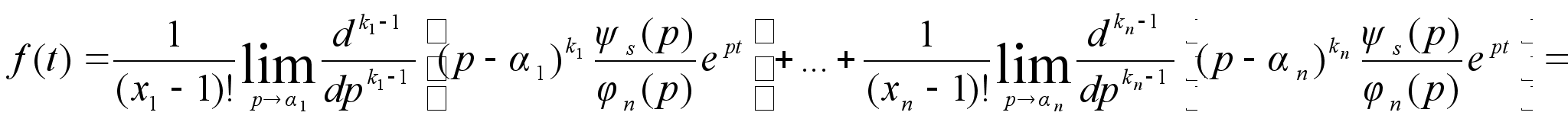
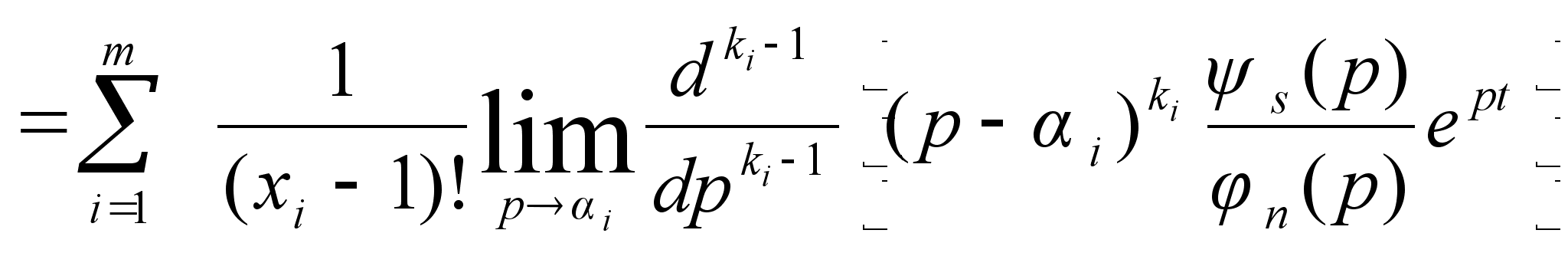 (3)
(3)
Например :
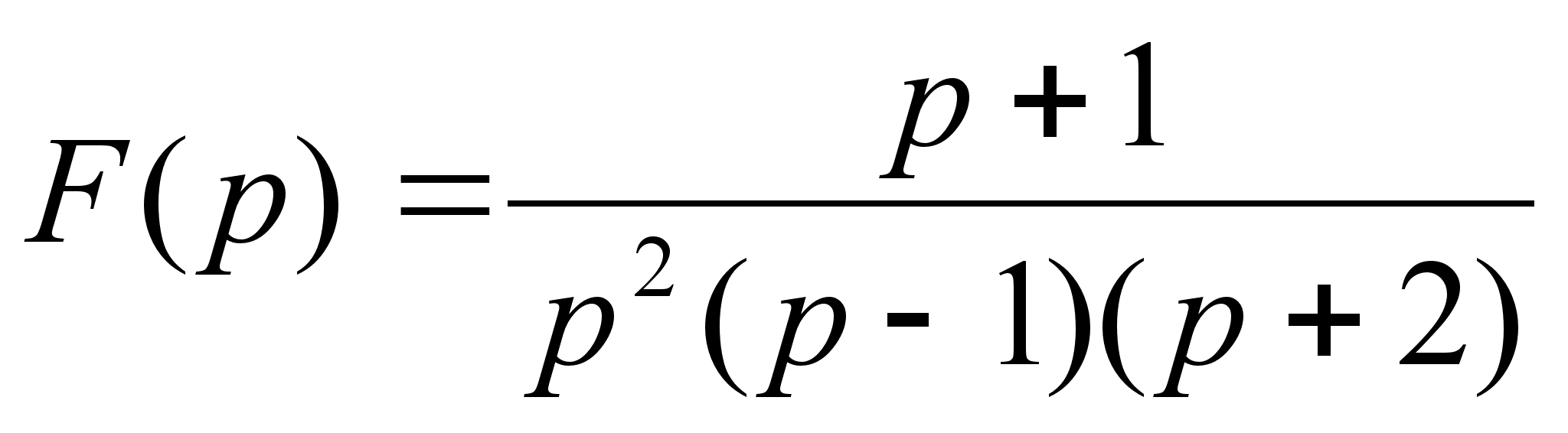
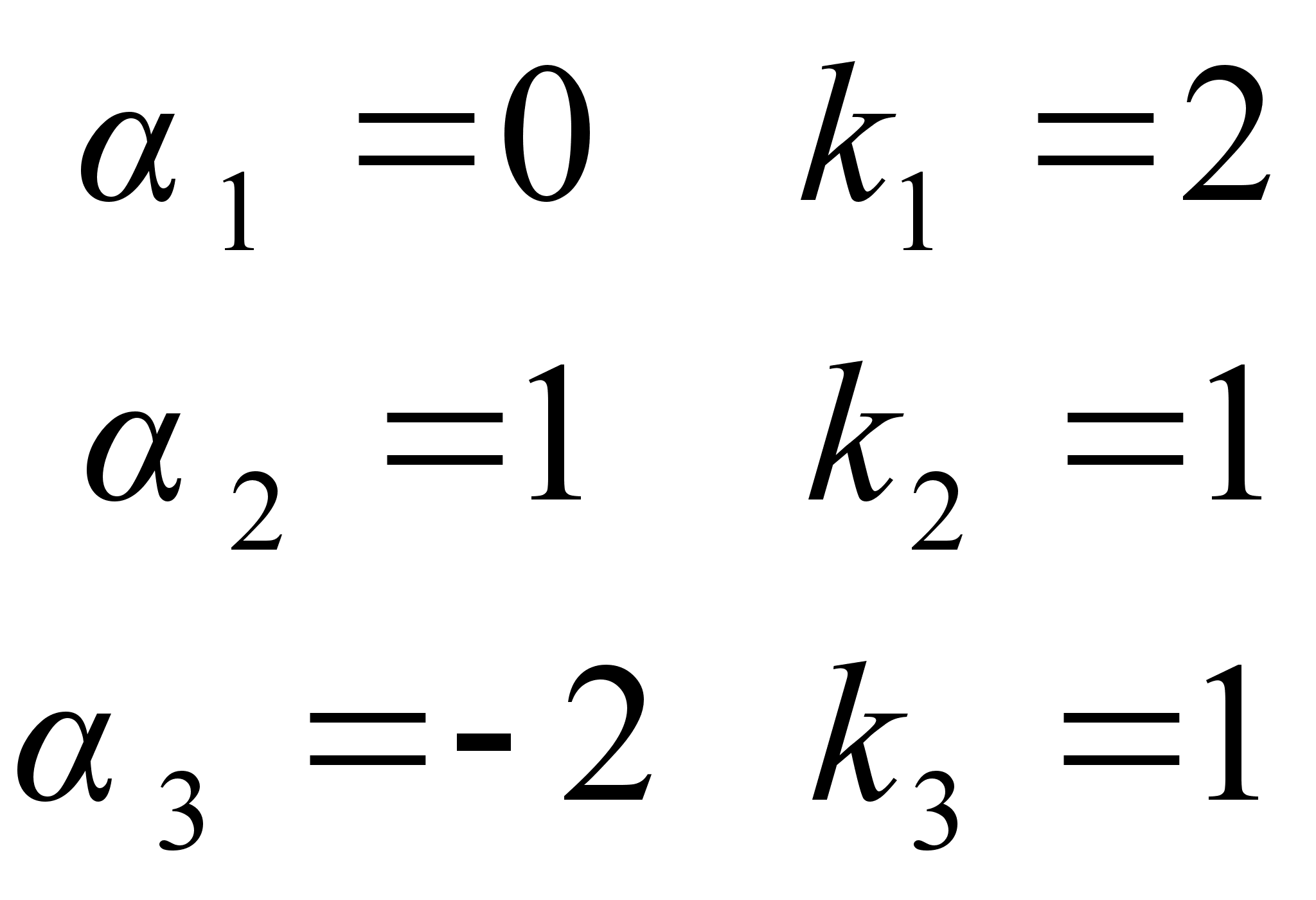
Связь
между преобразованиями
Фурье и Лапласа.
Преобразование
Лапласа имеет
вид :
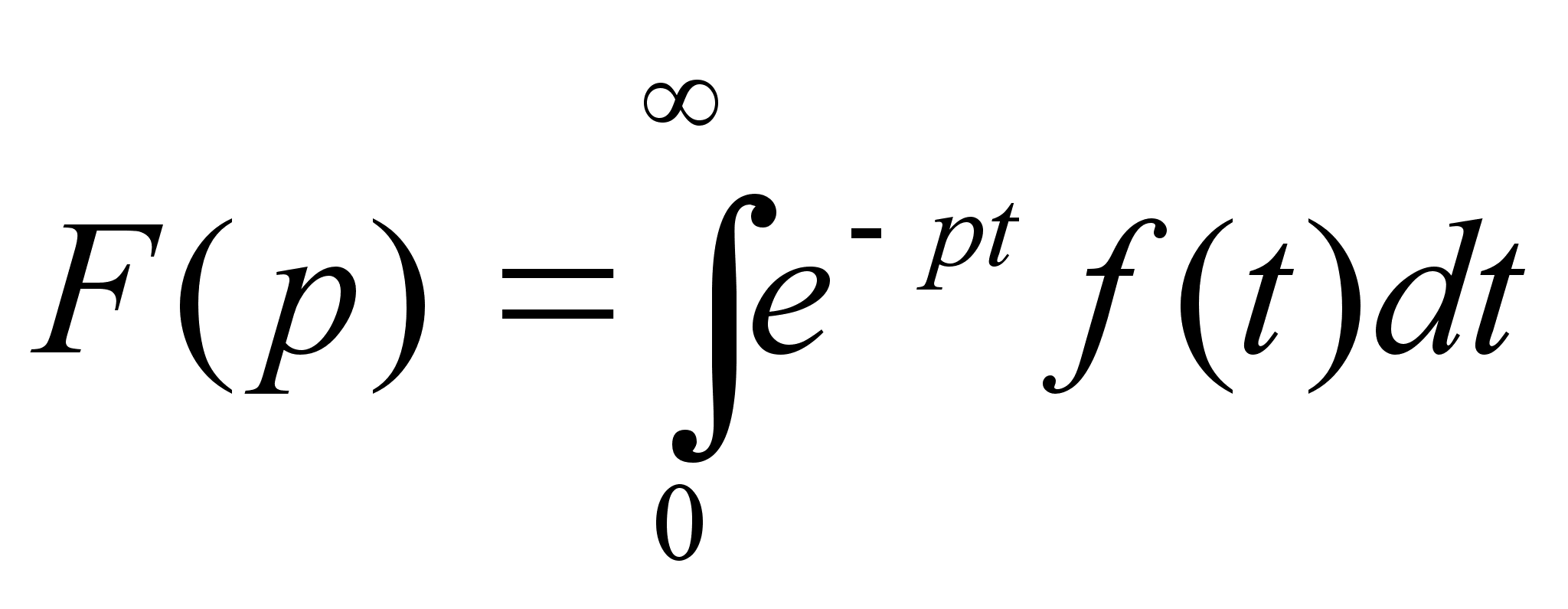 (1)
(1)
На f(t)
наложены
условия :
f(t) определена
и непрерывна
на всем интервале:
(- ;
)
f(t)
0 , t
(-
;0)
При M,
S0 >0
, для всех t
> 0 выполняется
условие |f(t)|S0t
Если отказаться
от условий 2 и
3, и считать, что
f(t) принимает
произвольное
значение при
t < 0, то вместо
(1) можно рассмотреть
следующий
интеграл :
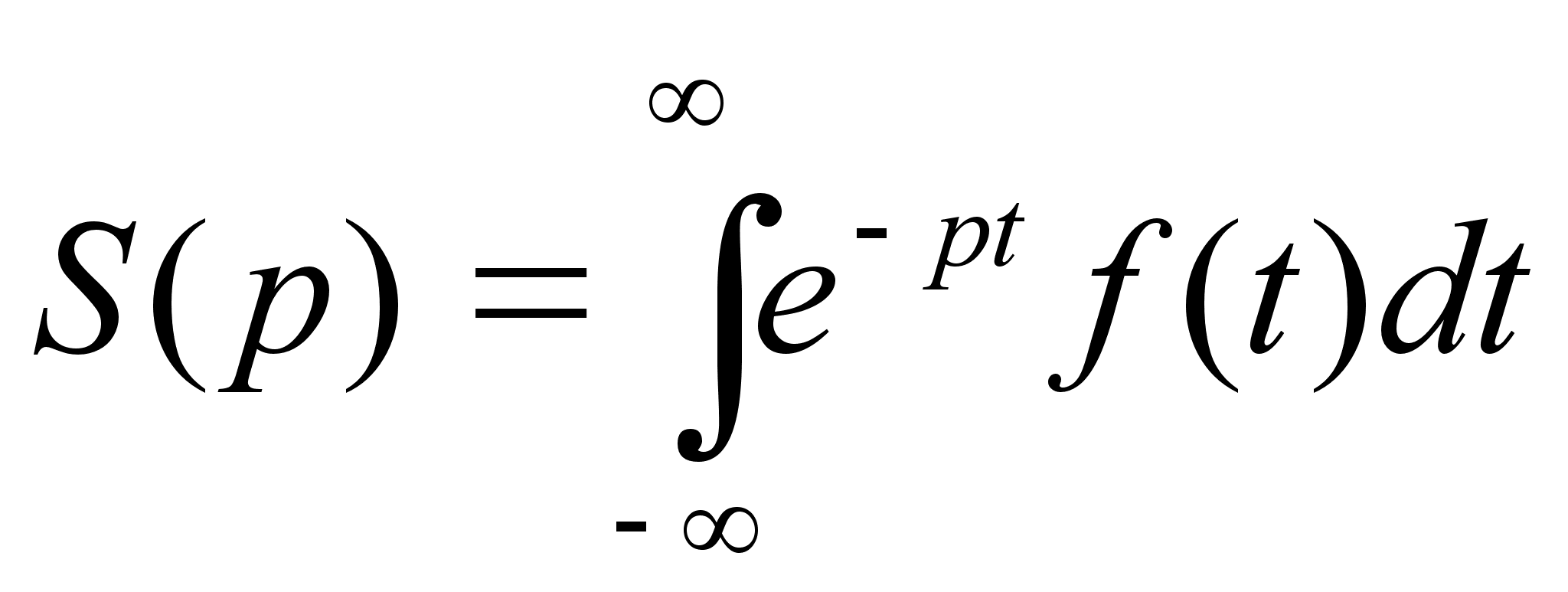 (2)
(2)
Формула (2) –
двустороннее
преобразование
Лапласа.
Пусть в (1) и (2)
p =a + in,
где a
и n
– действительные
числа.
Предположим,
что Re(p)
= a = 0, т.е.
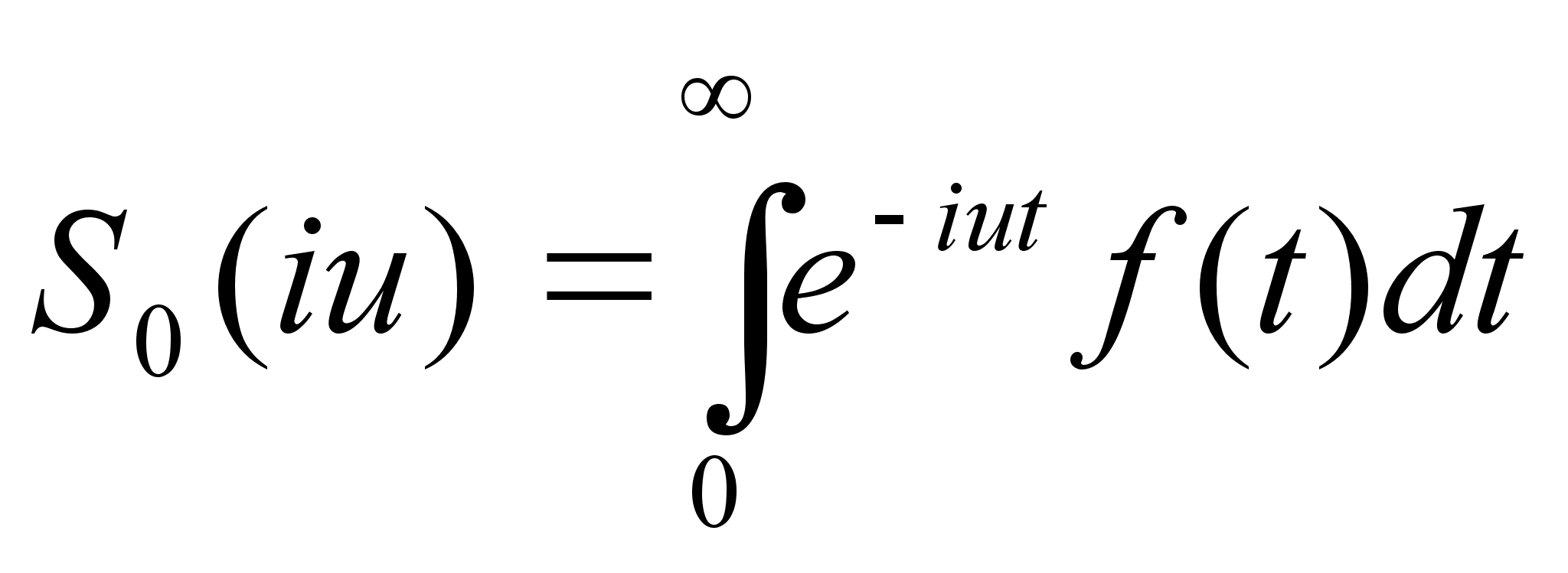 (4)
(4)
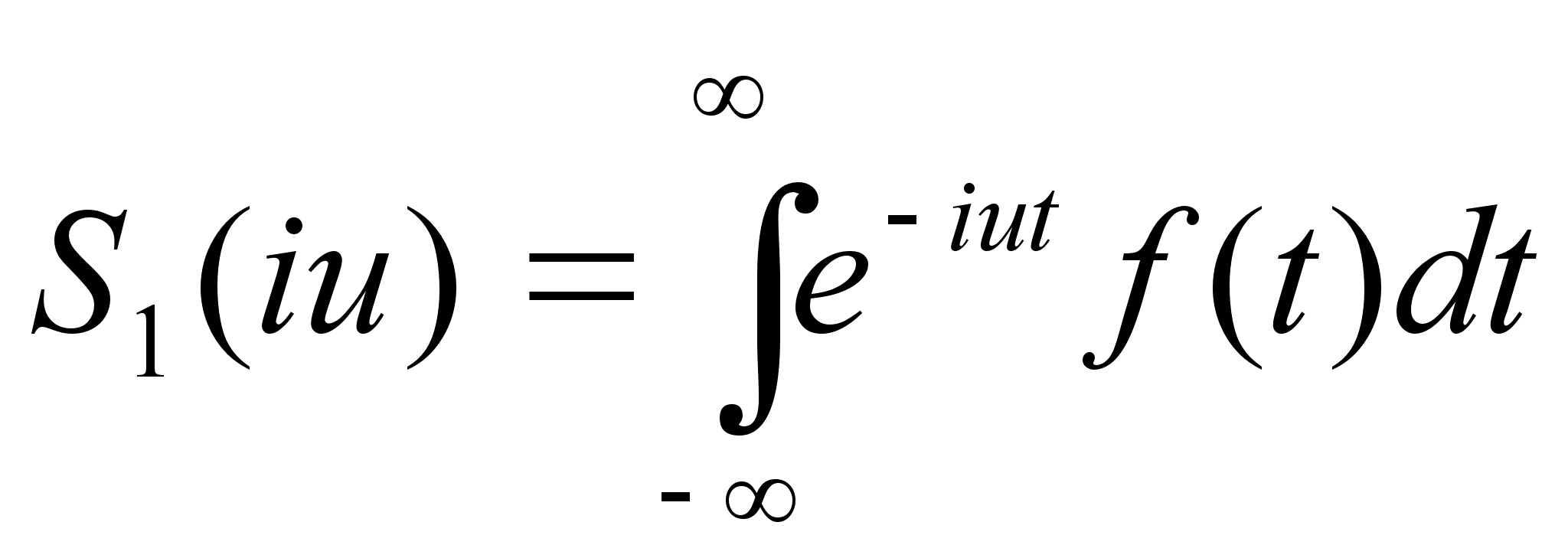 (5)
(5)
и (5) соответственно
односторонние
и двусторонние
преобразования
Фурье.
Для существования
преобразования
Фурье, функция
должна удовлетворять
условиям :
Должна быть
определена
на промежутке
(- ;
) , непрерывна
всюду, за исключением
конечного
числа точек
разрыва первого
рода.
Любой конечный
промежуток
оси t можно
разделить на
конечное число
промежутков,
в каждом из
которых функция
либо кусочно-гладкая,
либо кусочно-монотонная.
Функция абсолютно
интегрируема
:
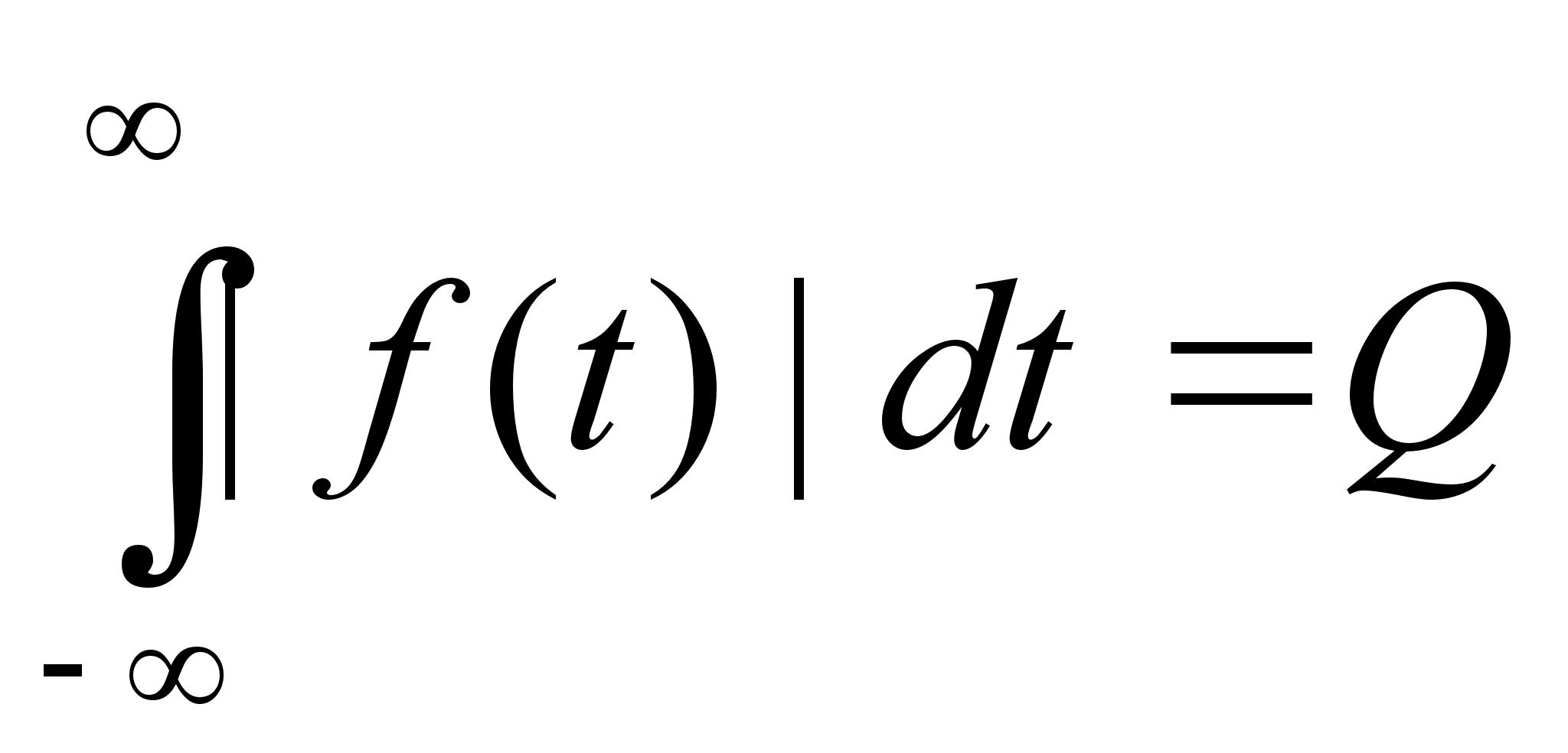 ,
это условие
выполняется,
если |f(t)|S0t
,
это условие
выполняется,
если |f(t)|S0t
Из существования
преобразования
Лапласа не
следует преобразование
Фурье. Преобразования
Фурье существуют
для более узкого
класса функций.
Преобразования
Фурье не существуют
для постоянной
и ограниченной
функции : f(t)
= C
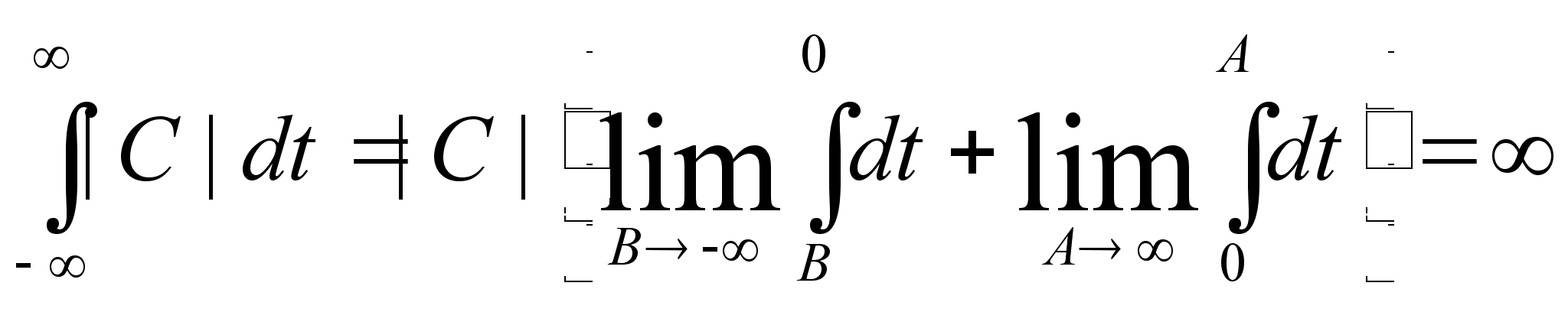
Аналогично
преобразования
Фурье не существуют
и для гармоничных
функций :
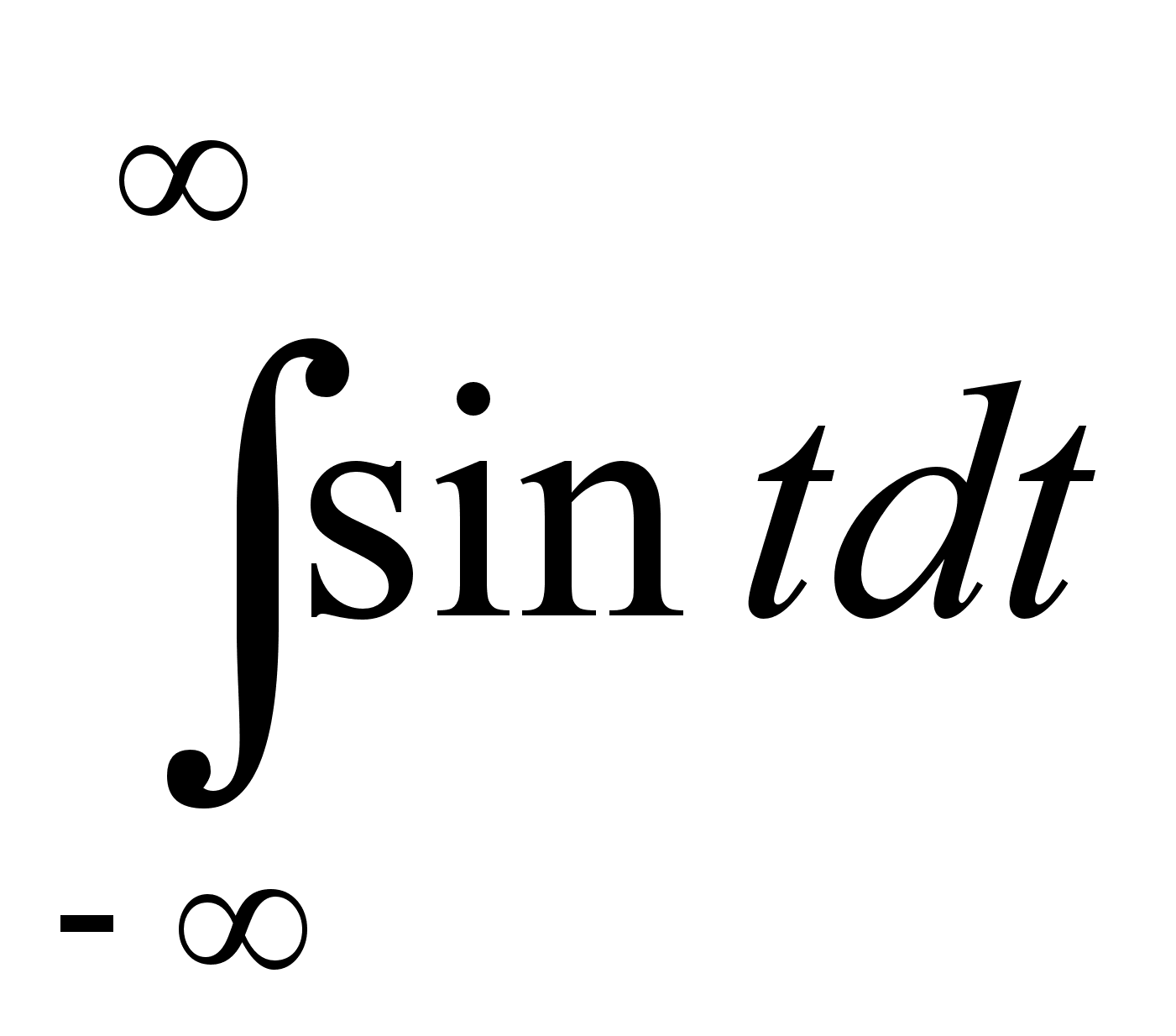 т.к.
т.к.
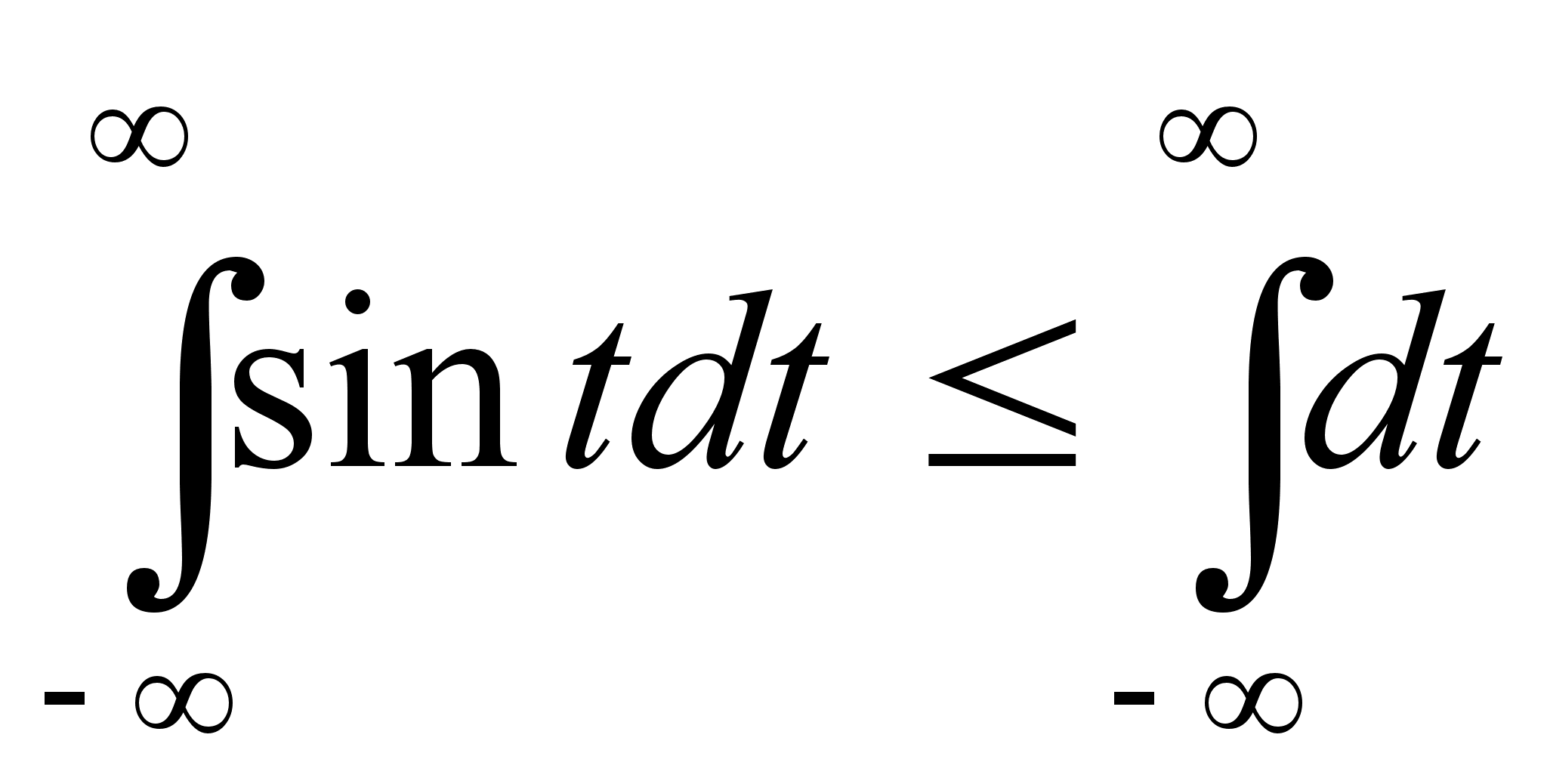
Если f(t)
= 0 при t>0
и преобразование
для этой функции
существует,
то оно может
быть получено
из таблицы
оригиналов
и изображений
для преобразования
Лапласа путем
замены параметра
t на iu,
но при этом
необходимо
убедиться, что
F(p) не
обращается
в число справа
от мнимой оси.
Если f(t)
0, t<0
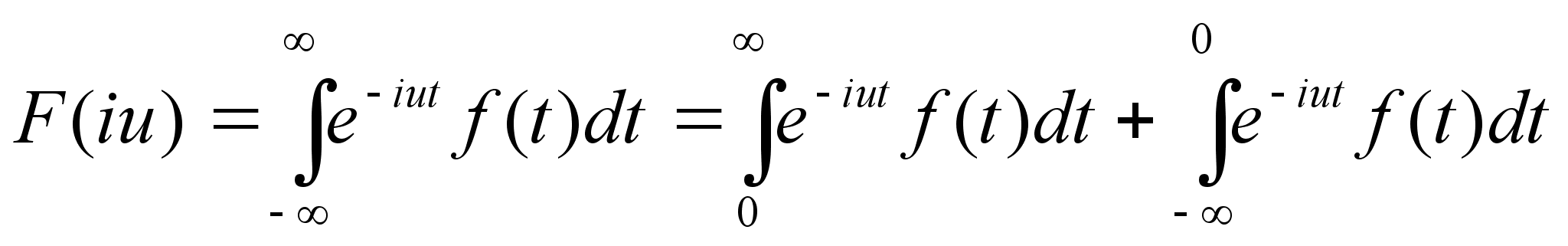 (6)
(6)
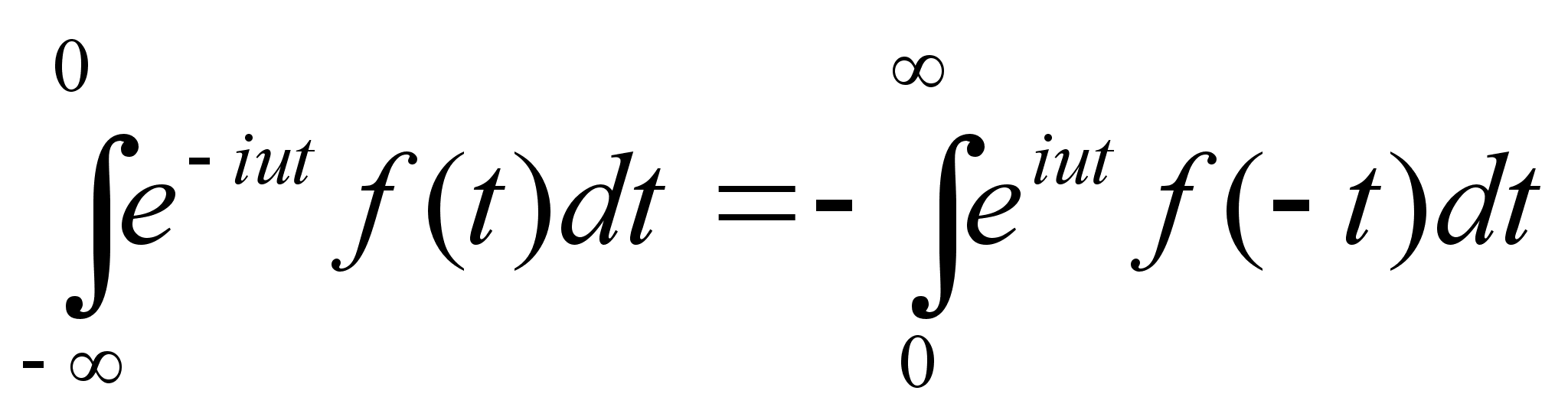
Обозначим
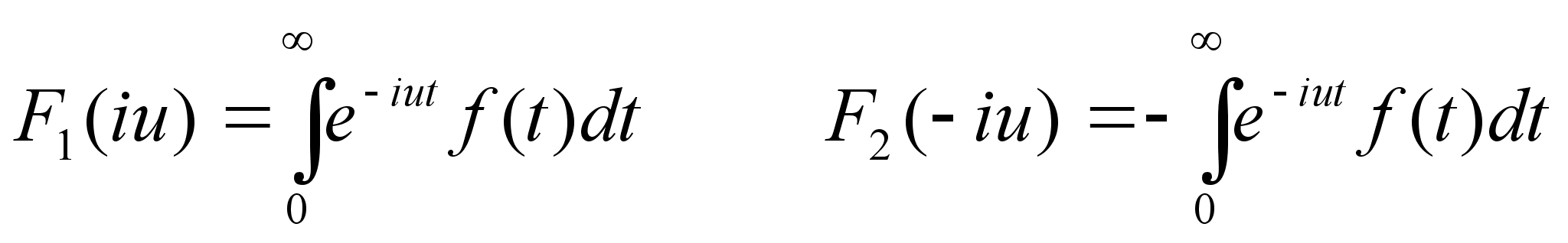
Очевидно, что
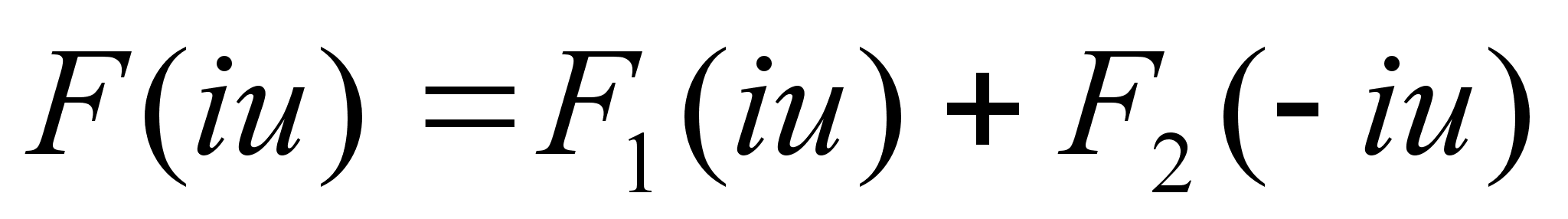 (6’)
(6’)
Функция (6) называется
спектральной
плотностью
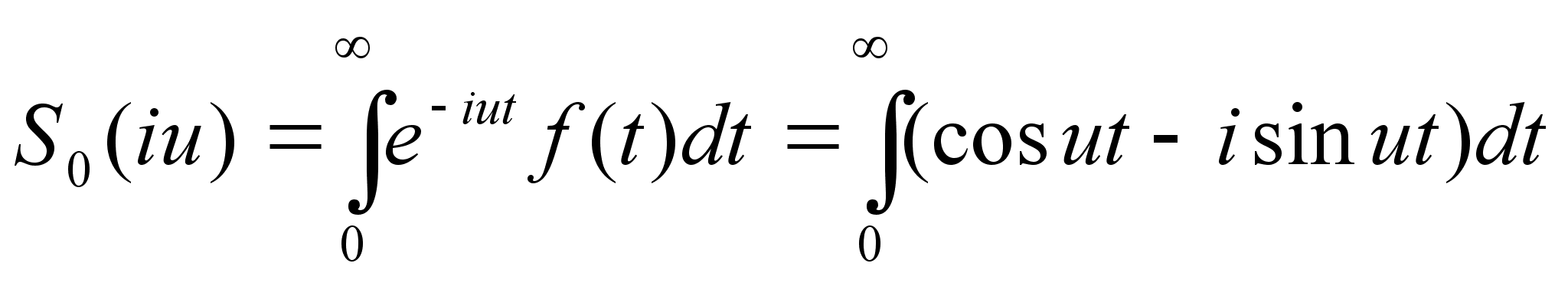
В связи с изложенным
можно указать
два пути отыскания
спектральной
плотности :
Вычисление
интеграла (5)
Использование
преобразования
Лапласа или
Фурье.
Непосредственное
вычисление
спектральной
плотности для
абсолютно
интегрируемой
функции.
Функция F(iu)
может быть
представлена,
как комплексная
функция действительной
переменной
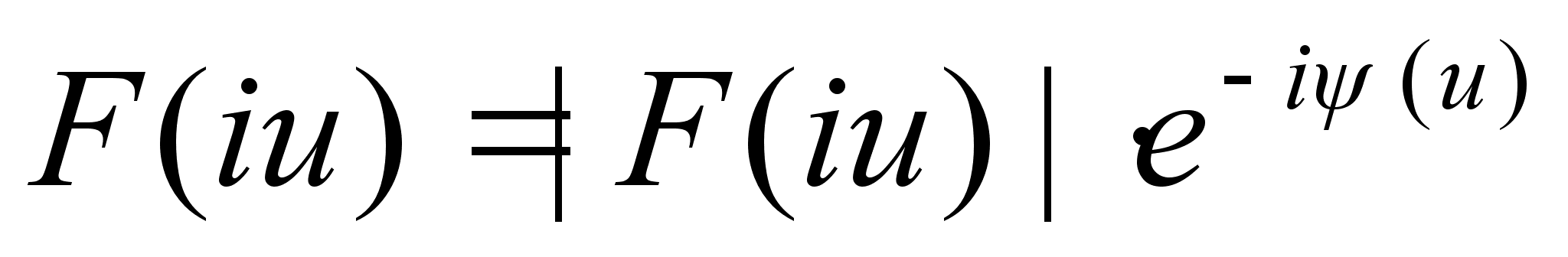 (7)
(7)
|F(iu)| -
амплитудное
значение спектральной
плотности,
(u) – фазовый
угол.
В алгебраической
форме : F(iu) =
a(u) +ib(u)
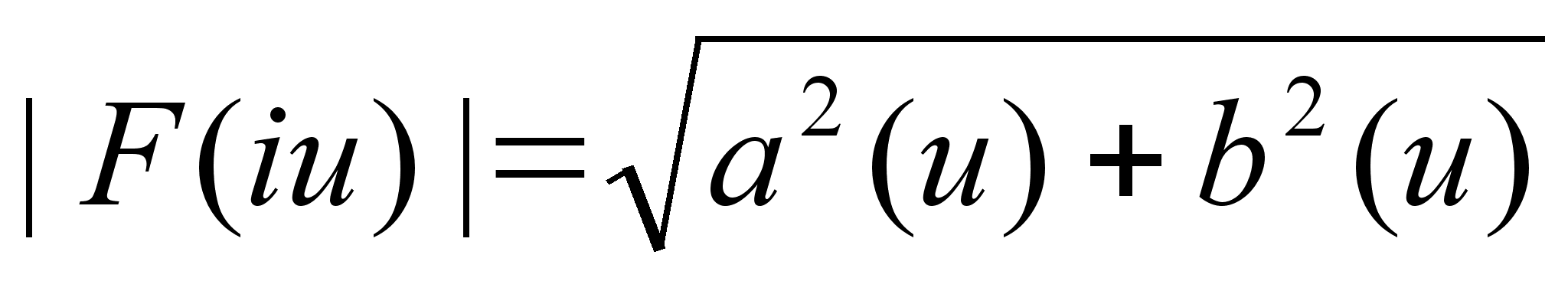 (8)
(8)
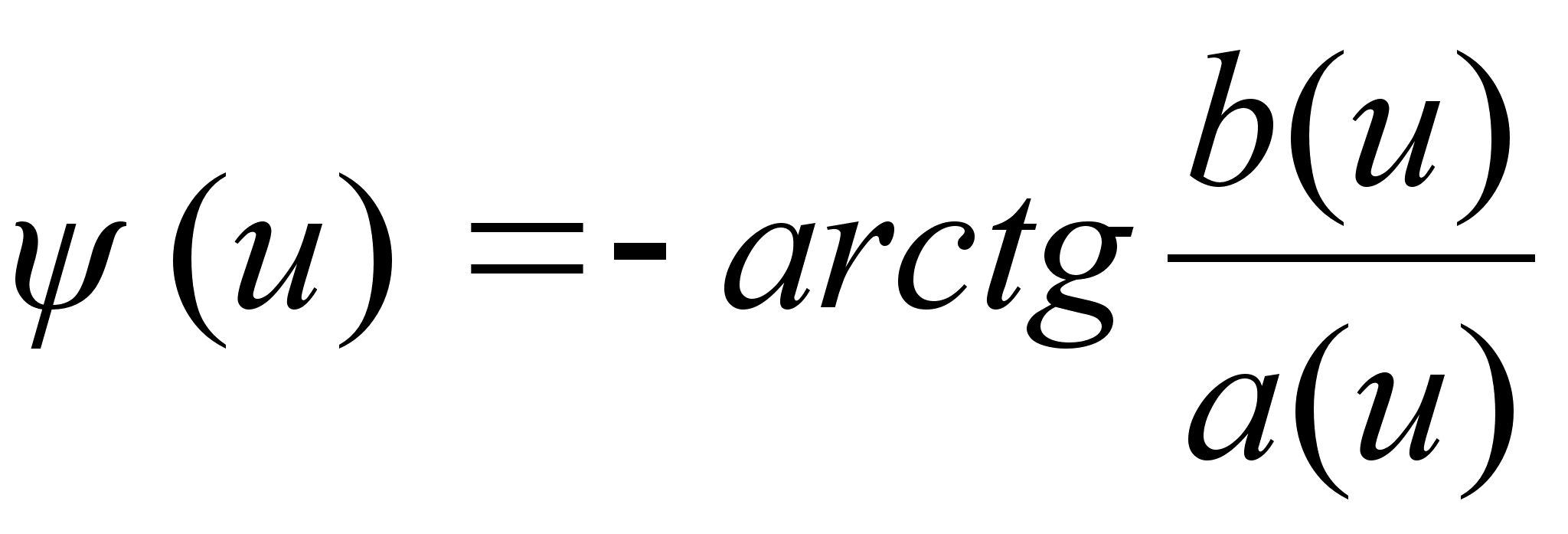 (9)
(9)
Для непосредственного
вычисления
спектральной
плотности
вычисляется
интеграл (6), а
затем по формулам
(8) и (9) определяется
амплитудное
значение |F(iu)|
и фазовый угол
(u).
Пример.
Найти спектральную
плотность
импульса :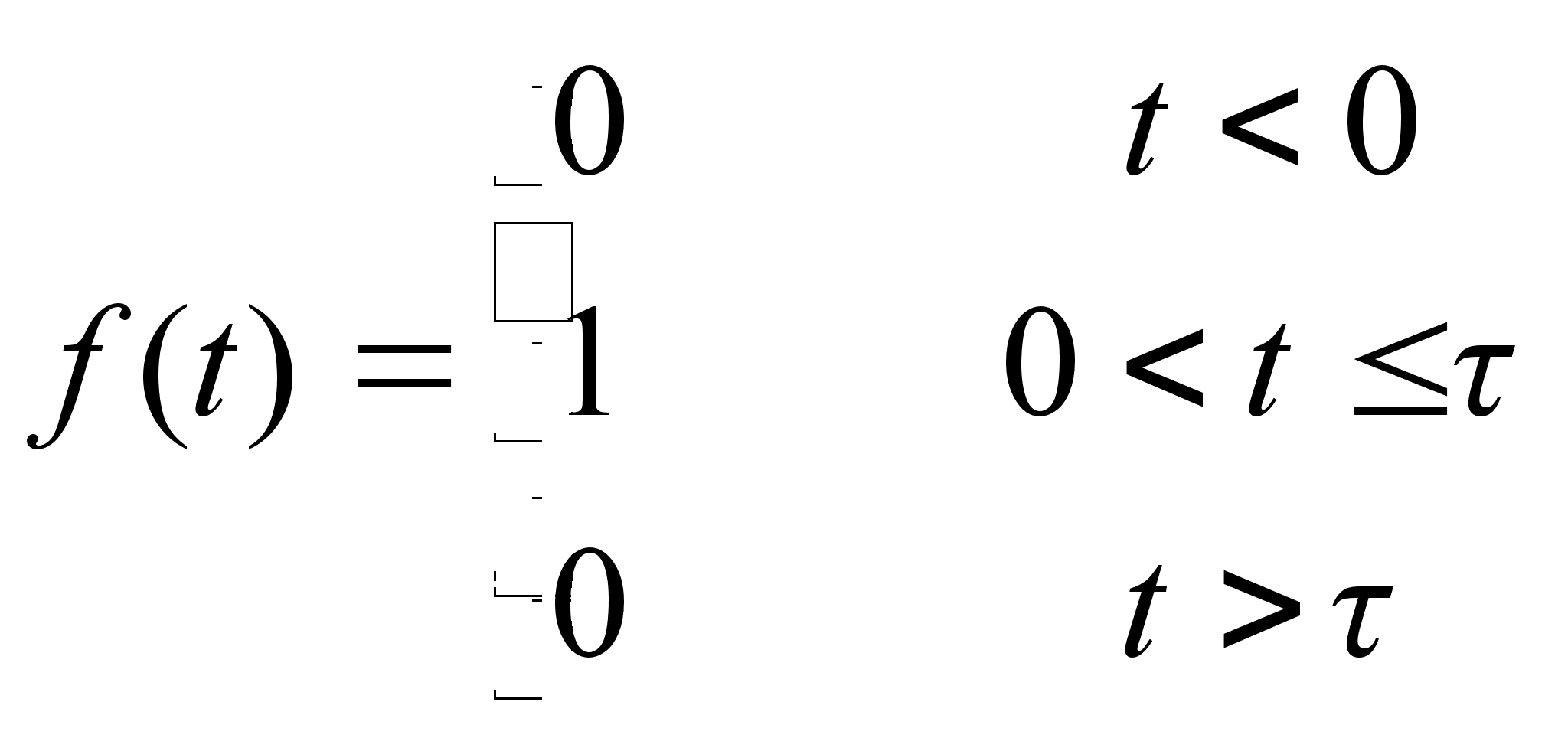
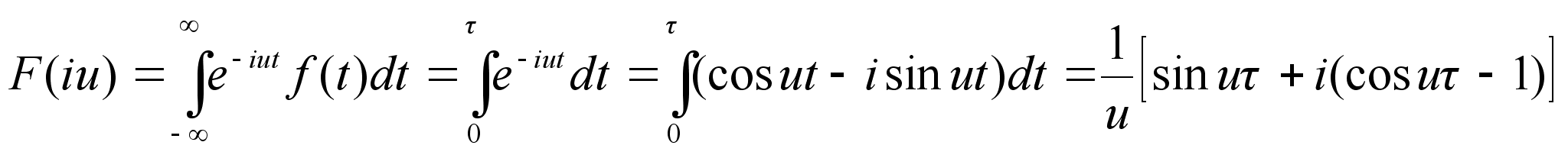
откуда
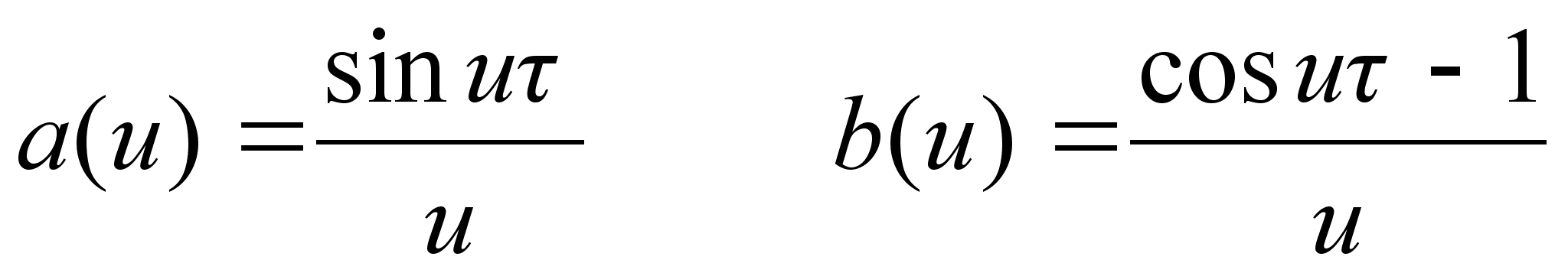 ,
далее
,
далее
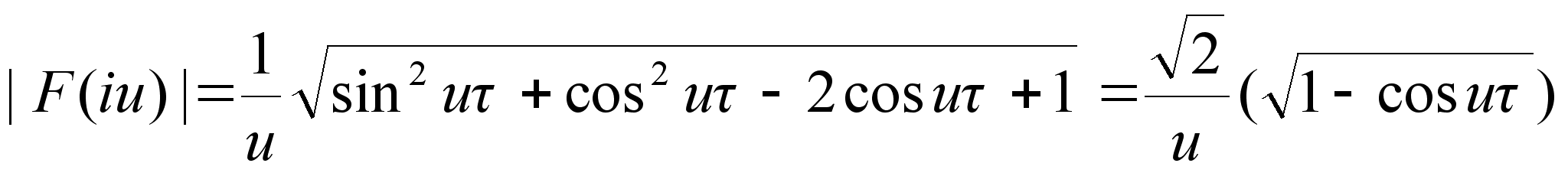
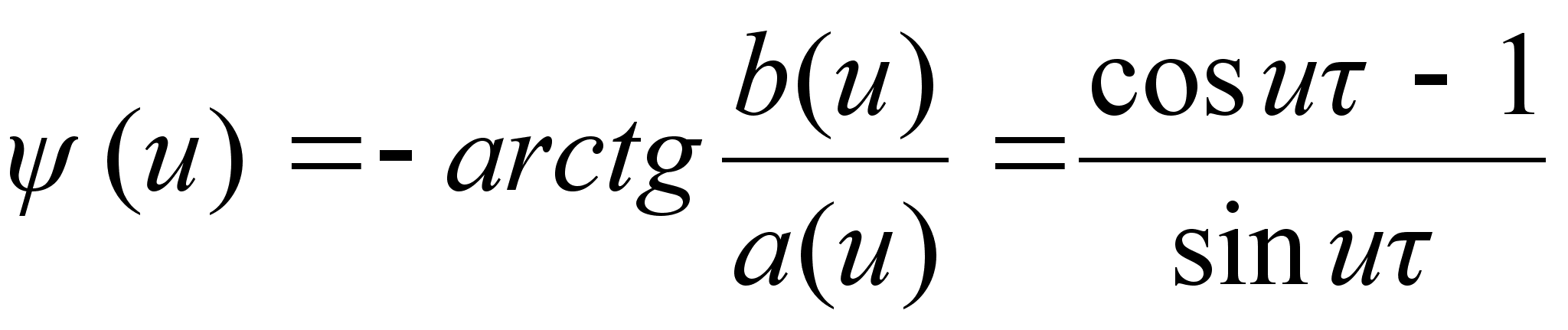
Отыскание
спектральной
плотности для
неабсолютно
интегрируемых
функций.
Прямое преобразование
Фурье для таких
функций не
существует,
существует
преобразование
Лагранжа.
Прямое преобразование
Фурье необходимо
:
Для облегчения
процесса решения
дифференциальных
и интегральных
уравнений.
Для исследования
амплитудной
и частотной
характеристик
спектральной
плотности,
определенной
всюду на числовой
оси.
Введем следующее
определение
спектральной
плотности для
неабсолютно
интегрируемых
функций:
Если для заданной
функции y=f(t)
существует
непрерывное
изображение
по Лапласу
F(p), то
спектральной
плотностью
функции называется
изображение
функции по
Лапласу при
p = iu.
Спектральной
плотностью
F1(iu)
неабсолютно
интегрируемой
функции называется
предел от
спектральной
плотности
F2(iu)
абсолютно
интегрируемой
функции.