ВОЛОГОДСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ
ФИЗИКО-МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ
КАФЕДРА МАТЕМАТИЧЕСКОГО АНАЛИЗА
Курсовая работа на тему:
«Интеграл Лебега»
Выполнила: студентка 3мфА
Сенченко Ю. В.
Проверила: Панфилова Т. Л.
Вологда
2000
Содержание.
1.
Введение.
1.1.Простые функции.
1.2.ИнтегралЛебега от простых функций.
2.
Определение интнгралаЛебега.
3.
Основные свойства интеграла.
4.
Предельный переход под знаком интеграла.
5.
Сравнение интегралов Римана и Лебега.
6.
Примеры.
7.
Литература.
1. Введение
Понятие интеграла Римана, известное из элементарного курса анализа, применимо лишь к таким функциям, которые или непрерывны или имеют «не слишком много» точек разрыва. Для измеримых функций, которые могут быть разрывны всюду, где они определены (или же вообще могут быть заданы на абстрактном множестве, так что для них понятие непрерывности просто не имеет смысла), римановская конструкция интеграла становится непригодной. Вместе с тем для таких функций имеется весьма совершенное и гибкое понятие интеграла, введенное Лебегом.
Основная идея построения интеграла Лебега состоит в том, что здесь, в отличие от интеграла Римана, точки х
группируются не по признаку их близости на оси х,
а по признаку близости значений функции в этих точках. Это сразу же позволяет распространить понятие интеграла на весьма широкий класс функций.
Кроме того, интеграл Лебега определяется совершенно одинаково для функций, заданных на любых пространствах с мерой, в то время как интеграл Римана вводится сначала для функций одного переменного, а затем уже с соответствующими изменениями переносится на случай нескольких переменных. Для функций же на абстрактных пространствах с мерой интеграл Римана вообще не имеет смысла.
Всюду, где не оговорено противное, будет рассматриваться некоторая полная s-аддитивная мера m, определенная на s-алгебре множеств с единицей X.
Все рассматриваемые множества А
ÌХ
будут предполагаться измеримыми, а функции f(
x) -
определенными для x
Î Х и
измеримыми.
1.1. Простые функции.
Определение 1. Функция f(
x),
определенная на некотором пространстве Х
с заданной на нем мерой, называется простой,
если она измерима и принимает не более, чем счетное число значений.
Реклама

Структура простых функций характеризуется следующей теоремой.
Теорема 1.
Функция
f(
x), принимающая не более чем счетное число различных значений
y1
, y2
, … , yn
, … ,
измерима в том и только том случае, если все множества
An
={x :
¦
(x)=yn
}
измеримы.
Доказательство.
Необходимость условия ясна, так как каждое An
есть прообраз одноточечного множества{
yn
},
а всякое одноточечное множество является борелевским. Достаточность следует из того, что в условиях теоремы прообраз f-1
(
B)
любого борелевского множества есть объединение  не более чем счетного числа измеримых множеств An
,
т. е. измерим. не более чем счетного числа измеримых множеств An
,
т. е. измерим.
Использование простых функций в построении интеграла Лебега будет основано на следующей теореме.
Теорема 2.
Для измеримости функции
f(
x) необходимо и достаточно, чтобы она могла быть представлена в виде предела равномерно сходящейся последовательности простых измеримых функций.
Доказательство.
Для доказательства необходимости рассмотрим произвольную измеримую функцию f(
x)
и положим fn
(х)=
m/п,
если т/п f(
x)
<(
m+1)/
n
(здесь т -
целые, а п -
целые положительные). Ясно, что функции fn
(
x)
простые; при п
®
f(
x)
<(
m+1)/
n
(здесь т -
целые, а п -
целые положительные). Ясно, что функции fn
(
x)
простые; при п
® они равномерно сходятся к f(
x),
так как çf(
x)-
fn
(
x)
ç£1/
n.
они равномерно сходятся к f(
x),
так как çf(
x)-
fn
(
x)
ç£1/
n.
1.2.Интеграл Лебега для простых функций.
Мы введем понятие интеграла Лебега сначала для функций, названных выше простыми, т. е. для измеримых функций, принимающих конечное или счетное число значений.
Пусть f—
некоторая простая функция, принимающая значения
y1
, y2
, … , yn
, … ; yi yj
при i
yj
при i j
, j
,
и пусть А —
некоторое измеримое подмножество X.
Естественно определить интеграл от функции f
по множеству А
равенством
 = = , где An
={
x:
x , где An
={
x:
x A,
f(
x)=
yn
},
(1) если ряд справа сходится. Мы приходим к следующему определению (в котором по понятным причинам заранее постулируется абсолютная сходимость ряда). A,
f(
x)=
yn
},
(1) если ряд справа сходится. Мы приходим к следующему определению (в котором по понятным причинам заранее постулируется абсолютная сходимость ряда).
Определение 2. Простая функция f
называется интегрируемой
или суммируемой
(по мере m) на множестве A, если ряд (1) абсолютно сходится. Если f
интегрируема, то сумма ряда (1) называется интегралом
от f
по множеству А.
В этом определении предполагается, что все у
n
различны. Можно, однако, представить значение интеграла от простой функции в виде суммы произведений вида ck
m(Bk
) и не предполагая, что все ck
различны. Это позволяет сделать следующая лемма.
Реклама

Лемма
. Пусть А=
 ,
Bi ,
Bi
 Bj
=
Æ при
i
Bj
=
Æ при
i j и пусть на каждом множестве
Bk
функция f принимает только одно значение c
k
; тогда j и пусть на каждом множестве
Bk
функция f принимает только одно значение c
k
; тогда
 = =
 ,
(2) причем функция f интегрируема на А в том и только том случае, когда ряд (2) абсолютно сходится. ,
(2) причем функция f интегрируема на А в том и только том случае, когда ряд (2) абсолютно сходится.
Доказательство
. Легко видеть, что каждое множество
А
n
={х: х
ÎА,
f(
x)=
yn
}
является объединением тех Bk
, для которых с
k
=
yn
.
Поэтому
 = =

 = =
 . .
Так как мера неотрицательна, то
 =
=
 =
=
 ,
,
т. е. ряды  и и  абсолютно сходятся или расходятся одновременно. Лемма доказана. абсолютно сходятся или расходятся одновременно. Лемма доказана.
Установим некоторые свойства интеграла Лебега от простых функций
A)  = = + + , ,
причем из существования интегралов в правой части равенства следует существование интеграла в левой.
Для доказательства предположим, что f
принимает значения fi
на множествах Fi
Ì
A,
ag —
значения gj
на множествах Gj
ÌA, так что
J1
=
 = =
 ,
(3) ,
(3)
J2
=
 = =
 .
(4) .
(4)
Тогда в силу леммы
J=
 = =
 ;
(5)
;
(5)
так что из абсолютной сходимости рядов (3) и (4) следует и абсолютная сходимость ряда (5); при этом
J=J1
+J2
.
Б) Для любого постоянного
k
 =
k
=
k
 ,
,
причем из существования интеграла в правой части следует существование интеграла в левой части.
(Проверяется непосредственно.)
В) Ограниченная на множестве А простая функция
f интегрируема на А, причем, если
½f(
x)
½£
M на
A
, то
½ ½£M
m
(A). ½£M
m
(A).
(Проверяется непосредственно.)
2. Определение интеграла Лебега
Классическое определение интеграла, данное О. Коши и развитое Б. Риманом, состоит, как известно, в следующем: рассматривается конечная функция f(
x),
заданная на сегменте [
a,
b]
; этот сегмент разбивается на части точками
x0
= a
<
x1
<
x2
<
¼
<
xn
= b
в
каждой части [
xk
,
xk
+1
]
выбирается точка x
k
и составляется риманова сумма
s =
 . .
Если сумма s при стремлении к нулю числа
l
= max(xk+1
– xk
).
стремится к конечному пределу I
, не зависящему ни от способа дробления [
a,
b]
, ни от выбора точек x
k
,
то этот предел I
называется интегралом Римана функции f(
x)
и обозначается символом
 . .
Иногда, желая подчеркнуть, что речь идет именно о римановом интеграле, пишут
(
R) . .
Функции, для которых интеграл Римана существует, называются интегрируемыми в смысле Римана или, короче, интегрируемыми (
R).
Для интегрируемости (R)
функции f(
x)
необходимо, чтобы она была ограниченной.
Еще Коши установил, что всякая непрерывная функция интегрируема (R).
Существуют также и разрывные функции, интегрируемые (R).
В частности, такова любая разрывная монотонная функция.
Легко построить, однако, ограниченную функцию, которая не будет интегрируемой (R).
Рассмотрим, например, функцию Дирихле  ,
которая определяется на сегменте [0, 1]
следующим образом ,
которая определяется на сегменте [0, 1]
следующим образом
 1, если
x рационально, 1, если
x рационально,
y(
x) =
0, если
x иррационально.
Легко видеть, что эта функция не интегрируема (R),
ибо сумма s
обращается в 0, если все точки x иррациональны и s = 1, если все
иррациональны и s = 1, если все  рациональны. рациональны.
Таким образом, риманово определение интеграла страдает существенными недостатками - даже очень простые функции оказываются неинтегрируемыми.
Нетрудно разобраться в причинах этого обстоятельства.
Дело заключается в следующем: при составлении сумм Римана s
, мы дробим сегмент [
a,
b]
на мелкие части [
x0
,
x1
], [
x1
,
x2
],
¼ ,[
xn
-1
,
xn
]
(назовем их через e0
,
e1
,
¼ ,
en
-1
), в каждой части ek
берем точку x
k
и, составив сумму
s =  , ,
требуем, чтобы она имела предел, не зависящий от выбора точек x
k
в множествах е
k
.
Иначе говоря, каждая точка х
из множества е
k
может быть взята за x
k
, а варьирование этой точки не должно заметно влиять на значение суммы s
. А это возможно лишь в том случае, когда варьирование точки x
k
мало изменяет величину f(
x
k
)
. Но что же объединяет между собой различные точки х
множества ek
? Их объединяет то, что они близки друг другу, ибо е
k
есть малый сегмент [
xk
,
xk
+1
].
Если функция f(
x)
непрерывна, то достаточная близость абсцисс х
влечет за собой и близость соответствующих значений функции и мы вправе ждать, что изменение точки x
k
в пределах множества ek
мало влияет на величину суммы s
, но для функция разрывной это вовсе не так.
Иначе можно сказать, что множества ek
составлены так, что только для непрерывных функций значение f(
x
k
)
можно считать нормальным представителем других значений функции на ek
.
Таким образом, самое определение риманова интеграла можно считать вполне оправданным лишь для функций непрерывных, для прочих же функций оно выглядит довольно случайным. Ниже мы убедимся, что для интегрируемости (
R)
необходимо, чтобы рассматриваемая функция не была «слишком разрывной».
Желая обобщить понятие интеграла на более широкие классы функций, Лебег предложил другой процесс интегрирования, в котором точки x
объединяются в множества ek
не по случайному признаку своей близости на оси Ох,
а по признаку достаточной близости соответствующих значений функции. С этой целью Лебег разбивает на части не сегмент [
a,
b],
расположенный на оси абсцисс, а сегмент [А, В],
лежащий на оси ординат и включающий все значения функции f(
x)
:
A = yo
<
y1
<
¼
<
yn
= B
Если составить множества ek
так:
ek
= E(yk
£
f
<
yk+1
),
то ясно, что различный точкам х
Î е
k
и в самом деле отвечают близкие значения функции, хотя, в отличие от римановского процесса, сами точки x
могут быть весьма далеки друг от друга.
В частности, хорошим представителем значений функции на множестве ek
может служить, например, yk
,
так что естественно положить в основу понятия интеграла сумму
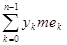 . .
Перейдем теперь к точному изложению вопроса.
Пусть на измеримом множестве E
задана измеримая ограниченная функция f(
x),
причем
A<f(x)<B.
(1)
Разобьем сегмент [А, В]
на части точками
yo
= A
<
y1
<
y2
<
¼
<
yn
= B
и соотнесем каждому полусегменту [у
k
, у
k+1
)
множество
ek
= E(yk
£
f
<
yk+1
)
Легко проверить четыре свойства множеств ek
:
1) Множества ek
попарно не пересекаются: ek
ek
¢
= 0 (
k
¹
k').
2) Эти множества измеримы.
3) E =
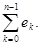
4) тЕ
= 
Введем теперь нижнюю и верхнюю суммы Лебега
s
и S
:
S = 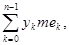 S = S = 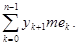
Если мы положим
l
= max (yk+1
– yk
),
то будем иметь
0
£
S –
s
£
l
mE.
(2)
Основное свойство сумм Лебега выражает
Лемма.
Пусть некоторому способу дробления сегмента [А, В] отвечают суммы Лебега
s0
и
S0
. Если ми добавим новую точку дробления 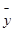 и снова найдем суммы Лебега
s и
S, то окажется и снова найдем суммы Лебега
s и
S, то окажется
s0
£
s, S
£
S0
.
Иначе говоря, от добавления новых точек деления нижняя сумма не уменьшается, а верхняя не увеличивается.
Доказательство.
Допустим, что
yi
<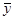 <
yi
+1
.
(3)
<
yi
+1
.
(3)
Тогда при k
¹
i
полусегменты [
yk
, у
k+1
),
а с ними и множества ek
,
фигурируют и в новом способе дробления. Полусегмент же [
yi
,
yi
+1
)
при переходе к новому способу заменяется двумя полусегментами
[
yi
,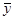 ), [ ), [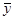 ,
yi
+1
), ,
yi
+1
),
в связи с чем и множество ei
разбивается на два множества
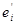 = E(yi
£
f
<
= E(yi
£
f
<
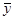 ), ), 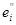 = E( = E(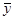 £
f
<
yi+1
).
£
f
<
yi+1
).
Очевидно, что
ei
=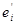 + +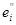 , , 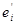 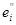 = 0, = 0,
так что
mei
=
m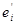 +
m +
m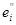 .
(4) .
(4)
Из сказанного ясно, что сумма s
получается из суммы s0
заменой слагаемого yi
mei
двумя слагаемымиyi
m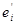 + + 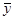 m
m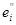 ,
откуда, в связи с (3) и с (4), и следует, что s
³
s0
. ,
откуда, в связи с (3) и с (4), и следует, что s
³
s0
.
Для верхних сумм рассуждение аналогично.
Следствие.
Ни одна нижняя сумма
s не больше ни одной верхней суммы
S.
Доказательство.
Рассмотрим два каких-нибудь способа дробления I и II, сегмента [А, В].
Пусть этим способам отвечают соответственно нижние суммы s1
и s2
и верхние суммы S1
и S2
.
Составим третий способ дробления [А, В] -
способ III, в котором точками деления служат точки деления обоих способов I и II. Если способу III отвечают суммы s3
иS3
, то, в силу леммы, s1
£
s3
,
S3
£
S2
,
откуда, в связи с тем, что s3
£
S3
, ясно, что s1
£
S2
, а это и требовалось доказать.
Выберем какую-нибудь определенную верхнюю сумму S0
. Так как для всякой нижней суммы s
будет s
£
S0
, то множество {
s}
всех нижних сумм Лебега оказывается ограниченный сверху. Пусть U
есть его точная верхняя граница U
= sup{
s}.
Тогда, ясно, что
U
£
S0
.
Ввиду произвольности суммы S0
, последнее неравенство доказывает, что множество {
S}
всех верхних сумм Лебега ограничено снизу. Назовем через V
его точную нижнюю границу
V =
inf{
S}.
Очевидно, при любом способе дробления будет
S
£
U
£
V
£
S.
Но, как мы отмечали, S –
s
£
l
mE
, откуда
0
£
V –
U
£
l
mE
и, так как l
произвольно мало, то
U =
V.
Определение.
Общее значение чисел U
и V
называется интегралом Лебега
функции f(
x)
по множеству Е
и обозначается символом
(
L)
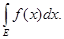
В тех случаях, когда смешение с другими видами интеграла исключено, пишут просто
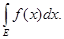
В частности, если Е
есть сегмент [а,
b],
употребляют символы
(
L)
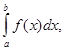
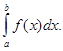
Из сказанного выше следует, что каждая измеримая ограниченная функция интегрируема в смысле Лебега,
или, короче, интегрируема (
L)
. Уже из этого замечания видно, что процесс интегрирования (
L)
приложим к гораздо более широкому классу функций, чем процесс интегрирования (
R).
В частности, совершенно отпадают все вопросы, связанные с признаками интегрируемости, которые для интегралов (
R)
имеют сравнительно сложный характер.
Теорема 1.
Если
l
® 0
, то суммы Лебега
s и
S стремятся
к интегралу
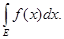
Теорема непосредственно вытекает из неравенств
S
£
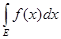 £
S, S – s
£
l
×
mE.
£
S, S – s
£
l
×
mE.
Из этой теоремы, между прочим, следует, что значение интеграла Лебега, которое в силу самого определения его связано с числами А
и В,
насамом деле от них не зависит.
Действительно, допустим, что
A <
f(
x) < В,
A <
f(
x) <
B*,
причем В* < В.
Раздробим сегмент [А, В]
на части
A = у0
< у1
<
¼ <
yn
= В,
причем включим и точку В*
в число точек деления В* = ут
.
Если мы составим множества ek
,
то легко убедиться, что
ek
= 0
(k
³
m).
Значит,
s = 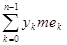 = = 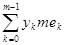 = s*, = s*,
где s*
есть нижняя сумма Лебега, построенная, исходя из сегмента [А, В*].
Сгущая точки дробления и переходя к пределу, найдем, что
I =
I*,
где I
и I*
суть значения интегралов Лебега, отвечающие сегментам [А, В]
и [А, В*].
Таким образом, изменение числа В
не отражается на величине интеграла. То же относится и к числу А.
Этот факт весьма существенен, ибо только теперь определение интеграла оказывается освобожденным от случайного характера выбора точек А
и В.
3. Основные свойства интеграла
В этом параграфе мы установим ряд свойств интеграла от ограниченной измеримой функции.
Теорема 1.
Если измеримая функция
f(
x)
на измеримом множестве Е удовлетворяет неравенствам
a
£
f(
x)
£
b,
то
a
×
mE
£
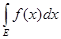 £
b
×
mE.
£
b
×
mE.
Это теорема обычно называется теоремой о среднем.
Доказательство.
Пусть n
натуральное число. Если мы положим
A =
a -
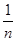 ,
B =
b + ,
B =
b +
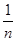 , ,
то окажется, что
A
<
f(
x)
<
B,
и суммы Лебега можно будет составлять, дробя сегмент [А, В].
Но еслиA
£
yk
£
B
, то, очевидно,
A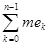 £
£
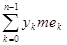 £
B
£
B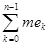
или, что то же самое,
A
×
mE
£
s
£
B
×
mE,
откуда и в пределе
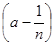 mE
£
mE
£
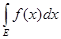 £
£
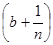 mE.
mE.
В силу произвольности числа n
, теорема доказана.
Из этой теоремы вытекает несколько простых следствий.
Следствие 1.
Если функция
f(
x) постоянна на измеримом множестве Е и
f(
x)
= с, то
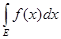 =
c
×
mE. =
c
×
mE.
Следствие 2.
Если функция
f(
x) не отрицательна (не положительна), то таков же и ее интеграл.
Следствие 3.
Если тЕ =
0
, то для любой ограниченной функции
f(
x), заданной на множестве Е, будет
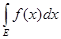 = 0. = 0.
Теорема 2.
Пусть на измеримом множестве Е задана измеримая ограниченная функция
f(
x). Если множество Е есть сумма конечного числа или счетного множества попарно не пересекающихся измеримых множеств
E =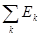 (Ek
(Ek
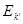 = 0, k
¹
k’
), = 0, k
¹
k’
),
то
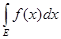 = =
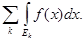
Свойство интеграла, выражаемое этой теоремой, называется его полной аддитивностью.
Доказательство.
Рассмотрим сначала простейший случай, когда число слагаемых равно двум
Е = 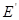 + +
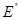 ( (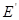
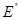 = 0). = 0).
Если на множестве Е
A < f(x) < B
и мы, раздробив сегмент [А, В]
точками у0
,
y1
,
¼
, у
n
,
составим множества
ek
= E(yk
£
f
<
yk+1
),
ek
’
= E’(yk
£
f
<
yk+1
),
ek
’’
= E’’(yk
£
f
<
yk+1
),
то, очевидно, будем иметь
ek
= ek
’
+ ek
’’
(ek
’
ek
’’
= 0),
откуда
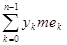 = =
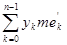 + +
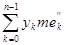
н в пределе, приl
® 0
,
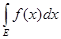 = = 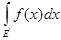 + + 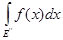
Итак, теорема доказана для случая двух слагаемых множеств. Пользуясь методом математической индукции, мы легко распространим теорему на случай любого конечного числа слагаемых множеств.
Остается рассмотреть случай, когда
E =
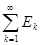 . .
В этом случае
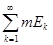 =
mE, =
mE,
так что при n
®
¥
будет
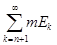 ® 0.
(*) ® 0.
(*)
Заметив это, положим
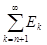 =
Rn
. =
Rn
.
Так как для конечного числа слагаемых множеств теорема уже доказана, то
 = =
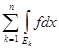 + +
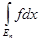 . .
В силу теоремы о среднем
A
×
mRn
£
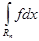 £
B
×
mRn
,
£
B
×
mRn
,
а в силу (*) мера mRn
множества Rn
стремится к нулю с возрастанием n
, откуда ясно, что
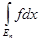 ® 0. ® 0.
Но это и означает, что
 = =
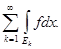
Из этой теоремы вытекает ряд следствий.
Следствие 1.
Если измеримые ограниченные функции
f(
x) и
g(
x), заданные на множестве Е, эквивалентны между собой, то
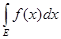 = =
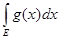 . .
Действительно, если
А = Е(
f
¹
g),
B =
E(
f =
g)
,
то mA = 0
и
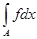 = =
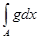 = 0. = 0.
На множестве же В
обе функции тождественны и
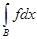 = =
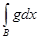 . .
Остается сложить это равенство с предыдущим.
В частности, интеграл от функции, эквивалентной нулю, равен нулю.
Само собою разумеется, что последнее утверждение необратимо. Например, если f(
x)
задана на сегменте [-1, +1]
, так:
 1 при
x
³ 0, 1 при
x
³ 0,
f(
x) =
-1 при
x
< 0,
то
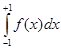 = =
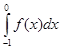 + +
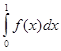 = -1 + 1 = 0, = -1 + 1 = 0,
хотя функция f(
x)
и не эквивалентна нулю.
Однако справедливо
Следствие 2.
Если интеграл от неотрицательной измеримой ограниченной функции
f(
x) равен нулю
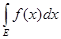 (
f(
x)
³ 0), (
f(
x)
³ 0),
то эта функция эквивалентна нулю.
В самом деле, легко видеть, что
E(
f
>0) =
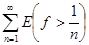 . .
Если бы f(
x)
не была эквивалентна нулю, то необходимо нашлось бы такое n0
, что
mE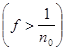 =
s
>
0. =
s
>
0.
Полагая
A = E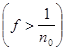 , B = B - A, , B = B - A,
мы имели бы, что
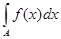 ³
³
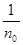 s, s,
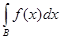 ³ 0,
³ 0,
и, складывая эти неравенства, мы получили бы
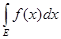 ³
³
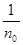 s, s,
что противоречит условию.
Теорема 3.
Если на измеримом множестве
Q заданы две измеримые ограниченные функции
f(
x) и
F(
x), то
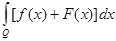 = =
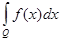 + +
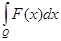 . .
Теорема 4.
Если на измеримом множестве Е задана измеримая ограниченная функция
f(
x)
и с есть конечная постоянная, то
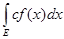 =
c =
c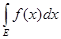 . .
Следствие.
Если
f(
x) и
F(х) измеримы и ограничены на множестве Е, то
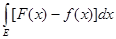 = =
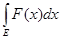 - -
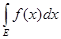 . .
Теорема 5.
Пусть
f(
x) и
F(х) измеримы и ограничены на измеримом множестве Е. Если
f(x)
£
F(x),
то
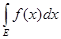 £
£
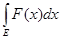 . .
Действительно, функция F(
x)—
f(
x)
не отрицательна, так что
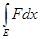 - -
 = =
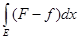 ³ 0. ³ 0.
Теорема 6.
Если функция
f(
x) измерима и ограничена на измеримом множестве
E, то
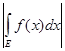 £ £
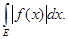
4. Предельный переход под знаком интеграла
Здесь мы рассмотрим следующий вопрос: пусть на измеримом множестве E
задана последовательность измеримых ограниченных функций
f1
(x), f2
(x), f3
(x),
¼
, fn
(x),
¼
которая в каком-нибудь смысле (везде, почти везде, по мере) сходится к измеримой ограниченной функции F(
x).
Спрашивается, будет ли справедливо соотношение
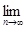
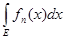 = =
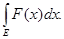 (1)
(1)
Если (1) верно, то говорят, что допустим предельный переход под знаком интеграла.
Легко видеть, что, вообще говоря, это не так. Например, если функции fn
(
x)
определены в сегменте [0, 1]
следующим образом:
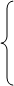 n при
x
Î n при
x
Î
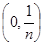 , ,
fn
(
x) =
0 при
x
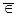
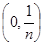 , ,
то при всяком x
Î [0, 1]
будет
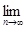 fn
(
x) = 0,
но fn
(
x) = 0,
но 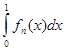 = 1, = 1,
и этот интеграл не стремится к нулю.
Поэтому естественно поставить вопрос о тех дополнительных ограничениях, которые нужно наложить на функцию fn
(
x),
чтобы равенство (1) все же имело место.
Мы ограничимся доказательством следующей теоремы.
Теорема (А. Лебег).
Пусть на измеримом множестве Е задана последовательность
f1
(
x),
f2
(
x),
f3
(
x),
¼ измеримых ограниченных функций, сходящаяся по мере к измеримой ограниченной функции
F(х)
fn
(x)
Þ
F(x).
Если существует постоянная К, такая, что при всех п и лри всех х
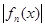 <
K, <
K,
то
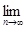
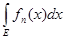 = =
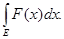 (1)
(1)
Доказательство.
Прежде всего заметим, что почти для всех х
Î
Е
будет
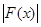 £
K.
(2) £
K.
(2)
В самом деле, из последовательности {
fn
(
x)}
можно (на основании теоремы Рисса) извлечь частичную последовательность {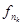 (
x)},
которая сходится к F(
x)
почти везде. Во всех точках, где (
x)},
которая сходится к F(
x)
почти везде. Во всех точках, где
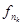 (x)
®
F(x),
(x)
®
F(x),
можно перейти к пределу в неравенстве 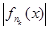 <
K,
что и приводит к (2). <
K,
что и приводит к (2).
Пусть теперь s
есть положительное число. Положим,
An
(
s) =
E(
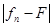 )
³
s),
Bn
(
s) =
E( )
³
s),
Bn
(
s) =
E(
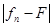 )
<
s. )
<
s.
Тогда
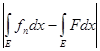 £ £
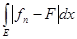 = =
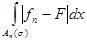 + +
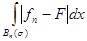 . .
В силу неравенства 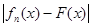 £ £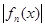 + + 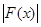 ,
почтидля всех х
из множества An
(
s)
будет ,
почтидля всех х
из множества An
(
s)
будет
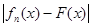 < 2
K, < 2
K,
так что по теореме о среднем
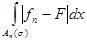 £ 2
K
×
mAn
(
s)
(3)
£ 2
K
×
mAn
(
s)
(3)
(то обстоятельство, что неравенство 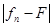 <
2К
может не выполняться на множестве меры 0, несущественно. Можно, например, функцию <
2К
может не выполняться на множестве меры 0, несущественно. Можно, например, функцию 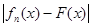 на этом множестве изменить, сделав ее равной нулю; тогда неравенство (3) будет выполняться во всех точках А.
Но так как изменение функции на множестве меры 0 не влияет на величину интеграла, то (3) верно и без такого изменения). на этом множестве изменить, сделав ее равной нулю; тогда неравенство (3) будет выполняться во всех точках А.
Но так как изменение функции на множестве меры 0 не влияет на величину интеграла, то (3) верно и без такого изменения).
С другой стороны, опять-таки в силу теоремы о среднем,
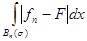 £
s
mBn
(
s)
£
s
mE.
£
s
mBn
(
s)
£
s
mE.
Сопоставляя это с (3), находим, что
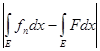 £
2K
×
mAn
(
s
) +
s
mE.
(4) £
2K
×
mAn
(
s
) +
s
mE.
(4)
Заметив это, возьмем произвольное e > 0
и найдем столь малое s> 0
, что
s
×
mE
<
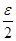 . .
Фиксировав это s
, мы, на основании самого определения сходимости по мере, будем иметь, что при n
®
¥
mAn
(
s)
® 0
и, стало быть, для n > N
окажется
2
K
×
mAn
(
s)
<
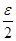 . .
Для этих n
неравенство (4) примет вид
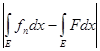 <
e, <
e,
что и доказывает теорему.
Легко понять, что теорема остается верной и в том случае, когда неравенство
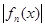 <
K <
K
выполняется только почти везде на множестве Е.
Доказательство остается прежним.
Далее, поскольку сходимость по мере общее обычной сходимости, то теорема и подавно сохраняет силу для того случая, когда
fn
(x)
®
F(x)
почти везде (и тем более везде).
5. Сравнение интегралов Римана и Лебега
Пусть на сегменте [а,
b]
задана (не обязательно конечная) функция f(х).
Пусть
x0
Î
[
a,
b]
и d > 0
. Обозначим через m
d
(
x0
)
и М
d
(х0
)
соответственно точную нижнюю и точную верхнюю границы функции f(
x)
наинтервале (х0
-
d
, x0
+
d
)
m
d
(
x0
) =
inf{
f(
x)},
M
d
(
x0
) =
sup{
f(
x)} (х0
-
d
<
x
<
x0
+
d
).
(Само собою разумеется, что мы принимаем во внимание лишь те точки интервала
(х0
-
d
, x0
+
d
), которые лежат также и на сегменте [а,
b].
)
Очевидно,
m
d
(
x0
)
£
f(
x0
)
£
M
d
(
x0
).
Если d
уменьшается, то m
d
(
x0
)
не убывает, aM
d
(
x0
)
не возрастает. Поэтому существуют определенные пределы
m(
x0
) =
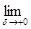 m
d
(
x0
),
M
d
(
x0
) =
m
d
(
x0
),
M
d
(
x0
) =
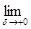 M
d
(
x0
),
M
d
(
x0
),
причем, очевидно,
m
d
(
x0
)
£
m(
x0
)
£
f(
x0
)
£
M(
x0
)
£
M
d
(
x0
).
Определение.
Функции т(х)
и М(х)
называются соответственно нижней и верхней функциями Бэра
для функции f(
x).
Теорема 1 (Р. Бэр).
Пусть функция
f(х) конечна в точке х0
. Для того чтобы
f(
x) была в этой точке непрерывна, необходимо и достаточно, чтобы было
m(
x0
) =
M(
x0
).
(*)
Доказательство.
Допустим, что функция f(х)
непрерывна в точке x0
. Взяв произвольное e > 0
, найдем такое d > 0
, что как только
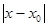 <
d,
<
d,
так сейчас же
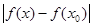 <
e.
<
e.
Иначе говоря, для всех х
Î
(х0
-
d
, x0
+
d
) будет
f(x0
) -
e
<
f(x)
<
f(x0
) +
e
.
Но отсюда следует, что
f(x0
) -
e
£
m
d
(x0
)
£
M
d
(x0
)
£
f(x0
) +
e
,
а стало быть, и тем более
f(x0
) -
e
£
m(x0
)
£
M(x0
)
£
f(x0
) +
e
,
откуда, ввиду произвольности e
, и вытекает (*). Итак, необходимость условия (*) доказана.
Пусть теперь, обратно, дано, что (*) выполнено. Тогда, очевидно,
m(
x0
) =
M(
x0
) =
f(
x0
)
и общее значение функций Бэра в точке x0
конечно.
Возьмем произвольное e > 0
и найдем столь малое d > 0
, что
m(
x0
) -
e
<
m
d
(
x0
)
£
m(
x0
),
M(
x0
)
£
M
d
(
x0
)
<
M(
x0
) +
e.
Эти неравенства означают, что
f(x0
) -
e
<
m
d
(x0
), M
d
(x0
)
<
f(x0
) +
e
.
Если теперь x
Î (х0
-
d
, x0
+
d
), то f(
x)
лежит между m
d
(
x0
)
и M
d
(
x0
)
, так что
f(x0
) -
e
<
f(x)
<
f(x0
) +
e
.
Иначе говоря, из того, что 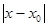 <
d
вытекает, что <
d
вытекает, что
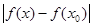 <
e,
<
e,
т. е. функция f(
x)
непрерывна в точке х0
.
Основная лемма.
Рассмотрим последовательность дроблений сегмента [а,
b]
a = 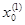 <
<
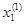 <
¼
<
<
¼
<
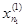 = b = b
. . . . . . . . . . . . . . . . . . . . . . . .
a = 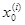 <
<
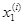 <
¼
<
<
¼
<
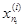 = b = b
. . . . . . . . . . . . . . . . . . . . . . . .
причем при
i
®
¥
l
i =
max[
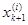 - -
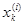 ]
® 0. ]
® 0.
Пусть 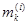 есть точная нижняя граница значений функции
f(
x) на сегменте есть точная нижняя граница значений функции
f(
x) на сегменте
[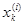 , , 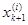 ].
Введем функцию
j
i
(
x)
, полагая ].
Введем функцию
j
i
(
x)
, полагая
j
i
(
x)
= 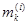 при
x
Î ( при
x
Î (
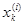 , ,
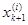 ) )
j
i
(
x) = 0 при
x =
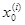 , ,
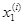 ,
¼ , ,
¼ ,
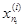 . .
Если
х0
не совпадает ни с одной точкой 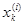 (
I = 1, 2, 3,
¼ ;
k = 0, 1, 2,
¼ ,
ni
)
, то (
I = 1, 2, 3,
¼ ;
k = 0, 1, 2,
¼ ,
ni
)
, то
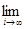 j
i
(x0
) = m(x0
). j
i
(x0
) = m(x0
).
Доказательство.
Фиксируем какое-нибудь i
и назовем через [
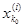 , , 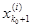 ]
тот из сегментов i
-го способа дробления, который содержит точку х0
.
Так как х0
не совпадает ни с одной из точек деления, то ]
тот из сегментов i
-го способа дробления, который содержит точку х0
.
Так как х0
не совпадает ни с одной из точек деления, то
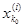 <
x0
<
<
x0
<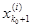
и, следовательно, при достаточно малых d > 0
будет
(х0
-
d
, x0
+
d
) Ì [
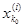 , , 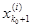 ], ],
откуда следует, что
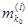 £
m
d
(
x0
)
£
m
d
(
x0
)
или, что то же самое, что
j
i
(x0
)
£
m
d
(x0
).
Устремив d
к нулю и перейдя к пределу, находим, что при любом i
j
i
(x0
)
£
m(x0
).
Этим самым лемма уже доказана для случая т(х0
) =
-
¥.
Пусть т(х0
)
>
-
¥
и пусть
h
<
m(x0
)
.
Тогда найдется такое d> 0
, что m
d
(
x0
)
>
h
.
Фиксировав это d
, найдем столь большое i0
, что при i
>
i0
будет
[
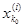 , , 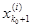 ]
Ì (х0
-
d
, x0
+
d
), ]
Ì (х0
-
d
, x0
+
d
),
где, как и выше, [
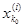 , , 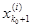 ]
есть сегмент, содержащий точку х0
.
Существование такого i0
следует из условияl
i
® 0
. ]
есть сегмент, содержащий точку х0
.
Существование такого i0
следует из условияl
i
® 0
.
Для таких i
будет
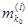 ³
m
d
(x0
)
>
h,
³
m
d
(x0
)
>
h,
или, что то же самое,
j
i
(x0
)
>
h.
Итак, для всякого h
<
m(
x0
)
найдется такое i0
,
что при i
>
i0
h
<
j
i
(x0
)
£
m(x0
),
а это и значит, что j
i
(
x0
)
®
m(
x0
).
Лемма доказана.
Следствие 1.
Функции Бэра т(х) и М(х) измеримы.
В самом деле, множество точек деления {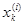 }
счетно и, стало быть, имеет меру нуль. Поэтому лемма означает, что j
i
(
x)
®
m(
x)
почти везде. }
счетно и, стало быть, имеет меру нуль. Поэтому лемма означает, что j
i
(
x)
®
m(
x)
почти везде.
Но j
i
(
x)
измерима, ибо это ступенчатая функция, значит измерима я функция т(
x).
Для верхней функции Бэра М(х)
рассуждение аналогично.
Следствие 2.
Если в условиях леммы исходная функция
f(
x)
ограничена, то
(
L)
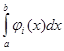 ® (
L)
® (
L)
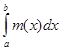 . .
Действительно, если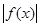 £
K
, то, очевидно, £
K
, то, очевидно,
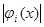 £
K, £
K,
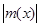 £
K,
£
K,
откуда прежде всего следует, что эти функции интегрируемы (
L)
, после чего остается сослаться на теорему Лебега о предельном переходе под знаком интеграла.
Перефразируем теперь следствие 2. Для этого заметим, что
(
L)
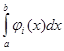 = =
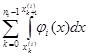 = =
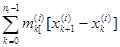 =
si
, =
si
,
где si
есть нижняя сумма Дарбу, отвечающая i
-му способу дробления. Таким образом, следствие 2 означает, что при i
®
¥
si
® (
L)
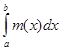 . .
Аналогично можно установить, что верхняя сумма Дарбу Si
при возрастании i
стремится к интегралу от верхней функции Бэра
Si
® (
L)
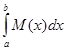 . .
Но в таком случае
Si
- si
®
(L) 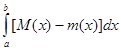 . .
С другой стороны, в курсе Анализа устанавливается, что для того, чтобы ограниченная функция f(
x)
была интегрируема (
R),
необходимо и достаточно, чтобы было Si
–
si
® 0
.
Сопоставляя это со сказанным выше, мы видим, что для интегрируемости (
R)
функции f(
x)
необходимо и достаточно, чтобы было
(
L)
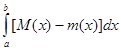 = 0.
(1) = 0.
(1)
Условие (1) во всяком случае выполнено, если разность М(х) - т(х)
эквивалентна нулю, но так как эта разность неотрицательна, то и обратно из (1) следует, что
т(х) ~ М(х).
(2)
Итак, интегрируемость (
R)
ограниченной функции f(
x)
равносильна соотношению (2).
Сопоставив этот результат с теоремой 1, получаем следующую теорему.
Теорема 2 (А. Лебег).
Для того чтобы ограниченная функция
f(
x) была интегрируема (R),необходимо и достаточно, чтобы она была непрерывна почти везде.
Эта замечательная теорема представляет собой наиболее простой и ясный признак интегрируемости (
R)
. В частности, она оправдывает сделанное в пункте 2 замечание, что интегрируемыми (
R)
могут быть только «не очень разрывные» функции.
Допустим теперь, что функция f(
x)
интегрируема (
R)
. Тогда она необходимо ограничена и почти везде будет
т(х) = М(х).
Но ведь
т(х)
£
f(
x)
£ М(х).
Значит, почти везде
f(
x) =
m(
x),
и f(
x)
, будучи эквивалентна измеримой функции т(х),
измерима сама. Так как всякая ограниченная измеримая функция интегрируема (
L)
, то такова же и f(
x)
, т. е. из интегрируемости какой-нибудь функции в смысле Римана вытекает ее интегрируемость в смысле Лебега.
Наконец, из эквивалентности функций f(
x)
и т(х)
следует, что
(
L)
 = (
L) = (
L)
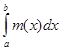 . .
Но, как известно из курса Анализа, в условиях основной леммы для интегрируемой (
R)
функции f(
x)
будет
si
® (
R)
 , ,
где si
есть нижняя сумма Дарбу, отвечающая i-
муспособу дробления. Сопоставляя это с тем, что, как показано нами,
si
® (
L)
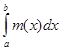 , ,
мы видим, что
(
R)
 = (
L) = (
L)
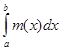 . .
Таким образом, имеет место
Теорема 3.
Всякая функция, интегрируемая (
R), необходимо интегрируема и (
L), и оба ее интеграла равны между собой.
В заключение отметим, что функция Дирихле y(
x)
(равная нулю в иррациональных и единице в рациональных точках) интегрируема (
L)
(ибо она эквивалентна нулю), но, как мы видели в пункте 2, не интегрируема (
R),
так что теорема 3 не обратима.
6. Примеры
1) Вычислить интеграл Лебега от функции 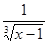 на интервале (1; 2). на интервале (1; 2).
Строим срезку
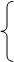
N,
f(
x)
³
N,
fN
(x) =
f(x), f(x)
<
N.
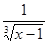 = N, = N,
x = 1 + 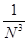 . .
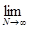
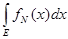 =
= 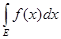 , ,
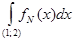 =
= 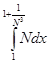 + + 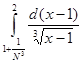 = Nx = Nx + + 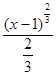 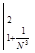 = N = N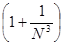 - N + - N + 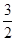 - -
-

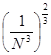 = =
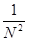 + +
 - -
 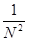 = - = -
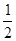
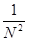 + +
 , ,

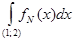 = =

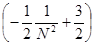 = =
 , ,
(
L)
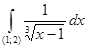 = =
 . .
2) Суммируемы ли функции 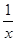 и и 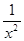 на интервале (0; 1). на интервале (0; 1).
f(
x) =
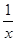 . .
Строим срезку
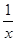 =
N, =
N,
x =
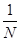 . .
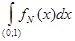 = =
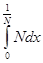 + +
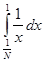 = =
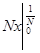 + +
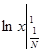 = 1 - = 1 -
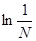 = 1 + = 1 +
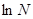 , ,
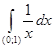 = =

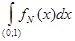 = =
 (1 + (1 +
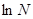 ) = +
¥, ) = +
¥,
значит функция f(
x) = 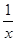 суммируемой не является.
суммируемой не является.
f(
x) =
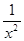 . .
Строим срезку
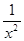 =
N, =
N,
x =
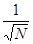 . .
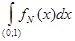 = =
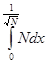 + +
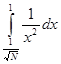 = =
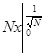 - -
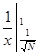 = =
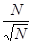 - (1 - - (1 -
 ) = ) =
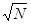 - 1 + - 1 +
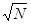 = =
= 2
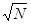 - 1, - 1,
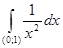 = =

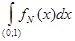 = =
 (2 (2
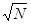 - 1) = +
¥, - 1) = +
¥,
значит функция f(
x) =
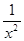 суммируемой не является.
суммируемой не является.
3) Суммируема ли функция f(
x) =
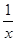 на отрезке [-1; 1],
где f(0) = 0.
на отрезке [-1; 1],
где f(0) = 0.
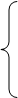 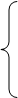 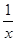 ,
x
> 0 0 ,
x
³ 0 ,
x
> 0 0 ,
x
³ 0
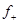 = =
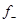 = =
0 ,
x
£ 0
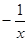 ,
x
< 0 ,
x
< 0
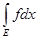 = =
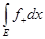 - -
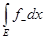 . .
Строим срезку
N =
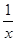 , ,
x =
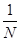 . .
(
L)
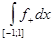 = =

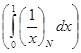 = =

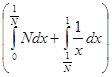 = =

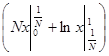 = =
=

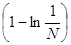 = =

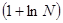 = +
¥. = +
¥.
Строим срезку
N = 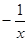 , ,
x = 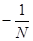 . .
(L)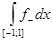 = =  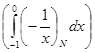 = =  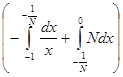 = =  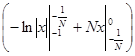 = =
=

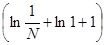 = =

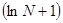 = +
¥, = +
¥,
значит функция f(
x) =
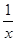 не является суммируемой на [-1 ;1].
не является суммируемой на [-1 ;1].
4) Суммируема ли функция f(
x) =
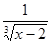 на [1; 3],
где f(2) = 1.
на [1; 3],
где f(2) = 1.
 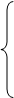 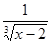 ,
x
> 2 0,
x
³ 2 ,
x
> 2 0,
x
³ 2
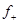 = 0,
x
< 2 = 0,
x
< 2 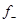 = =
1,
x = 2
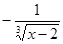 ,
x
< 2 ,
x
< 2
Строим срезку
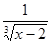 = N,
= N,
x = 2 + 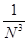 . .
(L)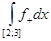 = =  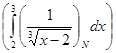 = =  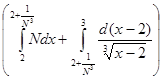 = =
=

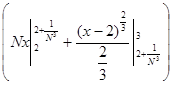 = =

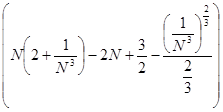 = =
=

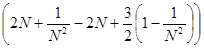 = =

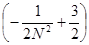 = =
 . .
Строим срезку
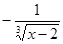 =
N, =
N,
x = 2 -
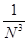 . .
(
L)
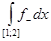 = =

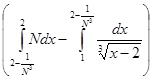 = =

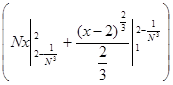 = =

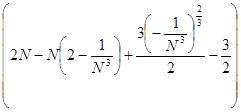 = =

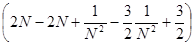 = =

функция f(
x)
суммируема на [1; 3].
7. Литература
1) Колмогоров, Фомин «Элементы функционального анализа».
2) Натансон И. П. «Теория функций вещественной переменной», С-П, 1999.
3) Очан «Сборник задач по математическому анализу».
|