А.М. Марченко, А.П. Плис
Рассмотрена проблема устранения циклических конфликтов при трассировке многослойного канала с любым расслоением при размещении контактов на любой стороне. Предложен алгоритм преобразования графа вертикальных ограничений к ациклическому виду путем расщепления его вершины на минимальное число новых вершин, который, в отличие от известных, использует информацию о контактах цепи, соответствующей выбранной вершине.
Одним из важных этапов автоматизированного проектирования топологии СБИС является трассировка каналов. Каналом называется односвязная прямоугольная область на поверхности кристалла, предназначенная для соединения контактов, принадлежащих одной и той же цепи. В первой постановке задачи контакты располагались на двух противоположных сторонах канала, а трассировка была разрешена в двух коммутационных слоях. При этом в одном слое размещались горизонтальные сегменты соединений, а в другом - вертикальные. Такой канал называется HV - каналом [1].
Качество решения задачи трассировки во многом определяет окончательный результат проектирования таких широко распространенных типов кристаллов, как тракты передачи данных, в которых каналы занимают около 20% общей площади. В канальной трассировке можно выделить три основные задачи:
1. Построение графа вертикальных ограничений.
2. Удаление циклов из графа вертикальных ограничений.
3. Укладка горизонтальных сегментов в канале.
Известно много эвристических алгоритмов канальной трассировки, которые эффективно решают задачу укладки горизонтальных сегментов при условии, что граф вертикальных ограничений не содержит циклов [2-4]. В то же время проблема построения графа вертикальных ограничений и удаления из него циклов изучена недостаточно полно. По мере совершенствования технологии изготовления СБИС проблема канальной трассировки постоянно усложняется. Например, увеличивается число коммутационных слоев, разрешается нарушать принятую модель расслоения соединений, контакты могут находиться на любой стороне канала и в любом слое. Перечисленные новые технологические требования приводят к усложнению графа вертикальных ограничений и превращают проблему его преобразования к ациклическому виду в крайне актуальную.
Реклама

Граф вертикальных ограничений (Vertical Constraints Graph) - это граф следующего вида: VCG=(X, U), где X - множество вершин, соответствующих горизонтальным сегментам цепей, U - множество ориентированных ребер. В случае двуслойного канала с принятым расслоением HV ребро ui?U соединяет вершины xm, xn? X, если существует пара противолежащих контактов, принадлежащих соответственно горизонтальным сегментам m, n, первый из которых расположен на верхней, а второй - на нижней сторонах канала.
В многослойном канале возможны более сложные вертикальные ограничения. Если контакты расположены один над другим в соседних вертикальных слоях, что может иметь место в VVH канале, то порядок соответствующих им горизонтальных сегментов представляется в графе дополнительными ребрами так, как это показано на рисунке 1.

Рис.1.
Если в канале существуют контакты, расположенные на боковых сторонах, то порядок их расположения также отражается в графе дополнительными ребрами. На рисунке 2 приведен пример канала, содержащего четыре цепи a, b, c, d с контактами на боковых сторонах, и соответствующий граф вертикальных ограничений.

Рис. 2.
Задача приведения VCG к ациклическому виду (задача 2) может быть сформулирована следующим образом: используя информацию о цепях в канале и о графе вертикальных ограничений, так изменить конфигурацию цепей, чтобы соответствующий VCG не имел циклов.
Основная идея, положенная в основу алгоритмов решения этой задачи, состоит в расщеплении вершины графа, которая участвует в создании цикла, на две или более части. Это соответствует разделению горизонтального сегмента на два или более новых сегмента. Такие механизмы были предложены Дойчем [2] (терминальный доглег) и Прессом [5] (нетерминальный доглег).
Эти варианты доглега отличаются друг от друга способами перераспределения контактов горизонтального сегмента между новыми сегментами. Местоположение контактов определяет существование и ориентацию ребер между соответствующими вершинами VCG, поэтому метод разделения контактов на группы в наибольшей степени влияет на успех процедуры удаления циклов. При терминальном доглеге контакты делятся по признаку левый - правый относительно контакта, по которому происходит разбиение. При этом в цепи может появиться несколько горизонтальных сегментов, но нет гарантии удаления циклов.
При нетерминальном доглеге, в свою очередь, контакты сегмента разделяются на две группы по признаку верхний - нижний. Этот метод гарантирует удаление всех циклов, проходящих через расщепляемую вершину, при условии, что верхние контакты порождают только выходящие ребра, а нижние - только входящие.
Реклама

Наличие в канале более двух коммутационных слоев и контактов на боковых сторонах приводит к тому, что контакт может порождать в VCG входящие и выходящие ребра одновременно. В этом случае разделения контактов на верхние и нижние недостаточно и для успешного разбиения вершины требуется дополнительный анализ графа и, возможно, многократный (мульти-) доглег. В данной статье предлагается алгоритм мульти-доглега, который способен эффективно расщеплять вершины в такой ситуации. Он состоит из следующих шагов:
1. Если в VCG нет циклов либо уже рассмотрены все его вершины, то завершить работу алгоритма.
2. Найти критическую вершину в VCG, выбирая среди еще не рассмотренных вершин.
3. Построить расширенный граф вертикальных ограничений.
4. Построить локальный граф контактов. Если в локальном графе контактов нет петель, то раскрасить его в минимальное число цветов, иначе вернуться на шаг 1.
5. Расщепить вершину в соответствии с цветами контактов.
6. Создать вертикальное соединение для доглега, если это возможно, и вернуться на шаг 1.
Рассмотрим отдельные шаги алгоритма более детально. На шаге 2 для каждой итерации выбирается критическая вершина в VCG. Критерием выбора является значение следующей функции:
f = cyclesa* width-b* priority-g , где
cycles - количество циклов, проходящих через данную вершину,
width - ширина, priority - приоритет соответствующей цепи,
a> 0, b³ 0, g³ 0 - коэффициенты важности перечисленных параметров, которые выбираются пользователем в зависимости от конкретной задачи.
Определенная таким образом функция выбора позволяет расщеплять большее количество циклов за одну итерацию, выбирать для доглега цепи меньшей ширины, а также не усложнять конфигурацию приоритетных цепей, например цепей земли/питания.
На шаге 3 для найденной критической вершины a строится расширенный граф вертикальных ограничений (Expanded Vertical Constraints Graph) следующего вида: EVCGa = ((X \ a)?Ka, Ua), где X - множество вершин исходного VCG, a - критическая вершина VCG, Ka - множество новых вершин, образованных контактами сегмента, соответствующего вершине a, Ua - множество ориентированных ребер, соединяющих новые вершины с другими вершинами VCG. Такой граф содержит более детальную информации о циклах, проходящих через критическую вершину. На рисунке 3 приведен пример EVCGa для канала, показанного на рисунке 2.
На шаге 4 строится локальный граф контактов для критической вершины a (Local Pin Graph): LPGa = (Ka, Va), где Va - множество неориентированных ребер. Ребро vi?Va соединяет вершины km, kn? Ka, если в графе EVCGa существует путь между вершинами km и kn. Локальный граф для вершины a изображен на рисунке 3.
Каждое ребро локального графа контактов соответствует как минимум одному циклу, проходящему через критическую вершину VCG, и указывает на контакты, образующие этот цикл. Таким образом, если ребро существует между парой вершин локального графа, то соответствующие им контакты должны быть назначены в различные группы при расщеплении вершины VCG. В этом случае соответствующие ребру циклы будут удалены.
Возможен случай, когда в локальном графе появляется петля. Петля не может быть удалена путем разбиения контактов на группы, так как контакт не может быть расщеплен на части. В этом случае проходящий через вершину цикл не может быть удален путем расщепления только данной вершины.
Использование локального графа контактов позволяет свести задачу разбиения контактов на группы к задаче раскраски неориентированного графа. Необходимо раскрасить локальный граф контактов в минимальное число цветов так, чтобы вершины, соединенные ребром, оказались раскрашены в разные цвета. Раскраска графа в минимальное число цветов будет соответствовать разбиению сегмента на минимальное число частей, достаточное для удаления циклов в VCG. Необходимо отметить, что, несмотря на сложность задачи раскраски произвольного графа в минимальное число цветов, для данного случая задача всегда может быть решена методом полного перебора, так как размерность локального графа контактов определяется числом контактов в цепи и для сигнальных цепей обычно не превышает 5.
Если локальный граф контактов не содержит нечетных циклов, то, по теореме Кенига [6], он может быть раскрашен в два цвета. В этом случае достаточно бинарного доглега. В остальных случаях требуется мульти-доглег. Пример раскраски локального графа контактов для вершины а показан на рисунке 3.
Граф вертикальных ограничений после одной процедуры мульти-доглега изображен на рисунке 3. Критическая вершина a расщеплена на три новые вершины (a’, a’’, a’’’) в соответствии с раскраской графа LPGa
, а ребра, относящиеся к a, построены заново для трех новых вершин.

Рис.3.
Чтобы завершить процедуру мульти-доглега, необходимо найти место для вертикального соединения между новыми сегментами. Эта задача решается на шаге 7 в соответствии с [5].
В общем случае итерации повторяются до тех пор, пока не будут удалены все циклы. Граф, рассмотренный в нашем примере, был приведен к ациклическому виду за один шаг. После этого была решена задача укладки горизонтальных сегментов в канале. Результат канальной трассировки показан на рисунке 4. Необходимо отметить, что это решение не удается получить ранее известными методами.
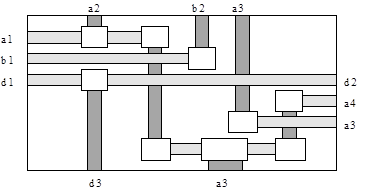
Рис.4.
Алгоритм мульти-доглега был реализован на языке С++. На рис. 5 представлен пример канала, который является сложным для задачи удаления циклов. Контакты фиксированы на верхней и нижней и упорядочены на левой и правой сторонах, VCG содержит 33 цикла. Алгоритм мульти-доглега удаляет циклы в этом примере за 9 итераций.

Рис.5.Трассировка сложного примера
Разработанный алгоритм приведения VCG к ациклическому виду обеспечивает, в отличие от известных алгоритмов, трассировку многослойных каналов с контактами, расположенными на любой стороне и в любом коммутационном слое, что является в настоящее время необходимым технологическим условием применения САПР СБИС.
Список
литературы
A.Hashimoto and J.Stivens. “Wire routing by optimization channel assignment within large apertures.” Proc. Of the 8th Design automation workshop, pp. 155-163, 1971.
Deutsch D.N. “A Dogleg Channel Router” in Proc. 13th Design Automat. Conf. June 1976, pp. 425-433.
T.Yoshimura, E. S. Kuh “Efficient algorithm for channel routing”, IEEE Transactions on Computer-Aided Design, CAD-1(1):25-30, January 1982.
H.H.Chen, E. Kuh “Glitter: A gridless variable-width channel routing”, IEEE Transactions on Computer-Aided Design, CAD-5(4):459-465, 1986.
Bryan Preas “Channel Routing With Non-Terminal Doglegs”, Proc. European Design Automation Conference (EDAC), March 1990, pp. 451-458.
Берж К. “Теория графов и ее применения”, Иностранная Литература, Москва, 1962.
|