Р.С. Шенгелов
Пока будем говорить об одной разведочно-эксплуатационной скважине. По данным стабилизировавшейся опытно-эксплуатационной откачки имеем уже неизменную удельную срезку:
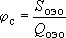
Казалось бы, теперь можно дать прогноз понижения в водозаборе при заявленном дебите:
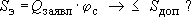
Однако, для этого нужно быть уверенным, что величина 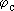 не зависит от дебита, т.е. сохранит свое значение при не зависит от дебита, т.е. сохранит свое значение при  , который чаще всего больше опытного (хотя и необязательно). В каких условиях этого можно ожидать ? , который чаще всего больше опытного (хотя и необязательно). В каких условиях этого можно ожидать ?
- если от дебита (т.е. и от понижения) не зависят параметры водоносной системы и характер действия граничных условий. Например, стационар в Звенигороде:
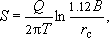
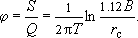
Видно, что при "устойчивых" 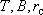 величина величина  не должна меняться при любых дебитах. Но ведь при увеличении дебита воронка углубляется и расширяется - следовательно, в нее попадут новые элементы опробуемой водоносной системы, которые окажут свое влияние на характер связи понижения и дебита (например, зоны с существенно отличными параметрами проводимости или перетекания). не должна меняться при любых дебитах. Но ведь при увеличении дебита воронка углубляется и расширяется - следовательно, в нее попадут новые элементы опробуемой водоносной системы, которые окажут свое влияние на характер связи понижения и дебита (например, зоны с существенно отличными параметрами проводимости или перетекания).
Поэтому ОЭО проводится в несколько "ступеней", т.е. при нескольких значениях дебита; затем строится ИНДИКАТОРНАЯ КРИВАЯ или "КРИВАЯ ДЕБИТА" - график в координатах 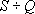 . .
Если удельная срезка  действительно = действительно =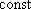 , то связь , то связь  и и 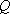 линейная, график является ПРЯМОЙ линией (рис. 1). линейная, график является ПРЯМОЙ линией (рис. 1).
 |
| Рис. 1 |
Сколько нужно "ступеней" для подтверждения линейности связи 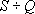 ? Строго говоря, достаточно двух, т.к. формально существует точка ? Строго говоря, достаточно двух, т.к. формально существует точка  = 0 при = 0 при 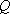 = 0. На практике предпочитают провести все же три ступени. = 0. На практике предпочитают провести все же три ступени.
Однако, в реальных условиях связь 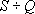 часто НЕЛИНЕЙНА, причем обычно часто НЕЛИНЕЙНА, причем обычно  возрастает с ростом возрастает с ростом 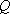 (кривая имеет выпуклость вверх). Генетические причины нелинейности кривой дебита разнообразны. (кривая имеет выпуклость вверх). Генетические причины нелинейности кривой дебита разнообразны.
БЕЗНАПОРНЫЕ ПОТОКИ : проводимость зависит от мощности (глубины) потока 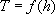 . Поэтому, чем больше дебит опробования, тем больше понижение - тем меньше . Поэтому, чем больше дебит опробования, тем больше понижение - тем меньше 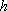 и, следовательно, тем меньше проводимость и, следовательно, тем меньше проводимость 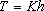 . Для таких условий возможно аналитическое описание формы кривой дебита. Общий вид связи . Для таких условий возможно аналитическое описание формы кривой дебита. Общий вид связи  и и 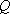 для стационарных радиальных потоков: для стационарных радиальных потоков:
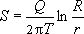 , ,
где  - радиальная координата точки наблюдения, - радиальная координата точки наблюдения, 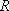 - "радиус питания" (при - "радиус питания" (при 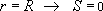 ). ).
Соответственно понижение в работающей скважине 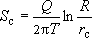 . .
Реклама

Аналитический вид выражения для 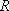 зависит от конкретной расчетной схемы - например, при работе скважины на расстоянии зависит от конкретной расчетной схемы - например, при работе скважины на расстоянии 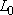 от уреза несовершенной реки (с параметром сопротивления ложа от уреза несовершенной реки (с параметром сопротивления ложа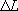 ) ) 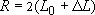 . .
Для условий безнапорного потока следует принимать 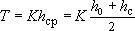 (рис.2), откуда (рис.2), откуда 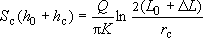 . .
Так как 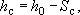 то то 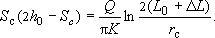
Отсюда: Q = 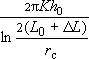 Sс
- Sс
- 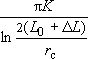 Sс
2
= Sс
2
=  Sс
- Sс
-  Sс
2
. Это уравнение параболы в координатах Sс
2
. Это уравнение параболы в координатах 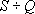 (рис. 3). (рис. 3).
 |
| Рис. 1. |
Рис. 2. |
Для использования такой кривой в целях прогноза (определение ожидаемого 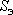 при расчетном эксплуатационном дебите при расчетном эксплуатационном дебите 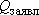 ) нужно ее экстраполировать, следовательно, нужно определить ее КОЭФФИЦИЕНТЫ. Это можно сделать путем обычного регрессионного анализа, но для этого нужно бы иметь побольше экспериментальных точек - малореально, так как дорого и хлопотно. ) нужно ее экстраполировать, следовательно, нужно определить ее КОЭФФИЦИЕНТЫ. Это можно сделать путем обычного регрессионного анализа, но для этого нужно бы иметь побольше экспериментальных точек - малореально, так как дорого и хлопотно.
Можно применить линейную анаморфозу в виде 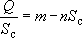 . .
Что такое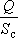 ? Это удельный дебит ? Это удельный дебит 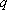 (величина, обратная удельной срезке). (величина, обратная удельной срезке).
Итак, если причиной нелинейности кривой дебита является именно зависимость проводимости от понижения в безнапорных потоках, то в координатах 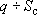 должен получаться линейный график (рис.4). Это важнейший диагностический признак! должен получаться линейный график (рис.4). Это важнейший диагностический признак!
Сколько нужно ступеней дебита, чтобы подтвердить линейность этого графика? Три, так как есть неизвестный свободный член.
Проведя минимум три ступени откачки с разными дебитами, получаем возможность определить прямо с графика коэффициенты прямой  и и  . После этого для прогноза понижения при заявленном дебите решаем квадратное уравнение: . После этого для прогноза понижения при заявленном дебите решаем квадратное уравнение:
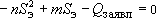
относительно 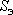 и сравниваем его с допустимым. и сравниваем его с допустимым.
 |
| Рис. 4 |
Другая распространенная причина нелинейности индикаторного графика - возникновение явлений ТУРБУЛЕНТНОСТИ в прискважинной зоне; при этом возникают дополнительные потери напора, величина которых зависит от дебита.
Пример, показывающий высокую действительную скорость при входе подземных вод в ствол скважины - учебная откачка на Звенигородском полигоне:
- Дебит Q = 40 л/с ≈ 3500 куб.м/сут
- Радиус фильтрового интервала rф
= 0.15 м
- Длина рабочей части фильтра lф
≈ 15 м
- Площадь боковой поверхности рабочей части Fф
= 2p rф
lф
≈ 14 кв.м
- Скорость фильтрации на боковой поверхности vф
= Q / Fф
= 3500 / 14 ≈ 250 м/сут
- Действительная скорость на боковой поверхности (при активной трещиноватости порядка nакт
≈ 3-5%):
uф
= vф
/nакт
≈ 5000-8300 м/сут ≈ 6-10 см/сек !
Это огромная скорость для подземных вод. Прямым следствием является постоянно наблюдаемый при учебных откачках вынос тонкой карбонатной взвеси в откачиваемой воде; расчетный радиус центральной скважины уже сейчас превышает фактический радиус бурения. На другом учебном кусте несколько лет назад вышла из строя центральная скважина в связи с осадкой технической обсадной колонны; расчетный радиус этой скважины по последним оценкам составлял около 5 м (!), что свидетельствует о значительном суффозионном выносе и, возможно, расширении трещин и карстовых каверн в прискважинной зоне.
Реклама

Возможность подобного рода негативных последствий при чрезмерно высоких скоростях входа воды в ствол скважин служит основанием для ограничения допустимой нагрузки на одну скважину, которая специально обосновывается с учетом строения водовмещающих отложений.
При значимом проявлении турбулентных составляющих потерь напора используется двучленная зависимость Дюпюи:
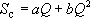 , откуда , откуда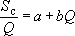 , ,
т.е. подобный генезис криволинейности графика  должен подтверждаться линейным характером связи должен подтверждаться линейным характером связи 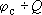 (рис. 5). (рис. 5).
Опять нужно минимум три ступени для доказательства линейности, так как есть неизвестный свободный член.
По графику находим коэффициенты a и b. Для прогноза понижений при заявленном дебите решается уравнение
Sc
= aQзаявл
+ bQ2
заявл
,
либо можно экстраполировать прямую на графике до Qзаявл
и получить φэ
.
 |
| Рис. 5 |
Есть еще целый ряд причин, заметно осложняющих форму кривых дебита:
- изменение сопротивления прискважинной зоны (размыв, разрушение стенок скважины, кольматация фильтра глинистыми частицами, выносимыми из заполнителя трещин и т.д.) - совершенно непрогнозируемая вещь !;
- изменение характера действия границ - например, ограниченный расход реки, частично перехватываемый при ОЭО;
- неоднородность пласта по вертикали ....
К тому же, эти причины могут проявляться совместно, т.е. очень часто нельзя или трудно применить стандартные приемы интерпретации типа вышерассмотренных. Что делать?
Пробуют разные системы координат, чтобы найти линейную связь между  и и 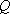 , затем как-то ее объясняют с генетических позиций и по ней экстраполируют понижения на величину , затем как-то ее объясняют с генетических позиций и по ней экстраполируют понижения на величину 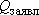 . Понятно, что такие формальные построения весьма уязвимы, поэтому рекомендуют ОЭО проводить при дебите, максимально близком к потребности, чтобы уменьшить риск экстраполяции по дебиту. . Понятно, что такие формальные построения весьма уязвимы, поэтому рекомендуют ОЭО проводить при дебите, максимально близком к потребности, чтобы уменьшить риск экстраполяции по дебиту.
ОБЩИЕ ЗАМЕЧАНИЯ ПО ГИДРАВЛИЧЕСКОМУ МЕТОДУ (в стационарной постановке ОЭО): в принципе сильный инструмент, так как  определяется экспериментально, по факту, а не частям. Но есть и явно уязвимые места: определяется экспериментально, по факту, а не частям. Но есть и явно уязвимые места:
- далеко не всегда ясны причины возникновения того или иного характера кривых дебита, так как "по определению" - месторождение имеет сложные условия; отсюда риск экстраполяции.
- кроме того, этот метод чрезвычайно консервативен - подсчет запасов возможен только для конкретных опробованных скважин, так как 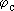 является индивидуальной характеристикой скважины ! является индивидуальной характеристикой скважины !
А как быть, если будущий водозабор должен состоять из нескольких скважин ?
Приходится проводить ОЭО из каждой (!) скважины системы, чтобы получить n2
удельных срезок:
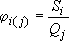 (удельная срезка в i -ой скважине от действия j -ой) (удельная срезка в i -ой скважине от действия j -ой)
Затем для каждой скважины рассчитывается ожидаемое понижение при заявленном дебите по принципу суперпозиции:
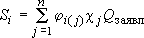
(если скважины равнодебитные, то 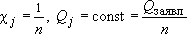 ). ).
Затем проверяем соответствие получаемых и допустимых понижений по каждой скважине. Если где-то что-то не сошлось: в гидродинамическом методе легко изменить (в уме!) схему расстановки или количество скважин, а при гидравлическом? Нужно бурить реальные новые скважины, проводить в них ОЭО, снова считать, сравнивать.....
|