Р.С.Шенгелов
Теперь рассмотрим особенности расчетов неупорядоченных площадных систем. Очень часто системы водозаборных скважин имеют именно такой характер: в силу особенностей условий строительства и землепользования, исторически сложившиеся и т.д. Их точный расчет всегда возможен по принципу суперпозиции (суммирования взаимодействий), но это может быть очень громоздко и трудоемко при выполнении многовариантных расчетов, так как количество скважин в системе может достигать десятков и даже сотен. Поэтому нередко используют методику приближенного расчета крупных площадных систем взаимодействующих скважин, который бывает вполне достаточен для решения двух важных задач:
а) расчет влияния таких систем на некоторые удаленные от них точки (почему-либо интересные - например, на соседний водозабор);
б) предварительная оценка возможного суммарного дебита таких систем.
Для приближенного расчета площадных систем используют идею "БОЛЬШОГО КОЛОДЦА", под которым понимается одна-единственная скважина с большим радиусом 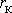 , эквивалентная всей системе, т.е. имеющая тот же суммарный дебит и дающая те же понижения в области влияния. Наиболее чисто этот прием обосновывается при отсутствии близкорасположенных границ - например, для "схемы Тейса". , эквивалентная всей системе, т.е. имеющая тот же суммарный дебит и дающая те же понижения в области влияния. Наиболее чисто этот прием обосновывается при отсутствии близкорасположенных границ - например, для "схемы Тейса".
Система состоит из  скважин с разными дебитами скважин с разными дебитами 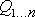 и разным временем ввода в действие и разным временем ввода в действие 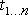 для каждой скважины (рис.1). для каждой скважины (рис.1).
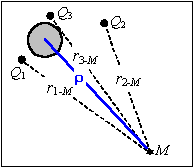 |
| Рис. 1. |
Определим по принципу сложения решений понижение уровня в некоторой точке 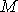 в момент t, полагая, что расчетное время достаточно для наступления квазистационарного режима в точке в момент t, полагая, что расчетное время достаточно для наступления квазистационарного режима в точке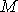 : :
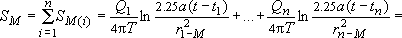
(введем долевые коэффициенты дебита 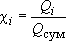 ) )
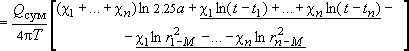 . .
Учитывая, что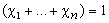 , а две подчеркнутые группировки однородных членов можно свернуть по свойствам логарифма: , а две подчеркнутые группировки однородных членов можно свернуть по свойствам логарифма:
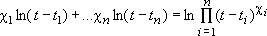 , ,
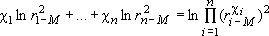 , ,
получим окончательное выражение в виде:
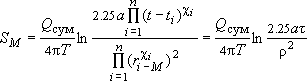 . .
Видно, что полученное выражение для 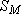 по форме аналогично действию одной скважины, находящейся на расчетном расстоянии по форме аналогично действию одной скважины, находящейся на расчетном расстоянии 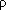 от точки от точки 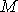 и действующей с суммарным дебитом и действующей с суммарным дебитом 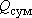 в течение расчетного времени в течение расчетного времени  . Такая скважина и называется "большим колодцом". Некоторые комментарии: . Такая скважина и называется "большим колодцом". Некоторые комментарии:
В частном случае равнодебитных скважин (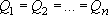 ) долевые коэффициенты также равны между собой ) долевые коэффициенты также равны между собой ; тогда ; тогда 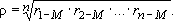
Очевидно, что при такой методике расчета 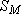 физическое положение "большого колодца" в принципе безразлично; важно только, что он находится на расчетном расстоянии физическое положение "большого колодца" в принципе безразлично; важно только, что он находится на расчетном расстоянии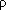 . Можно использовать и другую методику, не требующую специального вычисления . Можно использовать и другую методику, не требующую специального вычисления 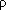 : предварительно рассчитывается положение центра (оси) "большого колодца" как центра тяжести системы скважин по их расходам, от которого и измеряется расчетное расстояние до точки : предварительно рассчитывается положение центра (оси) "большого колодца" как центра тяжести системы скважин по их расходам, от которого и измеряется расчетное расстояние до точки 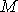 (рис. 2). (рис. 2).
Реклама

Координаты центра "большого колодца" в произвольной системе декартовых координат {X,Y} вычисляются с учетом координат и долевых коэффициентов дебита каждой скважины:
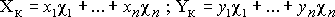 . .
По численным оценкам, погрешность расчетов понижений не превышает 3-5% для точек, удаленных от площадки системы скважин на расстояние, превышающее ее наибольший размер.
Другая полезная практическая задача: оценка возможного суммарного притока к системе скважин. Для этого рассчитывается радиус "большого колодца" 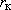 , т.е. точка , т.е. точка 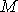 перемещается на стенку "большого колодца". При этом одна из скважин принимается за опорную и от нее рассчитываются расстояния до всех остальных; после этого оценивается перемещается на стенку "большого колодца". При этом одна из скважин принимается за опорную и от нее рассчитываются расстояния до всех остальных; после этого оценивается 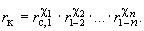
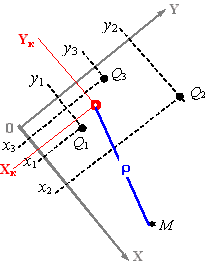 |
| Рис. 2. Определение координат центра "большого колодца" |
Теперь можно рассчитать потенциальный суммарный дебит системы как дебит "большого колодца" с радиусом 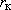 по любой формуле, отвечающей расчетной схеме; например, в "схеме Тейса": по любой формуле, отвечающей расчетной схеме; например, в "схеме Тейса":
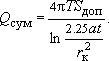
Конечно, такая оценка будет приближенной, так как приходится принимать некоторое единое для системы значение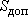 . .
В завершение характеристики гидродинамических расчетов коротко остановимся на МОДЕЛИРОВАНИИ РАБОТЫ ВОДОЗАБОРОВ. Оно применяется, если необходимо учесть выявленные при разведке особенности неоднородного распределения параметров, сложные граничные условия, структуру потока и др., которые явно не удается безболезненно упростить для аналитических расчетов. Принципиально моделирование "водозаборных" задач ничем не отличается от других. Специфика состоит лишь в обязательном наличии водозаборных скважин (хотя они могут быть и в других задачах - дренажи, закачка промстоков, подземное выщелачивание и т.п.).
Основная особенность моделирования скважин: если в блок модели подать дебит скважины 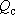 , то в нем при решении будет получен напор , то в нем при решении будет получен напор 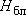 (или понижение (или понижение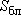 ), не отвечающий реальному напору (понижению) в скважине ), не отвечающий реальному напору (понижению) в скважине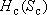 . Почему ? . Почему ?
В природе поток в непосредственной близости от скважины имеет практически радиальный характер, а распределение напоров подчиняется логарифмике Дюпюи:
Реклама

(1) 
В отличие от этого, на модели "приток" к водозаборному блоку происходит в виде линейных потоков из четырех смежных блоков (рис. 4.7); расход каждого из таких потоков:
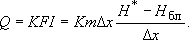
Так как 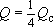 , то: , то:
(2) 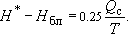
Если теперь почленно вычесть (2) из (1), то:
(3) 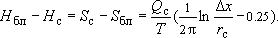
Таким образом, к напору/понижению, получаемому в "скважинном" блоке, следует сделать поправку по формуле (3). Особенно об этом надо помнить при работе с "чужими" программами численного моделирования, для которых, как правило, нет внятного описания многих деталей построения расчетных алгоритмов. Решить эту проблему (а это действительно проблема, так как разность 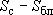 может быть весьма значительной) можно только путем тестирования программы по аналитическим решениям. может быть весьма значительной) можно только путем тестирования программы по аналитическим решениям.
Еще одно замечание: если в один блок сетки модели попадают несколько работающих водозаборных скважин, то их приходится объединять в одну эквивалентную, т.е. заменять их "большим колодцем" с суммарным дебитом, рассчитав его радиус по вышерассмотренным зависимостям.
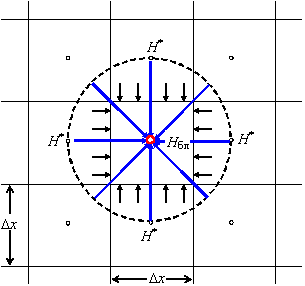 |
| Рис. 3. Характер притока к водозаборной скважине в РЕАЛЬНОМ (синие стрелки) фильтрационном потоке и на СЕТОЧНОЙ МОДЕЛИ (черные стрелки) |
Другой метод оценки эксплуатационных запасов и расчета водозаборов, являющийся альтернативой рассмотренному гидродинамическому - ГИДРАВЛИЧЕСКИЙ.
Вспомним, что для применения гидродинамического метода величина обобщенного фильтрационного сопротивления  рассматривается как совокупность всех значимых элементов строения области месторождения, отдельно разведуемых и затем "собираемых" для прогноза в виде расчетной фильтрационной схемы. Если же объективно трудно рассчитывать на построение достоверной фильтрационной схемы (сложные балансово-гидрогеодинамические условия, слишком большая необходимая плотность опытного опробования, отсутствие методик постановки и достоверной интерпретации опробования), то применяют (в какой-то мере - вынужденно) гидравлический метод. рассматривается как совокупность всех значимых элементов строения области месторождения, отдельно разведуемых и затем "собираемых" для прогноза в виде расчетной фильтрационной схемы. Если же объективно трудно рассчитывать на построение достоверной фильтрационной схемы (сложные балансово-гидрогеодинамические условия, слишком большая необходимая плотность опытного опробования, отсутствие методик постановки и достоверной интерпретации опробования), то применяют (в какой-то мере - вынужденно) гидравлический метод.
Его основной смысл - НЕПОСРЕДСТВЕННАЯ ЭКСПЕРИМЕНТАЛЬНАЯ (т.е. с помощью прямых полевых опытов) оценка  как единой "эмпирической" величины. Для этого при разведке выполняется ОЭО - достаточно длительные и достаточно мощные опытно-эксплуатационные откачки из скважин, заложенных непосредственно в точках будущего водозабора (такие скважины обычно называют разведочно-эксплуатационными). По сути, такое опробование является почти полной имитацией работы будущего водозабора. как единой "эмпирической" величины. Для этого при разведке выполняется ОЭО - достаточно длительные и достаточно мощные опытно-эксплуатационные откачки из скважин, заложенных непосредственно в точках будущего водозабора (такие скважины обычно называют разведочно-эксплуатационными). По сути, такое опробование является почти полной имитацией работы будущего водозабора.
Техника применения:
по результатам ОЭО для опробуемой скважины фиксируется т.н. СРЕЗКА уровня (несколько устаревший синоним термина "понижение";
затем рассчитывается УДЕЛЬНАЯ СРЕЗКА ("удельное понижение") как величина срезки (понижения) на единицу дебита:
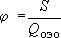 [ сут/м2
]. [ сут/м2
].
Видно, что и по смыслу, и по размерности  является фильтрационным сопротивлением - тем самым "обобщенным" сопротивлением области влияния ОЭО. Таким образом, проводя ОЭО, мы "одним ударом" определяем (в виде одного-единственного числа) ВСЮ СОВОКУПНОСТЬ ДЕЙСТВИЯ ГИДРОГЕОЛОГИЧЕСКИХ ФАКТОРОВ в зоне влияния опробования. является фильтрационным сопротивлением - тем самым "обобщенным" сопротивлением области влияния ОЭО. Таким образом, проводя ОЭО, мы "одним ударом" определяем (в виде одного-единственного числа) ВСЮ СОВОКУПНОСТЬ ДЕЙСТВИЯ ГИДРОГЕОЛОГИЧЕСКИХ ФАКТОРОВ в зоне влияния опробования.
Ясно, что  в ходе ОЭО будет изменяться в соответствии с развитием величины понижения даже при относительно постоянном дебите опробования в ходе ОЭО будет изменяться в соответствии с развитием величины понижения даже при относительно постоянном дебите опробования 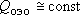 . Очевидно, что возможны два принципиальных варианта: . Очевидно, что возможны два принципиальных варианта:
- за время ОЭО достигнут устойчивый стационарный режим понижений - следовательно, удельная срезка достигла своего максимального в данных условиях значения;
- в течение всего времени ОЭО сохранялся нестационарный режим, т.е. достигнутое к моменту завершения ОЭО значение  не является предельным. не является предельным.
Существование одного из этих вариантов в конкретной ситуации определяется, в первую очередь, удаленностью питающих границ, способных обеспечить необходимую величину 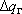 . .
|