Построение аэродинамически устойчивой расчетной модели надземного газопровода с односторонней связью
Дегтярева Наталья Владимировна Челябинск, асп. каф. стр. механики ЮУрГУ
Гибкие сооружения типа надземных газопроводов высокого давления часто подвержены аэродинамической неустойчивости, что проявляется в возникновении опасных вертикальных колебаний. Явление раскачивания газопровода в плоскости, перпендикулярной направлению ветрового потока, обусловлено совпадением частоты 9 срыва вихрей с боковой поверхности трубы с частотой со собственных колебаний газопровода. Это может привести к резкому возрастанию амплитуды колебаний и в итоге - к разрушению конструкции.
Несмотря на то, что явление ветрового резонанса достаточно хорошо изучено в специальной литературе [1, 2], вопросы гашения резонансных колебаний надземных газопроводов относятся к технически сложной проблеме, не получившей пока удовлетворительного решения. Частично эти вопросы рассматривались в [3].
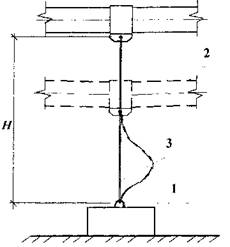
Рис. 1. Устройство гашения колебаний
В статье предложен способ ограничения резонансных амплитуд с помощью устройства, работающего по принципу односторонней связи (рис. 1). Устройство содержит фундаментный блок 1, соединенный с трубой 2 газопровода гибким тросом 3, и устанавливается в одном из пролетов газопровода, расчетная схема которого имеет вид неразрезной балки (рис. 2).
При аэродинамическом воздействии, направленном вниз, труба деформируется согласно расчетной схеме (рис. 2а). В этом случае односторонняя связь выключена из работы, и изгиб трубы соответствует низшей (первой) собственной форме колебаний (пунктирные линии на рис. 1 и 2а). При аэродинамическом возмущении, направленном вверх, труба при обратном движении вызывает натяжение троса, который совместно с фундаментным блоком начинает работать как дополнительная опорная связь. Это приводит к скачкообразному изменению расчетной схемы газопровода и, соответственно, к появлению новой собственной формы колебаний газопровода (рис. 26).

Рис. 2. Расчетная модель надземного газопровода с устройством гашения колебаний: а - устройство выключено из работы; б - устройство включено в работу
Таким образом, циклическое включение- выключение односторонней связи в процессе колебаний газопровода сопровождается циклической сменой его собственных форм, каждой из которых соответствует своя собственная частота. При включении односторонней связи в работу низшая собственная форма, отвечающая резонансной частоте юь заменяется следующей по номеру собственной формой с частотой ю2, более высокой по сравнению с основным тоном (со2 > Wi)- Данная форма с частотой аъ определяет движение системы в течение текущего полуцикла (рис. 26).
Реклама

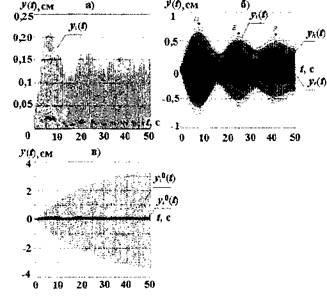
Рис. 3. Осциллограммы перемещения сечений в центре пролетов РДМ газопровода:
а - перемещения /-го сечения в пролете, где становлено устройство гашения; б - перемещения j'-го, fr-ro, г-го сечений (см. рис.2);
в - перемещения /-го сечения, где установлено устройство гашения \у° - перемещение в системе без устройства гашения; yf - перемещение с устройством гашения)
Теоретические исследования
Периодическая смена форм и частот приводит к автоматическому отстраиванию от резонансного режима. Поскольку процесс подавления низшей собственной формы происходит в каждом цикле колебаний, то резонансные амплитуды испытывают постоянные ограничения. Это не допускает развитие резонанса во времени и предопределяет эффективность работы устройства.
Для примера рассмотрен надземный газопровод высокого давления Кузнецкое-Байрамгулово, трасса которого пролегает через Аргаяшский район Челябинской области (труба 0 = 219 мм, шаг опор 1=15 м), где условия эксплуатации характеризуются повышенной аэродинамической активностью.
Динамический расчет выполнялся методом временного анализа, разработанным для дискретных диссипативных систем при нестационарных процессах [4]. Анализ параметров реакции расчетной модели газопровода осуществлялся при т = 11, q = 6, L = 15 м (рис. 3). Устройство гашения колебаний установлено в среднем (шестом) пролете расчетной схемы. Работу устройства можно оценить по осциллограммам перемещений для сечений г, г, k,j в центре пролетов: 6-го (рис. За), 5-го, 3-го и 1-го (рис. 36).
На рис. Зв приведено сравнение осциллограмм перемещений в базовой модели газопровода (у,°(0) и в модели с устройством гашения (у,(У)). Видно, что резонансные амплитуды в системе, где нет устройства гашения колебаний, непрерывно возрастают с течением времени. Включение односторонней связи в работу значительно снижает резонансные амплитуды, что свидетельствует об устойчивом характере колебаний. Так, для г-го сечения модели отношение максимальных резонансных амплитуд составило (t =50 с= 3,43/0,22 = 15,88.
По мере удаления от центрального пролета максимальные значения резонансных амплитуд средних сечений возрастают: у,(1) = 0,32 см (5-й пролет), y^t) = 0,65 см (3-й), y}(t) = 0,8 см (1-й) (рис. 36). Нумерация пролетов - слева направо и соответствует расчетной схеме, приведенной на рис. 2.
Реклама

Несмотря на рост амплитуд, все волнообразные огибающие резонансных амплитуд имеют максимальные значения перемещений для первой волны (точка D на осциллограмме перемещений у-го сечения (рис. 36)). В последующих волнах экстремумы (точки Е и F на рис. 36) на огибающих последовательно уменьшаются. Данный признак может служить показателем аэродинамической устойчивости динамической модели газопровода.
Выводы
Предложен способ гашения резонансных амплитуд в надземных газопроводах с помощью устройства односторонней связи.
Показана возможность вычисления реакции динамической системы с односторонней связью «газопровод - гаситель колебаний» при нестационарном процессе на основе временного анализа.
Построена аэродинамически устойчивая расчетная модель газопровода с максимальными резонансными амплитудами не более 0,8 см.
Список литературы
1 Динамический расчет сооружений на специальные воздействия // Справочник проектировщика. -М.: Стройиздат, 1981 - 216 с.
Бисплингхофф, Р.Л. Аэроупругость: монография / Р.Л. Бисплингхофф, X. Эшли, Р.Л. Халф- ман. - М.. ИЛ, 1958. - 799 с.
Потапов, А.Н. К вопросу об аэродинамической неустойчивости надземных газопроводов / А.Н. Потапов, А.Г Немелкова // Территория Неф- тегаз,-2005. - № 4.-С. 36-39
Потапов, А.Н. Динамический анализ дискретных диссипативных систем при нестационарных воздействиях: монография /А.Н. Потапов. - Челябинск: Изд-во ЮУрГУ, 2003. - 167 с.
|