Ю.М. Вишняков
В 60-70-х годах на теорию конечных автоматов (КА), как универсальный инструментарий описания и синтеза цифровых схем, возлагались большие надежды. Однако возможности технологического базиса и информационные технологии того времени ограничили практическое использование теории КА только рамками структурного синтеза. Абстрактный синтез так и остался предметом теоретических изысканий. Сегодня в автоматизированном проектировании происходит интенсивный переход к интегрированным инструментальным средствам, осуществляющим сквозную разработку проектов на всех уровнях. В таких системах наряду со стандартными средствами проектирования топологии и моделирования должны присутствовать и средства реализация проектных процедур логического синтеза. Таким образом сегодня сформированы практические потребности и имеются все условия, чтобы абстрактная теория КА заняла достойное место в автоматизированном проектировании. Однако в этом плане она должна быть переработана в контексте сквозного автоматизированного проектирования.
В рамках этой цели предлагаемая работа развивает абстрактный синтез в части построения непротиворечивых описаний КА на языке регулярных выражений.
Пусть заданы входной X={X1
,X2
,...,Xn
} и выходной Y={Y1
,Y2
,...,Ym
} алфавиты. КА перерабатывает входные слова (цепочки) aÎX* в выходные bÎY* в соответствии с алфавитным (автоматным) оператором b=F(a) (А-оператор). Доказано, что обрабатываемые КА множества цепочек, относятся к классу регулярных множеств (РМ), которые задаются через правила их порождения, называемые регулярными выражениями (РВ) [1].
В алгебре РВ по определению Æ, l (пустая цепочка), X1
, X2
, ..., Xn
являются элементарными РВ. Если e1
, e2
, e - РВ, то результаты операций e1
*e2 -
(конкатенации), e1
|e2
(ИЛИ), {e} (Клини), (e) (круглые скобки) также являются РВ. Также отметим, что порождаемое множество цепочек или язык РВ e обозначают через |e|.
Представим А-оператор через систему РВ (СРВ). Для этого выделим в X* подмножества регулярных цепочек E1
, E2
, ..., Em
(в общем случае бесконечных) таким образом, чтобы цепочка aÎE1
приводила к появлению на выходе КА буквы Y1,
aÎE2
- буквы Y2
, aÎEm
-.Ym
.
Для случая aÎX*\(E1
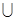 E2 E2
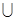 ... ...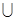 Em
) определим дополнительную букву Ym+1
. Также введем условие непротиворечивости Ei Em
) определим дополнительную букву Ym+1
. Также введем условие непротиворечивости Ei
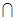 Ej
= Ej
=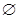 (i,j=1..m, i¹j). Представим каждое множество Ei
порождающим его регулярным выражением (РВ) ei
(|ei
|= Ei
). Тогда представляющая КА система соотношений вида (1) и называется СРВ: (i,j=1..m, i¹j). Представим каждое множество Ei
порождающим его регулярным выражением (РВ) ei
(|ei
|= Ei
). Тогда представляющая КА система соотношений вида (1) и называется СРВ:
Реклама

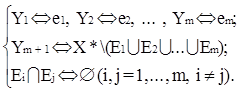 (1) (1)

Поскольку взаимно однозначное соответствие между языком и порождающим его РВ отсутствует (например, РВ а{a} и {a}a порождают различными способами один и тот же язык), построение непротиворечивой CРВ требует далеко нетривиальных действий. И в этой связи можно предположить, что средства исследования непротиворечивости СРВ нужно искать вне алгебры РВ.
Ближайшей моделью к РВ, которой может быть промоделирован разбор цепочек, является система переходов (СП), дуги которой взвешены буквами входного алфавита. КА с выходным алфавитом Y={0,1}, распознающий язык |e|, называют конечным распознавателем (КР). Представление КР в виде диаграммы состояний (рис.1), в которой начальная вершина S и конечная вершина Z связаны дугой e называется системой переходов (СП). Здесь любая цепочка aÎ|e| переводит КА из состояния S в состояние Z [2].
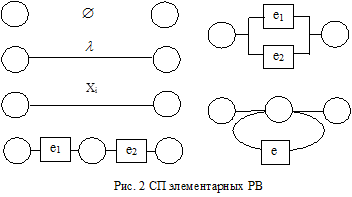
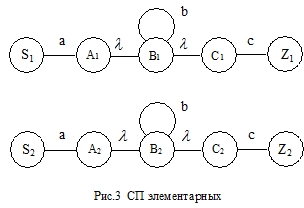
СП элементарных РВ приведены на рис.2. В соответствии с алгеброй РВ СП любого РВ e можно представить в виде композиции элементарных СП. Такую СП будем называть приведенной и обозначать через СПп
. Введем на СПп
ряд понятий.
Определение 1. Если из некоторого состояния Q исходит l-дуга в состояние A1
, из состояния A1
в состояние A2
и т.д. до состояния Т, а из состояния Т нет исходящих l-дуг, то будем говорить, что состояние Q связано с состоянием Т линейным l-путем.
Определение 2. Если из некоторого состояния Q исходит l-дуга в состояние А1
, а из состояния А1
в состояние А2
и т.д. состояния Ak
, а из состояния Ak
в состояние Q, то будем говорить, что состояние Q, A1
, A2
,..., Ak
входят в один и тот же кольцевой l-путь.
Длиной l-пути будем называть число входящих в него l-дуг.
Определение 3. Блоком состояний (БС) для некоторого состояния Q БС(Q) назовем множество состояний, включающих само состояние Q и все состояния , входящие в l-пути, исходящие из состояния Q.
Если из состояния Q не исходит l-путей, то БС(Q)= {Q}. В дальнейшем БС(Q), включающий более чем одно состояние, будем обозначать l- БС(Q).
Реклама

Определение 4. Если из состояния Q исходит один или несколько l-путей единичной длины, то l- БС(Q) назовем простым, в противном случае составным.
Введем на СП функцию разбора m, представляющую отображение {БС} Х ® БС. Ее по аналогии с функцией переходов запишем в виде БС=m(БС(Q),xi
). Цепочка a допускается КА, если существует функция разбора вида БС(Zi
)=m(БС(S),a), где S - начальное состояние, Zi
- заключительное состояние СП КА. Х ® БС. Ее по аналогии с функцией переходов запишем в виде БС=m(БС(Q),xi
). Цепочка a допускается КА, если существует функция разбора вида БС(Zi
)=m(БС(S),a), где S - начальное состояние, Zi
- заключительное состояние СП КА.
Пусть задана СРВ e1
, e2
, ..., em
и для каждого РВ выполнено независимое построение СПп
. Здесь S1
, S2
, ..., Sm
начальные и Z1
, Z2
, ..., Zm
заключительные состояния соответствующих СПп
. Введем следующую проверочную таблицу (ПТ), на основе которой будем одновременно строить функцию разбора для всех РВ. ПТ содержит m+1 столбец, где 1,2,...,m столбцы, соответствуют буквам входного алфавита X, а 0-столбец представляет БС, именующие строки. Множество строк ПТ разбито на группы, каждая из которых может содержать до m строк по числу РВ, и представляет БС для всех РВ, полученных на некотором шаге построения функции разбора. В клетку пересечения строки и столбца записывается вычисленное значение функции разбора для данного БС и входной буквы.
Алгоритм проверки непротиворечивости СРВ.
1. Построить пустую ПТ, сформировать БС(S1
), БС(S2
),..., БС(Sm
) и поименовать ими первую группу строк;
2. Для всех букв xi
ÎX вычислить функцию разбора;
3. Образовать новую группу строк и поименовать их новыми БС, полученными в п.2 и не содержащими заключительных состояний Zi
.
4. Повторять п.2 до тех пор, пока не перестанут образовываться новые БС, не содержащие заключительных состояний.
Выход: СРВ противоречива, если на некотором шаге для одной и той же входной буквы получены более чем один БС, содержащий заключительные состояния.
В качестве примера ниже представлены проверяемая на непротиворечивость СРВ, СП, входящих в нее РВ (рис.4), и соответствующая ПТ:
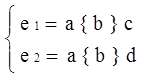 (2) (2)
Проверочная таблица
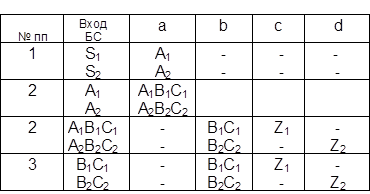
Как это видно из построения ПТ СРВ (2) является непротиворечивой.
Итак, предлагаемая в работе процедура проверки на непротиворечивость исходных описаний КА, может быть положена в основу построения одной из функциональных частей программной подсистемы логического синтеза интегрированной инструментальной среды САПР. Это позволит на ранних этапах проектирования выявить корректность исходного описания объекта проектирования.
Список литературы
Вавилов Е.Н., Портной Г.П. Синтез схем электронных цифровых машин. М.: Сов.радио, 1963. 440 с.
Грис Д. Конструирование компиляторов для цифровых вычислительных машин. М.: Мир, 1975, 545 с.
Вишняков Ю.М. Инструментарий разработчика СБИС. - Таганрог: ТРТУ, 1993. 178 с.
|