Тепловой расчет растепления грунтов в приустьевых зонах скважин
В.А. Ворков, С.А. Овчинникова, М.А. Федотенко
ОАО «Гипровостокнефть», г. Самара
Проектирование и эксплуатация объектов в местах распространения многолетнемерзлых грунтов является сложной инженерной задачей. Для обоснования возможности эксплуатации объектов необходимо проводить расчет растепления грунтов. В статье приведена методика расчета теплового поля в приустьевых зонах скважин. Решается задача нестационарного теплообмена с учетом смены теплофизических параметров грунтов.
В последние годы районы добычи нефти и газа все больше смещаются в сторону Восточной Сибири. В связи с перемещением районов промысла в области распространения многолетнемерзлых грунтов встает вопрос об учете их взаимодействия с проектируемыми сооружениями (здания, трубопроводные системы, скважины и т.д.). Проектирование сооружений в условиях вечномерзлых грунтов является сложной инженерной задачей, которая требует специального подхода, а также ставит необходимость в разработке собственного программного обеспечения или покупке расчетных комплексов для выполнения проектной документации. В настоящее время, как в России, так и за её пределами разработано большое количество расчетных методик для анализа температурного поля в областях распространения многолетнемерзлых грунтов [1]. Наряду с расчетными методиками, разрабатываются системы мониторинга температур для обеспечения дополнительной безопасности эксплуатации трубопроводных систем [2]. Одним из наиболее хорошо зарекомендовавших себя расчетных методов является метод конечных элементов (МКЭ), который является наиболее популярным приемом при проектировании и разработке различных систем в различных областях. Основными преимуществами метода являются:
универсальность, т.е. он применим к широкому кругу задач (прочностные расчеты, расчеты гидрогазодинамики, тепловые расчеты и т.д.);
отсутствие необходимости решать сложные дифференциальные уравнения (ссистема уравнений теории упругости и т.д.);
- большое количество разработанных при использовании метода конечных элементов
программных комплексов (Bentley AutoPIPE, ANSYS, MSC.Patran/Nastran и т.д.).
На сегодняшний день существует большое количество расчетных программ, основанных на МКЭ. Они могут обладать свойствами, необходимыми для решения каких-то конкретных задач. Например, программа Bentley AutoPIPE позволяет рассматривать только балочные системы трубопроводов. Наряду с узкоспециализированными расчетными комплексами существуют и универсальные инструменты. Наиболее популярным в настоящее время является расчетная программа ANSYS, которая обладает достаточным функционалом для решения широкого круга задач в различных областях (механика твердого деформированного тела, тепловые расчеты, механика жидкости и газа, электродинамика и т.д.).
Реклама

Одна из проблем при обустройстве и эксплуатации нефтяных скважин в районах распространения вечномерзлых грунтов - это тепловая деформация грунтов. Мерзлые грунты обладают специфическими реологическими, просадочными, пу- чинистыми и другими свойствами в зависимости от температуры. В связи с этим важной задачей является расчет тепловых полей нефтяных скважин на протяжении всего срока эксплуатации. На основании полученных данных можно делать выводы о безопасности работы рассматриваемого объекта. К решению теплотехнических задач существуют два подхода: стационарный [3] и нестационарный. Упрощенно говоря, стационарный тепловой расчет оценивает воздействие постоянных температурных воздействий на рассматриваемую систему, тогда как нестационарный определяет распределение температур и других тепловых величин. В данной работе применяется нестационарный тепловой анализ, как показывает практика стационарный расчет дает приемлемые результаты, но не позволяет получить данные в зависимости от времени, что очень часто является целью самого расчета.
Цель работы: разработать методику теплотехнического расчета грунтов в приустьевых зонах скважин для оценки их возможной эксплуатации в течении всего срока службы.
Для решения задачи о растеплении грунтов в приустьевых зонах скважин выбран программный комплекс ANSYS. Входными параметрами для расчета являются:
расположение скважин для расчета;
конструктивное исполнение скважин (теплотехнические данные о конструктивном исполнении колонн);
теплотехнические данные о мерзлых и талых грунтах в прилегающих районах к рассматриваемой области (коэффициенты тепловодности, массовая теплоемкость и плотность грунта в талом и мерзлом состоянии);
температурное распределение по глубине скважины;
климатические условия района проектирования (помесячное распределение температуры воздуха и высоты снежного покрова);
Реклама

данные о функционировании скважины (проектная производительность скважины, температура продукта, коэффициент теплопроводности продукта, плотность продукта, кинематическая вязкость продукта);
По исходным данным генерируется конечноэлементная расчетная модель для программного комплекса ANSYS. Для случая одиночной скважины может быть использована плоская модель с осесимметричной опцией. Выходными расчетными параметрами являются данные о тепловом распределении, по которым можно построить временные диаграммы на весь срок эксплуатации скважины. Данные о температурном поле позволяют сделать вывод о возможности эксплуатирования скважины с представленной в исходных данных конфигурацией.
Задача прогноза теплового взаимодействия скважин с многолетнемерзлыми породами приобрела особую актуальность в связи с освоением северных месторождений нефти и газа. За вторую половину XX века выполнено большое количество теоретических и экспериментальных исследований протаивания - промерзания пород вокруг скважин и связанных с этим процессов. Однако большинство из них имели дело с отдельной скважиной и не учитывали их совместное влияние на мерзлый массив при кустовом способе разработки месторождений [4, 5]. При определении влияния одиночной скважины на температурное поле грунтов может быть рассмотрена плоская модель. Для расчета взаимного влияния необходимо более сложные трехмерные модели. Построение трехмерных моделей не отличается большей сложностью по сравнению с плоскими, но вычисление результатов по ним требует намного больших компьютерных ресурсов [6]. Временные затраты могут различаться в сотни и даже тысячи раз.
Рассмотрим задачу о растеплении одиночной скважины, расположенной в зоне повсеместного распространения многолетнемерзлых грунтов. Конструкция добывающей скважины представлена на рис. 1. Для моделирования температурного взаимодействия модели «грунт-скважина» использовались плоские конечные элементы с осесимметричной опцией. Теплофизические параметры грунтов взяты по результатам инженерных изысканий.
Влияние окружающей среды учитывалось заданием конвективного теплообмена грунта с воздухом. Область моделирования является трехмерным фрагментом, ограниченным сверху дневной поверхностью, снизу плоскостью, расположенной на достаточно большой глубине, чтобы не оказывать влияния на процессы в интересующей части области.
Рассматриваемая область моделирования является трехмерным фрагментом, ограниченным сверху дневной поверхностью, снизу плоскостью, расположенной на достаточно большой глубине, чтобы не оказывать влияния на процессы в интересующей части области. Расчетная область представлена на рис. 2 для отображения включен режим осесимметричного поворота. В области расчета перпендикулярно дневной поверхности проходит ось скважины, пересекающая вертикально всю модель. Вдоль границы, соответствующей положению скважины, смоделирован слой тампонажного раствора посредством задания соответствующих теплофизических характеристик, заполняющий пространство между обсадными трубами и затруб- ное пространство.
На верхней границе расчетной области задаются условия конвективного теплообмена, позволяющие учитывать теплообмен грунта с атмосферой при наличии в зимнее время снежного покрова различной высоты. На левой вертикальной границе, соответствующей положению скважины, определена температура продукта и коэффициент теплоотдачи от продукта к эксплуатационной колонне. На нижней границе расчетной области принята постоянная температура грунта, согласно термометрическим данным. Решение задачи проводилось в нестационарной постановке. По результатам были получены температурные поля в самый теплый месяц года в течение всего срока эксплуатации скважины. Пример полученного температурного распределения представлен на рис. 3.
По данной методике проводились расчеты по проекту «0239 - Система сбора, подготовки, внутрипромыслового транспорта нефти и обустройства ВЧНГКМ. ПРМ. Фаза 4». Расчеты проверены государственной экспертизой, а по проекту принято положительное заключение. Для таких сложных инженерно-технических задач, как расчет растепления грунтов, очень важным является наличие точных и адекватных исходных данных. Это касается как данных, полученных по результатам инженерных изысканий, так и для теплотехнических данных перекачиваемых продуктов. Программный комплекс ANSYS позволяет учитывать реальные условия нагружения, но он, как и расчетчик, бессилен при неправильных входных данных. Ошибочные параметры не влияют в большинстве случаев на качественные результаты, но оказывают существенное влияние числовые данные для выходных значений. Так как в большинстве своем целью расчетов является не выявить теоретические закономерности, а получить конкретные цифры - достоверность входных параметров наряду с самой методикой является наиболее важной частью расчета.
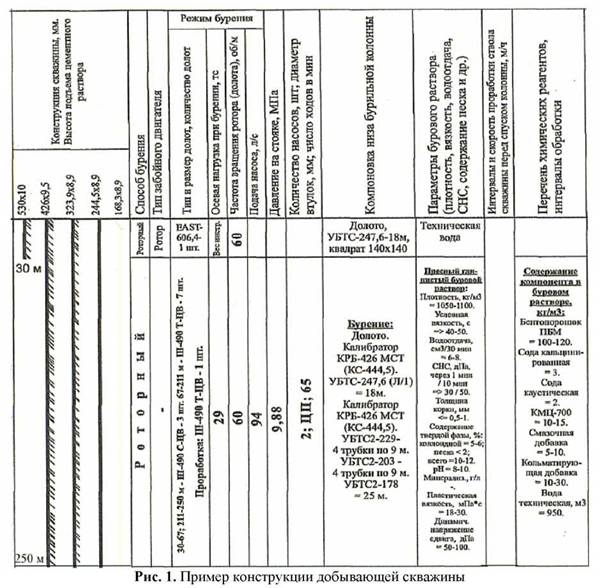
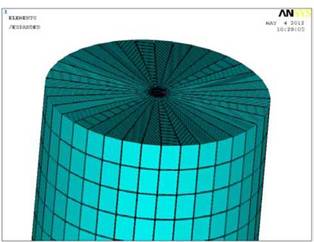
Рис. 2. Конечно-элементная модель
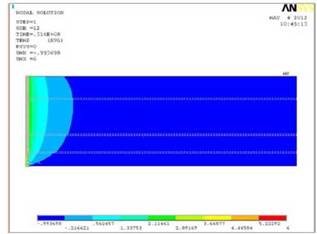
Рис. 3. Результаты расчета
Дополнительным затруднением при расчетах растепления являются как неполные данные по инженерным изысканиям, так и в некоторых случаях, полное их отсутствие. Для расчета двухфазного грунта, т.е. грунта в мерзлом и талом состоянии необходимы данные до и после растепления.
В некоторых расчетных областях фазовый переход происходит 2 раза в год, весной из мерзлого состояния в талое, а осенью наоборот. Значения расчетных значений для мерзлого и талого состояния грунта иногда сильно различаются, что вносит дополнительную погрешность в результаты расчета. В большинстве случаев приходится довольствоваться значениями из нормативных документов, которые соответствует этому типу грунта, а не натурными испытаниями образцов выработанных изыскателями.
Разработка численных расчетных методов включает в себя несколько последовательных этапов: подбор адекватной физической модели; численное моделирование расчетной модели; получение результатов работы; валидация решения. Последовательное выполнение всех этих этапов ведет к адекватному и точному решению. Однако расчеты производятся в большинстве своем в авральном порядке с минимальными временными затратами и порой одним человеком. Сложно сравнивать сложность и трудоемкость различных расчетов, но, к примеру, расчет, сопоставимый по сложности с расчетом в данной работе, выполнялся командой из нескольких инженеров в течение 5 месяцев [8]. В нашей практике сроки гораздо меньше. Следует отметить, что речь идет не о размерности задачи, а о поставленных сроках выполнения. Говорить о точности решения можно только после выполнения всех четырех этапов выполнения расчетов. Хорошим тоном при расчетах является проведение валидации расчета экспериментом или сопоставление его с существующими подтвержденными теоретическими моделями. К сожалению, в большинстве случаев мы не обладаем достаточными финансовыми и временными ресурсами для моделирования экспериментов, а тем более разработки валидирующих результаты расчетов теоретических обоснований.
Выводы: для проведения расчетов по определению температурного распределения необходимо использовать современные расчетные комплексы, которые позволяют учитывать широкий спектр граничных условий и условий нагружения.
Представленная методика очень чувствительна к исходным данным и требует экспериментального и теоретического подтверждения.
Список литературы
Пермяков, П.П. Расчет осадки грунтового основания нефтепровода ВСТО / П.П. Пермяков, А.П. Амосов, Г.Г. Попов // Энергетическая безопасность. 2011. №3. С. 52-54.
Паздерин, Д.С. Система мониторинга температур протяженных объектов в вечномерзлых грунтах / Д.С. Паздерин, Е.В. Амосова, Д.Ю. Кропачев // Технология транспорта нефти и газа. 2011. №4 (26) август. С. 3235.
Агафонов, А.В. Использование конечноэлементного анализа для расчета на прочность подземных трубопроводов с учетом тепловых деформаций грунтов / А.В. Агафонов, В.А. Ворков II Известия Самарского Научного Центра РАН. 2010. Т. 12, №4(3). С. 535-539.
Ермилов, ОМ. Сооружение и эксплуатация газовых скважин в районах Крайнего Севера / ОМ. Ермилов, Б.В. Дегтярев, А.Р. Курчиков. - Новосибирск: изд-во СО РАН, 2003. С. 222.
Медведский, Р.И. Строительство и эксплуатация скважин на нефть и газ в вечномерзлых породах. - М.: Недра, 1987. 230 с.
Горелик, Я.Б. Динамика протаивания мерзлых пород в зоне влияния двух скважин / Я.Б. Горелик, А.Б. Шаба- ров, Ю.С. Сысоев // Криосфера земли. 2008. Т. XII. №1. С. 59-65.
Васильев, Г.Г. Прокладка трубопроводов на много- летне-мерзлых грунтах с использованием грунтовых моделей / Г.Г. Васильев, М.А. Лежнев, Э.Н. Гайнулин // Наука и технологии трубопроводного транспорта нефти и нефтепродуктов. 2011. №3. С. 12-17.
Younger, Ray. Deep Thinking. ANSYS Advantage 2011. Volume V. Issue 2. P. 13-15.
|