| 
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«Самарский государственный
Технический университет»
|
К а ф е д р а «Высшая математика и
прикладная информатика»
ЛИНЕЙНАЯ АЛГЕБРА,
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ,
НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА.
Учебно-методическое пособие
по специальным разделам высшей математики
Самара 2005
Составители: Л.В. Лиманова, Л.А. МУРАТОВА
УДК 517.531, 519.2
Линейная алгебра, аналитическая геометрия, начала математического анализа.
Учебно-метод. пособ. по спец. главам высш. матем./ Самар. гос. техн. ун-т. Сост. Л.В. Лиманова,
Л.А. Муратова
. Самара, 2005. 49 с.
Представлены задачи и их решения из следующих разделов курса высшей математики: линейная алгебра, аналитическая геометрия, математический анализ.
Пособие предназначено для студентов всех специальностей СамГТУ.
Ил. . Библиогр.: 6 назв.
Печатается по решению редакционно-издательского совета СамГТУ
В соответствии с программой курса высшей математики для 1 семестра СамГТУ пособие охватывает такие разделы, как линейная алгебра, аналитическая геометрия, теория пределов, дифференциальное исчисление.
Пособие содержит тренировочный тест (стр.37) с типовыми задачами из указанных разделов.
Представлены подробные решения всех задач тренировочного теста, а также необходимый теоретический материал.
Пособие рекомендуется использовать для подготовки к экзамену по высшей математике. Внимательное изучение настоящего пособия позволит успешно справиться с этой задачей.
ЗАДАЧИ И РЕШЕНИЯ
Задача 1.
Найти сумму элементов 3-его столбца матрицы В
, если
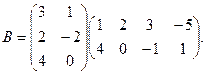
Решение.
При умножении матрицы размера 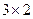 на матрицу размера на матрицу размера 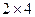 получится матрица размера получится матрица размера 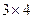 (3 строки и 4 столбца). Таким образом, в 3-м столбце будет 3 элемента: (3 строки и 4 столбца). Таким образом, в 3-м столбце будет 3 элемента: 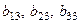 . Далее, умножение матриц осуществляется по правилу: элемент . Далее, умножение матриц осуществляется по правилу: элемент 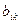 матрицы матрицы 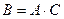 , стоящий в i
-той строке и к
-том столбце, равен сумме произведений соответствующих элементов i
-той строки матрицы А
и к
-го столбца матрицы С
. То есть, чтобы найти , стоящий в i
-той строке и к
-том столбце, равен сумме произведений соответствующих элементов i
-той строки матрицы А
и к
-го столбца матрицы С
. То есть, чтобы найти 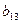 нужно 1-ю строку матрицы А
умножить на 3-й столбец матрицы С
: нужно 1-ю строку матрицы А
умножить на 3-й столбец матрицы С
:
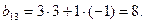
Аналогично, находим
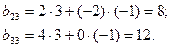
Тогда сумма этих элементов
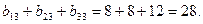
Задача 2.
Найти 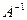 , если , если
Реклама

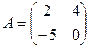 .
.
Решение.
Вычислим определитель матрицы А
:
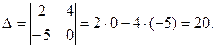
Так как 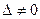 , то , то 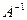 - существует. Обратную матрицу - существует. Обратную матрицу 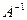 находим по схеме находим по схеме
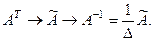
Здесь 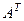 - транспонированная матрица, получается из матрицы А
, если поменять местами строки и столбцы: - транспонированная матрица, получается из матрицы А
, если поменять местами строки и столбцы:
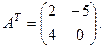
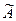 - союзная матрица, состоит из алгебраических дополнений элементов - союзная матрица, состоит из алгебраических дополнений элементов 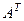 . .
Найдем алгебраические дополнения элементов 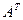 по формуле по формуле
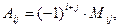
где 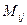 - минор - определитель, остающийся после вычеркивания строки i
и столбца j
матрицы - минор - определитель, остающийся после вычеркивания строки i
и столбца j
матрицы 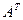 . .
Получим
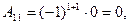 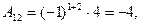
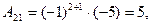 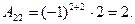
Итак,
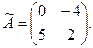
Наконец, находим обратную матрицу
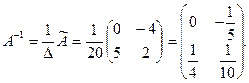
Задача 3.
Найти сумму элементов 3-ей строки матрицы 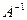 , если , если
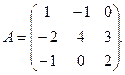
Решение.
Вычислим определитель матрицы А
:
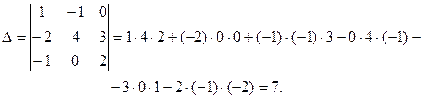
Запишем транспонированную матрицу
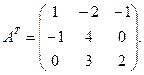
Так как надо найти сумму элементов 3-ей строки матрицы 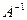 , достаточно определить алгебраические дополнения для 3-ей строки матрицы , достаточно определить алгебраические дополнения для 3-ей строки матрицы 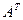 : :
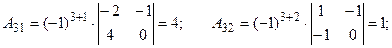
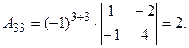
Тогда элементы 3-ей строки матрицы 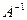 : :
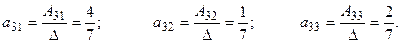
Их сумма равна 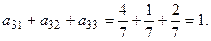
Задача 4.
Дана система уравнений
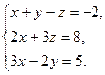
Найти 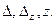
Решение.
Согласно формулам Крамера решение системы определяется соотношениями
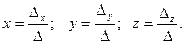
Найдем 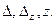
 - определитель из коэффициентов, стоящих перед неизвестными - определитель из коэффициентов, стоящих перед неизвестными
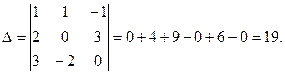
Чтобы найти 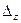 , необходимо элементы 3-его столбца определителя , необходимо элементы 3-его столбца определителя 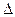 заменить на столбец свободных членов системы: заменить на столбец свободных членов системы:
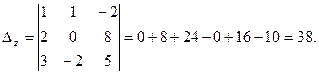
Находим z
:
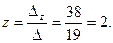
Задача 5.
Решить систему уравнений, приняв в качестве базисных переменных y
и z
:
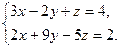
Решение.
Решаем систему методом Гаусса. Запишем расширенную матрицу системы – матрицу из коэффициентов при неизвестных и свободных членов.
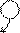   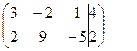 ~ ~ Среди коэффициентов при неизвестных есть 1, ей соответствует переменная z
. Назовем z
базисной переменной. Исключим базисную переменную z
из 2-го уравнения, для чего умножим 1-е уравнение на 5 и сложим со вторым. Получим эквивалентную исходной систему уравнений с матрицей
 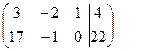 ~ ~
Умножим 2-е уравнение на (-1):
  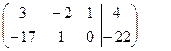 ~ ~ Считая новой базисной переменной у
, исключим её из 1-го уравнения. Для этого умножим 2-е уравнение на 2 и сложим с первым:
  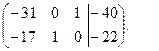
В каждом уравнении выбирают одну базисную переменную, оставшиеся переменные называют свободными (в данном случае это х
).
Запишем систему уравнений, соответствующую последней матрице:
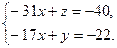
Выразив базисные переменные (у
и z
) через свободную (х
), получим общее решение системы уравнений
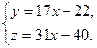
Задача 6. 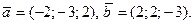 Найти
Найти 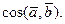
Решение.
Воспользуемся формулой
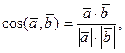
где 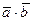 - скалярное произведение векторов - скалярное произведение векторов 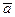 и
и 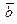 . .
Вычислим 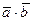 : :
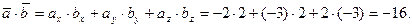
Найдем модули векторов
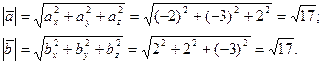
Тогда
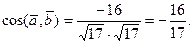
Задача 7.
Вектор 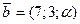 ортогонален вектору
ортогонален вектору 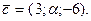 Найти
Найти 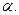
Решение.
Так как вектор 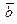 ортогонален вектору
ортогонален вектору 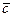 ,
то ,
то 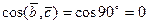 , и, значит, скалярное произведение этих векторов тоже равно нулю: , и, значит, скалярное произведение этих векторов тоже равно нулю:
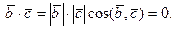
С другой стороны
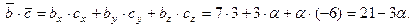
Итак,
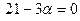 и
и 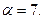
Задача 8.
Найти 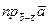 ,
если ,
если 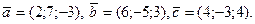
Реклама

Решение.
Проекция вектора 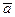 на вектор
на вектор 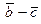 определяется по формуле
определяется по формуле
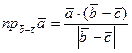 .
.
Найдем координаты вектора 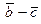 : :
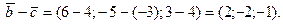
Вычислим скалярное произведение векторов 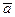 и
и 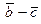
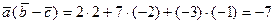
и модуль вектора 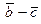
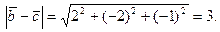
Тогда
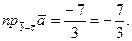
Задача 9.
Известно, что 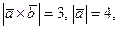 а угол между а угол между 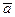 и
и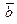 равен
равен 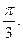 Найти Найти 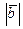 .
.
Решение.
Согласно определению векторного произведения 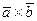 имеет место формула имеет место формула
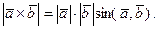
Тогда 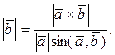
Подставив исходные данные, получим
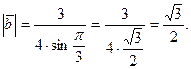
Задача 10.
Найти площадь треугольника с вершинами в точках 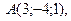 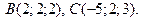
Решение.
Площадь треугольника, построенного на векторах 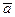 и
и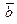 ,
может быть найдена по формуле: ,
может быть найдена по формуле:
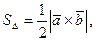
где
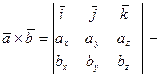 векторное произведение векторов векторное произведение векторов 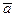 и
и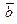 . .
Примем 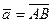 , , 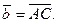 Вычислим координаты векторов Вычислим координаты векторов 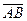 и и 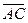 : :
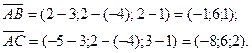
Найдем векторное произведение этих векторов
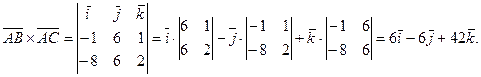
Тогда
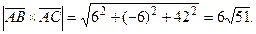
Следовательно,
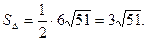
Задача 11.
Определить  , при котором компланарны векторы , при котором компланарны векторы 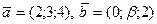 и
и 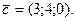
Решение.
Условие компланарности трех векторов имеет вид
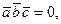
где 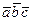 -
смешанное произведение векторов -
смешанное произведение векторов 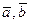 и
и 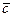 - вычисляется по формуле - вычисляется по формуле
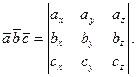
Подставляя исходные данные, получим
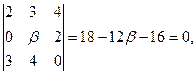 откуда откуда 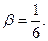
Задача 12.
Найти объём треугольной пирамиды с вершинами в точках 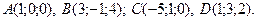
Решение.
Найдем координаты векторов 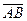 , ,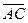 , ,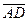 , на которых построена пирамида: , на которых построена пирамида:
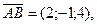 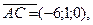 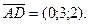
Вычислим смешанное произведение этих векторов
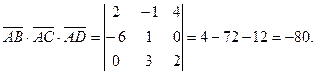
Объём треугольной пирамиды, построенной на векторах 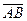 , ,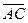 , ,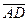 , равен , равен
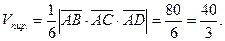
Задача 13.
Записать уравнение прямой, проходящей через точки 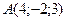 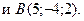
Решение.
Уравнение прямой, проходящей через две точки 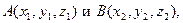 имеет вид имеет вид
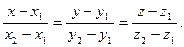
Подставляя координаты точек А
и В
, получим
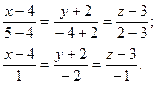
Задача 14.
Написать уравнение прямой, проходящей через точку 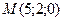 , перпендикулярно плоскости , перпендикулярно плоскости 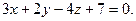
Решение.
Так как прямая перпендикулярна плоскости, то в качестве направляющего вектора 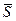 прямой можно взять нормальный вектор прямой можно взять нормальный вектор 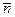 плоскости. плоскости.
Тогда
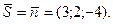
Поскольку уравнение прямой, проходящей через точку 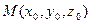 с направляющим вектором с направляющим вектором 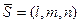 , имеет вид , имеет вид
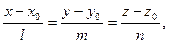
получим
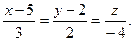
Задача 15.
Определить, при каких 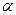 и и 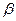 параллельны прямые параллельны прямые
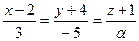 и и 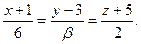
Решение.
Условие параллельности двух прямых – это условие коллинеарности их направляющих векторов 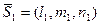 и и 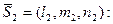
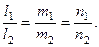
Подставляя координаты 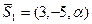 и и 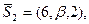 получим получим
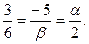
Тогда
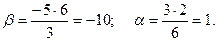
Задача 16.
Составить уравнение плоскости, проходящей через точки 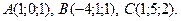
Решение.
Уравнение плоскости, проходящей через три точки 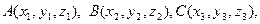 имеет вид имеет вид
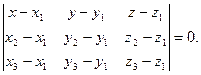
Вычисляем определитель
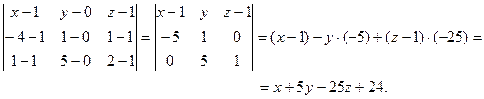
и получаем уравнение плоскости
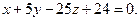
Задача 17.
Определить, при каком А
прямая 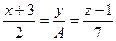 параллельна плоскости параллельна плоскости 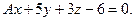
Решение.
Условие параллельности прямой и плоскости – это условие ортогональности направляющего вектора 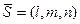 прямой и нормального вектора прямой и нормального вектора 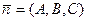 плоскости: плоскости:
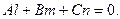
Применяя эту формулу для 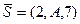 и и 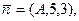 получим получим
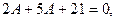 то есть то есть 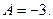
Задача 18.
Найти точку пересечения прямой
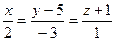
и плоскости 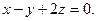
Решение.
Перейдем к параметрическим уравнениям прямой
 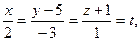 откуда откуда 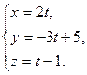
Найдем значение t
, соответствующее точке пересечения прямой и плоскости, для чего подставим полученные выражения в уравнение плоскости
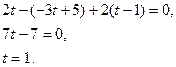
Подставляя 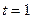 в параметрические уравнения прямой, найдем координаты точки пересечения прямой и плоскости в параметрические уравнения прямой, найдем координаты точки пересечения прямой и плоскости
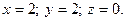
Задача 19.
Найти канонические уравнения прямой пересечения двух плоскостей
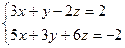
Решение.
Уравнение прямой пересечения двух плоскостей получим, решив совместно систему уравнений методом Гаусса.
Составим расширенную матрицу системы уравнений   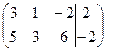 ~ ~
Возьмем у
в качестве базисной переменной и исключим у
из 2-го уравнения, для чего умножим 1-е уравнение на (-3) и сложим со вторым уравнением. Получим
 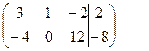 ~ ~
Разделим 2-е уравнение на (-4)
  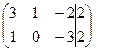 ~ ~ Возьмем в качестве следующей базисной переменной х
и исключим её из первого уравнения, умножив 2-е уравнение на (-3) и сложив с первым уравнением
  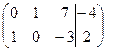
Запишем получившуюся систему уравнений:
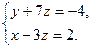
Выразим базисные переменные х
и у
через свободную переменную z
:
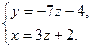
Обозначив 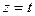 , получим параметрические уравнения прямой: , получим параметрические уравнения прямой:
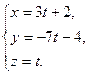
Исключив параметр 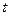 , перейдем к каноническим уравнениям прямой , перейдем к каноническим уравнениям прямой
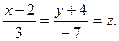
Задача 20.
Составить уравнение плоскости, проходящей через точки 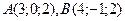 параллельно вектору параллельно вектору 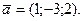
Решение.
Пусть 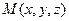 - произвольная точка искомой плоскости. Тогда векторы - произвольная точка искомой плоскости. Тогда векторы 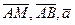 - компланарны. Запишем условие компланарности трех векторов: - компланарны. Запишем условие компланарности трех векторов:
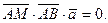
Так как
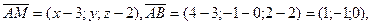
то
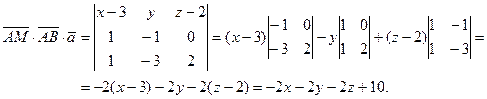 Тогда уравнение искомой плоскости будет иметь вид Тогда уравнение искомой плоскости будет иметь вид
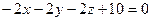 , или , или 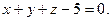
Задача 21.
Составить уравнение плоскости, проходящей через прямые
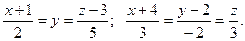
Решение.
Пусть 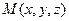 - произвольная точка искомой плоскости. Обозначим - произвольная точка искомой плоскости. Обозначим 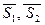 - направляющие векторы прямых, - направляющие векторы прямых, 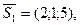 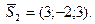 Уравнение искомой плоскости получим, записав условие компланарности векторов Уравнение искомой плоскости получим, записав условие компланарности векторов 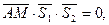 где А
– точка, лежащая в искомой плоскости (в качестве такой точки можно взять любую точку, принадлежащую любой из двух прямых, например, А
(-1; 0; 3). Так как где А
– точка, лежащая в искомой плоскости (в качестве такой точки можно взять любую точку, принадлежащую любой из двух прямых, например, А
(-1; 0; 3). Так как 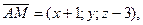 получим получим
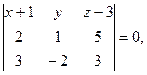 или или 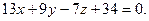
Задача 22.
Найти собственные значения матрицы
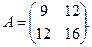
Решение.
Собственные значения 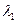 и и 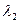 матрицы А
находим, решая характеристическое уравнение: матрицы А
находим, решая характеристическое уравнение:
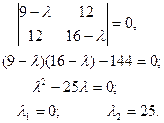
Задача 23.
Найти координаты вектора 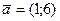 в базисе в базисе 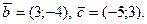
Решение.
При разложении вектора 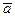 по базису по базису 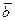 , , 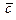 , необходимо представить , необходимо представить 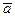 в виде в виде
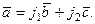
Здесь 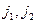 - есть координаты вектора - есть координаты вектора 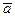 в базисе в базисе 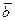 , , 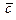 . .
Запишем это равенство в координатной форме
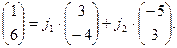
Оно равносильно системе уравнений
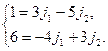
Решим систему, например, по формулам Крамера.
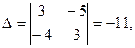 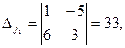 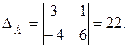
Тогда
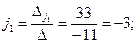 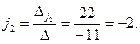
Значит, координаты вектора 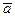 в базисе в базисе 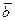 , , 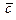
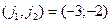 . .
Задача 24.
Определить вид и расположение кривой
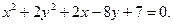
Решение.
Чтобы определить, какая кривая представлена данным уравнением, необходимо привести уравнение к каноническому виду. Для этого выделим полные квадраты при переменных x
и y
.
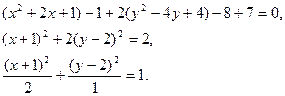
Полученное уравнение соответствует уравнению эллипса
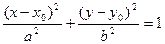
с полуосями 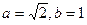 и центром в точке и центром в точке 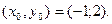
Задача 25.
Составить уравнение гиперболы, фокусы которой расположены на оси ординат симметрично относительно начала координат, если её действительная полуось равна 3, а расстояние между фокусами 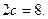
Решение.
Уравнение гиперболы, фокусы которой расположены на оси ординат симметрично относительно начала координат, имеет вид
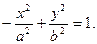
Действительная полуось этой гиперболы 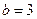 . Найдем а
из соотношения: . Найдем а
из соотношения:
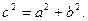
Так как 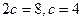 и и 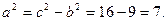
Итак, искомое уравнение гиперболы
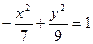 или или 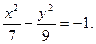
Задача 26.
Вычислить 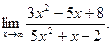
Решение.
Числитель и знаменатель дроби неограниченно возрастают при 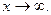 В этом случае говорят, что имеет место неопределенность вида В этом случае говорят, что имеет место неопределенность вида 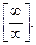 Разделим числитель и знаменатель дроби на старшую степень переменной, то есть на Разделим числитель и знаменатель дроби на старшую степень переменной, то есть на 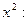
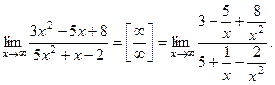
Так как при 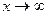 каждая из дробей каждая из дробей 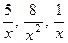 , ,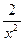 стремится к нулю, получим стремится к нулю, получим
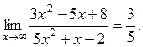
Задача 27.
Вычислить 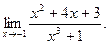
Решение.
При 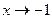 числитель и знаменатель дроби стремятся к 0. Это неопределенность вида числитель и знаменатель дроби стремятся к 0. Это неопределенность вида 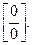 Разложим на множители числитель и знаменатель дроби и выполним сокращение: Разложим на множители числитель и знаменатель дроби и выполним сокращение:
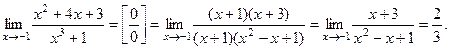
Задача 28.
Вычислить 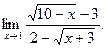
Решение.
В данном случае имеет место неопределенность вида 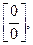 так как при так как при 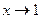 числитель и знаменатель стремятся к нулю. Умножим числитель и знаменатель дроби на выражения, сопряженные к ним, то есть на числитель и знаменатель стремятся к нулю. Умножим числитель и знаменатель дроби на выражения, сопряженные к ним, то есть на 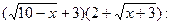
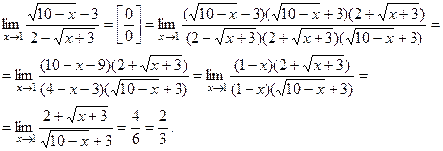
Задача 29.
Вычислить 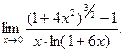
Решение.
При 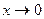 числитель и знаменатель – бесконечно малые величины. Заменим их эквивалентными бесконечно малыми. числитель и знаменатель – бесконечно малые величины. Заменим их эквивалентными бесконечно малыми.
Так как при 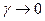 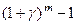 ~ ~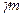 , , 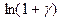 ~ ~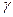 , то , то 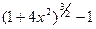 ~ ~ 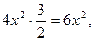 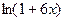 ~6x
. ~6x
.
Теперь можно воспользоваться формулой
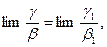 где где
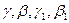 - бесконечно малые, причем - бесконечно малые, причем 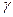 ~ ~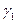 , , 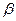 ~ ~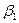 . .
Тогда
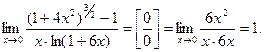
Задача 30.
Вычислить 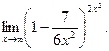
Решение.
Это неопределенность 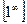 . Раскрываем её с помощью второго замечательного предела . Раскрываем её с помощью второго замечательного предела
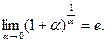
В данном случае 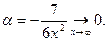 Поэтому Поэтому
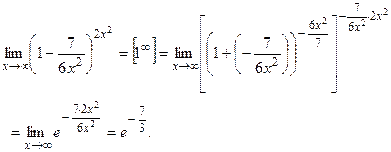
Задача 31.
Вычислить 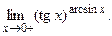
Решение.
При 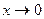 имеем неопределенность имеем неопределенность 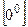 . .
Преобразуем выражение, используя свойства логарифмов:
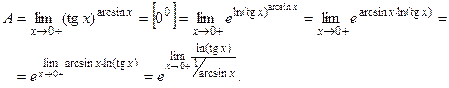
Так как 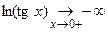 , , 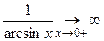 , имеем неопределенность , имеем неопределенность 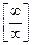 , которую раскрываем по правилу Лопиталя: , которую раскрываем по правилу Лопиталя:
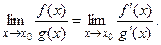
Тогда
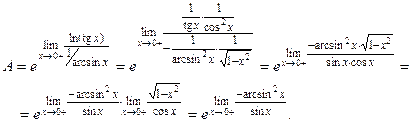
Так как 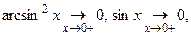 получили неопределенность получили неопределенность 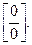 Её можно раскрыть, ещё раз применив правило Лопиталя, но проще использовать таблицу эквивалентных бесконечно малых: Её можно раскрыть, ещё раз применив правило Лопиталя, но проще использовать таблицу эквивалентных бесконечно малых:
при 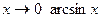 ~х
, ~х
, 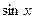 ~х
. ~х
.
Тогда 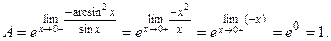
Задача 32.
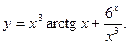 Найти Найти 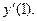
Решение.
Применяя формулы дифференцирования произведения и частного
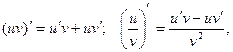
получим
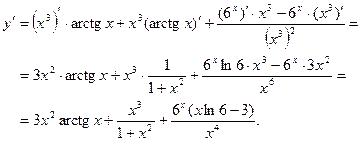
Подставим в производную 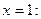
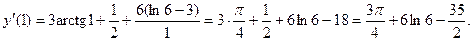 Замечание.
Здесь и далее используются формулы дифференцирования, приведенные в конце пособия. Замечание.
Здесь и далее используются формулы дифференцирования, приведенные в конце пособия.
Задача 33.
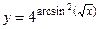 . Найти . Найти 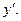
Решение.
Применим правило дифференцирования сложной функции: если 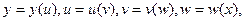 то то
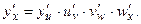
В данном случае
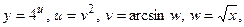
поэтому 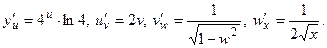
Тогда
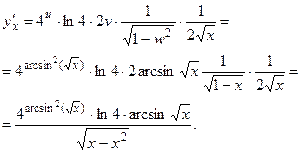
Задача 34.
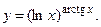 Вычислить Вычислить 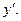
Решение.
Это показательно-степенная функция. Преобразуем её в показательную, используя свойства логарифмов:
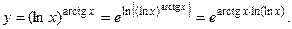
Получившуюся функцию дифференцируем как сложную
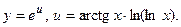
Тогда 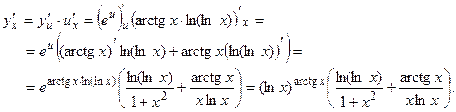
Задача 35.
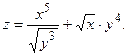 Вычислить Вычислить 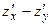 в точке в точке 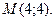
Решение.
Преобразуем данную функцию
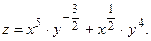
Вычислим частную производную 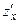 , считая у
константой: , считая у
константой:
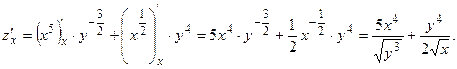
Найдем 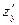 , считая х
константой: , считая х
константой:
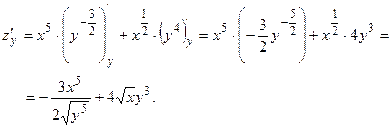
Подставим вместо х
и у
координаты точки 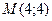
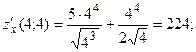 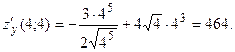
Тогда
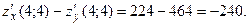
Задача 36.
Найти 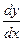 , если , если 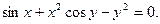
Решение.
Функция 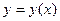 задана в неявном виде – уравнением задана в неявном виде – уравнением 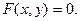 Воспользуемся формулой дифференцирования неявно заданной функции: Воспользуемся формулой дифференцирования неявно заданной функции:
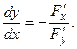
Так как
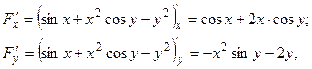
то
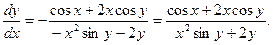
Задача 37.
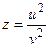 , где , где 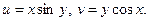 Найти Найти 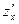 при при 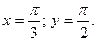
Решение.
Согласно формуле дифференцирования сложной функции
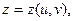 где где 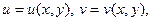
имеем
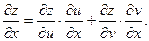
Так как
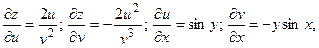 то то
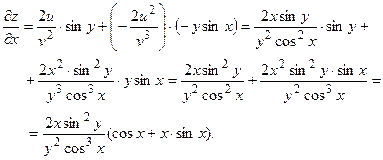
Тогда
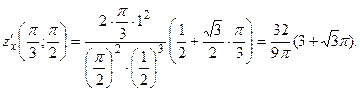
Задача 38.
Найти 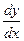 , если , если 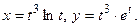
Решение.
Функция 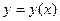 задана параметрически – уравнениями задана параметрически – уравнениями 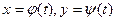 . .
В этом случае можно воспользоваться формулой
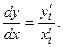
Так как
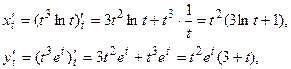
то
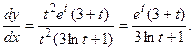
Задача 39.
Найти асимптоты кривой 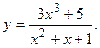
Решение.
Асимптоты бывают вертикальные и наклонные.
Прямая 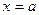 является вертикальной асимптотой кривой является вертикальной асимптотой кривой 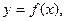 если если
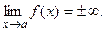
Прямая 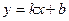 является наклонной асимптотой кривой является наклонной асимптотой кривой 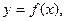 если существуют конечные пределы если существуют конечные пределы
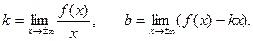
Так как знаменатель дроби 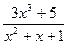 никогда не обращается в 0 (D
=-3<0), значит, не существует точек, обращающих саму дробь в бесконечность, и вертикальных асимптот нет. никогда не обращается в 0 (D
=-3<0), значит, не существует точек, обращающих саму дробь в бесконечность, и вертикальных асимптот нет.
Ищем наклонные асимптоты:
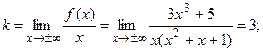
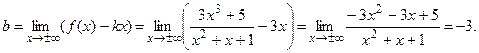
Тогда наклонная асимптота имеет вид
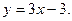
Задача 40.
Найти интервалы убывания функции
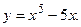
Решение.
Функция 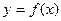 убывает, если убывает, если 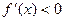 , и возрастает, если , и возрастает, если 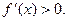 Найдем Найдем 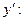
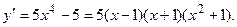
Определим знаки производной и промежутки монотонности функции:
Итак, функция убывает на интервале 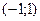 . .
Задача 41.
Найти интервалы выпуклости функции
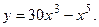
Решение.
Функция 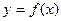 является выпуклой, если является выпуклой, если 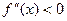 и вогнутой, если и вогнутой, если 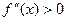 . Найдем . Найдем 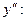
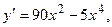
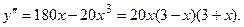
Определим знаки 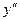 , а также промежутки выпуклости и вогнутости функции: , а также промежутки выпуклости и вогнутости функции:
Итак, функция выпукла при 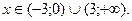
Задача 42.
Дана функция
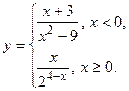
Найти точки разрыва и установить их характер.
Решение.
Функция 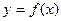 называется непрерывной в точке называется непрерывной в точке 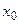 , если , если 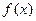 определена в некоторой окрестности этой точки и имеет в ней конечный предел, причем определена в некоторой окрестности этой точки и имеет в ней конечный предел, причем
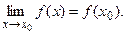
Последнее равенство означает, что
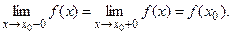
Точки, в которых не выполняется, хотя бы одно из перечисленных условий, называются точками разрыва функции 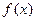 . Различают точки разрыва I и II рода. . Различают точки разрыва I и II рода.
Если 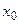 - точка разрыва и хотя бы один из односторонних пределов не существует или равен - точка разрыва и хотя бы один из односторонних пределов не существует или равен 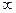 , то это разрыв II рода. , то это разрыв II рода.
В том случае, когда 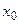 - точка разрыва, но односторонние пределы конечны, имеем разрыв I рода: - точка разрыва, но односторонние пределы конечны, имеем разрыв I рода:
устранимый, если 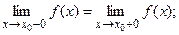
со скачком, если 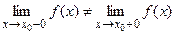
(величина скачка 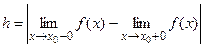 ). ).
Рассмотрим заданную функцию при 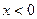 . Здесь . Здесь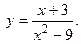 Функция не определена в точке Функция не определена в точке 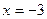 , значит в этой точке разрыв. , значит в этой точке разрыв.
Вычислим односторонние пределы:
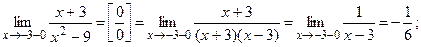
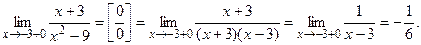
Итак, 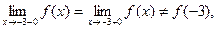 значит, при значит, при 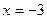 имеем устранимый разрыв I рода. имеем устранимый разрыв I рода.
Если 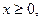 то то 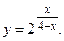 Функция не определена в точке Функция не определена в точке 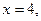 значит это точка разрыва. значит это точка разрыва.
Вычислим односторонние пределы.
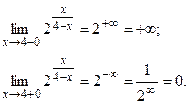
Так как 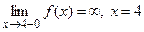 - точка разрыва II рода. - точка разрыва II рода.
В качестве точки, подозрительной на разрыв, следует рассмотреть 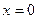 , так как при переходе через эту точку функция , так как при переходе через эту точку функция 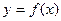 меняет свой вид. меняет свой вид.
В этой точке функция определена:
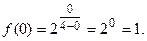
Найдем односторонние пределы:
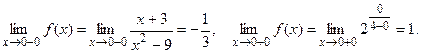
Итак, для точки 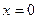 односторонние пределы конечны и различны, значит это разрыв I рода со скачком односторонние пределы конечны и различны, значит это разрыв I рода со скачком
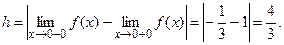
Таким образом, заданная функция имеет 3 точки разрыва: устранимый разрыв I рода при 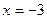 ; разрыв II рода при ; разрыв II рода при 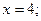 разрыв I рода со скачком при разрыв I рода со скачком при 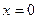 . .
Задача 43.
Найти максимальную скорость возрастания функции 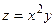 в точке М
(2;1). в точке М
(2;1).
Решение.
Известно, что максимальная скорость возрастания функции 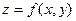 равна модулю градиента, а сам градиент – это вектор равна модулю градиента, а сам градиент – это вектор
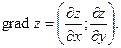
Найдем градиент функции 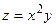 : :
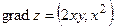
Вычислим градиент в точке М
(2;1):
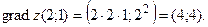
Тогда максимальная скорость возрастания функции
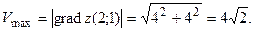
Задача 44.
Найти производную функции 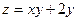 в точке М
(1;-3) в направлении вектора в точке М
(1;-3) в направлении вектора 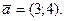
Решение.
Производная функции 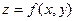 по направлению вектора по направлению вектора 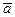 определяется по формуле определяется по формуле
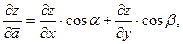
где 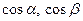 - направляющие косинусы вектора - направляющие косинусы вектора 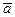 , ,
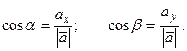
Найдем частные производные функции 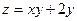 : :

Их значения в точке М
(1;-3) равны

Вычислим направляющие косинусы вектора 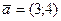
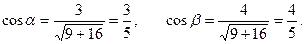
Тогда производная функции по направлению равна
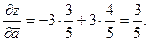
Задача 45.
Найти экстремум функции
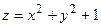 , ,
если 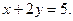
Решение.
I способ.
Необходимо найти экстремум функции 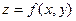 при условии, что переменные x
и y
подчиняются уравнению связи при условии, что переменные x
и y
подчиняются уравнению связи 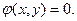
Составим функцию Лагранжа
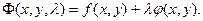
Точки экстремума находим, решая систему уравнений:
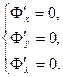
Так как 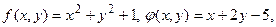 то то
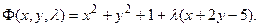
Находим 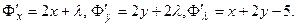
Решаем систему уравнений
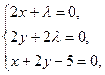 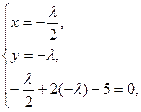 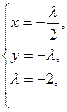 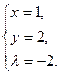
Итак, получена точка экстремума (1;2). Вычисляем 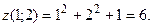 Определяем характер экстремума, сравнивая значение Определяем характер экстремума, сравнивая значение 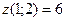 со значением функции в любой другой точке, удовлетворяющей условию со значением функции в любой другой точке, удовлетворяющей условию 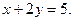 Например, Например, 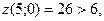 значит, в точке (1;2) – минимум. значит, в точке (1;2) – минимум.
II способ.
Преобразуем уравнение связи: 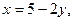 и подставим его в данную функцию и подставим его в данную функцию
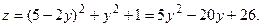
Получили функцию одной переменной у
. Исследуем её на экстремум:
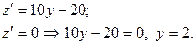
Определим знаки производной и промежутки монотонности функции:
Следовательно, точка 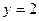 является точкой минимума. является точкой минимума.
Таким образом, функция 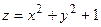 имеет минимум в точке с координатами имеет минимум в точке с координатами 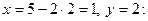
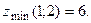
Задача 46.
Функцию 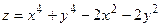 исследовать на экстремум в точках исследовать на экстремум в точках 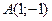 и и 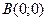 . .
Решение.
Функция  может достигать экстремума только в стационарной точке, то есть такой, что может достигать экстремума только в стационарной точке, то есть такой, что
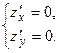
Найдем частные производные первого порядка
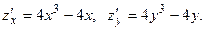
Подставив координаты точек 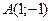 и и 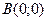 , убеждаемся, что обе точки стационарные. , убеждаемся, что обе точки стационарные.
А
: 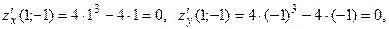
В
: 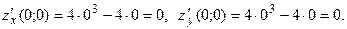
Согласно достаточным условиям экстремума в стационарной точке 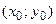 функция функция 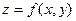 имеет имеет
1) минимум, если 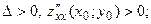
2) максимум, если 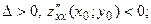
3) отсутствие экстремума, если 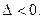
Здесь 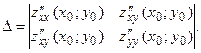
Вычисляем частные производные второго порядка
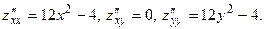
Рассмотрим точку 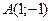 . .
Так как
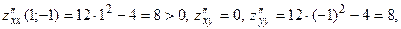
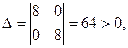 то в точке то в точке 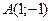 - минимум. - минимум.
Рассмотрим точку 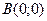 . .
Так как
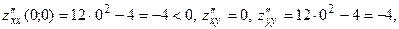
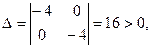 то в точке то в точке  - максимум. - максимум.
ТРЕНИРОВОЧНЫЙ ТЕСТ
| №
|
Задания
|
Варианты ответов
|
| 1
|
2
|
3
|
4
|
5
|
| 1
|
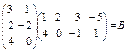 Найти сумму элементов Найти сумму элементов
3 столбца матрицы В
.
|
34
|
-18
|
28
|
-26
|
14
|
| 2а
|
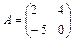 . Найти . Найти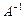 . .
|
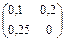
|
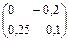
|
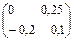
|
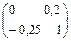
|
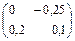
|
| 2б
|
Найти сумму элементов 3 строки матрицы 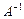 , если , если 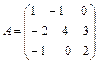 . .
|
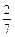
|
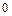
|
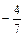
|
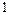
|
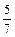
|
| 3а
|
Дана система уравнений
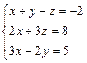 . .
Найти 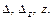
|
19,-38,-2
|
19,-19,-1
|
19,38,2
|
19,19,1
|
19,57,3
|
| 3б
|
Решить систему уравнений 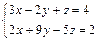 , ,
приняв в качестве базисных переменных 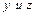 : :
|
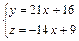
|
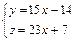
|
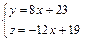
|
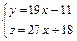
|
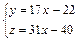
|
| 4а
|
Найти 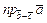 , если , если 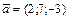 , , 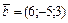 , , 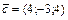 . .
|
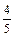
|
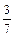
|
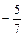
|
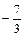
|
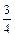
|
| 4б
|
Вектор 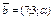
ортогонален вектору 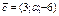 . .
Найти 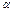 . .
|
7
|
-1
|
5
|
9
|
-3
|
| 4в
|
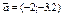 , , 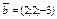 . .
Найти 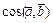 . .
|
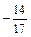
|
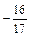
|
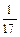
|
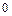
|
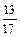
|
| 5а
|
Найти площадь треугольника с вершинами в точках 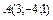 , , 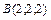 , , 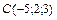 . .
|
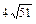
|
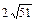
|
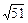
|
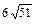
|
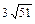
|
| 5б
|
Известно, что 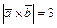 , , 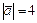 , а угол между , а угол между 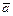 и и 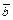 равен равен 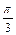 . Найти . Найти 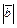 . .
|
0
|
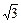
|
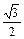
|
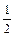
|
1
|
| 6а
|
Определить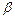 , при котором компланарны векторы , при котором компланарны векторы 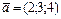 , , 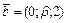 , , 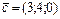 . .
|
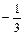
|
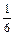
|
1
|
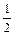
|
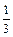
|
| 6б
|
Найти объем треугольной пирамиды с вершинами в точках 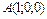 , , 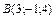 , , 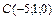 , , 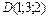 . .
|
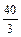
|
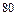
|
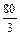
|
40
|
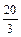
|
| 7а
|
Уравнение прямой, проходящей через точки 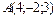 и и 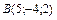 имеет вид: имеет вид:
|
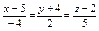
|
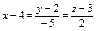
|
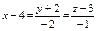
|
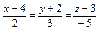
|
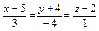
|
| 7б
|
Уравнение прямой, проходящей через точку 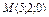 перпендикулярно плоскости перпендикулярно плоскости  имеет вид: имеет вид:
|
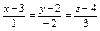
|
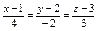
|
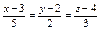
|
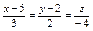
|
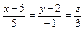
|
| 7в
|
Определить, при каких 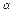 и и 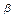 параллельны прямые параллельны прямые 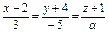 и и 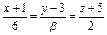
|
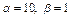
|
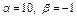
|
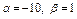
|
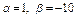
|
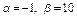
|
| 8а
|
Составить уравнение плоскости, проходящей через точки 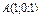 , , 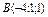 , , 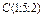 . .
|
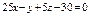
|
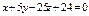
|
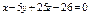
|
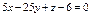
|
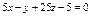
|
| 8б
|
Определить, при каком 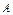 прямая прямая 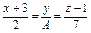 параллельна плоскости параллельна плоскости 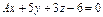 . .
|
1
|
-7
|
-3
|
2
|
5
|
| 9а
|
Найти собственные значения матрицы 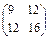
|
0 и 25
|
1 и 9
|
0 и 20
|
5 и 25
|
20 и 25
|
| 9б
|
Найти координаты вектора 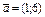 в базисе в базисе 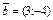 , , 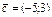 . .
|
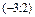
|
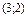
|
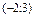
|
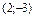
|
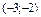
|
| 9в
|
Определить вид и расположение кривой 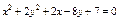
|
Гипербола с центром в точке 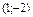
|
Парабола с вершиной в точке 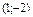
|
Эллипс с центром в точке 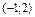
|
Гипербола с центром в точке 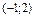
|
Эллипс
с центром в
точке 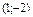
|
| 9г
|
Составить уравнение гиперболы, фокусы которой расположены на оси ординат симметрично относительно начала координат, если ее действительная полуось 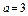 , а расстояние между фокусами , а расстояние между фокусами 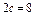 . .
|
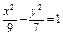
|
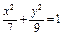
|
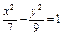
|
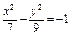
|
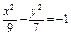
|
| 10а
|
Найти точку пересечения прямой 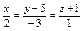 и плоскости и плоскости 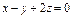
|
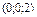
|
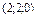
|
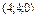
|
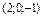
|
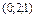
|
| 10б
|
Канонические уравнения прямой пересечения двух плоскостей 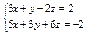 имеют вид: имеют вид:
|
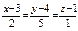
|
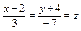
|
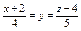
|
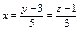
|
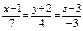
|
| 10в
|
Составить уравнение плоскости, проходящей через точки 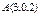 , , 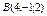 параллельно вектору параллельно вектору 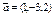 . .
|
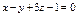
|
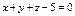
|
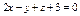
|
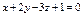
|
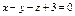
|
| 10г
|
Составить уравнение плоскости, проходящей через прямые: 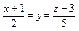 , , 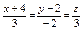
|
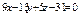
|
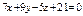
|
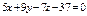
|
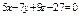
|
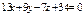
|
| 11а
|
Вычислить 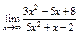
|
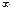
|
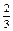
|
-5
|
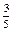
|
-4
|
| 11б
|
Вычислить 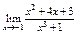
|
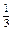
|
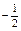
|
0
|
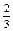
|
1
|
| 11в
|
Вычислить 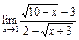
|
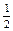
|
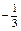
|
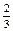
|
-1
|
0
|
| 12
|
Вычислить 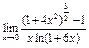
|
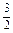
|
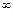
|
0
|
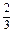
|
1
|
| 13
|
Вычислить 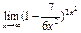
|
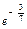
|
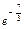
|
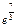
|
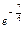
|
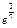
|
| 14
|
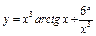 . Найти . Найти 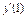 . .
|
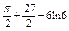
|
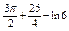
|
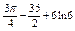
|
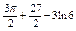
|
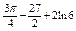
|
| 15
|
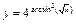 . .
Найти 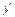 . .
|
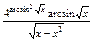
|
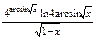
|
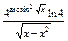
|
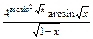
|
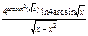
|
| 16
|
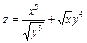 . Вычислить . Вычислить  в точке в точке  . .
|
-240
|
180
|
210
|
-160
|
280
|
| 17а
|
Найти 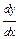 , если , если 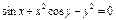 . .
|
0
|
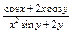
|
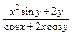
|
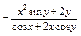
|
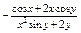
|
| 17б
|
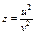 , где , где 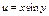 , , 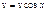 . Найти . Найти 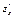 при при 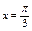 , , 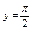 . .
|
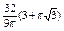
|
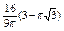
|
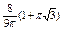
|
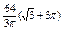
|
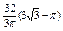
|
| 17в
|
Найти 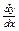 , если , если 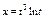 , , 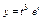 . .
|
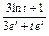
|
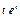
|
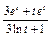
|
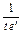
|
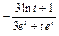
|
| 18а
|
Найти асимптоты кривой 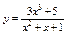 . .
|
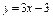
|
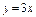
|
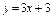
|
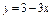
|
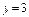
|
| 18б
|
Найти интервал(ы) убывания функции 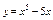 . .
|
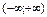
|
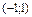
|
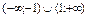
|
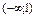
|
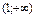
|
| 18в
|
Найти интервал(ы) выпуклости функции 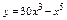 . .
|
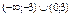
|
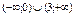
|
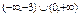
|
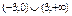
|
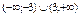
|
| 18г
|
Дана функция
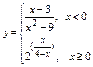 . Найти точки разрыва и установить их характер. . Найти точки разрыва и установить их характер.
|
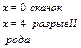
|
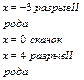
|
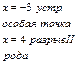
|
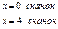
|
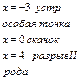
|
| 19а
|
Найти максимальную скорость возрастания функции 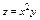 в точке в точке 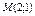 . .
|
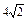
|
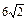
|
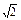
|
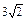
|
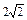
|
| 19б
|
Найти производную функции 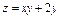 в точке в точке 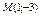 в направлении вектора в направлении вектора 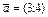 . .
|
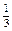
|
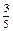
|
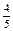
|
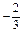
|
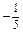
|
| 19в
|
Найти экстремум функции 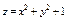 , если , если 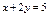 . .
|
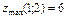
|
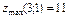
|
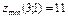
|
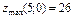
|
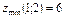
|
| 19г
|
Функцию 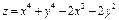 исследовать на экстремум в точках исследовать на экстремум в точках 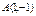 и и 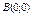 . .
|
А- точка максимума
В – точка максимума
|
А – точка минимума
В не является точкой экстремума
|
А- точка максимума
В – точка минимума
|
А- точка минимума
В – точка максимума
|
А – точка минимума
В – точка минимума
|
| 20а
|
Вычислить 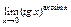 . .
|
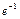
|
0
|
1
|
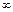
|
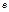
|
| 20б
|
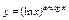 . Вычислить . Вычислить 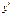 . .
|
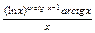
|
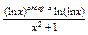
|
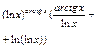
|
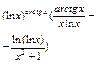
|
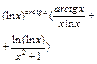
|
| № задания
|
1
|
2а
|
2б
|
3а
|
3б
|
4а
|
4б
|
4в
|
5а
|
5б
|
6а
|
6б
|
7а
|
7б
|
7в
|
| Правильный ответ
|
3
|
2
|
4
|
3
|
5
|
4
|
1
|
2
|
5
|
3
|
2
|
1
|
3
|
4
|
4
|
| № задания
|
8а
|
8б
|
9а
|
9б
|
9в
|
9г
|
10а
|
10б
|
10в
|
10г
|
11а
|
11б
|
11в
|
12
|
13
|
14
|
| Правильный ответ
|
2
|
3
|
1
|
5
|
3
|
4
|
2
|
2
|
2
|
5
|
4
|
4
|
3
|
5
|
2
|
3
|
| № задания
|
15
|
16
|
17а
|
17б
|
17в
|
18а
|
18б
|
18в
|
18г
|
19а
|
19б
|
19в
|
19г
|
20а
|
20б
|
| Правильный ответ
|
5
|
1
|
2
|
1
|
3
|
1
|
2
|
4
|
5
|
1
|
2
|
5
|
4
|
3
|
5
|
ТАБЛИЦА ПРОИЗВОДНЫХ ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
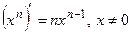 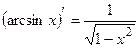
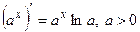 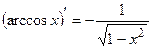
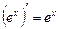 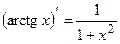
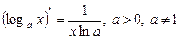 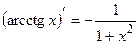
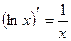 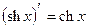
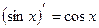 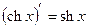
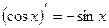 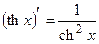
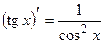 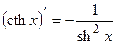
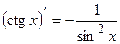
Правила дифференцирования функций
Пусть 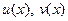 - дифференцируемые функции, - дифференцируемые функции, 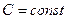 . Тогда . Тогда
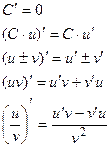
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- Задачи и упражнения по математическому анализу. Под ред. Б.П.Демидовича. М.:Наука, 1970. 472 с.
- Самарин Ю.П., Сахабиева Г.А. Математика-2 для студентов вузов. Самара, 2000. 96 с.
- Самарин Ю.П., Сахабиева Г.А. Математика-3 для студентов вузов. Самара, 2000. 45 с.
- Самарин Ю.П., Сахабиева Г.А. Математика-4 для студентов вузов. Самара, 2000. 84 с.
- Сборник задач по математике. Болгов В.А., Демидович Б.П., Ефимов А.В. и др. М.: Наука, 1993. 480 с.
- Фихтенгольц Г.М. курс дифференциального и интегрального исчисления. т.1.М.: Наука, 1970. 608 с.
ОГЛАВЛЕНИЕ
1. Задачи и решения ………………………………………………4
2. Тренировочный тест ………………………………….............37
3. Таблицы производных ………………………………………..47
4. Библиографический список…………………………………..48
|