| Санкт-Петербургский государственный университет телекоммуникаций
имени проф. М.А. Бонч-Бруевича
Курсовая работа по Передаче Дискретных Сообщений
«ПРОЕКТИРОВАЕНИЕ КОДИРУЮЩЕГО УСТРОЙСТВА ЦИКЛИЧЕСКОГО КОДА»
Выполнил студент гр ФП-91
Мишланов Дмитрий
Санкт-Петербург
2002
Задание на курсовую работу
Целью данной курсовой работы является изучение принципов построения циклических кодов и реализация кодирующего устройства.
Исходные данные.
Задан обнаруживающий ошибки циклический код (15,5).
Образующий полином P(x)= x10
+x9
+x8
+x6
+x5
+x3
+x2
+x+1
n= 25 = 11001
Основные определения и необходимые сведения
о циклических кодах.
Введение избыточности (добавление проверочных разрядов) является одним из методов борьбы с ошибками, возникающими в канале передачи данных. Избыточные (корректирующие) коды строят таким образом, что для передачи информации используется лишь часть кодовых комбинаций (разрешенные), отличающиеся друг от друга более чем в одном разряде. Все остальные комбинации не используются для передачи и относятся к числу неразрешенных.
При использовании корректирующих кодов ошибка в одном разряде приводит к замене разрешенной кодовой комбинации комбинацией неразрешенной, что позволяет обнаружить ошибку.
Коды, корректирующие ошибки, делятся на блочные и непрерывные.
Блочные разбивается на отдельные кодовые комбинации (блоки), которые кодируются и декодируются независимо друг от друга.
Блочные коды подразделяются на систематические и несистематические.
Систематические – те, в которых одни разряды являются информационными, другие – проверочными. Они обозначаются как (n,k) – коды, где n – длина или общее число разрядов кода; k – число информационных разрядов.
Двоичные блочные коды называются линейными, когда сумма по модулю 2 двух разрешенных кодовых комбинаций является также разрешенной комбинацией. К линейным кодам относятся циклические коды, обладающие корректирующими свойствами.
Циклические коды
относятся к блочным систематическим кодам. Они обеспечивают обнаружение и исправление, как независимых ошибок (одиночных и многократных), так и пачек ошибок. Основное свойство рассматриваемых кодов: если кодовая комбинация принадлежит циклическому коду, то комбинации, полученные циклической перестановкой элементов, также принадлежат этому коду.
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
Общим свойством всех разрешенных кодовых комбинаций циклических кодов является их делимость без остатка на некоторый выбранный полином, называемый производящим. Синдромом ошибки в этих кодах является наличие остатка от деления принятой кодовой комбинации на этот полином. Для того чтобы полиномы имели нужные свойства необходимо выполнение условия: полиномы должны быть неприводимыми, т.е. не делится ни на какой другой полином.
Основные характеристики кода.
1) Весом кодовой комбинации называется число единиц в ней.
2) Если две кодовые комбинации отличаются друг от друга, то мера этого отличия – кодовое расстояние. Оно определяется как число разрядов, в которых различаются эти кодовые комбинации. Наименьшее из всех кодовых расстояний в коде называется минимальным расстоянием dmin
. Минимальное кодовое расстояние связано с числом или кратностью обнаруживаемых s и исправляемых t ошибок следующим образом:
Dmin
>= s + 1
Dmin
>= 2t +1
3) Общее число всевозможных комбинаций кода длины n равно: N=2n
. Число разрешенных кодовых комбинаций определяется числом информационных разрядов и равно: M=2k
=2n
-
r
, где r- число проверочных разрядов. Таким образом, число разрешенных кодовых комбинаций в 2r
раз меньше общего числа комбинаций.
Анализ возможностей заданного циклического кода
Первой операцией построения циклического кода является умножение на x10
информационного полинома. Умножению информационного полинома на x10
соответствует добавление справа 10 нулей к двоичному представлению этого полинома.
Нахождение остатка от деления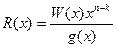 
  110010000000000 11101101111
  11101101111
001001011110 10110
 00000000000
010010111100
11101101111
 011110100110
11101101111
 000110010010
00000000000
 00110010010 R(x)=0110010010
2.1Составление порождающей матрицы и матрицы проверок
Образующий полином :
P(x)= x10
+x9
+x8
+x6
+x5
+x3
+x2
+x+1
Составим порождающую матрицу G состоящую из единичной и проверочной матриц.
10000 1111011011
01000 1000110110 00100 0100011011
00010 1101010110
 00001 0110101011
Количество разрешенных кодовых комбинаций = 2k
=32. Где к=5.
Найдем матрицу проверок Н(15,10)
. Она будет состоять из единичной матрицы размерностью 10x10 и матрицы размерности 10x5, которая получается из матрицы 5x10, составленной из проверочных элементов, входящих в матрицу G(15,5)
путем ее транспонирования.
11010 1000000000
Сервис онлайн-записи на собственном Telegram-боте
Попробуйте сервис онлайн-записи VisitTime на основе вашего собственного Telegram-бота:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно.
Зарегистрироваться в сервисе
10111 0100000000
10001 0010000000
10010 0001000000
01001 0000100000
Н(15,10)
= 11110 0000010000
10101 0000001000
01010 0000000100
11111 0000000010
 10101 0000000001
Согласно свойству циклического кода dmin
равно минимальному числу линейно зависимых столбцов матрицы проверок, т.е. минимальному числу столбцов поразрядная сумма по mod(2) равна нулю.
dmin
= 5
2.2Составление таблицы всех разрешенных кодовых комбинаций и определение их веса
Для получения 32 разрешенных кодовых комбинаций необходимо воспользоваться образующей матрицей, где 5 разрешенных комбинаций имеются в явном виде, а остальные разрешенные комбинации получаются при помощи сложения в различных сочетаниях строк этой матрицы.
Таблица всех разрешенных
,
ненулевых комбинаций
| чв
|
№к
|
№строки
|
Разрешённые кодовые комбинации (КК)
|
Вес
|
| И
|
Н
|
Ф
|
О
|
Р
|
П
|
Р
|
О
|
В
|
Е
|
Р
|
О
|
Ч
|
Н
|
Ые
|
| 
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
7
|
| 2
|
2
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
7
|
| 3
|
3
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
6
|
| 4
|
4
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
6
|
| 5
|
5
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
9
|
| 
|
6
|
1Å2
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
1
|
10
|
| 7
|
1Å3
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
5
|
| 8
|
1Å4
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
9
|
| 9
|
1Å5
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
6
|
| 10
|
2Å3
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
7
|
| 11
|
2Å4
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
5
|
| 12
|
2Å5
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
6
|
| 13
|
3Å4
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
8
|
| 14
|
3Å5
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
5
|
| 15
|
4Å5
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
9
|
| 
|
16
|
1Å2Å3
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
10
|
| 17
|
1Å2Å4
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
8
|
| 18
|
1Å2Å5
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
7
|
| 19
|
2Å3Å4
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
9
|
| 20
|
2Å3Å5
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
8
|
| 21
|
1Å3Å5
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
10
|
| 22
|
4Å5Å1
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
6
|
| 23
|
4Å5Å2
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
1
|
0
|
1
|
10
|
| 24
|
3Å5Å4
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
9
|
| 25
|
1Å3Å4
|
1
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
7
|
| 
|
26
|
1Å2Å3Å4
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
8
|
| 27
|
1Å2Å3Å5
|
1
|
1
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
9
|
| 28
|
2Å3Å4Å5
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
8
|
| 29
|
3Å4Å5Å1
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
1
|
0
|
1
|
0
|
10
|
| 30
|
1Å4Å5Å2
|
1
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
7
|
| 
|
31
|
1Å2Å3Å4Å5
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
9
|
| Кратность ошибки
|
Число вариантов комбинации ошибок кратности
|
Число вариантов комбинацийошибок приводящих к НО
|
Доля НО
|
| 1
|
15
|
0
|
0
|
| 2
|
105
|
0
|
0
|
| 3
|
455
|
0
|
0
|
| 4
|
1365
|
0
|
0
|
| 5
|
3003
|
3
|
0,001
|
| 6
|
5005
|
5
|
0,001
|
| 7
|
6435
|
6
|
0,001
|
| 8
|
6435
|
5
|
0,0008
|
| 9
|
5005
|
7
|
0,0014
|
| 10
|
3003
|
5
|
0,0017
|
| 11
|
1365
|
0
|
0
|
| 12
|
455
|
0
|
0
|
| 13
|
105
|
0
|
0
|
| 14
|
15
|
0
|
0
|
| 15
|
1
|
0
|
0
|
Dmin
=5
5>= s + 1 Þ s=4 кратность обнаружения ошибок
5>= 2t +1 Þ t = 2 кратность исправления ошибок
I.
Разработка схемы кодирующего устройства
Декодирующее устройство – это регистр сдвига с обратной связью. Количество триггеров регистра равно степени образующего полинома. Число сумматоров в регистре равно количеству знаков + в выражении для образующего полинома. Сумматоры ставятся перед триггерами, соответствующими ненулевым членам образующего полинома.
Таблица состояний регистра сдвига кодера цикличесого кода.
| №такта
|
G(x)
|
Т1
|
Т2
|
Т3
|
Т4
|
Т5
|
Т6
|
Т7
|
Т8
|
Т9
|
Т10
|
F(x)
|
| 1
|
1
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
| 2
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
| 3
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
| 4
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
| 5
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
|  6
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
| 7
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
| 8
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
| 9
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
| 10
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
| 11
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
| 12
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
| 13
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
| 14
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
| 15
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
Для обнаружения ошибок в принятой кодовой комбинации следует разделить её на образующий полином. Результат деления укажет на наличие или отсутствие ошибки в принятой кодовой комбинации. Если деление дает нулевой остаток, то ошибки отсутствуют или не обнаружены. Если же в результате деления полинома (принятой кодовой комбинации) на образующий полином остаток R’
(х) отличен от нуля , то это означает что принятая кодовая комбинация содержит ошибки. Вид ненулевого остатка R’
(х), называемого синдромом ошибки.
|
