| Министерство образования и науки Российской Федерации
Государственное образовательное учреждение высшего профессионального
образования
Хабаровский Государственный Технический Университет
Кафедра: Экономическая кибернетика
КОНТРОЛЬНАЯ РАБОТА
по дисциплине «Социально-экономическая статистика»
Вариант № 4
Выполнил:
студент 3 курса (1г/об.)
специальность-КЗУ-41 (3,5)
шифр 040440637
Гуляс Антон
Александрович
Проверил:
Хабаровск
2005
| |
Содержание
|
|
| |
Общая теория статистики
|
3
|
| 1
|
Задача 1
|
3
|
| 2
|
Задача 2
|
4
|
| 3
|
Задача 3
|
6
|
| 4
|
Задача 4
|
8
|
| 5
|
Задача 5
|
10
|
| |
Социально-экономическая статистика
|
11
|
| 6
|
Задача 1
|
11
|
| 7
|
Задача 2
|
11
|
| 8
|
Задача 3
|
12
|
| 9
|
Задача 4
|
13
|
| 10
|
Задача 5
|
14
|
| 11
|
Задача 6
|
15
|
ОБЩАЯ ТЕОРИЯ СТАТИСТИКИ
Вариант 4
Задача 1
Исходные данные:
| № завода
|
Среднегодовая стоимость основных производственных фондов, млн. руб.
Ф
|
Валовая продукция в сопоставимых ценах, млн. руб.
ВП
|
№ завода
|
Среднегодовая стоимость основных производственных фондов, млн. руб.
Ф
|
Валовая продукция в сопоставимых ценах, млн. руб.
ВП
|
| 1
|
7,1
|
7,4
|
12
|
6,6
|
6,8
|
| 2
|
7,2
|
7,3
|
13
|
9,8
|
11
|
| 3
|
9,5
|
9,9
|
14
|
2,5
|
2,7
|
| 4
|
9,9
|
9,2
|
15
|
9,9
|
9,6
|
| 5
|
6
|
5,5
|
16
|
4,8
|
3,8
|
| 6
|
9,1
|
10
|
17
|
5,9
|
9,1
|
| 7
|
7,5
|
10
|
18
|
4
|
3,7
|
| 8
|
8,6
|
9,1
|
19
|
6
|
4,8
|
| 9
|
10
|
9,58
|
20
|
3,3
|
3,8
|
| 10
|
7
|
9,2
|
21
|
7,9
|
11
|
| 11
|
7,4
|
9,8
|
22
|
5,8
|
7
|
Шаг интервала определим:
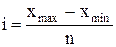
где хmax
, xmin
- соответственно максимальное и минимальное значение признака.
i = (10 - 2,5) / 5 = 1,5 млн.руб.
Группировка заводов по среднегодовой стоимости основных
производственных фондов
| № группы
|
Интервал, млн. руб.
|
Номера заводов
|
Число заводов
|
| 1
|
2,5 - 4
|
14 18 20
|
3
|
| 2
|
4 - 5,5
|
16
|
1
|
| 3
|
5,5 - 7
|
5 10 12 17 19 22
|
6
|
| 4
|
7 - 8,5
|
1 2 7 11 21
|
5
|
| 5
|
8,5 - 10
|
3 4 6 8 9 13 15
|
7
|
Уровень фондоотдачи вычисляется по формуле:
f=BП /Ф
Результаты вычислений представлены в таблице.
На основе полученной группировки можно сделать вывод, что между среднегодовой стоимостью основных производственных фондов и валовой продукцией существует прямолинейная зависимость.
Группировка заводов по среднегодовой стоимости
основных производственных фондов
| № группы
|
Интервал по среднегодовой стоимости основных производственных фондов, млн.руб.
|
Количество заводов
|
Среднегодовая стоимость основных производственных фондов, млн.руб.
|
Стоимость валовой продукции, млн.руб.
|
Фондоотдача, руб/руб
|
| всего
|
на 1 завод
|
всего
|
на 1 завод
|
| 1
|
2,5 - 4
|
3
|
9,8
|
3,3
|
10,2
|
3,4
|
1,041
|
| 2
|
4 - 5,5
|
1
|
4,8
|
4,8
|
3,8
|
3,8
|
0,792
|
| 3
|
5,5 - 7
|
6
|
37,3
|
6,2
|
43,4
|
7,2
|
1,164
|
| 4
|
7 - 8,5
|
5
|
37,1
|
7,4
|
45,5
|
9,1
|
1,226
Реклама

|
| 5
|
8,5 -10
|
7
|
23,5
|
3,4
|
68,38
|
9,8
|
2,910
|
| Итого
|
22
|
112,5
|
5,1
|
171,28
|
7,8
|
1,522
|
Задача 2
Исходные данные для расчетов
| Затраты, времени на одну деталь, мин
|
Число дет.,шт
|
| До 14
|
10
|
| 14 -16
|
15
|
| 16 -18
|
35
|
| 18 - 20
|
25
|
| 20 и более
|
|
| Итого
|
100
|
Расчетная таблица
| Затраты, времени на одну деталь, мин
|
Число дет., шт.
f
|
Середина интервала х
|
xf
|
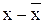
|
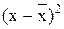
|
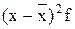
|
| До 14
|
10
|
13
|
130
|
-4,4
|
19,36
|
193,6
|
| 14-16
|
15
|
15
|
225
|
-2,4
|
5,76
|
86,4
|
| 16-18
|
35
|
17
|
595
|
-0,4
|
0,16
|
5,6
|
| 18-20
|
25
|
19
|
475
|
1,6
|
2,56
|
64
|
| 20 и более
|
15
|
21
|
315
|
3,6
|
12,96
|
194,4
|
| Итого
|
100
|
-
|
1740
|
-
|
|
544
|
а) Средние затраты времени на изготовление одной детали:
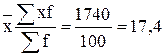 мин мин
б) Среднее квадратическое отклонение:
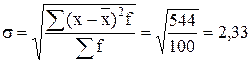 мин мин
Дисперсия: 
в) Коэффициент вариации:
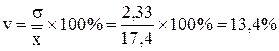 < 33% < 33% 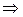 , рассматриваемая совокупность является качественно однородной и средняя типична. , рассматриваемая совокупность является качественно однородной и средняя типична.
г) Случайная ошибка выборочной средней при случайной бесповторной выборке:
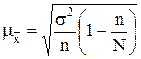 , ,
где n - объем выборки;
N - объем генеральной совокупности;
σ2
- выборочная дисперсия;
n/N - соотношение объема выборки и объема генеральной совокупности.
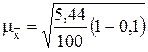 =0,221 мин =0,221 мин
Предельная ошибка выборки:
Δ = μх
× t,
где t - коэффициент доверия Лапласа. При вероятности 0,954 t=2
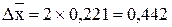 мин мин
Пределы, в которых находится средний тарифный разряд:
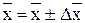 ; 17,4 – 0,442 ≤ ; 17,4 – 0,442 ≤ 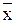 ≤ 17,4 – 0,442; 16,958 ≤ ≤ 17,4 – 0,442; 16,958 ≤ 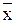 ≤ 17,842. ≤ 17,842.
С вероятностью 0,954 ожидаются средние затраты времени на изготовление одной детали на заводе в пределах 16,96 до 17,84 минут.
д) Границы генеральной доли находятся как:
ω - Δω
≤ р ≤ ω + Δω
,
где р - генеральная доля;
ω - выборочная доля: ω = 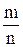 ; ;
где m - число единиц, обладающих данным признаком;
n - объем выборочной совокупности.
Δω
- предельная ошибка доли:
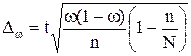 . При вероятности 0,954 t = 2. . При вероятности 0,954 t = 2.
ω = 10 / 100 = 0,1
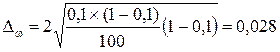
0,1 – 0,028 ≤ р ≤ 0,1 + 0,028; 0,072 ≤ р ≤ 0,128.
С вероятностью 0,954 можно утверждать, что границы удельного веса числа деталей с минимальными затратами времени на их изготовление будут находиться в пределах от 7,2% до 12,8%.
Задача 3
Исходные данные для расчетов
| |
Годы
|
| 1998
|
1999
|
2000
|
2001
|
2002
|
2003
|
| Розничный товарооборот, тыс.руб.
|
10820
|
11850
|
13050
|
14191
|
14470
|
14590
|
Для анализа динамики розничного товарооборота вычислим:
а) Базисный абсолютный прирост ΔУб
i
определяется как разность между сравниваемым уровнем Уi
и уровнем, принятым за постоянную базу сравнения Уoi
:
ΔУб
i
= Уi
- Уoi
- Цепной абсолютный прирост: ΔУц
i
– разность между сравниваемым уровнем Уi
и уровнем, который ему предшествует:
ΔУц
i
= Уi
- Уi
– 1
- Базисные коэффициенты роста: Трб.
i
.
= Уi
: Уoi
Реклама

- Цепные коэффициенты роста: Трц.
i
.
= Уi
: Уi
– 1
- Базисные темпы роста: Трб.
i
.
= Уi
: Уoi
× 100%
- Цепные темпы роста: Трц.
i
.
= Уi
: Уi
– 1
× 100%
- Базисный темп прироста: Тпб
= ΔУб
i
: Уoi
- Цепной темп прироста: Тпц
= ΔУц
i
: Уi
– 1
.
Полученные показатели представлены в таблице.
б) Среднегодовой розничный товарооборот:
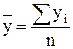 , где n - число периодов. , где n - число периодов.
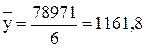 тыс.руб. тыс.руб.
в) Среднегодовой темп роста:
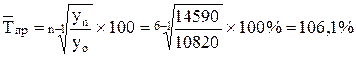
Среднегодовой темп прироста розничного товарооборота:
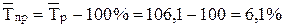
Показатели анализа динамики розничного товарооборота
| Годы
|
Розничный товарооборот, тыс.руб.
|
Абсолютный прирост, тыс.руб.
|
Коэффициент роста
|
Темпы роста, %
|
Коэффициент прироста
|
Темпы прироста, %
|
Аi
, тыс.руб.
|
| цепной
|
базисный
|
цепной
|
базисный
|
цепной
|
базисный
|
цепной
|
базисный
|
цепной
|
базисный
|
| 1998
|
10820
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
| 1999
|
11850
|
1030
|
1030
|
1,095
|
1,095
|
109,5
|
109,5
|
0,095
|
0,095
|
9,5
|
9,5
|
108,2
|
| 2000
|
13050
|
1200
|
2230
|
1,101
|
1,206
|
110,1
|
120,6
|
0,101
|
0,206
|
10,1
|
20,6
|
118,5
|
| 2001
|
14191
|
1141
|
3371
|
1,087
|
1,312
|
108,7
|
131,2
|
0,087
|
0,312
|
8,7
|
31,2
|
130,5
|
| 2002
|
14470
|
279
|
3650
|
1,020
|
1,337
|
102,0
|
133,7
|
0,020
|
0,337
|
2,0
|
33,7
|
141,9
|
| 2003
|
14590
|
120
|
3770
|
1,008
|
1,348
|
100,8
|
134,8
|
0,008
|
0,348
|
0,8
|
34,8
|
144,7
|
| Итого
|
78971
|
3770
|
-
|
1,348
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
Задача 4
Исходные данные для расчетов
| №
завода
|
Вид продукции
|
Выработка продукции,
шт. за период
|
Себестоимость единицы
продукции, тыс.руб.
|
| Базисный (q0
)
|
Отчетный (q1
)
|
Базисный (Z0
)
|
Отчетный (Z1
)
|
| Завод
№ 1
|
АМ-6
|
830
|
825
|
2,5
|
2,6
|
| ТБ-2
|
615
|
585
|
5,3
|
5,0
|
| Завод
№ 2
|
АМ-6
|
1100
|
1100
|
4,1
|
4,4
|
Вычислим:
а) Для завода № 1 (по двум видам продукции вместе):
Общий индекс затрат: 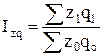 = = 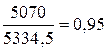 или 95% или 95%
Расчетная таблица
| Продукция
|
Выработка продукции, шт. период
|
Себестоимость единицы продукции, тыс.руб.
|
Z0
q0
|
Z1
q1
|
Z0
q1
|
| Базисный
(q0
)
|
Отчетный
(q1
)
|
Базисный
(Z0
)
|
Отчетный
(Z1
)
|
| АМ-6
|
830
|
825
|
2,5
|
2,6
|
2075
|
2145
|
2062,5
|
| ТБ-2
|
615
|
585
|
5,3
|
5,0
|
3259,5
|
2925
|
3100,5
|
| Сумма
|
1445
|
1410
|
-
|
-
|
5334,5
|
5070
|
5163
|
Общий индекс себестоимости продукции:
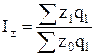 = = 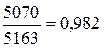 или 98,2%. или 98,2%.
Общий индекс физического объема:
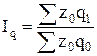 = = 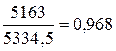 или 96,8%. или 96,8%.
Затраты на производство в отчетном периоде по сравнению с базисным сократились на 5%, в том числе в результате изменения себестоимости единицы продукции на 1,8% и объемов выпуска – на 3,2%.
Абсолютный прирост затрат:
а) Общий: 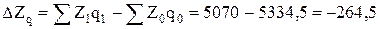 тыс.руб. тыс.руб.
б) В результате изменения:
- себестоимости единицы продукции:
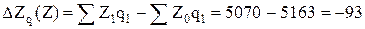 тыс.руб. тыс.руб.
- объемов производства:
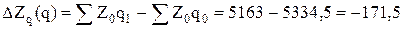 тыс.руб. тыс.руб.
Затраты на производство в отчетном периоде по сравнению с базисным сократились на 264,5 тыс.руб., в том числе в результате изменения себестоимости единицы продукции на 93 тыс.руб. и объемов выпуска – на 171,5 тыс.руб.
Покажите взаимосвязь между исчисленными индексами:
Izq
= Iq
× Iz
; 0,95 = 0,981 × 0,968 – верно.
б) Для двух заводов вместе (по продукции АМ-6):
- индекс себестоимости переменного состава:
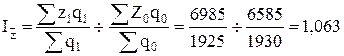 или 106,3% или 106,3%
- индекс себестоимости постоянного состава:
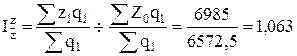 или 106,3% или 106,3%
- индекс влияния изменения структуры производства продукции на динамику средней себестоимости:
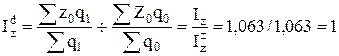 или 100% или 100%
Расчетная таблица
| Завод
|
Выработка продукции, шт. период
|
Себестоимость единицы продукции, тыс.руб.
|
Z0
q0
|
Z1
q1
|
Z0
q1
|
| Базисный
(q0
)
|
Отчетный
(q1
)
|
Базисный
(Z0
)
|
Отчетный
(Z1
)
|
| №1
|
830
|
825
|
2,5
|
2,6
|
2075
|
2145
|
2062,5
|
| №2
|
1100
|
1100
|
4,1
|
4,4
|
4510
|
4840
|
4510
|
| Сумма
|
1930
|
1925
|
-
|
-
|
6585
|
6985
|
6572,5
|
Средняя себестоимость продукции АМ-6 по двум заводам в отчетном периоде по сравнению с базисным возросла на 6,3%, в том числе в результате изменения себестоимости единицы продукции на 6,3%. Т.о. структурные сдвиги в выпуске продукции на средней себестоимости не отразились.
Задача 5
Исходные данные для расчетов
| Продукция
|
Общие затраты на производство продукции, тыс.руб. за квартал
|
Измен. количества произв. продукции в 3-м квартале по сравнению со 2-м., %
|
| 2-й
|
3-й
|
| А
|
1520
|
1600
|
- 4
|
| Б
|
1780
|
1840
|
1
|
| Итого
|
3300
|
3440
|
-
|
Вычислим общий индекс:
а) Затрат на производство обуви: 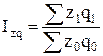 = = 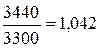 или 104,2 %. или 104,2 %.
б) Физического объема производства обуви: 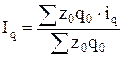 , ,
где iq
- индивидуальный индекс физического объема.
Продукция А: iq
= 100 – 4 = 96 %
Продукция Б: iq
= 100 + 1 = 101 %
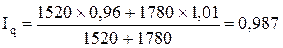 или 98,7 % или 98,7 %
в) Себестоимости производства обуви, используя взаимосвязь индексов:
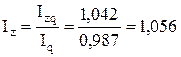 или 105,6 % или 105,6 %
Затраты на производство продукции в III квартале по сравнению со II возросли на 4,2%, в том числе в результате изменения себестоимости единицы продукции – на 5,6 %. Из-за изменения объемов производства общие затраты снизились на 1,3 %.
СОЦИАЛЬНО-ЭКОНОМИЧЕСКАЯ СТАТИСТИКА
Вариант 4
Задача 1
Общие индексы:
1. Стоимости приобретенных товаров: 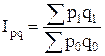 , ,
где р1
, р0
- это цена за единицу продукции;
q1,
q0
- физический объем реализованных товаров.
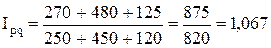 или 106,7 % или 106,7 %
2. Цен: 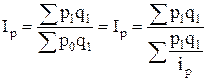 , ,
где iр
- индивидуальный индекс цен
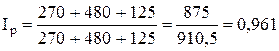 или 96,1 % или 96,1 %
3. Физического объема: 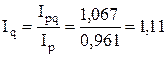 или 111 % или 111 %
Т.о. стоимость приобретенных товаров в отчетном периоде по сравнению с базисным возросла на 6,7 %, в том числе в результате изменения объема продаж на 11 %. Из-за изменения цен стоимость снизилась на 3,9 %.
Задача 2
Абсолютная экономия (перерасход) фонда заработной платы:
ΔФЗП = ФЗП1
– ФЗП0
,
где ФЗП1
, ФЗП0
- фонд заработной платы соответственно в отчетном и базисном периодах.
ΔФЗП = 17,5 – 15,6 = 1,9 тыс.руб.
Относительная экономия (перерасход) фонда заработной платы:
IФЗП
= ФЗП1
/ ФЗП0
= 17,5 / 15,6 = 1,121 или 112,2 %
Абсолютное изменение фонда заработной платы за счет:
а) Изменения численности рабочих:
ΔФЗП (Т) = (Т1
– Т0
) × ФЗП0
/ Т0
= Т1
× ФЗП0
/ Т0
– ФЗП0
,
где Т - численность промышленно-производственного персонала
ΔФЗП (Т) = 125 × 15,6 / 120 – 15,6 = 0,56 тыс.руб.
б) Изменения средней заработной платы:
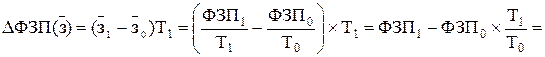
= 17,5 – 15,6 × 125 / 120 = 1,25 тыс.руб.
Проверка: ΔФЗП = ΔФЗП(Т) + 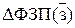
1,9 ≈ 1,25 + 0,56 – верно.
Т.о., фактический фонд заработной платы в отчетном периоде по сравнению с базисным возрос на 1,9 тыс.руб., в том числе в результате изменения численности рабочих и средней заработной платы соответственно на 0,56 и 1,25 тыс.руб.
Задача 3
Среднесписочная численность рабочих:
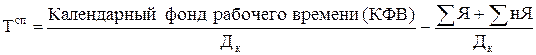 , ,
где ∑Я - сумма явок;
∑нЯ - сумма неявок;
Дк
- календарные дни в периоде
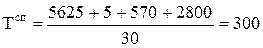 чел. чел.
Средняя фактическая продолжительность рабочего месяца:
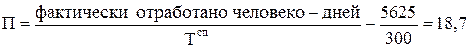 дней дней
Средняя фактическая продолжительность рабочего дня:
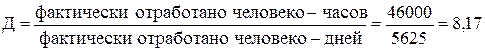 часов часов
Коэффициент использования календарного фонда времени:
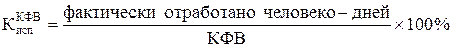
КФВ = ∑Я + ∑нЯ = 5625 + 5 + 570 + 2800 = 9000 чел.-дн.
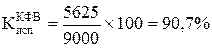
Коэффициент использования максимально-возможного фонда времени:
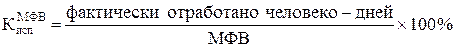
МФВ = КФВ – ОО – ПВ,
где ОО - очередные отпуска;
ПВ - праздничные и выходные дни.
МФВ = 9000 – 470 – 2800 = 5730
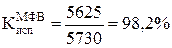
Задача 4
Определим:
1. Индекс покупательной способности рубля:
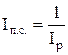 , ,
где Iр
- индекс цен.
Iр
= 100 + 12 = 112%
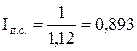 или 89,3%, т.е. покупательская способность рубля составляет 89,3%. или 89,3%, т.е. покупательская способность рубля составляет 89,3%.
2. Индекс номинальной заработной платы:
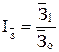 , ,
где 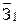 ; ; 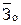 - среднемесячная заработная плата соответственно в отчетном и базисном периодах - среднемесячная заработная плата соответственно в отчетном и базисном периодах
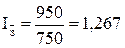 или 126,7% или 126,7%
Средняя номинальная заработная плата в отчетном периоде по сравнению с базисным периодом возросла на 26,7 %.
3. Индекс реальной заработной платы:
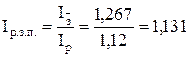 или 113,1% или 113,1%
Средняя реальная заработная плата в отчетном периоде по сравнению с базисным периодом возросла на 13,1%
4. Индекс конечных доходов в текущих ценах:
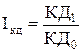 , ,
где КД1
, КД0
- конечные доходы в отчетном и базисном периодах соответственно
КД1
= 950 + 180 = 1130 руб.
КД0
= 750 + 152 = 902 руб.
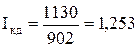 или 125,3 % или 125,3 %
Конечные доходы рабочих в отчетном периоде по сравнению с базисным возросли на 25,3%.
5. Индекс реальных доходов:
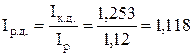 или 111,8 % или 111,8 %
Конечные доходы рабочих в отчетном периоде по сравнению с базисным возросли на 11,8%.
Задача 5
Валовая продукция по факту:
ВП1
= 900 + 30 + 15 + 12 + (12 – 16) = 953 тыс.руб.
Товарная продукция по факту:
ТП1
= 900 + 30 + 15 + 12 = 957 тыс.руб.
Процент выполнения плана по валовой продукции:
Iвп
= ВП1
/ ВП0
= 953 / 940 = 1,014 или 101,4%, т.е. план по выпуску валовой продукции перевыполнен на 1,4%.
Процент выполнения плана по товарной продукции:
Iтп
= ТП1
/ ТП0
= 957 / 870 = 1,1 или 110 %, т.е. план по выпуску товарной продукции перевыполнен на 10%.
Задача 6
Сумма, погашенная в конце года, будет определена по формуле:
S = Р × (1 + t ×i),
где Р - начальная сумма кредита;
t - период открытия кредита;
i - процентная ставка
S = 40 × (1 + 2 × 0,04) = 43,2 тыс.руб.
|