|
Чибуничев А.Г.
В настоящее время вопросам обработки цифровых изображений, полученных камерами на ПЗС, уделяется большое внимание в исследованиях советских и зарубежных ученых [1 —10]. В основном эти исследования направлены на повышение точности и надежности определения координат точек изображений и их отождествления на смежных снимках. Так, например, положение маркированных точек на изображении определяется с точностью 0, 01—0, 05 пиксела изображения [4; 10] по макетным снимкам и 0, 03—0, 09 величины пиксела [3, 7, 8, 9] по реальным изображениям, полученным различными камерами на ПЗС.
Для немаркированных точек точность отождествления одноименных точек на паре реальных снимков значительно ниже и колеблется в пределах 0, 5—10 пикселов изображения [6]. При этом надежность отождествления маркированных точек на тест-объекте достигает — 90% [5] и 50—80% на реальных снимках (также по маркированным точкам)[5, 9]. Точность и надежность определения координат точек цифрового изображения и их отождествления на смежных снимках зависит от качества самих изображений (параметров . камеры, условий съемки) и в значительной степени от алгоритмов их обработки. Используя цифровую фотограмметрическую систему на базе персонального компьютера, описанную в [2], можно организовать обработку цифровых изображений с более высокой точностью и надежностью. Напомним, что в [2] речь идет о стереонаблюдениях и измерениях цифровых изображений на разделенном экране персонального компьютера. Вопрос о надежности отождествления одноименных точек стереопары в данном случае отпадает, так как выполняются стереонаблюдения.
С целью ускорения процесса измерений предлагается использовать измерительную марку, высвечиваемую на экране в виде «окна», величина которого подбирается немного больше по размерам маркированных точек. Процесс измерений в этом случае заключается только в том, чтобы данная маркированная точка попала в соответствующее «окно» (Р1 и Р2) на левом и правом снимке. Это существенно ускоряет процесс измерений и не требует от наблюдателя большой квалификации. Если измеряются немаркированные точки, то размер измерительной марки целесообразно устанавливать 20X20— 30x30 пикселов изображения, так как в таких пределах осуществляется наиболее точно корреляция двух изображений согласно исследованиям, выполненным в [9].
Реклама

После наведения измерительной марки на выбранную точку вырезаются два фрагмента изображений по периметру «окна» и : и запоминаются в отдельных файлах для дальнейшей их обработки с целью получения координат х и у соответствующих точек на левом ( ) и правом ( ) снимках. Выделение фрагментов изображений и происходит из исходных изображений и, хранящихся в памяти ПК.
Здесь следует заметить, что выделение фрагментов изображений Р'1 и Р’2 происходит, естественно, из исходных изображений Р1 и Р1, хранящихся в памяти ПК. При этом дисплей служит только для стереонаблюдений и не является измерительной частью системы. Поэтому требования к дисплею в данном случае могут быть невысокими, особенно при измерениях только по маркированным точкам (такие задачи часто имеют место в инженерной фотограмметрии). Для этих целей может быть использован стандартный дисплей ПК вместо отдельного графического дисплея.
Теперь рассмотрим получение координат х, у, - по фрагментам изображений. Остановимся здесь только на случае маркированных точек. Для нахождения соответствующих координат точки левого и правого снимков достаточно найти координаты центра маркированной точки на этих снимках. Большинство авторов [4, 8, 10] решает этот вопрос следующим образом. Фрагмент изображения рассматривают как некоторое материальное тело и применяют к нему известный из математического анализа метод вычисления моментов различного порядка [11]. Для дискретного изображения размером m х n пикселей можно записать
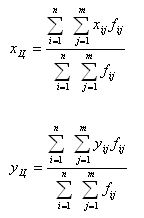 (1) (1)
где fij — значения плотностей пикселей или их функции. Выражения (2.1) являются универсальными в смысле формы маркированных точек. Однако они очень чувствительны к шумам. Поэтому для повышения точности определения координат хЦ, уЦ сначала выполняют предварительную обработку изображения (используя чаще методы пространственной области) путем свертки изображения с гауссоидой вида
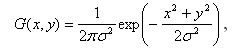 (2) (2)
что позволяет сгладить изображение. Затем выполняют пороговое удаление шумов. Пороговое значение плотности изображения: получают на основе эмпирических формул. Получена следующая оптимальная формула для изображения с уровнем квантования, равным 256:
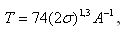 (3) (3)
где 2G — ширина распространения функции Гаусса (2);
А — размер маркированной точки.
Реклама

Как показали исследования [10], такой подход дает хорошие результаты. Точность данного метода достигает 0, 01 пикселя. Однако этот путь имеет существенные недостатки. Имеется в виду необходимость подбора оптимальной ширины функции Гаусса, от которой в значительной степени зависит точность определения координат хЦ, уЦ. Выбор величины 2G, в свою очередь, зависит от уровня шума, уровня квантования изображения и размеров маркированной точки. Достаточно сказать, что изменение величины 2а на 0, 5 приводит к размыванию границ на 1 пиксель. Кроме того, вычисление центра фигуры на основе (1) совершенно не защищено от влияния локального шума, наличие которого может привести к грубым ошибкам. Источником такого шума могут быть блики, тени, посторонние изображения объектов, попавшие в пределы окна с маркированной точкой и т. д.
В данной работе предлагается другой подход, основанный на использовании уравнения фигуры маркированной точки для определения координат хЦ, уЦ. В этом случае появляется возможность подавлять пиксели, принадлежащие не только общему, но и локальным шумам.
Вычислительная процедура состоит из двух этапов. Первый этап заключается в выделении границ маркированной точки. На втором этапе определяются координаты хЦ, уЦ на основе уравнения фигуры.
Выделение границ маркированной точки основано на вычислении первой производной функции изображения f(x, у). Первая производная в любой точке изображения получается из величины градиента в этой точке. Существует много способов вычисления производных от изображения. Наибольшее распространение получили способы, основанные па свертке изображения в некоторой окрестности с центром в точке (х, у) с так называемой маской (оператором) H тех же размеров. Градиент изображения G можно записать в общем виде как двумерный вектор:
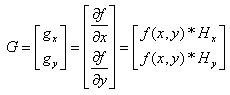 (4) (4)
где Нx, Hy — маски;
* — обозначение операции свертки.
В качестве Нх, Ну использован оператор Собеля для окрестности 3x3:
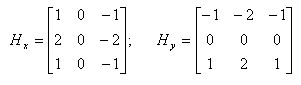 (5) (5)
Величина градиента в точке вычисляется как
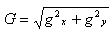 (6) (6)
Определение координат центра маркированной точки рассмотрим на примере круга:
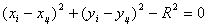 (7) (7)
Это уравнение составляется для всех точек, имеющих ненулевые значения градиентов в пределах фрагмента изображения. Решение выполняется по способу наименьших квадратов методом последовательных приближений. Каждому уравнению присваивается вес в зависимости от величины градиента:
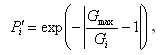 (8) (8)
где Gmax — максимальное значение градиента в пределах фрагмента изображения; Gi — значение градиента для данного (i) пикселя изображения.
Вес, вычисленный по (8), играет роль фильтра, который подавляет энергетические шумы (порядка 20%) и сужает область пикселей, принадлежащих границе контура, которая получается размытой из-за условий съемки и преобразований (6) примерно до +/-1 пикселя.
С целью уменьшения влияния локальных шумов, соизмеримых по энергии пикселей с уровнем сигнала на маркированной точке вводится второй вес также для каждого пикселя:
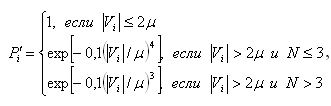 (9) (9)
где Vi —невязка в i-м уравнении (7);
ц — средняя квадратическая ошибка единицы веса;
N — номер итерации.
Полученные таким образом координаты геометрического центра маркированной точки хц, уц на левом и правом снимках используются в качестве измеренных для дальнейшей аналитической обработки снимков, причем с весом, полученным из уравнивания.
Экспериментальные исследования данного метода подтвердили его эффективность. Координаты центра маркированной точки можно определять, в некоторых случаях с точностью 0, 01 пикселя изображения. Подробные экспериментальные исследования приводятся в следующей статье.
Список литературы
1. Путятин Е.П., Аверин С.А. Обработка изображений в робототехнике. М.: Машиностроение, 1990, 320 с.
2. Чибуничев А.Г. О возможностях применения цифровых методов фотограмметрии для решения инженерных задач, -Изв. вузов. Геодезия и аэрофотосъемка, 1990, № 6, с. 76—82.
3. Bosseman W., Godding R., Riechmann W. Photogrammetric Investigation of CCD Cameras, C. – R. Ph. M. M. V., Corn. V. Symposium, Switzerland, September, 1990, v. 1395, p. 119-126
4. El Hakim S. F. A Hierarchial Approach to Stereo vision. – Photog. Eng. And Rem. Sen., 1989, vol. 55. № 4. p. 443-448
5. Hwang J. T., Chang R. G. Comparing the image matching methods of the two-stage and FFT. C. – R. Ph. M. M. V., Com. V. Symposium, Switzerland, September, 1990, v. 1395, p. 1035-1042
6. Greenfield J.S. A Stereo Visision Approach to Automatic Stereo Matching in Photogrammetry. – Report № 381. The Ohio State University Columbus, July, 1987, 137 p.
7. Luhmann T. Image recording systems for close-range photogrammetry. C. – R. Ph. M. M. V., Com. V. Symposium, Switzerland, September, 1990, v. 1395, p. 86-95
8. Mikhail E. M., Akey M. L., Mitchell O. R. Detection andsub-pixel-location of photogrammetric targets in digital images. – Photogrammetria, 1984, 39(3), p. 63-83
9. Rosenholm D. Emperical Invesligation of Optimal Window Size Using the Least Square Image Matching Method. – Photogrammetria, 1987, vol. 42, p. 113-125
10. Trinder J. C. Precision of Digital Target Location. - Photog. Eng. And Rem. Sen., 1989, vol. 55. № 6. p. 883-886
11.Бермант А. Ф. Краткий курс математического анализа. М.: Наука, 1965, 663 с.
|