| Определение напряжений сдвига в условиях резания с помощью модификации Макгрегора–Фишера
Матюха П.Г., Полтавец В.В.
Донецкий национальный технический университет
Силы, необходимые для осуществления процесса резания, зависят от параметров среза, определяемых кинематикой процесса, контактных явлений между стружкой, поверхностью резания и поверхностью инструмента, от сопротивления обрабатываемого материала пластическому деформированию.
В общем случае сопротивление материала пластическому деформированию, определяемое совместным влиянием процессов упрочнения и разупрочнения, является функцией температуры, величины деформации и скорости деформации [1], т.е.
σ=f(T, ε, ε),
где σ — текущее значение напряжения сопротивления деформации, МПа;
T — температура деформации, К;
ε — относительный сдвиг;
ε — скорость относительного сдвига, с−1;
В зоне стружкообразования сопротивление материала пластической деформации приближенно характеризуется средней величиной напряжения сдвига τs по условной плоскости сдвига [1].
Для определения величины τ s в температурно–скоростных условиях, характерных для резания, предложены ряд методик:
- расчет τs по измеренной твердости стружки [1, 2];
- расчет касательного напряжения т по осевому эффективному напряжению в момент прекращения деформации при сжатии образцов [3];
- расчет τ и σ по измеренной твердости пластически деформированного тела Нп [3];
- расчет напряжений сдвига по стандартным механическим характеристикам сам обрабатываемого материала [3];
- экспериментальное определение условного напряжения резания при обработке холодных [4] либо подогретых заготовок [1];
- расчет τs графоаналитическим методом по результатам испытаний на разрыв образцов, нагретых до различных температур, с учетом скорости деформации [5];
- определение τ s с помощью модификации К. Макгрегора и И. Фишера [1, 6].
Как показал анализ перечисленных методик, достоинством определения τs с помощью модификации Макгрегора–Фишера является возможность нахождения напряжений сдвига по данным стандартных испытаний, приведенным в технической литературе, что значительно упрощает определение напряжений сдвига в температурно–скоростных условиях, характерных для резания.
Реклама

Модификац ия К. Макгрегора и И. Фишера базируется на экспериментально проверенном факте, в соответствии с которым напряжение σ является функцией только абсолютной температуры, т.е.
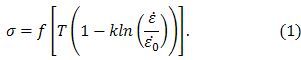
Постоянная k в уравнении (1) может быть выбрана так, что изменение напряжения при температуре T0 и нулевой скорости относительного сдвига будет таким же, как и при скорости относительного сдвига и температуре деформации. При этом температура деформации является температурой, модифицированной по скорости деформации
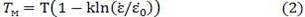
Из (2) ясна идея модификации, заключающаяся в том, что если известна зависимость какой–либо характеристики обрабатываемого материала (например, σв, НV) от температуры, то всегда можно найти зависимость этой характеристики от скорости деформации по уравнению (2).
Определение τs в температурно–скоростных условиях, характерных для резания, осуществляется в четыре этапа.
На первом этапе по данным о влияния скорости деформации и температуры на величину σ, имеющимся для обрабатываемого материала в технической литературе, рассчитывают коэффициент k
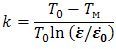
На втором этапе определяют отношение T o/Tм диапазоне скоростей резания, характерных для исследуемого процесса обработки.
На третьем этапе, используя отношение Tм/Т и имеющиеся зависимости характеристик обрабатываемого материала (σв, НV) от температуры, полученные стандартным методом испытания при низкой скорости деформации, находят зависимости модифицированных характеристик (σвм, НVм) от температуры, которая учитывает скорость деформации для конкретных условий резания.
На четвертом этапе, используя полученные зависимости модифицированных характеристик от температуры, а также известные [3] соотношения τs = 0, 185(НVм) или τs=σвм/√3, получают уравнения, описывающие влияние температурно–скоростных факторов на величину касательных напряжений в условиях резания.
С помощью описанной методики были определены напряжения сдвига при алмазном шлифовании быстрорежущих, высоколегированных и титановых сплавов. Установлено, что влияние температурно–скоростных факторов на величину касательных напряжений при шлифовании этих материалов может быть описано линейной зависимостью
Реклама

τs=С − αТ. (3)
Параметры уравнения (3) для расчета напряжений сдвига приведены в табл. 1.
Таблица 1 — Значения С и α в уравнении (3) для высоколегированных, быстрорежущих сталей и титановых сплавов сталей и титановых сплавов
| Обрабатываемый материал
|
Состояние
|
С, МПа
|
α, МПа/К
|
| Быстрорежущие стали Р18, Р14Ф4, Р12ФЗ
|
Закаленные
|
1761
|
0, 185
|
| Высоколегированные стали Х12Ф1, Х12М, 9Х5Ф, Х6ВФ, Х6ВЗФМ
|
Закаленные
|
1697
|
0, 148
|
| Титановый сплав ВТ–14
|
Отожженный
|
671
|
0, 236
|
| Титановый сплав ВТ–14
|
Термически упрочненный
|
829
|
0, 317
|
| Титановый сплав ВТ–3–1
|
Отожженный
|
770
|
0, 329
|
| Титановый сплав ВТ–3–1
|
Термически упрочненный
|
899
|
0, 357
|
Выводы
1. Модификация Макгрегора–Фишера позволяет получить зависимости, отражающие влияние температурно–скоростных условий резания на величину касательных напряжений в условной плоскости сдвига без проведения трудоемких экспериментов;
2. Получены уравнения, описывающие влияние температурно–скоростных факторов на величину касательных напряжений в условиях шлифования, и определены параметры уравнений для быстрорежущих, высоколегированных сталей и титановых сплавов.
Список литературы
Лоладзе Т.Н. Прочность и износостойкость режущего инструмента. — М.: Машиностроение, 1983. — 352 с.
Томленов А.Д. Теория пластического деформирования металлов. — М.: Металлургия, 1972. — 408 с.
Розенберг А.И., Еремин А.Н. Элементы теории процесса резания металлов. — Свердловск: Машгиз, 1956. — 319 с.
Маслов Е.Н. Теория шлифования материалов. — М.: Машиностроение, 1974. — 316 с.
Корчак С.Н. Производительность процесса шлифования стальных деталей. — М.: Машиностроение, 1974. — 280 с.
Евсеев Д.Г., Сальников А.Н. Физические основы процесса шлифования. — Саратов: Изд–во Саратовского университета, 1978. — 129 с.
|