|
Азартные игры были главной причиной возникновения и развития теории вероятностей. Эта теория, как и любая другая математическая теория, устанавливает свои законы и теоремы, которые приводят к некоторой путанице. Действительно, кажется странным, что случай может регулироваться законами, потому что если это так, и если мы знаем эти законы, мы можем выиграть в случайной игре — действительно несбыточная мечта. Первое, что нужно прояснить, это то, что случайной является игра, в которой игрок не может иметь никакого влияния на исход игры. Ни шахматы, ни спортивный бридж не являются случайными играми. А вот бросание монеты и рулетка — случайные игры.
Математическое ожидание
В некоторых играх, таких как обычная лотерея или бинго, игрок не принимает никакого участия, выходящего за рамки приобретения билета. Другие, такие как игры казино (рулетка и блэк джек), допускают более активное участие игрока, который может управлять ставками и выбирать тип игры. Вообще говоря, чем меньше участие, чем больше выигрыш. В любом случае, у нас есть четкое ощущение, что в выигрыше всегда оказывается казино. Это потому, что с математической точки зрения, игра не является справедливой. Понятие справедливой игры тесно связано с математическим ожиданием, которое впервые было введено голландским математиком Яном де Виттом (1625–1672) в трактате о пожизненной ренте (1671).
В игре, где известны вероятности событий, которые в ней происходят, математическое ожидание, обозначаемое буквой 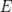 , представляет собой средний выигрыш за игру. Игра считается справедливой, когда математическое ожидание равно нулю. Посмотрим на примере, как найти математическое ожидание. Предположим, что кто-то предлагает следующую игру: мы бросаем кости, если выпадает , представляет собой средний выигрыш за игру. Игра считается справедливой, когда математическое ожидание равно нулю. Посмотрим на примере, как найти математическое ожидание. Предположим, что кто-то предлагает следующую игру: мы бросаем кости, если выпадает  , то вы платите € , то вы платите € 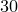 , а если что-то другое, то вы выигрываете € , а если что-то другое, то вы выигрываете € 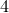 . Первое, что нужно сделать, это вычислить вероятность каждого события. Вероятность . Первое, что нужно сделать, это вычислить вероятность каждого события. Вероятность 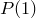 того, что выпадет того, что выпадет  , равна , равна 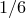 (один благоприятный случай из шести возможных), а вероятность выпадения любого другого числа равна (один благоприятный случай из шести возможных), а вероятность выпадения любого другого числа равна 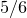 . Математическое ожидание рассчитывается как сумма всех вероятностей, умноженных на соответствующие доходы или убытки, (доход берем со знаком “плюс’’, убыток — со знаком “минус’’). В нашем случае математическое ожидание будет равно . Математическое ожидание рассчитывается как сумма всех вероятностей, умноженных на соответствующие доходы или убытки, (доход берем со знаком “плюс’’, убыток — со знаком “минус’’). В нашем случае математическое ожидание будет равно
Реклама

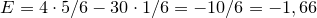 евро. евро.
Это сумма средней прибыли, которую получит наш противник, если мы согласимся на игру. Эта игра будет справедливой, если при выпадении чего-либо, отличного от  , мы будем получать , мы будем получать 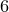 евро в случае подвижного, поскольку: евро в случае подвижного, поскольку:
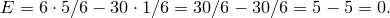
В некоторых случаях интуиция может помочь определить, является ли игра благоприятной, неблагоприятной или несправедливой, но существует много ситуаций, в которых эта интуиция не является полезным инструментом, и становится необходимым использовать карандаш и бумагу. Есть множество примеров, которые показывают, как интуиция может ввести в заблуждение. Например, на собрании, в котором участвуют 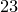 человека, вероятность встретить человека, день рождения которого в тот же день, что и у вас, несколько выше, чем вероятность выпадения орла при бросании монеты. человека, вероятность встретить человека, день рождения которого в тот же день, что и у вас, несколько выше, чем вероятность выпадения орла при бросании монеты.
Вот еще один пример. Предположим, что два игрока 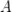 и и  играют в следующую игру. Игрок играют в следующую игру. Игрок 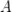 случайным образом берет одну карту из колоды в случайным образом берет одну карту из колоды в 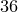 карт. Если у него валет, дама или король, игрок карт. Если у него валет, дама или король, игрок  должен заплатить € должен заплатить € 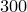 , если туз, то игрок , если туз, то игрок  платит игроку платит игроку 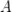 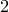 €, и если любая другая карта, то также проигрывает €, и если любая другая карта, то также проигрывает 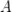 , который должен заплатить игроку , который должен заплатить игроку  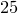 €. Кто выиграет? Сначала найдем вероятность каждого исхода. В колоде 36 карт, из которых только €. Кто выиграет? Сначала найдем вероятность каждого исхода. В колоде 36 карт, из которых только 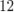 валетов, королей и дам, поэтому вероятность вытянуть одну из этих карт: валетов, королей и дам, поэтому вероятность вытянуть одну из этих карт:
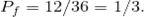
Так как есть только 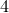 туза, то вероятность вытянуть один из них туза, то вероятность вытянуть один из них
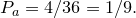
Исключим валетов, дам, королей и тузов, оставшихся карт в колоде, в общей сложности 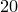 , поэтому вероятность вытянуть карту, отличную от перечисленных: , поэтому вероятность вытянуть карту, отличную от перечисленных:
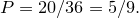
Теперь мы можем применить формулу для расчета математического ожидания игры.

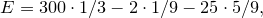
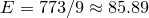 €. €.
Это средняя прибыль игрока 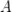 . Ясно, что игра не является справедливой. . Ясно, что игра не является справедливой.
|