| Министерство Образования и Науки Украины
Харьковский национальный университет
А.А. Тензор, В.В. Невязкин
Современные методы теории функции Зильберта
ТОМ 3
Харьков 2008
DSFGIH904
ДЖ7ПИВО61
Издание третье, дополненное и недоделанное
Р е ц е н з е н т ы :
Бюншман, Треугольник, Хвилиппов, Петросян,
Штрассерман, Штольц, Коклюшкин
© 2008 А.А. Тензор, В.В. Невязкин кафедра теории функции Зильберта
ОГЛАВЛЕНИЕ
:
| Теория полиномов Зильберта-Зажигалкина
|
4
|
| Лирическое отступление
|
7
|
| Принцип Максима Понтрягина
|
8
|
| Обобщение принципа Максима Понтрягина
|
9
|
| 3гономе3ческие функции
|
10
|
| Определение функции Зильберта
|
11
|
| Замечательно
|
12
|

Задачки 13
Вопросы к экзамену 13
Список использованной макулатуры 15
Теория полиномов Зильберта-Зажигалкина
Интегруй – не интегруй, Всё равно получишь …!
Народная мудрость
Определение
.
C a b c
[ , , '] – пространство функций, непрерывных в треугольнике ABC
' .
Определение
.
Говорят, что, а слышится “што”
!
Определение
.
Если ∀ε∃δ, то говорят, что выполнено условие Коши-Зильберта
.
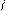 Определение
.
Говорят, что на C a b c
[ , , '] задан полином Зажигалкина zh
(x
), если ∀x x
1
, 2
∈C a b c
[ , , '] ∃zh x
( ) ∈C
32
(C a b c
[ , , ']) : Определение
.
Говорят, что на C a b c
[ , , '] задан полином Зажигалкина zh
(x
), если ∀x x
1
, 2
∈C a b c
[ , , '] ∃zh x
( ) ∈C
32
(C a b c
[ , , ']) :
1. ∀ε∃δ(выполнено условие Коши-Зильберта);
2. ∀ξ∃η;
3.  для ∀ разбиения T
многоугольника ATBCEB
на треугольники, измеримые по Зильберту, sup для ∀ разбиения T
многоугольника ATBCEB
на треугольники, измеримые по Зильберту, sup x x
1
− <2
ξ η≥[ ] 1+ . x x
1
− <2
ξ η≥[ ] 1+ .
T
Тогда полином Зажигалкина имеет вид.
Упражнение
.
Доказать, что пространство C a b c
[ , , '] является банаховым пространством.
Определение
.
На пространстве C a b c
*[ , , '] (C
со снежинкой) два функционала называются квазиэквивалентными
, если при действии на них полиномом Зажигалкина получается одно и то же почти всюду на C a b c
[ , , '] отрицательное число. Это число называется константой Мопиталя
.
Замечание
.
На линейные ограниченные функционалы можно подействовать ещё и вектором.
Теорема
.
Полином Зажигалкина всегда и только всегда является квазиполиномом с выколотой границей, если все его коэффициенты кроме, быть может, j
-ого представляют собой константы Мопиталя.
Единственное свойство полиномов Зажигалкина
:
Реклама

Определения полинома Зажигалкина по Коши и по Гейне квазиэквивалентны.
Теоремка
(Зильберта-Зажигалкина)
∀ n
-угольник конформным преобразованием можно перевести в правильный m
-угольник так, что граница перейдёт во внутренность, а внутренность – в границу.
Утверждение
.
Полином Зажигалкина n
-ой степени сходится к n
-угольнику “отнюдь не сразу”
.
Леммка
.
Полином Зажигалкина является 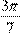 -периодическим. -периодическим.
Доказательство
.
Полином Зажигалкина определён на пространстве C a b c
[ , , '] и непрерывен в треугольнике ⇒ он 3πпериодичен.
Далее методом мат. дедукции доказывается 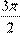 -периодичность, и так далее до -периодичность, и так далее до 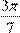 . .
Теорема
(
признак слаборавномерной полунепрерывности сверху)
Полином Pn
(x
) слаборавномерно полунепрерывен сверху, если он представим в виде криволинейной комбинации квазиполиномов Зажигалкина.
(Доказывается методом усилий)
Лемма
.
Подграфик полинома Зажигалкина монотонно выпуклый чутьчуть влево.
Доказательство
.
Введём начало координат – точку 0, и конец координат – точку ∞ . Переименуем вершины треугольника так, координат
Картина Шмалевича “круг и треугольник”
чтобы полином Зажигалкина чувствовал себя в нём конформно. Далее методом логических догадок приходим к выводу, что теорема верна.
Очень важное замечание
:
Зажигалкин ЖЖОТ!
Теорема
.
В силу теоремы Зильберта-Зажигалкина (там что-то про n
- и m
угольники -) теорию полиномов, непрерывных в треугольнике можно обобщить до m
-угольников класса гладкости, равного константе Мопиталя.
Лирическое отступление
Из чего же, из чего же, из чего же Сделана формула Грина?
Из производных, из интегралов, Из градиентов и функционалов Сделана формула Грина!
***
Принцип Максима Понтрягина
Потрясающая теорема
.
Рассмотрим функционал «ШЫ
» (от франц. shit)
b b
 < ШЫ
, zh
>= tg
∫∫
(lh
τ+ c dc
') ' , < ШЫ
, zh
>= tg
∫∫
(lh
τ+ c dc
') ' ,
a a
где lh x
( ) – гиперболический логарифм x
.
Этот функционал достигает апогея (неистово стремится к max) тогда и только тогда, когда max стремится к функционалу «ШЫ
».
Определение
.
В таком случае говорят, что ШЫ
=XO
(max) («хо большое
»).
Определение
.
Условием ГорЭлектроТрансверсальности
называется перпендикулярность функционала ШЫ
железнодорожным путям, т. е. равенство нулю скалярного произведения. Напомним, что в пространстве C a b c
[ , , '] скалярное произведение – это произведение интеграла и матрицы
b
1
⎛a
2 −λ b
2 c
2' ⎞
⎜ ⎟
(ABC ABC
1 1 1', 2 2 2')=−(∫dc
1',⎜ b
2 c
2'−λ a
2 ⎟)
a
1 ⎜⎝ c
2' a
2 b
2 −λ⎟⎠
Теорема (без доказательства)
.
Реклама

В случае, когда матрица диагонализируется, скалярное произведение равно π.
Теорема (без формулировки)
.
Доказательство
.
В силу формулировки теоремы, из (1), (2) и (3) следует (4). Значит, в силу непрерывности функции Зильберта З(х) и по условию ГорЭлектроТрансверсальности, выполняется и требуемое условие (5). Теорема доказана.
Следствие
.
Если в предыдущей теореме вместо функции Зильберта З(х) везде подставить полином Зажигалкина zh
, теорема останется верной при ∀t
и доказывается точно так же.
Упражнение
.
r r r
Доказать, что тройка векторов {ШЫ З х
, ( ), zh
} образует базис в пространстве C a b c
[ , , '] (использовать метод ортогонализации
Грамма-Шмидта запрещается).
Обобщение принципа Максима Понтрягина
Рассмотрим замыкание пространства C a b c
[ , , '], а именно

пространство C a b c
[ , , '] непрерывных в криволинейном треугольнике ABC
' функций (примеры криволинейных треугольников были рассмотрены в томе 1).
r r r
На этом пространстве векторы {ШЫ З х
, ( ), zh
} мона интегрировать, косинусировать и брать от них невязку с двойным пересчётом.
Вопрос
.
Почему нельзя тангенцировать?
Определение
.
Зильбертов кирпич – это кирпич в пространстве C a b c
[ , , '] со сторонами a
, b
, 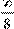 . .
Вопрос
.
Можно ли из зильбертовых кирпичей построить дачу? 3гономе3ческие функции
sinn x
Определение
.
Функция синнус
на пространстве Зильберта определяется следующим образом: sinn(x
)=sin(n
⋅ x
)
Эта функция названа так в честь эстонского математика Отто Синнуса.
Функция синнус похожа на обычный синус, только она гораздо медленнее стремится к 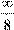 , потому что ей некуда спешить! , потому что ей некуда спешить!
narccos x
Определение
.
Функция нарккосинус
выражается через арккосинус так:
narccos(x
)=n
⋅arcos(x
)
gensec x
Определение
.
Функция генсеконс
:
⎡g
= 9.8⎤
gensec(x
)= g e n
⋅ ⋅ ⋅sec(x
)= ⎢ ⎥
= 26.46⋅n
⋅sec(x
).
⎣e
= 2,7⎦
Основное 3гономе3ческое тождество
Теорема
.
Функции нарккосинус и генсеконс связаны тождеством:
narccos2
(x
)+ gensec2
(x
)=1991.
***
Теперь, когда теоретическая основа положена и все теоремы доказаны, можно наконец дать определение функции Зильберта
З(х).
Определение (функции Зильберта)
Итак, рассмотрим конформное отображение Г матриц из пространства Зильберта Zn
в пространство функций, непрерывных в треугольнике C a b c
[ , , '].
Подействуем полиномом Зажигалкина на вектор нормали к пространству LC a b c
2
[ , , ']. По теореме Зильберта-Лиувилля, получим оператор Ы
, умноженный на константу Ц
. Эта константа является кусочно-непрерывной на кривоугольном отрезке [a b c
, , '] , поэтому её можно, и, более того, желательно разделить на 0, особенно если 0 попадёт в тот кусочек, где она разрывна.
Далее интегрируем оператор Ы
от А
до Я
. Применяя метод Симпсона к полученному выражению, найдём значение sinnΘ(η) в точках излома.
Таким образом, наша задача сводится к полноценной задаче Гольца с тремя закреплёнными концами и одним ослабленным. Эта задача записывается в виде:
J
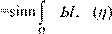 < Θ >ds
→minn (1) < Θ >ds
→minn (1)
Условия ГорЭлектроТрансверсальности:
⎧J
(0) =π
,
⎪ 2
 ⎪
⎨⎪J
(π
2) =∞
8 , (2) ⎪
⎨⎪J
(π
2) =∞
8 , (2)
⎪J
(Ц Ц
) = !
⎩
Решение этой задачи называется функцией Зильберта
З(х).
Это конец!
Замечательно
.
Теория функции Зильберта является фундаментальной
. Это означает, что любая последовательность теорем сходится к любой доказанной теореме, значит, и все теоремы из этой последовательности также верны. Эта теория такG
полная
, т. к. любая её подтеория является сходящейся, и очень сепарабельная
(хрен его знает, что это такое!).
1. Найти максимум минимума супремума инфинума функции
Зильберта в точке 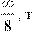 .е. .е.
 p{inf{ ( )}}}}| ? p{inf{ ( )}}}}| ?
Решение. Начнём с конца. Рассмотрим разбиение T
пространства Зильберта Zn
. Тогда sup{inf{ ( )}}З х
=З х
( ) .
T T
Согласно теореме об экстремуме,
max{min{ ( )}}З х
= min{max{ ( )}}З х
=З х
( ) .
Z Z Z Z
⎛∞⎞
Остаётся посчитать З
⎜  ⎟ . Воспользуемся таблицами мат. стати- ⎟ . Воспользуемся таблицами мат. стати-
⎝ 8 ⎠
⎛∞⎞ π
 стики: З
⎜ ⎟= . стики: З
⎜ ⎟= .
⎝ 8 ⎠ 2
Ответ: 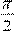 . .
2. Доказать очевидное неравенство:
Минус вторая производная функции f
не равна минус первой производной от её минус первой производной.
− f
"( )x
≠−(− f
'( ))'x
.
1. Минус первая и минус вторая производные. Теорема Зильберта-Штольца.
2. Матьожидание и писдерсия.
3. Сходимость “так сказать”, “как надо” и “как не надо”, “да нет, наверное”, “отнюдь не сразу”, “из ряда вон”.
4. Очень сильная и очень слабая сходимость.
5. Одно-, дву- и треугольники, измеримые по Зильберту.
6. Шестиугольник ATBCEB. Теорема существования и единственности.
7. Определение кривой и очень кривой.
8. Понятие кусочно-гадкой функции. Её свойства.
9. Оператор «Ы». Операторы GSM и SDMA.
10. Условия Коши-Зильберта.

11. Пространство C a b c
[ , , '], пространство C a b c
[ , , '].
12. Пространство LC a b c
2
[ , , '].
13. Пространство Зильберта Zn
.
14. Полином Зажигалкина. Теорема Зильберта-Зажигалкина.
15. Признак слаборавномерной полунепрерывности полинома Зажигалкина сверху.
16. Принцип Максима Понтрягина. Обобщение.
17. Определение функции Зильберта.
СПИСОК ИСПОЛЬЗОВАННОЙ
МАКУЛАТУРЫ
:
1. В методичке по теории функции Зильберта использован конспект студентов 4-го курса мех-мата (один по всем предметам), где все имена и теоремы вымышленные, любое сходство с уже существующими случайно.
2. Немного фантазии на лекции, и не такое можно придумать!
Также здесь фигурируют фразы и выражения некоторых преподавателей с мех-мата, большой им привет!
Тираж 76 экземпляров.
Цена – бесплатно, то есть даром!
|