КОНТРОЛЬНАЯ РАБОТА № 11
ВАРИАНТ 3
1. Монета подброшена 3 раза. Найти вероятность того: что герб появится два раза
Применяя классическое определение вероятности, находим:
— общее количество событий (Г, Г, Г), (ГГЦ), (Г,Ц,Г), (Г, Ц, Ц), (Ц, Г, Г), (ЦГЦ), (Ц, Ц, Ц), т.е. n =8.
Событию А (герб появляется два раза) соответствуют три случая — (Г, Г, Ц), (Г, Ц, Г) и (Ц, Г, Г), m =3
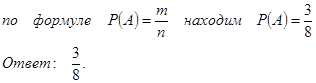
2. Из 10 радиоламп 4 неисправны. Случайно взяты 4 лампы. Найти вероятность того, что среди них окажется хотя бы одна неисправная
Введем обозначения.
Событие А — хотя бы одна лампа неисправна.

Четыре детали из десяти можно выбрать 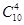 способами (число сочетаний из 10 элементов по 4. способами (число сочетаний из 10 элементов по 4.
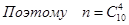 . .
Случай — наступило событие А 1
:
Три неисправных лампы из шести можно выбрать 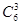 различными способами, а одну из четырех неисправных — различными способами, а одну из четырех неисправных — 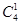 . .
Каждый набор исправных ламп может сочетаться с каждым набором неисправных, поэтому количество благоприятных событий 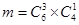 , получаем: , получаем:

Для событий А 2
две исправных лампы из 6 — 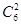 способов две неисправных из способов две неисправных из 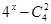 , ,


3. Из урны, содержащей 4 белых, 6 красных и 5 черных шаров случайно извлекли 3 шара. Найти вероятность того, что два из них одного цвета
Обозначим искомое событие через А (два шара одного цвета).
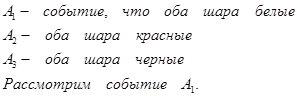
Имеем 4 белых и 11 шаров не белых.
Для события А 1
количество событий, что из четырех белых в выборке будут два белых — 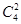 , количество событий — из 11 — один шар — , количество событий — из 11 — один шар — 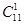 , тогда число благоприятных событий , тогда число благоприятных событий 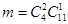 . .
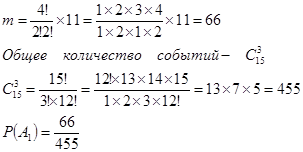
Событие А 2
.
Имеем 6 красных, 9 — других цветов.
Из 6 красных — 2 красных — 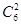 событий. событий.
Из 9 других цветов — 1 —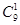 событий, а общее число благоприятных событий — событий, а общее число благоприятных событий —
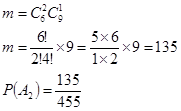
Событие А 3
.
Имеем 5 черных шаров и 10 других.
Из 5 черных — 2 — 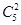 событий. событий.
Из 10 других — 1 — 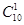 событий. Общее число благоприятных событий событий. Общее число благоприятных событий
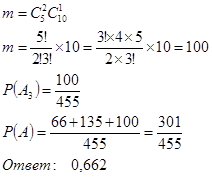
4. В ящике 5 мячей, из которых три — новые. Для игры взяли два мяча, после игры вернув их в ящик. Для второй игры случайно взяли еще два мяча. Найти вероятность того, что они оба новые
Здесь имеем два независимых события. Применяем формулу умножения вероятностей
Для того, чтобы вероятность события искомого (А) не была равна нулю в ящике после наступления события В (взяли первый раз два мяча) должно остаться либо три, либо два мяча новых.
Обозначим через В1 — взяли два мяча подержанных.
Реклама

Число вариантов, что из двух мячей взяли два равно 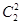 . .
Число вариантов, что из трех мячей не взяли ни одного равно 
Общее число благоприятных событий
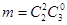 . .
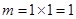
Общее количество событий — 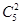 . .
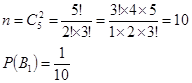
Для события А вычислим вероятность наступления при условии наступления события 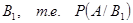 . .
Имеем в ящике 5 шаров, из них три новых, тогда число благоприятных событий будет состоять из суммы:
1) Из 2-х старых мячей в выборке не оказалось ни одного — 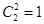 . .
2) Из 3-х новых мячей в выборке 2 новых — 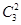 . .
Общее число благоприятных событий:
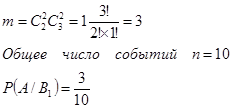
Обозначим через В 2
— (взяли первый раз один новый мяч и один старый).
Число событий — из трех мячей взяли один равно — 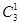 , число вариантов — из двух мячей взяли один равно — , число вариантов — из двух мячей взяли один равно — 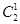 , общее число благоприятных вариантов равно — , общее число благоприятных вариантов равно — 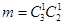 . .
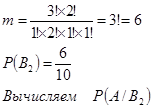
Имеем три старых и два новых мяча. Количество благоприятных событий:
— из трех старых — ни одного — 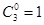
— из двух новых — два — 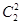 будет равно будет равно 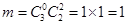
Вероятность 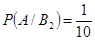 . .
Вероятность наступления события А будет равна:
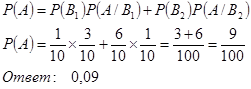
5. Пассажир может ждать летной погоды трое суток, после чего едет поездом. По прогнозам вероятность летной погоды в первые сутки 0,5, во вторые — 0,6, в третьи — 0,8, Х — число полных суток до отъезда пассажира.
Найти:
А) ряд распределения Х.
Вероятность того, что пассажир не будет ждать равна вероятности летней погоды в первые сутки, т.е. Р(0)=0,5.
Вероятность, что пассажир улетит через сутки равна вероятности того, что в первые сутки будет нелетная погода, а во вторые — летная, т.е.
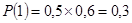 . .
Вероятность того, что пассажир улетит через двое суток равна вероятности трех независимых событий: первые сутки — нелетная погода; вторые — нелетная; третьи — летная
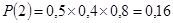
Вероятность того, что пассажир уедет поездом через трое суток равна вероятности того, что все трое суток погода нелетная
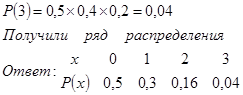
Б) функцию распределения F ( x ).
Функцию F ( x ) строим с помощью формулы:
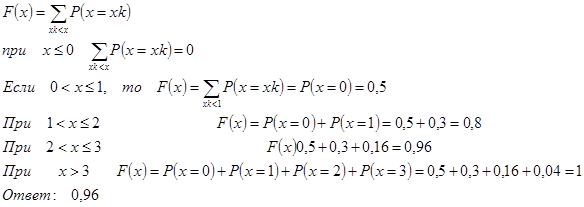
В) m x
ищем по формуле:
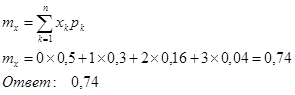
Г) D x
применяем формулу:
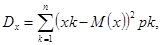
т.е. дисперсия равна математическому ожиданию квадрата ее отклонения:
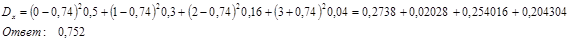
Д) 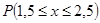 В данном промежутке x принимает только одно значение x =2, следовательно: В данном промежутке x принимает только одно значение x =2, следовательно:
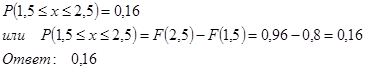
6. Дана функция распределения случайной величины
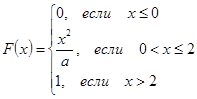
Найти:
А) константу а.
Из условия непрерывности F ( x ) следует 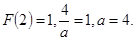
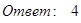
Б) р( x ), по определению 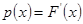 , т.к. F ’( x ) при , т.к. F ’( x ) при 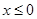 равно (0)’=0, при равно (0)’=0, при 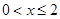
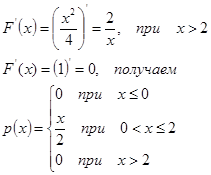
В) m x
. Математическое описание непрерывной случайной величины, все значения которой принадлежат промежутку [α, β] определяется формулой:
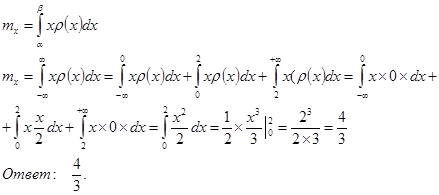
Г) D x
. Дисперсия непрерывной случайной величины X с плотностью распределения p ( x ) определяется формулой:
Реклама

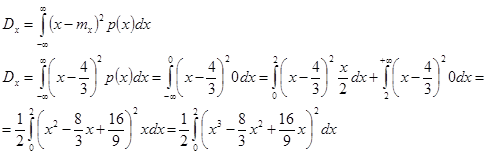
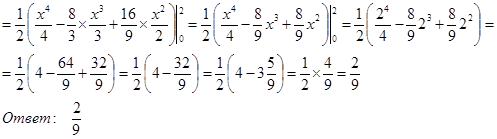
Д) 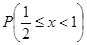 . Находим по формуле . Находим по формуле 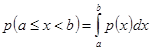 , получаем , получаем
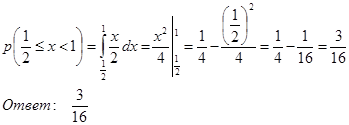
7. Изделие считается высшего сорта, если отклонение его размера от номинала не превышает по модулю 3,45 мм. Случайные отклонения X распределены нормально, причем 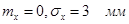 . .
Определить вероятность того, что случайно взятое изделие — высшего сорта
Вероятность того, что отклонение случайной величины X , распределенной по нормальному закону, от математического ожидания 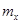 , не превзойдет по абсолютной величине Δ равна: , не превзойдет по абсолютной величине Δ равна:
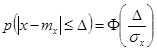
Исключая вероятность будет равна
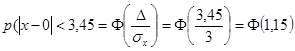
По таблице находим
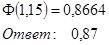
|