Федеральное агентство по образованию (Рособразование)
|
| Архангельский государственный технический университет |
| Кафедра вычислительных систем и телекоммуникаций |
| (наименование кафедры) |
| ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ |
| по |
Интеллектуальные информационные системы |
| (наименование дисциплины) |
| студенту |
ОИТ |
образования |
5 |
курса |
1251 |
группы |
| (фамилия, имя, отчество студента) |
| ТЕМА: |
Генетический алгоритм |
| ИСХОДНЫЕ ДАННЫЕ: |
| 1) Дать обзор моделированию нейронных сетей |
| 2) Смоделировать нейронную сеть |
| 3) Обучит сеть при помощи генетического алгоритма |
Срок проектирования с «18» декабря 2009г. По «24» декабря 2009г.
|
| Руководитель проекта |
ассистент |
| (должность) |
(подпись) |
(и.,о., фамилия) |
ЛИСТ ЗАМЕЧАНИЙ
СОДЕРЖАНИЕ
ВВЕДЕНИЕ . 2
1 МОДЕЛИРОВАНИЕ РАБОТЫ НЕЙРОННОЙ СЕТИ . 2
2 АЛГОРИТМ ОБРАТНОГО РАСПРОСТРОНЕНИЯ ОШИБКИ . 2
3 ГЕНЕТИЧЕСКИЙ АЛГОРИТМ .. 2
4 ЭФФЕКТИВНОСТЬ ГЕНЕТИЧЕСКИХ АЛГОРИТМОВ . 2
4.1 Показатели эффективности генетических алгоритмов . 2
4.2 Скорость работы генетических алгоритмов . 2
4.3 Устойчивость работы генетических алгоритмов . 2
4.4 Направления развития генетических алгоритмов . 2
ЗАКЛЮЧЕНИЕ . 2
СПИСОК ЛИТЕРАТУРЫ .. 2
ПРИЛОЖЕНИЕ . 2
Принятие решения в большинстве случаев заключается в генерации всех возможных альтернатив, их оценке и выборе лучшей среди них. Принять "правильное" решение - значит выбрать такой вариант из числа возможных, в котором с учетом всех разнообразных факторов и противоречивых требований будет оптимизирована некая общая ценность, то есть решение будет в максимальной степени способствовать достижению поставленной цели.
Область применения генетических алгоритмов достаточно обширна. Они успешно используются для решения ряда больших и экономически значимых задач в бизнесе и инженерных разработках. С их помощью были разработаны промышленные проектные решения, позволившие сэкономить многомиллионные суммы. Финансовые компании широко используют эти средства для прогнозирования развития финансовых рынков при управлении пакетами ценных бумаг. Наряду с другими методами эволюционных вычислений генетические алгоритмы обычно используются для оценки значений непрерывных параметров моделей большой размерности, для решения комбинаторных задач, для оптимизации моделей, включающих одновременно непрерывные и дискретные параметры. Другая область применения - использование в системах извлечения новых знаний из больших баз данных, создание и обучение стохастических сетей, обучение нейронных сетей, оценка параметров в задачах многомерного статистического анализа, получение исходных данных для работы других алгоритмов поиска и оптимизации.
1
МОДЕЛИРОВАНИЕ РАБОТЫ НЕЙРОННОЙ СЕТИ
Под нейронными сетями (НС) подразумеваются вычислительные структуры, которые моделируют простые биологические процессы, обычно ассоциируемые с процессами человеческого мозга. Адаптируемые и обучаемые, они представляют собой распараллеленные системы, способные к обучению путем анализа положительных и отрицательных воздействий. Элементарным преобразователем в данных сетях является искусственный нейрон или просто нейрон, названный так по аналогии с биологическим прототипом.
Реклама

Как отмечалось, искусственная нейронная сеть (ИНС, нейросеть) - это набор нейронов, соединенных между собой. Как правило, передаточные (активационные) функции всех нейронов в сети фиксированы, а веса являются параметрами сети и могут изменяться. Некоторые входы нейронов помечены как внешние входы сети, а некоторые выходы - как внешние выходы сети. Подавая любые числа на входы сети, мы получаем какой-то набор чисел на выходах сети. Таким образом, работа нейросети состоит в преобразовании входного вектора X в выходной вектор Y, причем это преобразование задается весами сети. Практически любую задачу можно свести к задаче, решаемой нейросетью.
Моделирование сети начинается с выбора архитектуры. На данном этапе необходимо учесть:
- какие нейроны мы хотим использовать (число входов, передаточные функции);
- каким образом следует соединить их между собой;
- что взять в качестве входов и выходов сети.
На втором этапе нам следует «обучить» выбранную сеть, т.е. подобрать такие значения ее весов, чтобы сеть работала нужным образом. Необученная сеть подобна ребенку - ее можно научить чему угодно. В используемых на практике нейросетях количество весов может составлять несколько десятков тысяч, поэтому обучение - действительно сложный процесс. Для многих архитектур разработаны специальные алгоритмы обучения, которые позволяют настроить веса сети определенным образом.
В зависимости от функций, выполняемых нейронами в сети, можно выделить три их типа:
- входные нейроны - это нейроны, на которые подается входной вектор, кодирующий входное воздействие или образ внешней среды; в них обычно не осуществляется вычислительных процедур, информация передается с входа на выход нейрона путем изменения его активации;
- выходные нейроны - это нейроны, выходные значения которых представляют выход сети;
- промежуточные нейроны - это нейроны, составляющие основу искусственных нейронных сетей.
Обучить нейросеть - значит, сообщить ей, чего мы от нее добиваемся. Этот процесс очень похож на обучение ребенка алфавиту. Показав ребенку изображение буквы «А», мы спрашиваем его: «Какая это буква?» Если ответ неверен, мы сообщаем ребенку тот ответ, который мы хотели бы от него получить: «Это буква А». Ребенок запоминает этот пример вместе с верным ответом, т.е. в его памяти происходят некоторые изменения в нужном направлении. Мы будем повторять процесс предъявления букв снова и снова до тех пор, когда все буквы будут твердо запомнены. Такой процесс называют «обучение с учителем».
Реклама

При обучении сети мы действуем совершенно аналогично. У нас имеется некоторая база данных, содержащая примеры (набор рукописных изображений букв). Предъявляя изображение буквы «А» на вход сети, мы получаем от нее некоторый ответ, не обязательно верный. Нам известен и верный (желаемый) ответ, в данном случае нам хотелось бы, чтобы на выходе с меткой «А» уровень сигнала был максимален. Обычно в качестве желаемого выхода в задаче классификации берут набор (1, 0, 0,...), где 1 стоит на выходе с меткой «А», а 0 - на всех остальных выходах. Вычисляя разность между желаемым ответом и реальным ответом сети, мы получаем (для букв русского алфавита) 33 числа - вектор ошибки. Алгоритм обучения - это набор формул, который позволяет по вектору ошибки вычислить требуемые поправки для весов сети. Одну и ту же букву (а также различные изображения одной и той же буквы) мы можем предъявлять сети много раз. В этом смысле обучение скорее напоминает повторение упражнений в спорте - тренировку.
Оказывается, что после многократного предъявления примеров веса сети стабилизируются, причем сеть дает правильные ответы на все (или почти все) примеры из базы данных. В таком случае говорят, что «сеть выучила все примеры», «сеть обучена», или «сеть натренирована». В программных реализациях можно видеть, что в процессе обучения функция ошибки (например, сумма квадратов ошибок по всем выходам) постепенно уменьшается. Когда функция ошибки достигает нуля или приемлимого малого уровня, тренировку останавливают, а полученную сеть считают натренированной и готовой к применению на новых данных.
Важно отметить, что вся информация, которую сеть имеет о задаче, содержится в наборе примеров. Поэтому качество обучения сети напрямую зависит от количества примеров в обучающей выборке, а также от того, насколько полно эти примеры описывают данную задачу. Так, например, бессмысленно использовать сеть для предсказания финансового кризиса, если в обучающей выборке кризисов не представлено. Считается, что для полноценной тренировки требуется хотя бы несколько десятков (а лучше сотен) примеров.
Математически процесс обучения можно описать следующим образом. В процессе функционирования нейронная сеть формирует выходной сигнал Y в соответствии с входным сигналом X, реализуя некоторую функцию Y = G(X). Если архитектура сети задана, то вид функции G определяется значениями синоптических весов и смещений сети. Пусть решением некоторой задачи является функция Y = = F(X), заданная парами входных - выходных данных (X 1
, Y 1
), (X 2
, Y 2
), ..., (X w
, Y w
), для которых Y k
= F(X k
) (к = 1, 2, …,N).
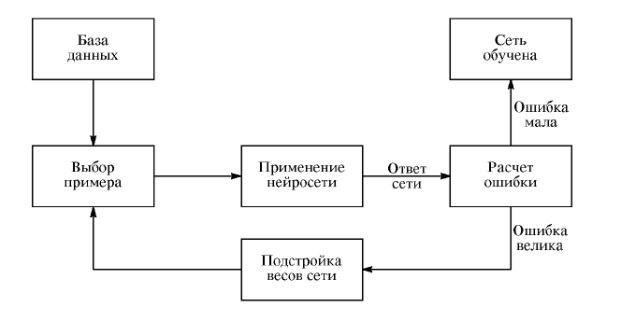
Рисунок 5- Схема обучения сети
2
АЛГОРИТМ ОБРАТНОГО РАСПРОСТРОНЕНИЯ ОШИБКИ
Алгоритм обратного распространения ошибки (back propagation) - это итеративный градиентный алгоритм обучения, который используется с целью минимизации среднеквадратичного отклонения текущего выхода и желаемого выхода многослойных нейронных сетей.
Алгоритм обратного распространения используется для обучения многослойных нейронных сетей с последовательными связями вида. Нейроны в таких сетях делятся на группы с общим входным сигналом. Нейроны выполняют взвешенное (с синоптическими весами) суммирование элементов входных сигналов; к данной сумме прибавляется смещение нейрона. Над полученным результатом выполняется активационной функцией затем нелинейное преобразование. Значение функции активации есть выход нейрона.
В многослойных сетях оптимальные выходные значения нейронов всех слоев, кроме последнего, как правило, неизвестны, и трех- или более слойный персептрон уже невозможно обучить, руководствуясь только величинами ошибок на выходах НС. Наиболее приемлемым вариантом обучения в таких условиях оказался градиентный метод поиска минимума функции ошибки с рассмотрением сигналов ошибки от выходов НС к ее входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы. Этот алгоритм обучения НС получил название процедуры обратного распространения.
В данном алгоритме функция ошибки представляет собой сумму квадратов рассогласования (ошибки) желаемого выхода сети и реального. При вычислении элементов вектора-градиента использован своеобразный вид производных функций активации сигмоидального типа. Алгоритм действует циклически (итеративно), и его циклы принято называть эпохами. На каждой эпохе на вход сети поочередно подаются все обучающие наблюдения, выходные значения сети сравниваются с целевыми значениями и вычисляется ошибка. Значение ошибки, а также градиента поверхности ошибок используется для корректировки весов, после чего все действия повторяются. Начальная конфигурация сети выбирается случайным образом, и процесс обучения прекращается, либо когда пройдено определенное количество эпох, либо когда ошибка достигнет некоторого определенного уровня малости, либо когда ошибка перестанет уменьшаться (пользователь может сам выбрать нужное условие остановки).
Приведем словесное описание алгоритма.
Шаг 1. Весам сети присваиваются небольшие начальные значения.
Шаг 2. Выбирается очередная обучающая пара (X, Y) из обучающего множества; вектор X подается на вход сети.
Шаг 3. Вычисляется выход сети.
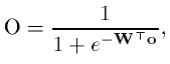
где W - вектор весов выходного нейрона, o k
- вектор выходов нейронов скрытого слоя с элементами
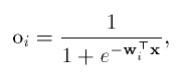
w i
обозначает вектор весов, связанных с i-м скрытым нейроном, i = 1, 2, ..., L.
Шаг 4. Вычисляется разность между требуемым (целевым, Y) и реальным (вычисленным) выходом сети.
Шаг 5. Веса сети корректируются так, чтобы минимизировать ошибку.
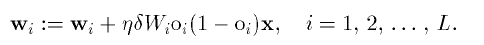
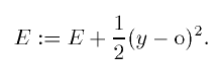
Шаг 6. Шаги со 2-го по 5-й повторяются для каждой пары обучающего множества до тех пор, пока ошибка на всем множестве не достигнет приемлемой величины.
Шаги 2 и 3 подобны тем, которые выполняются в уже обученной сети.
Вычисления в сети выполняются послойно. На шаге 3 каждый из выходов сети вычитается из соответствующей компоненты целевого вектора с целью получения ошибки. Эта ошибка используется на шаге 5 для коррекции весов сети.
Шаги 2 и 3 можно рассматривать как «проход вперед», так как сигнал распространяется по сети от входа к выходу. Шаги 4 и 5 составляют «обратный проход», поскольку здесь вычисляемый сигнал ошибки распространяется обратно по сети и используется для подстройки весов
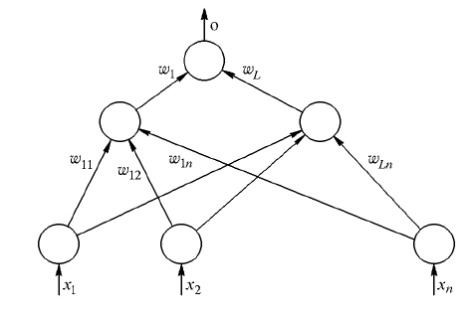
Рисунок 6 –Двухслойная сеть
Рассмотренная процедура может быть легко обобщена на случай сети с произвольным количеством слоев и нейронов в каждом слое. Обратим внимание, что в данной процедуре сначала происходит коррекция весов для выходного нейрона, а затем - для нейронов скрытого слоя, т.е. от конца сети к ее началу. Отсюда и название - обратное распространение ошибки. Ввиду использования для обозначений греческой буквы S, эту процедуру обучения называют еще иногда обобщенным дельта - правилом.
Дадим изложенному геометрическую интерпретацию.
В алгоритме обратного распространения вычисляется вектор градиента поверхности ошибок. Этот вектор указывает направление кратчайшего спуска по поверхности из данной точки, поэтому, если мы «немного» продвинемся по нему, ошибка уменьшится. Последовательность таких шагов (замедляющаяся по мере приближения к дну) в конце концов приведет к минимуму того или иного типа. Определенную трудность здесь представляет вопрос о том, какую нужно брать длину шагов (что определяется величиной коэффициента скорости обучения η ).
При большой длине шага сходимость будет более быстрой, но имеется опасность перепрыгнуть через решение или (если поверхность ошибок имеет особо вычурную форму) уйти в неправильном направлении. Классическим примером такого явления при обучении нейронной сети является ситуация, когда алгоритм очень медленно продвигается по узкому оврагу с крутыми склонами, прыгая с одной его стороны на другую. Напротив, при маленьком шаге, вероятно, будет схвачено верное направление, однако при этом потребуется очень много итераций. На практике величина шага берется пропорциональной крутизне склона (так что алгоритм замедляет ход вблизи минимума) с некоторой константой ( η ), которая, как отмечалось, называется коэффициентом скорости обучения. Правильный выбор скорости обучения зависит от конкретной задачи и обычно осуществляется опытным путем; эта константа может также зависеть от времени, уменьшаясь по мере продвижения алгоритма.
Обычно этот алгоритм видоизменяется таким образом, чтобы включать слагаемое импульса (или инерции). Этот член способствует продвижению в фиксированном направлении, поэтому если было сделано несколько шагов в одном и том же направлении, то алгоритм «увеличивает скорость», что (иногда) позволяет избежать локального минимума, а также быстрее проходить плоские участки.
Таким образом, алгоритм действует итеративно, и его шаги принято называть эпохами. На каждой эпохе на вход сети поочередно подаются все обучающие наблюдения, выходные значения сети сравниваются с целевыми значениями и вычисляется ошибка. Значение ошибки, а также градиента поверхности ошибок используется для корректировки весов, после чего все действия повторяются. Начальная конфигурация сети выбирается случайным образом, и процесс обучения прекращается, либо когда пройдено определенное количество эпох, либо когда ошибка достигнет некоторого определенного уровня малости, либо когда ошибка перестанет уменьшаться (пользователь может сам выбрать нужное условие остановки).
Классический метод обратного распространения относится к алгоритмам с линейной сходимостью и известными недостатками его являются: невысокая скорость сходимости (большое число требуемых итераций для достижения минимума функции ошибки), возможность сходиться не к глобальному, а к локальным решениям (локальным минимумам отмеченной функции), возможность паралича сети (при котором большинство нейронов функционирует при очень больших значениях аргумента функций активации, т.е. на ее пологом участке; поскольку ошибка пропорциональна производной, которая на данных участках мала, то процесс обучения практически замирает).
Для устранения этих недостатков были предложены много-численные модификации алгоритма обратного распространения, которые связаны с использованием различных функций ошибки, различных процедур определения направления и величины шага и т. п.
Программируемая НС, предназначена для распознавания образа нуля и единицы.
3
ГЕНЕТИЧЕСКИЙ АЛГОРИТМ
Генетический алгоритм (англ. genetic algorithm) — это эвристический алгоритм поиска, используемый для решения задач оптимизации и моделирования путем последовательного подбора, комбинирования и вариации искомых параметров с использованием механизмов, напоминающих биологическую эволюцию. Является разновидностью эволюционных вычислений (англ. evolutionary computation). Отличительной особенностью генетического алгоритма является акцент на использование оператора «скрещивания», который производит операцию рекомбинации решений-кандидатов, роль которой аналогична роли скрещивания в живой природе. «Отцом-основателем» генетических алгоритмов считается Джон Холланд (англ. John Holland), книга которого «Адаптация в естественных и искусственных системах» (англ. Adaptation in Natural and Artificial Systems) является основополагающим трудом в этой области исследований.
Генетические алгоритмы являются разновидностью методов поиска с элементами случайности и имеют цель нахождение лучшего решения по сравнению с имеющимся, а не оптимальным решением задачи. Это связано с тем, что для сложной системы часто требуется найти хоть какое-нибудь удовлетворительное решение, а проблема достижения оптимума отходит на второй план. При этом другие методы, ориентированные на поиск именно оптимального решения, вследствие чрезвычайной сложности задачи становятся вообще неприменимыми. В этом кроется причина появления, развития и роста популярности генетических алгоритмов. Хотя, как и всякий другой метод поиска, этот подход не является оптимальным методом решения любых задач. Дополнительным свойством этих алгоритмов является невмешательство человека в развивающийся процесс поиска. Человек может влиять на него лишь опосредованно, задавая определенные параметры.
Преимущества генетических алгоритмов становятся еще более прозрачными, если рассмотреть основные их отличия от традиционных методов:
1) Генетические алгоритмы работают с кодами, в которых представлен набор параметров, напрямую зависящих от аргументов целевой функции. Причем интерпретация этих кодов происходит только перед началом работы алгоритма и после завершения его работы для получения результата. В процессе работы манипуляции с кодами происходят совершенно независимо от их интерпретации, код рассматривается просто как битовая строка.
2) Для поиска генетический алгоритм использует несколько точек поискового пространства одновременно, а не переходит от точки к точке, как это делается в традиционных методах. Это позволяет преодолеть один из их недостатков - опасность попадания в локальный экстремум целевой функции, если она не является унимодальной, то есть имеет несколько таких экстремумов. Использование нескольких точек одновременно значительно снижает такую возможность.
3) Генетические алгоритмы в процессе работы не используют никакой дополнительной информации, что повышает скорость работы. Единственной используемой информацией может быть область допустимых значений параметров и целевой функции в произвольной точке.
4) Генетический алгоритм использует как вероятностные правила для порождения новых точек анализа, так и детерминированные правила для перехода от одних точек к другим. Одновременное использование элементов случайности и детерминированности дает значительно больший эффект, чем раздельное.
Прежде чем рассматривать непосредственно работу генетического алгоритма, введем ряд терминов, которые широко используются в данной области.
Генетический алгоритм работает с кодами безотносительно их смысловой интерпретации. Поэтому сам код и его структура описываются понятием генотип, а его интерпретация, с точки зрения решаемой задачи, понятием - фенотип. Каждый код представляет, по сути, точку пространства поиска. С целью максимально приблизиться к биологическим терминам, экземпляр кода называют хромосомой, особью или индивидуумом. Далее для обозначения строки кода мы будем в основном использовать термин "особь".
На каждом шаге работы генетический алгоритм использует несколько точек поиска одновременно. Совокупность этих точек является набором осо¬бей, который называется популяцией. Количество особей в популяции назы¬вают размером популяции. На каждом шаге работы генетический алгоритм обновляет популяцию путем создания новых особей и уничтожения ненужных. Чтобы отличать популяции на каждом из шагов и сами эти шаги, их называют поколениями и обычно идентифицируют по номеру. Например, популяция, полученная из исходной популяции после первого шага работы алгоритма, будет первым поколением, после следующего шага - вторым и т. д.
В процессе работы алгоритма генерация новых особей происходит на основе моделирования процесса размножения. При этом, естественно, порождающие особи называются родителями, а порожденные - потомками. Родительская пара, как правило, порождает пару потомков. Непосредственная генерация новых кодовых строк из двух выбранных происходит за счет работы оператора скрещивания, который также называют кроссинговером (от англ., crossover). При порождении новой популяции оператор скрещивания может применяться не ко всем парам родителей. Часть этих пар может переходить в популяцию следующего поколения непосредственно. Насколько часто будет возникать такая ситуация, зависит от значения вероятности применения оператора скрещивания, которая является одним из параметров генетического алгоритма.
Моделирование процесса мутации новых особей осуществляется за счет работы оператора мутации. Основным параметром оператора мутации также является вероятность мутации.
Поскольку размер популяции фиксирован, то порождение потомков должно сопровождаться уничтожением других особей. Выбор пар родителей из популяции для порождения потомков производит оператор отбора, а выбор особей для уничтожения - оператор редукции. Основным параметром их работы является, как правило, качество особи, которое определяется значением целевой функции в точке пространства поиска, описываемой этой особью.
Таким образом, можно перечислить основные понятия и термины, используемые в области генетических алгоритмов:
- генотип и фенотип;
- особь и качество особи;
- популяция и размер популяции;
- поколение;
- родители и потомки.
К характеристикам генетического алгоритма относятся:
- размер популяции;
- оператор скрещивания и вероятность его использования;
- оператор мутации и вероятность мутации;
- оператор отбора;
- оператор редукции;
- критерий останова.
Операторы отбора, скрещивания, мутации и редукции называют еще генетическими операторами.
Критерием останова работы генетического алгоритма может быть одно из трех событий:
1) Сформировано заданное пользователем число поколений.
2) Популяция достигла заданного пользователем качества (например, значение качества всех особей превысило заданный порог).
3) Достигнут некоторый уровень сходимости. То есть особи в популяции стали настолько подобными, что дальнейшее их улучшение происходит чрезвычайно медленно.
Характеристики генетического алгоритма выбираются таким образом, чтобы обеспечить малое время работы, с одной стороны, и поиск как можно лучшего решения, с другой.
Последовательность работы генетического алгоритма
Рассмотрим теперь непосредственно работу генетического алгоритма. Общая схема его работы представлена на рисунке 7.
  


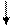

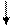





Рисунок 7 – Схема работы генетического алгоритма
Программируемый генетический алгоритм используется для поиска минимального значения функции ошибки нейрона.
Оператор скрещивания призван моделировать природный процесс наследования, то есть обеспечивать передачу свойств родителей потомкам.
Рассмотрим простейший оператор скрещивания. Он выполняется в два этапа. Пусть особь представляет собой строку из т
элементов. На первом этапе равновероятно выбирается натуральное число k
от 1 до т-1.
Это число называется точкой разбиения. В соответствии с ним обе исходные строки разбиваются на две подстроки. На втором этапе строки обмениваются своими подстроками, лежащими после точки разбиения, то есть элементами с k +1-го по m -й. Так получаются две новые строки, которые наследовали частично свойства обоих родителей. Этот процесс проиллюстрирован ниже.
Вероятность применения оператора скрещивания обычно выбирается достаточно большой, в пределах от 0,9 до 1, чтобы обеспечить постоянное появление новых особей, расширяющих пространство поиска. При значении вероятности меньше 1 часто используют элитизм .
Это особая стратегия, которая предполагает переход в популяцию следующего поколения элиты, то есть лучших особей текущей популяции, без каких-либо изменений. Применение элитизма способствует сохранению общего качества популяции на высоком уровне. При этом элитные особи участвуют еще и в процессе отбора родителей для последующего скрещивания. Количество элитных особей определяется обычно по формуле:
К =
(1 - Р) *
N
,
(7.2)
где К-
количество элитных особей, Р -
вероятность применения оператора скрещивания, N -
размер популяции.
В случае использования элитизма все выбранные родительские пары подвергаются скрещиванию, несмотря на то, что вероятность применения оператора скрещивания меньше 1. Это позволяет сохранять размер популяции постоянным.
Оператор мутации служит для моделирования природного процесса мутации. Его применение в генетических алгоритмах обусловлено следующими соображениями. Исходная популяция, какой бы большой она ни была, охватывает ограниченную область пространства поиска. Оператор скрещивания, безусловно, расширяет эту область, но все же до определенной степени, поскольку использует ограниченный набор значений, заданный исходной популяцией. Внесение случайных изменений в особи позволяет преодолеть это ограничение и иногда значительно сократить время поиска и улучшить качество результата.
Как правило, вероятность мутации, в отличие от вероятности скрещивания, выбирается достаточно малой. Сам процесс мутации заключается в замене одного из элементов строки на другое значение. Это может быть перестановка двух элементов в.строке, замена элемента строки значением элемента из другой строки, в случае битовой строки может применяться инверсия одного из битов и т. д.
В процессе работы алгоритма все указанные выше операторы применяются многократно и ведут к постепенному изменению исходной популяции. Поскольку операторы отбора, скрещивания, мутации и редукции по своей сути направлены на улучшение каждой отдельной особи, то результатом их работы является постепенное улучшение популяции в целом. В этом и заключается основной смысл работы генетического алгоритма - улучшить популяцию решений по сравнению с исходной.
После завершения работы генетического алгоритма из конечной популяции выбирается та особь, которая дает экстремальное (максимальное или минимальное) значение целевой функции и является, таким образом, результатом работы генетического алгоритма. За счет того, что конечная популяция лучше исходной, полученный результат представляет собой улучшенное решение.
4
ЭФФЕКТИВНОСТЬ ГЕНЕТИЧЕСКИХ АЛГОРИТМОВ И СРЕДСТВА ЕЕ ПОВЫШЕНИЯ
Эффективность генетического алгоритма при решении конкретной задачи зависит от многих факторов, и в частности от таких, как генетические операторы и выбор соответствующих значений параметров, а также способа представления задачи на хромосоме. Оптимизация этих факторов приводит к повышению скорости и устойчивости поиска, что существенно для применения генетических алгоритмов.
Скорость генетического алгоритма оценивается временем, необходимым для выполнения заданного пользователем числа итераций. Если критерием останова является качество популяции или ее сходимость, то скорость оценивается временем достижения генетическим алгоритмом одного из этих событий.
Устойчивость поиска оценивается степенью устойчивости алгоритма к попаданию в точки локальных экстремумов и способностью постоянно увеличивать качество популяции от поколения к поколению.
Два этих фактора - скорость и устойчивость - и определяют эффективность генетического алгоритма для решения каждой конкретной задачи.
Основным способом повышения скорости работы генетических алгоритмов является распараллеливание. Причем этот процесс можно рассматривать с двух позиций. Распараллеливание может осуществляться на уровне организации работы генетического алгоритма и на уровне его непосредственной реализации на вычислительной машине.
Во втором случае используется следующая особенность генетических алгоритмов. В процессе работы многократно приходится вычислять значения целевой функции для каждой особи, осуществлять преобразования оператора скрещивания и мутации для нескольких пар родителей и т. д. Все эти процессы могут быть реализованы одновременно на нескольких параллельных системах или процессорах, что пропорционально повысит скорость работы алгоритма.
В первом же случае применяется структурирование популяции решений на основе одного из двух подходов:
1)Популяция разделяется на несколько различных подпопуляций ,
которые впоследствии развиваются параллельно и независимо. То есть скрещивание происходит только между членами одного демоса. На каком-то этапе работы происходит обмен частью особей между подпопуляциями на основе случайной выборки. И так может продолжаться до завершения работы алгоритма. Данный подход получил название концепции островов.
2)Для каждой особи устанавливается ее пространственное положение в популяции. Скрещивание в процессе работы происходит между ближайшими особями. Такой подход получил название концепции скрещивания в локальной области.
Оба подхода, очевидно, также могут эффективно реализовываться на параллельных вычислительных машинах. Кроме того, практика показала, что структурирование популяции приводит к повышению эффективности генетического алгоритма даже при использовании традиционных вычислительных средств.
Еще одним средством повышения скорости работы является кластеризация. Суть ее состоит, как правило, в двухэтапной работе генетического алгоритма. На первом этапе генетический алгоритм работает традиционным образом с целью получения популяции более "хороших" решений. После завершения работы алгоритма из итоговой популяции выбираются группы наиболее близких решений. Эти группы в качестве единого целого образуют исходную популяцию для работы генетического алгоритма на втором этапе. Размер такой популяции будет, естественно, значительно меньше, и, соответственно, алгоритм будет далее осуществлять поиск зна-чительнд^эыстрее. Сужения пространства поиска в данном случае не происходит, поскольку применяется исключение из рассмотрения только ряда очень похожих особей, существенно не влияющих на получение новых видов решений.
Устойчивость или способность генетического алгоритма эффективно формировать лучшие решения зависит в основном от принципов работы генетических операторов (операторов отбора, скрещивания, мутации и редукции). Рассмотрим механизм этого воздействия подробнее.
Как правило, диапазон влияния можно оценить, рассматривая вырожденные случаи генетических операторов.
Вырожденными формами операторов скрещивания являются, с одной стороны, точное копирование потомками своих родителей, а с другой, порождение потомков, в наибольшей степени отличающихся от них.
Преимуществом первого варианта является скорейшее нахождение лучшего решения, а недостатком, в свою очередь, тот факт, что алгоритм не сможет найти решения лучше, чем уже содержится в исходной популяции, поскольку в данном случае алгоритм не порождает принципиально новых особей, а лишь копирует уже имеющиеся. Чтобы все-таки использовать достоинства этой предельной формы операторов скрещивания в реальных генетических алгоритмах, применяют элитизм', речь о котором шла выше.
Во втором случае алгоритм рассматривает наибольшее число различных особей, расширяя область поиска, что, естественно, приводит к получению более качественного результата. Недостатком в данном случае является значительное замедление поиска. Одной из причин этого, в частности, является то, что потомки, значительно отличаясь от родителей, не наследуют их полезных свойств.
В качестве реальных операторов скрещивания используются промежуточные варианты. В частности, родительское воспроизводство с мутацией и родительское воспроизводство с рекомбинацией и мутацией. Родительское воспроизводство означает копирование строк родительских особей в
строки потомков. В первом случае после этого потомки подвергаются воздействию, мутации. Во втором случае после копирования особи-потомки обмениваются подстроками, этот процесс называется рекомбинацией и был описан в предыдущих параграфах. После рекомбинации п 髒 томки также подвергаются воздействию мутации. Последний подход получил наибольшее распространение в области генетических алгоритмов.
Наиболее распространенными при этом являются одноточечный, двухточечный и равномерный операторы скрещивания. Свои названия они получили от принципа разбиения кодовой строки на подстроки. Строка может соответственно разбиваться на подстроки в одном или двух местах. Или строки могут образовывать особи-потомки, чередуя свои элементы.
Основным параметром оператора мутации является вероятность его воздействия. Обычно она выбирается достаточно малой. Чтобы, с одной стороны, обеспечивать расширение области поиска, а с другой, не привести к чересчур серьезным изменениям потомков, нарушающим наследование полезных параметров родителей. Сама же суть воздействия мутации обычно определяется фенотипом и на эффективность алгоритма особого воздействия не оказывает.
Существует также дополнительная стратегия расширения поискового пространства, называемая стратегией разнообразия.
Если генетический алгоритм использует данную стратегию, то каждый порожденный потомок подвергается незначительному случайному изменению. Отличие разнообразия и мутации в том, что оператор мутации вносит в хромосому достаточно значительные изменения, а оператор разнообразия - наоборот. В этом заключается основная причина стопроцентной вероятности применения разнообразия. Ведь если часто вносить в хромосомы потомков незначительные изменения, то они могут быть полезны с точки зрения как расширения пространства поиска, так и наследования полезных свойств. Отметим, что стратегия разнообразия применяется далеко не во всех генетических алгоритмах, поскольку является лишь средством повышения эффективности.
Еще одним важнейшим фактором, влияющим на эффективность генетического алгоритма, является оператор отбора. Слепое следование принципу "выживает сильнейший" может привести к сужению области поиска и попаданию найденного решения в область локального экстремума целевой функции. С другой стороны, слишком слабый оператор отбора может привести к замедлению роста качества популяции, а значит, и к замедлению поиска. Кроме того, популяция при этом может не только не улучшаться, но и ухудшаться. Самыми распространенными операторами отбора родителей являются:
- случайный равновероятный отбор;
- рангово-пропорциональный отбор;
- отбор пропорционально значению целевой функции.
Виды операторов редукции особей с целью сохранения размера популяции практически совпадают с видами операторов отбора родителей. Среди них можно перечислить:
- случайное равновероятное удаление;
- удаление К наихудших;
- удаление, обратно пропорциональное значению целевой функции.
Поскольку процедуры отбора родителей и редукции разнесены по дей
ствию во времени и имеют разный смысл, сейчас ведутся активные иссле
дования с целью выяснения, как влияет согласованность этих процедур на
эффективность генетического алгоритма. /
Одним из параметров, также влияющих на устойчивость и скорость поиска, является размер популяции, с которой работает алгоритм. Классические генетические алгоритмы предполагают, что размер популяции должен быть фиксированным. Такие алгоритмы называют алгоритмами стационарного состояния. В этом случае оптимальным считается размер 21о§ 2
(и), где п -
количество всех возможных решений задачи.
Однако практика показала, что иногда бывает полезно варьировать размер популяции в определенных пределах. Подобные алгоритмы получили название поколенческих
[82]. В данном случае после очередного порождения потомков усечения популяции не происходит. Таким образом, на протяжении нескольких итераций размер популяции может расти, пока не достигнет определенного порога, После чего популяция усекается до своего исходного размера. Такой подход способствует расширению области поиска, но вместе с тем не ведет к значительному снижению скорости, поскольку усечение популяции, хотя и реже, но все же происходит.
4.
4 Направления развития генетических алгоритмов
Практическая деятельность человека ставит перед наукой все новые исследовательские задачи 祥 Область применения генетических алгоритмов постоянно расширяется, что требует их совершенствования и исследования. Перечислим несколько новых задач, которые могут решаться с использованием генетических алгоритмов, и связанные с ними направления исследований в этой области:
1) разработка новых методов тестирования генетических алгоритмов;
разработка адаптивных генетических алгоритмов;
2) расширение круга решаемых с использованием генетических алгоритмов задач;
3) максимальное приближение генетических алгоритмов к естественному эволюционному процессу.
До недавнего времени в качестве критерия качества большинства конкретных генетических алгоритмов использовалась эффективность решения задачи получения битового вектора с максимальным числом единичных разрядов. Чем быстрее алгоритм находил наилучшее решение, тем он считался эффективнее. Сейчас эта задача уже не является объективным средством тестирования алгоритмов, что свидетельствует об их бурном развитии не только с точки зрения применимости к тем или иным классам задач, но и с точки зрения их внутреннего построения и принципов работы.
В области исследований, направленных на повышение эффективности генетических алгоритмов, большое значение приобрели идеи создания адаптивных генетических алгоритмов, которые могут изменять свои параметры в процессе работы. Они стали продолжением развития идеи поколенческих алгоритмов, которые в процессе работы изменяют размер популяции. Адаптивные алгоритмы способны изменять не только этот параметр, но и суть генетических операторов, вероятность мутации и даже генотип алгоритма. Как правило, данные изменения происходят путем выбора параметров из нескольких вариантов, определенных перед началом работы алгоритма.
Идея адаптивных генетических алгоритмов получила свое воплощение в концепции, представляющей многоуровневые генетические алгоритмы. Нижний уровень такого алгоритма непосредственно выполняет задачу улучшения популяции решений. Верхние уровни представляют собой генетические алгоритмы, решающие оптимизационную задачу по улучшению параметров алгоритма нижнего уровня. При этом в качестве целевой функции используется обычно скорость работы алгоритма нижнего уровня и скорость улучшения им популяции от поколения к поколению.
Традиционные оптимизационные задачи имеют целевую функцию с фиксированной областью значений, называемой также ландшафтом. В последнее время потребовалось решение задач, в которых ландшафт со временем может изменяться. То есть целевая функция при одних и тех же значениях аргументов в разные моменты времени может принимать различные значения. Создание алгоритмов, способных работать с такими задачами, является сейчас одной из актуальных и одновременно сложных проблем в области генетических алгоритмов.
До сих пор продолжается дискуссия между сторонниками универсальных и проблемно-ориентированных представлений задач при использовании эволюционных вычислений. Можно говорить, что в этом вопросе чаша весов, склоняется в сторону универсальных, в которых можно осуществлять изменения на уровне генотипа значительно проще и эффективнее, чем на уровне фенотипа.
Перспективным направлением развития является добавление к генетическим операторам ламарковских операторов, которые позволяют вводить в рассмотрение признаки, приобретенные особью не в результате наследования, а в течение своего жизненного цикла. Это еще более приближает модель генетических алгоритмов к природным процессам и, по мнению ученых, способно повысить их эффективность.
Идея приближения генетических алгоритмов к реальному эволюционному процессу нашла свое отражение и в предложениях ввести в рассмотрение такие понятия, как вид и пол, учитывать взаимодействие особей в популяции в процессе "жизни", причем особей как одного вида, так и различных. Это позволит моделировать процессы сотрудничества, отношений хозяев и паразитов и т. д.
Помимо этих новых течений в области исследования генетических алгоритмов ведутся работы и в традиционных направлениях. Создаются все новые разновидности операторов отбора, скрещивания и мутации. Конструируются адаптивные алгоритмы, совершенствуются методы распараллеливания вычислений и структурирования популяций. Одновременно разрабатываются методики оценки эффективности и тестирования генетических алгоритмов.
Таким образом, генетические алгоритмы представляют собой одну из важных и активно развивающихся парадигм обширной области алгоритмов поиска оптимальных решений. И в последнее время, с развитием методов компьютерной поддержки принятия решений, они приобретают все большее значение.
В ходе данной работы была построена модель нейрона, нейронной сети. Для обучения сети был использовании алгоритм обратного распространения ошибки, являющийся наиболее распространённым алгоритмом при обучении нейронных сетей. Для обучения сети был применен генетический алгоритм. Программирование и обучение нейронных сетей очень интересное и увлекательное занятие. Роль генетических алгоритмом и нейронных сетей в настоящее время очень велика, поэтому знание и умение программировать их необходимо знать.
1) Курс лекций по дисциплине «Интеллектуальные ИС», Гурьев А.Т. , 2008
2) Лабораторный практикум по дисциплине «Интеллектуальные ИС», 2008г.
3) Методические пособия по дисциплине «Интеллектуальные ИС», 2008г.
4) Нейрокомпьютерная техника, Ф.Уоссермен, 1992.
5) Нейронные сети: основные положения, С.Короткий, 2008г.
(обязательное)
using System;
using System.Collections.Generic;
using System.Text;
using System.Collections;
using System.IO;
namespace neuro
{
struct SandY//резултат работы нейрона
{
public double S;//сумма
public double Y;//значение активизационной функции
}
class Program
{
static Random ver = new Random();
static int s = 0;// для рандомайза
static int[] NMinIndexesValue(int N, double[] mass)// Возвращает N индексов для наименьших значений mass
{
int[] resultMin = new int[N];
double[] arr = new double[mass.Length];
int[] ind = new int[mass.Length];
for (int i = 0; i < mass.Length; i++)
{
arr[i] = mass[i];
ind[i] = i;
}
double x;
int x1;
for (int i = 0; i < mass.Length; i++)
{
for (int j = mass.Length - 1; j > i; j--)
{
if (arr[j - 1] > arr[j])
{
x = arr[j - 1];
x1 = ind[j - 1];
arr[j - 1] = arr[j];
ind[j - 1] = ind[j];
arr[j] = x;
ind[j] = x1;
}
}
}
for (int n = 0; n < N; n++)
{
resultMin[n] = ind[n];
}
return resultMin;
}
static void mutation(double[][] W)// оператор мутации
{
Random rnd = new Random(s);
int rnd1 = rnd.Next(0, 5);
int rnd2 = rnd.Next(0, 5);
double[] temp = new double[W[rnd1].Length];
double[] temp2 = new double[W.Length];
//меняет местами случайную строку и случайный столбец - и все портит =)
for (int j = 0; j < W[rnd1].Length; j++)
{
temp[j] = W[rnd1][j];
}
for (int i = 0; i < W.Length; i++)
{
temp2[i] = W[i][rnd2];
W[i][rnd2] = temp[i];
}
for (int j = 0; j < W[rnd1].Length; j++)
{
W[rnd1][j] = temp2[j];
}
if (s > 500)
s = 0;
else
s++;
}
static double[][][] Screshivanie(double[][] W1, double[][] W2)// оператор скрещивания , возвращает двух потомков
{
Random rnd = new Random(s);
int rnd1 = rnd.Next(0,5);
double[] temp = new double[W1[0].Length];
double[][][] resultW = new double[2][][];// для двух потомков
double[][][] resultW_temp = new double[2][][];
resultW[0] = new double[W1.Length][];
resultW[1] = new double[W1.Length][];
resultW_temp[0] = new double[W1.Length][];
resultW_temp[1] = new double[W1.Length][];
int rnd2 = rnd.Next(0, 5);
for (int i = 0; i < W1.Length; i++)
{
resultW_temp[0][i] = new double[W1[i].Length];
resultW_temp[1][i] = new double[W1[i].Length];
resultW[0][i] = new double[W1[i].Length];
resultW[1][i] = new double[W1[i].Length];
for (int j = 0; j < W1[i].Length; j++ )
{
resultW_temp[0][i][j] = W1[i][j];
resultW_temp[1][i][j] = W2[i][j];
resultW[0][i][j] = W1[i][j];
resultW[1][i][j] = W2[i][j];
}
}
//меяет одну случайных строки между двумя массивами
//проверяем не равны ли строки у родителей
bool[] str1 = new bool[resultW_temp[0].Length];
bool[] str2 = new bool[resultW_temp[0].Length];
for (int i = 0; i < resultW_temp[0].Length; i++)
{
str1[i] = true;
str2[i] = true;
}
for (int i = 0; i < resultW_temp[0].Length; i++)
{
for (int j = 0; j < resultW_temp[0][i].Length; j++)
{
if (resultW[0][i][j] != resultW_temp[1][i][j])
{
str1[i] = false;
break;
}
}
}
for (int i = 0; i < resultW_temp.Length; i++)
{
for (int j = 0; j < resultW_temp[0].Length; j++)
{
if (resultW[0][i][j] != resultW_temp[1][i][j])
{
str2[i] = false;
break;
}
}
}
if (!str1[rnd1])//если случайные строки не равны
{
for (int j = 0; j < resultW_temp[0].Length; j++)
{
resultW[0][rnd1][j] = resultW_temp[1][rnd1][j];
resultW[1][rnd1][j] = resultW_temp[0][rnd1][j];
}
}
else
{
//выбираем первую не равную пару строк
for (int i = 0; i < resultW_temp.Length; i++)
{
if (!str1[i])
{
for (int j = 0; j < resultW_temp[0].Length; j++)
{
resultW[0][i][j] = resultW_temp[1][i][j];
resultW[1][i][j] = resultW_temp[0][i][j];
}
break;
}
else//если таких пар не найдено то меняем случайные строки
{
for (int j = 0; j < resultW_temp[0].Length; j++)
{
resultW[0][rnd1][j] = rnd.NextDouble() * 0.1;
resultW[1][rnd1][j] = rnd.NextDouble() * 0.1;
}
}
}
}
if (s > 500)
s = 0;
else
s++;
return resultW;
}
static SandY neuro(double[][] X, double[][] W)// типа нейрон
{
SandY result;
double alfa = 1;// коэфицент сигмоидности
result.S = 0;// результирующая сумма
for (int i = 0; i < X.Length; i++)
{
for (int j = 0; j < X[i].Length; j++)
{
result.S += X[i][j] * W[i][j];// комбинаторим
}
}
result.Y = 1 / (1 + Math.Exp(alfa * result.S));// функция активизации
return result;
}
static void Main(string[] args)
{
double[][] input_x0 = new double[5][];
double[][] input_x1 = new double[5][];
double[][][] weight = new double[2][][];// веса для двух нейрон
for (int i = 0; i < 5; i++)
{
input_x0[i] = new double[5];
input_x1[i] = new double[5];
}
int seed = 0;
for (int n = 0; n < 2; n++)//заполняем веса случайными значениями от 0,0 до 1,0
{
weight[n] = new double[5][];
for (int i = 0; i < 5; i++)
{
weight[n][i] = new double[5];
for (int j = 0; j < 5; j++)
{
weight[n][i][j] = new Random(seed).NextDouble()*0.1;
seed++;
}
}
}
//тестовая матрица для 0
input_x0[0][0] = 0;
input_x0[0][1] = 1;
input_x0[0][2] = 1;
input_x0[0][3] = 1;
input_x0[0][4] = 0;
input_x0[1][0] = 1;
input_x0[1][1] = 0;
input_x0[1][2] = 0;
input_x0[1][3] = 0;
input_x0[1][4] = 1;
input_x0[2][0] = 1;
input_x0[2][1] = 0;
input_x0[2][2] = 0;
input_x0[2][3] = 0;
input_x0[2][4] = 1;
input_x0[3][0] = 1;
input_x0[3][1] = 0;
input_x0[3][2] = 0;
input_x0[3][3] = 0;
input_x0[3][4] = 1;
input_x0[4][0] = 0;
input_x0[4][1] = 1;
input_x0[4][2] = 1;
input_x0[4][3] = 1;
input_x0[4][4] = 0;
//тестовая матрица для 1
input_x1[0][0] = 0;
input_x1[0][1] = 0;
input_x1[0][2] = 1;
input_x1[0][3] = 0;
input_x1[0][4] = 0;
input_x1[1][0] = 0;
input_x1[1][1] = 1;
input_x1[1][2] = 1;
input_x1[1][3] = 0;
input_x1[1][4] = 0;
input_x1[2][0] = 0;
input_x1[2][1] = 0;
input_x1[2][2] = 1;
input_x1[2][3] = 0;
input_x1[2][4] = 0;
input_x1[3][0] = 0;
input_x1[3][1] = 0;
input_x1[3][2] = 1;
input_x1[3][3] = 0;
input_x1[3][4] = 0;
input_x1[4][0] = 0;
input_x1[4][1] = 0;
input_x1[4][2] = 1;
input_x1[4][3] = 0;
input_x1[4][4] = 0;
double nu = 0.01;//скорость обучения,которая на самом деле никакая ни скорость а шаг изменения веса
SandY [] neuro_data = new SandY[2];
double[] y = new double[2];// результат
double[] d0 = new double[2];// идеальные значения для 0
double[] d1 = new double[2];//идеальные значения для 1
d0[0] = 1.0;
d0[1] = 0.0;
d1[0] = 0.0;
d1[1] = 1.0;
int step = 0;
double[] delta = new double[2];
/*
Console.WriteLine("=============================================");
Console.WriteLine("по алгоритму обратного распространения ошибки");
Console.WriteLine("=============================================");
/////////////////////////////////////////////////
//по алгоритму обратного распространения ошибки//
/////////////////////////////////////////////////
while(step <=1000000)
{
step++;
for (int neuron = 0; neuron < 2; neuron ++ )// всего два нейрона
{
neuro_data[neuron] = neuro(input_x0, weight[neuron]);
Console.Write(" Нейрон : {0} Y={1} S={2}\n\n", neuron, neuro_data[neuron].Y, neuro_data[neuron].S);
}
if (Math.Abs(neuro_data[0].Y - neuro_data[1].Y) >= 0.9)
break;
for (int neuron = 0; neuron < 2; neuron++)
{
delta[neuron] = (d0[neuron] - neuro_data[neuron].Y) * neuro_data[neuron].Y * (1 - neuro_data[neuron].Y);
for (int i = 0; i < 5; i++)
{
for (int j = 0; j < 5; j++)
{
weight[neuron][i][j] = weight[neuron][i][j] - nu * delta[neuron] * input_x0[i][j];
}
}
}
}
if (neuro_data[0].Y > neuro_data[1].Y)
Console.WriteLine(" Результат 0");
else
Console.WriteLine(" Результат 1");
*/
//////////////////////////////
//по генетическому алгоритму//
//////////////////////////////
Console.WriteLine("=============================================");
Console.WriteLine("=========по генетическому алгоритму==========");
Console.WriteLine("=============================================");
//целевая функция - это функция ошибки нейрона E(w) = 1/2*(y-d)^2
// где y - реальное значение ф-ции активизации для нейрона, d - идеальное значенние
int kolPopul = 8;
double[][][][] weightGA = new double[2][][][];// матрицы весов для 2- х нейронов
for (int n = 0; n < 2; n++)
{
weightGA[n] = new double[kolPopul][][];// матрицы весов для 4- х особей каждого нейрона
seed = 0;
for (int o = 0; o < kolPopul; o++)//заполняем веса случайными значениями от 0,0 до 0,1
{
weightGA[n][o] = new double[5][];
for (int i = 0; i < 5; i++)
{
weightGA[n][o][i] = new double[5];
for (int j = 0; j < 5; j++)
{
//Console.WriteLine(new Random(seed).NextDouble()*0.1);
weightGA[n][o][i][j] = new Random(seed).NextDouble() * 0.1;
seed++;
}
}
}
}
double[][] F = new double[2][]; // массив для хранения значений целевой функции для 4-х поколеий для двух нейронов
for (int n = 0; n < 2; n++)
{
F[n] = new double[kolPopul];
}
double[][] F_temp = new double[2][]; // массив для хранения значений целевой функции для расширенной популяции для двух нейронов
for (int n = 0; n < 2; n++)
{
F_temp[n] = new double[kolPopul + kolPopul];
}
double[][] F_potomki = new double[2][]; // массив для хранения значений целевой функции для потомков для двух нейронов
for (int n = 0; n < 2; n++)
{
F_potomki[n] = new double[kolPopul];
}
int k = 0;
SandY[] neuro_dataGA = new SandY[2];
while (k < 10)//количество поколений
{
Console.WriteLine("============== Поколение {0} =================", k);
k++;
for (int neuron = 0; neuron < 2; neuron++)
{
Console.WriteLine("======== Нейрон {0} ========", neuron);
for (int n_osob = 0; n_osob < kolPopul; n_osob++)// вычисляем значение целевой функции для каждой особи
{
neuro_dataGA[neuron] = neuro(input_x0, weightGA[neuron][n_osob]);
F[neuron][n_osob] = (0.5*(neuro_dataGA[neuron].Y - d0[neuron]) * (neuro_dataGA[neuron].Y - d0[neuron]));// целевая ф - я
Console.WriteLine(F[neuron][n_osob]);
}
//выбираем 4 пары особей для скрещивания
int[] bestParent = new int[4]; //четыре родителя
bestParent = NMinIndexesValue(4, F[neuron]);//находим четырех лучших родителей
Console.WriteLine("Особи для размножения");
Console.WriteLine(F[neuron][bestParent[0]]);
Console.WriteLine(F[neuron][bestParent[1]]);
Console.WriteLine(F[neuron][bestParent[2]]);
Console.WriteLine(F[neuron][bestParent[3]]);
Console.WriteLine("####################");
double[][][][] potomki = new double[4][][][];
for (int num = 0; num < 4; num++)
{
potomki[num] = new double[2][][];
}
//скрещиваем как-бы случайным образом родителей и плодим потомков
int vm = ver.Next(1, 4);
potomki[0] = Screshivanie(weightGA[neuron][bestParent[0]], weightGA[neuron][bestParent[vm]]);
vm = ver.Next(0, 3);
potomki[1] = Screshivanie(weightGA[neuron][bestParent[3]], weightGA[neuron][bestParent[vm]]);
vm = ver.Next(0, 4);
potomki[2] = Screshivanie(weightGA[neuron][bestParent[1]], weightGA[neuron][bestParent[vm]]);
vm = ver.Next(0, 4);
potomki[3] = Screshivanie(weightGA[neuron][bestParent[2]], weightGA[neuron][bestParent[vm]]);
vm = ver.Next(0,7);//определяет для кого из потомков случайным образом сработает мутация
if (vm == 0)
{
mutation(potomki[0][0]);
}
if (vm == 1)
{
mutation(potomki[0][1]);
}
if (vm == 2)
{
mutation(potomki[1][0]);
}
if (vm == 3)
{
mutation(potomki[1][1]);
}
if (vm == 4)
{
mutation(potomki[2][0]);
}
if (vm == 5)
{
mutation(potomki[2][1]);
}
if (vm == 6)
{
mutation(potomki[3][0]);
}
if (vm == 7)
{
mutation(potomki[3][1]);
}
Console.WriteLine(" Целевая ф - я потомков ");
double[][][] temp_weight = new double[kolPopul + kolPopul][][];
int nomer = 0;
for (int num = 0; num < 4; num++)//переписываем веса потомков в один массив
{
for (int n = 0; n < 2; n++)
{
temp_weight[nomer] = potomki[num][n];
double temp_y = neuro(input_x0, potomki[num][n]).Y;
F_potomki[neuron][nomer] = (0.5*(temp_y - d0[neuron]) * (temp_y - d0[neuron]));// целевая ф - я
Console.WriteLine(F_potomki[neuron][nomer]);
nomer++;
}
}
for (int num = 0; num < kolPopul; num++)// добавляем к массиву веса родителей
{
temp_weight[num + kolPopul] = weightGA[neuron][num];
}
Console.WriteLine("Целевая ф-я расширенной популяции");
for (int n_osob = 0; n_osob < kolPopul + kolPopul; n_osob++)//вычисляем значение целевой функции для каждой особи
{
double temp_y = neuro(input_x0, temp_weight[n_osob]).Y;
F_temp[neuron][n_osob] = (0.5*(temp_y - d0[neuron]) * (temp_y - d0[neuron]));// целевая ф - я
}
//Удаляем 4 особи с самым большим значением целевой функции
//на след. итерацию переходят 4 особи с наименьшими значениями целевой ф-ции
int[] minimum = new int[kolPopul];
minimum = NMinIndexesValue(8, F_temp[neuron]);
for (int n = 0; n < kolPopul; n++)//копируем данные из промежуточного массива в исходный
{
weightGA[neuron][n] = temp_weight[minimum[n]];
}
}
}
Console.ReadKey();
}
}
}
|