ОБРАБОТКА РЕЗУЛЬТАТОВ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ
РЕФЕРАТ
по дисциплине «Метрология, стандартизация и сертификация»
 СОДЕРЖАНИЕ СОДЕРЖАНИЕ
Введение ………………………………………………………………стр.3-4
Последовательность обработки результатов……………..................стр.5-9
Заключение…………………………………………………………….стр.10
Список использованной литературы…………………………………стр.11
 ВВЕДЕНИЕ ВВЕДЕНИЕ
Измерения — один из важнейших путей познания природы человеком. Они играют огромную роль в современном обществе. Наука и промышленность не могут существовать без измерений. Практически нет ни одной сферы деятельности человека, где бы интенсивно не использовались результаты измерений, испытаний и контроля.
Диапазон измерительных величин и их количество постоянно растут и поэтому возрастает и сложность измерений. Они перестают быть одноактным действием и превращаются в сложную процедуру подготовки и проведения измерительного эксперимента и обработки полученной информации.
Другой причиной важности измерений является их значимость. Основа любой формы управления, анализа, прогнозирования, контроля или регулирования — достоверная исходная информация, которая может быть получена лишь путем измерения требуемых физических величин, параметров и показателей. Только высокая и гарантированная точность результатов измерений обеспечивает правильность принимаемых решений.
Методической основой стандартизации являются математические методы, включая предпочтительные числа и ряды предпочтительных чисел, параметрические ряды, а также унификация деталей и узлов, агрегатирование, комплексная и опережающая стандартизация.
Предпочтительные числа и ряды предпочтительных чисел необходимы для выбора оптимального ряда параметров и типоразмеров готовых изделий. Набор установленных значений параметров составляет параметрический ряд, который строится по системе предпочтительных чисел.
 Прямые многократные измерения делятся на равно- и неравноточные. Равноточными называются измерения, которые проводятся средствами измерений одинаковой точности по одной и той же методике при неизменных внешних условиях. При равноточных измерениях среднее квадратичное отклонение (СКО) результатов всех рядов измерений равны между собой. Прямые многократные измерения делятся на равно- и неравноточные. Равноточными называются измерения, которые проводятся средствами измерений одинаковой точности по одной и той же методике при неизменных внешних условиях. При равноточных измерениях среднее квадратичное отклонение (СКО) результатов всех рядов измерений равны между собой.
Перед проведением обработки результатов измерений необходимо удостовериться в том, что данные из обрабатываемой выборки статистически подконтрольны, группируются вокруг одного и того же центра и имеют одинаковую дисперсию. Устойчивость изменений часто оценивают интуитивно на основе длительных наблюдений. Однако существуют математические методы решения поставленной задачи — так называемые методы проверки однородности. Применительно к измерениям рассматривается однородность групп наблюдений, необходимые признаки которой состоят в оценке несмещенности средних арифметических и дисперсий относительно друг друга.
Реклама

Задача обработки результатов многократных измерений заключается в нахождении оценки измеряемой величины и доверительного интервала, в котором находится ее истинное значение. Обработка должна проводится в соответствии с ГОСТ 8.207—76 ГСИ. «Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. Общие положения».
ПОСЛЕДОВАТЕЛЬНОСТЬ ОБРАБОТКИ РЕЗУЛЬТАТОВ ПРЯМЫХ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ
 Определение точечных оценок закона распределения результатов измерений. На этом этапе определяются: Определение точечных оценок закона распределения результатов измерений. На этом этапе определяются:
• среднее арифметическое значение х измеряемой величины ;
• СКО результата измерения S x
;
• СКО среднего арифметического значения S x
̅
. Грубые погрешности и промахи исключаются, после чего проводится повторный расчет оценок среднего арифметического значения и его СКО. В ряде случаев для более надежной идентификации закона распределения результатов измерений могут определяться другие точечные оценки: коэффициент асимметрии, эксцесс и контрэксцесс, энтропийный коэффициент.
Определение закона распределения результатов измерений или случайных погрешностей измерений. В последнем случае от выборки результатов измерений х 1
, х 2
, х 3
,-.., х n
переходят к выборке отклонений от среднего арифметического D х 1
, D х 2
, D х 3
,..., D х n
, где D x i
= x i
- х ̅ .
Первым шагом при идентификации закона распределения является построение по исправленным результатам измерений x i
, где I = 1, 2,..., n , вариационного ряда (упорядоченной выборки), а также у i
, где у i
= min ( x i
) и у n
= m ах(х i ). В вариационном ряду результаты измерений (или их отклонения от среднего арифметического) располагают в порядке возрастания. Далее этот ряд разбивается на оптимальное число m , как правило, одинаковых интервалов группирования длиной h = ( y 1
+ y n
) / m .
Реклама

 Оптимальным является такое число интервалов m , при котором возможное максимальное сглаживание случайных флуктуации данных сопровождается с минимальным искажением от сглаживания самой кривой искомого распределения. Для практического применения целесообразно использовать предложенные m min
= 0,55 n 0,4
и m max
= 1,25 n 0,4
, которые получены для наиболее часто встречающихся на практике распределений с эксцессом, находящимся в пределах от 1,8 до 6, т.е. от равномерного до распределения Лапласа. Оптимальным является такое число интервалов m , при котором возможное максимальное сглаживание случайных флуктуации данных сопровождается с минимальным искажением от сглаживания самой кривой искомого распределения. Для практического применения целесообразно использовать предложенные m min
= 0,55 n 0,4
и m max
= 1,25 n 0,4
, которые получены для наиболее часто встречающихся на практике распределений с эксцессом, находящимся в пределах от 1,8 до 6, т.е. от равномерного до распределения Лапласа.
Искомое значение m должно находится в пределах от m mjn
до m max
, быть нечетным, так как при четном m в островершинном или двухмодальном симметричном распределении в центре гистограммы оказываются два равных по высоте столбца и середина кривой распределения искусственно уплощается. В случае, если гистограмма распределения явно двухмодальная, число столбцов может быть увеличено в 1,5-2 раза, чтобы на каждый из двух максимумов приходилось примерно по m интервалов. Полученное значение длины интервала группирования h всегда округляют в большую сторону, иначе последняя точка окажется за пределами крайнего интервала.
Далее определяют интервалы группирования экспериментальных данных в виде D 1
= (у 1
, y 1
+ h ); D 2
= ( y 1
+ h , y 1
+ 2 h );....; D m
= ( y n
- h ; у n
), и подсчитывают число попаданий n k
(частоты) результатов измерений в каждый интервал группирования. Сумма этих чисел должна равняться числу измерений. По полученным значениям рассчитывают вероятности попадания результатов измерений (частости) в каждый из интервалов группирования по формуле p k
= n k
/ n , где k = l , 2,..., m .
Проведенные расчеты позволяют построить гистограмму, полигон и кумулятивную кривую. Для построения гистограммы по оси результатов откладываются интервалы D k
в порядке возрастания номеров и на каждом интервале строится прямоугольник высотой p k
. В этом случае площадь под гистограммой равна единице. При увеличении числа интервалов и соответственно уменьшении их длины гистограмма все более приближается к гладкой кривой — графику плотности распределения вероятности.
 Полигон представляет собой ломаную кривую, соединяющую середины верхних оснований каждого столбца гистограммы. Полигон представляет собой ломаную кривую, соединяющую середины верхних оснований каждого столбца гистограммы.
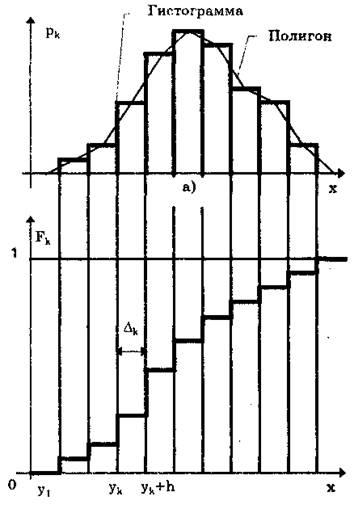
Рисунок 1-Гистограмма, полигон (а) и кумулятивная кривая (б)
Эти точки при построении полигона соединяют между собой отрезками прямых линий. В результате совместно с осью х образуется замкнутая фигура, площадь которой в соответствии с правилом нормирования должна быть равна единице (или числу наблюдений при использовании частостей).
Кумулятивная кривая — это график статистической функции распределения. Для ее построения по оси результатов наблюдений х (рисунок 1,6) откладывают интервалы D k
в порядке возрастания номеров и
на каждом интервале строят прямоугольник высотой p
По виду построенных зависимостей может быть оценен закон распределения результатов измерений.
Оценка закона распределения по статистическим критериям .
При числе наблюдений n >
50 для идентификации закона распределения используется критерий Пирсона (хи-квадрат) или критерий Мизеса—Смирнова ( w 2
). При 50 > n > 15 для проверки нормальности закона распределения применяется составной критерий ( d -критерий), приведенный в ГОСТ 8.207-76. При n < 15 принадлежность экспериментального распределения к нормальному не проверяется.
Определение доверительных границ случайной погрешности. Если удалось идентифицировать закон распределения результатов измерений, то с его использованием находят квантильный множитель z p
при заданном значении доверительной вероятности Р. В этом случае доверительные границы случайной погрешности А = ± z p
S .
Определение границ неисключенной систематической погрешности q результата измерений. Под этими границами понимают найденные нестатистическими методами границы интервала, внутри которого находится неисключенная систематическая погрешность. Она образуется из ряда составляющих: как правило, погрешностей метода и средств измерений, а также субъективной погрешности. Границы неисключенной систематической погрешности принимаются равными пределам допускаемых основных и дополнительных погрешностей средств измерений, если их случайные составляющие пренебрежимо малы. Доверительная вероятность при определении границ 6 принимается равной доверительной вероятности, используемой при нахождении границ случайной погрешности.
 Определение доверительных границ погрешности результата измерения D р
. Данная операция осуществляется путем суммирования СКО случайной составляющей S x
̅
и границ неисключенной систематической Определение доверительных границ погрешности результата измерения D р
. Данная операция осуществляется путем суммирования СКО случайной составляющей S x
̅
и границ неисключенной систематической  составляющей q в зависимости от соотношения q / S x
̅
. Результат измерения записывается в виде х = х ̅ ± D p
при доверительной вероятности Р = Р . При отсутствии данных о виде функции распределения составляющих погрешности результаты измерений представляют в виде х, S -. п.8 при доверительной вероятности Р = Р д
. составляющей q в зависимости от соотношения q / S x
̅
. Результат измерения записывается в виде х = х ̅ ± D p
при доверительной вероятности Р = Р . При отсутствии данных о виде функции распределения составляющих погрешности результаты измерений представляют в виде х, S -. п.8 при доверительной вероятности Р = Р д
.
 ЗАКЛЮЧЕНИЕ ЗАКЛЮЧЕНИЕ
Многократные измерения проводят с целью уменьшения влияния случайных составляющих погрешностей измерения.
Применение рядов предпочтительных чисел представляет собой параметрическую стандартизацию, которая позволяет получить значительный эффект на всех стадиях жизненного цикла изделий (проектирование, изготовление, эксплуатация и др.) Стандартами параметров охватывается большой диапазон характеристик изделий: материалы, заготовки, размерный режущий инструмент, оснастка, контрольные калибры, узлы по присоединительным размерам, выходные параметры электродвигателей и многое другое, что используется в той или иной отрасли промышленности.
ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА
1. Пустыльник Е.И. Статистические методы анализа и обработки наблюдений. – М.:Изд. «Наука», 1968. –288 с.
2.
Шаловников Э.А. Метрология, стандартизация и сертификация. Методические указания и контрольные задания для студентов специальностей 21.02.03 (АГ) и 1804 (АЭ) дневной и заочной форм обучения.- Изд-во УГНТУ, Уфа, 1999.
|