Агентство по образованию и науки РФ
Пензенский государственный университет
Кафедра: "Информационно-измерительная техника"
Курсовая работа
по дисциплине: "Надёжность и техническая диагностика оборудования"
на тему:
"Составление алгоритмов поиска неисправностей"
Выполнил: студент гр.05ТО1
Кострицын Д.
Принял: д. т. н., профессор
Цыпин Б.В.
Пенза 2008
Задание 1. Для заданной функциональной модели составить таблицу состояний

Рис.1
Таблица 1
| Состояния |
Проверки |
| S1=100000 |
П1 |
П2 |
П3 |
П4 |
П5 |
П6 |
| 0 |
0 |
0 |
0 |
0 |
0 |
| S2=010000 |
1 |
0 |
0 |
0 |
0 |
0 |
| S3=001000 |
1 |
1 |
0 |
1 |
1 |
1 |
| S4=000100 |
1 |
1 |
1 |
0 |
0 |
0 |
| S5=000010 |
1 |
1 |
1 |
1 |
0 |
1 |
| S6=000001 |
1 |
1 |
1 |
0 |
0 |
0 |
Предположим, что система находится в состоянии S 2 (010000), которое соответствует неисправности второго элемента X 2. Тогда реакция Z 2 этого элемента недопустима. Второй элемент предшествует третьему X 3 и четвертому X 4, а четвертый - пятому X 5 и шестому X 6 элементам. Следовательно, реакции элементов Z 3, Z 4, Z 5, Z 6 также недопустимы. Исходы проверок П2, П3, П4, П5, П6 отрицательны, так как на них влияет состояние элемента X 2. Исход проверки П1 положителен, так как на него не влияет состояние элемента X 2.
Таким образом, в строке S 2 таблицы состояний (табл.1) будет записан код 100000. Аналогичным образом проводится анализ функциональной модели для других состояний.
Тождественность строк S 4 и S 6 таблицы означает, что отказ элемента X 4 проявляется так же, как и отказ элемента X 6. Поэтому с помощью всех возможных проверок нельзя определить, какой из этих двух элементов отказал. Такие состояния называются неразличимыми. Неразличимость состояний объясняется тем, что элементы X 4 и X 6 взаимоохвачены обратной связью, то есть соединены в кольцо.
Задание 2. Составить все возможные алгоритмы последовательного поиска неисправностей
Приведем пример составления последовательного алгоритма (рис.2) для функциональной модели рис.1. Первая проверка выбирается произвольно, например П3. До начала проверок неисправным может быть любой узел объекта.
При положительном исходе проверки неисправными могут быть только узлы, ею не охваченные. Тогда возможны только состояния S 4, S 5, S 6 системы. Для дальнейшей локализации неисправностей выбираем проверку П4. Положительному исходу проверки соответствует состояние S 5, а отрицательному - S 46. Мы получили конечные результаты. Аналогично составляется другая ветвь данного алгоритма.
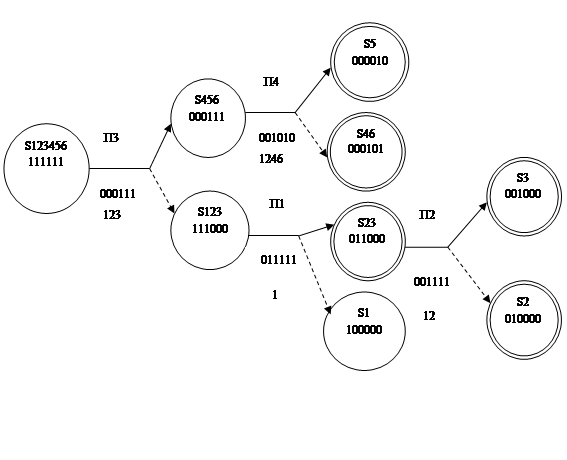
Рис.2
Рассмотрим ещё один алгоритм поиска неисправностей (рис.3).
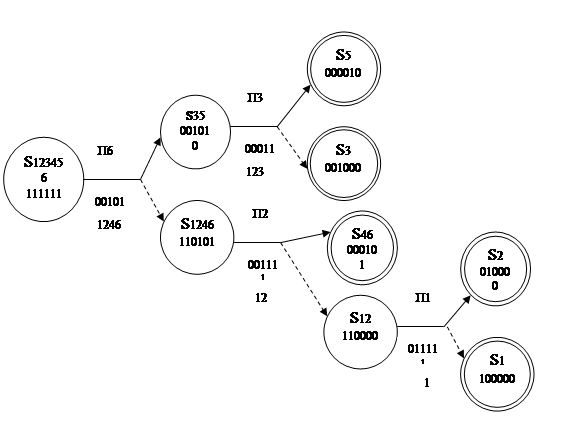
Рис.3
Реклама

Задание 3.
Таблица 2
Условная вероятность
| Номер варианта |
q1 |
q2 |
q3 |
q4 |
q5 |
q6 |
| 3 |
0 ,15 |
0,05 |
0,1 |
0,2 |
0,3 |
0,2 |
Таблица 3
Условная трудоёмкость
| Номер варианта |
t1 |
t2 |
t3 |
t4 |
t5 |
t6 |
| 2 |
0, 0 5 |
0, 25 |
0, 3 |
0, 4 |
0,2 |
0,1 |
Для заданных значений qi и ti выбрать квазиоптимальный по информационному критерию алгоритм и рассчитать для него среднее и максимальное время локализации неисправностей.
Функциональная модель 2
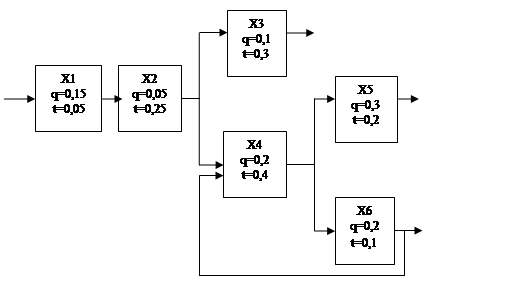
Рис.4
Составим по модели (рис.4) таблицу состояний, включив в неё только обязательные проверки и исключив проверки на разветвляющихся выходах.
| Состояния |
Проверки |
| 1 |
3 |
5 |
6 |
| 1 |
0 |
0 |
0 |
0 |
| 2 |
1 |
0 |
0 |
0 |
| 3 |
1 |
0 |
1 |
1 |
| 4 |
1 |
1 |
0 |
0 |
| 5 |
1 |
1 |
0 |
1 |
| 6 |
1 |
1 |
0 |
0 |
Оценим эффективность всех проверок:
Вычислим вероятности положительных исходов проверок по формуле:
Р (П i +) =∑ qi (1)
i Є M н
Вероятность положительного исхода проверки Р (П i +) определяется суммой условных вероятностей отказов элементов подмножества Мн, не охваченных данной проверкой.
Р (П1+) = q 2+ q 3+ q 4+ q 5+ q 6=0,05+0,1+ 0,2+0,3+0,2=0,85
Р (П3+) = q 4+ q 5+ q 6=0,2+0,3+0,2=0,7
Р (П5+) = q 3 =0,1
Р (П6+) = q 3+ q 5=0,1+0,3=0,4
Информативность проверок определим по графику: I (П1) =0,6;
I (П3) =0,88; I (П5) =0,5; I (П6) =0,97
Вычислим эффективность каждой из проверок по формуле:
Fi = I (П i ) / ti (2)
Эффективность проверки определяется как отношение получаемого в результате проверки количества информации к затратам времени на проверку:
F 1=0,6/0,05=12 F 3=0,88/ 0,3=2,93; F 5=0,5/0,2=2,5;
F 6=0,97/0,1=9,7
В качестве первой выбираем проверку П1, обладающую максимальной эффективностью.
2. Определим информационное состояние, соответствующее положительному результату П1, перемножая код исходного состояния S 0 на код проверки П1: 111111*011111=011111. Информационное состояние, соответствующее положительному результату - S 23456.
Находим информационное состояние, соответствующее отрицательному результату проверки, перемножая код исходного состояния S 0 на инверсный код проверки П1: 111111*100000=100000. Искомое состояние S 1 - конечный результат.
3. Проведём для состояния S 23456 оценку эффективности всех возможных проверок П3, П5, П6 т.е. проверок, не имеющих всех нулей или всех единиц в строках возможных неисправностей:
3.1 Расчет проводится по формуле: n
Р (П i +) = Pi /∑ Pi ; (3)
i=1
Р ( П 3+) =q4+q5+q6/q2+q3+q4+q5+q6=0,2+0,3+0,2/0,05+0,1+0,2+0,3+0,2=0,7/0,85=0,82
Р ( П 5+) =q3/q2+q3+q4+q5+q6=0,1/0,85=0,12;
P ( П 6+) =q3+q5/q2+q3+q4+q5+q6=0,1+0,3/0,85=0,47
3.2 Определим информативность этих проверок:
I (П3) =0,68; I (П5) =0,54; I (П6) =0,99
3.3 Вычислим эффективности проверок:
F 3=0,68/0,3=2,266; F 5=0,54/0,2=2,7; F 6=0,99/0,1=9,9
Выбираем проверку П6, обладающую наибольшей эффективностью. Она должна проводиться в состоянии S 23456.
Реклама

4. Найдём информативные состояния, соответствующие положительному результату проведения проверки П6 в состоянии S 23456: 011111*001010=001010 - S 35; отрицательному результату соответствуют состояния: 011111*110101=010101- S 246.
5.1 В состоянии S 35 возможны проверки П3 и П5. Оценим эффективность проверок:
Р (П3+) = q 5/ q 3+ q 5=0,3/0,1+0,3=0,75;
Р (П5+) = q 3/ q 3+ q 5=0,1/0,4=0,25
5.2 Информативность определяем по графику: I (П3) =0,8; I (П5) =0,82
5.3 F 3=0,8/0,3=2,66; F 5=0,82/0,2=4,1
Выбираем проверку П5.
6. В состоянии S 246 возможна единственная проверка П3: при положительном исходе 010101*000111=000101 - S 46; при отрицательном исходе 010101*111000=010000 - S 2. Состояния S 46 и S 2 являются конечными.
Таким образом, выбраны все проверки и составлен оптимальный алгоритм поиска неисправностей.
 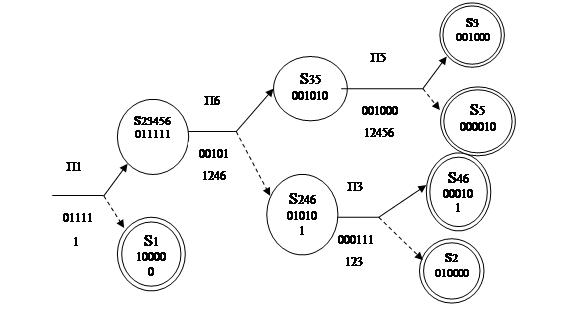
Рис.5
Среднее время локализации неисправностей для найденного алгоритма:
t ср= q 1* t 1+ ( q 3+ q 5) * ( t 1+ t 6+ t 5) + ( q 4+ q 6+ q 2) * ( t 1+ t 6+ t 3) =0,15*0,05+ (0,1+0,3) * (0,05+0,1++0,2) + (0,2+0,2+0,05) * (0,01+0,1+0,3) =0,0075+0,14+0,1845=0,332 (4)
Максимальное время локализации неисправностей:
tmax = t 1+ t 6+ t 5 + t 3=0,05+0,1+0,2+0,3=0,65 (5)
*
Библиография
1. Цыпин Б.В. Оптимизация поиска неисправностей при технической диагностике оборудования: Учеб. пособие/ Б.В. Цыпин, Ю.М. Крысин, А.Г. Схиртладзе, В.А. Скрябин. - Пенза: Изд-во Пенз. гос. ун-та, 2002. - 112с.
|