| Основные представления о специальной и общей теории относительности
Введение
1 Основные представления об общей теории относительности
1.1 Принцип эквивалентности и геометризация тяготения
1.2 Классические опыты по проверке ОТО
1.3 Черные дыры
1.4 Пульсар PSR 1913+16 и гравитационные волны
1.5 Гравитационные линзы и коричневые карлики
2 Основные представления о специальной теории относительности
2.1 Эйнштейновский принцип относительности
2.2 Синхронизация часов
2.3 Преобразование Лоренца
2.4 Преобразование скорости
2.5 Собственное время, события и мировые линии частиц
2.6 Геометрический смысл преобразований Лоренца
2.7 Замедление времени
2.8 Лоренцево сокращение длины
2.9 Релятивистские парадоксы
3 Динамика специальной теории относительности
3.1 Энергия и импульс частицы
3.2 Релятивистские преобразования энергии и импульса
3.3 Частицы с нулевой массой покоя
Заключение
Список использованных источников
ВВЕДЕНИЕ
Название “теория относительности” возникло из наименования основного принципа (постулата), положенного Пуанкаре и Эйнштейном в основу из всех теоретических построений новой теории пространства и времени.[ГАсГ1]
Содержанием теории относительности является физическая теория пространства и времени, учитывающая существующую между ними взаимосвязь геометрического характера.
Название же “принцип относительности” или “постулат относительности”, возникло как отрицание представления об абсолютной неподвижной системе отсчета, связанной с неподвижным эфиром, вводившимся для объяснения оптических и электродинамических явлений.
Дело в том, что к началу двадцатого века у физиков, строивших теорию оптических и электромагнитных явлений по аналогии с теорией упругости, сложилось ложное представление о необходимости существования абсолютной неподвижной системы отсчета, связанной с электромагнитным эфиром. Зародилось, таким образом, представление об абсолютном движении относительно системы, связанной с эфиром, представление, противоречащее более ранним воззрениям классической механики (принцип относительности Галилея). Опыты Майкельсона и других физиков опровергли эту теорию “неподвижного эфира” и дали основание для формулировки противоположного утверждения, которое и получило название “принципа относительности”. Так это название вводится и обосновывается в первых работах Пуанкаре и Эйнштейна.
Реклама

Эйнштейн пишет: “.. неудавшиеся попытки обнаружить движение Земли относительно “светоносной среды” ведут к предположению, что не только в механике, но и в электродинамике никакие свойства явлений не соответствуют понятию абсолютного покоя, и даже более того,- к предположению, что для всех координатных систем, для которых справедливы уравнения механики, имеют место те же самые электродинамические и оптические законы, как это уже доказано для величин первого порядка. Мы намерены это положение (содержание которого в дальнейшем будет называться “принципом относительности”) превратить в предпосылку... “ /1/. А вот что пишет Пуанкаре: “Эта невозможность показать опытным путем абсолютное движение Земли представляет закон природы; мы приходим к тому, чтобы принять этот закон, который мы назовем постулатом относительности, и примем его без оговорок.”
Но крупнейший советский теоретик Л. И. Мандельштам в своих лекциях по теории относительности /2/ разъяснял: “Название “принцип относительности” - одно из самых неудачных. Утверждается независимость явлений от неускоренного движения замкнутой системы. Это вводит в заблуждение многие умы”. На неудачность названия указывал и один из творцов теории относительности, раскрывший ее содержание в четырехмерной геометрической форме, - Герман Минковский. В 1908 г. он утверждал: “... термин “постулат относительности” для требования инвариантности по отношению к группе , кажется мне слишком бедным. Так как смысл постулата сводится к тому, что в явлениях нам дается только четырехмерный в пространстве и времени мир, но что проекции этого мира на пространство и на время могут быть взяты с некоторым произволом, мне хотелось бы этому утверждению дать название: постулат абсолютного мира” .
Таким образом, мы видим, что названия “принцип относительности” и “теория относительности” не отражают истинного содержания теории.
Общая теория относительности (ОТО) — современная теория тяготения, связывающая его с кривизной четырехмерного пространства-времени.
В своем, так сказать, классическом варианте теория тяготения была создана Ньютоном еще в XVII веке и до сих пор верно служит человечеству. Она вполне достаточна для многих, если не для большинства, задач современной астрономии, астрофизики, космонавтики. Между тем ее принципиальный внутренний недостаток был ясен еще самому Ньютону. Это теория с дальнодействием: в ней гравитационное действие одного тела на другое передается мгновенно, без запаздывания. Ньютоновская гравитация так же соотносится с общей теорией относительности, как закон Кулона с максвелловской электродинамикой. Максвеллу удалось изгнать дальнодействие из электродинамики. В гравитации это сделал Эйнштейн.
Реклама

Начать рассказ следует с замечательной работы Эйнштейна 1905 года /3/, в которой была сформулирована специальная теория относительности и которая завершила в идейном отношении развитие классической электродинамики. У этой работы несомненно были предшественники, среди которых нельзя не упомянуть работы Лоренца и Пуанкаре. В их статьях уже содержались многие элементы специальной теории относительности. Однако ясное понимание, цельная картина физики больших скоростей появились лишь в упомянутой работе Эйнштейна. Не случайно, несмотря на наличие прекрасных современных учебников, ее до сих нор можно рекомендовать для первого знакомства с предметом не только студентам, но и старшеклассникам.
Что же касается ОТО, то все ее основополагающие элементы были созданы Эйнштейном.
Впрочем, предчувствие того, что физика может быть связана с кривизной пространства, можно найти в трудах замечательных ученых прошлого века Гаусса, Римана, Гельмгольца, Клиффорда. Гаусс, который пришел к идеям неевклидовой геометрии несколько ранее Лобачевского и Бойаи, но так и не опубликовал своих исследований в этой области, не только считал, что «геометрию приходится ставить в один ряд не с арифметикой, существующей чисто a priori, а скорее с механикой». Он пытался проверить экспериментально, путем точных (для того времени) измерений геометрию нашего пространства. Его идея вдохновила Римана, полагавшего, что наше пространство действительно искривлено (а на малых расстояниях даже дискретно). Жесткие ограничения на кривизну пространства были получены из астрономических данных Гельмгольцем. Клиффорд считал материю рябью на искривленном пространстве.
Однако все эти блестящие догадки и прозрения были явно преждевременны. Создание современной теории тяготения было немыслимым без специальной теории относительности, без глубокого понимания структуры классической электродинамики, без осознания единства пространства-времени. Как уже отмечалось, ОТО была создана в основном усилиями одного человека. Путь Эйнштейна к построению этой теории был долгим и мучительным. Если его работа 1905 года «К электродинамике движущихся сред» появилась как бы сразу в законченном виде, оставляя вне поля зрения читателя длительные размышления, тяжелый труд автора, то с ОТО дело обстояло совершенно иначе. Эйнштейн начал работать над ней с 1907 года. Его путь к ОТО продолжался несколько лет. Это был путь проб и ошибок, который хотя бы отчасти можно проследить по публикациям Эйнштейна в эти годы. Окончательно задача была решена им в двух работах, доложенных на заседаниях Прусской Академии наук в Берлине 18 и 25 ноября 1915 года. В них были сформулированы уравнения гравитационного поля в пустоте и при наличии источников.
В последнем этапе создания ОТО принял участие Гильберт. Вообще значение математики (и математиков) для ОТО очень велико. Ее аппарат, тензорный анализ, или абсолютное дифференциальное исчисление, был развит Риччи и Леви-Чивита. Друг Эйнштейна, математик Гроссман познакомил его с этой техникой.
И все же ОТО — это физическая теория, в основе которой лежит ясный физический принцип, твердо установленный экспериментальный факт.
Специальная теория относительности (СТО) - фундаментальная физическая теория пространственно-временных свойств всех физических процессов.
Основой СТО явились представления о свойствах пространства, времени и движения, разработанные в классической механике Галилеем и Ньютоном, но углублённые и в ряде положений существенно изменённые и дополненные Эйнштейном в связи с теми экспериментальными фактами, которые были обнаружены в физике к концу XIX столетия при изучении электромагнитных явлений.
Целью настоящей работы является рассмотрение основных представлений о специальной и общей теории относительности, существующих в современной физике. Все рассматриваемые в работе разделы соответствуют основным принципам теории общей и специальной теории относительности.
1 Основные представления об общей теории относительности
1.1 Принцип эквивалентности и геометризация тяготения
Факт этот по существу был установлен еще Галилеем. Он хорошо известен каждому успевающему старшекласснику: все тела движутся в поле тяжести (в отсутствие сопротивления среды) с одним и тем же ускорением, траектории всех тел с заданной скоростью искривлены в гравитационном поле одинаково. Благодаря этому, в свободно падающем лифте никакой эксперимент не может обнаружить гравитационное поле. Иными словами, в системе отсчёта, свободно движущейся в гравитационном поле, в малой области пространства-времени гравитации нет. Последнее утверждение — это одна из формулировок принципа эквивалентности /4/.
Данное свойство поля тяготения отнюдь не тривиально. Достаточно вспомнить, что в случае электромагнитного поля ситуация совершенно иная. Существуют, например, подзаряженные, нейтральные тела, которые электромагнитного поля вообще не чувствуют. Так вот, гравитационно- нейтральных тел нет, не существует ни линеек, ни часов, которые не чувствовали бы гравитационного поля. Эталоны привычного евклидова пространства меняются в поле тяготения.
Геометрия нашего пространства оказывается неевклидовой.
Некоторое представление о свойствах такого пространства можно получить на простейшем примере сферы, поверхности обычного глобуса. Рассмотрим на ней сферический треугольник — фигуру, ограниченную дугами большого радиуса. (Дуга большого радиуса, соединяющая две точки на сфере, — это кратчайшее расстояние между ними: она естественный аналог прямой на плоскости.) Выберем в качестве этих дуг участки меридианов, отличающихся на 90o
долготы, и экватора (рис. 1). Сумма углов этого сферического треугольника отнюдь не равна сумме углов π,треугольника на плоскости:
Заметим, что превышение суммы углов данного треугольника над может быть выражено через его площадь S и радиус сферы R:
Можно доказать, что это соотношение справедливо для любого сферического треугольника. Заметим также, что обычный случай треугольника на плоскости тоже вытекает из этого равенства: плоскость может рассматриваться как сфера с R→∞
Перепишем формулу (2) иначе:
Отсюда видно, что радиус сферы можно определить, оставаясь на ней, не обращаясь к трехмерному пространству, в которое она погружена. Для этого достаточно измерить площадь сферического треугольника и сумму его углов. Иными словами, K (или R) является внутренней характеристикой сферы. Величину K принято называть гауссовой кривизной, она естественным образом обобщается на произвольную гладкую поверхность: Здесь углы и площадь относятся к малому треугольнику на поверхности, ограниченному линиями кратчайших расстояний на ней, а кривизна, вообще говоря, меняется от точки к точке, является величиной локальной. И в общем случае, так же как и для сферы, K служит внутренней характеристикой поверхности, не зависящей от ее погружения в трехмерное пространство. Гауссова кривизна не меняется при изгибании поверхности без ее разрыва и растяжения. Так, например, конус или цилиндр можно разогнуть в плоскость, и поэтому для них, так же как для плоскости, K = 0.
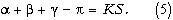 |
На соотношения (3), (4) полезно взглянуть несколько иначе. Вернемся к рисунку 1. Возьмем на полюсе вектор, направленный вдоль одного из меридианов, и перенесем его вдоль этого меридиана, не меняя угла между ними (в данном случае нулевого), на экватор. Далее, перенесем его вдоль экватора, снова не меняя угла между ними (на сей раз π/2), на второй меридиан. И наконец, таким же образом вернемся вдоль второго меридиана на полюс. Легко видеть, что, в отличие от такого же переноса по замкнутому контуру на плоскости, вектор окажется в конечном счете повернутым относительно своего исходного направления на π/2, или на Этот результат, поворот вектора при его переносе вдоль замкнутого контура на угол, пропорциональный охваченной площади, естественным образом обобщается не только на произвольную двумерную поверхность, но и на многомерные неевклидовы пространства. Однако в общем случае n-мерного пространства кривизна не сводится к одной скалярной величине K(x). Это более сложный геометрический объект, имеющий n2
(n2
- 1)/12 компонентов. Его называют тензором кривизны, или тензором Римана, а сами эти пространства — римановыми. В четырехмерном римановом пространстве-времени общей теории относительности тензор кривизны имеет 20 компонентов.
1.2 Классические опыты по проверке ОТО
В начале предыдущего раздела уже отмечалось, что гравитационное поле влияет на движение не только массивных тел, но и света. В частности, фотон, распространяясь в поле Земли вверх, совершает работу против силы тяжести и поэтому теряет энергию. Как известно, энергия фотона пропорциональна его частоте, которая, естественно, тоже падает. Этот эффект — красное смещение — был предсказан Эйнштейном еще в 1907 году. Нетрудно оценить его величину. Работа против силы тяжести, очевидно, пропорциональна gh, где g — ускорение свободного падения, а h — высота подъема. Произведение gh имеет размерность квадрата скорости. Поэтому результат для относительного смещения частоты выглядит из соображений размерности так:
где c = 3 .
1010
см/с — скорость света. При g≈103
см/с2
, h~103
см относительное смещение ничтожно мало ~10-15
. Неудивительно, что экспериментально красное смещение удалось наблюдать лишь спустя полвека, с появлением техники, использующей эффект Мёссбауэра. Это сделали Паунд и Ребка.
Еще один эффект, предсказанный Эйнштейном на заре ОТО, — отклонение луча света в поле Солнца. Его величину нетрудно оценить следующим образом. Если характерное, прицельное, расстояние луча от Солнца равно ρ , то радиальное ускорение составляет GM/ρ2
где G — ньютоновская гравитационная постоянная, а M — масса Солнца. За характерное время пролета ρ/cрадиальная компонента скорости фотона изменится на GM/(ρc) и угол отклонения составит соответственно Удобно ввести часто используемую в ОТО характеристику массивного тела, так называемый гравитационный радиус:
Наивное использование полуклассических соображений действительно приводит к ответу
Именно этот результат был получен Эйнштейном в одном из первоначальных вариантов ОТО. Первая мировая война воспрепятствовала проверке, неблагоприятной для теории. Окончательный, правильный результат ОТО вдвое больше: Гравитационный радиус Солнца rg
≈3 км, а прицельный параметр естественно сделать как можно ближе к обычному радиусу Солнца, который составляет 7 .
105
км. Таким образом, для луча света, проходящего вблизи поверхности Солнца, угол отклонения равен 1,75". Измерения, проведенные группой Эддингтона во время солнечного затмения 1919 года, подтвердили последнее предсказание. Это был подлинный триумф молодой общей теории относительности.
И наконец, к числу классических тестов ОТО относится также вращение перигелия орбиты Меркурия. Замкнутые эллиптические орбиты — это специфика нерелятивистского движения в притягивающем потенциале 1/r. Неудивительно, что в ОТО орбиты планет незамкнуты. Малый эффект такого рода удобно описывать как вращение перигелия эллиптической орбиты. Задолго до появления ОТО астрономы знали, что перигелий орбиты Меркурия поворачивается за столетие примерно на 6000" . Поворот этот в основном объяснялся гравитационными возмущениями движения Меркурия со стороны других планет Солнечной системы. Оставался, однако, неустранимый остаток — около 40" в столетие. В 1915 году Эйнштейн объяснил это расхождение в рамках ОТО.
Из простых соображений размерности можно ожидать, что поворот перигелия за один оборот составляет где R — радиус орбиты. Аккуратный расчет в рамках ОТО для орбиты, близкой к круговой, дает
При радиусе орбиты Меркурия R≈0.6.
108
км это дает 43" в столетие, снимая таким образом существовавшее расхождение. Ясно, кстати, чем выделяется в этом отношении Меркурий: это планета, ближайшая к Солнцу, планета с наименьшим радиусом орбиты R. Поэтому вращение перигелия орбиты у нее максимально.
1.3 Черные дыры
Однако роль ОТО отнюдь не сводится к исследованию малых поправок к обычной ньютоновской гравитации. Существуют объекты, в которых эффекты ОТО играют ключевую роль, важны стопроцентно. Это так называемые черные дыры.
Еще в XVIII веке Митчел и Лаплас независимо заметили, что могут существовать звезды, обладающие совершенно необычным свойством: свет не может покинуть их поверхность. Рассуждение выглядело примерно так. Тело, обладающее радиальной скоростью v, может покинуть поверхность звезды радиусом R и массой M при условии, что кинетическая энергия этого тела mv2
/2 превышает энергию притяжения GMm/R,т.е. при v2
> 2GM/R. Применение последнего неравенства к свету (как мы теперь понимаем, совершенно не обоснованное) приводит к выводу: если радиус звезды меньше чем то свет не может покинуть ее поверхность, такая звезда не светит! Последовательное применение ОТО приводит к такому же выводу, причем, поразительно, правильный критерий количественно совпадает с наивным, необоснованным. Величина rg
, гравитационный радиус, уже встречалась раньше (см. формулу (7)).
Черная дыра — вполне естественное название для такого объекта. Свойства его весьма необычны. Черная дыра возникает, когда звезда сжимается настолько сильно, что усиливающееся гравитационное поле не выпускает во внешнее пространство ничего, даже свет. Поэтому из черной дыры не выходит никакая информация.
Занятно выглядит падение пробного тела на черную дыру. По часам бесконечно удаленного наблюдателя это тело достигает гравитационного радиуса лишь за бесконечное время. С другой стороны, по часам, установленным на самом пробном теле, время этого путешествия вполне конечно.
Многочисленные результаты астрономических наблюдений дают серьезные основания полагать, что черные дыры — это не просто игра ума физиков-теоретиков, а реальные объекты, существующие по крайней мере в ядрах галактик.
1.4 Пульсар PSR 1913+16 и гравитационные волны
Нобелевская премия по физике за 1993 год была присуждена Халсу и Тейлору за исследование пульсара PSR 1913+16 (буквы PSR означают пульсар, а цифры относятся к координатам на небесной сфере: прямое восхождение 19h
13h
, склонение +16o
). Исследование свойств излучения этого пульсара показало, что он является компонентом двойной звезды. Иными словами, у него есть компаньон, и обе звезды вращаются вокруг общего центра масс. Расстояние между этим пульсаром и его компаньоном составляет всего 1,8 .
106
км. Если бы невидимый компаньон был обычной звездой с характерным радиусом ~106
км, то наблюдались бы, очевидно, затмения пульсара. Однако ничего подобного не происходит. Подробный анализ наблюдений показал, что невидимый компонент — это не что иное, как нейтронная звезда.
Существование нейтронных звезд было предсказано теоретически еще в 30-е годы. Они образуются в результате бурного гравитационного сжатия массивных звезд, сопровождающегося взрывом сверхновых. После взрыва давление в оставшемся ядре массивной звезды продолжает нарастать, электроны с протонами сливаются (с испусканием нейтрино) в нейтроны. Образуется очень плотная звезда с массой, несколько большей массы Солнца, но очень малого размера, порядка 10 — 15 км, не превышающего размер астероида. Несомненно, наблюдение нейтронных звезд уже само по себе является выдающимся открытием.
Кроме того, тщательное исследование движения этой двойной звезды дало новое подтверждение предсказания ОТО, касающегося незамкнутости эллиптических орбит. Поскольку гравитационные поля в данной системе очень велики, периастр орбиты вращается несравненно быстрее, чем перигелий орбиты Меркурия, он поворачивается на 4,2o
в год. Изучение этого и других эффектов позволило также определить с высокой точностью массы пульсара и нейтронной звезды. Они равны, соответственно, 1,442 и 1,386 массы Солнца. Но и это далеко не все.
Еще в 1918 году Эйнштейн предсказал на основе ОТО существование гравитационного излучения. Хорошо известно, что электрически заряженные частицы, будучи ускоренными, излучают электромагнитные волны. Аналогично, массивные тела, двигаясь с ускорением, излучают гравитационные волны — рябь геометрии пространства, распространяющуюся тоже со скоростью света.
Следует заметить, что аналогия эта неполна (впрочем, как практически и всякая иная). Одно из отличий между электромагнитными и гравитационными волнами, имеющее довольно существенный характер, состоит в следующем. В отличие от случая электромагнитного поля плотность энергии гравитационного поля, гравитационной волны локально, в данной точке, можно всегда обратить в ноль подходящим выбором системы координат. В свое время, лет 60 — 70 назад, это обстоятельство рассматривалось как серьезная трудность теории. Затем, однако, смысл его был прояснен, и проблема была снята. Тем не менее, по-видимому, стоит остановиться на этом вопросе в данной, по существу научно-популярной, статье по следующей причине. В последние годы в нашей стране в некоторых публикациях, претендующих на серьезный научный характер, а также в научно-популярной литературе появились утверждения о том, что возможность обращения в ноль локальной плотности энергии гравитационного поля является коренным, принципиальным дефектом ОТО.
На самом же деле ничего страшного в этом факте нет. Он — прямое следствие принципа эквивалентности. Действительно, как уже упоминалось выше, переходя в систему, связанную со свободно падающим лифтом, мы обращаем в ноль напряженность гравитационного поля. Вполне естественно, что в этой системе равна нулю и плотность энергии гравитационного поля. (Это соображение принадлежит С.И. Литерату, учителю средней школы N 130 г. Новосибирска.)
Отсюда, однако, вовсе не следует, что гравитационные волны — всего лишь игра ума, математическая абстракция. Это в принципе наблюдаемое физическое явление. Так, например, стержень, находящийся в поле гравитационной волны, испытывает деформации, меняющиеся с ее частотой. Увы, оговорка «в принципе» отнюдь не случайна: масса любого объекта на Земле настолько мала, а движение его столь медленно, что генерация гравитационного излучения в земных условиях совершенно ничтожна, не видно сколько-нибудь реального способа зарегистрировать такое излучение. Существует ряд проектов создания детекторов гравитационного излучения от космических объектов. Однако и здесь реальных результатов до сих пор нет.
Следует также сказать, что, хотя плотность энергии гравитационного поля в любой точке можно по своему желанию обратить в ноль выбором подходящей системы координат, полная энергия этого поля во всем объеме, полный его импульс имеют совершенно реальный физический смысл (конечно, если поле достаточно быстро убывает на бесконечности). Столь же наблюдаемой, хорошо определенной величиной является и потеря энергии системой за счет гравитационного излучения.
Все это имеет самое прямое отношение к пульсару PSR 1913+16. Эта система также должна излучать гравитационные волны. Их энергия в данном случае огромна, она сравнима с полной энергией излучения Солнца. Впрочем, даже этого недостаточно, чтобы непосредственно зарегистрировать эти волны на Земле. Однако энергия гравитационных волн может черпаться только из энергии орбитального движения звезд. Падение последней приводит к уменьшению расстояния между звездами. Так вот, тщательные измерения импульсов радиоизлучения от пульсара PSR 1913+16 показали, что расстояние между компонентами этой двойной звезды уменьшается на несколько метров в год в полном согласии с предсказанием ОТО. Любопытно, что потеря энергии двойной звездой за счет гравитационного излучения была впервые рассчитана Ландау и Лифшицем, они поместили этот расчет в качестве учебной задачи в первое издание своей замечательной книги —Теория поля», которое вышло в 1941 году.
1.5 Гравитационные линзы и коричневые карлики
И наконец, сюжет, еще более свежий, чем пульсар PSR 1913+16. Он тесно связан, однако, с идеей, возникшей еще на заре ОТО. В 1919 году Эддингтон и Лодж независимо заметили, что, поскольку звезда отклоняет световые лучи, она может рассматриваться как своеобразная гравитационная линза. Такая линза смещает видимое изображение звезды-источника по отношению к ее истинному положению.
Первая наивная оценка может привести к выводу о полной безнадежности наблюдения эффекта. Из простых соображений размерности можно было бы заключить, что изображение окажется сдвинутым на угол порядка rg
/d, где rg
— гравитационный радиус линзы, а d — характерное расстояние в задаче. Даже если взять в качестве линзы скопление, состоящее из 104
звезд, а для расстояния принять оценку d~10 световых лет, то и тогда этот угол составил бы всего 10-10
радиан. Разрешение подобных углов практически невозможно.
Однако такая наивная оценка просто неверна. Это следует, в частности, из исследования простейшего случая соосного расположения источника S, линзы L и наблюдателя O (рис. 2). Задача эта была рассмотрена в 1924 году Хвольсоном (профессор Петербургского университета, автор пятитомного курса физики, широко известного в начале века) и спустя 12 лет Эйнштейном. Обратимся к ней и мы. Ясно, что для всякого расстояния d1
между источником и линзой, d — между линзой и наблюдателем для любого гравитационного радиуса rg
линзы (звезды или скопления звезд) найдется такое минимальное расстояние ρ между лучом из источника и линзой, при котором этот луч попадает в приемник. При этом изображения источника заполняют окружность, которую наблюдатель видит под углом φ Углы φ и θ1
малы, так что φ=h/d,φ1
=h/d а, кроме того, h=ρ Отсюда легко находим С другой стороны, для θ справедлива, очевидно, формула (8). Таким образом,
И наконец, интересующий нас угол составляет
Таким образом, правильный порядок величины угловых размеров изображения не rg
/d, а √rg
/d (мы считаем здесь, что все расстояния по порядку величины одинаковы). Он оказался намного больше первой, наивной, оценки, и это радикально меняет ситуацию с возможностью наблюдения эффектов гравитационных линз. 
Изображение источника в виде окружности (ее принято называть кольцом Эйнштейна), создаваемое гравитационной линзой при аксиально-симметричном расположении, реально наблюдалось. Сейчас известно
несколько источников в радиодиапазоне, которые выглядят именно так, кольцеобразно.
Если, однако, гравитационная линза не лежит на прямой, соединяющей источник с наблюдателем, картина оказывается иной. В случае сферически-симметричной линзы возникают два изображения (рис. 3), одно из которых лежит внутри кольца Эйнштейна, соответствующего осесимметричной картине, а другое — снаружи. Подобные изображения также наблюдались, они выглядят как двойные квазары, как квазары-близнецы.
Если источник движется, то перемещаются и оба изображения. Пока яркости обоих сравнимы с яркостью источника, для оценки углового расстояния между ними можно по-прежнему использовать выражение (10). Если масса звезды, действующей в качестве линзы, невелика, скажем на два — три порядка величины меньше массы Солнца, то разрешить такой угол между изображениями, ~0,001", практически немыслимо. Тем не менее обнаружить подобное явление можно. Дело в том, что при сближении изображений их суммарная яркость растет. Явление это, так называемое микролинзирование, имеет достаточно специфический характер: рост яркости и ее последующее падение происходят симметрично во времени, причем изменение яркости происходит одинаково на всех длинах волн (угол отклонения (10) не зависит от длины волны).
Поиски микролинзирования, которые велись на протяжении нескольких лет двумя группами астрономов, австралийско-американской и французской, не просто привели к обнаружению эффекта. Таким образом был открыт новый класс небесных тел: слабосветящиеся карликовые звезды, так называемые коричневые карлики, именно они играют роль микролинз. Все это произошло совсем недавно. Если еще в январе 1994 года было известно лишь два — три подобных события, то в настоящее время они уже исчисляются десятками. Поистине первоклассное открытие в астрономии.
2 Основные представления о специальной теории относительности
2.1 Эйнштейновский принцип относительности
Специальная теория относительности (СТО) наряду с предположением о том, что
a) пространство - трёхмерно, однородно и изотропно, (что означает, что в пространстве нет выделенных мест и направлений)
б) время - одномерно и однородно, (нет выделенных моментов времени)
использует следующие два основополагающие принципа:
1. Никакими физическими опытами внутри замкнутой физической системы нельзя определить, покоится ли эта система или движется равномерно и прямолинейно (относительно системы бесконечно удаленных тел). Этот принцип называют принципом относительности
Галилея - Эйнштейна, а соответствующие системы отсчёта - инерциальными
.
2. Существует предельная скорость (мировая константа
c) распространения физических объектов и воздействий, которая одинакова во всех инерциальных системах отсчета. Со скоростью c распространяется свет в вакууме.
Прямая проверка независимости скорости света от скорости источника была выполнена А.М. Бонч-Бруевичем в 1956 г. с использованием света, испускаемого экваториальными краями солнечного диска. Скорости диаметрально противоположных участков диска (за счет вращения Солнца) отличаются на 3,5·103
м/с, а скорость испущенного ими света изменялась на 65 240м/c. В пределах точности эксперимента, которая составляла [(v)/( v)] 7·10-2
, зависимость скорости света от скорости источника не наблюдалось.
Таким образом, все физические явления, включая распространение света (и, следовательно, все законы природы
), в различных инерциальных системах отсчета выглядят совершенно одинаково. Такая особенность Законов Природы носит название лоренцевой инвариантности
(от латинского invariantis - неизменяющийся).
Согласно СТО, если скорость частицы меньше скорости света в вакууме c в некоторой инерциальной системе отсчета в данный момент времени, то она не может быть сделана равной или большей c ни кинематически - переходом в другую систему отсчета, ни динамически - изменением скорости частицы, приложенными к ней силами. Поэтому распространение электромагнитных волн в вакууме является самым быстрым способом распространения взаимодействия в физических системах.
Это положение принято распространять на все типы частиц и взаимодействий, хотя прямая проверка осуществлена только для электромагнитного взаимодействия.
Существование предельной скорости распространения взаимодействия приводит к ограничениям на модели в релятивистской физике. Оказывается, например, недопустимой модель абсолютно твердого тела, так как под воздействием приложенной к нему силы, все точки тела мгновенно изменяют свои механические состояния.
2.2 Синхронизация часов
В упомянутой статье Эйнштейн проанализировал свойства времени и кажущееся "очевидным" понятие одновременности. Он показал, что классическая механика приписывает времени такие свойства, которые, вообще говоря, не согласуются с опытом и являются правильными только при малых скоростях движения. Одним из центральных пунктов эйнштейновского анализа понятия времени является синхронизация часов
, т.е. установление единого времени в пределах одной инерциальной системы отсчета. Если двое часов находятся в одной точке пространства (т.е. в непосредственной близости), то их синхронизация производится непосредственно - стрелки ставятся в одно и то же положение (полагают, что часы совершенно одинаковы и абсолютно точны).
Синхронизацию часов, находящихся в двух разных точках пространства, Эйнштейн предложил проводить с помощью световых сигналов. Испустим из точки A в момент t1
короткий световой сигнал, который отразится от некоторого зеркала B и вернется в точку A в момент t2
(Рис. 4). Времена распространения сигнала туда и обратно конечны (скорость сигнала конечна!) и одинаковы (изотропия пространства!). Поэтому часы в точке B будут согласованы с показаниями часов в точке A в моменты испускания (t1
) и возвращения (t2
) сигнала соотношениями
| t1
= tB
- h/c, t2
= tB
+ h/c,
|
|
где h = rAB
- расстояние между точками A и B. Отсюда положение, в которое нужно поставить стрелки часов B в момент прихода сигнала: tb
= (t1
+ t2
)/2. Таким способом можно синхронизовать показания всех часов, неподвижных друг относительно друга в некоторой инерциальной системе отсчета S.

Рис. 4

Рис. 5
Мысленные эксперименты с движущимися часами, аналогичные только что описанному, показывают, что здесь синхронизация невозможна и единого для всех инерциальных систем времени не существует
. Расмотрим пример с "эйнштейновским поездом" (см. Рис. 5).
Пусть наблюдатель A находится посередине длинного поезда, движущегося со скоростью сравнимой со скоростью света, а наблюдатель B стоит на земле вблизи железнодорожного полотна. Устройства, находящиеся в хвосте и в голове поезда на одинаковых расстояниях от A, испускают две короткие вспышки света, которые достигают наблюдателей A и B одновременно - в тот момент, когда они поравняются друг с другом. Какие выводы сделают из одновременного прихода к ним световых сигналов наблюдатели в поезде и на земле?
Наблюдатель A: Сигналы испущены из точек, удаленных от меня на равные расстояния, следовательно, они и испущены были одновременно.
Наблюдатель B: Сигналы пришли ко мне одновременно, но в момент испускания голова поезда была ко мне ближе, поэтому сигнал от хвоста поезда прошел больший путь, следовательно он и был испущен раньше, чем сигнал от головы.
Этот пример показывает, что часы в системе "поезд" синхронизованы только с точки зрения наблюдателя, который в ней неподвижен. С точки зрения наблюдателя на земле, часы, расположенные на поезде в разных точках (в голове, в хвосте и в середине поезда) показывают разное время. События, одновременные в одной системе отсчета (световые вспышки в системе отсчета поезда), не являются одновременными в другой системе отсчета земли. Синхронизация часов находящихся в разных системах отсчета невозможна. Этот вывод не исключает совпадения показаний часов в отдельный момент времени - например, наблюдатели A и B в момент встречи могут установить одинаковые показания своих часов. Но уже в любой последующий момент показания часов разойдутся.
2.3 Преобразования Лоренца
Преобразования Лоренца, обобщающие формулы Галилея перехода от одной инерциальной системы отсчета в другую, можно получить из анализа еще одного мысленного эксперимента. Пусть начала координат систем отсчета S и S
в начальный момент t = t
совпадают и оси координат в них имеют одинаковую ориентацию (см. Рис. 6). В этот момент времени в их общем начале координат пусть произошла световая вспышка. С точки зрения наблюдателя, находящегося в системе S, в ней распространяется сферическая электромагнитная волна, которая за время t пройдет расстояние r = c t ( 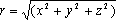 ) от начала координат. ) от начала координат.
Но наблюдатель в движущейся системе S
также регистрирует сферическую световую волну, распространяющуюся из начала координат этой системы (точки 0
) со скоростью света в вакууме c. По его часам за время t
волна пройдет расстояние r
= c t
, где 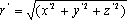 . Это связано с тем, что физические явления в инерциальных системах происходят одинаковым образом. Иначе, регистрируя различия, можно было бы найти "истинно" покоящуюся систему отсчета, что невозможно. . Это связано с тем, что физические явления в инерциальных системах происходят одинаковым образом. Иначе, регистрируя различия, можно было бы найти "истинно" покоящуюся систему отсчета, что невозможно.
Теперь ясно, что координаты точек волнового фронта в системе S и S
связаны уравнением
| c2
t2
- (x2
+ y2
+ z2
) = 0 = c2
t2
- (x2
+ y2
+ z2
),
|
|
(11)
|
решение которого и является искомым обобщением преобразований перехода из одной инерциальной системы координат в другую.
Опуская сам формальный вывод, который использует общие соображения об однородности и изотропии пространства и однородности времени (из которых, например, следует, что связь "штрихованных" и "нештрихованных" координат должна быть линейной), можно получить, что в условиях рассматриваемого мысленного эксперимента, параметры {x
,y
,z
,t
} связаны с параметрами {x,y,z,t} соотношениями
| x
=
|
x - V t
|
, y
= y, z
= z, t
=
|
t - x V/c2
|
.
|
|
(12)
|
Преобразования Лоренца оставляют неизменными уравнения Максвелла, однако проверка этого утверждения выходит за рамки школьной программы по физике.
Легко видеть, что уравнения Ньютона теперь не сохраняют свой вид при преобразовании (12). Поэтому второй закон Ньютона необходимо модифицировать. Новая механика, основанная на принципе относительности Эйнштейна, называется релятивистской
(от латинского relativus - относительный).
При безразмерном параметре V/c 1 формулы (4) переходят в формулы (1). Поэтому в теории относительности выполняется принцип соответствия
- при малых скоростях движения частиц и систем отсчета релятивистские выражения переходят в формулы ньютоновой механики. Этот переход является характерной чертой любой физической теории: старые знания не перечеркиваются новыми достижениями, а включаются них как предельный частный случай.
Обратное преобразование координат системы S в координаты системы S
можно получить из (12), поменяв местами штрихованные и нештрихованные координаты и проведя замену V - V:
| x =
|
x
+ V t
|
, y = y
, z = z
, t =
|
t
+ x
V/c2
|
.
|
|
(5)
|

Рис. 6
2.4 Преобразование скорости
Если частица движется относительно движущейся системы координат S
со скоростью 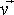 , то ее скорость , то ее скорость 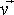 в системе отсчета S может быть найдена с помощью преобразований Лоренца (12). в системе отсчета S может быть найдена с помощью преобразований Лоренца (12).
Если закон движения частицы в движущейся системе координат имеет вид
| x
= v
t
, y
= z
= 0,
|
|
то в покоящейся (лабораторной) системе координат этот закон, очевидно, имеет вид
Выполнив подстановку (13), найдем, что
Эта формула определяет релятивистский закон сложения скоростей.
При = V/c 0 релятивистский закон сложения скоростей (13) с точностью до линейных по членов переходит в формулу преобразования скоростей в классической механике:
Из (13) следует, что скорость частицы меньшая скорости света в вакууме (v
c) в одной системе отсчета, останется меньше скорости света в вакууме (v c) в любой другой системе отсчета, движущейся по отношению к первой с досветовой скоростью V c. Если же 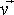
= (c,0,0), то
= (c,0,0), то 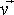 = (c,0,0): скорость света одна и та же во всех системах отсчета. = (c,0,0): скорость света одна и та же во всех системах отсчета.
Более общее преобразование скорости можно получить из формулы (14), если в ней перейти к дифференциалам координат и времени и использовать, что vx
= dx/dt, vy
= dy/dt, vz
= dz/dt и аналогичные выражения для vx
, vy
, vz
. После преобразования получившегося соотношения, получим
| vx
=
|
vx
+ V
1 - V vx
/c2
|
, vy
=
|
1 - V vx
/c2
|
, vz
=
|
1 - V vx
/c2
|
.
|
|
2.5 Собственное время, события и мировые линии частиц
В качестве часов наблюдатели в системах S, S
могут использовать любой периодический процесс, например, излучение атомов или молекул на определенных фиксированных частотах. Время, отсчитываемое по часам, движущимся вмемте с данным объектом, называется собственным временем
этого объекта. Для измерения длин можно взять некоторый эталон - линейку. Собственной длиной
линейки называется ее длина l0
в той системе, в которой она покоится. Величина l0
равна модулю разности координат концов линейки в один и тот же момент времени.
Совокупность декартовых координат 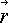 = (x,y,z) и момента времени t в некоторой инерциальной системе отсчета определяют событие
. Событием является, например, нахождение точечной частицы в момент времени t в точке пространства, указанной вектором = (x,y,z) и момента времени t в некоторой инерциальной системе отсчета определяют событие
. Событием является, например, нахождение точечной частицы в момент времени t в точке пространства, указанной вектором 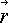 . .
Множество всех событий образуют "четырехмерный Мир Минковского". Отдельные точки в четырехмерном пространстве указывают координаты и время некоторого "события". Последовательность кинематических состояний любого тела (его координаты в разные моменты времени) изображается мировой линией
(Рис. 7).

Рис. 7
Если частицы движутся только вдоль оси 0x, то наглядно представить "Мир Минковского" можно с помощью плоскости координат (с t, x). Время удобно умножить на скорость света, чтобы обе координаты имели одинаковую размерность. Это можно сделать, поскольку скорость света - универсальная мировая константа.

Рис. 8
Мировыми линиями (в отличие от траекторий классической механики) обладают не только движущиеся, но и покоящиеся в данной инерциальной системе отсчета тела. Так, мировая линия тела, покоящегося в начале координат, будет совпадать с временной осью 0 ct, а тела, покоящегося в пространственной точке xa
- является прямой AB, параллельной оси времени. Мировая линия тела, движущегося с постоянной скоростью V - (и при t = 0, находящегося в точке x(0) = 0) - прямая CD; мировая линия светового луча, испущенного из начала координат в напралении оси x - биссектриса координатного угла OF; мировая линия тела, движущегося с переменной скоростью v(t) - кривая MN (cм. Рис. 8а))
2.6 Геометрический смысл преобразований Лоренца
Выясним теперь геометрический смысл преобразований Лоренца. Еще раз запишем его только для x и t в виде
| x
= (x - ct), ct
= (ct - x).
|
|
Это линейное однородное преобразование, очень похожее на преобразование поворота на угол в плоскости XY:
| x
= x cos+ y sin, y
= - x sin+y cos.
|
|
Новые оси x
, y
, получающиеся в результате поворота изображены на Рис. 8 б).
Важнейшим свойством преобразования поворота является сохранение расстояния между любыми двумя точками: r12
= r
12
.
Здесь:
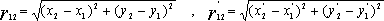
Введем величину, зависящую от параметров двух событий { [(r1
)\vec],t1
} и { [(r2
)\vec],t2
} и определенную равенством
| s12
= [ c2
(t2
- t1
)2
- (x2
- x1
)2
- (y2
- y1
)2
- (z2
- z1
)2
]1/2
.
|
|
(15)
|
Она называется пространственно - временным интервалом.
Прямой подстановкой формул (12) можно проверить, что величина пространственно - временного интервала между двумя событиями является инвариантом преобразований Лоренца:
В двумерном случае 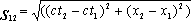 можно рассматривать как "расстояние" между точками плоскости ct, x. Но квадрат разности координат входит в s12
со знаком "минус". Пространство, в котором расстояние между точками определено формулой (15) называется псевдоевклидовым
. Наряду с отмеченным сходством, между евклидовым и псевдоевклидовым пространствами имеются принципиальные различия. В евклидовом пространстве расстояние между любыми точками r2
12
0, равенство нулю означает, что точки совпадают. В псевдоевклидовом пространстве s2
12
может иметь любой знак, а его обращение в нуль возможно для двух совершенно различных точек пространства - времени. можно рассматривать как "расстояние" между точками плоскости ct, x. Но квадрат разности координат входит в s12
со знаком "минус". Пространство, в котором расстояние между точками определено формулой (15) называется псевдоевклидовым
. Наряду с отмеченным сходством, между евклидовым и псевдоевклидовым пространствами имеются принципиальные различия. В евклидовом пространстве расстояние между любыми точками r2
12
0, равенство нулю означает, что точки совпадают. В псевдоевклидовом пространстве s2
12
может иметь любой знак, а его обращение в нуль возможно для двух совершенно различных точек пространства - времени.
Найдем положение новых осей (x
, ct
) на псевдоевклидовой плоскости. Отложим координата x, ct на прямоугольных осях. (Рис. 9). Точка x
= 0, сопадающая с началом координат системы S
, движется в системе S со скоростью V. Ее мировая линия будет представлять собой ось времени ct
системы S
. Эта ось будет наклонена к оси ct на угол = arctg (V/c). Ось x
новой системы можно определить условием ct
= 0. Но тогда в старой системе координат это будет прямая ct = x, проходящая через начало координат и составляющая с осью x тот же угол = arctg (V/c).
Приходим к выводу, что новая система координат косоугольна! Если попытаться найти связь между отрезками x
, ct
и x, ct, посто проектируя отрезки (так как это делается в эвклидовом случае), то получится неправильный результат. Преобразования Лоренца не только поворачивают оси, но и искажают масштабы координат по осям!
Итак, основной результат состоит в том, что преобразования Лоренца можно интерпретировать, как псевдоевклидово вращение
системы координат в пространстве Минковского.

Рис. 9
С помощью Рис. 9 можно дать геометрическую интерпретацию различным следствиям из преобразований Лоренца. Вспомним, например, относительность одновременности. В системе S линии равного времени - прямые параллельные оси 0x. В системе S
- это прямые, параллельные 0x
, не совпадающие с линиями равного времени в системе S. Поэтому события, одновременные в S, не будут в общем случае одновременными в S. Например, между одновременными в системе S событиями A и B в системе S
пройдет промежуток времени t
= A
B
/c, причем событие B произойдет раньше.
Как ясно из вышеизложенного, на псевдоевклидовой плоскости квадрат интервала s2
12
может быть как положительным, так и равным нулю и отрицательным.
Если s2
12
0, его называют времениподобным
, при s2
12
0 - пространственноподобным
, при s2
12
= 0 - светоподобным
или нулевым
.
Характер интервала тесно связан c причинностью
- он определяет возможность причинной связи событий, происходящих в пространственно - временных точках 1 и 2. Если s2
12
0, то из точки 1 можно послать сигнал со скоростью 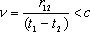 , который вызовет событие 2. В случае s2
12
= 0 это также возможно, но сигнал должен посылаться с предельной скоростью c. События, разделенные пространственноподобным интервалом, не могут быть причинно обусловлены, т.к. сигналы не могут распространяться со скоростью , который вызовет событие 2. В случае s2
12
= 0 это также возможно, но сигнал должен посылаться с предельной скоростью c. События, разделенные пространственноподобным интервалом, не могут быть причинно обусловлены, т.к. сигналы не могут распространяться со скоростью 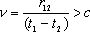 . .
2.7 Замедление времени
Рассмотрим часы, покоящиеся в начале координат движущейся системы (x
= 0), которые перемещаются относительно лабораторной системы координат со скоростью V, так что их координата x = V t пропорциональна времени, определяемому неподвижными часами. Инвариантность интервала позволяет, тогда, определить показания движущихся часов:
| t
= t
|
________
1 - V2
/c2
|
.
|
|
(17)
|
Время, измеряемое часами, движущимися относительно лабораторной системы отсчета, замедляется.
Как ни покажется странным, но тот же вывод справедлив относительно замедления темпа хода часов в лабораторной системе координат с точки зрения наблюдателя из движущейся системы отсчета, т.е. "движущиеся" и "покоящиеся" часы взаимно отстают друг от друга.
С последним замечанием тесно связан широко известный парадокс близнецов
(см. ниже раздел "Задачи").
Замедление хода времени в движущейся системе отсчета было экспериментально подтверждено американскими физиками Б. Росси и Д.Х. Холлом в 1941 году. Они наблюдали увеличение среднего времени жизни мюонов, двигавшихся со скоростью v c, в 6 8 раз по сравнению с временем жизни неподвижных мюонов.
Особая ценность этого эксперимента состоит в том, что процесс распада мюонов определяется слабым взаимодействием, в то время как СТО была построена для описания систем с электромагнитным взаимодействием.
2.8 Лоренцево сокращение длины
Стержень, расположенный вдоль оси 0
X
движущейся системы отсчета и покоящийся в ней, имеет длину l0
. Если один из концов стержня (для простоты) сосвпадает с началом координат этой системы, то в момент t = 0 по часам лабораторной системы отсчета координаты концов стержня определяются преобразованием Лоренца:
| x1
= 0, x2
= l = l0
|
________
1 - V2
/c2
|
.
|
|
(18)
|
Длина движущегося стержня в лабораторной системе отсчета уменьшается в направлении движения. Это изменение длины называется сокращением Лоренца - Фитцджеральда
.
Поскольку поперечные размеры тела не изменяются, то легко видеть, что объем тела также уменьшается:
| V = V0
|
________
1 - V2
/c2
|
.
|
|
(19)
|
3
Динамика специальной теории относительности
3.1 Энергия и импульс частицы
Под массой частицы m
будем понимать ее массу, измеряемую в системе покоя частицы - массу покоя.
Релятивистским импульсом частицы массы m
, движущейся в выбранной инерциальной системе отсчета со скоростью 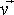 , называется векторная величина , называется векторная величина 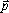 , определяемая формулой , определяемая формулой
Релятивистский импульс имеет ту же размерность, что и импульс в классической механике. При v
/c
0, 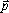 m m
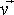 (с точностью до линейных по v
/c
слагаемых). (с точностью до линейных по v
/c
слагаемых).
Энергией
частицы в релятивистской физике называется величина E
, определяемая выражением
Энергия имеет ту же размерность и измеряется в тех же единицах, что и энергия в ньютоновской механике.
Энергия частицы в той системе отсчета, в которой она покоится, называется ее энергией покоя
E
0
:
При = v
/c
0 релятивистское выражение для энергии частицы может быть записано в виде
| E
= mc
2
+
|
m
v
2
2
|
= E
0
+
|
m
v
2
2
|
.
|
|
Второе слагаемое совпадает с кинетической энергией частицы в классической теории. Разность E
- mc
2
= T
называют кинетической энергией релятивистской частицы.
Из формул (20) и (21) находим полезную формулу для скорости частицы:
3.2 Релятивистские преобразования энергии и импульса
Рассмотрим вновь две инерциальные системы отсчета, движущиеся друг относительно друга со скоростью V
в направлении оси x
.
Закон преобразования для величин (E
, 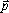 ) и (E
, ) и (E
, 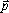
), измеряемых в системах S
и S
, имеет форму преобразования (23):
), измеряемых в системах S
и S
, имеет форму преобразования (23):
| E
¢
=
|
E
- V
px
|
, px
¢
=
|
px
- E
V
/c
2
|
, py
¢
= py
, pz
¢
= pz
.
|
|
(23)
|
Таким образом,энергия и импульс частицы зависят от выбора системы отсчета, однако существует величина, которая имеет абсолютный смысл. Из формул (23) следует, что
| æ
ç
è
|
E
¢
c
|
ö
÷
ø
|
2
|
-
|
®
p
|
¢
2
=
|
æ
ç
è
|
E
c
|
ö
÷
ø
|
2
|
-
|
®
p
|
2
= m
2
c
2
,
|
|
из которого следует, что масса частицы одинакова во всех системах отсчета и, следовательно, является релятивистским инвариантом
.

Рис. 10
Используя последнее выражение можно легко получить соотношение, связывающее энергию и импульс в релятивистской физике:
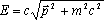
.
Эта зависимость энергии от импульса изображена на Рис. 10. При малых значениях импульса E
= m
c
2
+ p
2
/2 m
, а при достаточно больших импульсах E
= p
c
.
Иногда формулу (21), записывают в виде E
= m
(v
) c
2
, вводя "релятивистскую массу" частицы, зависящую от скорости:
Саму же формулу (21) истолковывают, как "эквивалентность" энергии и массы в релятивистской физике. Однако такое утверждение приводит лишь к путанице (а в преждние времена вело даже к ожесточенным идеологическим спорам). Масса и энергия совершенно разные характеристики частицы. Масса - инвариант, а энергия - динамическая характеристика, зависящая от выбора системы отсчета. Взаимосвязь энергии и массы частицы имеет место только в системе покоя частицы.
Поэтому понятие "массы, зависящей от скорости" [(m
)/([(1 - (v
/c
)2
)])] лишено физического смысла!
3.3 Частицы с нулевой массой покоя
Если в формулах (20,21) формально положить скорость частицы v
= c
, то энергия и импульс частицы обращаются в бесконечность. Это значит, что частица с отличной от нуля массой покоя не может двигаться со скоростью света. В релятивистской механике однако предполагается, что существовуют частицы с массой покоя равной нулю, всегда движущиеся со скоростью света. Из (22) видно, что для таких частиц модуль импульса и энергия связаны соотношением:
откуда следует, что здесь
в соответствии с тем, что m
= 0.
К частицам с нулевой массой покоя относятся, например, фотоны - кванты электромагнитного поля. В больших деталях их свойства будут обсуждены в разделе "Квантовая теория" - задание N 5.
3.3 Релятивистский эффект Доплера
Рассмотрим плоскую монохроматическую волну
| E
(
|
®
r
|
,t
) = E
0
cos
|
æ
è
|
®
k
|
·
|
®
r
|
- w t
|
ö
ø
|
.
|
|
(23)
|
Здесь - частота волны, а 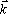 = k = k
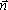 - волновой вектор (k
= [()/( c
)] - волновое число, - волновой вектор (k
= [()/( c
)] - волновое число, 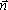 - единичный вектор в направлении распространения волны (см. Рис. 11).) - единичный вектор в направлении распространения волны (см. Рис. 11).)

Рис. 11
Выясним закон преобразования частоты и волнового вектора при переходе в другую инерциальную систему отсчета. Будем для определенности считать, что волна распространяется под углом к оси 0x
, вдоль которой со скоростью V
движется "штрихованная" система отсчета S
. Из Рис. 11 видно, что существуют пространственно - временные точки, в которых векторы поля обращаются в нуль (узловые точки волны - те точки, в которых косинус равен нулю). Ясно, что это свойство поля носит объективный характер и должно выполняться во всех инерциальных системах отсчета. Отсюда следует, что фаза электромагнитной волны должна быть инвариантна!
| ®
k
|
·
|
®
r
|
- wt
=
|
®
k
|
¢
|
·
|
®
r
|
¢
|
-w¢
t
¢
.
|
|
В декартовых координатах это условие принимает вид:
| kx
x
+ky
y
+ kz
z
-w t
= kx
¢
x
¢
+ky
¢
y
¢
+ kz
¢
z
¢
- w¢
t
¢
.
|
|
(24)
|
Поскольку x
, y
, z
, t
связаны с x
¢
, y
¢
, z
¢
, t
¢
преобразованием Лоренца , то для обеспечения инвариантности фазы необходимо, чтобы выполнялись преобразования
| w¢
=
|
w- V
kx
|
, kx
¢
=
|
kx
- V
/c
2
w
|
, ky
¢
= ky
, kz
¢
= kz
.
|
|
(25)
|
Прямой подстановкой формул (25) в соотношение (24) можно проверить его выполнение.
Найдем теперь связю между частотой 0
в системе источника волны и частотой той же волны в системе наблюдателя.
Полагая в первой формуле из (25)
= 0
, kx
= [()/( c
)] cos, где - угол распространения волны относительно V
в системе наблюдателя (приемника), найдем
Эта формула выражает собой эффект Доплера
- изменение частоты волны, вызанное относительным движением источника и приемника.
При V
/c
1 из (26) имеем
| Dw = w- w0
= w0
(V
/c
) cosq.
|
|
Частота волны возрастает при сближении источника и наблюдателя ( в этом случае проекция скорости на направление луча V
= V
cos0) и убывает при их удалении (V
0) продольный эфект Доплера
. Если относительная скорость направлена перпендикулярно лучу зрения (cos = 0), то уменьшение частоты представляет собой эффект, квадратичный по V
/c
:
| Dw = -
|
w0
2
|
æ
ç
è
|
V
c
|
ö
÷
ø
|
2
|
|
- поперечный эффект Доплера
.
При выводе последних двух формул учтено, что при V
/c
1
| 1
1 - (V
/c
)cosq
|
» 1 + (V
/c
)cosq,
|
________
Ö1 - (V
/c
)2
|
» 1 - (V
/c
)2
/2.
|
|
Красное смещение (в сторону волн большей длины) наблюдаемое на Земле в спектрах излучения далеких галактик по сравнению с эталонными линиями интерпретируется как эффект раширения Метагалактики (наблюдаемой части Вселенной) - взаимного удаления галактик друг от друга. В 1928 г. Э. Хабблом было обнаружено, что скорости разбегания галактик приблизительно пропорциональны расстоянию до них:
Константа Хаббла H
50 100 км/(с·Мпк). Значение H
-1
13 млрд. лет определяет время, истекшее с начала расширения Метагалактики при условии постоянной скорости расширения.
Заключение
ОТО — завершенная физическая теория. Она завершена в том же смысле, что и классическая механика, классическая электродинамика, квантовая механика. Подобно им, она дает однозначные ответы на физически осмысленные вопросы, дает четкие предсказания для реально осуществимых наблюдений и экспериментов. Однако, как и всякая иная физическая теория, ОТО имеет свою область применимости. Так, вне этой области лежат сверхсильные гравитационные поля, где важны квантовые эффекты. Законченной квантовой теории гравитации не существует.
ОТО — удивительная физическая теория. Она удивительна тем, что в ее основе лежит, по существу, всего один экспериментальный факт, к тому же известный задолго до создания ОТО (все тела падают в поле тяжести с одним и тем же ускорением). Удивительна тем, что она создана в большой степени одним человеком. Но прежде всего ОТО удивительна своей необычайной внутренней стройностью, красотой. Не случайно Ландау говорил, что истинного физика-теоретика можно распознать по тому, испытал ли человек восхищение при первом же знакомстве с ОТО.
Примерно до середины 60-х годов ОТО находилась в значительной мере вне основной линии развития физики. Да и развитие самой ОТО отнюдь не было весьма активным, оно сводилось в большой степени к выяснению определенных тонких мест, деталей теории, к решению пусть важных, но достаточно частных задач.
Вероятно, одна из причин такой ситуации состоит в том, что ОТО возникла в некотором смысле слишком рано, Эйнштейн обогнал время. С другой стороны, уже в его работе 1915 года теория была сформулирована в достаточно завершенном виде. Не менее важно и то обстоятельство, что наблюдательная база ОТО оставалась очень узкой. Соответствующие эксперименты чрезвычайно трудны. Достаточно напомнить, что красное смещение удалось измерить лишь спустя почти 40 лет после того, как было обнаружено отклонение света в поле Солнца.
СТО возникла больше для решения специальных задач и никоим образом не противоречит принципам ОТО. Она лишь дополнение реального состояния науки с точки зрения потребности современной физики и естествознания. Релятивизм не мертв, он лишь отражение состояния научно-технической мысли того времени.
Тем не менее, в настоящее время СТО — бурно развивающаяся область современной физики. Это результат огромного прогресса наблюдательной астрономии, развития экспериментальной техники, впечатляющего продвижения в теории.
Список использованных источников
1. “Принцип относительности” Лоренц, Пуанкаре, Эйнштейн и Минковский; ОНТИ ; 1935 г., стр. 134
2. Полное собрание трудов, Л. И. Мандельштам; Том 5, стр. 172
3. А.Эйнштейн. К электродинамике движущихся сред. - М.: 1966.
4. "Общая теория относительности"; Н. В. Мицкевич; Москва., 1927 г
5. "Парадоксы теории относительности"; Я. П. Терлецкий; Москва., 1965 г.
6. Л.В. Тарасов, Современная физика в средней школе. М.: Просвещение, 1990.
7. В.Н. Дубровский, Я.А. Смородинский, Е.Л. Сурков, Релятивистский мир. (Библиотечка "Квант", выпуск 34). М.: Наука, 1984.
8. Э.Тейлор, Дж. Уилер, Физика пространства - времени. М.: Мир, 1969.
9. И.И. Гольденблат, Парадоксы времени в релятивистской механике. М.: Наука, 1972.
10. И.М. Гельфгат, Л.Э. Генденштейн, Л.А. Кирик, 1001 задача по физике с ответами, указаниями, решениями. Москва - Харьков, Илекса. 1997.
11. И.И. Воробьев Теория относительности в задачах. М.: Наука, 1989.
12. П.В. Елютин, Г.А. Чижов, Словарь-справочник по элементарной физике. Часть 3. М., 1995.
13. Эйнштейн, Л.Инфельд. Эволюция физики. - М.: 1966.
14. В.Л.Гинзбург. О теории относительности. - М.: Наука, 1970.
15. Г.Линдер. Картины современной физики. - М.: Мир, 1977.
16. А.В.Горелов. Элементы теории относительности- элементарное изложение специальной теории относительности.
17. П.А.М.Дирак. Воспоминания о необычайной эпохе. - М.: Наука, 1990.
[ГАсГ1]
|