МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ГОСУДАРСТВЕННОЕ ОБЩЕОБРАЗОВАТЕЛЬЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«УССУРИЙСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ»
Физико–математический факультет
Курсовая работа по математическому анализу
Тема: «Непрерывная, но не дифференцируемая функции»
Выполнила: Пляшешник Ксения
студентка 131 группы
Руководитель: Делюкова Я.В.
Уссурийск – 2011г.
Содержание
Введение.............................................................................................. 3
Историческая справка......................................................................... 4
Основные определения и теоремы..................................................... 5
Пример непрерывной функции без производной........................... 10
Решение упражнений........................................................................ 13
Заключение........................................................................................ 21
Список литературы........................................................................... 22
Курсовая работа посвящена изучению связи между непрерывностью и существованием производной функции одной переменной. Исходя из цели ставились задачи:
1. Изучить учебную литературу;
2. Изучить пример непрерывной функции, не имеющей производной ни в одной точке, построенной ван-дер-Варденом;
3. Прорешать систему упражнений.
Историческая справка
Ба́ртель Лее́ндерт ван дер Ва́рден (нидерл. Bartel Leendert van der Waerden , 2 февраля 1903, Амстердам , Нидерланды — 12 января 1996, Цюрих , Швейцария) — голландский математик.
Обучался в Амстердамском университете, затем в Гёттингенском университете , где на него огромное влияние оказала Эмми Нётер.
Основные работы в области алгебры , алгебраической геометрии, где он (наряду с Андре Вейлем и О.Зарисским) поднял уровень строгости, и математической физики , где он занимался приложением теории групп к вопросам квантовой механики (наряду с Германом Вейлем и Ю.Вигнером ). Его классическая книга Современная алгебра (1930) стала образцом для последующих учебников по абстрактной алгебре и выдержала множество переизданий.
Ван дер Варден — один из крупнейших специалистов по истории математики и астрономии в Древнем мире. Его Пробуждающаяся наука (Ontwakende wetenschap 1950, русский перевод 1959) даёт развёрнутое изложение истории математики и астрономии в Древнем Египте, Вавилоне и Греции. В Приложении к русскому переводу этой книги опубликована статья «Пифагорейское учение о гармонии» (1943) — фундаментальное изложение пифагорейских взглядов на музыкальную гармонию .
Забиваем Сайты В ТОП КУВАЛДОЙ - Уникальные возможности от SeoHammer
Каждая ссылка анализируется по трем пакетам оценки: SEO, Трафик и SMM.
SeoHammer делает продвижение сайта прозрачным и простым занятием.
Ссылки, вечные ссылки, статьи, упоминания, пресс-релизы - используйте по максимуму потенциал SeoHammer для продвижения вашего сайта.
Что умеет делать SeoHammer
— Продвижение в один клик, интеллектуальный подбор запросов, покупка самых лучших ссылок с высокой степенью качества у лучших бирж ссылок.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз,
а первые результаты появляются уже в течение первых 7 дней.
Зарегистрироваться и Начать продвижение
Основные определения и теоремы
Предел функции в точке. Левые и правые пределы
Определение (предел по Коши, на языке 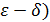 Число Число 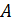 называется пределом функции называется пределом функции 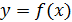 в точке в точке  , если , если 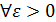 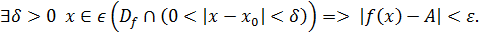
Определение (на языке окрестности) Число 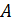 называется пределом функции называется пределом функции 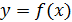 в точке в точке  , если для любой , если для любой 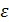 -окрестности числа -окрестности числа 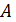 сущесвует сущесвует 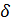 - окрестность точки - окрестность точки  такая, что как только такая, что как только 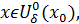 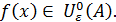
Определение (по Гейне) Число 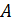 называется пределом функции называется пределом функции 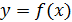 в точке в точке  , если для любой последовательности , если для любой последовательности 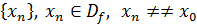 , сходящейся к , сходящейся к  ( то есть ( то есть 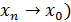 , соответствующая последовательность значений функции сходится к числу , соответствующая последовательность значений функции сходится к числу 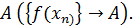
Определение Число 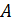 называется левым пределом функции называется левым пределом функции 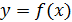 в точке в точке  , если , если 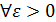 
Определение Число 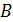 называется правым пределом функции называется правым пределом функции 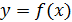 в точке в точке  , если , если 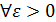 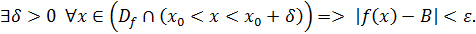
Теорема (необходимое и достаточное условие существования предела)
Для того чтобы в точке  существовал предел функции существовал предел функции 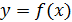 необходимо и достаточно, чтобы существовали левые и правые пределы равные между собой. необходимо и достаточно, чтобы существовали левые и правые пределы равные между собой.
Понятие производной. Односторонние производные.
Рассмотрим функцию 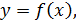 заданную на множестве заданную на множестве 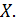
1. В озьмем 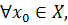 возьмем приращение возьмем приращение 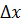 . Дадим точке . Дадим точке 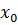 приращение приращение 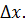 Получим Получим 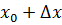 . .
2.
Вычислим значение функции в точках 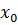 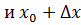 . . 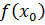 и и 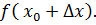
3. Найдем приращение функции в точке 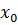 . .
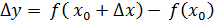
4. Составим отношение приращения функции в точке к приращению аргумента 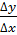 . .
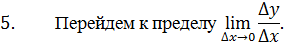
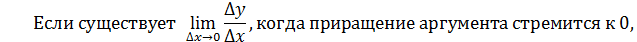
причем приращение аргумента может быть как положительным, так и отрицательным, то этот предел называется производной в точке  и обозначают и обозначают 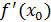 . Он может быть и бесконечным. . Он может быть и бесконечным.
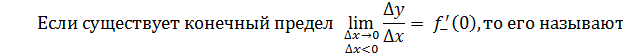
левой (левосторонней) производной функции 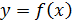 в точке в точке  , а если , а если
существует конечный предел 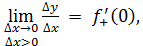 то его называют правосторонней производной функции то его называют правосторонней производной функции 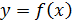 в точке в точке  . .
Функция 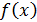 имеет в точке имеет в точке 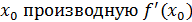 тогда и только тогда, когда в точке тогда и только тогда, когда в точке  совпадают ее левая и правая производные: совпадают ее левая и правая производные:
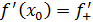 ( (
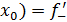 ( (
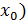 . .
Рассмотрим функцию 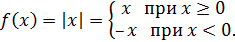 Найдем односторонние производные в точке Найдем односторонние производные в точке 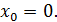
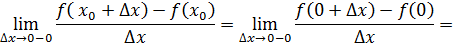
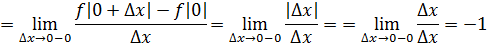
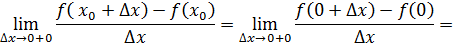
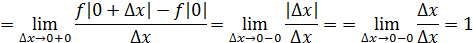
Следовательно, 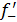 ( (
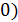 =-1; =-1;
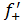 ( (
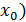 =1
и =1
и 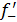 ( (
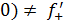 ( (
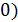 ,
то есть в точке ,
то есть в точке 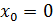 функция производной не имеет. функция производной не имеет.
Различные определения непрерывности функции в точке.
Определение 1 (основное) Функция 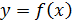 называется непрерывной в точке называется непрерывной в точке 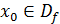 , если предел функции при , если предел функции при 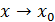 равен значению функции в этой точке. равен значению функции в этой точке.
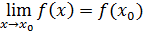
Определение 2 (на языке 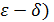 Функция Функция 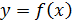 называется непрерывной в точке называется непрерывной в точке  , если , если 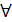 ε, ε, 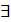 δ>0, такое что δ>0, такое что 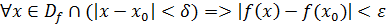 . .
Сервис онлайн-записи на собственном Telegram-боте
Попробуйте сервис онлайн-записи VisitTime на основе вашего собственного Telegram-бота:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно.
Зарегистрироваться в сервисе
Определение 3 (по Гейне, на языке последовательности) Функция 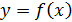 называется непрерывной в точке называется непрерывной в точке  , если для любой последовательности сходящейся к точке , если для любой последовательности сходящейся к точке  соответствующая последовательность значений функции сходится к соответствующая последовательность значений функции сходится к 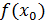 . .
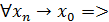 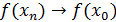
Определение 4 (на языке приращений) Функция 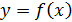 называется непрерывной в точке называется непрерывной в точке  , если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции. , если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Понятие дифференцируемой функции
Определение 1 Функция 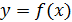 , заданная на множестве , заданная на множестве 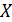 ( (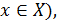 называется дифференцируемой в точке называется дифференцируемой в точке 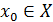 , если ее приращение в этой точке , если ее приращение в этой точке  можно представить как можно представить как 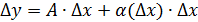 (*), где A - const , независящая от (*), где A - const , независящая от 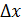 , , 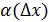 - бесконечно малая при - бесконечно малая при 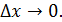
Определение 2 Функция, дифференцируемая в любой точке множества, называется дифференцируемой на множестве.
Связь между дифференцируемостью и непрерывностью
Теорема. Если функция дифференцируема в точке  , то она непрерывна в точке , то она непрерывна в точке  . .
Доказательство.
Пусть задана функция 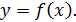 Функция дифференцируема в точке Функция дифференцируема в точке 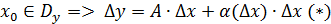 , где , где 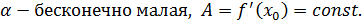
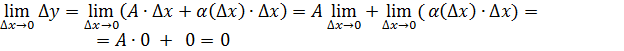
При 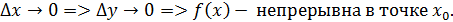
Обратная теорема. Если функция непрерывна, то она дифференцируема.
Обратная теорема неверна.
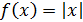 в в 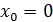 - не дифференцируема, хотя непрерывна. - не дифференцируема, хотя непрерывна.
Классификация точек разрыва
Определение Функция не являющаяся непрерывной в точке 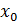 является разрывной в точке является разрывной в точке  , а саму точку , а саму точку  называют точкой разрыва. называют точкой разрыва.
Существуют две классификации точек разрыва: I и II рода.
Определение Точка  называется точкой разрыва I рода, если в этой точке существуют конечные односторонние пределы неравные друг другу. называется точкой разрыва I рода, если в этой точке существуют конечные односторонние пределы неравные друг другу.
Определение Точка 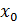 называется точкой устранимого разр ыва
, если называется точкой устранимого разр ыва
, если 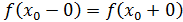 , но они не равны значению функции в точке , но они не равны значению функции в точке 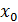 . . 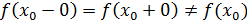
Определение Точка 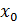 называется точкой разрыва II рода, если в этой точке односторонние пределы равны называется точкой разрыва II рода, если в этой точке односторонние пределы равны 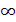 или один из односторонних пределов бесконечен или в точке или один из односторонних пределов бесконечен или в точке 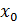 не существует предела. не существует предела.
·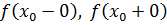 –
бесконечные; –
бесконечные;
·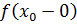 –
бесконечный или –
бесконечный или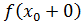 –
бесконечный; –
бесконечный;
·
Признаки равномерной сходимости рядо
в
Признак Вейерштрасса.
Если члены функционального ряда 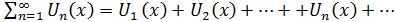 (1) удовлетворяют в области (1) удовлетворяют в области 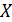 неравенствам неравенствам 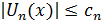 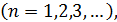 где где 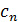 - член некоторого сходящегося числового ряда - член некоторого сходящегося числового ряда 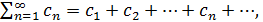 то ряд (1) сходится в то ряд (1) сходится в 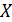 равнмерно. равнмерно.
Теорема 1 Пусть функции 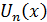 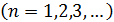 определены в промежутке определены в промежутке 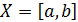 и все непрерывны в некоторой точке и все непрерывны в некоторой точке 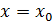 этого промежутка. Если ряд(1) в промежутке этого промежутка. Если ряд(1) в промежутке 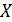 сходится равномерно, то и сумма ряда сходится равномерно, то и сумма ряда 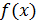 в точке в точке 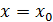 также будет непрерывна. также будет непрерывна.
Пример непрерывной функции без производной
Первый пример такого рода был построен Вейерштрассом; его функция определяется рядом:
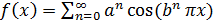 , ,
где 0< a <1, а b есть нечетное натуральное число (причем ab >1+ π). Этот ряд мажорируется сходящейся прогрессией π). Этот ряд мажорируется сходящейся прогрессией 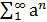 , следовательно (признаки равномерной сходимости рядов), сходится равномерно, и его сумма является всюду непрерывной функцией от x . Кропотливым исследованием Вейерштрассу удалось показать, что тем не менее ни в одной точке для нее не существует конечной производной. , следовательно (признаки равномерной сходимости рядов), сходится равномерно, и его сумма является всюду непрерывной функцией от x . Кропотливым исследованием Вейерштрассу удалось показать, что тем не менее ни в одной точке для нее не существует конечной производной.
Здесь будет рассмотрен более простой пример ван-дер-Вардена, построенный по существу на той же идее, лишь колеблющиеся кривые у= cosωχ заменены колеблющимися ломаными.
Итак, обозначим через 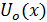 абсолютную величину разности между числом χ и ближайшим к нему целым числом. Эта функция будет линейной в каждом промежутке вида абсолютную величину разности между числом χ и ближайшим к нему целым числом. Эта функция будет линейной в каждом промежутке вида 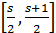 , где s -целое; она непрерывна и имеет период 1. Ее график представляет собой ломаную, он изображен на рис.1; отдельные звенья ломаной имеют угловой коэффициент ±1. , где s -целое; она непрерывна и имеет период 1. Ее график представляет собой ломаную, он изображен на рис.1; отдельные звенья ломаной имеют угловой коэффициент ±1.
 
Положим, затем, для к=1,2,3,…:
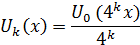
Эта функция будет линейной в промежутках вида 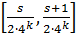 ; она также непрерывна и имеет период ; она также непрерывна и имеет период 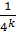 . Ее график также ломаная, но с более мелкими зубчиками; на рис.1(б), например, изображен график функции . Ее график также ломаная, но с более мелкими зубчиками; на рис.1(б), например, изображен график функции 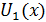 . Во всех случаях угловые коэффициенты отдельных звеньев ломаной и здесь равны ±1. . Во всех случаях угловые коэффициенты отдельных звеньев ломаной и здесь равны ±1.
Определим теперь, для всех вещественных значений x , функцию f ( x ) равенством
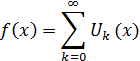
Так как, очевидно, 0≤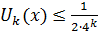 ( k =0,1,2,…), так что ряд мажорируется сходящейся прогрессией ( k =0,1,2,…), так что ряд мажорируется сходящейся прогрессией 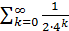 , то (как и в случае функции Вейерштрасса) ряд сходится равномерно, и функция , то (как и в случае функции Вейерштрасса) ряд сходится равномерно, и функция 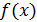 всюду непрерывна. всюду непрерывна.
Остановимся на любом значении 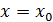 . Вычисляя его с точностью до . Вычисляя его с точностью до  (где n =0,1,2,…), по недостатку и по избытку, мы заключим его между числами вида: (где n =0,1,2,…), по недостатку и по избытку, мы заключим его между числами вида:
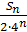 ≤ ≤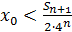 , где , где 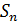 -целое. -целое.
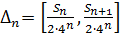 ( n =0,1,2,…). ( n =0,1,2,…).
Очевидно, что замкнутые промежутки оказываются вложенными один в другой. В каждом из них найдется такая точка 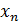 , что расстояние ее от точки , что расстояние ее от точки 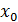 равно половине длины промежутка. равно половине длины промежутка.
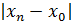 = =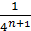 ; ;
Ясно, что с возрастанием n варианта 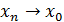 . .
Составим теперь отношение приращений
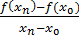 = =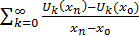
Но при k > n , число 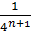 есть целое кратное периодам есть целое кратное периодам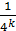 функции функции 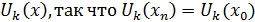 , соответствующие члены ряда обращаются в 0 и могут быть опущены. Если же k ≤ n , то функция , соответствующие члены ряда обращаются в 0 и могут быть опущены. Если же k ≤ n , то функция 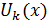 , линейная в промежутке , линейная в промежутке 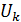 , будет линейной и в содержащемся на нем промежутке , будет линейной и в содержащемся на нем промежутке 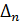 , причем , причем
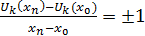 (k=0,1,…,n). (k=0,1,…,n).
Таким образом, имеем окончательно 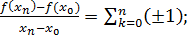 иными словами, это отношение равно четному целому числу при нечетном n и нечетному числу при четном n . Отсюда ясно, что при иными словами, это отношение равно четному целому числу при нечетном n и нечетному числу при четном n . Отсюда ясно, что при 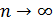 отношение приращений ни к какому конечному пределу стремится не может, так что наша функция при отношение приращений ни к какому конечному пределу стремится не может, так что наша функция при 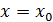 конечной производной не имеет. конечной производной не имеет.
Решение упражнений
Упражнение 1 ([2], №909)
Функция 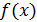 определена следующим образом: определена следующим образом: 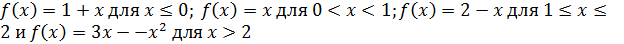 . Исследовать непрерывность . Исследовать непрерывность 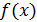 и выяснить существование и выяснить существование 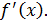
Решение
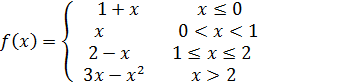
На 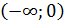 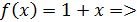 непрерывна как многочлен; непрерывна как многочлен;
На (0;1) 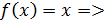 непрерывна как многочлен; непрерывна как многочлен;
На (1;2) 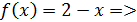 непрерывна как многочлен; непрерывна как многочлен;
На (2;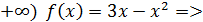 непрерывна как элементарная функция. непрерывна как элементарная функция.
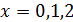 - точки подозрительные на разрыв - точки подозрительные на разрыв
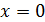
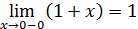
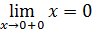
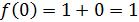
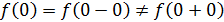
Так как левый предел равен значению функции в точке, то функция разрывна в точке 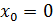 . .
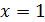
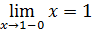
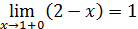
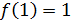
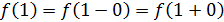
Так как левый предел равен правому пределу и равен значению функции в точке 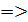 функция непрерывна в точке функция непрерывна в точке 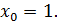
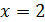
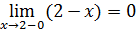
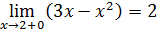
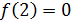
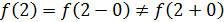
Так как левый предел равен значению функции в точке, то функция разрывна в точке 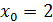 . .
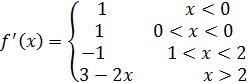
1 способ. В точке 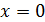 не существует конечной производной функции не существует конечной производной функции 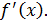 Действительно, предположим противное. Пусть в точке Действительно, предположим противное. Пусть в точке 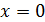 существует конечная производная функции существует конечная производная функции 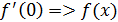 непрерывна в точке непрерывна в точке 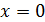 (по теореме 1: Если функция дифференцируема в точке (по теореме 1: Если функция дифференцируема в точке 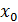 , то она непрерывна. , то она непрерывна.
2 способ. Найдем односторонние пределы функции 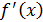 в точке x =0. в точке x =0.
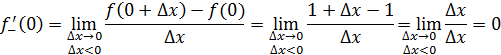
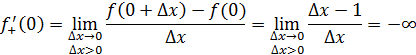
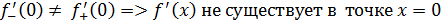
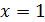
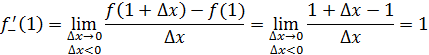
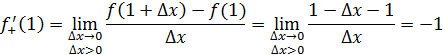
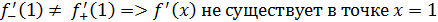
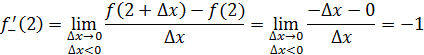
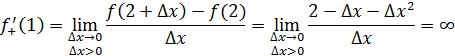
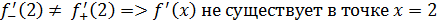
Упражнение 2
([1], №991)
Показать, что функция 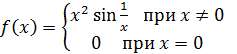 имеет разрывную производную. имеет разрывную производную.
Решение.
Найдем производную функции.
При 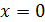
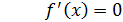
При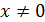
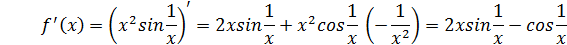
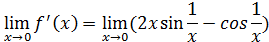
Предел 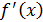 не существует не существует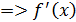 разрывна в точке разрывна в точке 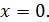
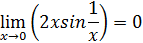
Так как 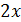 – бесконечно малая функция, – бесконечно малая функция, 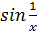 - ограниченная. - ограниченная.
Докажем, что функция 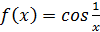 в точке в точке 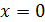 предела не имеет. предела не имеет.
Для доказательства достаточно показать, что существуют две последовательности значений аргумента сходящиеся к 0, что 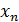 не сходится к не сходится к 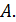
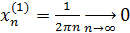
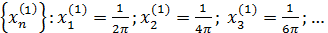
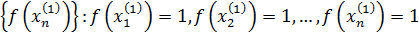
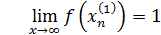
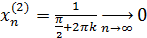
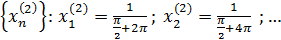
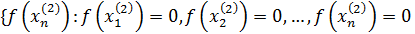
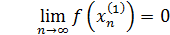
Вывод: функция 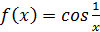 в точке в точке 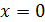 предела не имеет. предела не имеет.
Упражнение 3 ([1], №995)
Показать, что функция 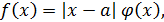 где где 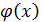 - непрерывная функция и - непрерывная функция и 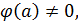 не имеет производной в точке не имеет производной в точке 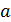 . Чему равны односторонние производные . Чему равны односторонние производные 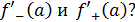
Решение.
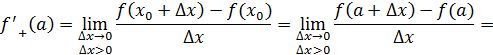
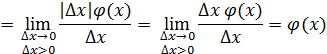
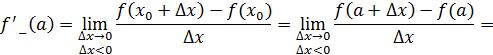
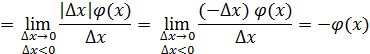
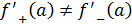
Односторонние пределы не равны 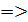 функция функция 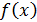 не имеет производной в точке не имеет производной в точке 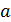 . .
Упражнение 4 ([1], №996)
Построить пример непрерывной функции, не имеющей производной функции в данных точках: 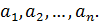
Решение.
Рассмотрим функцию 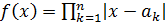 в точках в точках 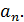
Найдем односторонние пределы 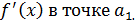
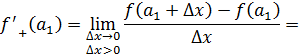
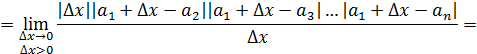
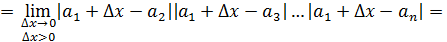
=
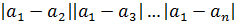
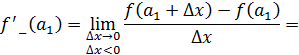
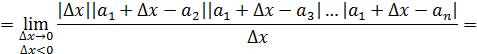
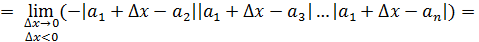
=
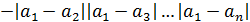
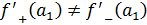
Односторонние пределы не равны 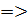 функция функция 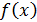 не имеет производной в точке не имеет производной в точке 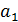 . Аналогично, функция не имеет производных в остальных точках . Аналогично, функция не имеет производных в остальных точках 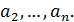
Упражнение 5 ([4], №125)
Показать, что функция 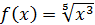 не имеет производной в точке не имеет производной в точке 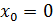 . .
Решение
Возьмем приращение 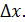 Дадим точке Дадим точке 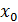 приращение приращение 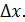 Получим Получим 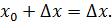
Найдем значение функции в точках 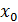 и и 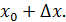
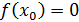
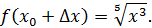
Найдем приращение функции в точке 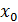
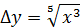
Составим отношение приращения функции в точке к приращению аргумента
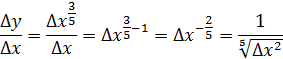
Перейдем к пределу
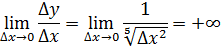
Вывод: не имеет конечной производной в точке 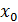 . .
Упражнение 6
([4], №128)
Показать, что функция 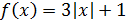 не имеет производной в точке не имеет производной в точке 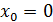 . .
Решение
Возьмем приращение 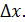 Дадим точке Дадим точке 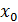 приращение приращение 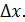 Получим Получим 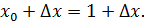
Найдем значение функции в точках 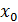 и и 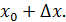
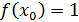
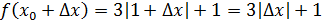
Найдем приращение функции в точке 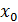
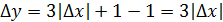
Составим отношение приращения функции в точке к приращению аргумента
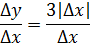
Перейдем к пределу
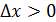
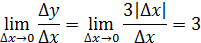
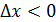

Вывод: не имеет конечной производной в точке 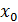 . .
Упражнение 7
([4], №131)
Исследовать функцию на непрерывность
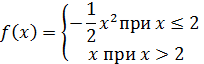
Решение.
На 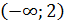 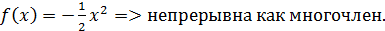
На 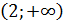 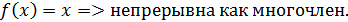
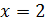 – точка подозрительная на разрыв – точка подозрительная на разрыв
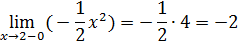
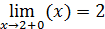
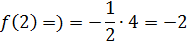
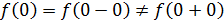
Так как левый предел равен значению функции в точке, то функция непрерывна  в точке в точке 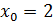 существует разрыв I рода. существует разрыв I рода.
В курсовой работе излагается материал, связанный с понятием « Непрерывная, но не дифференцируемая функции », цели данной работы достигнуты, задачи решены.
1. Б. П. Демидович, / Сборник задач по курсу математического анализа. Учебное пособие для студентов физико-математического факультета педагогических институтов. – М.: Просвещение, 1990 –624с.
2. Г. Н. Берман, / Сборник задач по курсу математического анализа. – М.: Наука, 1977 – 416с.
3. Г. М. Фихтенгольц, / Курс дифференциального и интегрального исчисления т.II. - М., Наука, 1970- 800с.
4. И.А. Виноградова, /Задачи и упражнения по математическому анализу ч.1. – М.:Дрофа,2001 – 725с.
5. Ресурс Интернет \ http://ru.wikipedia.org/wiki.
6. Ресурс Интернет \http://www.mathelp.spb.ru/ma.htm.
|