Министерство Образования и Науки Украины
Харьковский национальный университет имени Н.Н. Зильберта
А.А. Тензор, В.В. Невязкин
Нелинейная теория функции Зильберта
в частных производных
ТОМ 2
Харьков 2007
XFVBGD4567
ВДОПШ26986
Издание второе
Предназначено для студентов старших курсов
© 2007 А.А. Тензор, В.В. Невязкин кафедра теории функции Зильберта
ОГЛАВЛЕНИЕ
:
Дифференциальная геометрия 4
Теория вероятности 5
Теоретическая механика 5
Функциональный анализ 6
| Уравнения математической физики |
7 |
| Численные методы |
8 |
| Задачи |
9 |
| Список использованной литературы |
11 |
 Методы оптимизации и теория управления 7 Методы оптимизации и теория управления 7
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
Определение
.
Кривая называется кривой
, если она кривая.
Определение
.
Кривая называется очень кривой
, если она очень кривая.
Теорема
Рассмотрим кривую кривую.
∞
Она измерима по Зильберту ⇔ её радиус кривизны → . .
8 Следствие
.
Прямая измерима по Зильберту. Её мера равна её длине.
Доказательство (теоремы)
.
Достаточность
. Рассмотрим такую кривую γ , радиус кривизны которой R
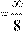 . Значит, . Значит,
кривизна γ :
 1 8 1 k
= = = ⋅ 8 = 0 8 ⋅ = 0. 1 8 1 k
= = = ⋅ 8 = 0 8 ⋅ = 0.
R
∞ ∞
Следовательно, γ – прямая.
Необходимость
. Поскольку кривизна прямой равна k
=0, мы можем записать:
1 ∞
 k
= 0 = 0·8 ⇒ R
= = . k
= 0 = 0·8 ⇒ R
= = .
k
8
Теорема доказана условно.
ТЕОРИЯ ВЕРОЯТНОСТИ
В теории функции Зильберта существует сходимость “да нет, наверное”, а именно:
Определение
.
Последовательность { } сходится “да нет, наверное
” к числу ξ ∈ Z
(пространство Зильберта): ξ k
⎯⎯→ НЕТ
⎯ !
ξ ⇔ когда она не сходится к этому числу. сходится “да нет, наверное
” к числу ξ ∈ Z
(пространство Зильберта): ξ k
⎯⎯→ НЕТ
⎯ !
ξ ⇔ когда она не сходится к этому числу.
Определение
.
Писдерсией
π D x
[ ] называется величина, матьожидание которой равно 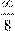 . .
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
В случае, когда все связи идеальные и стационарные,
 ∂ q
k
верно, что = 0, что значительно упрощает все формулы и ∂ q
j ∂ q
k
верно, что = 0, что значительно упрощает все формулы и ∂ q
j
теоремы из этого курса!
Окончательный результат:
Если в формуле вместо y
подставить y
, то формула останется верной для ∀ y
.
Этот факт даётся без доказательства.
ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ
Определение
.
Если последовательность имеет предел, который её удовлетворяет, то последовательность остаётся довольной
.
Теорема
.
Если последовательность имеет предел, то и предел её тоже имеет.
(Доказательство было приведено в курсе дифференциальных уравнений)
Реклама

– А что говорит Хвилиппов?
– Хвилиппов молчит!
Аксиома
.
Если ты разговаривал с Хвилипповым, то ты – Литрович, а если Хвилиппов тебе отвечал, – это алкоголизм!
Теорема
.
Если в обеих частях неравенства стоит одно и то же, то это равенство!
Доказательство
.
Необходимость
. Обозначим через α что-то, что стоит в обеих частях неравенства:
α > α .
Положим на α и заменим его на неотрицательную константу Ц:
Ц>Ц ≥ 0.
Константы сокращаются, и мы получаем верное равенство:
0 > 0 ⇒ 0 = 0 .
Что и требовалось доказать.
Достаточность
. Доказать самостоятельно или при помощи водки
 . .
 почувствуй вкус диffуров. почувствуй вкус диffуров.
МЕТОДЫ ОПТИМИЗАЦИИ и ТЕОРИЯ УПРАВЛЕНИЯ
Минус первая и минус вторая производные
Определение
.
Минус первой производной функции f
называется такая величина: − f
' .
Определение
.
Минус вторая производная функции f
: − f
′′ .
Рассмотрим функционал
ы
ЖЫ
( y
) = ∫ ( f
'( y y y
, ', *) − f y y y
( , ', *) ) dx
→ inf (*)
ж
Замечание.
Из курса русского языка известно:
«ЖИ–ШИ пишется с И»
,
но в данном случае «Ы»
– это оператор!
Оператор «Ы»
Определение
.
Оператором «Ы»
называется дифференциальный оператор, который функции Ж
ставит в соответствие интеграл (*).
УРАВНЕНИЯ МАТ. ФИЗИКИ
Задача.
Найти функцию Грея для системы:
⎧ ∞
⎪Δ u
=  8 , x
5
= 0, 8 , x
5
= 0,
⎪
⎨ 0, x
6
= 0,
⎪
u
= З
( x y z
, , ), x
i
≥ 0.
⎪
⎩
Подсказка.
Если x y
, ∈ M
решать эту задачу, нужно извлечь корешок из u
, x
, y
и z
. З
( x,y,z
) – функция Зильберта.
ЧИСЛЕННЫЕ МЕТОДЫ
Теорема
Если вам лень делать оценку по Рунге, позовите Рунге, и он сам её сделает!
Проверить самостоятельно.
Определение
. Обратным элементом к бесконечности ∞ явля-
 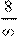 ∞ ∞
ется конечность
, а обратным к  является . является .
8
Точные значения этих величин даёт метод подгонки под ответ с двойным пересчётом.
Лабораторная работа №13
Вычисление сингулярных интегралов методом подгонки под ответ
Вычислить сингулярный интеграл
b
f x
( )  b
− a b
− a
I z
( ) = ∫
a
 x
− z dx
; z
j
= + a jh
0
; j
= 1, n
0
− 1; h
0
= x
− z dx
; z
j
= + a jh
0
; j
= 1, n
0
− 1; h
0
=  n
0 . n
0 .
с заданной точностью ε = 10 −
24
на отрезке [1;1.05] с помощью метода подгонки под ответ с двойным пересчётом. Для этого потребуется методичка с ответами и дискета с готовой программой.
На печать вывести N
, π , количество итераций и невязку в виде таблицы:
| N
|
π |
количество
итераций
k
|
невязка R
|
ЗАДАЧИ
1. Вычислить ё.
d e
2
Реклама

Решение: ё
=  2
= 0, т.к. e
≈ 2,7 = const
и от t
не зависит, а 2
= 0, т.к. e
≈ 2,7 = const
и от t
не зависит, а
dt
производная от константы равна 0. Ответ: ё
=0.
dx
2. Вычислить интеграл ∫
 dx
. dx
.
dx
1 dx
1
 Решение: ∫
dx
= d
∫
x
= d
ln | x
| + C
. Решение: ∫
dx
= d
∫
x
= d
ln | x
| + C
.
3. Построить треугольник, у которого все углы равны 0 0
. Решение:
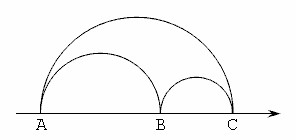
Рис. 1. Треугольник с тремя нулевыми углами
В пространстве Лобачевского (в верхней полуплоскости) такой треугольник имеет 3 угла по 0 0
.
4. Вопрос: метод Зильберта решения СЛАУ точный или приближённый? (Ответ – невязка мнимая, так что этот метод даёт результат точнее, чем есть искомая величина)
5. Найти минус третью производную функции f x
( ) = x
3
.
Решение: Минус третья производная: − f
′′′ ( ) x
= − ( x
3
) ′′′ = − 6 .
Ответ: –6.
6*. Построить конформное отображение из области «ВАСЯ» на правую полуплоскость (левую полу-ёлку):
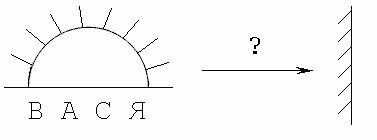
СПИС
ОК ИСПОЛЬ
ЗОВА ННОЙ
ЛИТЕ
РА ТУРЫ
:
1. Хвилиппов А. У. «Сборник задач по диффурам»
2. конспекты студентов мех-мата по:
- дифф. геометрии,
- матанализу,
- диффурам,
- теормеху,
- функану,
- теорверу,
- комплану,
- методам оптимизации, - численным методам.
Также здесь фигурируют фразы и выражения некоторых преподавателей с мех-мата, кто знает, тот поймёт.
Тираж 40 экземпляров.
Отпечатано на ксероксе в коридоре на 6-м этаже ХНУ им. В. Н.
Каразина.
Цена ксерокопии 20 коп.
|