ГОУ ВПО «Сургутский государственный университет
Ханты-Мансийского автономного округа — Югры»

Кафедра прикладной математики
Курсовая работа по предмету «Численные методы» на тему
Расчёт распространения тепла вдоль многослойного цилиндра
Выполнил студент группы 11 – 71
факультета Информационных технологий
Илинбаев Николай Геннадьевич
Проверил к.ф.-м.н., доцент кафедры ПМ
Моргун Дмитрий Алексеевич
« »

Сургут — 2010
Содержание
1 Введение
К уравнениям в частных производных приводят задачи газодинамики, теплопроводности, переноса излучения, распротранения нейтронов, теории упругости, электромагнитных полей, процессов переноса в газах, квантовой механики и многие другие.
Уравнения математической физики используются для расчётов распространения тепла, концентрации, волн. Для просмотра изменений температуры в различных точках заданной области применимы формулы теплопроводности. В данной работе рассматривается однородное уравнение теплопроводности и его решение интегро-интерполяционным методом.
Интегро-интерполяционный метод особенно полезен для уравнений с негладкими или разрывными коэффициентами, поскольку именно интегральная запись законов сохранения выделяет из всех математически допустимых решений таких уравнений физически правильное обобщённое решение.
2 Решение задачи
2.1 Интегро-интерполяционный метод
Интегро-интерполяционный метод, один из вариантов которого называется методом баланса
, наиболее надёжен и применим во всех случаях. В этом методе после выбора шаблона область G(r,t) разбивают на ячейки, определённым образом связанные с шаблоном. Дифференциальное уравнение интегрируют по ячейке и по формулам векторного анализа приводят к интегральной форме, соответствующей физическому закону сохранения. Приближенно вычисляя полученные интегралы по каким-либо квадратурным формулам, составляют разностную схему.
Например, для установления теплопроводности с переменным коэфициентом u t
= ( ku x
) x
выберем шаблон и сопосавим ему ячейку. Обозначая средние точки интервалов сетки полуцелыми индексами, выполним интегрирование по ячееке:
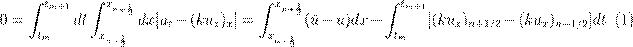
Это соотношение является точным. В правой части приближенно вычислим первый интеграл по формуле правых прямоугольников. Получим следущиее выражение:
Реклама

( y
ˆ n
− y
n
)( x
n
+1 /
2 − x
n
−1 /
2 ) = τ
[( k
ˆ y
ˆ x
) n
+1 /
2 − ( k
ˆ y
ˆ x
) n
−1 /
2 ] (2)
Заменяя в правой части производные разностями и учитывая, что на равномерной сетке x n
+1 /
2
− x n
−1 /
2
= h
, получим разностную схему
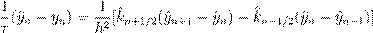 (3) (3)
Если k
= const
, то схема совпадает с неявной схемой.
Интегро-интерполяционный метод особенно полезен для уравнений с негладкими или разрывными коэффициентами, поскольку именно интегральная запись законов сохранения выделяет из всех математически допустимых решений таких уравнений физически правильное обобщённое решение.
3 Тестовые расчеты
Решим тестовую задачу. Зададим начальные значения: начальная температура по всему цилиндру = 1; температура на левом конце стержня = 10; температура на правом конце стержня = 15; коэфициенты теплопроводности K1=7, K2=35, K3=7.
Тогда расчеты изменений температуры дадут следущие результаты. Полученные графики:
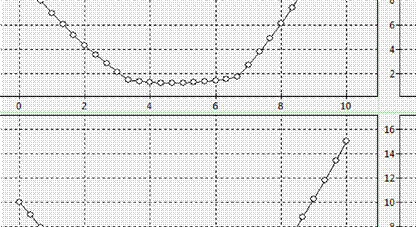
Рис.1. График распределения температуры при t
1
.
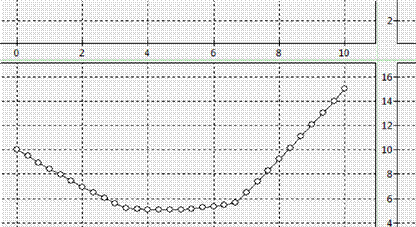
Рис.2. График распределения температуры при t
2
.
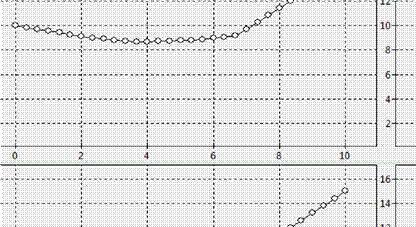
Рис.3. График распределения температуры при t
3
.
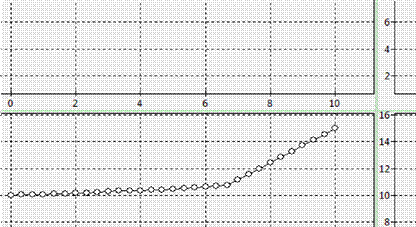
Рис.4. График распределения температуры при t
4
.
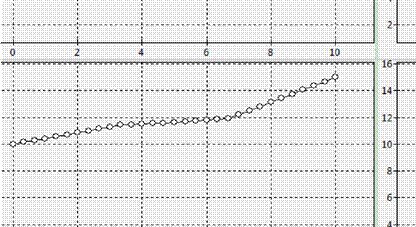
Рис.5. График распределения температуры при t
5
.
Из графиков видно, что температура плавно возрастает от краёв цилиндра к его середине.
4 Заключение
Поставленная задача на расчёт распространения тепла вдоль многослойного цилиндра успешно завершена. Начальные данные для решаемой задачи: температура на левом конце цилиндра, температура на правом конце цилиндра, коэфициенты теплопроводности на разных участках цилиндра. При вводе начальных данных в задачу просматриваются изменения температуры, продвигающиеся от концов цилиндра к его середине.
5 Литература
Список литературы
1. Калиткин Н. Н. Численные методы. М: Наука, 1978.
6 Приложение
Код программы: [1]
unit part1; {$mode objfpc}{$H+} interface
uses
Classes, SysUtils, FileUtil, LResources, Forms, Controls, Graphics, Dialogs,
Buttons, ExtCtrls, Menus, StdCtrls, ComCtrls, Arrow, CheckLst, ActnList,
TAGraph, TASeries; type
{ TForm1 }
TForm1 = class(TForm)
K1Edit: TLabeledEdit;
K2Edit: TLabeledEdit;
K3Edit: TLabeledEdit; Uslovie: TBitBtn;
BtStart1: TBitBtn;
BtClose: TBitBtn;
Chart1: TChart;
Chart1LineSeries1: TLineSeries;
Label1: TLabel;
Label2: TLabel;
Label3: TLabel;
Label4: TLabel;
Label5: TLabel;
Label6: TLabel;
Label7: TLabel;
Label8: TLabel;
RightTemp: TLabeledEdit;
Реклама

LeftTemp: TLabeledEdit;
Menu1: TMainMenu;
MenuItem1: TMenuItem;
MenuItem2: TMenuItem;
MenuItem3: TMenuItem; MenuItem4: TMenuItem; redaktor: TNotebook;
Page1: TPage;
Page2: TPage;
GoY: TUpDown;
GoX: TUpDown;
MashtabY: TUpDown; MashtabX: TUpDown; procedure stopClick(Sender: TObject); procedure UslovieClick(Sender: TObject); procedure BtStart1Click(Sender: TObject); procedure FormActivate(Sender: TObject); procedure MenuItem3Click(Sender: TObject); procedure MenuItem4Click(Sender: TObject); procedure GoYClick(Sender: TObject; Button: TUDBtnType); procedure GoXClick(Sender: TObject; Button: TUDBtnType); procedure MashtabYClick(Sender: TObject; Button: TUDBtnType); procedure MashtabXClick(Sender: TObject; Button: TUDBtnType); procedure VremenaTimer(Sender: TObject);
private
{ private declarations } public
{ public declarations } end;
const n=31; n1=10;//n1-номер узла до которого сохраняется K1.
Aconst=0; Bconst=10; type mass=array[1..n] of double; var
Form1: TForm1;
stepY,Ymin,Ymax,stepX,Xmin,Xmax,w1,w2:double;
Khigh,Lupa:double;
T1,T2,T4,T3:boolean;
{-----------------------------------------------------------------} K,X,XU,B,Aew,Ap,U:mass; shag,dt:double; j:integer;
K1const,K2const,K3const:double; implementation procedure Delay(millisecond: integer); begin sleep(millisecond);
Form1.chart1.repaint; end;
function fun1(Afun1:double):double; begin fun1:=1; end;
procedure ProcedureInit; var i:integer; begin shag:=(Bconst-Aconst)/(n-1); for i:=1 to n do
begin
X[i]:=Aconst+shag*(i-1); B[i]:=fun1(X[i]); end;
for i:=1 to n-1 do
begin
XU[i]:=(X[i]+X[i+1])/2;
if i>2*n1 then K[i]:=K3const else if i>n1 then K[i]:=K2const else K[i]:=K1const;
Aew[i]:=K[i]/shag/shag; end;
end;
procedure TForm1.BtStart1Click(Sender: TObject); var i,ii:integer; begin dt:=0.1;//(j*dt)-дельта-тэ для времени for ii:=1 to 50 do begin
delay(50);
Chart1LineSeries1.Clear; for i:=2 to n-1 do
begin
Ap[i]:=1/(j*dt)+Aew[i-1]+Aew[i]; end;
Chart1LineSeries1.AddXY(X[1],B[1]); for i:=2 to n-1 do begin
U[i]:=(B[i+1]*Aew[i]+B[i-1]*Aew[i-1]+B[i]/(j*dt))/Ap[i]; Chart1LineSeries1.AddXY(X[i],U[i]); end;
Chart1LineSeries1.AddXY(X[n],B[n]); for i:=2 to n-1 do
begin B[i]:=U[i]; end; inc(j); end; end;
procedure TForm1.UslovieClick(Sender: TObject); begin
Chart1LineSeries1.Clear;
K1const:=StrToInt(K1Edit.text);
K2const:=StrToInt(K2Edit.text);
K3const:=StrToInt(K3Edit.text);
ProcedureInit;
B[1]:=StrToInt(LeftTemp.text); B[n]:=StrToInt(RightTemp.text); j:=1;
Form1.BtStart1.enabled:=true; end;
procedure TForm1.stopClick(Sender: TObject); begin end;
procedure TForm1.FormActivate(Sender: TObject); begin
Khigh:=20;stepX:=2;stepY:=2;Lupa:=1;//все коэффициенты chart1.Extent.Xmax:=chart1.Extent.Xmax+Khigh; Chart1.Extent.useXmax:=true;
chart1.Extent.Ymax:=chart1.Extent.Ymax+Khigh; Chart1.Extent.useYmax:=true;
chart1.Extent.Xmin:=chart1.Extent.Xmin-1; Chart1.Extent.useXmin:=true; chart1.Extent.Ymin:=chart1.Extent.Ymin-1;
Chart1.Extent.useYmin:=true; end;
procedure TForm1.MenuItem3Click(Sender: TObject); begin close;
end;
procedure TForm1.MenuItem4Click(Sender: TObject); begin showmessage (’Сделал Илинбаев Н. Г., группа 1171, подгруппа А ’)
end;
procedure TForm1.GoYClick(Sender: TObject; Button: TUDBtnType); begin
stepY:=2; case button of
btNext: begin chart1.Extent.Ymax:=chart1.Extent.Ymax+stepX; Chart1.Extent.useYmax:=true;
chart1.Extent.Ymin:=chart1.Extent.Ymin+stepX;
Chart1.Extent.useYmin:=true;
end; btPrev: begin chart1.Extent.Ymax:=chart1.Extent.Ymax-stepX; Chart1.Extent.useYmax:=true;
chart1.Extent.Ymin:=chart1.Extent.Ymin-stepX;
Chart1.Extent.useYmin:=true; end; end;
end;
procedure TForm1.GoXClick(Sender: TObject; Button: TUDBtnType); begin
case button of
btNext: begin chart1.Extent.Xmax:=chart1.Extent.Xmax+stepX; Chart1.Extent.useXmax:=true;
chart1.Extent.Xmin:=chart1.Extent.Xmin+stepX;
Chart1.Extent.useXmin:=true;
end; btPrev: begin chart1.Extent.Xmax:=chart1.Extent.Xmax-stepX; Chart1.Extent.useXmax:=true;
chart1.Extent.Xmin:=chart1.Extent.Xmin-stepX;
Chart1.Extent.useXmin:=true; end; end;
end;
procedure TForm1.MashtabYClick(Sender: TObject; Button: TUDBtnType); begin
case button of
btPrev: begin chart1.Extent.Ymax:=chart1.Extent.Ymax+Lupa; Chart1.Extent.useYmax:=true;
chart1.Extent.Ymin:=chart1.Extent.Ymin-Lupa;
Chart1.Extent.useYmin:=true;
end;
btNext: begin
chart1.Extent.Ymax:=chart1.Extent.Ymax-Lupa; Chart1.Extent.useYmax:=true;
chart1.Extent.Ymin:=chart1.Extent.Ymin+Lupa;
Chart1.Extent.useYmin:=true; end; end;
end;
procedure TForm1.MashtabXClick(Sender: TObject; Button: TUDBtnType); begin
case button of
btPrev: begin chart1.Extent.Xmax:=chart1.Extent.Xmax+Lupa; Chart1.Extent.useXmax:=true;
chart1.Extent.Xmin:=chart1.Extent.Xmin-Lupa;
Chart1.Extent.useXmin:=true;
end; btNext: begin chart1.Extent.Xmax:=chart1.Extent.Xmax-Lupa; Chart1.Extent.useXmax:=true;
chart1.Extent.Xmin:=chart1.Extent.Xmin+Lupa;
Chart1.Extent.useXmin:=true; end; end;
end;
procedure TForm1.VremenaTimer(Sender: TObject); begin end;
initialization
{$I part1.lrs} end.
[1]
Код программы, реализующей решение расчёт распределения тепла вдоль многослойного цилиндра
|