Министерство образования Республики Беларусь
Министерство образования и науки
Российской Федерации
Государственное учреждение высшего
профессионального образования
«Белорусско-Российский университет»
Кафедра « Экономики»
КОНТРОЛЬНАЯ РАБОТА
по дисциплине «Планирование и прогнозирование
экономики»
студентки 3 курса экономического факультета
заочного отделения группы КДЗ-072
Картузовой Натальи Ивановны
Шифр 070921
Вариант 21
Могилев 2010 г.
СОДЕРЖАНИЕ
1 Использование экономико-математического программирования в макроэкономическом прогнозировании………………………………….. 3
2 Прогнозирование уровня инфляции в стране……………………. 8
3 Задача………………………………………………………………. 11
Список использованных источников………………………………. 12
1 Использование экономико-математического программирования в макроэкономическом прогнозировании.
Идея оптимизации составляет одно из отличий подхода экономиста к анализу хозяйственной деятельности и решению экономических проблем. Программирование занимается решением задач по нахождению оптимальности. Поэтому оно хорошо подходит для анализа рационального поведения. В анализе оптимальности существует множество возможных величин, характеризующих результаты деятельности фирмы или экономики в целом. Программирование является исключительно математическим методом и не имеет никакого экономического содержания. Это означает, что результаты, полученные с помощью программирования, сами по себе ничего не говорят о деятельности хозяйствующих субъектов. Оно может только помочь оценить экономическую информацию, которую получили или готовы получить.
Преимущества программирования
:
· Обеспечивает логически согласованную последовательность различных предпосылок;
· Позволяет использовать различные виды информации;
· Решает задачи большой размерности, учитывающие огромные объемы информации, различного типа ограничения и обеспечивающие реализацию многих альтернатив;
· Решает задачи с известной степенью точности;
· Могут систематически изучаться;
· Позволяют пояснить многие проблемы, связанные с разграничением задач и мерой ответственности между экспертами и политиками.
Использование экономико-математических методов предполагает формализованное описание экономического процесса и следующие этапы построения модели:
Реклама

1. формулируется предмет и цели исследования;
2. в экономической системе выделяются структурные или функциональные элементы, соответствующие данной цели, выявляются наиболее важные качественные характеристики этих элементов;
3. словесно, качественно описываются взаимосвязи между элементами модели;
4. вводятся символические обозначения для учитываемых характеристик экономического объекта и формализуются взаимосвязи между ними. Тем самым формулируется математическая модель;
5. проводятся расчеты математической модели и анализируются полученные решения.
Целевая функция
описывает цель оптимизации и представляет собой зависимость показателей, по которым ведется оптимизация, от независимых переменных. Влияние каждой из переменных на величину целевой функции выражается коэффициентом – значением показателя, экстремум которого используется в качестве критерия оптимальности.
Система ограничений
отражает объективные экономические связи и зависимости в виде системы равенств и неравенств.
В экономико-математическом анализе используется широкий спектр математических методов. Наиболее простым является метод линейного программирования
– направление математики, изучающее методы решения задач на экстремальные значения, которые характеризуются линейной зависимостью между переменными (неизвестными величинами) и линейным критерием. Необходимым условием постановки задачи является: 1) ограничение на ресурсы; 2) выбор количественно оцениваемого критерия оптимального плана.
Показатель, по которому оценивается мера эффективности плана, его оптимальность, называется критерием оптимальности. Критерий оптимальности должен удовлетворять следующим требованиям: 1) быть единственным, 2) количественно определяться, 3) находиться в линейной зависимости.
В общем виде задача линейного программирования выглядит следующим образом:
целевая функция: F ( X ) = c 1
x 1
+ c 2
x 2
+ …. c n
x n
max ;
условия ограничения в виде равенств или неравенств:
a 11
x 1
+ a 12
x 2
+ … a 1
n
x n
= b 1
a 21
x 2
+a 22
x 2
+ … a 2n
x n
= b 2
условие неотрицательности: х 1
> 0, x 2
>0 … x n
> 0.
Условие неотрицательности для экономического анализа имеет важное значение, так как свидетельствует о реальности протекаемого процесса.
В задачах линейного программирования исходные данные обычно определяются неточно. Поэтому важную роль играют методы стохастического линейного программирования, рассматривающего задачи, целевая функция и ограничения которых могут содержать случайные параметры.
Реклама

НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
применяется в силу того, что в экономике существует большое количество нелинейных зависимостей. В этом случае целевая функция или условия ограничения становятся нелинейными относительно искомых переменных. Переменные входят в уравнения не в первой, а во второй или более высокой степени, перемножаются или делятся друг на друга. Данная форма программирования применяется в тех случаях, когда эффективность возрастает или убывает непропорционально изменению масштабов производства.
В общем виде задача нелинейного программирования может быть записана:
1) целевая функция F ( X ) = 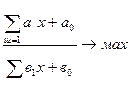
2) условия ограничения 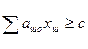
3) условие неотрицательности: х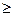 0; 0;
Могут быть различные комбинации целевой функции и условий ограничения с точки зрения сочетания линейности и нелинейности.
В числе методов нелинейного программирования можно выделить квадратичное и выпуклое программирование. Выпуклое программирование
представляет собой совокупность специальных методов решения, у которых выпуклы либо целевые функции, либо условия ограничения. Выпуклой считается область, если прямая, соединяющая две точки этой области, лежит полностью внутри данной области. Целью решения такой задачи является отыскание такого множества переменных, которое обеспечивает минимум выпуклой функции или максимум вогнутой. (Используется метод Лагранжа, матричные модели).
Квадратичное программирование
– совокупность методов решения особого рода экстремальных задач, в которых условия ограничения линейны, а целевая функция является многочленом второй степени. Для решения такого типа задач могут применяться методы решения общей задачи выпуклого программирования.
ЦЕЛОЧИСЛЕННОЕ ПРОГРАММИРОВАНИЕ
применяется в тех случаях, когда переменные принимают целочисленные значения (0,1,2 …). Простое округление результатов при расчетах может привести к значительным плановым ошибкам. Поэтому задачи целочисленного программирования требуют специальных методов решения. Различают задачи:
а) дискретного программирования.
В этом случае вводится искусственная переменная R и условия задачи принимают вид:
целевая функция P = ax + by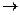 max ; max ;
ограничения x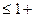 R ; y R ; y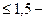 R /2; R R /2; R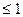
условия неотрицательности x 0; y 0; R 0.
Решение заключается в максимизации первоначальной целевой функции путем перебора переменных x , y , R , которые расположены в искусственно выпуклой области.
б) целочисленного программирования с булевыми переменными
. Булевой переменной называют переменную, которая принимает значения 1 и 0. Использование таких переменных позволяет решать задачи о включении или не включении заданий в план.
Математическая модель имеет вид: целевая функция: 
Условия ограничения: 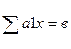 х = х =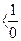 
ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ -
позволяет установить соотношение между экстремальными значениями целевой функции в задачах, характеризующихся различной продолжительностью процесса и различными начальными состояниями. При этом необходимо учитывать последствия найденного оптимального решения для последующих расчетов. Такой подход обуславливает выработку оптимальной стратегии. Процесс решения является многошаговым. Полученные на каждом этапе соотношения последовательно связаны между собой: полученные результаты вводятся в уравнения следующего шага. При решении вариантных задач они разбиваются на отдельные этапы, каждый из которых решается самостоятельно. Тем самым сложная задача со многими переменными сводится к многим задачам с малым числом переменных. Это значительно сокращает объем вычислений и ускоряет процесс принятия управленческих решений.
К недостаткам
следует отнести отсутствие единого универсального метода решения. Практически каждая задача, решаемая этим методом, характеризуется своими особенностями и трудностями и требует поиска наиболее приемлемой для ее решения методики. При поиске решения может оказаться, что процесс, рассматриваемый как многошаговый, имеет очень много состояний. В таком случае необходимо искать другие методы решения.
Динамическое программирование эффективно при определении оптимальной стратегии случайного (стохастического) процесса. Его протекание может быть различным в зависимости от случая, но вероятность каждого течения определена. Случайный процесс может быть непрерывным или дискретным. В рассматриваемом процессе независимой переменной является время, функция от независимой переменной – случайна. Случайный процесс характеризуется множеством значений его состояния. В зависимости от того, непрерывные или дискретные эти значения, случайный процесс будет непрерывным или дискретным.
При использовании динамического программирования необходимо:
· четко сформулировать задачу;
· сформировать целевую функцию и условия ограничения;
· подготовить исходную информацию по изучаемому процессу;
· определить альтернативные варианты развития процесса;
· выбрать оптимальный метод решения задачи;
· произвести расчеты;
· провести анализ и оценку полученных результатов.
Экономические процессы характеризуются большими совокупностями однородных объектов. Поэтому нет необходимости изучать каждый элемент совокупности. Объектом исследования является определенная выборка. Полученные характеристики такой выборки могут использоваться для сравнительной оценки элементов различных совокупностей или их характеристик, установления связей между отдельными величинами и прогнозирования на этой основе развития системы в будущем. Это предполагает использование статистических методов
в прогнозировании.
Математическая статистика включает корреляционный, регрессионный, дисперсионный, факторный анализ и т.д.
В экономике между различными явлениями могут быть две формы зависимости: функциональная и корреляционная. Функциональная
– зависимость, которая точно проявляется в каждом отдельном случае и подчинена принципу строго определенного соответствия между количественными признаками. Корреляционная
– зависимость между явлениями и показателями, которая проявляется только в среднем, в массе наблюдений.
Построение корреляционной модели
предполагает постановку задачи, сбор статистических данных. Эти данные набираются на основе первичных документов и отчетных данных. Некоторые показатели могут быть получены только после предварительной обработки полученной информации. При сборе данных необходимо определить количество выборочных наблюдений - выборочную совокупность.
После сбора данных осуществляется корреляционный анализ, состоящий из трех этапов: а) определяется форма связи исследуемых показателей (уравнение регрессии); б) проверяется теснота связи выбранных показателей, т.е. насколько полно выбраны факториальные признаки, как велико влияние неучтенных факторов; в) определяются численные значения постоянных коэффициентов уравнения.
Дисперсионный анализ
– метод проверки гипотезы с помощью критериев, основанных на вычислении дисперсии. Наибольшее применение он находит для проверки связи между различными признаками.
Факторный анализ
предполагает, что исследуемый процесс – многомерная случайная величина х = (х 1
… х n
), подчиняющаяся нормальному распределению.
В факторном анализе считается, что факторы, оказывающие влияние, надо определить; случайные величины независимы между собой. Наиболее перспективными направлениями факторного анализа является: сокращение числа экономических показателей, характеризующих какое-либо экономическое явление без существенной потери точности; получение обобщенных индексов; классификация экономических объектов, характеризующаяся набором независимых признаков; возможность построения и последующей статистической проверки гипотезы о сущности экономических явлений.
Цель
факторного анализа – отыскание таких комбинаций х 1
, …х n
, которые были бы как можно ближе к значению факторов f 1
,… f n
.
Обычно это двухстадийный процесс. Сначала оценивается факторная структура, т.е. необходимое число факторов для объяснения корреляции между переменными и нагрузки факторов на эти переменные. Затем – значения индивидуальных членов выборки для самих факторов. Важное место в содержательном факторном анализе занимает интерпретация факторов. Для оценки факторных нагрузок используют метод максимального правдоподобия, центроидный метод и т.д. При этом возможны различные предположения, например о некоррелированности факторов, о равенстве нулю какой-либо заранее выбранной факторной нагрузки и т.д.
2 Прогнозирование уровня инфляции в стране.
Термин "инфляция" (от лат. inflatio — вздутие) впервые стал употребляться в Северной Америке в период Гражданской войны 1861—1865 гг. и обозначал процесс разбухания бумажно-денежного обращения.
В самом общем виде инфляция представляет собой обесценение бумажных денег, т.е. переполнение сферы обращения бумажными деньгами, не обеспеченными товарами. Однако такое определение инфляции нельзя считать полным. Инфляция — это сложное социально-экономическое явление, порождаемое диспропорциями воспроизводства.
Под инфляцией следует понимать дисбаланс спроса и предложения, а также нарушение других пропорций национального хозяйства, проявляющееся в росте цен.
Проблема инфляции сложна и многогранна. Инфляционные процессы приводят к широкому спектру негативных последствий.
Социально-экономические последствия инфляции: обесценение и перераспределение доходов, материализация денежных средств, падение интереса к долгосрочным целям, обесценение денежных сбережений, уменьшение реальной процентной ставки и скрытая конфискация денежных средств.
Высокие темпы инфляции оказывают разрушительное воздействие на производство: подавляют стимулы к занятию производственной и инвестиционной деятельностью, нарушают стабильность денежной национальной единицы, дезорганизуют финансовую систему государства. Экономика, втянутая в инфляцию, особенно если процесс перерастает в галопирующую или гиперинфляцию, скатывается в полосу затяжного и глубокого экономического кризиса. Примером может служить ситуация, сложившаяся в Беларуси в 90-е годы.
Для выработки наиболее эффективных мер, способствующих снижению инфляции, необходимо выявлять причины, осуществлять прогнозирование инфляции и анализировать степень воздействия тех или иных мер на инфляционные процессы.
Прогнозированию инфляции в переходный период в странах СНГ стала придаваться особая значимость. В прогнозных расчетах заинтересованы правительство, хозяйствующие субъекты и население. Результаты прогнозов служат основой для разработки мер и принятия управленческих решений. Это обусловливает необходимость применения синтеза методов прогнозирования, позволяющих избежать серьезных ошибок в прогнозах.
Прогнозирование инфляции можно осуществлять на основе индексов потребительских цен:
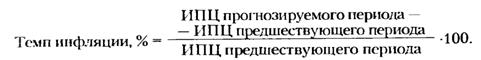
Однако для характеристики инфляции в условиях несбалансированной экономики только лишь индекса потребительских цен недостаточно. Необходимо учитывать скрытую инфляцию, или неудовлетворенный спрос. В этих условиях индекс инфляции ( J и
) можно рассчитать по формуле:
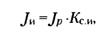
(1)
где J p
— индекс потребительских цен;
К с
— коэффициент скрытой инфляции, или неудовлетворенного спроса.
В свою очередь коэффициент скрытой инфляции может быть определен как
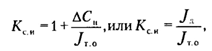
где С и — прирост неудовлетворенного спроса или вынужденных сбережений;
J д — индекс денежных доходов населения;
J т.о — индекс товарооборота и услуг.
Альтернативным .методом определения индекса инфляции является метод, основанный на использовании индексов расходов, доходов и цен:
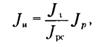
где J д — индекс доходов;
J рс — индекс расходов;
J р — индекс цен.
Этот метод является приближенным. Главное его достоинство - наличие информации в центральных планирующих органах: баланса денежных доходов и расходов населения и других данных.
Учитывая, что инфляция происходит в силу влияния множества факторов, целесообразно прогнозные расчеты осуществлять на основе многофакторных моделей с применением корреляционно-регрессионного метода, позволяющего установить наличие корреляционной связи между прогнозируемой инфляцией и влияющими на нее факторами, определить форму связи, сформировать уравнение и на его основе осуществить прогноз инфляции. Общий вид многофакторной модели:
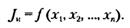
Среди важнейших факторов следует выделить: изменение курса валюты, рост денежной массы, изменение ставки рефинансирования национального банка. При этом по каждому фактору необходимо учитывать временной лаг. При изменении ситуации временной лаг меняется. Изменчивость временного лага является одним из фундаментальных макроэкономических факторов. Знание временной связи между инфляцией и ее факторами позволяет осуществить более точное прогнозирование инфляционных процессов и умело управлять ими.
В мировой практике распространенным методом прогнозирования инфляции является расчет ее уровня па основе дефлятора ВВП. Сущность этого метода состоит в следующем. На основе данных по инфляции в предшествующем периоде и учета влияния факторов в прогнозируемом периоде определяется инфляция на определенный прогнозируемый период. Выделяются следующие факторы: изменение денежных доходов, субсидий, экспортных и импортных цен ближнего и дальнего зарубежья, процентных ставок по кредитам и депозитам и др.
По каждому фактору определяются его прогнозируемая величина и изменение. Затем данные в абсолютном выражении по соответствующему фактору в периоде, предшествующем прогнозируемому, делятся на ВВП в том же периоде, и этот результат умножается на процентное изменение фактора в прогнозируемом периоде по сравнению с предшествующим.
Результаты по каждому фактору суммируются и, исходя из уровня инфляции предшествующего периода и влияния факторов, рассчитывается инфляция в прогнозируемом периоде
Поскольку инфляционные процессы проявляются при росте цен, прогнозирование инфляции должно осуществляться в сочетании с прогнозированием индексов изменения цен.
Западные экономисты при анализе тенденций развития инфляционных процессов часто обращаются к прогнозированию движения цен на отдельные виды товаров, пытаясь с помощью этих прогнозов определить возможные темпы инфляции. В последнее время в основе этих прогнозов, как правило, находится динамика либо цен на энергоносители (нефть, газ), либо заработной платы (расходы на заработную плату в США и других странах составляют существенную долю в издержках предприятий).
В рыночной экономике избавиться от инфляции невозможно. Однако можно ее сделать умеренной и управляемой.
Задача.
В базисном периоде пассажирооборот автомобильного транспорта составил 4 млрд.пасс.км; численность населения - 2 млн. чел.
В прогнозируемом периоде доходы в расчете на душу населения возрастут на 5 %, численность населения увеличится на 0,1 млн. чел. Соотношение темпов роста подвижности населения и денежных доходов, сложившихся в предыдущие годы, равно 1,1.
Технико-экономические показатели использования пассажирского автомобильного транспорта следующие: коэффициент выпуска автобусов на линию – 0,75; среднесуточный пробег автобусов – 250 км; коэффициент использования пробега – 0,8; средняя вместимость автобуса – 40 чел.; коэффициент использования вместимости – 0,9.
Исходя из данных о росте численности, доходах населения и технико-экономических показателей использования автобусного парка, рассчитать по региону на прогнозируемый период: рост транспортной подвижности населения, объем пассажирооборота и потребность в автомобильном пассажирском транспорте.
Решение:
рассчитаем:
1 )
транспортную подвижность населения: пассажирооборот / численность населения. = 4 млрд пасс км / 2 млн чел. = 2000 км.
2) рост транспортной подвижности населения:
Рост доходов = 5%
Рост подвиж. = 5,5% или 1,055
Рост доходов = 1,1
3) подвижность населения в прогнозируемом периоде: 200*1,055=2110 км.
4) пассажирооборот в прогнозируемом периоде: = подвижность * численность = 2110 км * (2 + 0,1)= 2110*2,1 = 4431млн. км.
5) пассажирооборот 1 автомобиля:
0,75*250*365*0,8*40*0,9=1971 тыс. км.
6) потребность в пассажирском транспорте: общий пассажирооборот / пассажирооборот 1 авт = 4431 млн ткм / 1971 тыс ткм = 2248 шт
Ответ: рост транспортной подвижности населения составил 5,5%; объем пассажирооборота – 4431 млн.км.; потребность в автомобильном пассажирском транспорте – 2248 шт.
Список использованных источников
1 Карасев А.И. Математические модели и модели в планировании. / А.И.Карасев, Н.Ш.Кремер, Т.И.Савельев.- М.: 1987.
2 Прогнозирование и планирование экономики: Учеб. пособие / Под общ. ред. В.И.Борисевича, Г.А.Кандауровой. – Мн.: Интерпрессервис; Экоперспектива, 2001.- 380 с.
3 Статистическое моделирование и прогнозирование / Под ред. А.Г.Гринберга.- М.: 1980.
|