МЕХАНИКА СПЛОШНОЙ СРЕДЫ
ОСНОВНЫЕ ЗАКОНЫ МЕХАНИКИ СПЛОШНОЙ СРЕДЫ
1. Сохранение массы. Уравнение неразрывности
Материальный континуум обладает свойством, называемым массой.
Суммарная масса некоторой части сплошной среды, занимающей в момент t
объем пространства V,
выражается интегралом
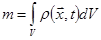 (1.1) (1.1)
где 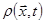 - непрерывная функция координат, называемая плотностью. Закон сохранения массы,
утверждает, что масса выделенной части среды остается постоянной и, следовательно, материальная производная от (1.1) равна нулю. Если в формуле (4.52) положить P
'
ij
. ( x , t
)
ss
р (х, 0, то получим выражение для скорости изменения массы т - непрерывная функция координат, называемая плотностью. Закон сохранения массы,
утверждает, что масса выделенной части среды остается постоянной и, следовательно, материальная производная от (1.1) равна нулю. Если в формуле (4.52) положить P
'
ij
. ( x , t
)
ss
р (х, 0, то получим выражение для скорости изменения массы т
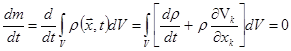 (1.2) (1.2)
Поскольку это равенство верно для произвольного объема V,
подинтегральное выражение само должно обращаться в нуль, т. е.
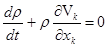 или или 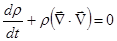 (1.3) (1.3)
Это уравнение называется уравнением неразрывности
(или непрерывности). Раскрывая оператор материальной производной, его можно написать в другой равнозначной форме
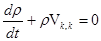 , или , или 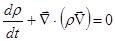 (1.4) (1.4)
В несжимаемой
среде плотность массы каждой частицы не зависит от времени, т. е. 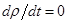 , и уравнение (1.3) принимает вид
, и уравнение (1.3) принимает вид
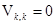 , или , или 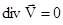 . (1.5) . (1.5)
Поле скорости 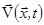 в несжимаемой среде можно поэтому представить выражением в несжимаемой среде можно поэтому представить выражением
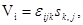 или или 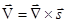 , (1.6) , (1.6)
где функция 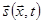 называется векторным потенциалом называется векторным потенциалом
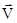 . .
Уравнение неразрывности можно записывать в лагранжевой, или материальной, форме. Для сохранения массы требуется, чтобы выполнялось уравнение
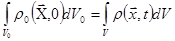 . (1.7) . (1.7)
Здесь оба интеграла взяты по одним и тем же частицам, т. е. V -
это объем, который теперь занимает среда, заполнявшая в момент t
= 0 объем 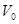 .
Используя (4.1) и (4.38), интеграл в правой части (1.7) можно преобразовать следующим образом: .
Используя (4.1) и (4.38), интеграл в правой части (1.7) можно преобразовать следующим образом:
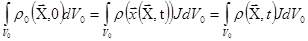 (1.8) (1.8)
Соотношение (1.8) должно иметь силу для произвольно выбранного объема 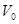 , и поэтому , и поэтому
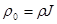 (1.9) (1.9)
Это означает, что произведение 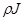 не зависит от времени, так как объем V
произволен, т. е. что не зависит от времени, так как объем V
произволен, т. е. что
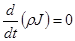 (1.10) (1.10)
Уравнение (1.10) является лагранжевой дифференциальной формой
уравнения неразрывности.
2. Теорема об изменении количества движения. Уравнения движения
Уравнения равновесия
На рис. 2.1 изображен движущийся объем сплошной среды V
в момент t.
На него действуют массовые силы с плотностью распределения 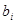 . На каждом бесконечно малом элементе . На каждом бесконечно малом элементе 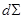 поверхности, ограничивающей рассматриваемый объем, действует вектор напряжения поверхности, ограничивающей рассматриваемый объем, действует вектор напряжения 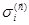 . Во всей области, занятой средой, определено поле скоростей . Во всей области, занятой средой, определено поле скоростей 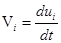 .
Общее количество движения
системы масс, заполняющих объем V,
определяется интегралом .
Общее количество движения
системы масс, заполняющих объем V,
определяется интегралом
Реклама

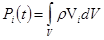 . (2.1) . (2.1)
Основываясь на втором законе Ньютона, теорема об изменении количества движения
утверждает, что скорость изменения со временем количества движения некоторой части континуума равна результирующей сил, действующих на рассматриваемую область. Если внутренние силы, действующие между частицами данного объема (рис. 2.1), подчиняются третьему закону Ньютона о действии и противодействии, то теорема об изменении количества движения для этой системы масс выражается уравнением
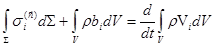 , ,
или (2.2)
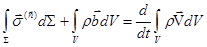 . .
После подстановки 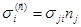 в первый интеграл и преобразования интеграла по поверхности в интеграл по объему (согласно теореме Гаусса — Остроградского) это уравнение примет вид в первый интеграл и преобразования интеграла по поверхности в интеграл по объему (согласно теореме Гаусса — Остроградского) это уравнение примет вид
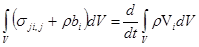
или (2.3)
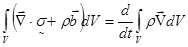
Распишем материальную производную правой части (2.3) и воспользуемся уравнением неразрывности в форме (1.10). Это даст
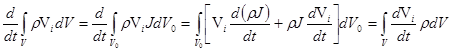 . (2.4) . (2.4)
Подстановка этого выражения в правую часть (2.3) и объединение членов приводят к интегральной форме теоремы об изменении количества движения:
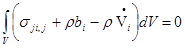
или (2.5)
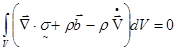
Так как объем V
произволен, само подинтегральное выражение (2.5) должно обращаться в нуль. Полученные таким образом уравнения
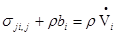 , или , или 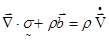 (2.6) (2.6)
называются уравнениями движения.
Для случая равновесия, когда отсутствуют ускорения, из (2.6) получаются уравнения, называемые у равнениями равновесия
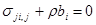 , или , или 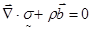 (2.7) (2.7)
3. Теорема об изменении момента количества движения
Будем предполагать, что момент количества движения
для сплошной среды равен моменту вектора количества движения относительно какой-либо точки. Так, для части континуума, изображенной на рис. 2.1, полный момент количества движения относительно начала координат по определению равен интегралу
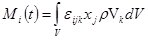 , или , или 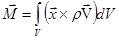 , (3.1) , (3.1)
где 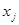 - радиус-вектор элемента объема dV. Теорема об изменении момента количества движения
утверждает, что скорость изменения момента количества движения произвольно выбранной части континуума относительно любой точки равна главному моменту (относительно той же точки) массовых и поверхностных сил, действующих на рассматриваемую область среды. Для объема V
сплошной среды можно написать уравнение момента количества движения в интегральной форме: - радиус-вектор элемента объема dV. Теорема об изменении момента количества движения
утверждает, что скорость изменения момента количества движения произвольно выбранной части континуума относительно любой точки равна главному моменту (относительно той же точки) массовых и поверхностных сил, действующих на рассматриваемую область среды. Для объема V
сплошной среды можно написать уравнение момента количества движения в интегральной форме:
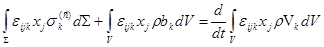 , ,
или (3.2)
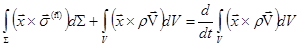
Уравнение (3.2) справедливо для таких сред, в которых силы взаимодействия частиц равны по величине, коллинеарны и противоположны по направлению, а распределенные моменты отсутствуют. Уравнение момента количества движения не всегда представляет собой новое дифференциальное уравнение. Если в (3.2) подставить 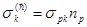 и предположить симметрию тензора напряжений, то уравнение будет удовлетворено тождественно при учете только соотношения (2.6). Если же симметрия тензора напряжений не предполагается заранее, то она получается как прямое следствие уравнения (3.2), которое после подстановки и предположить симметрию тензора напряжений, то уравнение будет удовлетворено тождественно при учете только соотношения (2.6). Если же симметрия тензора напряжений не предполагается заранее, то она получается как прямое следствие уравнения (3.2), которое после подстановки 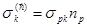 сводится к виду сводится к виду
Реклама

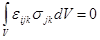 , или , или 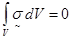 (3.3) (3.3)
В силу произвольности объема V
это ведет к равенствам
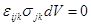 , или , или 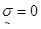 , (3.4) , (3.4)
откуда видно, что 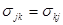 . .
ЗАДАНИЕ ДЛЯ РАСЧЕТНОЙ РАБОТЫ
По заданному в эйлеровых координатах закону распределения компонент тензора истинных напряжений, полагая плотность постоянной, определить:
1. Закон распределения массовых сил, при котором среда находится в равновесии.
2. Построить эпюры нормальных и касательных составляющих вектора напряжений на границе куба со сторонами 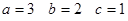 . .
3. Найти главный вектор поверхностных (определить нормальную и касательную составляющие) сил и массовых сил.
4. Найти главный момент поверхностных и массовых сил. Убедиться в их равновесии.
5. Полагая массовые силы отсутствующими, найти поле ускорений в эйлеровых координатах.
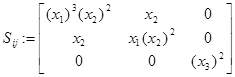
Выполнение расчетной работы
По заданному в эйлеровых координатах закону распределения компонент тензора истинных напряжений, полагая плотность постоянной, определить:
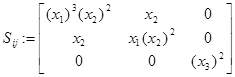
1. Определим закон распределения массовых сил, при котором среда находится в равновесии, для этого составим уравнение движения:
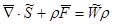
Условие равновесия : 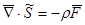 . .
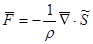
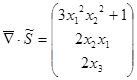
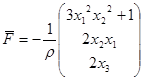
2. Построить эпюры нормальных и касательных составляющих вектора напряжений на границе куба со сторонами 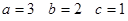 . .
Построим нормальные составляющие.
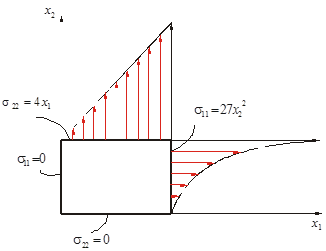
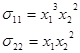
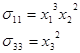
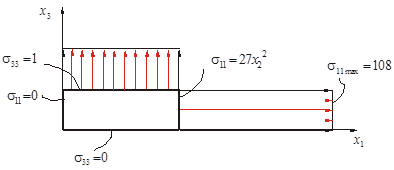 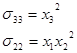
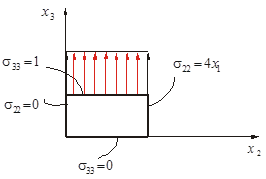
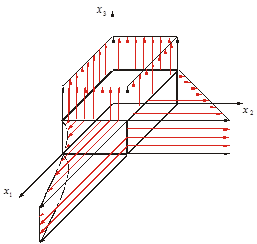
Построим касательные составляющие.
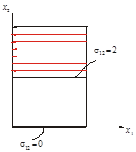
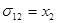
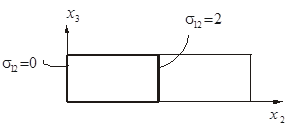
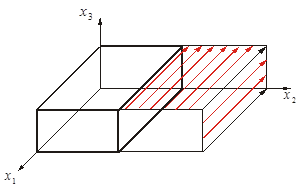
3. Найти главный вектор поверхностных (определить нормальную и касательную составляющие) сил и массовых сил.
Найдем главный вектор массовых сил: 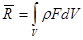 . .
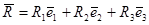 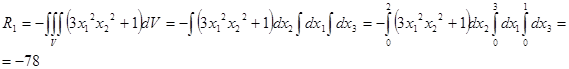
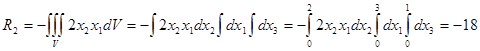
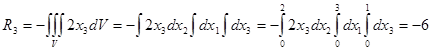
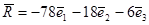
Найдем главный вектор поверхностных сил: 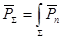 . .
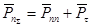
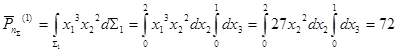

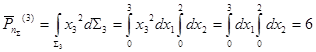
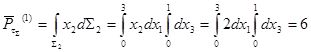
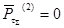
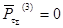
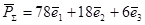
Т.к. 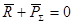 , то система находится в равновесии. , то система находится в равновесии.
4. Найти главный момент поверхностных и массовых сил. Убедиться в их равновесии.
Найдем главный момент поверхностных сил относительно центра заданного объема, т.е. параллепипида со сторонами 3 x 2 x 1.
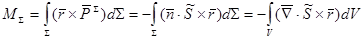
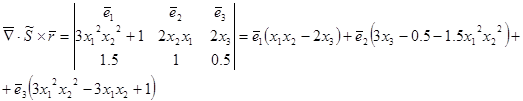
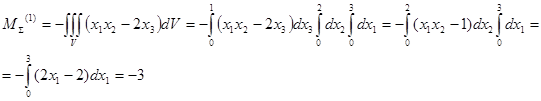
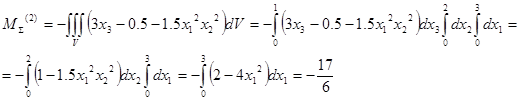
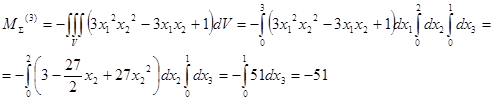
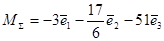
Найдем главный момент массовых сил:
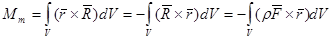
Но 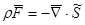 , поэтому , поэтому 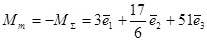 и условие равновесия автоматически выполняется. и условие равновесия автоматически выполняется.
5. Полагая массовые силы отсутствующими, найти поле ускорений в эйлеровых координатах.

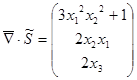
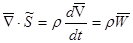

|