| Расчет трубки цевки
Цевка имеет трубчатую структуру (рисунок 3.6).
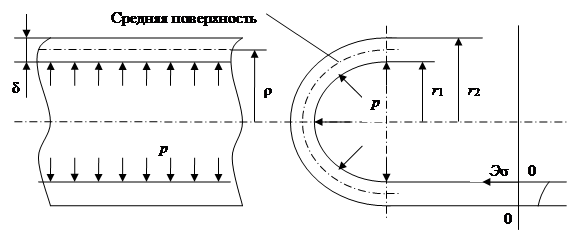
Рисунок 3.6 – Расчетная схема трубы цевки
Толщина стенки δ = 2 мм, что имеет сопоставимые размеры с внутренним радиусом r
1
= 4 мм и наружным радиусом r
2
= 6 мм цевки. Радиус кривизны срединной поверхности определяется по формуле:
ρ = (r
1
+ r
2
)/2, (3.2)
ρ = (4 + 6)/2 = 5 мм
В этом случае используется теория расчета толстостенных труб по методу Ламе. В общем случае нагружения трубы без дна можно записать следующую систему уравнений [20]:
σt
= 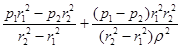 , ,
σx
= 0, (3.3)
σr
= 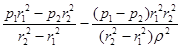 , ,
где σt
– кольцевые главные нормальные напряжения, МПа;
σx
– осевые главные нормальные напряжения, МПа;
σr
– радиальные главные нормальные напряжения, МПа;
р
1
– внутреннее давление в трубе, МПа;
р
2
– наружное давление, МПа;
r
1
, r
2
– внутренний и наружный радиусы трубы, м;
ρ – радиус кривизны срединной поверхности, м.
В нашем случае цевка нагружена только внутренним давлением, то есть р
1
= р
, р
2
= 0. Давление внутри трубы соответствует давлению нагнетаемого фарша. Шнековые шприцы развивают давление р
= 0,2 МПа.
При этих условиях уравнения (3.3) примут вид:
σt
= 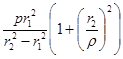 , ,
σx
= 0, (3.4)
σr
= 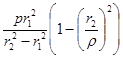 , ,
Определим указанные напряжения:
σt
= 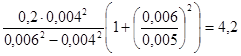 МПа МПа
σx
= 0
σr
= 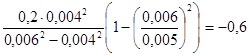 МПа МПа
Используем первую теорию прочности и определим главные нормальные напряжения (объемно-напряженное состояние):
σ1
= σmax
= σt
= 4,2 МПа
σ2
= σх
= 0
σ3
= σmin
= σr
= - 0,6 МПа
Эквивалентное напряжение в материале:
σэ
= σ1
– σ3
, (3.5)
σэ
= 4,2 – (-0,6) = 4,8 МПа
Для материала цевки – сталь 10Х13Г18Д ГОСТ 14959-91 – допускаемое напряжение принимается равным [σ] = 200 МПа. Так как эквивалентное напряжение оказалось меньше допускаемого 4,8 МПа < 200 МПа, то условие прочности цевки выполняется.
Расчет конической части цевки
Для расчета конической части цевки используем безмоментную теорию оболочек. Коническое расширение цевки предназначено для ее соединения со шприцем (рисунок 3.7).
Радиус основания конуса составляет величину R = 30 мм, угол полураствора α = 410
.
Реклама


Рисунок 3.7 – Расчетная схема конической части цевки
Для расчета используется уравнение Лапласа [20]:
σm
/ρm
+ σt
/ρt
= р
/δ, (3.6)
где σm
– меридиональные напряжения, МПа;
ρm
– радиус кривизны оболочки в меридиональном направлении, м;
σt
– окружные напряжения, МПа;
ρt
– радиус кривизны оболочки в окружном направлении, м;
р
– давление внутри оболочки, МПа;
δ – толщина стенки, м.
Если использовать метод сечения, то получается второе уравнение из условия равновесия отсеченной части. В этом случае
σm
= 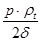 , ,
(3.7)
σt
= 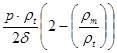
Для оболочки конической формы имеем:
ρm
= ∞, ρt
= R
/cosα, (3.8)
Получаем формулы для определения искомых величин:
σm
= 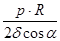 , ,
(3.9)
σt
= 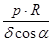
В оболочке развивается давление р
= 0,2 МПа (давление нагнетаемого фарша), толщина стенки δ = 2 мм:
σm
= 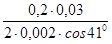 = 2 МПа, = 2 МПа,
σt
= 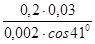 = 4 МПа = 4 МПа
Используем первую теорию прочности и определим главные напряжения:
σ1
= 4 МПа, σ2
= 2 МПа, σ3
= 0
Эквивалентное напряжение определяем по формуле (3.5):
σэ
= σ1
– σ2
= 4 – 0 = 4 МПа
Проверяем условие прочности:
σэ
≤ [σ], (3.10)
где [σ] – допускаемое напряжение, [σ] = 200 МПа.
4 МПа < 200 МПа
Условие прочности выполняется, следовательно, конструкция выдержит рабочие нагрузки без разрушения.
Расчет сварного шва
Для крепления конической части цевки к трубе используется сварка в среде аргона неплавящимся вольфрамовым электродом (рисунок 3.8).

Рисунок 3.8 – Сварное соединение трубки и конической части цевки
Шов является тавровым кольцевым. Его рассчитывают по касательным напряжениям среда при действии осевой нагрузки, определяемой давление р
:
F
= p
· S
= p
· (πd
2
)/4, (3.11)
где F
– осевое усилие в шве, Н;
S
– площадь поперечного сечения трубки, м2
;
d
– наружный диаметр цевки, м.
При диаметре цевки d
= 0,012 м и давлении р
= 0,2 МПа имеем:
F
= 0,2 · 106
· (3,14 · 0,0122
)/4 = 400 Н
Касательные напряжения определяются по формуле [11]:
τ = F
/(0,7 · k
· l
) ≤ [τ'], (3.12)
где τ - касательное напряжение, МПа;
k
– катет шва, мм;
l
– длина шва, мм;
[τ'] – допускаемое напряжение на срез для сварного шва, МПа.
При данном способе сварки катет шва равен толщине свариваемых деталей, то есть k
= δ = 2 мм.
Длина шва определяется длиной окружности:
Реклама

l
= πd
=3,14 · 12 = 38 мм (3.13)
Допускаемое напряжение [τ'] выбираем по рекомендациям для полуавтоматической сварки в среде аргона [11]:
[τ'] = 0,65[σр
], (3.14)
где [σр
] – допускаемое напряжение растяжения для основного металла, МПа.
[σр
] = σт
/[S], (3.15)
где σт
– предел текучести основного металла, МПа;
[S] – нормативный коэффициент запаса прочности.
Для стали марки 10Х13Г18Д предел текучести составляет величину σт
= 400 МПа. Нормативный коэффициент запаса прочности легированных сталей равен [S] = 1,5…1,7, тогда
[σр
] = 400/1,7 = 235 МПа
По формуле (3.14) определяем величину допускаемых напряжений среза:
[τ'] = 0,65 · 235 = 141 МПа
Проверяем прочность сварного шва по условию (3.12):
τ = 400/(0,7 · 2 · 38) = 7,5 МПа ≤ 141 МПа
Условие прочности сварного шва выполняется.
Расчет установочной штанги
Установочная штанга удерживает ролики тормозного устройства в требуемом положении относительно отверстии выхода сосисок. Длина штанги
L
= 800 мм. Она изготовлена из трубы диаметром d
= 16 мм и с толщиной стенки δ = 3 мм. Трубка нагружена изгибающим моментом от массы тормозного устройства (m
= 0,8 кг). Закрепление штанги консольное, защемленное (рисунок 3.5). Расчетная схема представлена на рисунке 3.9.
Рисунок 3.9 – Расчетная схема штанги
Определим изгибающий момент в опасном сечении (место защемления):
М
изг
= mgL
, (3.16)
где g – ускорение свободного падения, м/с2
.
М
изг
= 0,8 · 10 ·0,8 = 6,4 Н·м
Условие прочности выглядит следующим образом:
σ = М
изг
/W
≤ [σ], (3.17)
где σ – напряжение в опасном сечении, МПа;
W
– момент сопротивления поперечного сечения, м3
;
[σ] – допускаемое напряжение для материала штанги, МПа.
Для стали 10Х13Г18Д имеем [σ] = 200 МПа.
Штанга имеет трубчатое сечение с наружным диаметром d
= 16 мм и внутренним диаметром d
1
= 12 мм (толщина стенки δ = 2 мм), тогда момент сопротивления равен:
W
= π(d
3
– d
1
3
)/32 = 3,14(0,0163
– 0,0123
)/32 = 2,32 · 10-7
м3
σ = 6,4/(2,32 · 10-7
) = 27,5 МПа < 200 МПа
Условие прочности выполняется, однако в условиях нагружения штанги недопустимым может оказаться прогиб конца консольного участка. Вычислим прогиб у
:
у
= (mg
· L
3
)/(3 · E
· J
), (3.18)
где E
– модуль Гука (модуль упругости первого рода), МПа;
J
– момент инерции поперечного сечения трубки, м4
.
Для стали E
= 2,1 · 105
МПа. Момент инерции трубки равен:
J
= π(d4
– d1
4
)/64 = 3,14(0,0164
– 0,0124
)/64 = 2,2 · 10-9
м4
у
= (0,8 · 0,83
)/(3 · 2,1 · 105
· 2,2 · 10-9
) = 0,0012 м = 1,2 мм
По условиям отсутствия перекоса сосиски в тормозке допустимое значение прогиба [у
] = 5 мм, то есть прогиб находится в допустимых пределах (1,2 мм < 5 мм).
Расчет прочности полиамидной оболочки
После выхода сосиски из шприца она удерживается между роликами тормозного устройства. Эти ролики, обжимая сосиску, создают необходимые условия для удержания готовой сосиски от прокручивания. Однако деформация фарша в готовом изделии ведет к увеличению внутреннего давления, что может привести к прорыву оболочки. Рассмотрим деформацию сосиски между роликами (рисунок 3.10).
Первоначальное поперечное сечение сосиски – круглое с диаметром D
. Попадая между роликами, происходит деформация, и сечение сосиски становится эллипсовидным с полуосями D
/2 и a
/2 (а
– расстояние между роликами). Для лучших условий охватывания сосиски роликами и с целью предотвратить разрыв оболочки ролики сделаны фасонными, чтобы обеспечить эллиптическое отверстие в пространстве между собой.
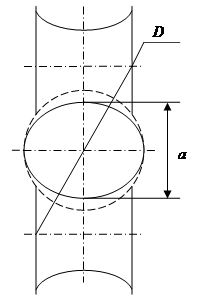 
Рисунок 3.10 – Деформация сосиски между роликами
Сделаем допущение, что фарш является абсолютно упругой системой. Тогда энергия, идущая на деформацию, запасается в фарше в виде потенциальной энергии. После снятия нагрузки первоначальная форма восстанавливается полностью, остаточных деформаций не остается. Условие сохранения энергии в деформированном поперечном слое сосиски выглядит следующим образом [17]:
р
1
S
1
= р
2
S
2
, (3.19)
где р
1
– первоначальное давление фарша внутри сосиски, Па;
р
2
– давление фарша в зоне деформации, Па;
S
1
– площадь сечения сосиски до деформации, м2
;
S
2
– площадь сечения сосиски после деформации, м2
.
До деформации давление в сосиске можно принять р
1
= 2 · 105
Па, площадь S
1
= (πD
2
)/4. Площадь эллипса определяется по формуле:
S
2
= π · D
/2 · a
/2 = D
· a
· π/4, (3.20)
Делаем допущение, что деформация сечения сосиски не выходит за пределы окружности, ограничивающей первоначальное сечение. В действительности большая полуось эллипса будет больше радиуса D
/2. Но принятое допущение позволяет рассмотреть самый неблагоприятный случай нагружения. Если условие прочности оболочки выполняется при неблагоприятных допущениях, то в реальной ситуации заведомо условие прочности выполнится. Из формулы (3.19) с учетом (3.20) выразим давление в деформированном слое:
р
2
= р
1
· S
1
/S
2
= р
1
· ((πD
2
)/4)/((π/4)Da
) = р
1
· D
/a
, (3.21)
Расстояние между роликами а
рекомендуется выдерживать в пределах 2/3 от диаметра оболочки, т.е. а
= 2/3 · D
.
р
2
= р
1
· D
/(2/3 · D
) = 3/2 · р
1
= 3/2 · 2 = 3 · 105
Па
При допустимом давление в оболочке р
= 5 · 105
Па условие прочности оболочки выполняется (3 · 105
Па < 5 · 105
Па).
|