Кафедра высшей математики
Курсовая работа
по линейной алгебре и аналитической геометрии
на тему:
Исследование кривых и поверхностей второго порядка
Дубна, 2002
Оглавление
ВВЕДЕНИЕ
ИССЛЕДОВАНИЕ КРИВОЙ ВТОРОГО ПОРЯДКА
Теоретическая часть
Практическая часть
ВЫВОД
ИССЛЕДОВАНИЕ ФОРМЫ ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Теоретическая часть
Практическая часть
ВЫВОД
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
Цель
1. Целью данной курсовой работы является исследование кривой и формы поверхности второго порядка. Закрепление полученных теоретических знаний и практических навыков по изучению и анализу свойств кривых и поверхностей второго порядка.
2. Ознакомление с пакетами программ Microsoft® Word и Microsoft® Excel.
Постановка задачи
I
.
Для данного уравнения кривой второго порядка:
1. Определить тип данной кривой с помощью инвариантов.
2. Привести уравнение кривой к каноническому виду, применяя преобразования параллельного переноса и поворота координатных осей.
3. Найти фокусы, директрисы и ассимптоты данной кривой (если они есть).
4. Построить каноническую систему координат и данную кривую в общей системе координат.
II
. Для данного канонического уравнения поверхности второго порядка:
1. Исследовать форму поверхности методом сечений плоскостями, построить линии, полученные в сечениях;
2. Построить поверхность в канонической системе координат.
Теоретическая часть
Пусть кривая Г задана в декартовой прямоугольной системе координат xOy
уравнением:
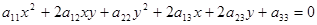 . (1.1) . (1.1)
Если хотя бы один из коэффициентов 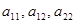 отличен от нуля, то кривую Г называют кривой второго порядка. отличен от нуля, то кривую Г называют кривой второго порядка.
Теорема 1.
Для произвольной кривой второго порядка Г существует такая декартова прямоугольная система координат XO
¢
Y
, что в этой системе кривая Г имеет уравнение одного из следующих канонических
видов:
1) 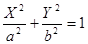 , а
³b
> 0
— эллипс, , а
³b
> 0
— эллипс,
2) 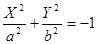 — мнимый эллипс, — мнимый эллипс,
3) 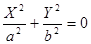 — две мнимые пересекающиеся прямые — две мнимые пересекающиеся прямые
(точка),
4) 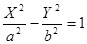 — гипербола, — гипербола,
5) 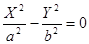 — две пересекающиеся прямые, — две пересекающиеся прямые,
6) 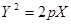 — парабола, — парабола,
7) 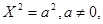 — две параллельные прямые, — две параллельные прямые,
8) 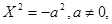 — две мнимые параллельные прямые, — две мнимые параллельные прямые,
9) 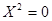 — две совпадающие прямые. — две совпадающие прямые.
В этих уравнениях a
,b
,p
—
положительные параметры.
Систему координат XO¢Y назовем канонической системой координат, а систему координат xOy — общей системой координат.
Реклама

Классификация кривых второго порядка
В зависимости от значения инварианта 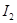 принята следующая классификация кривых второго порядка: принята следующая классификация кривых второго порядка:
· если  кривая второго порядка Г называется кривой эллиптического
типа. кривая второго порядка Г называется кривой эллиптического
типа.
· если 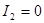 кривая второго порядка Г называется кривой параболического
типа. кривая второго порядка Г называется кривой параболического
типа.
· если 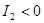 кривая второго порядка Г называется кривой гиперболического
типа. кривая второго порядка Г называется кривой гиперболического
типа.
Кривая второго порядка Г называется центральной
, если 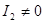 . Кривые эллиптического и гиперболического
типа являются центральными кривыми
. . Кривые эллиптического и гиперболического
типа являются центральными кривыми
.
Центром
кривой второго порядка Г называется такая точка плоскости, по отношению к которой точки этой кривой расположены симметрично парами. Точка 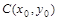 является центром кривой второго порядка, определяемой уравнением (1.1), в том и только в том случае, когда ее координаты удовлетворяют уравнениям: является центром кривой второго порядка, определяемой уравнением (1.1), в том и только в том случае, когда ее координаты удовлетворяют уравнениям:
 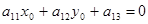 (2.1) (2.1)
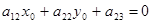 (2.1) (2.1)
Определитель этой системы равен 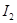 . Если . Если 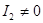 , то система имеет единственное решение. В этом случае координаты центра могут быть определены по формулам: , то система имеет единственное решение. В этом случае координаты центра могут быть определены по формулам:
 , , 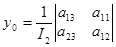 . (2.2) . (2.2)
Из теорем 1 и 2 получается следующая классификация кривых второго порядка с помощью инвариантов:
1) эллипс 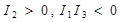
2) мнимый эллипс 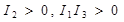
3) две мнимые пересекающиеся прямые (точка) 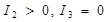
4) гипербола 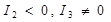
5) две пересекающиеся прямые 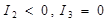 (2.3) (2.3)
6) парабола 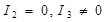
7) две параллельные прямые 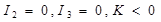
8) две мнимые параллельные прямые 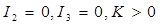
9) две совпадающие прямые 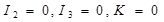
Дано: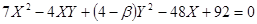 
Определить тип кривой с помощью инвариантов в зависимости от β:
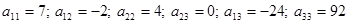
Вычислим инварианты:
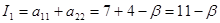
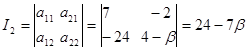
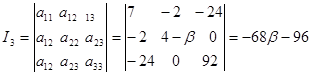
1. Если  , то имеем линии эллиптического типа , то имеем линии эллиптического типа
Этих β будет эллипс
При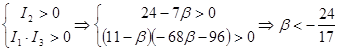
При
2. Если 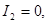 то пишем линии параболического типа, при этом, чтобы была парабола то пишем линии параболического типа, при этом, чтобы была парабола 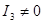
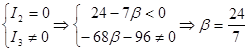
3. Если 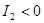 , то получаем линии гиперболического типа. , то получаем линии гиперболического типа.
При 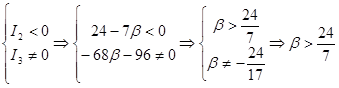 гипербола гипербола
При 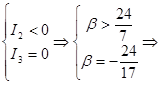 корней нет, т.е. таких двух пересекающихся прямых, не существует. корней нет, т.е. таких двух пересекающихся прямых, не существует.
Значение 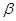 |
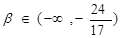 |
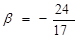 |
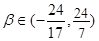 |
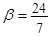 |
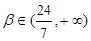 |
| Тип кривой |
Мнимая точка |
Точка |
Эллипс |
Парабола |
Гипербола |
Исследуем кривую при β=0 , тогда получим:
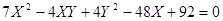
Сперва повернём на угол φ:
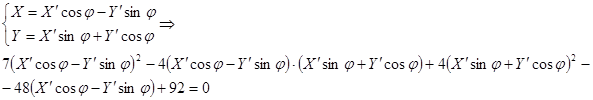 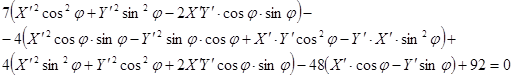 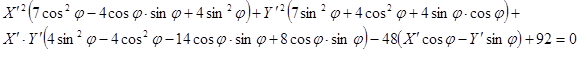
Найдём угол φ,такой чтобы коэффициент при был равен 0: был равен 0:
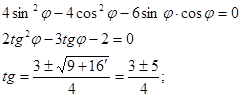
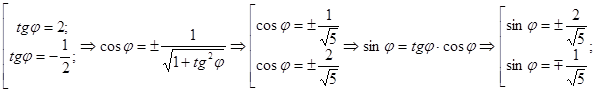
 Пусть Пусть 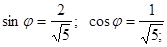
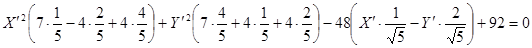
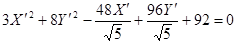
Сгруппируем члены уравнения и дополним до полного квадрата:
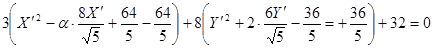
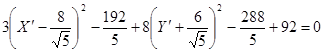
Произведём перенос системы координат:
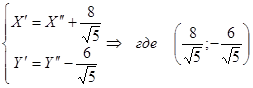 координаты нового центра O системы координат координаты нового центра O системы координат 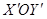
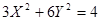
т.е. мы правильно определили каноническое уравнение
 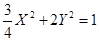
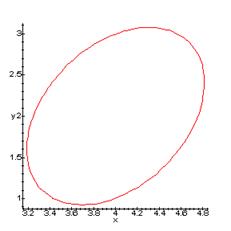
Определим фокус 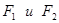 эллипс. эллипс.
Расстояние между 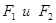 найдём по: найдём по:
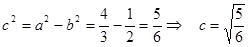
В системе координат
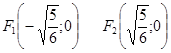
Эксцентрический эллипс 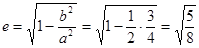
Директрисы 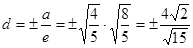
Вывод
Исследовав общее уравнение кривой второго порядка и приведя его к каноническому виду, мы установили, что данная кривая — эллипс.
Мы получили каноническое уравнение гиперболы при помощи преобразований параллельного переноса и поворота координатных осей.
Исследование формы поверхности второго порядка
Реклама

Теоретическая часть
Поверхностью второго порядка
S
называется геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида:
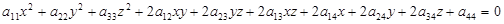 , ,
где по крайней мере один из коэффициентов 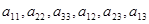 отличен от нуля. отличен от нуля.
Уравнение (3.1) называют общим уравнением
поверхности второго порядка S
,
а систему координатOxyz
называют общей системой координат
.
Теорема:
Для произвольной поверхности S
, заданной общим уравнением существует такая декартова прямоугольная система координат  что в этой системе поверхность S
имеет уравнение одного из следующих семнадцати канонических видов. что в этой системе поверхность S
имеет уравнение одного из следующих семнадцати канонических видов.
1) 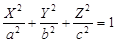 — эллипсоид, — эллипсоид,
2) 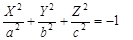 — мнимый эллипсоид, — мнимый эллипсоид,
3) 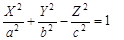 — однополостный гиперболоид, — однополостный гиперболоид,
4) 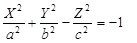 — двуполостный гиперболоид, — двуполостный гиперболоид,
5) 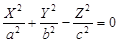 — конус, — конус,
6) 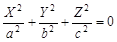 — мнимый конус (точка), — мнимый конус (точка),
7) 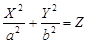 — эллиптический параболоид, — эллиптический параболоид,
8) 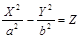 — гиперболический параболоид, — гиперболический параболоид,
9) 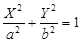 — эллиптический цилиндр, — эллиптический цилиндр,
10) 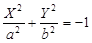 — мнимый эллиптический цилиндр, — мнимый эллиптический цилиндр,
11) 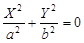 — две мнимые пересекающиеся плоскости (ось — две мнимые пересекающиеся плоскости (ось
O
'Z
),
12) 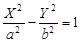 — гиперболический цилиндр, — гиперболический цилиндр,
13) 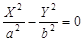 — две пересекающиеся плоскости, — две пересекающиеся плоскости,
14) 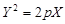 — параболический цилиндр, — параболический цилиндр,
15) 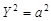 — две параллельные плоскости, — две параллельные плоскости,
16) 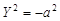 — две мнимые параллельные плоскости, — две мнимые параллельные плоскости,
17) 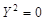 — две совпадающие плоскости (плоскость XOZ
). — две совпадающие плоскости (плоскость XOZ
).
В выше перечисленных уравнениях a
,
b
,
c
,
p
— положительные параметры. Систему координат  называют канонической. называют канонической.
Исследование формы поверхности второго порядка методом сечения плоскостями
Если дано каноническое уравнение поверхности S
,
то представление о поверхности можно получить по форме линий пересечения ее плоскостями:
Z
=
h
— параллельными координатной плоскости XO
'
Y
,
X
=
h
— параллельными координатной плоскости YO
'
Z
,
Y
=
h
— параллельными координатной плоскости XO
'
Z
.
Практическая часть
Дано:
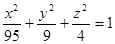 ; ;
Это эллипсоид в прямоугольной декартовой системе координат Oxyz, где оси OX, OY, OZ — оси симметрии.
1. Рассмотрим линии  плоскостями Z=h (h=const): плоскостями Z=h (h=const):
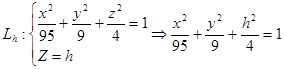 (1) (1)
Плоскость Z
=
h
параллельна плоскости Oxy.
Уравнения проекций 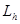 на Oxy имеют вид: на Oxy имеют вид:
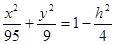
Если 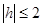 , то , то 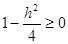 , и тогда поделим обе части уравнения на , и тогда поделим обе части уравнения на 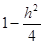 , получим: , получим:
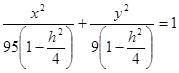
Это уравнение эллипсов с полуосями 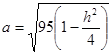 , , 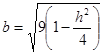 ; увеличивающиеся с уменьшением ; увеличивающиеся с уменьшением 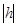 , центр эллипса (0;0;h) , центр эллипса (0;0;h)
При различных h
имеем:
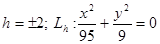
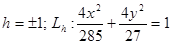
Если 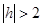 , тогда , тогда 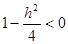 и значит линии и значит линии  удовлетворяющих уравнению(1) нет. удовлетворяющих уравнению(1) нет.
2. Рассмотрим 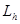 полученные в сечениях эллипсоида плоскостями X=h
: полученные в сечениях эллипсоида плоскостями X=h
:
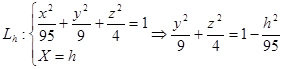 (2) (2)
Уравнение проекций 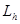 на YOZ. на YOZ.
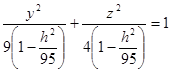
Это уравнение эллипсов с полуосями 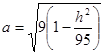 , , 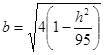 ; ;
Если 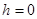 , то a=3, b=2, и , то a=3, b=2, и 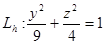
Если 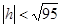 , тогда мы получаем семейство эллипсов: , тогда мы получаем семейство эллипсов:
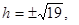 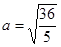 , , 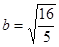 ; ;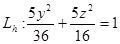
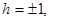 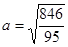 , , 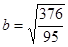 ; ;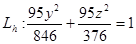
Если 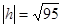 , тогда , тогда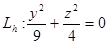 — это уравнение точки с координатами (h
;0;0). — это уравнение точки с координатами (h
;0;0).
Если 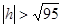 , тогда , тогда 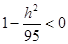 и значит линии и значит линии 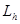 удовлетворяющих уравнению (2) нет. удовлетворяющих уравнению (2) нет.
3. Рассмотрим 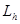 полученные в сечениях эллипсоида плоскостями Y=h
: полученные в сечениях эллипсоида плоскостями Y=h
:
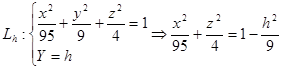 (3) (3)
Уравнения эллипсов, проекций 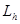 на YOZ и имеют центры (0;h
;0). на YOZ и имеют центры (0;h
;0).
Полуоси 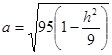 , , 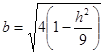
Если 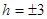 , тогда , тогда 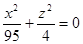 , уравнение точек с координатами (0;h
;0). , уравнение точек с координатами (0;h
;0).
Если 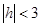 , тогда мы получаем семейство эллипсов: , тогда мы получаем семейство эллипсов:
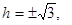 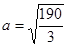 , , 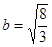 ; ;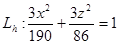
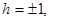 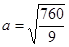 , , 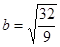 ; ;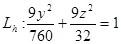
Если 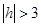 , тогда , тогда 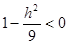 и значит линии и значит линии 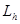 удовлетворяющих уравнению (3) нет. удовлетворяющих уравнению (3) нет.
Построим однополостный гиперболоид
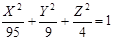
в канонической системе координат  проанализировав уравнение поверхности и результаты исследования методом сечения ее плоскостями. проанализировав уравнение поверхности и результаты исследования методом сечения ее плоскостями.
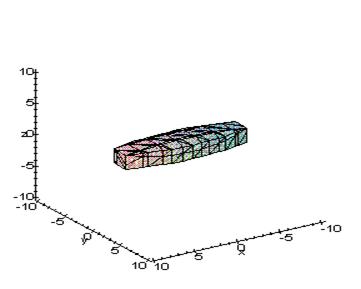
Проанализировав уравнение эллипсоида 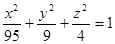 , получили некоторые представления о форме эллипсоида. , получили некоторые представления о форме эллипсоида.
Из уравнения следует, что оси OX, OY, OZ — оси симметрии, плоскости XOY, YOZ, XOZ — плоскости симметрии.
Рассекая поверхность плоскостями y
=
h
,z
=
h
,x
=
h
,
в сечениях имеем эллипсы, наибольшие из которых получаются в плоскостях x=0, y=0, z=0, полуоси их уменьшаются с увеличением  , вершины эллипсов имеют координаты , вершины эллипсов имеют координаты 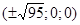 по оси X; по оси X; 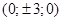 по оси Y; по оси Y; 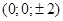 по оси Z. по оси Z.
1. Копылова Т. В. Конспект лекций по линейной алгебре;
2. Копылова Т. В. Линейная алгебра. — Дубна: Международный университет природы, общества и человека «Дубна», 1996;
3. Ефимова Л. В., Демидович Б. П. Линейная алгебра и основы математического анализа. — М: Наука, 1993.
|