ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовому проекту по деталям машин
Выполнила:
Проверил:
СОДЕРЖАНИЕ
Лист
1 Техническое задание
2 Кинематический расчёт привода
2.1 Подбор электродвигателя
3 Расчёт клиноременной передачи привода
4 Расчёт зубчатых передач редуктора
4.1 Разбивка передаточного числа между ступенями редуктора
4.2 Расчёт конической передачи
4.3 Расчёт цилиндрической передачи
4.4 Выбор параметров и расчёт геометрии зубчатых колёс
5 Эскизная компоновка редуктора
5.1 Проектный расчёт валов на кручение, выбор типа и
схемы установки подшипников
5.2 Основные размеры корпусов, крышек, болтов,
винтов редуктора
6 Расчёт валов на сложное сопротивление
6.1 Расчёт ведущего вала
6.2 Расчёт промежуточного вала
6.3 Расчёт ведомого вала
7 Проверочный расчёт подшипников по динамической
грузоподъёмности
7.1 Расчёт подшипников ведущего вала
7.2 Расчёт подшипников промежуточного вала
7.3 Расчёт подшипников ведомого вала
8 Список литературы
1 Техническое задание
Привод состоит из клиноременной передачи и коническо-цилиндрического редуктора.
Ч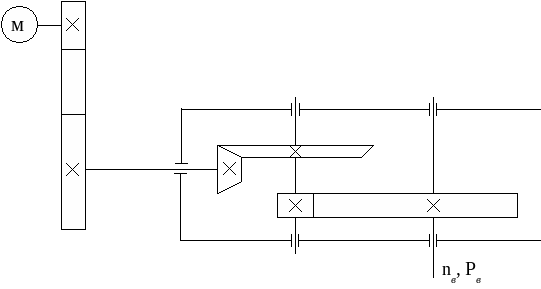
астота вращения выходного вала редуктора 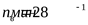 , мощность на выходном валу , мощность на выходном валу 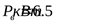 , нагрузка спокойная, передача реверсивная, требуемая долговечность , нагрузка спокойная, передача реверсивная, требуемая долговечность 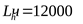 . .
2 Кинематический расчёт привода
2.1 Подбор электродвигателя
По мощности на выходном валу 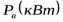 определяем расчётную мощность электродвигателя определяем расчётную мощность электродвигателя
 , ,
где 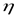 - КПД привода, равный ([3], с.14) - КПД привода, равный ([3], с.14)
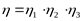
где 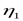 - КПД клиноременной передачи; - КПД клиноременной передачи;
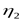 - КПД конической передачи редуктора; - КПД конической передачи редуктора;
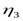 - КПД цилиндрической передачи редуктора. - КПД цилиндрической передачи редуктора.
Принимаем ([3] c. 15)
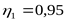 , , 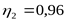 , , 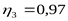 ; ;
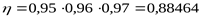 . .
Тогда
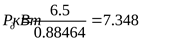
Общее передаточное число привода
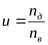
где 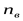 - частота вращения выходного вала привода; - частота вращения выходного вала привода;
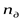 - частота вращения вала электродвигателя. - частота вращения вала электродвигателя.
Откуда получаем
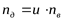
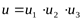
где  - передаточное число клиноременной передачи; - передаточное число клиноременной передачи;
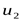 - передаточное число конической передачи редуктора; - передаточное число конической передачи редуктора;
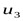 - передаточное число цилиндрической передачи редуктора. - передаточное число цилиндрической передачи редуктора.
Предварительно принимаем ([3] c. 15)
 , , 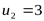 , , 
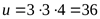 , ,
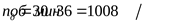 . .
Принимаем ([3] приложение таблица 2) 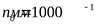 . .
С учётом полученной частоты вращения вала электродвигателя и расчётной мощности 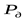 (кВт) по каталогу ([3] приложение таблица 2) выбираем двигатель, номинальная мощность которого P должна быть равна или больше расчётной мощности двигателя, т.е. (кВт) по каталогу ([3] приложение таблица 2) выбираем двигатель, номинальная мощность которого P должна быть равна или больше расчётной мощности двигателя, т.е.
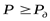
Принимаем двигатель
Тип двигателя 4А132МВ6УЗ
Мощность 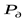 , кВт 7.5 , кВт 7.5
Реклама

Частота вращения, мин-1 970
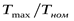 2,2 2,2
Так как частота вращения выбранного электродвигателя не совпадает с полученной ранее, необходимо откорректировать принятые передаточные числа.
Изменим передаточное число редуктора
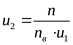
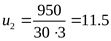
3 Расчёт клиноременной передачи привода
1) Крутящий момент на быстроходном валу
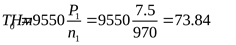
2) При данном моменте принимаем ([3] таблица 2.12) сечение “Б” с размерами
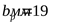 ; ; 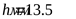 ; ;  ; ; 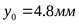 ; ; 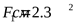 . .
3) Диаметр меньшего шкива в соответствии с рекомендациями ([3] таблица 2.12) 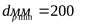 , но т.к. нет жёстких ограничений к габаритам передачи, то для повышения долговечности ремня принимаем , но т.к. нет жёстких ограничений к габаритам передачи, то для повышения долговечности ремня принимаем 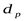 следующим за минимальным ([3] таблица 2.12) следующим за минимальным ([3] таблица 2.12) 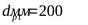 . .
4) Диаметр большего шкива ([3] формула 2.2)
 , ,
где 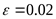 - коэффициент скольжения прорезиненного ремня. - коэффициент скольжения прорезиненного ремня.
Принимаем стандартный диаметр по ГОСТ 17383-73 ([3] таблица 2.12)
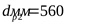 . .
5) Фактическое передаточное число передачи ([3] формула 2.3)
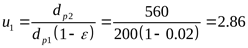 . .
6) Скорость ремня ([3] формула 2.4)
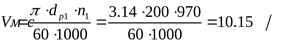 . .
7) Частота вращения ведомого вала
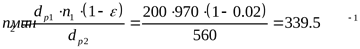 . .
8) Межосевое расстояние согласно рекомендациям ([3] таблица 2.14)
 . .
9) Расчётная длина ремня ([3] по формуле 2.6)
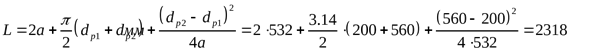
Стандартная длина ремня ([3] с. 26) L=2240мм.
10) По стандартной длине L уточняем действительное межосевое расстояние ([3] формула 2.9)
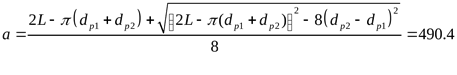
Минимальное межосевое расстояние для удобства монтажа и снятия ремней ([3] с. 27)
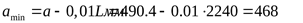 . .
Максимальное межосевое расстояние для создания натяжения и подтягивания ремня при вытяжке
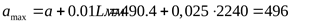 . .
11) Угол обхвата на меньшем шкиве ([3] формула 2.10)
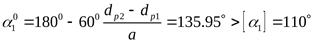 . .
12) Исходная длина ремня ([3] таблица 2.15)
L0=3750мм
Относительная длина 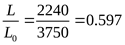 . .
13) Коэффициент длины определяется методом интерполяции по таблице 219 [3]
СL=0,878.
14) Исходная мощность при 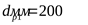 и и 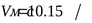 ([3] таблица 2.15) методом интерполирования ([3] таблица 2.15) методом интерполирования 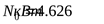 . .
15) Коэффициент угла обхвата ([3] таблица 2.18) 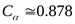 . .
16) Поправка к крутящему моменту на передаточное число (таблица 2.20)
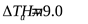 . .
17) Поправка к мощности ([3] с. 28)
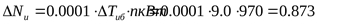
18) Коэффициент режима работы при указанной нагрузке ([3] таблица 2.8)
Ср=0,8.
19) Допускаемая мощность на один ремень ([3] формула 2.24)
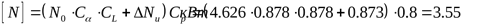 . .
20) Расчётное число ремней ([3] по формуле 2.25)
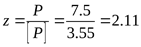 . .
21) Коэффициент, учитывающий неравномерность нагрузки ([3] с. 28)
Сz=0,95.
22) Действительное число ремней в передаче ([3] формула 2.26)
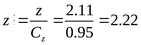 . .
Принимаем число ремней  . .
23) Сила начального натяжения одного клинового ремня ([3] формула 2.28)
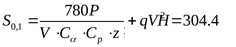 . .
где q – масса одного погонного метра ремня ([3] таблица 2.12).
24) Усилие, действующее на валы передачи ([3] формула 2.29)
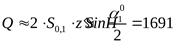
25) Размеры обода шкивов ([3] таблица 2.21)
 ; ; 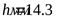 ; ; 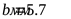 ; ; 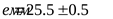 ; ; 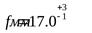 ; ; 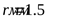 ; ; 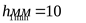 ; ; 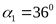 ; ;  . .
26) Наружные диаметры шкивов ([3] формула 2.32)
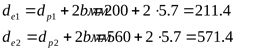
27) Ширина обода шкивов ([3] формула 2.33)
Реклама

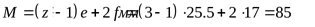 . .
4 Расчёт зубчатых передач редуктора
4.1 Разбивка передаточного числа между ступенями редуктора
В двухступенчатых коническо-цилиндрических редукторах передаточное число тихоходной (цилиндрической) ступени рекомендуется ([3] с. 56)
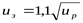
где uр – передаточное число редуктора
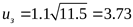
Принимаем из стандартного ряда передаточных чисел зубчатых передач ([3] приложение таблица 8)
 ; ; 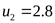 . .
4.2 Расчёт конической передачи
4.2.1 Выбор материала и допускаемых напряжений для шестерни и колеса
1) Назначаем материал ([3] таблица 3.12) для шестерни и колеса – сталь 40ХН (поковка); термообработка – нормализация.
Для шестерни -  , ,  , 280 НВ1; , 280 НВ1;
для колеса -  , ,  , 250 НВ2. , 250 НВ2.
2) Определяем допускаемое напряжение изгиба для шестерни ([3] формула 3.51)
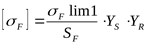 . .
Предварительно находим предел выносливости зубьев при изгибе, соответствующий эквивалентному числу циклов перемены напряжений ([3] формула 3.52)
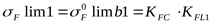 , ,
где предел выносливости при изгибе, соответствующий эквивалентному числу циклов перемены напряжений ([3] таблица 3.19)
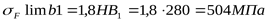 . .
Коэффициент, учитывающий влияние двухстороннего приложения нагрузки (таблица 3.20)
реверсивная передача - 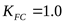
Коэффициент долговечности ([3] формула 3.53)
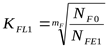
При 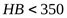 ([3] c. 77) ([3] c. 77)  ; ;
базовое число циклов перемены напряжения ([3] c. 77) 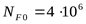
эквивалентное (суммарное) число циклов перемены напряжения ([3] формула 3.54)
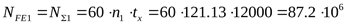
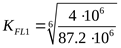 , ,
но т.к. 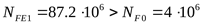 ([3] с. 77) ([3] с. 77)
принимаем 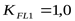
Соответственно 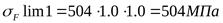
Коэффициент безопасности ([3] формула 3.56)
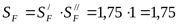
где 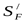 - коэффициент, учитывающий нестабильность характеристики материала ([3] таблица 3.19) - коэффициент, учитывающий нестабильность характеристики материала ([3] таблица 3.19)  ; ;
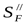 - коэффициент, учитывающий способ получения заготовки и условия эксплуатации передачи ([3] таблица 3.21) - коэффициент, учитывающий способ получения заготовки и условия эксплуатации передачи ([3] таблица 3.21)  . .
Коэффициент, учитывающий чувствительность материала к концентрации напряжений ([3] формула 3.57)  . .
Коэффициент, учитывающий шероховатость переходной поверхности зуба ( [3] формула 3.58)  . .
Допускаемое напряжение изгиба для зубьев шестерни
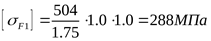 . .
3) Допускаемое напряжение изгиба для зубьев колеса определяем аналогично предыдущему расчёту
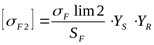 , ,
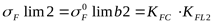 , ,
где
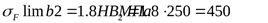 , ,
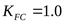 , ,
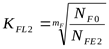 . .
При НВ<350 
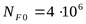
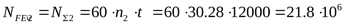
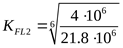
но т.к. 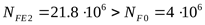 ,* ,*
то принимаем 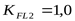
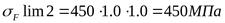 . .
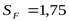 ; ;  ; ;  . .
Допускаемое напряжение изгиба для зубьев колеса
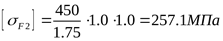 . .
4) Допускаемое напряжение изгиба при расчёте на действие максимальной нагрузки ([3] таблица 3.19), для шестерни
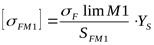 . .
Предварительно находим предельное напряжение, не вызывающее остаточных деформаций или хрупкого излома зуба ([3] таблица 3.19)
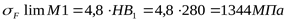
Коэффициент безопасности ([3] с. 76)
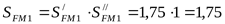 , ,
где 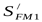 - коэффициент, учитывающий нестабильность характиристики материала; - коэффициент, учитывающий нестабильность характиристики материала;
 ([3] таблица 3.19, см. с. 80); ([3] таблица 3.19, см. с. 80);
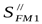 - коэффициент, учитывающий способ получения заготовки и условия эксплуатации передачи ([3] таблица 3.21); - коэффициент, учитывающий способ получения заготовки и условия эксплуатации передачи ([3] таблица 3.21);
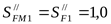
Коэффициент, учитывающий чувствительность материала к концентрации напряжений ([3] формула 3.57)

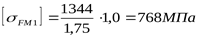
5) Допускаемое напряжение изгиба при действии максимальной нагрузки для колеса
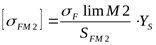
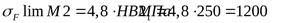
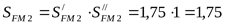

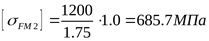 . .
6) Допускаемое контактное напряжение для шестерни ([3] формула 3.33)
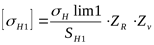 . .
Предварительно находим предел контактной выносливости поверхностей зубьев, соответствующий эквивалентному числу циклов перемены напряжений ([3] формула 3.34)
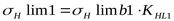 , ,
здесь предел выносливости соответствующий базовому числу циклов перемены напряжений ([3] таблица 3.17)
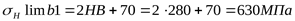 ; ;
коэффициент долговечности ([3] формула 3.35)
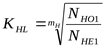 , ,
где базовое число циклов перемены напряжений ([9] рисунок 3.16)
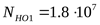
эквивалентное (суммарное) число циклов перемены напряжений
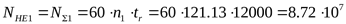 . .
Отношение 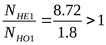 поэтому коэффициент долговечности определяем по формуле 3.38 [3] поэтому коэффициент долговечности определяем по формуле 3.38 [3]
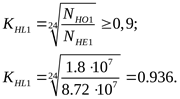
Принимаем 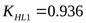 . .
Предел контактной выносливости
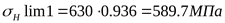 . .
Коэффициент безопасности для зубьев с однородной структурой материала ([3] с. 75)

Коэффициент, учитывающий шероховатость сопряжённых поверхностей ([3] таблица 3.18)

Коэффициент, учитывающий окружную скорость ([3] с. 75)

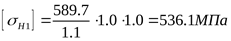 . .
7) Допускаемое контактное напряжение для колеса
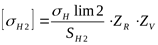 ; ;
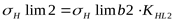 ; ;
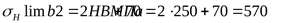 ; ;
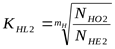 ; ;
 ; ;
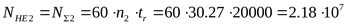 ; ;
т.к. 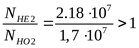 , ,
то
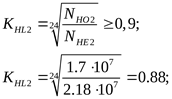
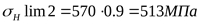 ; ;
 ; ;  ; ; 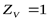 ; ;
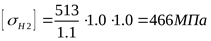 . .
8) Допускаемое контактное напряжение передачи ([3] формула 3.41)
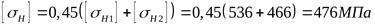 . .
Проверяем условие ([3] формула 3.42)
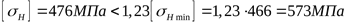 , ,
т.е. условие выполнено, поэтому принимаем допускаемое контактное напряжение передачи  . .
9) Допускаемое контактное напряжение при расчёте на действие максимальной нагрузки ([3] с. 80)
для шестерни
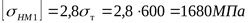 ; ;
для колеса
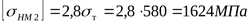 . .
4.2.2 Расчёт передачи на контактную выносливость
Согласно рекомендациям ([3] с. 61) принимаем пропорционально понижающие зубья (форма I).
Вычисляем начальный диаметр шестерни по большему торцу ([3] таблица 3.14, формула 3.20)

Предварительно определяем величины, необходимые для расчёта.
Номинальный крутящий момент на шестерне ([3] формула 3.12)
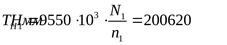
Ориентировочная окружная скорость зубчатых колёс ([3] формула 3.27)
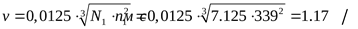 . .
При данной скорости требуемая степень точности зубчатых колёс ([3] таблица 3.33) – 9-я.
Коэффициент, учитывающий распределение нагрузки между зубьями для прямозубых передач ([3] c. 82)  . .
Коэффициент ширины венца ([3] формула 3.63) 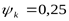 . .
Коэффициент, учитывающий распределение нагрузки по ширине венца ([3] рисунок 3.20,а), при отношении (Iб – роликовые подшипники)
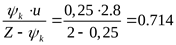 , , 
Коэффициент динамической нагрузки ([3] таблица 3.16)  для степени точности зубчатых колёс на единицу грубее установленной ([3] с. 80). для степени точности зубчатых колёс на единицу грубее установленной ([3] с. 80).
Коэффициент, учитывающий форму сопряжённых поверхностей ([3] формула 3.28).

Коэффициент, учитывающий механические свойства материалов сопряжённых колёс ([3] формула 3.29)
 . .
Выбираем число зубьев ([3] таблица 3.11) шестерни  и коэффициент торцевого перекрытия и коэффициент торцевого перекрытия 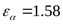 . .
Коэффициент, учитывающий суммарную длину контактных линий ([3] формула 3.30)
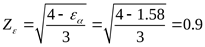 ; ;
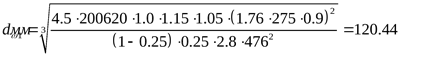 . .
Внешний окружной модуль
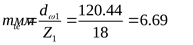 . .
Полученный модуль округляем по стандарту ([3] приложение таблица 9)
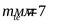 . .
Пересчитываем начальный диаметр
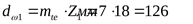 . .
Число зубьев плоского колеса ([3] таблицы 3.9)
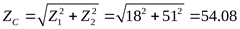 , ,
где 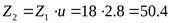 . .
Внешнее конусное расстояние ([3] таблица 3.9)
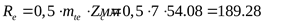
Рабочая ширина зубчатого венца ([3] таблица 3.1) при 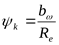
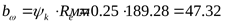 . .
Принимаем по стандарту ([3] приложение таблица 8) 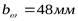
Проверяем условие ([3] формула 3.64)
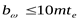 , т.е. , т.е.  условие соблюдено. условие соблюдено.
4.2.3 Проверочный расчёт зубьев на контактную выносливость
Средний нормальный модуль зацепления ([3] формула 3.4)
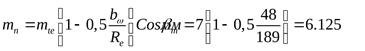 . .
Средний начальный диаметр шестерни ([3] с. 80)
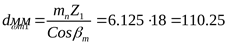 . .
Расчётная окружная скорость на среднем начальном диаметре шестерни
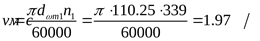 . .
При данной скорости ([3] таблица 3.33) требуемая степень точности передачи – 9-я, что совпадает с ранее принятой степенью точности.
Коэффициент, учитывающий окружную скорость передачи ([3] рисунок 3.17) 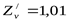 . .
Уточняем коэффициент динамической нагрузки ([3] таблица 3.16) 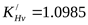 . .
Начальный диаметр шестерни по большему торцу ([3] формула 3.48)
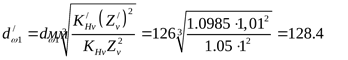 , ,
где  (см. определение (см. определение 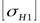 и и 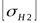 ). ).
Вновь определяем окружной модуль
 . .
Полученный модуль округляем до стандартного 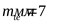 . .
Диаметр начальной окружности по большему торцу, соответствующий стандартному модулю
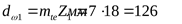 . .
4.2.4 Проверочный расчёт передачи на контактную прочность при действии максимальной нагрузки
Фактическое напряжение при расчёте на контактную выносливость ([3] таблица 3.14 формула 3.19)

Расчётное напряжение от максимальной нагрузки ([3] формула 3.60)
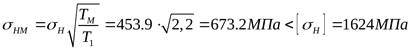
где отношение 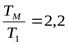 (задано при выборе электродвигателя). 4.2.5 Проверочный расчёт зубьев на выносливость по напряжениям изгиба (задано при выборе электродвигателя). 4.2.5 Проверочный расчёт зубьев на выносливость по напряжениям изгиба
Изгибающее напряжение для зуба шестерни ([3] таблица 3.14, формула 3.22)
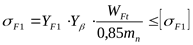 . .
Находим эквивалентное число зубьев для шестерни и колеса ([3] формула 3.7)
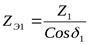 , , 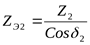
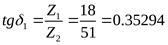 ([3] таблица 3.9) ([3] таблица 3.9)

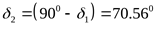
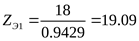 ; ; 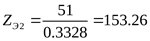 . .
Определяем коэффициенты, учитывающие форму зуба ([3] рисунок 3.21)
 ; ; 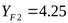 . .
Коэффициент, учитывающий влияние наклона зуба на его напряжённое состояние, для прямозубых колёс ([3] с. 77) 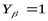 . .
Расчётная удельная нагрузка ([3] формула 3.25/)
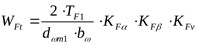 , ,
где 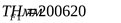 ; ;
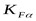 - коэффициент, усиливающий распределение нагрузки между зубьями ([3] c. 82), - коэффициент, усиливающий распределение нагрузки между зубьями ([3] c. 82), 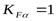 ; ;
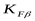 - коэффициент, учитывающий распределение нагрузки по ширине венца ([3] рисунок 3.20,б), при отношении - коэффициент, учитывающий распределение нагрузки по ширине венца ([3] рисунок 3.20,б), при отношении
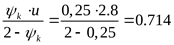 , , 
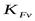 - коэффициент, учитывающий динамическую нагрузку ([3] таблица 3.16) при скорости - коэффициент, учитывающий динамическую нагрузку ([3] таблица 3.16) при скорости  , , 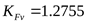 . .
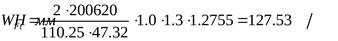 . .
Напряжение изгиба для зуба шестерни
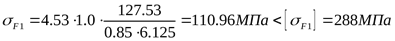 , ,
для зуба колеса
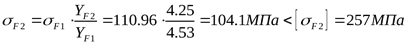
4.2.6 Проверочный расчёт зубьев при изгибе максимальной нагрузкой. Расчётное напряжение от максимальной нагрузки ([3] формула 3.61)
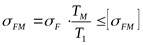
для зуба шестерни
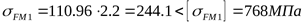 , ,
для зуба колеса
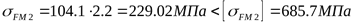 . .
4.2.7 Окончательно принимаем параметры передачи
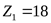 ; ;  ; ; 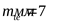 ; ; 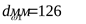 ; ; 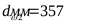 ; ; 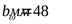 ; ;  ; ;  . .
4.3 Расчёт цилиндрической передачи
Расчёт цилиндрической передачи ведётся аналогично конической.
4.3.1 Выбор материала и допускаемых напряжений для шестерни и колеса
1) Назначаем материал ([3] таблица 3.12) для шестерни и колеса сталь 40ХН (поковка), термообработка – нормализация;
для шестерни  , ,  , 280НВ1; , 280НВ1;
для колеса 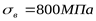 , , 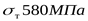 , 250НВ2. , 250НВ2.
2) Определяем допускаемое напряжение изгиба для шестерни
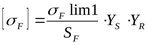
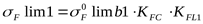


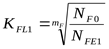
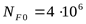
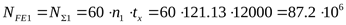
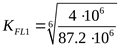 , ,
но т.к. 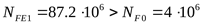 ([3] с. 77) ([3] с. 77)
принимаем 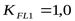 . .
Соответственно  . .
Коэффициент безопасности ([3] формула 3.56)
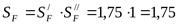 , ,
 ; ;  ; ;  ; ;  , ,
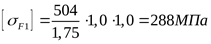 . .
3) Допускаемое напряжение изгиба для зубьев колеса определяем аналогично предыдущему расчёту
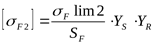 , ,
 , ,
где
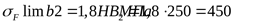 , ,
 , ,
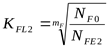 . .
При НВ<350 
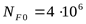
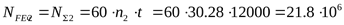
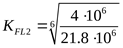
но т.к. 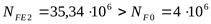 ,* ,*
то принимаем 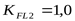
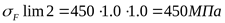 . .
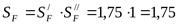
 ; ;    . .
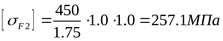
4) Допускаемое напряжение изгиба при расчёте на действие максимальной нагрузки ([3] таблица 3.19) для шестерни
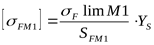 . .

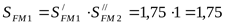 , ,
где  , , 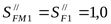 , ,  . .
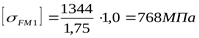 . .
5) Допускаемое напряжение изгиба при действии максимальной нагрузки для колеса

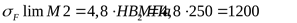
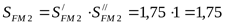
 , , 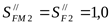 , ,  . .
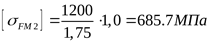 . .
6) Допускаемое контактное напряжение для шестерни ([3] формула 3.33)
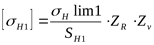 . .
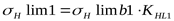 , ,
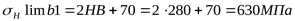 ; ;
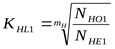 , ,
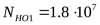
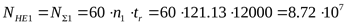 . .
Отношение 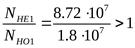 поэтому коэффициент долговечности определяем по формуле 3.38 [3] поэтому коэффициент долговечности определяем по формуле 3.38 [3]
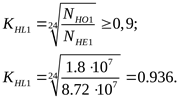
Принимаем 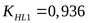 . .
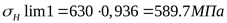 . .
 ; ;  ; ; 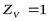 ; ;
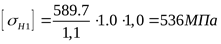 . .
7) Допускаемое контактное напряжение для колеса
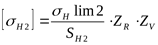 ; ;
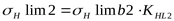 ; ;
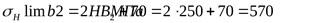 ; ;
 ; ;
 ; ;
 ; ;
т.к. 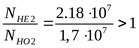 , ,
то
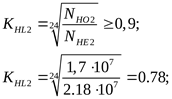
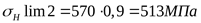 ; ;
 ; ;  ; ; 
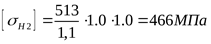 . .
8) Допускаемое контактное напряжение передачи ([3] формула 3.41)
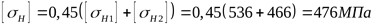 . .
Проверяем условие ([3] формула 3.42)
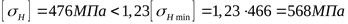 , ,
т.е. условие выполнено, поэтому принимаем допускаемое контактное напряжение передачи  . .
9) Допускаемое контактное напряжение при расчёте на действие максимальной нагрузки ([3] с. 80)
для шестерни
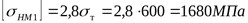 ; ;
для колеса
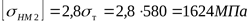 . .
4.3.2 Расчёт передачи на контактную выносливость
Начальный диаметр шестерни ([3] таблица 3.13, формула 3.16)
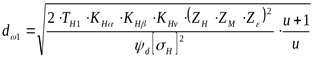
Номинальный крутящий момент на шестерне ([3] формула 3.12)
 . .
Ориентировочная окружная скорость ([3] формула 3.27)
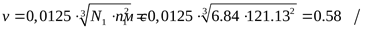
При данной скорости требуется степень точности зубчатых колёс ([3] таблица 3.33) – 9-я.
Коэффициент, учитывающий распределение нагрузки между зубьями ([3] рисунок 3.13), 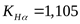 . .
Коэффициент ширины зубчатого венца при несимметричном расположении опор ([3] таблица 3.15)
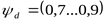 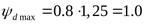 . .
Проверяем условие ([3] формула 3.26)
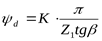
Принимаем ([3] с.71) K=2
угол наклона ([3] с. 60)  ; ;
минимальное число зубьев шестерни ([3] таблица 3.3)  ; ;
расчётное число зубьев шестерни ([3] c. 58)
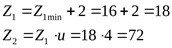
Соответственно
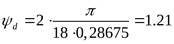
Коэффициент, учитывающий распределение нагрузки по ширине венца ([3] рисунок 3.14,б) 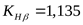 . .
Коэффициент, учитывающий динамическую нагрузку ([3] таблица 3.16) 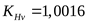 . .
Коэффициент, учитывающий форму сопряжённых поверхностей ([3] формула 3.28/) 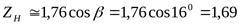 . .
Коэффициент, учитывающий механические свойства материалов сопряжённых колёс ([3] формула 3.29) 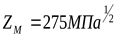 . .
Коэффициент, учитывающий суммарную длину контактных линий ([3] формула 3.31)
 , ,
где  - коэффициент торцевого перекрытия ([3] формула 3.3) - коэффициент торцевого перекрытия ([3] формула 3.3)
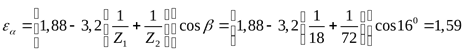
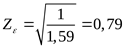 . .
Тогда
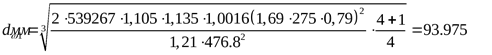
Модуль зацепления ([3] формула 3.46)
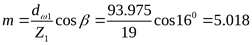 . .
Полученный модуль округляем до стандартного значения ([3] приложение, таблица 9) m=5мм.
По стандартному модулю пересчитываем начальный диаметр
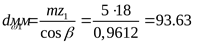 . .
4.3.3 Проверочный расчёт передачи на контактную выносливость
Определяем расчётную окружную скорость ([3] формула 3,47) при начальном диаметре шестерни 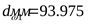
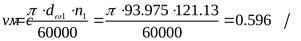 . .
При данной скорости требуемая степень точности передачи – 9-я, что соответствует принятой ранее. Уточняем по скорости 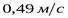 коэффициенты: коэффициенты:
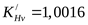 ([3] таблица 3.16); ([3] таблица 3.16);  ([3] рисунок 3.13); ([3] рисунок 3.13);  ([3] рисунок 3.17). ([3] рисунок 3.17).
Уточняем начальный диаметр шестерни ([3] формула 3.48)
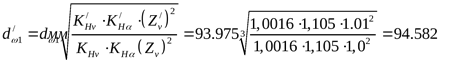 . .
По уточнённому начальному диаметру 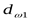 находим модуль зацепления находим модуль зацепления
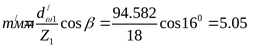 . .
Полученный модуль вновь округляем до стандартного значения 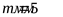 , что совпадает с ранее принятой величиной модуля. Следовательно диаметр начальной окружности шестерни , что совпадает с ранее принятой величиной модуля. Следовательно диаметр начальной окружности шестерни 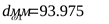 . .
Ширина зубчатого венца при  ([3] таблица 3.1) ([3] таблица 3.1)
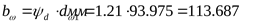 . .
Принимаем 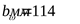 . .
4.3.4 Проверочный расчёт зубьев на контактную прочность при действии максимальной нагрузки
Расчётное напряжение от максимальной нагрузки ([3] формула 3.60)
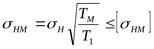 , ,
где действующее напряжение при расчёте на контактную выносливость ([3] таблица 3.13 формула 3.15)
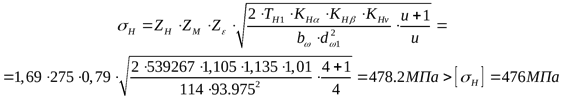
Отклонение действующих контактных напряжений от допустимых составляет 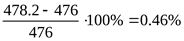 , что допустимо. , что допустимо.
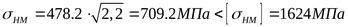 . .
4.3.5 Проверочный расчёт зубьев на выносливость по напряжениям изгиба
Расчётное напряжение изгиба ([3] таблица 3.13, формула 3.17)
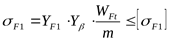
Предварительно определяем величины необходимые для расчёта.
Эквивалентное число зубьев шестерни и колеса ([3] с. 76)
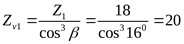 ; ; 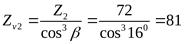 . .
Коэффициенты, учитывающие форму зуба и шестерни и колеса ([3] рисунок 3.18)  , ,  . .
Коэффициент, учитывающий влияние наклона зуба на его напряжённое состояние ([3] формула 3.50) 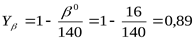 . .
Расчётная удельная нагрузка ([3] формула 3.25/)
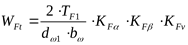 , ,
где коэффициент, учитывающим распределение нагрузки между зубьями ([3] формула 3.40) 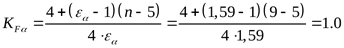 , ,
где n – порядковый номер степени точности.
Коэффициент, учитывающий распределение нагрузки по ширине венца ([3] рисунок 3.14,г)  . .
Коэффициент, учитывающий динамическую нагрузку ([3] таблица 3.16)

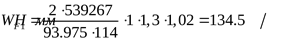 . .
Напряжение изгиба в зубьях шестерни
 ; ;
в зубьях колеса ([3] таблица 3.13, формула 3.17/)
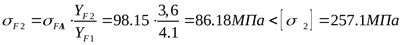 . .
4.3.6 Проверочный расчёт при изгибе максимальной нагрузкой
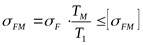
для зубьев шестерни 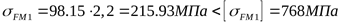
для зубьев колеса 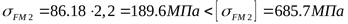
4.3.7 Принимаем окончательно параметры передачи
 ; ;  ; ; 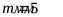 ; ;  ; ; 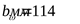 ; ; 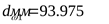 ; ;
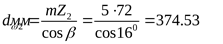 . .
Определим межосевое расстояние
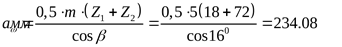 . .
Проверим межосевое расстояние
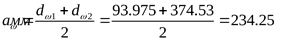 . .
4.3.8 Округлим межосевое расстояние до целого стандартного числа, для чего принимаем угол наклона 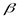 ([3] формула 3.2/) ([3] формула 3.2/)
Принимаем межосевое расстояние 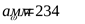 , что соответствует стандартной величине ([3] приложение таблица 8), соответственно угол наклона , что соответствует стандартной величине ([3] приложение таблица 8), соответственно угол наклона
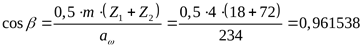

Пересчитываем начальные диаметры
шестерни 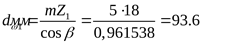 ; ;
колеса 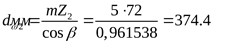 . .
Проверяем межосевое расстояние
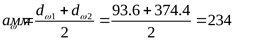 . .
4.4 Выбор параметров и расчёт геометрии зубчатых колёс
4.4.1 Основные размеры цилиндрической передачи ([3] таблица 3.5)
Угол наклона зуба на диаметре d 
Угол профиля рейки в торцевом сечении 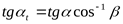 , , 
Угол зацепления в нормальном сечении 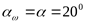
Угол зацепления в торцевом сечении 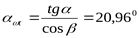
Межосевое расстояние 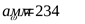
Делительный и начальный диаметры:
шестерни 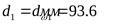
колеса 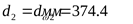
Диаметр вершин зубьев;
шестерни 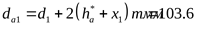
колеса 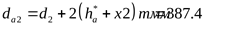
Диаметр впадин:
шестерни 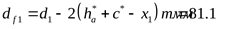
колеса 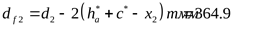
4.4.2 Основные размеры конической передачи ([3] таблица 3.9)
Число зубьев плоского колеса 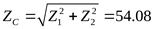
Ширина зубчатого венца 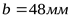 , , 
Внешнее конусное расстояние 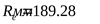
Среднее конусное расстояние 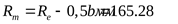
Диаметр внешней делительной
(начальной) окружности
шестерни 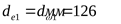
колеса 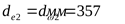
Средний делительный диаметр
шестерни 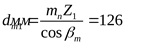
колеса 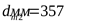
Глубина захода 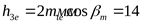
Радиальный зазор 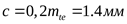
Высота зуба у торца 
Высота головки зуба у торца:
шестерни 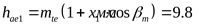
колеса 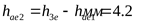
Высота ножки зуба у торца;
шестерни 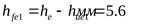
колеса 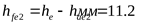
Угол делительного конуса:
шестерни 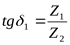 ; ; 
колеса 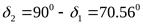
Угол ножки зуба
шестерни 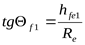 ; ; 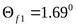
колеса 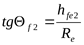 ; ; 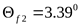
Угол конуса вершин
шестерни 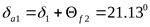
колеса 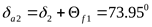
Угол конуса впадин
шестерни 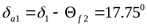
колеса 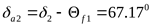
Внешний диаметр вершин
шестерни 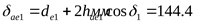
колеса 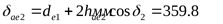
5. Эскизная компановка редуктора
5.1 Проектный расчёт валов на кручение, выбор типа и схемы установки подшипников
Т.к. на настоящем этапе расстояние между опорами неизвестны, ориентировочно диаметр вала в опасном сечении определяется из условий прочности на кручение при пониженных допускаемых напряжениях ([3] формула 4.1)
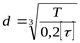
где Т – крутящий момент, Н-мм;
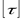 - допускаемое напряжение на кручение: - допускаемое напряжение на кручение:
 - допускаемое напряжение на кручение для ведущего вала; - допускаемое напряжение на кручение для ведущего вала;
 - допускаемое напряжение на кручение для промежуточного вала; - допускаемое напряжение на кручение для промежуточного вала;
 - допускаемое напряжение на кручение для ведомого вала. - допускаемое напряжение на кручение для ведомого вала.
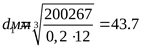 принимаем принимаем 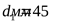
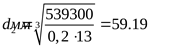 принимаем принимаем 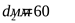
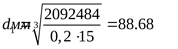 принимаем принимаем 
Первоначально внутренний диаметр подшипника выбираем по принятому (округлённому до нуля или пяти) ориентировочному диаметру вала, рассчитанному по формуле 4.1 с добавлением приблизительно 5мм. Для ведущего и промежуточного валов принимаем подшипники - роликовые конические средней серии, для ведомого – шарикоподшипники радиальные лёгкой серии. Критические роликоподшипники ведущего и промежуточного валов устанавливаем по прямой схеме – в распор.
Ось конической шестерни располагаем в плоскости симметрии корпуса, шестерню устанавливаем на консоли вала, расстояние между подшипниками предварительно принимаем равным (2,5…3,5)d, где d – диаметр вала, определённый при ориентировочном расчёте.
5.2 Основные размеры корпусов, крышек, болтов, винтов редуктора ([3] таблица 4.3)
Толщина стенки корпуса редуктора 
Толщина стенки крышки редуктора 
Толщина верхнего фланца корпуса 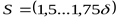 , , 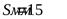
Толщина нижнего фланца корпуса 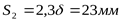
Толщина фланца крышки редуктора 
Диаметр фундаментных болтов 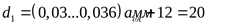
Число фундаментных болтов 
Диаметр болтов, стягивающих
корпус и крышку у бобышек 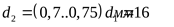
Диаметр болтов, стягивающих
фланцы корпуса и крышки 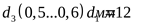
Ширина опорной поверхности
Нижнего фланца корпуса 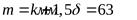
Толщина рёбер конуса 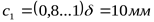
Минимальный зазор между колесом
и корпусом 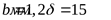
Координата стяжного болта 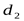
у бобышек 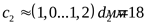
6 Расчёт валов на сложное сопротивление
6.1 Расчёт ведущего вала
1
) Определение составляющих усилия в зацеплении ([3] таблица 5.2)
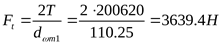
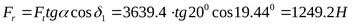
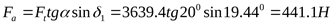
2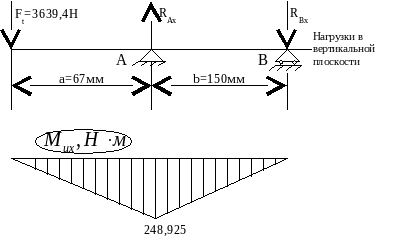 ) Составление расчётной схемы, определение опорных реакций и построение эпюр изгибающих моментов в различных плоскостях ) Составление расчётной схемы, определение опорных реакций и построение эпюр изгибающих моментов в различных плоскостях
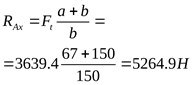
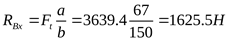
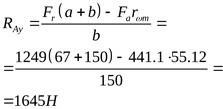 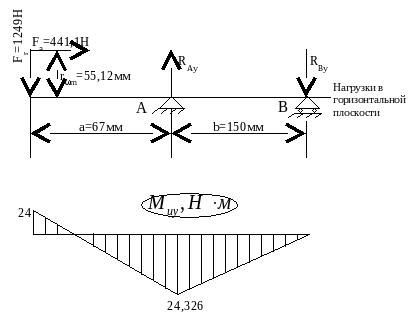
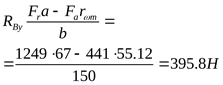
3) Построение эпюры суммарных изгибающих моментов
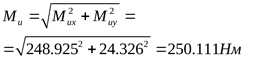
([3] формула 5.1)
4) Построение эпюры крутящего момента
5) Построение эпюры приведенных моментов
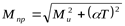 ([3] формула5.2) ([3] формула5.2)
 (реверсивная передача[3] с.171) (реверсивная передача[3] с.171)
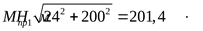
 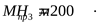
6) Расчётный диаметр вала ([3] формула 5.3)
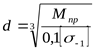
где 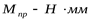 , , 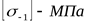 ([3] таблица 5.3) ([3] таблица 5.3)
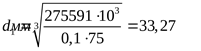
6.2 Расчёт промежуточного вала
1) Определение составляющих усилий в зацеплении
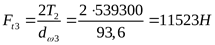
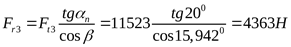
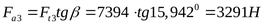
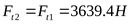
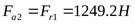

2) Составление расчётной схемы, определение опорных реакций и построение эпюр изгибающих моментов в различных плоскостях
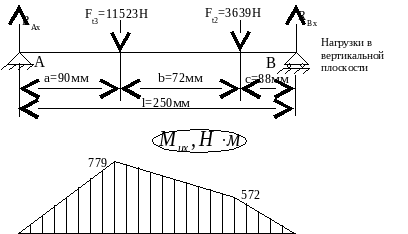
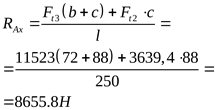
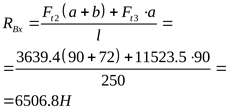
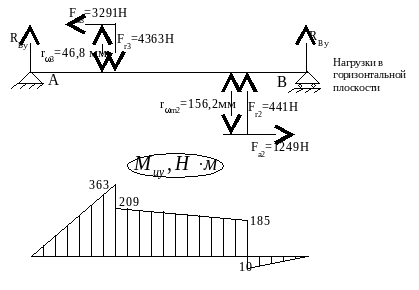
3) Построение эпюры суммарных изгибающих моментов
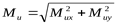 ([3] формула 5.1) ([3] формула 5.1)
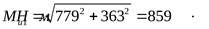
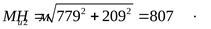
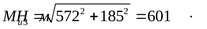
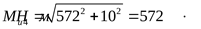
4) Построение эпюры крутящего момента
5) Построение эпюры приведенных моментов
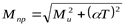 , , 
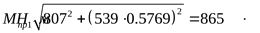
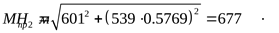
6) Расчётный диаметр вала ([3] формула 5.3)
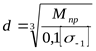
где 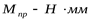 , , 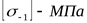 ([3] таблица 5.3) ([3] таблица 5.3)
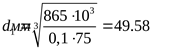 ; ;
6.3 Расчёт ведомого вала
1) Определение составляющих усилия в зацеплении
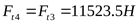

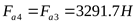
2) Составление расчётной схемы, определение опорных реакций и построение эпюр изгибающих моментов в различных плоскостях
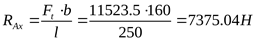
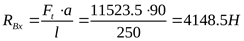
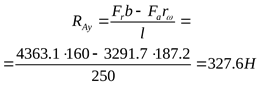 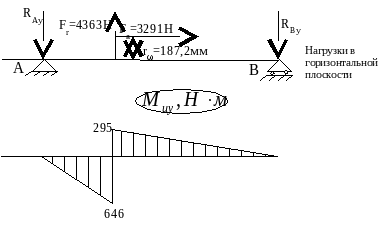
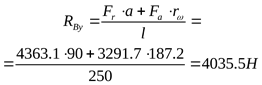
3) Построение эпюры суммарных изгибающих моментов
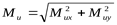
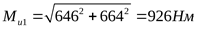
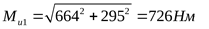
4) Построение эпюры крутящего момента
5) Построение эпюры приведенных моментов
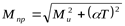 , , 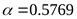
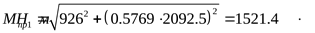
6) Расчётный диаметр вала
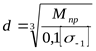
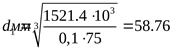
7 Проверочный расчёт подшипников по динамической грузоподъёмности
7.1 Расчёт подшипников ведущего вала
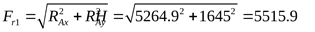
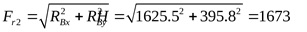
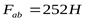 - воспринимает подшипник 2 - воспринимает подшипник 2
Посадочные диаметры – 35мм
Lh=12000ч
V=Ks=Kт=1
n=339мин-1
1) Принимаем предварительно подшипники 7307, у которых
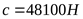 , , 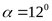 , , 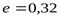
2) Осевые составляющие радиальных нагрузок FS ([3] формула 6.10)
подшипник 1:
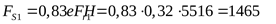
подшипник 2:
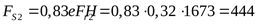
3) Расчётная осевая нагрузка
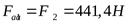
4) Находим отношение ([3] формула 6.9)
подшипник 1:
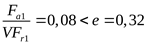 , принимаем коэффициенты , принимаем коэффициенты 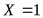 , , 
подшипник 2:
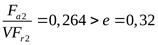 , принимаем коэффициенты , принимаем коэффициенты 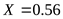 , , 
5) Эквивалентная расчётная нагрузка ([3] таблица 6.5 формула 5)
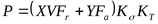
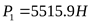
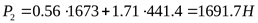
Поскольку для обеих опор подшипники выбирают одинаковые, дальнейший расчёт ведём по наиболее нагруженному подшипнику опоры 1.
6) Находим методом интерполяции отношение 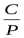 ([3] приложение таблица 21) ([3] приложение таблица 21)
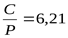 , отсюда требуемая грузоподъёмность , отсюда требуемая грузоподъёмность  , что гораздо меньше реальной грузоподъёмности (С=48100Н) и обеспечит большой запас долговечности подшипников. , что гораздо меньше реальной грузоподъёмности (С=48100Н) и обеспечит большой запас долговечности подшипников.
7.2 Расчёт подшипников промежуточного вала
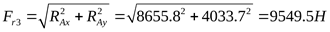
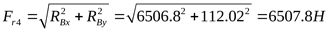
Посадочные диаметры d=45мм
Lh=12000ч
V=Ks=KT=1
n=121мин-1
1) Принимаем предварительно подшипник 7309, у которого
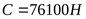 , ,  , , 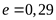
2) Осевые составляющие радиальных нагрузок 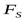
подшипник 1:
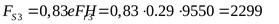
подшипник 2:
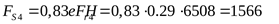
3) Расчётная осевая нагрузка
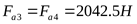
4) Находим отношение ([3] формула 6.9)
подшипник 1:
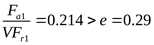 , принимаем коэффициенты , принимаем коэффициенты 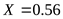 , , 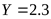
подшипник 2:
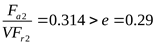 , принимаем коэффициенты , принимаем коэффициенты 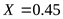 , , 
5) Эквивалентная расчётная нагрузка ([3] таблица 6.5 формула 5)
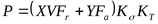
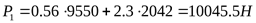
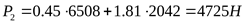
Поскольку для обеих опор подшипники выбирают одинаковые, дальнейший расчёт ведём по наиболее нагруженному подшипнику опоры 1.
6) Находим методом интерполяции отношение 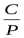 ([3] приложение таблица 21) ([3] приложение таблица 21)
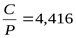 , отсюда требуемая грузоподъёмность , отсюда требуемая грузоподъёмность 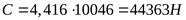 , что несколько меньше реальной грузоподъёмности (С=76100Н) и обеспечит запас долговечности подшипников. , что несколько меньше реальной грузоподъёмности (С=76100Н) и обеспечит запас долговечности подшипников.
7.3 Расчёт подшипников ведомого вала
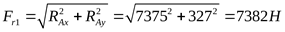
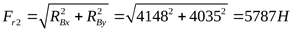
, 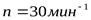 , , 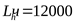 , , 
1) Принимаем предварительно 210 шарикоподшипник, у которого 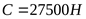 , , 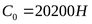 . .
2) Выбираем коэффициенты X и Y.
Поскольку 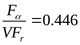 , ,
то 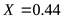 , , 
3) Определяем эквивалентную нагрузку
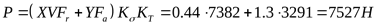 . .
4) Находим методом интерполяции отношение 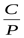 ([3] приложение таблица 21) ([3] приложение таблица 21)
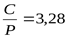 , отсюда требуемая грузоподъёмность , отсюда требуемая грузоподъёмность 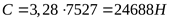 , что несколько меньше реальной грузоподъёмности (С=27500Н) и обеспечит запас долговечности подшипников. , что несколько меньше реальной грузоподъёмности (С=27500Н) и обеспечит запас долговечности подшипников.
СПИСОК ЛИТЕРАТУРЫ
1. Баласанян Р.А. Атлас деталей машин
2. Дунаев П.Ф., Леликов О.П. Конструирование узлов и деталей машин. – М.: Высшая школа, 1998.
3. Киркач Н.Ф., Баласанян Р.А. Расчёт и проектирование деталей машин. Изд. 3-е. – Х.: Основа, 1991.
|