Задача 1
При выборочном бесповторном собственно-случайном отборе 5% коробок конфет со стандартным весом 20 кг получены следующие данные о недовесе.
| Недовес 1 коробки, кг |
0,4-0,6 |
0,6-0,8 |
0,8-1,0 |
1,0-1,2 |
1,2-1,4 |
| Число обследованных коробок |
10 |
18 |
36 |
26 |
10 |
Определите:
1) средний недовес одной коробки конфет и его возможные пределы
(с вероятностью Р=0,954);
2) долю коробок с недовесом до 1 кг;
3) возможные пределы доли коробок с недовесом до 1 кг
(с вероятностью 0,683). Сделайте выводы.
Решение:
1) средний недовес одной коробки конфет и его возможные пределы
(с вероятностью Р=0,954);
| Недовес 1 коробки, кг |
Число обследованных коробок f |
Середина интервала х |
хf |
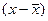 |
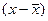 2 2
|
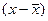 2
f 2
f |
| 0,4-0,6 |
10 |
0,5 |
5 |
-0,416 |
0,17306 |
1,73056 |
| 0,6-0,8 |
18 |
0,7 |
12,6 |
-0,216 |
0,04666 |
0,83981 |
| 0,8-1,0 |
36 |
0,9 |
32,4 |
-0,016 |
0,00026 |
0,00922 |
| 1,0-1,2 |
26 |
1,1 |
28,6 |
0,184 |
0,03386 |
0,88026 |
| 1,2-1,4 |
10 |
1,3 |
13 |
0,384 |
0,14746 |
1,47456 |
| Итого: |
100 |
- |
91,6 |
- |
- |
4,9344 |
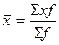 =91,6/100=0,9 – средний недовес одной коробки =91,6/100=0,9 – средний недовес одной коробки
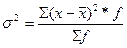 =4,9344/100=0,493 =4,9344/100=0,493
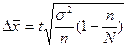 =2* =2*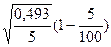 =0,193 =0,193
Вычислим пределы среднего недовеса одной коробки для всей партии:
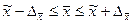
0,9-0,23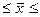 0,9+0,23 0,9+0,23
0,7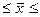 1,13 1,13
С вероятностью 0,954 (т.е. в 95,4 коробках из 100) можно утверждать, что средний недовес колеблется в пределах от 0,7 до 1,13 кг.
2) долю коробок с недовесом до 1 кг;
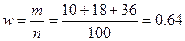
3) возможные пределы доли коробок с недовесом до 1 кг
(с вероятностью 0,683). Сделайте выводы.
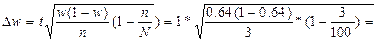 0,27 0,27
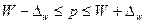
0,64-0,27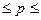 0,64+0,27 0,64+0,27
0,37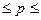 0,91 0,91
С вероятностью 0,683 (то есть в 68,3 коробках из 100) можно гарантировать, что доля недовеса до 1 кг будет находиться в пределах от 0,37 до 0,91 кг.
Задача 2
Ежегодные темпы прироста реализации товара «А» составили в % к предыдущему году:
1998 – 5,5;
1999 – 6,2;
2000 – 8,4;
2001 – 10,5;
2002 – 9,2
Исчислите за приведённые годы базисные темпы роста по отношению к 1997 г. и среднегодовой темп прироста за 1998 – 2002 гг.
Решение
Приведём исходные данные в таблице
| Год |
Темп прироста цепной, % |
| 1997 |
- |
| 1998 |
5,5 |
| 1999 |
6,2 |
| 2000 |
8,4 |
| 2001 |
10,5 |
| 2002 |
9,2 |
Воспользуемся связью цепных и базисных темпов роста
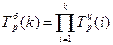
Составим расчётную таблицу
| Год |
Темп прироста цепной, % |
Темп роста цепной |
Темп роста базисный |
Темп прироста базисный, % |
| 1997 |
- |
- |
1,000 |
- |
| 1998 |
5,5 |
1,055 |
1,055 |
5,5 |
| 1999 |
6,2 |
1,062 |
1,120 |
12,0 |
| 2000 |
8,4 |
1,084 |
1,215 |
21,5 |
| 2001 |
10,5 |
1,105 |
1,342 |
34,2 |
| 2002 |
9,2 |
1,092 |
1,466 |
46,6 |
При этом среднегодовой темп роста за 1998 – 2002 гг. равен
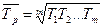
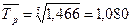 , ,
или 108,0%
Тогда среднегодовой темп роста за 1998 – 2002 гг. равен 108,0% - 100%=8,0%
Задача 3
Имеются следующие выборочные данные о расходах на платные услуги домохозяйств района:
| Домохозяйство |
Обследовано домохозяйств |
Доля расходов на платные услуги, % |
| Городское |
400 |
30 |
| Сельское |
100 |
10 |
Определите для домохозяйств района:
1. общую дисперсию;
2. среднюю из групповых дисперсий;
3. межгрупповую дисперсию, используя правило сложения дисперсий;
4. эмпирический коэффициент детерминации;
5. эмпирическое корреляционное отношение. Поясните полученные показатели.
Решение:
- общую дисперсию по правилу сложения дисперсии;
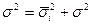
Обследовано домохозяйств
f
|
Доля расходов на платные услуги х |
(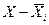 ) ) |
(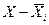 )2 )2
|
(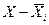 )2
f )2
f |
| 400 |
30 |
4 |
16 |
6400 |
| 100 |
10 |
-16 |
256 |
25600 |
| 500
|
32000
|
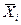 = =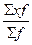 =32000/500=26 =32000/500=26
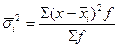 =32000/500=64 =32000/500=64
Домохозяйство
f
|
Доля расходов на платные услуги х |
(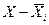 ) ) |
(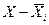 )2 )2
|
(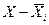 )2
f )2
f |
| 400 |
30 |
10 |
100 |
40000 |
| 100 |
10 |
-10 |
100 |
10000 |
| 500
|
40
|
50000
|
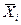 =40/2=20 =40/2=20
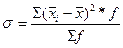 =50000/500=100 =50000/500=100
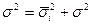 =100+64=164 =100+64=164
- эмпирическое корреляционное отношение.
Реклама

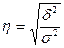 = =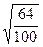 =0,80 =0,80
Чем значение корреляционного отношения ближе к единице, тем теснее, ближе к функциональной зависимости связь между признаками.
- эмпирический коэффициент детерминации
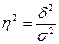 =0,64 =0,64
Этоозначает,
что на 64% вариация расходов обусловлена тем, что услуги являются платными и 36% бесплатными.
Задача 4
По отделению банка имеются следующие данные о вкладах населения:
| Виды вкладов |
Базисный период |
Отчетный период |
| Количество счетов |
Остаток вкладов, тыс. руб. |
Количество счетов |
Остаток вкладов, тыс. руб. |
| Депозитный |
10000 |
10200 |
10500 |
11200 |
| Срочный |
2500 |
5400 |
4200 |
5800 |
| Выигрышный |
500 |
250 |
400 |
280 |
| Итого:
|
13000
|
15850
|
15100
|
17280
|
Определите
1) Средний размер вклада в базисном и отчетном периодах.
2) Индексы среднего размера вклада:
· переменного состава;
· постоянного состава;
· структурных сдвигов.
Покажите взаимосвязь рассчитанных индексов.
Решение:
1)
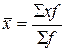
(баз)= 15850/13000=1,219 тыс.руб.
(отч)= 17280/15100=1,144 тыс.руб.
2) Индекс переменного состава:
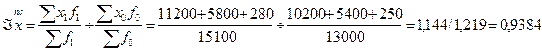
Следовательно, средний размер вклада по данным трем видам в отчетном году снизился на 6,16%
Индекс постоянного состава:
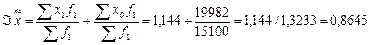
Следовательно, средний размер вклада по данным видам снизился на 13,5% в результате изменения только одного фактора – самого вклада по каждому виду.
Индекс структурных сдвигов:
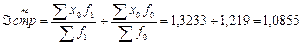
Следовательно, увеличение доли видов вклада с меньшим его размером в общей сумме привело к увеличению среднего вклада по трем видам вместе на 8,55%.
3) Покажите взаимосвязь рассчитанных индексов:
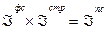 1,0855*0,8645=0,9384 1,0855*0,8645=0,9384
Задача 5
Валовой выпуск товаров и услуг в рыночных ценах в производственной сфере Российской Федерации за отчётный период составил 5130,2 млрд. руб., в непроизводственной сфере – 1520,9 млрд. руб. Условно исчисленная продукция финансового посредничества в экономике составила 126,8 млрд. руб. Определите валовую добавленную стоимость по сферам деятельности и в целом по экономике, если промежуточное потребление в производственной сфере составило 2790,5 млрд. руб., в непроизводственной – 680,3 млрд. руб.
Решение
Валовая добавленная стоимость (ВДС) определяется как разность между стоимостью выпуска товаров и услуг (ВВ) и промежуточным потреблением (ПП)
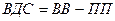
В производственной сфере
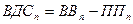
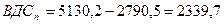 млрд. руб. млрд. руб.
дисперсия корреляционный валовый стоимость прирост
В непроизводственной сфере
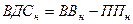
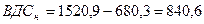 млрд. руб. млрд. руб.
В целом по экономике
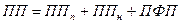
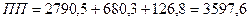 млрд. руб. млрд. руб.
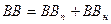
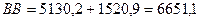 млрд. руб. млрд. руб.
Тогда
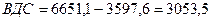 млрд. руб. млрд. руб.
Имеются следующие данные по области на начало текущего года (тыс. чел.)
| Население рабочего возраста1 |
880 |
| Нетрудоспособное население рабочего возраста1 |
58,5 |
| Фактически работающие пенсионеры и подростки12 |
31,8 |
| Из общей численности трудоспособного населения занято работой и учёбой в других областях2 |
12,8 |
| Занято частным предпринимательством2 |
181,8 |
| Занято на производственных предприятиях2 |
564,1 |
| Учащиеся с отрывом от производства рабочего возраста2 |
35,9 |
| Занято в домашнем хозяйстве и уходом за детьми2 |
68,4 |
| Из общей численности занятых и учащихся проживает в других областях2 |
9,3 |
Определите
1) численность трудовых ресурсов двумя методами;
2) коэффициенты занятости трудовых ресурсов (с учётом и без учёта учащихся)
Решение
Трудовые ресурсы – это население обоего пола, способное к труду по возрасту и состоянию здоровья. Численность трудовых ресурсов определяется двумя методами:
-по источникам формирования (демографический метод) – исходя из численности населения в трудоспособном возрасте за исключением инвалидов I и II групп и лиц, получающих пенсию по возрасту на льготных условиях. В трудовые ресурсы включаются работающие лица нетрудоспособного возраста. В настоящее время границами трудоспособного возраста в России считают 16-54 года – для женщин и 16 – 59 лет – для мужчин
Реклама

-по фактической занятости (экономический метод) – как совокупность всего фактически занятого населения, включая работающих пенсионеров и подростков, а также лиц трудоспособного возраста, занятых в домашнем хозяйстве и уходом за детьми, учащихся с отрывом от производства старше 16 лет, безработных
1) Демографический метод
880-58,5=821,5
– трудоспособное население рабочего возраста
821,5+31,8=853,3
– трудовые ресурсы
ТР=880-58,5+31,8=853,3 тыс. чел.
Экономический метод
Занятые
181,8+564,1+68,4+31,8+35,9=882
В других областях
9,3+12,8=22,1
ТР=882-22,1=859,9 тыс. чел.
Численное расхождение возможно из – за не точных данных
2) Всего учащихся 35,9
Коэффициент занятости с учётом учащихся равен
Кз
=859,9/882=0,975
Коэффициент занятости без учёта учащихся равен
Кз
=(859,9-35,9)/882=0,934
Задача 7
Имеются следующие данные о движении основных производственных фондов, тыс. руб.:
| 1. Первоначальная стоимость ОПФза вычетом износа на начало года |
3875 |
| 2. Сумма износа на начало года |
2075 |
| 3. Введено в действие новых ОПФ за год |
1090 |
4. Выбыло в течение года ОПФ:
по полной стоимости
по остаточной стоимости
|
670
300
|
| 5. Начислено амортизации на полное восстановление ОПФ за год |
60,3 |
| 6. Объем продукции (работ, услуг) |
3800 |
| 7. удельный вес активной части ОПФ |
55% |
Определите:
1) Коэффициент годности ОПФ на начало года;
2) коэффициенты ввода и выбытия;
3) Фондоотдачу всех ОПФ и активной части;
4)Фондоемкость продукции
Решение:
1)Кгодности=
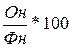 = =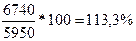
2) полную стоимость ОПФ на начало и конец года;
Фн=3875+2075=5950 тыс. руб.
Фк=Фн+Фп-Фв=5950+1090-670=6370 тыс. руб.
3) коэффициенты вода и выбытия ОПФ на начало года
Кввода=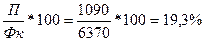
Квыбытия=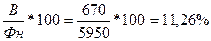
Кизноса=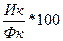 = =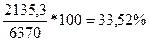
Кгодности=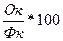 = =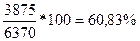
4) Фондоотдача = Объем продукции / Стоимость
ОС = 3800/6679,7 = 0,99 (р. с 1р. средств)
Фондоотдача (акт.части)= Объем продукции / Стоимость
ОС = 3800/3673,8 = 1,03(р. с 1р. средств)
Фондоемкость = Стоимость ОС / Объем продукции = 6679,7/3800 = 1,01
Баланс по полной восстановительной стоимости за вычетом износа
| Наличие на начало года |
Введено |
Выбыло всего |
Наличие на конец года |
| Ликвидировано |
Выбыло |
Износ за год |
| 1 |
2 |
3 |
4 |
5 |
6 |
| 5950 |
1090 |
670 |
60,3 |
6679,7 |
1. Гусаров В.М. Теория статистики: Учебное пособие. – М.: Юнити, 2003.
2. Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник. – 4-ое изд. перераб. и доп. – М.: Финансы и статистика, 2002.
3. Статистика: Учебное пособие под ред. Ионина В.Г. – 2-ое изд. перераб. и доп. – М.: ИНФРА-М, 2005.
4. Теория статистики: Учебник под ред. Р.А. Шмойловой – 4-ое изд., перераб. и доп. – М.: Финансы и статистика, 2005.
|