Федеральное агентство по образованию
ГОУ ВПО «Московский Государственный Открытый Университет»
Чебоксарский политехнический институт
Кафедра: Управление и информатика в технических системах
специальность 220201
Курсовая работа
Оптимальная система автоматического управления
Выполнил: студент V курса д/о
ФУИТС шифр: 604020
Белоусов А.В.
Проверил: пр. Изосимова Т.
Чебоксары 2008
Содержание
Введение
Задание
1. Анализ методов определения минимального, максимального
значения функции без ограничения
1.1 Методы прямого поиска
1.2 Градиентные методы
1.3 Методы второго порядка
2. Нахождение экстремума функции без ограничения
2.1 Метод наискорейшего спуска
2.2 Метод сопряженных направлений
3. Анализ методов определения минимального, максимального
значения функции при наличии ограничений
3.1 Методы возможных направлений
3.2 Методы проекции градиента
3.3 Методы линеаризации
3.4 Методы штрафов
4. Нахождение экстремума функции при наличии ограничения
4.1 Метод симплексных процедур
5. Синтез оптимальной по быстродействию системы с помощью принципа максимума Понтрягина
Звулючение
Список литературы
Приложение
Введение
В наиболее общем смысле теория оптимизации представляет собой совокупность фундаментальных математических результатов и численных методов, ориентированных на нахождение и идентификацию наилучших вариантов из множества альтернатив и позволяющих избежать полного перебора и оценивания возможных вариантов. Процесс оптимизации лежит в основе всей инженерной деятельности, поскольку классические функции инженера заключаются в том, чтобы, с одной стороны, проектировать новые, более эффективные, менее дорогостоящие технические системы и, с другой стороны, разрабатывать методы повышения качества функционирования существующих систем.
Эффективность оптимизационных методов, позволяющих осуществить выбор наилучшего варианта без непосредственной проверки всех возможных вариантов, тесно связана с широким использованием достижений в области математики путем реализации итеративных вычислительных схем, опирающихся на строго обоснованные логические процедуры и алгоритмы, на базе применения вычислительной техники. Поэтому для изложения методологических основ оптимизации требуется привлечение важнейших результатов теории матриц, элементов линейной алгебры и дифференциального исчисления, а также положений математического анализа. Математические понятия и конструкции используются не только для того, чтобы повысить уровень строгости представления материала, но и потому, что они составляют терминологическую базу изложения, которая позволяет упростить описание и определение структурных элементов рассматриваемых вычислительных процедур и облегчить их понимание.
Реклама

Поскольку размерность инженерных задач, как правило, достаточно велика, а расчеты требуют значительного времени, оптимизационные методы ориентированы главным образом на реализацию с помощью ЭВМ.
Задание
Вариант 2
Дана несепарабельная функция двух переменных:
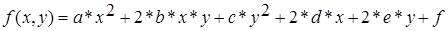 , ,
где 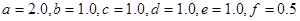 . .
Дана начальная точка поиска -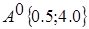 , где , где 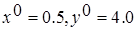 . .
Получим функцию:
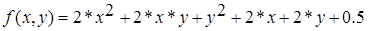 . .
1) Найти безусловный экстремум функции f(x,y) методами:
-наискорейшего спуска;
-сопряженных направлений.
Точность вычислений:
/xi
+1
-xi
/<0.01
/yi
+1
-yi
/<0.01
/f(xi+1
,yi+1
)-f(xi
,yi
)/<0.01
2) Найти условный экстремум функции f(x,y) методом симплексных процедур при наличии следующих ограничений:
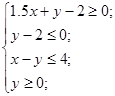
3) Выполнить синтез оптимальной по быстродействию системы с помощью принципа максимума Понтрягина (критерий по быстродействию), передаточная функция объекта имеет вид:
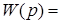
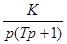 , где K=1, Т=1. , где K=1, Т=1.
- разработать модель для данного типа ОСАУ;
- провести исследование ОСАУ с применением программного продукта
“20 SimPro 2.3”;
- снять переходные и импульсные характеристики.
1. Анализ методов определения минимального, максимального
значения функции без ограничения
В данном разделе будет рассматриваться задача безусловной оптимизации, т.е. данная задача характеризуется тем, что минимум функции f: R
m
R
ищется на всем пространстве:
f(x) min, x R
m
.
Методы безусловной оптимизации функции многих переменных отличаются относительно высоким уровнем развития по сравнению с другими методами нелинейного программирования. Условно их можно разбить на три широких класса по типу используемой информации:
1) Методы прямого поиска, основанные на вычислении только значений целевой функции.
2) Градиентные методы, в которых используются точные значения первых производных f (x).
3) Методы второго порядка, в которых наряду с первыми производными используются также вторые производные функции f (x).
Здесь предполагается, что f (x) непрерывна и унимодальная. Если рассматриваемые методы применяются для анализа мультимодальных функций, то приходится ограничиваться идентификацией локальных минимумов. К особенностям этих методов можно отнести:
Реклама

1) относительная простота соответствующих вычислительных процедур, которые быстро реализуются и легко корректируются;
2) не требуют явного выражения целевой функции в аналитическом виде;
3) может требовать более значительных затрат времени по сравнению с методами, основанными на производных.
Метод поиска по симплексу
Процедура симплексного метода базируется на регулярном симплексе. Регулярный симплекс в N-мерном пространстве представляет собой многогранник, образованный N+1 равностоящими друг от друга точками - вершинами. Так в задаче с двумя переменными симплексом является равносторонний треугольник, с тремя - тетраэдр.
Работа алгоритма симплексного поиска начинается с построения регулярного симплекса в пространстве независимых переменных и оценивания значений целевой функции в каждой из вершин симплекса. При этом отбрасывается вершина, которой соответствует наибольшее значение целевой функции.
Преимущества метода:
· сравнительная простота логической структуры метода и, соответственно, программы для ЭВМ;
· используется сравнительно небольшое число заранее установленных параметров;
· невысокий уровень требований к ЭВМ.
· алгоритм эффективен даже в тех случаях, когда ошибка вычисления значений целевой функции велика, т.к. при его реализации используют наибольшие значения функции в вершинах, а не меньшие.
Недостатки метода:
· возникает проблема масштабирования, поскольку все координаты вершин симплекса зависят от одного масштабного множителя. Чтобы избежать такого рода проблем в практических задачах, следует промасштабировать все переменные с тем, чтобы их значения были сравнимы по величине;
· алгоритм работает достаточно медленно, т.к. полученная на предыдущих итерациях информация не используется для ускорения поиска;
· не существует простого способа расширения симплекса. Требуется перерасчет значений целевой функции во всех точках образца.
Метод поиска Хука-Дживса
Процедура поиска Хука-Дживса представляет собой комбинацию "исследующего поиска" и "ускоряющего поиска по образцу".
Исследующий поиск ориентирован на выявление локального характера поведения целевой функции и определение направлений вдоль "оврагов". Для проведения исследующего поиска необходимо задать величину шага, которая может быть различной для разных координатных направлений и изменяться в процессе поиска. Поиск начинается в некоторой исходной точке. Если значение целевой функции в пробной точке не превышает значение функции в исходной точке, то шаг поиска рассматривается как успешный. В противном случае необходимо вернуться в предыдущую точку и сделать шаг в противоположное направление с последующей проверкой значения целевой функции. После перебора всех N координат исследующий поиск завершается. Полученную в результате точку называют "базовой точкой".
Поиск по образцу заключается в реализации единственного шага из полученной базовой точки xk
вдоль прямой, соединяющей эту точку с предыдущей базовой точкой xk-1
. Новая точка образца xk+1
определяется в соответствии с формулой
xk+1
= xk
+ (xk
- xk-1
).
Как только движение по образцу не приводит к уменьшению целевой функции, точка xk+1
фиксируется в качестве временной базовой точки и вновь проводится исследующий поиск. Если в результате получается точка с меньшим значением целевой функции, чем в точке xk
, то она рассматривается как новая базовая точка xk+1
.
С другой стороны, если исследующий поиск неудачен, то необходимо вернуться в точку xk
и провести исследующий поиск с целью выявления нового направления минимизации. В конечном счете, возникает ситуация, когда такой поиск не приводит к успеху. В этом случае требуется уменьшить величину шага путем введения некоторого множителя и продолжить исследующий поиск. Поиск завершается, когда величина шага становится достаточно малой.
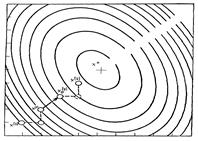
Рис. 1.1 - Метод поиска Хука-Дживса
Преимущества метода:
· несложная стратегия поиска;
· невысокий уровень требований к ЭВМ;
· широкое применение в инженерных приложениях.
Недостатки:
· при значительных нелинейных эффектах алгоритм вырождается в последовательность исследующих поисков без переходов к ускоряющему поиску по образцу.
1.2 Градиентные методы.
Важность прямых методов неоспорима, т.к. в практических задачах информация о значениях целевой функции является единственно надежной информацией, которой располагает инженер. Однако, если существует и непрерывны целевая функция f(x) и ее первые производные, aтакже они могут быть записаны в аналитическом виде (или с достаточно высокой точностью вычислены при помощи численных методов), то целесообразно использовать методы, основанные на использовании градиента целевой функции.
Все методы основаны на итерационной процедуре, реализуемой в соответствии с формулой
xk
+1
= xk
+ k
s(xk
),
где xk
- текущее приближение к решению x*
;
k
- параметр, характеризующий длину шага,
s(xk
) - направление поиска в N - мерном пространстве управляемых переменных xi
, i = 1, 2,..., N.
Способ определения k
и s(xk
) на каждой итерации связан с особенностями применяемого метода. Обычно выбор k
осуществляется путем решения задачи минимизации f(x) в направлении s(xk
). Поэтому при реализации градиентных необходимо использовать эффективные алгоритмы одномерной минимизации.
Простейший градиентный метод
В основе метода лежит следующая итерационная модификация формулы
xk
+1
= xk
+ k
s(xk
),
xk+1
= xk
- k
f(xk
),
где - заданный положительный коэффициент;
f(xk
) - градиент целевой функции первого порядка.
Недостатки:
· необходимость выбора подходящего значения ;
· медленная сходимость к точке минимума ввиду малости f(xk
) в окрестности этой точки.
Метод наискорейшего спуска
Свободен от первого недостатка простейшего градиентного метода, т.к. k
вычисляется путем решения задачи минимизации f(xk
) вдоль направления f(xk
) с помощью одного из методов одномерной оптимизации
xk+1
= xk
- k
f(xk
).
Данный метод иногда называют методом Коши.
Алгоритм характеризуется низкой скоростью сходимости при решении практических задач. Это объясняется тем, что изменения переменных непосредственно зависит от величины градиента, которая стремится к нулю в окрестности точки минимума и отсутствует механизм ускорения на последних итерациях. Поэтому, учитывая устойчивость алгоритма, методнаискорейшего спуска часто используется как начальная процедура поиска решения (из точек, расположенных на значительных расстояниях от точки минимума).
Метод сопряженных направлений
Общая задача нелинейного программирования без ограничений сводится к следующему: минимизировать f(x), xÎEn
, где f(x) является целевой функцией. При решении этой задачи мы используем методы минимизации, которые приводят к стационарной точке f(x), определяемой уравнением Ñf(x*
)=0.
Метод сопряженных направлений относится к методам минимизации без ограничений, использующим производные. Задача: минимизировать f(x), xÎEn
, где f(x) является целевой функцией n независимых переменных.
Важной особенностью является быстрая сходимость за счет того, что при выборе направления используется матрица Гессе, которая описывает область топологии поверхности отклика. В частности, если целевая функция квадратичная, то можно получить точку минимума не более чем за количество шагов, равное размерности задачи.
Для применения метода на практике его необходимо дополнить процедурами проверки сходимости и линейной независимости системы направлений
1.3 Методы второго порядка
Метод Ньютона
Последовательное применение схемы квадратичной аппроксимации приводит к реализации оптимизационного метода Ньютона по формуле
xk+1
= xk
- 2
f(xk-1
) f(xk
).
Недостатком метода Ньютона является его недостаточная надежность при оптимизации не квадратичных целевых функций. Поэтому его часто модифицируют:
xk+1
= xk
- k
2
f(xk-1
) f(xk
),
где k
- параметр, выбираемый таким образом, чтобы f(xk+1
) ® min.
2. Нахождение экстремума функции без ограничения
2.1 Метод наискорейшего спуска
Алгоритм данного метода отражается поисковой формулой:
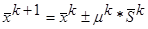 (2.1) (2.1)
где k – номер итерации, S – направление, в котором делается следующая итерации, 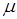 - величина шага в этом направлении. Знак « - » берется при поиске минимума. Если двигаться не в произвольном направлении S, а по градиенту, то формула выглядит так: - величина шага в этом направлении. Знак « - » берется при поиске минимума. Если двигаться не в произвольном направлении S, а по градиенту, то формула выглядит так:
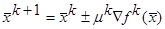 (2.2) (2.2)
где 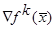 - градиент функции. - градиент функции.
Градиент функции в некоторой точке – вектор, показывающий направление наибольшей скорости увеличения функции
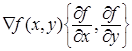 . .
Дана функция: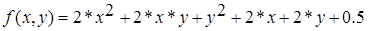
с начальной точкой 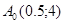 . .
Воспользуемся теоремой Ферма для определения экстремума:
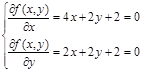 (2.3) (2.3)
Решим полученную систему:
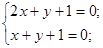 => =>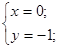 , точка , точка  - точка безусловного экстремума. - точка безусловного экстремума.
1) Найдем градиент функции в точке 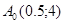 : :
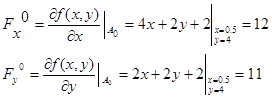
Оптимальную величину шага можно найти по формуле:
 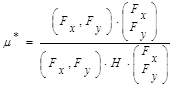 , (2.4) где Н – матрица Гессе. , (2.4) где Н – матрица Гессе.
Матрицу Гессе определяется по формуле:
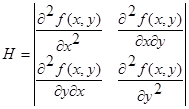 (2.5) (2.5)
Тогда получаем: 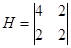 . .
Найдем величину оптимального шага:
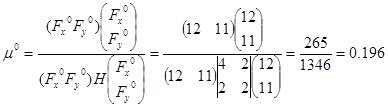
Подставим все найденные значения в формулу (2.2) и найдем координаты точки  : :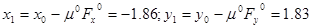
Получили новую точку с координатами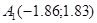
Проверка:
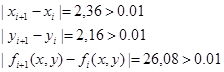
2) Точку 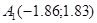 примем за начальную: примем за начальную:
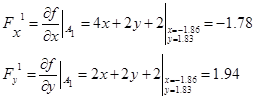
Найдем оптимальную величину шага:
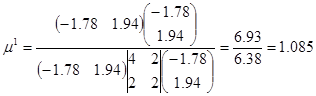
Находим 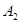 с помощью величины шага: с помощью величины шага:
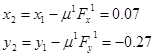
Получили новую точку с координатами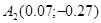
Проверка:
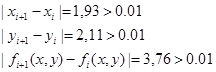
3) Точку 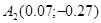 примем за начальную: примем за начальную:
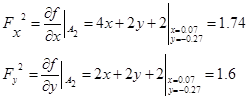
Определяем величину шага:
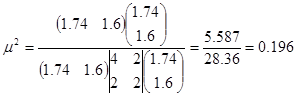
Находим 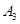 : :
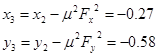
Получили новую точку с координатами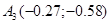
Проверка:
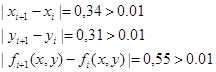
И так далее до выполнения условий точности вычисления экстремума функции:
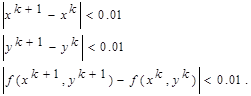
Рассматриваемый метод является градиентным методом второго порядка. Назовем некоторые направления 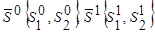 . Эти направления называются сопряженными по отношению к некоторой положительно определенной матрице Гессе (Н), если выполняется соотношение: . Эти направления называются сопряженными по отношению к некоторой положительно определенной матрице Гессе (Н), если выполняется соотношение:
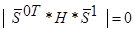 (2.6) (2.6)
При единичной матрице Гессе сопряженность направлений означает их ограниченность:
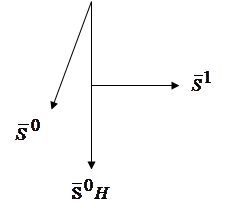
Рис. 2.1
Дана функция:
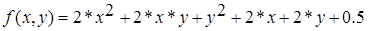
с начальной точкой 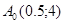 . .  - точка безусловного экстремума. - точка безусловного экстремума.
1) Найдем градиент функции в точке 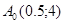 : :
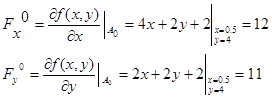
Выберем
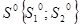 , ,
где 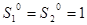 , имеем , имеем 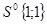 . .
1) Из начальной точки 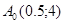 мы должны шагнуть по направлению мы должны шагнуть по направлению 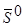 . Для этого найдем оптимальный шаг по формуле: . Для этого найдем оптимальный шаг по формуле:
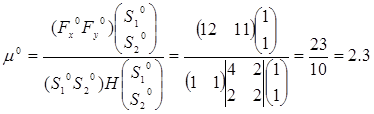
Находим координаты  с помощью величины шага: с помощью величины шага:
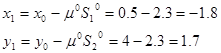
Получили новую точку с координатами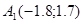
2) Примем точку 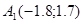 за начальную. Определяем: за начальную. Определяем:
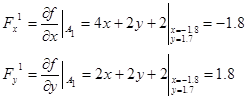
Найдем координаты сопряженного вектора 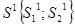 : :
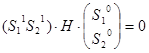 , тогда имеем: , тогда имеем: 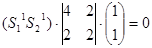 ; ;
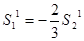 , пусть , пусть 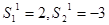 , тогда , тогда 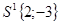
Найдем оптимальный шаг:
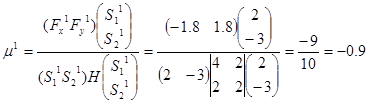
Находим координаты 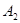 с помощью величины шага: с помощью величины шага:
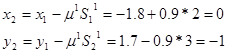
Получили новую точку с координатами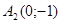 - точка минимума. - точка минимума.
Значение функции в этой точке равно 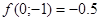 . .
3. Анализ методов определения минимального, максимального
значения функции при наличии ограничений
Напомним, что общая задача условной оптимизации выглядит так
f(x) min, x ,
где — собственное подмножество R
m
. Подкласс задач с ограничениями типа равенств
выделяется тем, что множество задается ограничениями вида
fi
(x) = 0,
гдеfi
: R
m
R
(i = 1, ..., k).
Таким образом, = {x R
m
: fi
(x) = 0, i = 1, ..., k}.
Нам будет удобно писать у функции f индекс "0". Таким образом, задача оптимизации с ограничениями типа равенств
записывается в виде:
f0
(x) min, (3.1)
fi
(x) = 0, i = 1, ..., k. (3.2)
Если обозначить теперь через f функцию на R
m
со значениями в R
k
, координатная запись которой имеет вид f(x) = (f1
(x), ..., fk
(x)), то (3.1)–(3.2) можно также записать в виде f0
(x) min, f(x) = .
Геометрически задача с ограничениями типа равенств — это задача о поиске наинизшей точки графика функции f0
над многообразием (см. рис. 3.1).
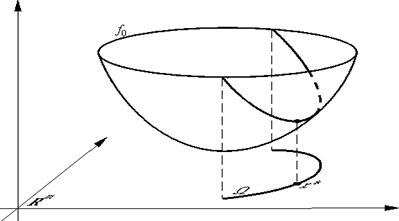
Рис. 3.1
Точки, удовлетворяющие всем ограничениям (т. е. точки множества ), обычно называют допустимыми
. Допустимая точка x* называется условным минимумом функции
f0
при ограничениях fi
(x) = 0, i = 1, ..., k (или решением задачи (1)–(2)), если при всех допустимых точках x f0
(x*) f0
(x). (3.3)
Если (3.3) выполняется только для допустимых x, лежащих в некоторой окрестности Vx*
точки x*, то говорят о локальном условном минимуме
. Естественным образом определяются понятия условных строгих локального
и глобального минимумов
.
Правило множителей Лагранжа.
Описываемый ниже необходимый признак локального условного минимума был сформулирован Лагранжем. Определим F: R
m
R
k+1
, положив F(x) = (f0
(x), f1
(x), ..., fk
(x)). Заданная на R
m
×R
k+1
скалярная функция Лагранжа
M по определению принимает значения в R
и задается равенством
M(x, ) = (, F(x)) = 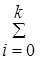 i
fi
(x) (x R
m
, R
k+1
). i
fi
(x) (x R
m
, R
k+1
).
Координаты вектора , т. е. числа 0
, 1
, ..., k
называются множителями Лагранжа
или двойственными переменными
. Оказывается, имеет место следующая теорема, часто именуемая правилом множителей Лагранжа
:
Теорема.
Пусть F C1
и x* — локальный условный минимум функции f0
при ограничениях fi
(x) = 0 (i = 1, ..., k). Тогда найдется ненулевой вектор * такой, что x* является стационарной точкой функции x M(x, *):
Mx
(x, *)|x
=
x
*
=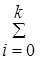 *i
f i
(x*)= Q *i
f i
(x*)= Q
Правило множителей Лагранжа доставляет необходимое условие локального условного минимума и поэтому позволяет искать точки, "подозрительные" на экстремум. В самом деле, для нахождения точки (x*, *) R
m+k+1
, т. е. для нахождения m + k + 1 неизвестных, мы имеем m + k уравнений
f(x) = , Mx
(x, )= .
Поскольку, очевидно, множители Лагранжа можно искать с точностью до постоянного множителя, то в общей ситуации этих уравнений хватает для отыскания x*.
Регулярные точки.
Допустимая точка x задачи (3.1)–(3.2) называется регулярной
, если векторы {f i
(x)}k
i=1
линейно независимы. Оказывается, что если x* — регулярная точка минимума, то в векторе * можно считать *0
ненулевым, а поскольку множители Лагранжа определяются с точностью до множителя, можно считать, что *0
= 1. Чтобы сформулировать это утверждение более точно, введем следующие обозначения. Пусть R
k
, а функция Лагранжа в регулярном случае
определяется равенством
L(x, ) = f0
(x) + (, f(x)) = f0
(x) +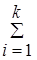 i
fi
(x) (x R
m
, R
k
). i
fi
(x) (x R
m
, R
k
).
Очевидно, L(x, ) = M(x, ), где = (1, ).
Теорема (правило множителей Лагранжа в регулярном случае).
Пусть F C1
, а x* — регулярное локальное решение задачи (3.1)–(3.2). Тогда найдется ненулевой вектор * R
k
такой, что
Lx
(x*, *)= .
Одно достаточное условие локального минимума.
Говорят, что линейный оператор A положительно определен на подпространстве
E, если (Ax, x) > 0 при всех x E. Касательным подпространством к многообразию
в точке y называется множество Ty
= {x R
m
: (f (y), x) = 0, i = 1, ..., k}. Касательной гиперплоскостью к многообразию
в точке y называется множество
y
= {x R
m
: fi
(y) + (f (y), xy) = 0, i = 1, ..., k}.
Теорема (достаточное условие минимума).
Пусть F C2
, а x* — регулярнаястационарная точкафункции Лагранжа, т. е., в частности, L(x*, *) = при некотором ненулевом * R
k
. Тогда, если Lxx
(x*, *)положительно определен на Tx*
, то точка x* является локальным решением задачи(3.1)–(3.2).
Методы решения задач с ограничениями типа равенств.
Мы будем рассматривать ниже только регулярный случай. Один из естественных подходов к решению задач типа (3.1)–(3.2) основывается на необходимом условии экстремума — правиле множителей Лагранжа. Если бы можно было утверждать, что решению x* задачи (3.1)–(3.2) соответствует экстремум (x*, *) функции ЛагранжаL, то к функции L можно было бы применять разработанные методы решения безусловных задач. Однако, так утверждать нельзя. В самом деле, если в точке x ограничения не выполняются, то за счет выбора функцию L (поскольку по она линейна) можно сделать как сколь угодно большой положительной, так и сколь угодно большой отрицательной. Поэтому естественно искать решение x* как первые m координат стационарной точкифункции Лагранжа, например, методом Ньютона, мы приходим к методу Ньютона решения задач с ограничениями типа равенств
— это просто метод Ньютона решения уравнения L(x, ) = (в регулярном случае):
L(xn
, n
) + L(xn
, n
)(xn
+1
xn
, n+1
n
) =
в "координатной" форме
Lx
(xn
,n
) + Lxx
(xn
,n
)(xn
+1
xn
) + Lx
(xn
,n
)(n+1
n
) = ,
L
(xn
,n
) + Lx
(xn
,n
)(xn
+1
xn
) + L
(xn
,n
)(n+1
n
) = .
Остается подставить в эти уравнения явные выражения производных функции Лагранжа (учитывая, в частности, что L
(xn
,n
) = ):
f 0
(xn
)+ [f (xn
)]*n
+ (f 0
(xn
)+ 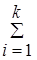 n
i
f i
(xn
)) (xn
+1
xn
) +[f (xn
)]*(n+1
n
) = ,f(xn
) + f (xn
)(xn
+1
xn
) = n
i
f i
(xn
)) (xn
+1
xn
) +[f (xn
)]*(n+1
n
) = ,f(xn
) + f (xn
)(xn
+1
xn
) =
и мы получаем m+k линейных уравнений для нахождения m+k неизвестных (xn
+1
, n+1
).
Описанный метод обладает всеми достоинствами и всеми недостатками метода Ньютона решения безусловных задач, в частности, он лишь локально сходится и требует большого объема вычислений. Поэтому попытаемся модифицировать градиентный метод, приспособив его к решению условной задачи (3.1)–(3.2). Поскольку, как сказано выше, точка (x*, *) - это седловая точкафункции Лагранжа, то естественно пытаться с помощью градиентного метода минимизировать ее по x, одновременно максимизируя ее по :
xn
+1
= xn
Lx
(xn
,n
), n+1
= n
+ L
(xn
,n
),
или, что то же xn
+1
= xn
(f 0
(xn
)+ [f (xn
)]*n
), n
+1
= n
+ f(xn
).
Можно доказать, что этот метод (его обычно называют методом Эрроу — Гурвица
) при естественных ограничениях на гладкость и при условии положительной определенности оператора Lxx
(x*,*) локальнолинейно сходится.
Описанные методы относятся к разряду двойственных методов
, поскольку в итерационном процессе участвуют как прямые (x), так и двойственные () переменные.
Можно строить также прямые методы
решения условных задач. Например, реализовать идею о том, что следующее приближение градиентного метода. Приближение xn
+1
ищется как минимум функции x (f 0
(xn
),x xn
) + ||x xn
||2
на касательной гиперплоскости xn
. Здесь "штрафной член" ||x xn
||2
позволяет "минимизировать" линейную функцию x (f 0
(xn
),x xn
). Таким образом, мы приходим к прямому методу
xn
+1
= argmin [(f 0
(xn
),x xn
) + ||x xn
||2
], (3.4)
fi
(xn
) + (f i
(xn
),x xn
) = 0, i = 1, ..., k. (3.5)
Ограничения (3.5) в этом методе — это, очевидно, линеаризации ограничений (3.2) в точке xn
: минимум ищется на касательной гиперплоскости xn
.
Один из распространенных методов решения задач с ограничениями, с которым мы еще столкнемся — так называемый метод штрафов
. Он позволяет сводить задачу с ограничениями к задаче без ограничений и суть его заключается в наказании за невыполнение ограничений. Именно, вместо минимизации функции f0
с ограничениями (3.2) минимизируется функция fs
(x) = f0
(x) + s||f(x)||2
без ограничений, в которой s — положительный параметр.
Теперь рассмотрим постановку задач с ограничениями типа неравенств gj
(x) 0, j = 1, ..., l (6).
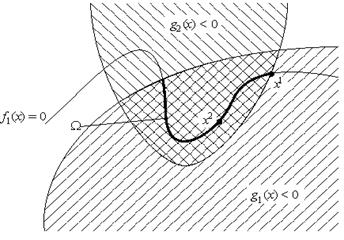
Рис. 3.2
Как и в предыдущем параграфе определяются допустимые точки, локальный и
глобальный,
строгий и нестрогий минимумы. Так же мы будем использовать обозначения f и g для функций из R
m
в R
k
и R
l
, соответственно, определяемые координатами fi
и gj
. Поэтому задачу (3.1)- (3.3), (3.6) можно записывать в виде
f(x) = , g(x) .
(напомним, что неравенство g(x) означает покоординатные неравенства).
f0
(x) min, f(x) = , g(x) .
Через J(x)
будет обозначаться множество индексов так называемых активных ограничений
: J(x) = {j {1, ..., l}: gj
(x) = 0} — это номера ограничений, которые в данной точке существенны.
Теорема (обобщенное правило множителей Лагранжа).
Пусть f0
, f, g C1
, а x* — локальное решение задачи f0
(x) min, f(x) = , g(x) . Тогда найдутся такие *0
R
, * R
k
, * R
l
, не равные одновременно нулю, такие, что *j
0 при j J(x*) и
*0
f 0
(x*)+  *i
f i
(x*)+
*i
f i
(x*)+ *j
gj
(x*) = . (3.7)
*j
gj
(x*) = . (3.7)
Регулярный случай.
Так же, как и в случае ограничений-равенств, в случае общей задачи нелинейной оптимизации, необходимый признак, информативен только в случае, если *0
0. В этой ситуации, так же как и в предыдущем параграфе можно разделить (3.7) на *0
и, следовательно, считать его равным единице. Это позволяет ввести функцию Лагранжа L: R
m
×R
k
×R
k
R
(в регулярном случае) равенством
(x, , ) = f0
(x) + (, f(x)) + (, g(x)).
Условие регулярности в случае общей задачи выглядит сложнее. Именно, допустимая точка x называется регулярной
, если векторы f 1
(x),..., f k
(x) линейно независимы и для некоторого ненулевого вектора
hR
m
(f i
(x),h) = 0 при i = 1, ..., kи (gj
(x),h) < 0 при j J(x).
Геометрически, эти условия означают, что, во-первых, вектор h является касательным к многообразию, выделяемому ограничениями-равенствами (т. е. ортогонален всем градиентам f i
(x)),и, во-вторых, он образует с градиентами gj
(x)активных ограничений (указывающими, очевидно, вовне множества ) тупой угол
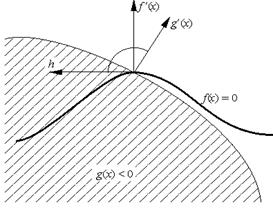
Рис. 3.3
Эти методы основываются на следующем простом понятии. Вектор (направление) z в допустимой точке x назовем возможным
, если малое перемещение в этом направлении уменьшает значение функции f0
и не выводит из множества допустимых точек, т. е. если при достаточно малых s точка xs
= x + sz допустима и f(xs
) < f(x). Если теперь на каждом шаге сдвигаться в возможном направлении на достаточно малое расстояние, то мы очевидно получим релаксационную последовательность, которая во многих случаях будет сходиться к решению задачи. Методы этого типа называются методами возможных направлений
.
Проекцией
P
x точки x R
m
на множество R
m
называется любая ближайшая к x точка множества :
||x P
x|| ||x y|| при всех y .
В тех случаях, когда проекцию точки на множество допустимых точек найти достаточно легко (например, когда — линейное подпространство, полупространство, шар, R
m
и т. д.) используют метод проекции градиента
:
xn
+1
= P
(xn
n
f 0
(xn
))
(см. рис. 3.3) являющийся прямым обобщением градиентного метода
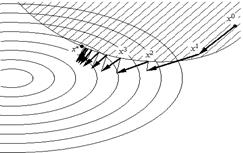
Рис. 3.4
Можно доказать, например, что если функция f0
C1
сильно выпукла и f удовлетворяет условию Липшица, а множество замкнуто и ограничено, то метод проекции градиента сходится со скоростью геометрической прогрессии.
Суть этих методов, как следует из названия, состоит в линеаризации минимизируемой функции и ограничений в очередной точке xn
строящейся релаксационной последовательности и объявлении следующим значением xn
+1
решения получающейся линейной задачи, т. е. задачи
(f 0
(xn
),x xn
) min, (3.8)
gi
(xn
) + (gi
(xn
),x xn
) 0,i = 1, ..., l. (3.9)
Чтобы эта (линейная) задача была разрешима либо добавляют штраф в минимизируемую функцию, заменяя (3.8), например, задачей
(f 0
(xn
), x xn
) + ||x xn
||2
min,
либо добавляя к (20) простые ограничения, которые делают множество допустимых точек этой задачи ограниченным, например, (линейные) ограничения
xi
xn
i
n
0, xi
+ xn
i
n
0 (i = 1, ..., m).
Основная идея здесь заключается в переходе от задачи (1), (3) к задаче безусловной оптимизации, в которой "наказывается" либо удаление от множества допустимых точек (внешний штраф
), либо приближение изнутри множества к его границе (внутренний штраф
). Различают методы внешних штрафов и внешних штрафов. При методе внешних штрафов задачу решают тем или иным методом решения безусловных задач, увеличивая на каждом шаге штраф s. Как и в случае задач с ограничениями-равенствами, основным недостатком метода штрафов является рост числа обусловленности s. На несколько другой идее основываются так называемые методы внутренних штрафов
или барьеров
. Образно его можно описать так: у границы множества возводятся барьеры, не позволяющие приближаться к его границе.
Вывод
: ни один метод или класс методов не выделяется своей собственной высокой эффективностью при решении оптимизационных задач различных типов, т.е. универсальностью. Инженер вынужден приспосабливать применяемый метод к конкретным характеристикам решаемой задачи.
4. Нахождение экстремума функции при наличии ограничения
4.1 Метод симплексных процедур
Дана функция:
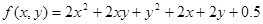 . .
Заданы ограничения:
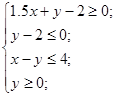
Симплексом в пространстве n-измерений называют выпуклый многогранник, имеющий (n+1) вершин, не лежащих в подпространстве размерности, меньшей n.
Решение задачи нахождения условного экстремума функции двух переменных может находиться либо на границах выпуклого многогранника, либо на его вершинах.
1) 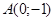 - точка безусловного экстремума. Полученная точка безусловного экстремума находится вне выпуклого многогранника и не удовлетворяет условию ограничения. Соответственно, полученная точка не является условным экстремумом. - точка безусловного экстремума. Полученная точка безусловного экстремума находится вне выпуклого многогранника и не удовлетворяет условию ограничения. Соответственно, полученная точка не является условным экстремумом.
2) Найдем экстремум для каждой грани по задаче Лагранжа.
Для грани j1 сконструируем вспомогательную функцию. Для этого сложим условный экстремум и некоторое число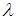 , умноженное на левую часть уравнения связи с правой нулевой частью. , умноженное на левую часть уравнения связи с правой нулевой частью.
Получим:
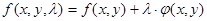 , ,
где 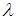 - множитель Лагранжа. Множитель Лагранжа характеризует положение гиперплоскости в точке решения задачи на условный экстремум функции. - множитель Лагранжа. Множитель Лагранжа характеризует положение гиперплоскости в точке решения задачи на условный экстремум функции.
Найдем для первого условия значения координат возможной точки экстремума. Получим для грани j1:
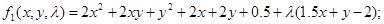
Исследуем полученную функцию на экстремум Ферма:
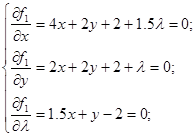 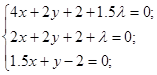 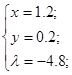
Решая систему, получим координаты точки условного экстремума: 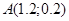 . .
Выполним проверку, лежит ли точка A в данных ограничениях:
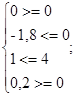 точка А может быть т. экстремума. точка А может быть т. экстремума.
Значение целевой функции в данной точке равно: 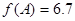
Для грани j2 вспомогательная функция для этой грани будет иметь вид:

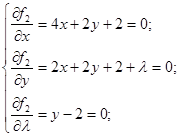 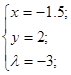 Имеем точку Имеем точку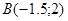 . .
Проверка:
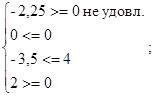 точка B лежит за пределами ограничений. точка B лежит за пределами ограничений.
Для грани j3 вспомогательная функция для этой грани будет иметь вид:
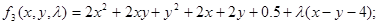
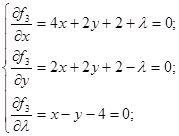 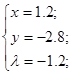 имеем точку имеем точку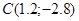 . .
Проверка:
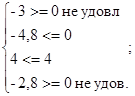 точка С лежит за пределами ограничений. точка С лежит за пределами ограничений.
Для грани j4 вспомогательная функция для этой грани будет иметь вид:
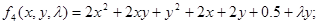
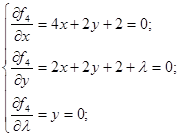 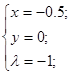 имеем точку имеем точку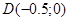 . .
Проверка:
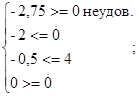 точка D лежит за пределами ограничений. точка D лежит за пределами ограничений.
3) Исследуем вершины четырехгранника.
Рис. 4.1.
Находим координаты вершины фигуры, полученной при пересечении неравенств.
Пересечение 1 и 2 неравенства (точка P1):
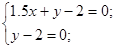 имеем имеем 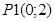 , значение функции в этой точке , значение функции в этой точке 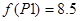
Пересечение 2 и 3 неравенства (точка P2):
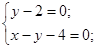 имеем имеем 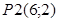 , значение функции в этой точке , значение функции в этой точке 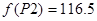
Пересечение 3 и 4 неравенства (точка P3):
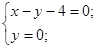 имеем имеем 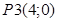 , значение функции в этой точке , значение функции в этой точке 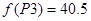
Пересечение 1 и 4 неравенства (точка P4):
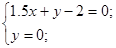 имеем имеем 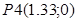 , значение функции в этой точке , значение функции в этой точке 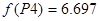
Вывод:
Минимальное значение функции достигается в точке 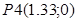 , ,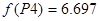 . .
Максимальное значение функции достигается в точке 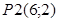 , ,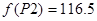 . .
5. Синтез оптимальной по быстродействию системы с помощью принципа максимума Понтрягина
Критерий управления, как отмечалось ранее, в этом случае
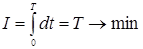 (5.1) (5.1)
Мера ошибки в критерии H =1, а верхний предел T не известен. Начальная Х(0) = Х0
и конечная Х(T) = ХT
точки закреплены.
Запишем функцию Гамильтона и условия трансверсальности:
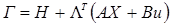
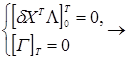 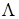 (T) и (T) и 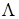 (0)-произвольны. (0)-произвольны.
Согласно принципу максимума Понтрягина, стратегия управления состоит в минимизации функции Гамильтона относительно u. Минимум Г будет тогда, когда
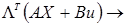 min по и min по и
или
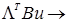 min по и min по и
Отсюда
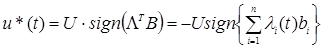 (5.2) (5.2)
Таким образом, стратегия управления и характер u*(t) определены: оптимальное управление - это релейное управление, максимальное по величине, причем переключение управления производится тогда, когда функция 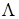 Т
В пересекает ось времени t. Т
В пересекает ось времени t.
По изложенной методике определим оптимальное управление 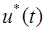 , которое произвольное начальное состояние (х10
, x20
) переводит в начало координат за минимальное время Т. , которое произвольное начальное состояние (х10
, x20
) переводит в начало координат за минимальное время Т.
Представим объект (1) в виде уравнения состояния (нормальная форма)
 (5.3) (5.3)
В рассматриваемом примере матрица 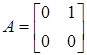 , вектор , вектор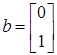 . Образуем матрицу . Образуем матрицу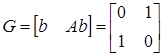 . .
Матрица G— невырожденная, поэтому система (5.3) будет нормальной. Характеристические числа матрицы A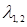 = 0, поэтому система удовлетворяет условиям теоремы об n-интервалах. Оптимальное управление u*(t) является кусочно-постоянным и имеет не более двух интервалов постоянства. = 0, поэтому система удовлетворяет условиям теоремы об n-интервалах. Оптимальное управление u*(t) является кусочно-постоянным и имеет не более двух интервалов постоянства.
Таким образом, управляющие последовательности в зависимости от начального состояния будут: {+ 1}, {-1},{+1,-1}, {-1, + 1}.
Обозначим u* = ∆=±1 и найдем общее решение системы при и* = ∆.
Имеем 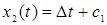 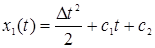
Пусть при t = 0, х1
= х10
, х2
= х20
. Тогда, исключив время tиз полученных выше равенств, найдем уравнение фазовых траекторий системы:
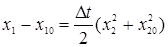 . .
Обозначим 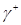 – множество начальных состояний, которые переводятся в начало координат управляющей последовательностью и*={+1}, – множество начальных состояний, которые переводятся в начало координат управляющей последовательностью и*={+1}, 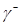 – множество начальных состояний, которые переводятся в начало координат управляющей последовательностью и*={—1}. Эти множества описываются уравнениями – множество начальных состояний, которые переводятся в начало координат управляющей последовательностью и*={—1}. Эти множества описываются уравнениями
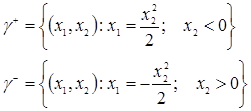
Если принять 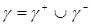 то множество то множество 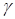 запишется в виде запишется в виде
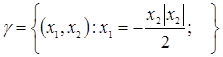
Закон управления
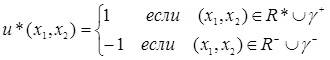 (5.4) (5.4)
Линия 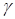 представляет собой линию переключения. представляет собой линию переключения.
Введем функцию 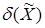 , характеризующую расстояние от текущего положения фазовой точки , характеризующую расстояние от текущего положения фазовой точки 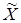 (x1
,x2
) до линии переключения: (x1
,x2
) до линии переключения:
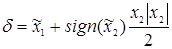 (5.5) (5.5)
Когда фазовая точка окажется на линии переключения, то правая часть уравнения (5) будет равна нулю (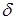 = 0) и управляющее устройство должно произвести переключение знака управления на противоположный.
= 0) и управляющее устройство должно произвести переключение знака управления на противоположный.
Пока фазовая точка находится над линией переключения, 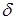 > 0 и управление должно быть отрицательным и (t) = -U .
> 0 и управление должно быть отрицательным и (t) = -U .
Когда фазовая точка находится под линией переключения, 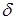 < 0 и управление должно быть положительным и (t) = +U .
< 0 и управление должно быть положительным и (t) = +U .
Таким образом, в зависимости от знака должен выбираться изнак управления:
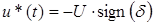
Все изложенное позволяет записать алгоритм
оптимальногопо быстродействию регулятора для объекта (1):
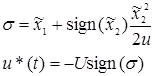
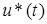 =0, если =0, если 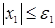 , ,  х2 х2
Дано:
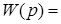
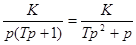 , ,
где K=1, Т=1.
Решение:
Представим знаменатель дроби в виде уравнения 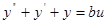
Получим 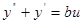
Заменим y на 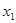
Получим: 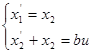 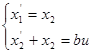
Продифференцируем уравнения
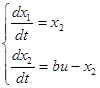
Получим
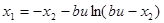
Обозначим 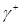 – множество начальных состояний, которые переводятся в начало координат управляющей последовательностью и*={+1}, – множество начальных состояний, которые переводятся в начало координат управляющей последовательностью и*={+1}, 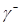 – множество начальных состояний, которые переводятся в начало координат управляющей последовательностью и*={—1}. Эти множества описываются уравнениями – множество начальных состояний, которые переводятся в начало координат управляющей последовательностью и*={—1}. Эти множества описываются уравнениями
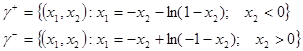
Закон управления
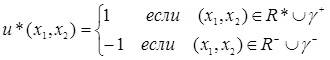
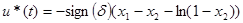
Разработаем модель для данного типа ОСАУ.
По алгоритму решения, составим структурную схему системы, реализующей выведенный закон управления.
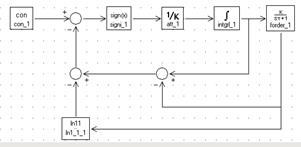
Рис. 5.1. Структурная схема модели для снятия переходной хар-ки.
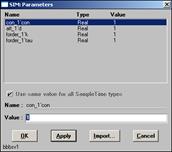
Рис. 5.2. Вводимые данные
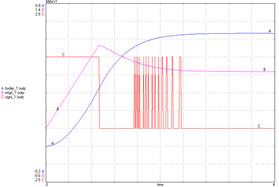
Рис. 5.3. Переходная характеристика ОСАУ
Для определения импульсной характеристики объекта необходимо изменить структуру модели решения задачи, заменив блок ступенчатого входного воздействия con
, на блок pulsgen
- импульсное воздействие, выходом которого является прямоугольный импульс.
При подготовке эксперимента задать параметры блока pulsgen
где: Т1
=-1- время начала импульса;
Т2
=1 время окончания импульса;
P=1 высота импульса.
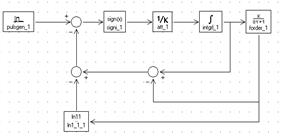
Рис. 5.4. Структурная схема модели для снятия импульсной хар-ки.
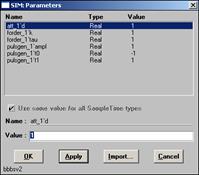
Рис. 5.5. Вводимые данные
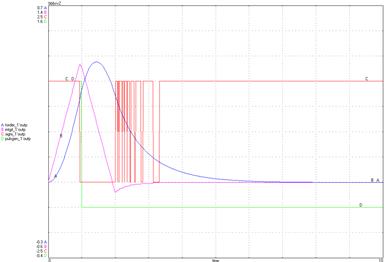
Рис. 5.6. Импульсная характеристика ОСАУ
Заключение
В теоретической части курсовой работы были рассмотрены методы поиска безусловного экстремума функции (методы прямого поиска, градиентные методы, методы второго порядка) и методы поиска экстремума функции при наличии ограничений (методы возможных направлений, методы проекции градиента, методы линеаризации, методы штрафов), указаны их основные достоинства и недостатки. В практической части произведен поиск безусловного и условного минимума несепарабельной функции двух переменных расчетным путем, выполнена алгоритмизация поиска безусловного экстремума функции двух переменных методами наискорейшего спуска и сопряженных направлений. На языке Си++ реализованы алгоритмы вышеназванных методов, а также выполнен поиск условного минимума методом симплексных процедур. Метод наискорейшего спуска для данной функции сошелся быстрее метода Зейделя-Гаусса, но для наиболее точного результата требует ввода достаточно малой величины критерия точности e. Методом симплексных процедур найден минимум функции в точке, лежащей внутри треугольника ограничений.
С
писок литературы
1. Акулич И. Л. Математическое программирование в примерах и задачах. – М: Высшая школа, 1986.
2. Болтянский В. Г. Математические методы оптимального управления. – М: Наука, 1969.
3. Банди Б. Методы оптимизации (вводный курс). - М.: Радио и связь,1988.
4. Васильев Ф.П. Численные методы решения экстремальных задач. - М.: Наука, 1980.
5. Моисеев Н.Н., Иванилов Ю.П., СтоляровЕ.М. «Методы оптимизации», "Наука", М., 1978.
6. Полак Э. «Численные методы оптимизации», "Наука", М., 1974.
7. Сухарев А.Г., Тимохов А.В., Федоров В.В. Курс методов оптимизации. - М.: Наука, 1986.
8. Сеа Ж. Оптимизация. Теория и алгоритмы. - М.: Мир, 1973.
9. Поляк Б.Т. Введение в оптимизацию. - М.: Наука, 1983.
10. Цирлин А.М. «Оптимальное управление технологическими процессами»: учебное пособие для вузов. – М.:1986.-400с.
11. Чураков Е.П. «Оптимальные и адаптивные системы»: учебное пособие для вузов.-М.:1987.-256с.
12. Иванов В. А., Фалдин Н. В. Теория оптимальных систем автоматического управления. – М: Наука, 1981.
Приложение
Код программы метода наискорейшего спуска
#include <stdio.h>
#include <conio.h>
#include <math.h>
main ()
{
clrscr ();
float x[20];
float y[20];
float dx,dy,df,df1,df2,Fx,Fy,m1,m2,m;
int i=-1;
x[0]=0.5;
y[0]=4;
printf("---------METOD NAISKOR SPUSKA---------\n");
printf(" f(x,y)=2x^2+2xy+y^2+2x+2y+0.5\n");
printf("--------------------------------------\n");
do
{
i++;
printf("-----------A%d(%2.3f;%2.3f)------------\n",i,x[i],y[i]);
Fx=4*x[i]+2*y[i]+2;
Fy=2*x[i]+2*y[i]+2;
printf("Fx%d=%2.3f Fy%d=%2.3f\n",i,Fx,i,Fy);
m1=Fx*Fx+Fy*Fy;
m2=(4*Fx+2*Fy)*Fx+(2*Fx+2*Fy)*Fy;
m=m1/m2;
printf("mu%d=%2.3f\n",i,m);
x[i+1]=x[i]-m*Fx;
y[i+1]=y[i]-m*Fy;
dy=fabs(y[i+1]-y[i]);
dx=fabs(x[i+1]-x[i]);
df2=2*x[i+1]*x[i+1]+2*x[i+1]*y[i+1]+y[i+1]*y[i+1]+2*x[i+1]+2*y[i+1]+0.5;
df1=2*x[i]*x[i]+2*x[i]*y[i]+y[i]*y[i]+2*x[i]+2*y[i]+0.5;
df=fabs(df2-df1);
printf("delta x=%2.3f\ndelta y=%2.3f\ndelta f=%2.3f\n\n",dx,dy,df);
getch();
}
while (!((dy<0.01)&(df<0.01)&(dx<0.01)));
printf("---------------------------------------\n");
printf("iskomaya tochka A%d(%2.3f;%2.3f)",i+1,x[i+1],y[i+1]);
getch();}
 Результат работы программы Результат работы программы
--------METOD NAISKOR SPUSKA---------
f(x,y)=2x^2+2xy+y^2+2x+2y+0.5
-------------------------------------------
-----------A0(0.500;4.000)------------
Fx0=12.000 Fy0=11.000
mu0=0.197
delta x=2.363
delta y=2.166
delta f=26.087
-----------A1(-1.863;1.834)------------
Fx1=-1.782 Fy1=1.944
mu1=1.086
delta x=1.935
delta y=2.111
delta f=3.775
-----------A2(0.072;-0.276)------------
Fx2=1.736 Fy2=1.592
mu2=0.197
delta x=0.342
delta y=0.313
delta f=0.546
-----------A3(-0.270;-0.590)------------
Fx3=-0.258 Fy3=0.281
mu3=1.086
delta x=0.280
delta y=0.305
delta f=0.079
-----------A4(0.010;-0.895)------------
Fx4=0.251 Fy4=0.230
mu4=0.197
delta x=0.049
delta y=0.045
delta f=0.011
-----------A5(-0.039;-0.941)------------
Fx5=-0.037 Fy5=0.041
mu5=1.086
delta x=0.041
delta y=0.044
delta f=0.002
-----------A6(0.002;-0.985)------------
Fx6=0.036 Fy6=0.033
mu6=0.197
delta x=0.007
delta y=0.007
delta f=0.000
---------------------------------------
iskomaya tochka A7(-0.006;-0.991)
Код программы метода сопряженных направлений
#include <stdio.h>
#include <conio.h>
#include <math.h>
main ()
{
clrscr ();
float x[10];
float y[10];
float Fx,Fy,m1,m2,m;
int i,S1=1,S2=1;
x[0]=0.5;
y[0]=4;
printf("--------METOD SOPR. NAPRAVLENIY--------\n");
printf(" f(x,y)=2x^2+2xy+y^2+2x+2y+0.5\n");
printf("---------------------------------------\n");
for (i=0;i<2;i++)
{
printf(" A%d(%2.3f;%2.3f)\n",i,x[i],y[i]);
printf(" ---------------\n");
Fx=4*x[i]+2*y[i]+2;
Fy=2*x[i]+2*y[i]+2;
printf("S1=%d S2=%d\nFx%d=%2.3f Fy%d=%2.3f\n",S1,S2,i,Fx,i,Fy);
m1=Fx*S1+Fy*S2;
m2=(4*S1+2*S2)*S1+(2*S1+2*S2)*S2;
m=m1/m2;
printf("mu%d=%2.3f\n\n",i,m);
x[i+1]=x[i]-m*S1;
y[i+1]=y[i]-m*S2;
S1=2;
S2=-3; }
printf("---------------------------------------\n");
printf("iskomaya tochka A2(%2.3f;%2.3f)\n",x[2],y[2]);
getch();}

Результат работы программы
--------METOD SOPR. NAPRAVLENIY--------
f(x,y)=2x^2+2xy+y^2+2x+2y+0.5
---------------------------------------
A0(0.500;4.000)
---------------
S1=1 S2=1
Fx0=12.000 Fy0=11.000
mu0=2.300
A1(-1.800;1.700)
---------------
S1=2 S2=-3
Fx1=-1.800 Fy1=1.800
mu1=-0.900
---------------------------------------
iskomaya tochka A2(0.000;-1.000)
Код программы метода симплексных процедур
#include <stdio.h>
#include <conio.h>
#include <math.h>
float fun (float x,float y)
{return(2*x*x+2*x*y+y*y+2*x+2*y+0.5);}
float n1 (float x,float y)
{return(1.5*x+y-2);}
float n2 (float x,float y)
{x=x;
return(y-2);}
float n3 (float x,float y)
{return(x-y-4);}
float n4 (float x,float y)
{x=x;
return(y);}
main (){
clrscr ();
float a=2,b=1,c=1,d=1,e=1,f=0.5;
float na=1.5,nb=1.0,nc=-2.0;
float x,y,z,k,t;
int i,h=1,m;
printf("-----METOD SIMPLEX PROCEDURE-----\n");
printf(" f(x,y)=2x^2+2xy+y^2+2x+2y+0.5\n\n");
printf("1)1.5x+y-2>=0;\n2)y-2<=0;\n3)x-y<=4;\n4)y>=0\n");
printf("----------------------------------\n");
float max=0;
printf("f1(x,y,z)=2x^2+2xy+y^2+2x+2y+0.5+z(1.5x+y-2)\n");
x=((2*b*nc/nb)-2*d-2*c*nc*na+(2*e*na/nb))/(2*a-(2*b*na/nb)-na*2*b/nb+2*c*na*na);
y=(-nc/nb)-(na/nb)*x;
max=fun(x,y);
printf ("x=%2.3f\ny=%2.3f\nA%d(%2.3f;%2.3f)\n",x,y,h,x,y);
if ((n1(x,y)>=0)&(n2(x,y)<=0)&(n3(x,y)<=0)&(n4(x,y)>=0))
{printf("tochka udovl nerav f(A%d)=%2.3f\n",h,fun(x,y));
if (fun(x,y)>max) max=fun(x,y),k=x,t=y,m=h;
else max=max; }
else
printf("tochka ne udovletv neravenstvu\n");
printf("-----------------------------------\n");
na=0.0;nb=1.0;nc=-2.0;h=h+1;
printf("f2(x,y,z)=2x^2+2xy+y^2+2x+2y+0.5+z(y-2)\n");
x=((2*b*nc/nb)-2*d-2*c*nc*na+(2*e*na/nb))/(2*a-(2*b*na/nb)-na*2*b/nb+2*c*na*na);
y=(-nc/nb)-(na/nb)*x;
fun(x,y);
printf ("x=%2.3f\ny=%2.3f\nA%d(%2.3f;%2.3f)\n",x,y,h,x,y);
if ((n1(x,y)>=0)&(n2(x,y)<=0)&(n3(x,y)<=0)&(n4(x,y)>=0))
{printf("tochka udovl nerav f(A%d)=%2.3f\n",h,fun(x,y));
if (fun(x,y)>max) max=fun(x,y),k=x,t=y,m=h;
else max=max;}
else
printf("tochka ne udovletv neravenstvu\n");
printf("------------------------------------\n");
na=1.0;nb=-1.0;nc=-4.0;h=h+1;
printf("f3(x,y,z)=2x^2+2xy+y^2+2x+2y+0.5+z(x-y-4)\n");
x=((2*b*nc/nb)-2*d-2*c*nc*na+(2*e*na/nb))/(2*a-(2*b*na/nb)-na*2*b/nb+2*c*na*na);
y=(-nc/nb)-(na/nb)*x;
fun(x,y);
printf ("x=%2.3f\ny=%2.3f\nA%d(%2.3f;%2.3f)\n",x,y,h,x,y);
if ((n1(x,y)>=0)&(n2(x,y)<=0)&(n3(x,y)<=0)&(n4(x,y)>=0))
{printf("tochka udovl nerav f(A%d)=%2.3f\n",h,fun(x,y));
if (fun(x,y)>max) max=fun(x,y),k=x,t=y,m=h;
else max=max; }
else
printf("tochka ne udovletv neravenstvu\n");
printf("-------------------------------------\n");
na=0.0;nb=1.0;nc=0.0;h=h+1;
printf("f4(x,y,z)=2x^2+2xy+y^2+2x+2y+0.5+z(y)\n");
x=((2*b*nc/nb)-2*d-2*c*nc*na+(2*e*na/nb))/(2*a-(2*b*na/nb)-na*2*b/nb+2*c*na*na);
y=(-nc/nb)-(na/nb)*x;
fun(x,y);
printf ("x=%2.3f\ny=%2.3f\nA%d(%2.3f;%2.3f)\n",x,y,h,x,y);
if ((n1(x,y)>=0)&(n2(x,y)<=0)&(n3(x,y)<=0)&(n4(x,y)>=0))
{printf("tochka udovl nerav f(A%d)=%2.3f\n",h,fun(x,y));
if (fun(x,y)>max) max=fun(x,y),k=x,t=y,m=h;
else max=max; }
else
printf("tochka ne udovletv neravenstvu\n\n");
printf("---------------------------------------------\n");
printf("Nahodim znacheniya funkzii v vershinah figuri\n");
printf("---------------------------------------------\n");
x=0.0;y=2;h=h+1;
printf ("A%d(%2.3f;%2.3f)\nf%d(A%d)=%2.3f\n",h,x,y,h,h,fun(x,y));
printf ("---------------\n");
if (fun(x,y)>max) max=fun(x,y),k=x,t=y,m=h;
else max=max;
x=6.0;y=2;h=h+1;
printf ("A%d(%2.3f;%2.3f)\nf%d(A%d)=%2.3f\n",h,x,y,h,h,fun(x,y));
printf ("---------------\n");
if (fun(x,y)>max) max=fun(x,y),k=x,t=y,m=h;
else max=max;
x=4.0;y=0.0;h=h+1;
printf ("A%d(%2.3f;%2.3f)\nf%d(A%d)=%2.3f\n",h,x,y,h,h,fun(x,y));
printf ("---------------\n");
if (fun(x,y)>max) max=fun(x,y),k=x,t=y,m=h;
else max=max;
x=1.33;y=0;h=h+1;
printf ("A%d(%2.3f;%2.3f)\nf%d(A%d)=%2.3f\n",h,x,y,h,h,fun(x,y));
printf ("-----------------------------------\n");
if (fun(x,y)>max) max=fun(x,y),k=x,t=y,m=h;
else max=max;
printf("Maximalnoe znach funkzii f%d=%2.3f\nA%d(%2.3f;%2.3f)-tochka maximuma\n",m,max,m,k,t);
getch ();}
Результат работы программы
-----METOD SIMPLEX PROCEDURE-----
f(x,y)=2x^2+2xy+y^2+2x+2y+0.5
1)1.5x+y-2>=0;
2)y-2<=0;
3)x-y<=4;
4)y>=0
----------------------------------
f1(x,y,z)=2x^2+2xy+y^2+2x+2y+0.5+z(1.5x+y-2)
x=1.200
y=0.200
A1(1.200;0.200)
tochka udovl nerav f(A1)=6.700
-----------------------------------
f2(x,y,z)=2x^2+2xy+y^2+2x+2y+0.5+z(y-2)
x=-1.500
y=2.000
A2(-1.500;2.000)
tochka ne udovletv neravenstvu
------------------------------------
f3(x,y,z)=2x^2+2xy+y^2+2x+2y+0.5+z(x-y-4)
x=1.200
y=-2.800
A3(1.200;-2.800)
tochka ne udovletv neravenstvu
------------------------------------
f4(x,y,z)=2x^2+2xy+y^2+2x+2y+0.5+z(y)
x=-0.500
y=0.000
A4(-0.500;0.000)
tochka ne udovletv neravenstvu
---------------------------------------------------------
Nahodim znacheniya funkzii v vershinah figuri
---------------------------------------------------------
A5(0.000;2.000)
f5(A5)=8.500
-------------------
A6(6.000;2.000)
f6(A6)=116.500
-------------------
A7(4.000;0.000)
f7(A7)=40.500
-------------------
A8(1.330;0.000)
f8(A8)=6.698
--------------------------------------------------------------------
Maximalnoe znach funkzii f6=116.500
A6(6.000;2.000)-tochka maximuma
|