Задача 1.
Найти общий интеграл дифференциального уравнения. (Ответ представить в виде 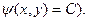
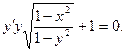

Задача 2.
Найти общий интеграл дифференциального уравнения.
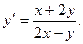
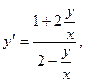
Введем замену 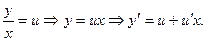
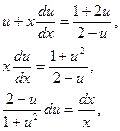
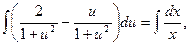
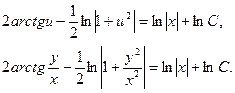
Задача 3.
Найти общий интеграл дифференциального уравнения.
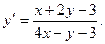
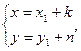
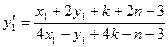
Пусть 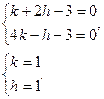
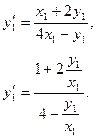
Введем замену 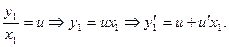


Задача 4.
Найти решение задачи Коши.
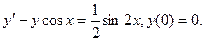
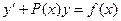 , ,
Пусть 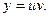
Разделим переменные в этом дифференциальном уравнении относительно функции 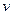 , находим , находим
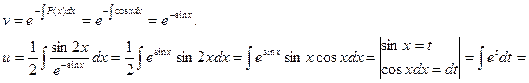
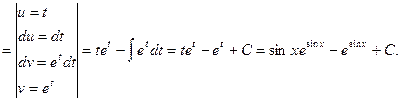
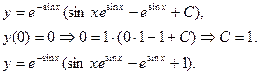
Задача 5.
Решить задачу Коши.
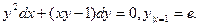
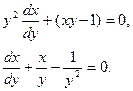
Пусть 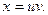
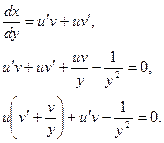
Разделим переменные в этом дифференциальном уравнении относительно функции 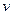 , находим , находим
1) 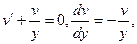
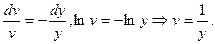
2) 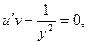
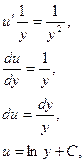
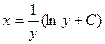 -общее решение ДУ. -общее решение ДУ.
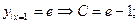
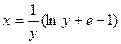 -частное решение ДУ. -частное решение ДУ.
Задача 6.
Найти решение задачи Коши.
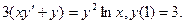
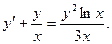
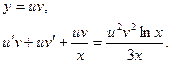
1) Пусть 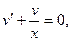
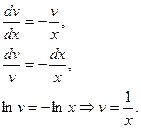
2) 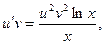
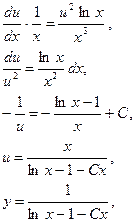
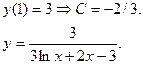
Задача 7.
Найти общий интеграл дифференциального уравнения.
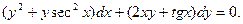
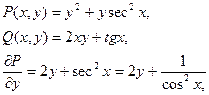
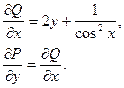
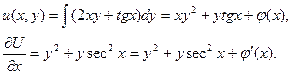
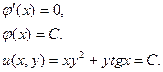
Задача 8.
Для данного дифференциального уравнения методом изоклин построить интегральную кривую, проходящую через точку.
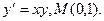
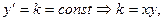
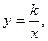 т.е. гипербола. т.е. гипербола.
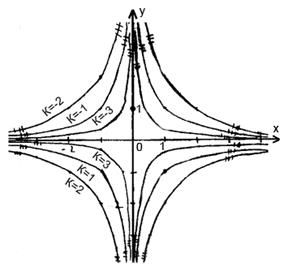
Задача 9.
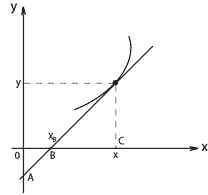
Найти линию, проходящую через точку 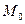 , если отрезок любой ее касательной между точкой касания и осью , если отрезок любой ее касательной между точкой касания и осью 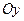 делится на точке пересечения с осью абсцисс в отношении делится на точке пересечения с осью абсцисс в отношении 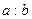 (считая от оси (считая от оси 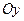 ). ).
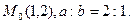
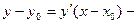 уравнение касательной. уравнение касательной.
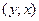 -координаты произвольной точки, принадлежащие касательной. -координаты произвольной точки, принадлежащие касательной.
По условию
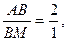
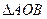 и и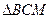 подобны. подобны.
 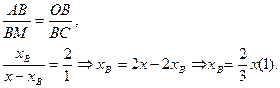
Точка 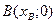 принадлежит касательной, поэтому подставим координаты координаты точки принадлежит касательной, поэтому подставим координаты координаты точки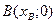 в уравнение касательной. в уравнение касательной.
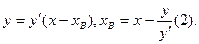
Подставим (1) в (2).
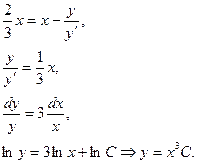
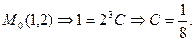
Отсюда, 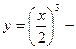 уравнение искомой линии. уравнение искомой линии.
Задача 10.
Найти общее решение дифференциального уравнения.
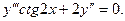
Замена: 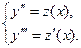
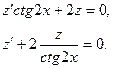
Предположим, что 
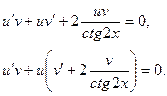
Пусть 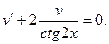
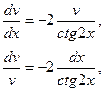

Задача 11.
Найти решение задачи Коши.
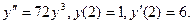
Замена: 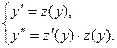
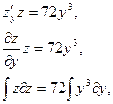
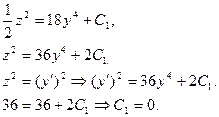
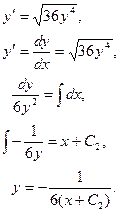
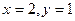 , , 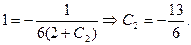
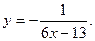
Задача 12.
Найти общее решение дифференциального уравнения.
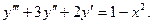
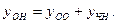
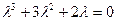 -характеристическое уравнение. -характеристическое уравнение.
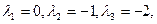
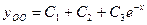 -общее решение однородного уравнения. -общее решение однородного уравнения.
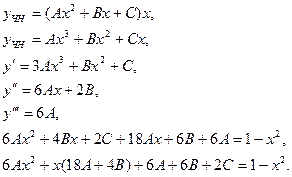
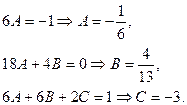
Отсюда 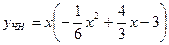 - частное решение неоднородного уравнения. - частное решение неоднородного уравнения.
Общее решение
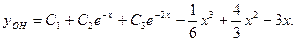
Задача 13.
Найти общее решение дифференциального уравнения.
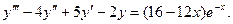
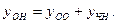
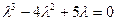 -характеристическое уравнение. -характеристическое уравнение.
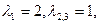
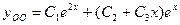 -общее решение однородного уравнения. -общее решение однородного уравнения.
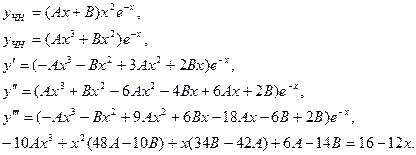
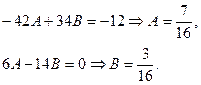
Отсюда 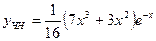 - частное решение неоднородного уравнения. - частное решение неоднородного уравнения.
Общее решение
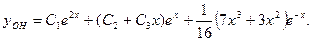
Задача 14.
Найти общее решение дифференциального уравнения.

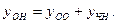
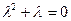 -характеристическое уравнение. -характеристическое уравнение.
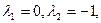
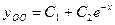 -общее решение однородного уравнения. -общее решение однородного уравнения.
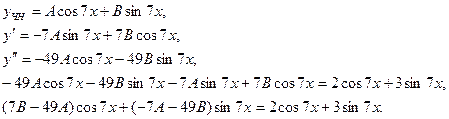
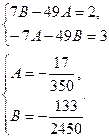
Отсюда 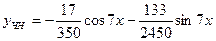 - частное решение неоднородного уравнения. - частное решение неоднородного уравнения.
Общее решение
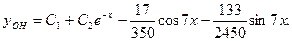
Задача 15.
Найти общее решение дифференциального уравнения.
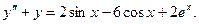
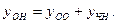
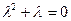 -характеристическое уравнение. -характеристическое уравнение.
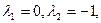
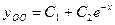 -общее решение однородного уравнения. -общее решение однородного уравнения.
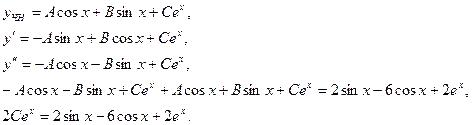
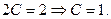
Отсюда 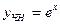 - частное решение неоднородного уравнения. - частное решение неоднородного уравнения.
Общее решение
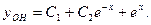
Задача 16.
Найти решение задачи Коши.
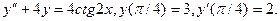
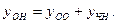
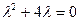 -характеристическое уравнение. -характеристическое уравнение.
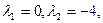
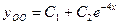 -общее решение однородного уравнения. -общее решение однородного уравнения.
Реклама

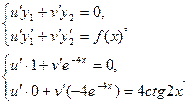
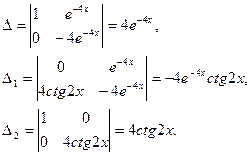
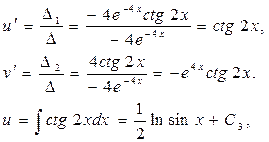
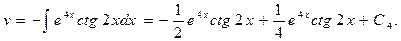
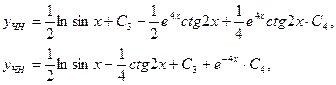
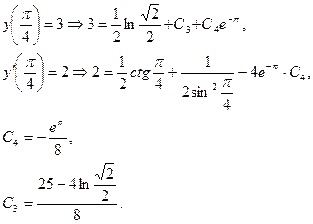
Общее решение
|