| 
Государственная (итоговая) аттестация выпускников IX классов общеобразовательных учреждений 2009 г.
(в новой форме) по ГЕОМЕТРИИ
Демонстрационный вариант экзаменационной работы
подготовлен Федеральным государственным научным учреждением
«ФЕДЕРАЛЬНЫЙ ИНСТИТУТ ПЕДАГОГИЧЕСКИХ ИЗМЕРЕНИЙ»

Экзаменационная работа для проведения государственной итоговой аттестации выпускников IX классов общеобразовательных учреждений 2009 года (в новой форме)
по ГЕОМЕТРИИ
Демонстрационный вариант 2009 года
Пояснения к демонстрационному варианту
экзаменационной работы
При ознакомлении с Демонстрационном вариантом 2009 года следует иметь в виду, что приведенные в нем задания не отражают всех вопросов содержания, которое будет проверяться на государственной (итоговой) аттестации выпускников IX классов по новой форме в 2009 году. Полный перечень вопросов, контролируемых на итоговой аттестации в IX классе в 2009 году, приведен в кодификаторе, помещенном на сайте www.fipi.ru
.
Назначение демонстрационного варианта состоит в том, чтобы дать возможность любому выпускнику, сдающему экзамен, и широкой общественности составить представление о структуре вариантов экзаменационной работы по числу, разнообразию форм, уровней сложности заданий. Приведенные критерии оценки выполнения заданий с развернутым ответом (части 3), включенные в демонстрационный вариант, позволят составить представление о требованиях к полноте и правильности записи развернутого ответа.
Эти сведения позволят выпускникам выработать стратегию подготовки к сдаче выпускного экзамена в соответствии с целями, которые ставятся перед ними.
Экзаменационная работа для проведения государственной итоговой аттестации выпускников IX классов общеобразовательных учреждений 2009 года (в новой форме)
по ГЕОМЕТРИИ
Демонстрационный вариант 2009 года
Инструкция по выполнению работы
На выполнение экзаменационной работы по геометрии дается
3 часа (180 мин). Работа состоит из трех частей и содержит 15 заданий.
Часть 1
содержит 8 несложных заданий. К первым четырем заданиям приведены 4 варианта ответа, из которых только один верный. При выполнении этих заданий обведите кружочком номер
выбранного ответа в экзаменационной работе. Если вы ошиблись при выборе ответа, то зачеркните отмеченную цифру и обведите нужную:
Реклама

  1) 26 2) 20 3) 15 4) 10 1) 26 2) 20 3) 15 4) 10
К заданиям 5 – 8 дайте только ответ (решение записывать не нужно). Ответ записывается в экзаменационной работе в отведенном для этого месте. В случае записи неверного ответа зачеркните его и запишите рядом новый.
Часть 2
содержит 5 более сложных заданий. К заданиям 9 – 12 необходимо дать только ответ, к заданию 13 – записать решение.
Часть 3
содержит 2 самых сложных задания, при выполнении которых требуется записать обоснованное решение.
При выполнении работы разрешается использовать линейку, угольник, циркуль и транспортир. Использование калькулятора не допускается.
Советуем выполнять задания в том порядке, в котором они даны в работе. С целью экономии времени пропускайте задание, которое не удается выполнить сразу, и переходите к следующему. Если после выполнения всей работы у вас останется время, то можно вернуться к пропущенным заданиям.
За каждый правильный ответ в зависимости от сложности задания дается один или более баллов. Баллы, полученные вами за все задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать как можно большее количество баллов.
Желаем успеха!
Часть 1
При выполнении заданий с выбором ответа (задания 1 – 4) обведите кружком номер выбранного ответа в экзаменационной работе.
Диагонали прямоугольника KMNP
пересекаются в точке С
. Найдите ∠MNС
, если ∠MСN
= 46°.
1) 67° 2) 46° 3) 23° 4) 44°
Через точку А
окружности с центром О
проведена касательная АВ
. Найдите радиус окружности, если ОВ
= 8, ∠АОВ
= 60°.
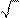 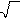 1) 43 2) 8 3) 4 2 4) 4 1) 43 2) 8 3) 4 2 4) 4
Внешний угол при основании равнобедренного треугольника равен 140°. Найдите угол между боковыми сторонами этого треугольника.
1) 70° 2) 100° 3) 40° 4) 80°
А
 Используя данные, указанные на рисунке, найдите высоту СН
. Используя данные, указанные на рисунке, найдите высоту СН
.
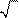 1) 15 2) 7,5 3) 63 4) 7,2 9 1) 15 2) 7,5 3) 63 4) 7,2 9
В
С
12
При выполнении заданий с кратким ответом (задания 5 – 8) запишите ответ в месте, указанном в тексте задания.
Длина окружности равна 29 π. Найдите радиус этой окружности. Ответ: ____________
С
 Используя данные, указанные на рисунке, найдите АС
, если известно, что АВ
|| CD
. Ответ: ____________ Используя данные, указанные на рисунке, найдите АС
, если известно, что АВ
|| CD
. Ответ: ____________
А D
Найдите боковую сторону равнобедренной трапеции, если ее основания равны 9 и 19, а высота равна 12. Ответ: ____________
В параллелограмме ABCD
на стороне ВС
отмечена точка К
так, что ВК=АВ
.
Найдите ∠ВСD
, если ∠КАD
= 20°. Ответ: ____________
Часть 2
При выполнении заданий с кратким ответом (задания 9 – 11) запишите ответ в месте, указанном в тексте задания. При этом единицы измерений (градусы, метры и др.) писать не нужно.
Реклама

Сторона равностороннего треугольника MLN
равна 6 см. Найдите

скалярное произведение векторов LM
и LN
.
Ответ: ____________
Радиус окружности, описанной около правильного двенадцатиугольника
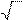 А
1
А
2
…А
12
, равен 5 3 . Найдите длину диагонали А
1
А
5
. А
1
А
2
…А
12
, равен 5 3 . Найдите длину диагонали А
1
А
5
.
Ответ: ____________
 Имеется лист фанеры прямоугольной формы, длина и ширина которого соответственно равны 10 дм и 5 дм. Из него, как показано на рисунке, вырезаны две одинаковые части в форме равнобедренных треугольников. Сколько килограммов краски потребуется, чтобы покрасить получившуюся фигуру, если длина отрезка АВ
равна 6 дм, а на 1 дм2
поверхности расходуется 0,012 кг краски? Имеется лист фанеры прямоугольной формы, длина и ширина которого соответственно равны 10 дм и 5 дм. Из него, как показано на рисунке, вырезаны две одинаковые части в форме равнобедренных треугольников. Сколько килограммов краски потребуется, чтобы покрасить получившуюся фигуру, если длина отрезка АВ
равна 6 дм, а на 1 дм2
поверхности расходуется 0,012 кг краски?
Ответ: ____________
При выполнении задания 12 обведите кружком номера ответов, которые вы выбрали как правильные. После слова «Ответ» запишите номера выбранных ответов, например 123.
Укажите, какие из перечисленных ниже утверждений всегда верны.
1) Все углы ромба – острые. 2) Все высоты ромба равны.
3) Диагонали ромба взаимно перпендикулярны.
4) Радиус окружности, вписанной в ромб, равен стороне этого ромба.
5) В ромбе с углом в 60° одна из диагоналей равна его стороне.
Ответ: ____________
Для записи ответов на задания 13 – 15 используйте отдельный лист или бланк. Запишите сначала номер выполняемого задания, а затем его решение.
ВР
и DК
– высоты параллелограмма АВСD
, проведенные из вершин тупых углов, причем точка P
лежит между точками C
и D
, а точка K
лежит между
точками B
и C
. Отрезки ВР
и DК
пересекаются в точке О
. Докажите, что треугольники СКD
и СРВ
подобны, а углы КОВ
и ВСD
равны.
Часть 3
В равнобедренный треугольник АВС
с основанием ВС
вписана окружность.
Она касается стороны АВ
в точке М.
Найдите радиус этой окружности, если AM
= 10
и BM
= 15
.
Высоты треугольника ABC
пересекаются в точке Н
, а медианы – в точке М
.
Точка K
– середина отрезка МН
. Найдите площадь треугольника AKC
, если известно, что AB
= 6
, CH
= 3
, ∠BAC
= 45
°
.
Система оценивания экзаменационной работы по геометрии
Часть 1
За верное выполнение заданий этой части выставляется 1 балл.
За выполнение заданий 1-4 с выбором ответа выставляется 1 балл при условии, если обведен только один номер верного ответа. Если обведены и не перечеркнуты два и более ответов, в том числе правильный, то ответ не засчитывается.
За выполнение заданий 5-8 с кратким ответом выставляется 1 балл при условии, если записано правильное число.
| № задания
|
Ответ
|
№ задания
|
Ответ
|
| 1
|
1
|
5
|
14,5
|
| 2
|
4
|
6
|
25
|
| 3
|
2
|
7
|
13
|
| 4
|
4
|
8
|
40
|
Часть 2
Задания 9-11 оцениваются в 1 балл.
В зависимости от числа указанных верных ответов за выполнение задания 12 выставляется от 0 до 2 баллов: указаны все 3 верных ответа и при этом не указаны неверные ответы – 2 балла; указано не менее двух верных ответов и при этом указано не более одного неверного ответа – 1 балл; во всех остальных случаях – 0 баллов.
| № задания
|
Ответ
|
| 9
|
18
|
| 10
|
15
|
| 11
|
0,48
|
| 12
|
235
|
Задание 13 оценивается в зависимости от полноты и правильности ответа по приведенным ниже критериям. За выполнение задания 13 выставляется от 0 до 2 баллов.
Часть 3
Задания 14 и 15 оцениваются в зависимости от полноты и правильности ответа по приведенным ниже критериям. За выполнение задания 14 выставляется от 0 до 2 баллов, задания 15 – от 0 до 3 баллов.
| № задания
|
Ответ
|
| 14
|
7,5
|
| 15
|
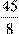
|
Критерии оценивания выполнения заданий с развернутым ответом
№№ 13-15
В работу включены три задания с развернутым ответом, существенно различающиеся по уровню сложности. Выполнение этих заданий оценивается экспертами.
Ниже для каждого из заданий №№ 13–15 приводится один из возможных
вариантов решения, который может быть представлен в работах учащихся, и даются критерии их оценивания.
Подчеркнем, что приведенные записи решений не являются эталонами выполнения работы, которым обязаны следовать учащиеся.
ЗАДАНИЕ № 13
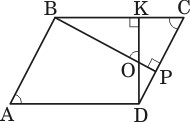
ВР
и DК
– высоты параллелограмма АВСD
, проведенные из вершин тупых углов, причем точка P
лежит между точками C
и D
, а точка K
лежит между точками B
и C
. Отрезки ВР
и DК
пересекаются в точке О
. Докажите, что треугольники СКD
и СРВ
подобны, а углы КОВ
и ВСD
равны.
Образец возможного решения:
1)  У треугольников СКD
и СРВ
∠C
- общий. Следовательно, прямоугольные треугольники СКD
и СВР
подобны (по двум углам). У треугольников СКD
и СРВ
∠C
- общий. Следовательно, прямоугольные треугольники СКD
и СВР
подобны (по двум углам).
2) Пусть у прямоугольного треугольника СРВ
∠BCP
=α, тогда ∠KBO
=∠CBP
= 90°
−α по свойству острых углов прямоугольного треугольника.
Тогда∠BOK
= 90°
−∠KBO
= 90°
−(90°
−α)=α.
То есть ∠BOK
=∠BCD
.
Что и требовалось доказать.
| Балл
|
Содержание критерия
|
| 2
|
Доказаны оба из предложенных в задаче утверждений.
|
| 1
|
Доказано только одно из утверждений.
|
| 0
|
Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1 и 2 балла.
|
ЗАДАНИЕ № 14
В равнобедренный треугольник АВС
с основанием ВС
вписана окружность. Она касается стороны АВ
в точке М.
Найдите радиус этой окружности, если AM
= 10
и BM
= 15
.
Образец возможного решения:
1) Пусть АН
– высота равнобедренного треугольника АВС
. Из свойств равнобедренного треугольника АВС
следует, что АН
– биссектриса этого треугольника. Поэтому центр О
вписанной в треугольник окружности лежит
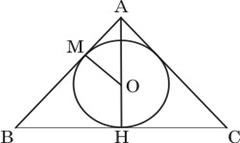 на отрезке АН
, и окружность касается основания ВС
данного треугольника в точке H
. 2) Поскольку отрезки касательных к окружности, проведенные из одной точки, равны, получаем: BH
= BM
= 15
. на отрезке АН
, и окружность касается основания ВС
данного треугольника в точке H
. 2) Поскольку отрезки касательных к окружности, проведенные из одной точки, равны, получаем: BH
= BM
= 15
.
3) В прямоугольном треугольнике ABH
AB
= AM
+ MB
, AB
= 25
и
 AH
= AB
2
− BH
2
, AH
= 20
. AH
= AB
2
− BH
2
, AH
= 20
.
4) Прямоугольный треугольник ABH
подобен прямоугольному
AH BH
 треугольнику AOM
(по двум углам). Откуда = . Получаем: треугольнику AOM
(по двум углам). Откуда = . Получаем:
AM OM
BH AM
· 15
OM
=  , OM
= , OM
=  . .
AH
2
Ответ: 7,5
.
Критерии оценивания задания № 14 учитывают только правильность хода решения, но не включают требование к его обоснованию.
| Балл
|
Содержание критерия
|
| 2
|
Ход решения правильный. Решение завершено.
Все преобразования и вычисления выполнены верно.
Получен верный ответ.
|
| 1
|
Ход решения правильный. Решение завершено.
Допустима описка или негрубая ошибка в вычислениях и преобразованиях, не влияющая на правильность хода решения.
В результате этих недочетов возможен неверный ответ.
|
| 0
|
Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1 и 2 балла.
|
ЗАДАНИЕ № 15
Высоты треугольника ABC
пересекаются в точке Н
, а медианы – в точке М
. Точка K
– середина отрезка МН
. Найдите площадь треугольника AKC
, если известно, что AB
= 6
, CH
= 3
, ∠BAC
= 45
°
.
Образец возможного решения:
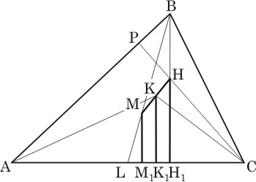 По условию высоты треугольника По условию высоты треугольника
ABC
пересекаются, следовательно, точка Н
их пересечения расположена внутри этого треугольника.
1) Пусть СР
– высота, а BL
– медиана треугольника ABC
.
Обозначим: H
1
,K M
1
, 1
– основания перпендикуляров, проведенных соот-
ветственно из точек H
,K M
, к прямой
АС
. В прямоугольном треугольнике APC
∠PAC
= 45
°
, следовательно, ∠PCA
= 45
°
.
2) В прямоугольном треугольнике HH C
1
∠HCH
1
= 45
°
, следовательно,
  °
3 2 3 2 °
3 2 3 2
катеты равны: CH
1
= HH
1
, HH
1
= CH
·sin45
, HH
1
=, CH
1
=.
2 2
В прямоугольном равнобедренном треугольнике BH A
1
катеты равны:
  AH
1
= BH
1
, BH
1
= AB
·sin45
°
, BH
1
= 3 2
, AH
1
= 3 2
. AH
1
= BH
1
, BH
1
= AB
·sin45
°
, BH
1
= 3 2
, AH
1
= 3 2
.
3) Треугольник BH L
1
подобен треугольнику MM L
1
(по двум углам), и
 BH
1
BL
3 BH
1
BL
3
= = (по свойству медиан треугольника). Отсюда
MM
1
ML
1
 MM
1
= MM
1
=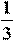 BH
1
, MM
1
= 2
. BH
1
, MM
1
= 2
.
4) Из теоремы Фалеса следует, что отрезок KK
1
является средней линией
 HH
1
+ MM
1
5 2 HH
1
+ MM
1
5 2
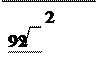 трапеции HH M M
1 1
, поэтому KK
1
=, KK
1
=. трапеции HH M M
1 1
, поэтому KK
1
=, KK
1
=.
4
5) Поскольку AC
= AH
1
+ H C AC
1
, = .
2
1
45
Отсюда S
ΔAKC
=  AC KK
· 1
, S
ΔAKC
= AC KK
· 1
, S
ΔAKC
=  . .
2
8
| Содержание критерия
|
Балл
|
| Найден верный способ решения.
Приведена последовательность всех шагов решения: 1) найдена величина угла ∠PCA
;
|
3
|
| 2) решены прямоугольные треугольники HH C
1
и BH A
1
;
3) установлено подобие треугольников BH L
1
и MM L
1
, и найдена сторона MM
1
;
4) вычислена средняя линия KK
1
трапеции HH M M
1 1
;
5) вычислена площадь треугольника AKC
.
Обоснованы ключевые моменты выбранного способа решения: а) прямоугольные треугольники BH L
1
и MM L
1
подобны;
б) отрезок KK
1
является средней линией трапеции HH M M
1 1
.
Верно выполнены все преобразования и вычисления. Получен верный ответ.
|
|
| Приведена верная последовательность всех шагов решения.
Явно описаны или могут быть отмечены на чертеже свойства представленных в условии фигур и их элементов, которые играют ключевую роль в решении задачи.
Допустимо отсутствие обоснований или неточности в обоснованиях ключевых моментов решения. Приведенные в решении обоснования не содержат грубых ошибок.
Допустима одна описка и/или вычислительная ошибка, не влияющие на правильность дальнейшего хода решения. В результате ошибки или описки может быть получен неверный ответ.
|
2
|
| Ход решения правильный, но решение, возможно, не завершено: найдены величина угла ∠PCA
и длины отрезков
HH
1
,H C H A
1
, 1
и BH
1
.
Допустимо отсутствие обоснований ключевых моментов решения. Приведенные в решении обоснования не содержат грубых ошибок. Допустимы ошибки в вычислениях или в преобразованиях, не влияющие на правильность хода решения. В результате этих ошибок может быть получен неверный ответ.
|
1
|
| Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла.
|
0
|
|