| 
Государственная (итоговая) аттестация выпускников IX классов общеобразовательных учреждений 2009 г.
(в новой форме) по АЛГЕБРЕ
Демонстрационный вариант экзаменационной работы
подготовлен Федеральным государственным научным учреждением
«ФЕДЕРАЛЬНЫЙ ИНСТИТУТ ПЕДАГОГИЧЕСКИХ ИЗМЕРЕНИЙ»

Экзаменационная работа для проведения государственной итоговой аттестации выпускников IX классов общеобразовательных учреждений 2009 года (в новой форме) по АЛГЕБРЕ
Демонстрационный вариант 2009 года
Пояснения к демонстрационному варианту экзаменационной работы
При ознакомлении с Демонстрационным вариантом 2009 года следует иметь в виду, что при сохранении перечня разделов, выносимых на проверку, содержание конкретных заданий в КИМ 2009 года может быть другим.
Полный перечень элементов содержания, которые могут контролироваться на экзамене, приведен в кодификаторе, помещенном на сайте www.fipi.ru
. Последовательность блоков содержания в КИМ 2009 года также может варьироваться.
Назначение демонстрационного варианта заключается в том, чтобы дать возможность любому участнику экзамена и широкой общественности составить представление о структуре будущей экзаменационной работы, числе и форме заданий, а также их уровне сложности. Приведенные критерии оценки выполнения заданий с развернутым ответом, включенные в этот вариант, позволят составить представление о требованиях к полноте и правильности записи развернутого ответа.
Экзаменационная работа для проведения государственной итоговой аттестации выпускников IX классов общеобразовательных учреждений 2009 года (в новой форме) по АЛГЕБРЕ
Демонстрационный вариант 2009 года
Инструкция по выполнению работы
Работа состоит из двух частей. В первой части 16 заданий, во второй – 5. На выполнение всей работы отводится 4 часа. Время на выполнение первой части ограничено: на нее отводится 60 минут.
При выполнении заданий первой части нужно указывать только ответы.
При этом:
- если к заданию приводятся варианты ответов (четыре ответа, из них верный только один), то надо обвести кружком цифру, соответствующую верному ответу;
- если ответы к заданию не приводятся, то полученный ответ надо вписать в отведенном для этого месте.
Если вы ошиблись при выборе ответа, то зачеркните отмеченную цифру и обведите нужную:
Реклама

  1) 26 2) 20 3) 15 4) 10 1) 26 2) 20 3) 15 4) 10
В случае записи неверного ответа зачеркните его и запишите новый:
 Ответ: х
= – 12 х
= 3 Ответ: х
= – 12 х
= 3
Все необходимые вычисления, преобразования и прочее выполняйте в черновике. Если задание содержит рисунок, то на нем можно проводить нужные линии, отмечать точки.
Задания второй части выполняются на отдельных листах или бланках с записью хода решения. Текст задания можно не переписывать, необходимо лишь указать его номер.
Советуем выполнять задания в том порядке, в котором они даны в работе.
С целью экономии времени пропускайте задание, которое не удается выполнить сразу, и переходите к следующему. Если после выполнения всей работы у вас останется время, то можно вернуться к пропущенным заданиям.
Желаем успеха!
Часть 1
Расположите в порядке возрастания числа: 0,0902; 0,09; 0,209.
1) 0,209; 0,0902; 0,09 2) 0,09; 0,0902; 0,209
3) 0,09; 0,209; 0,0902 4) 0,0902; 0,09; 0,209
 Какое из чисел 0,004 , 4000 , 400 является рациональным? Какое из чисел 0,004 , 4000 , 400 является рациональным?
1) 0,004
2)  4000 4000
3) 400
4) ни одно из этих чисел
Дневная норма потребления витамина С составляет 60 мг. Один мандарин в среднем содержит 35 мг витамина С. Сколько примерно процентов
дневной нормы витамина С получил человек, съевший один мандарин?
1) 170%
2) 58%
3) 17%
4) 0,58%
a
+
b
Найдите значение выражения при а
= 8,4; b
= –1,2; с
= – 4,5.
c
Ответ: ______________________
Цена килограмма орехов a
рублей. Сколько рублей надо заплатить за 300 граммов этих орехов?
a
1) (р.) 300
2) 300a
(р.) 3) 0,3a
(р.)
10a
4) (р.)
3
В каком случае выражение преобразовано в тождественно равное?
1) 3(x
− = −y
) 3x y
2) (3+ x
)( x
−3) = 9 − x
2
3) ( x
− y
)
2
= x
2
− y
2
4) ( x
+ 3)
2
= x
2
+ 6x
+ 9
3 1
Упростите выражение + . 2x x
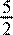 1) 4
5
4) 5 1) 4
5
4) 5
3x
2) 3) 2x
2
2x
Найдите частное 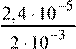 . Ответ запишите в виде десятичной дроби. . Ответ запишите в виде десятичной дроби.
Ответ: ______________________
Решите уравнение 3− 2x
= 6 − 4(x
+ 2).
Ответ: ______________________
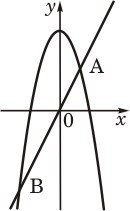
Прямая y
= 2x
пересекает параболу y
= −x
2
+8 в двух точках. Вычислите координаты точки А
.
Ответ: ______________________
Путь от поселка до железнодорожной станции пешеход прошел за 4 ч, а велосипедист проехал за 1,5 ч. Скорость велосипедиста на 8 км/ч больше скорости пешехода. С какой скоростью ехал велосипедист?
Какое уравнение соответствует условию задачи, если буквой х
обозначена скорость велосипедиста (в км/ч)?
1) 4
−1
 ,5
= 8 2) x
+8 = x
3) 1,5( x
+8) = 4x
4) 4( x
−8) =1,5x x x
4 1,5 ,5
= 8 2) x
+8 = x
3) 1,5( x
+8) = 4x
4) 4( x
−8) =1,5x x x
4 1,5
Реклама

Решите неравенство 10x
− 4(2x
−3) > 4.
1) x
> −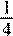 2) x
>8 3) x
> −4 4) x
< −4 2) x
>8 3) x
> −4 4) x
< −4
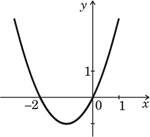 На рисунке изображен график функции y
= x
2
+ 2x
. На рисунке изображен график функции y
= x
2
+ 2x
.
Используя график, решите неравенство x
2
+ 2x
> 0.
1) (−∞; 0)
2) (−∞; − 2)∪(0; + ∞)
3) (–2; 0)
4) (−2; + ∞)
Каждой последовательности, заданной формулой n
-го члена (левый столбец), поставьте в соответствие верное утверждение (правый столбец).
А) xn
= n
2
1) Последовательность – арифметическая прогрессия
Б) yn
= 2n
2) Последовательность – геометрическая прогрессия
В) zn
= 2n
3) Последовательность не является прогрессией
Ответ:
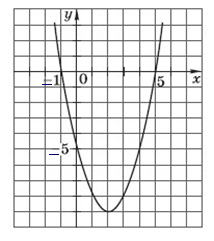 График какой квадратичной функции изображен на рисунке? График какой квадратичной функции изображен на рисунке?
1) y
= x
2
+ 4x
−5
2) y
= −x
2
− 6x
−5 3) y
= x
2
− 4x
−5
4) y
= −x
2
+ 6x
−5
Фирма начала продавать две новые модели телефонов — А и В. На графиках показано, как росло в течение года количество проданных телефонов. (По горизонтальной оси откладывается время, прошедшее с начала продаж, в месяцах; по вертикальной — число телефонов, проданных с начала продаж, в тыс. шт.). Сколько всего телефонов этих двух моделей было продано за первые десять месяцев?
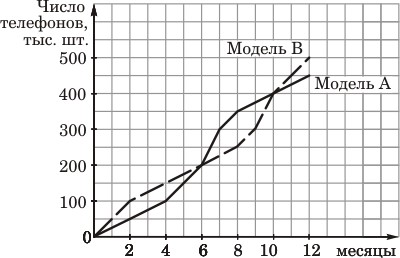
Ответ: ______________________
Часть 2
Задания этой части (17—21) выполняйте с записью решения.
Постройте график функции y
= 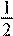 x
2
+ 4x
+ 5. Укажите наименьшее x
2
+ 4x
+ 5. Укажите наименьшее
значение этой функции.
 Выясните, имеет ли корни уравнение x
2
+ 2x
5 + 2x
= −11. Выясните, имеет ли корни уравнение x
2
+ 2x
5 + 2x
= −11.
Найдите сумму всех натуральных чисел, не превосходящих 160, которые не делятся на 4.
Найдите наименьшее значение выражения (2x
+ y
+ 3)2
+ (3x
− 2y
+8)2
и значения x
и y
, при которых оно достигается.
Найдите все значения k
, при которых прямая y
= kx
пересекает в трех различных точках ломаную, заданную условием:
⎧2x
+ 4, если x
< −3
⎪
y
= ⎨−2, если
−3≤ x
≤ 3 ⎪
⎩2x
−8, если x
> 3.
Система оценивания экзаменационной работы по алгебре
Ответы на задания с кратким и развернутым ответом приводятся в одной из возможных форм. Правильный ответ учащегося, данный в какой-либо иной форме, например, −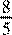 вместо –1,6, необходимо засчитывать. вместо –1,6, необходимо засчитывать.
Часть 1
| Номер задания
|
Ответ
|
| 1
|
2
|
| 2
|
3
|
| 3
|
2
|
| 4
|
– 1,6
|
| 5
|
3
|
| 6
|
4
|
| 7
|
4
|
| 8
|
0,012
|
| 9
|
– 2,5
|
| 10
|
А(2; 4)
|
| 11
|
4
|
| 12
|
3
|
| 13
|
2
|
| 14
|
312
|
| 15
|
3
|
| 16
|
800 тыс.
|
Часть 2
Пояснительная записка
. Требования к выполнению заданий с развернутым ответом заключаются в следующем: решение должно быть математически грамотным и полным, из него должен быть понятен ход рассуждений учащегося. Оформление решения должно обеспечивать выполнение указанных выше требований, а в остальном может быть произвольным. Если решение ученика удовлетворяет этим требованиям, то ему, в зависимости от полноты и правильности выполнения, выставляется полный или «частичный» балл.
Ниже предлагаются две модели начисления баллов. Выбор модели предоставляется регионам.
За выполнение заданий части 1 (№№ 1 – 16) учащийся получает:
по модели 1 – 0,5 балла; по модели 2 – 1 балл.
По модели 1
учащийся, демонстрирующий умение решить ту или иную задачу второй части, получает установленный балл (задание № 17 – 2 балла, №№ 18 и 19 – 4 балла, №№ 20 и 21 – 6 баллов) или балл, на 1 меньше установленного (в случае, если решение содержит несущественный недочет или даже несущественную ошибку). Поэлементное оценивание не предусматривается.
По модели 2
в зависимости от полноты и правильности решения учащемуся выставляется от 0 до максимального балла за каждое задание. Максимальный балл за задание: № 17 – 2 балла, №№ 18 и 19 – 3 балла, №№ 20 и 21 – 4 балла.
При оценивании по любой из моделей должно выполняться следующее требование: выполнение задания оценивается положительным баллом (любым в соответствии с принятой моделью) только в том случае, когда из записей учащегося можно сделать вывод о том, что в принципе он знает ход решения
.
Решения Задание 17
Постройте график функции y
=  x
2
+ 4x
+ 5. Укажите наименьшее x
2
+ 4x
+ 5. Укажите наименьшее
значение этой функции.
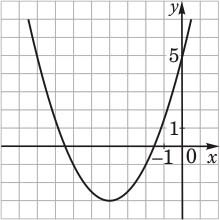 //Ответ
: график изображен на рисунке; у
наим.
= –3. //Ответ
: график изображен на рисунке; у
наим.
= –3.
//Решение
. График — парабола, ветви которой направлены вверх. Найдем
b
−4
координаты вершины: x
= − = x
= = −4;
2a
0 1
y
= 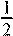 ·16 −16 + 5 = −3. ·16 −16 + 5 = −3.
Наименьшее значение функции равно –3.
Замечание
. Учащийся может вычислить координаты вершины параболы и другим способом.
Модель 1 и модель 2
| Баллы
|
Критерии оценки выполнения задания
|
| 2
|
Правильно построен график, верно указано наименьшее значение функции.
|
| 1
|
Правильно построен график, но отсутствует ответ на вопрос; или при правильных вычислениях допущены очевидные погрешности при построении графика (например, «негладкая» вершина).
|
| 0
|
Другие случаи, не соответствующие указанным критериям.
|
Комментарий
. В случае отсутствия вычислений в чистовике при правильном построении параболы решение должно быть засчитано.
Задание 18
Выясните, имеет ли корни уравнение x
2
+ 2x
5 + 2x
= −11.
//Ответ
: не имеет.
   //Решение
. Представим уравнение в виде x
2
+ 2( 5 +1)x
+11= 0. Определим знак дискриминанта: D
= ( 5 +1)2
−11= 5+ +1 2 5 −11= 2 5 −5. //Решение
. Представим уравнение в виде x
2
+ 2( 5 +1)x
+11= 0. Определим знак дискриминанта: D
= ( 5 +1)2
−11= 5+ +1 2 5 −11= 2 5 −5.
1
Так как 2 5 −5 = 20 − 25 < 0, то уравнение корней не имеет.
 Замечание
. Уравнение может быть представлено в виде x
2
+ (2 5 + 2)x
+11= 0; учащийся может вычислить дискриминант D
квадратного уравнения. Замечание
. Уравнение может быть представлено в виде x
2
+ (2 5 + 2)x
+11= 0; учащийся может вычислить дискриминант D
квадратного уравнения.
Критерии оценивания Модель 1
| Баллы
|
Критерии оценки выполнения задания
|
| 4
|
Уравнение правильно приведено к виду ax
2
+ bx
+ c
= 0, правильно найдено выражение D
1
(или D
), определен его знак и дан верный ответ.
|
| 3
|
Ход решения правильный, решение доведено до конца, но:
допущена одна ошибка вычислительного характера, с ее учетом все дальнейшие шаги выполнены верно; или: при верно вычисленном дискриминанте допущена ошибка
при определении его знака; или: при определении знака дискриминанта записано верное
неравенство, но не показано, как оно получено.
|
| 0
|
Другие случаи, не соответствующие указанным критериям.
|
Комментарий
. Ошибки в составлении выражения D
1
(или D
), в применении формулы квадрата двучлена считаются существенными, и решение при их наличии не засчитывается.
Модель 2
| Баллы
|
Критерии оценки выполнения задания
|
| |
Уравнение правильно приведено к виду ax
2
+ bx
+ c
= 0, правильно
|
| 3
|
найдено выражение D
1
(или D
), определен его знак и дан верный ответ.
|
| 2
|
Ход решения правильный, решение доведено до конца, но допущена одна ошибка вычислительного характера, с ее учетом все дальнейшие шаги выполнены верно; или при определении знака дискриминанта записано верное
неравенство, но не показано, как оно получено.
|
| |
Ход решения верный: уравнение правильно приведено к виду
|
| 1
|
ax
2
+ bx
+ c
= 0, правильно найдено выражение D
1
(или D
), но решение не доведено до конца (не выполнено сравнение полученного выражения с нулем, не сделан вывод о наличии корней).
|
| 0
|
Другие случаи, не соответствующие указанным критериям.
|
Комментарий
. Ошибки в составлении выражения D1
(или D
), в применении формулы квадрата двучлена считаются существенными, и решение при их наличии не засчитывается.
Задание 19
Найдите сумму всех натуральных чисел, не превосходящих 160, которые не делятся на 4.
//Ответ
: 9600. //Решение
. Пусть S
— искомая сумма; S
= S
− S
, где S
— сумма всех
1 2 1
натуральных чисел, не превосходящих 160, S
– сумма всех натуральных чисел,
2
кратных 4 и не превосходящих 160.
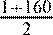 Найдем S
: S
=·160 =161· 80. Найдем S
: S
=·160 =161· 80.
1 1
В последовательности (a
) чисел, кратных 4 и не превосходящих 160, n
a
= 4, a
=160. Найдем число членов этой последовательности. Так как она
1 n
задается формулой a
= 4n
, то 4n
=160, n
= 40. n
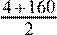 Теперь найдем S
: S
=· 40 =82 · 40. Теперь найдем S
: S
=· 40 =82 · 40.
2 2
Получим: S
= S
− S
=161· 80 −82 · 40 = 40 322( −82) = 9600.
1 2
Критерии оценивания Модель 1
| Баллы
|
Критерии оценки выполнения задания
|
| 4
|
Найден правильный ход решения, все его шаги выполнены верно, получен верный ответ.
|
| 3
|
Ход решения правильный, решение доведено до конца, но допущена одна описка, или непринципиальная ошибка вычислительного характера (например, при вычислении S
или S
), с ее учетом
1 2
дальнейшие шаги выполнены верно.
|
| 0
|
Другие случаи, не соответствующие указанным критериям.
|
Модель 2
| Баллы
|
Критерии оценки выполнения задания
|
| 3
|
Найден правильный ход решения, все его шаги выполнены верно, получен верный ответ.
|
| 2
|
Ход решения правильный, решение доведено до конца, но допущена одна описка или непринципиальная ошибка вычислительного характера (например, при вычислении S
или S
), с ее учетом
1 2
дальнейшие шаги выполнены верно.
|
| 1
|
Ход решения правильный, решение доведено до конца, но допущена ошибка, свидетельствующая о непонимании некоторых содержательных аспектов задания (например, неправильно найдено количество чисел, кратных 4; или суммировались числа, строго меньшие 160, а не меньшие либо равные 160).
|
| 0
|
Другие случаи, не соответствующие указанным критериям.
|
Задание 20
Найдите наименьшее значение выражения (2x
+ y
+ 3)2
+ (3x
− 2y
+8)2
и значения x
и y
, при которых оно достигается.
//Ответ
: наименьшее значение выражения равно 0, оно достигается при x
= −2, y
=1.
//Решение
. При любых значениях х
и у
(2x
+ y
+ 3)2
+ (3x
− 2y
+8) ≥ 0. Значение, равное 0, достигается только в том случае, когда 2x
+ y
+ 3 и 3x
− 2y
+8 равны нулю одновременно.
⎧2x
+ y
+ 3= 0
Составим систему уравнений ⎨ . Решив ее, получим: ⎩3x
− 2y
+8 = 0
x
= −2, y
=1.
Таким образом, наименьшее значение выражения равно 0, оно достигается при x
= −2, y
=1.
Критерии оценивания Модель 1
| Баллы
|
Критерии оценки выполнения задания
|
| 6
|
Найден правильный способ решения, все его шаги выполнены верно, решение содержит пояснения, получен правильный ответ.
|
| 5
|
При правильном решении отсутствуют какие-либо пояснения; или при правильном ходе решения дан неполный ответ (не
указано наименьшее значение выражения); или правильно составлена система уравнений, но при ее
решении допущена вычислительная ошибка.
|
| 0
|
Другие случаи, не соответствующие указанным критериям.
|
Модель 2
| Баллы
|
Критерии оценки выполнения задания
|
| 4
|
Найден правильный способ решения, все его шаги выполнены верно, решение содержит пояснения, получен правильный ответ.
|
| 3
|
При правильном решении отсутствуют какие-либо пояснения, или они содержат логические погрешности.
|
| 2
|
Правильно составлена система уравнений, имеются пояснения, но при решении системы допущена вычислительная ошибка (ответ может быть неверным) или дан неполный ответ (не указано наименьшее значение выражения).
|
| 1
|
При верном ходе решения имеют место какие-либо два из указанных выше недостатков.
|
| 0
|
Другие случаи, не соответствующие указанным критериям.
|
Задание 21
Найдите все значения k
, при которых прямая y
= kx
пересекает в трех различных точках ломаную, заданную условием:
⎧2x
+ 4, если x
< −3
⎪
y
= ⎨−2, если
−3≤ x
≤ 3 ⎪
⎩2x
−8, если x
> 3.
//Ответ
: 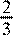 < k
< 2. Другие возможные формы ответа: < k
< 2. Другие возможные формы ответа: 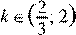 или ( или (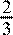 ; 2). ; 2).
//Решение
. Построим ломаную, заданную условиями:
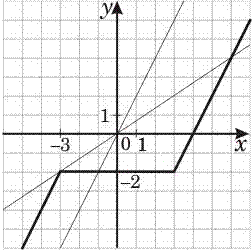 ⎧2x
+ 4, если x
< −3 ⎧2x
+ 4, если x
< −3
⎪ y
= ⎨−2, если
−3≤ x
≤ 3
⎪
⎩2x
−8, если x
> 3.
Прямая y
= kx
пересекает в трех различных точках эту ломаную, если ее угловой коэффициент больше углового коэффициента прямой, проходящей через точку (– 3; – 2), и меньше углового коэффициента прямой, параллельной прямым y
= 2x
−8 и y
= 2x
+ 4.
Найдем угловой коэффициент
прямой, проходящей через
точку (−3; − 2 : 2) − = −3k
, k
= 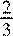 . Угловой коэффициент k
прямой, параллельной прямой y
= 2x
−8, равен 2. Прямая y
= kx
имеет с ломаной три общие точки при . Угловой коэффициент k
прямой, параллельной прямой y
= 2x
−8, равен 2. Прямая y
= kx
имеет с ломаной три общие точки при  < k
< 2. < k
< 2.
Критерии оценивания Модель 1
| Баллы
|
Критерии оценки выполнения задания
|
| 6
|
Правильно построена ломаная, верно найдено множество значений коэффициента k
.
|
| 5
|
Правильно построена ломаная, решение доведено до конца, но вместо k
= 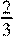 указано k
= указано k
= 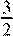 , или вместо строгого неравенства при записи , или вместо строгого неравенства при записи
множества значений k
записано нестрогое неравенство.
|
| 0
|
Другие случаи, не соответствующие указанным критериям.
|
Комментарий. Если график построен неправильно, или график построен правильно, но дальнейшие шаги отсутствуют, то решение не засчитывается.
Модель 2
| Баллы
|
Критерии оценки выполнения задания
|
| 4
|
Правильно построена ломаная, верно найдено множество значений коэффициента k
.
|
| 3
|
Правильно построена ломаная, решение доведено до конца, но вместоk
= 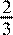 указано k
= указано k
= 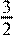 , или вместо строгого неравенства при , или вместо строгого неравенства при
записи множества значений k
записано нестрогое неравенство.
|
| 2
|
2
Правильно построена ломаная, получено одно из неравенств (k
>
3 или k
< 2), но вторая граница значений k
не указана.
|
| 1
|
Идея решения присутствует, но оно не доведено до конца: а именно, построена ломаная и проведены две граничные прямые или какаянибудь прямая, пересекающая ломаную в трех точках, дальнейшие шаги отсутствуют.
|
| 0
|
Другие случаи, не соответствующие указанным критериям.
|
Комментарий
. Если график построен неправильно, или график построен правильно, но дальнейшие шаги отсутствуют, то решение не засчитывается.
|