| МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
Учреждение образования
"Гомельский государственный университет
имени Франциска Скорины"
Математический факультет
Кафедра алгебры и геометрии
Курсовая работа
КОНГРУЭНЦИИ ФРАТТИНИ УНИВЕРСАЛЬНЫХ АЛГЕБР
Исполнитель:
студентка группы H.01.01.01 М-43
Селюкова Н.В.
Научный руководитель:
доктор физико-математических наук,
профессор кафедры Алгебры и геометрии
Монахов В. С.
Гомель 2004
Содержание
Введение
1. Основные определения, обозначения и используемые результаты
2. Свойства централизаторов конгруэнции универсальных алгебр
3. Конгруэнция Фраттини, подалгебра Фраттини и их свойства
Список литературы
Введение
Одно из направлений исследований самых абстрактных алгебраических систем, в частности, универсальных алгебр, связано с изучением, определенным образом выделенных подсистем таких систем. Например, в группах - это силовские подгруппы, подгруппа Фраттини, подгруппа Фиттинга, в алгебрах Ли --- это подалгебра Картана, Фраттини и т.д. Разработка новых методов исследований мультиколец, универсальных алгебр, нашедших свое отображение в книге Л. А. Шеметкова и А. Н. Скибы ``Формации алгебраических систем''(1), дает мощный импульс в реализации этого направленияи в универсальных алгебрах. В этой курсовой работе решается задача, связанная с изучением свойств подалгебр Фраттини и конгруэнции Фраттини универсальных алгебр, принадлежащих некоторому фиксированному мальцевскому многообразию. В частности, получены новые результаты, указывающие на связь подалгебры Фраттини с фраттиниевой конгруэнцией (теоремы (4)и(5)). Установлено одно свойство подалгебры Фраттини нильпотентной алгебры (теорема(2)). Как следствие, из полученных результатов следуют аналогичные результаты теории групп и мультиколец.
Перейдем к подробному изложению результатов курсовой работы, состоящей из введения, трех параграфов и списка литературы, состоящего из пяти наименований.
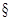 1 носит вспомагательный характер. Здесь приведены все необходимые определения, обозначения и используемые в дальнейшем результаты. 1 носит вспомагательный характер. Здесь приведены все необходимые определения, обозначения и используемые в дальнейшем результаты.
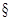 2 носит реферативный характер. Здесь приводятся с доказательствами результаты работ , касающееся свойств централизаторов конгруэнций. 2 носит реферативный характер. Здесь приводятся с доказательствами результаты работ , касающееся свойств централизаторов конгруэнций.
Реклама

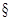 3 является основным. На основе введенного здесь понятия --- конгруэнции Фраттини, устанавливаются некотоые свойства подалгебры Фраттини универсальной алгебры. В частности, доказывается, что подалгебра Фраттини нильпотентной алгебры 3 является основным. На основе введенного здесь понятия --- конгруэнции Фраттини, устанавливаются некотоые свойства подалгебры Фраттини универсальной алгебры. В частности, доказывается, что подалгебра Фраттини нильпотентной алгебры 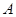 нормальна в нормальна в 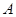 (теорема(3)). (теорема(3)).
1. Основные определения и используемые результаты
Определение 1.1
Пусть 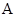 --- некоторое непустое множество и пусть --- некоторое непустое множество и пусть 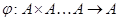 , отображение , отображение 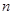 -ой декартовой степени -ой декартовой степени 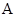 в себя, тогда в себя, тогда 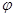 называют называют 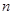 -арной алгебраической операцией
. -арной алгебраической операцией
.
Определение 1.2
Универсальной алгеброй
называют систему 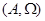 состоящую из некоторого множества состоящую из некоторого множества 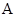 с заданной на нем некоторой совокупностью операций с заданной на нем некоторой совокупностью операций 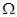 . .
Определение 1.3
Пусть 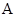 --- некоторая универсальная алгебра и --- некоторая универсальная алгебра и 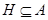 ( (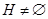 ), тогда ), тогда 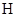 называют подалгеброй универсальной алгебры называют подалгеброй универсальной алгебры
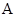 , если , если 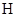 замкнута относительно операций из замкнута относительно операций из 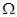 . .
• Для любой операции 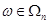 , где , где 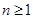 и и 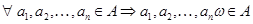 . .
• Для любой операции  элемент элемент 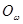 фиксируемый этой операцией в фиксируемый этой операцией в 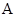 принадлежит принадлежит 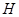 . .
Определение 1.4
Всякое подмножество 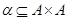 называется бинарным отношением
на называется бинарным отношением
на 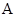 . .
Определение 1.5
Бинарное отношение называется эквивалентностью
, если оно:
• рефлексивно 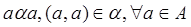
• транзитивно 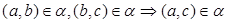 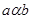 и и 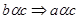
• симметрично 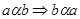 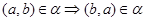
Определение 1.6
Пусть 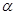 некоторая эквивалентность на некоторая эквивалентность на 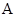 , тогда через , тогда через  обозначают множество обозначают множество 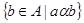 . Такое множество называют класс разбиения по эквивалентности . Такое множество называют класс разбиения по эквивалентности 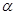 содержащий элемент содержащий элемент 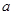 . Множество всех таких классов разбиения обозначают через . Множество всех таких классов разбиения обозначают через 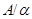 и называют фактормножеством
множества и называют фактормножеством
множества 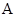 по эквивалентности по эквивалентности 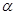 . .
Определим 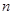 -арную операцию на фактормножестве -арную операцию на фактормножестве 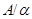 следующим образом: следующим образом:
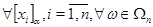
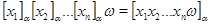
Определение 1.7
Эквивалентность 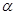 на алгебре на алгебре 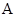 называется ее конгруэнцией
на называется ее конгруэнцией
на 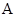 , если выполняется следующее условие: , если выполняется следующее условие:
Для любой операции 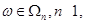 для любых элементов для любых элементов 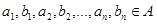 таких, что таких, что 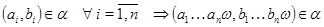 имеет место имеет место 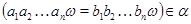 . .
Определение 1.8
Если 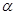 и и 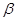 --- конгруэнции на алгебре --- конгруэнции на алгебре 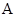 , , 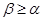 , то конгруэнцию , то конгруэнцию 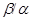 на алгебре на алгебре 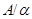 назовем фактором
на назовем фактором
на 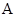 . .
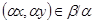 тогда и только тогда, когда тогда и только тогда, когда 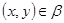 . .
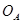 или или 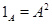 или 1 --- соответственно наименьший и наибольший элементы решетки конгруэнций алгебры или 1 --- соответственно наименьший и наибольший элементы решетки конгруэнций алгебры 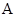 . .
Лемма 1.1 (Цорна).
Если любая цепь частично упорядоченного множества 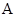 содержит максимальные элементы, то и само множество содержит максимальные элементы, то и само множество 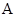 содержит максимальные элементы. содержит максимальные элементы.
Определение 1.9
Пусть 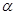 --- бинарное отношение на множестве --- бинарное отношение на множестве 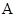 . Это отношение называют частичным порядком на . Это отношение называют частичным порядком на 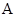 , если оно рефлексивно, транзитивно, антисимметрично.
, если оно рефлексивно, транзитивно, антисимметрично.
Определение 1.10
Множество с заданным на нем частичным порядком называют частично упорядоченным множеством
.
Теорема Мальцев А.И.
Конгруэнции на универсальной алгебре 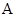 перестановочны тогда и только тогда, когда существует такой тернарный оператор перестановочны тогда и только тогда, когда существует такой тернарный оператор 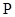 , что для любых элементов , что для любых элементов 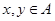 выполняется равенство выполняется равенство 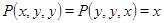 . В этом случае оператор . В этом случае оператор 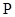 называется мальцевским. называется мальцевским.
Реклама

Определение 1.11
Алгебра 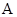 называется нильпотентной
, если существует такой ряд конгруэнций называется нильпотентной
, если существует такой ряд конгруэнций 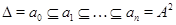 , называемый центральным
, что , называемый центральным
, что 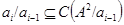 для любого для любого  . .
Определение 1.12
Подалгебра алгебры 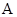 называется собственной
, если она отлична от самой алгебры называется собственной
, если она отлична от самой алгебры 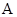 . .
Определение 1.13
Подалгебра 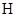 универсальной алгебры универсальной алгебры 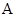 называется нормальной
в называется нормальной
в 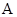 , если , если 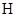 является смежным классом по некоторой конгруэнции является смежным классом по некоторой конгруэнции 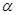 алгебры алгебры 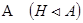 . .
Определение 1.14
Пусть 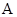 и и 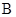 --- универсальные алгебры с одной и той же сигнатурой, отображение --- универсальные алгебры с одной и той же сигнатурой, отображение 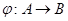 называется гомоморфизмом
, если называется гомоморфизмом
, если
1) 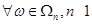 и и 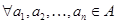 имеет место имеет место 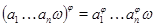 ; ;
2) 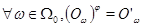 , где , где 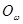 и и 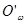 элементы фиксируемой операцией элементы фиксируемой операцией 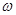 в алгебрах в алгебрах 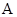 и и 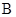 соответственно. соответственно.
Определение 1.15
Гомоморфизм 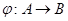 называется изоморфизмом
между называется изоморфизмом
между 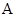 и и 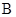 , если обратное к нему соответствие , если обратное к нему соответствие 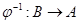 также является гомоморфизмом. также является гомоморфизмом.
Теорема Первая теорема об изоморфизмах
Пусть 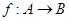 - гомоморфизм, - гомоморфизм, 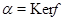 --- конгруэнция, тогда --- конгруэнция, тогда 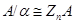 . .
Теорема Вторая теорема об изоморфизмах
Пусть 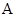 --- есть --- есть 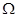 -алгебра, -алгебра, 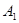 --- подалгебра алгебры --- подалгебра алгебры 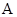 и и 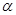 --- конгруэнция на --- конгруэнция на 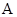 . Тогда . Тогда 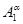 является подалгеброй алгебры является подалгеброй алгебры 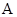 , , 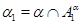 --- конгруэнцией на --- конгруэнцией на 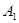 и и 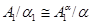 . .
Теорема Третья теорема об изоморфизмах
Пусть 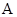 --- есть --- есть 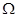 -алгебра и -алгебра и 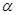 и и 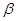 --- такие конгруэнции на --- такие конгруэнции на 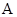 , что , что 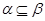 . Тогда существует такой единственный гомоморфизм . Тогда существует такой единственный гомоморфизм 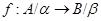 , что , что 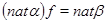 . Если . Если 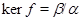 , то , то 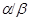 является конгруэнцией на является конгруэнцией на 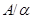 и и 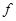 индуцирует такой изоморфизм индуцирует такой изоморфизм 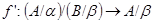 . .
2. Свойства централизаторов конгруэнции универсальных алгебр
Определение 2.1
Пусть 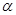 и и 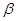 --- конгруэнции на алгебре --- конгруэнции на алгебре 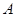 . Тогда . Тогда 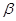 централизует централизует
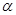 (записывается: (записывается: 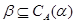 ), если на ), если на 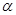 существует такая конгруэнция существует такая конгруэнция 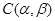 , что: , что:
1) из 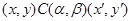
всегда следует 
2) для любого элемента 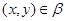
всегда выполняется 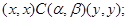
3) если 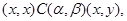
то 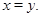
Под термином "алгебра" в дальнейшем будем понимать универсальную алгебру. Все рассматриваемые алгебры предполагаются входящими в фиксированное мальцевское многообразие 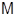 . .
Следующие свойства централизуемости, полученные Смитом , сформулируем в виде леммы.
Лемма 2.1
Пусть 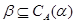 . Тогда: . Тогда:
1) существует единственная конгруэнция 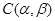 , удовлетворяющая определению 2.1; , удовлетворяющая определению 2.1;
2) 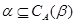 ; ;
3) если 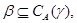
то 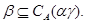
Из леммы 2.1. и леммы Цорна следует, что для произвольной конгруэнции 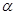 на алгебре на алгебре 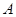 всегда существует наибольшая конгруэнция, централизующая всегда существует наибольшая конгруэнция, централизующая 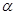 . Она называется централизатором
конгруэнции . Она называется централизатором
конгруэнции 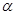 в в 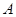 и обозначается и обозначается 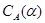 . .
В частности, если 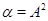 , то централизатор , то централизатор 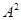 в в 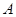 будем обозначать будем обозначать 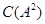 . .
Лемма 2.2
Пусть 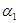 , , 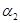 --- конгруэнции на алгебре --- конгруэнции на алгебре 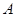 , , 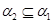 , , 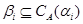 , , 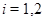 . Тогда справедливы следующие утверждения: . Тогда справедливы следующие утверждения:
1) 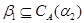 ; ;
2) 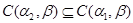 , где , где 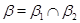 ; ;
3) если выполняется одно из следующих отношений:
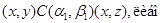

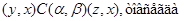
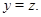
4) из 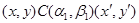 всегда следует всегда следует 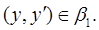
Доказательство:
1) Очевидно, что 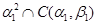 --- конгруэнция на --- конгруэнция на 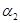 , удовлетворяющая определению 2.1. В силу пункта 1) леммы 2.1. и , удовлетворяющая определению 2.1. В силу пункта 1) леммы 2.1. и 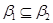 . .
2) 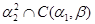 --- конгруэнция на --- конгруэнция на 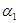 , удовлетворяющая определению , удовлетворяющая определению
2.1. Значит 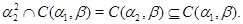
3) Пусть 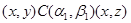 . .
Тогда 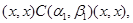
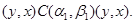
Применим к последним трем соотношениям мальцевский оператор 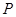 такой, что такой, что 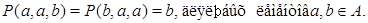
Тогда получим 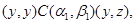
т.е. 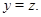
Аналогичным образом показываются остальные случаи из пункта 3).
4) Пусть 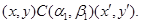
Тогда справедливы следующие соотношения:
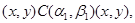
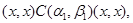
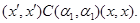
Следовательно, 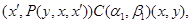
где 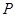 --- мальцевский оператор. --- мальцевский оператор.
Тогда 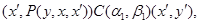
то есть 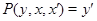 . .
Так как 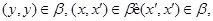
то 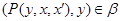 . .
Таким образом 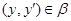 . Лемма доказана. . Лемма доказана.
Следующий результат оказывается полезным при доказательстве последующих результатов.
Лемма. 2.3
Любая подалгебра алгебры 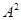 , содержащая диагональ , содержащая диагональ 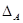 , является конгруэнцией на алгебре , является конгруэнцией на алгебре 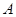 . .
Доказательство:
Пусть 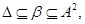 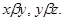
Тогда из 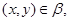 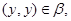 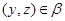
следует, что 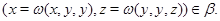
Аналогичным образом из 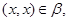 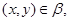 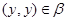
получаем, что 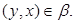
Итак, 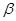 симметрично и транзитивно. Лемма доказана. симметрично и транзитивно. Лемма доказана.
Лемма 2.4
Пусть 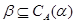 . Тогда . Тогда 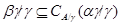 для любой конгруэнции для любой конгруэнции 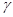 на алгебре на алгебре 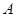 . .
Доказательство:
Обозначим 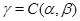 и определим на алгебре и определим на алгебре 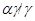 бинарное отношение бинарное отношение 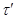 следующим образом: следующим образом: 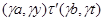
тогда и только тогда, когда 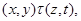
где 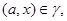 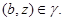
Используя лемму 2.3, нетрудно показать, что 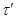 --- конгруэнция на алгебре --- конгруэнция на алгебре 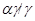 , причем , причем 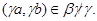
Пусть 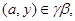
то есть 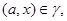 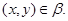
Тогда 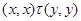
и, значит 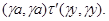
Пусть, наконец, имеет место 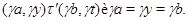
Тогда справедливы следующие соотношения:
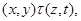
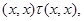
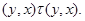
применяя мальцевчкий оператор  к этим трем соотношениям, получаем к этим трем соотношениям, получаем 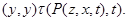
Из леммы 2.2 следует, что 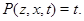
Так как 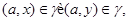 то то 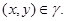
Значит, 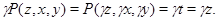
Но 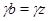 , следовательно, , следовательно, 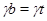 . .
Итак, 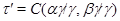
и удовлетворяет определению 2.1. Лемма доказана.
Лемма 2.5
Пусть 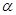 , , 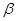 --- конгруэнции на алгебре --- конгруэнции на алгебре 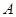 , , 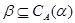 и и 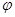 --- изоморфизм, определенный на --- изоморфизм, определенный на 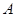 . .
Тогда для любого элемента 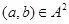 отображение отображение 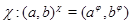 определяет изоморфизм алгебры определяет изоморфизм алгебры 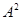 на алгебру на алгебру  , при котором , при котором 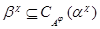 . .
В частности, 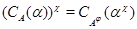 . .
Доказательство.
Очевидно, что 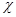 --- изоморфизм алгебры --- изоморфизм алгебры 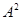 на алгебру на алгебру 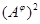 , при котором конгруэнции , при котором конгруэнции 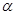 , , 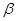 изоморфны соответственно конгруэнциям изоморфны соответственно конгруэнциям 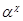 и и 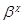 . .
Так как 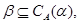
то определена конгруэнция 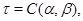
удовлетворяющая определению 2.1.
Изоморфизм 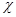 алгебры алгебры 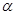 на алгебру на алгебру 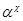 индуцирует в свою очередь изоморфизм индуцирует в свою очередь изоморфизм 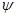 алгебры алгебры 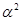 на алгебру на алгебру 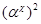 такой, что такой, что
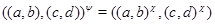
для любых элементов 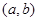 и и 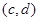 , принадлежащих , принадлежащих 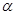 . Но тогда легко проверить, что . Но тогда легко проверить, что 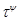 --- конгруэнция на алгебре --- конгруэнция на алгебре 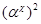 , изоморфная конгруэнции , изоморфная конгруэнции 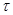 . .
Это и означает, что 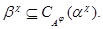
Лемма доказана.
Определение 2.2
Если 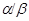 и и 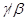 --- факторы на алгебре --- факторы на алгебре 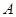 такие, что такие, что 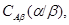 то конгруэнцию то конгруэнцию 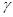 обозначим через обозначим через 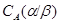 и назовем централизатором фактора и назовем централизатором фактора
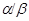 в в 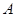 . .
Определение 2.3
Факторы 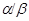 и и 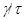 назыавются перспективными
, если либо назыавются перспективными
, если либо 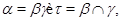 либо либо 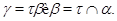
Теорема
Пусть 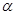 , , 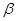 , , 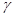 , , 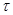 --- конгруэнции на алгебре --- конгруэнции на алгебре 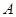 . Тогда: . Тогда:
1) если 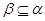 , то , то 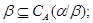
2) если 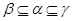 , то , то 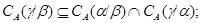 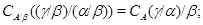
3) если 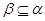 , , 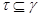 и факторы и факторы 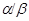 , , 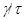 перспективны, то перспективны, то 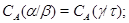
4) если 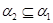 - конгруэнции на - конгруэнции на 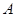 и и 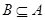 , то , то 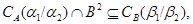
где 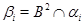 , , 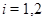 . .
Доказательство.
1) Так как конгруэнция 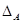 централизует любую конгруэнцию и централизует любую конгруэнцию и 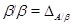 , то , то 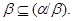
2) Из первого пункта лемы 2.2 следует, что 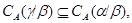
а в силу леммы 2.4 получаем, что 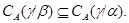
Пусть 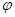 - изоморфизм - изоморфизм 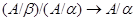 . Обозначим . Обозначим
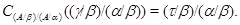
По лемме 2.5 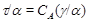 , а по определению , а по определению 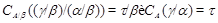
Следовательно, 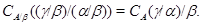
3) Очевидно, достаточно показать, что для любых двух конгруэнции 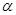 и и 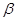 на алгебре на алгебре 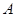 имеет место равенство имеет место равенство 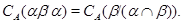
Покажем вналале, что 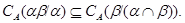
Обозначим 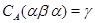 . Тогда, согласно определению 2.1. на алгебре . Тогда, согласно определению 2.1. на алгебре 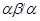 существует такая конгруэнция существует такая конгруэнция 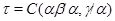 , что выполняются следующие свойства: , что выполняются следующие свойства:
а) если 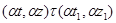 , то , то 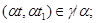
б) для любого элемента 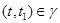 , , 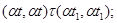
в) если 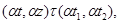 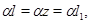
то 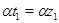
Построим бинарное отношение 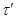 на алгебре на алгебре 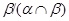 следующим образом: следующим образом: 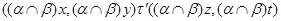
тогда и только тогда, когда 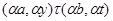
и 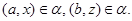
Покажем, что 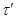 --- конгруэнция на --- конгруэнция на 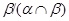 . .
Пусть 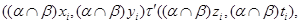
для 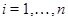 . Тогда . Тогда 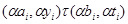
и 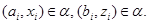
Так как 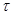 --- конгруэнция, то для любой --- конгруэнция, то для любой 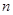 -арной операции -арной операции 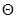 имеем имеем
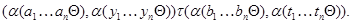
Очевидно, что 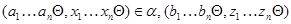
и 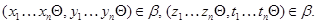
Следовательно, 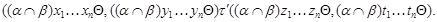
Очевидно, что для любой пары 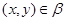 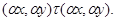
Значит, 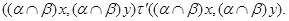
Итак, по лемме 2.3, 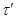 - конгруэнция на - конгруэнция на 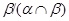 . Покажем теперь, что . Покажем теперь, что  удовлетворяет определению 2.1, то есть удовлетворяет определению 2.1, то есть 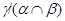 централизует централизует 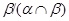 . Пусть . Пусть 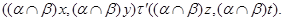
Тогда 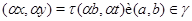
Так как 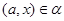 , ,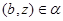 и и 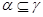 , то , то 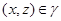 . Следовательно, . Следовательно,  удовлетворяет определению 2.1. удовлетворяет определению 2.1.
Если 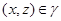 , то , то 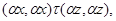
значит, 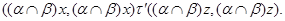
Пусть, наконец, имеет место (1) и 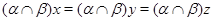
Тогда 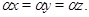
Так как 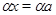 и и 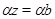 , то , то 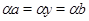 , следовательно, , следовательно, 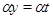 . Из (2) следует, что . Из (2) следует, что 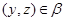 , а по условию , а по условию  . Значит, . Значит, 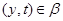 и поэтому и поэтому
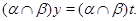
Тем самым показано, что конгруэнция 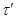 удовлетворяет определению 2.1, то есть удовлетворяет определению 2.1, то есть 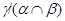 централизует централизует 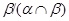 . .
Докажем обратное включение.
Пусть 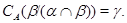
Тогда на алгебре 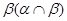 определена конгруэнция определена конгруэнция 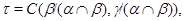 удовлетворяющая определению 2.1. Построим бинарное отношение удовлетворяющая определению 2.1. Построим бинарное отношение  на алгебре на алгебре 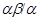 следующим образом: следующим образом:
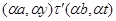
тогда и только тогда, когда
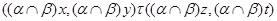
и 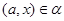 , , 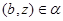 . .
Аналогично, как и выше, нетрудно показать, что 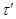 --- конгруэнция на алгебре --- конгруэнция на алгебре 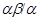 . Заметим, что из доказанного включения в одну сторону следует, что . Заметим, что из доказанного включения в одну сторону следует, что 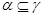 . Покажем поэтому, что . Покажем поэтому, что 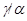 централизует централизует 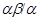 . .
Так как 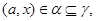 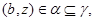 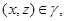 то то 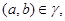
то есть 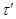 удовлетворяет условию 1) определения 2.1. удовлетворяет условию 1) определения 2.1.
Если 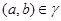 , то , то 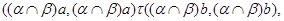
следовательно, 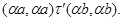
Пусть имеет место (3) и 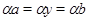 . .
Так как 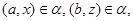
то 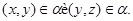
Из (4) следует, что 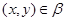 , следовательно, , следовательно, 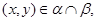
то есть 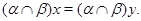
На основании леммы 2.2 заключаем, что 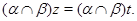
Следовательно, 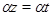 . .
А так как 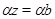 , то , то 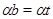 , то есть , то есть 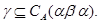
4) Обозначим 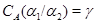 . Пусть . Пусть 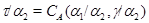
и удовлоетворяет определению 2.1.
Определим бинарное отношение 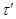 на на 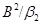 следующим образом следующим образом
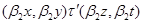
тогда и только тогда, когда
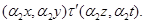
Аналогично, как и выше, нетрудно показать, что 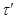 --- конгруэнция, удовлетворяющая определению 2.1. --- конгруэнция, удовлетворяющая определению 2.1.
Это и означает, что 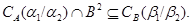
Теорема доказана.
Как следствия, из доказанной теоремы получаем аналогичные свойства централизаторов в группах и мультикольцах.
3. Конгруэнция Фраттини, подалгебра Фраттини и их свойства
Определение 3.1
Конгруэнция 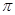 универсальной алгебры универсальной алгебры 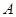 называется фраттиниевой
, если называется фраттиниевой
, если 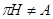 , для любой собственной подалгебры , для любой собственной подалгебры 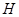 из из 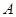 ; ;
Определение 3.2
Собственная подалгебра 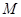 универсальной подалгебры универсальной подалгебры 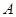 называется максимальной
, если из того, что для некоторой подалгебры называется максимальной
, если из того, что для некоторой подалгебры 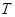 выполняется выполняется 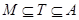 , всегда следует, что либо , всегда следует, что либо 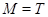 , либо , либо 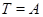 . .
Будем в дальнейшем рассматривать алгебры с условием максимальности и минимальности для подалгебр.
Теорема
Конгруэнция 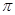 универсальной алгебры универсальной алгебры 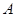 является фраттиниевой тогда и только тогда, когда для любой максимальной подалгебры является фраттиниевой тогда и только тогда, когда для любой максимальной подалгебры 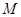 из из 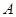 имеет место равенство имеет место равенство 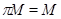 . .
Доказательство:
Пусть 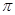 --- фраттиниева конгруэнция алгебры --- фраттиниева конгруэнция алгебры 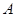 и и 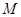 --- максимальная подалгебра из --- максимальная подалгебра из 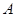 . .
Так как 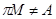 и и 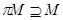 , то , то 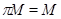 . .
Обратно. Пусть 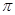 удовлетворяет свойству удовлетворяет свойству 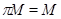 и пусть и пусть 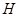 --- любая собственная подалгебра алгебры --- любая собственная подалгебра алгебры 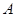 . .
Так как выполняется условие максимальности для подалгебр, то найдется такая максимальная подалгебра 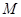 алгебры алгебры 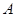 , что , что 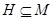 , но , но 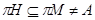 . .
Тем самым теорема доказана.
Определение 3.3
Пусть 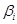 --- конгруэнция на универсальной алгебре --- конгруэнция на универсальной алгебре 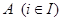 , тогда , тогда 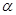 называется конгруэнцией, порожденной конгруэнцией называется конгруэнцией, порожденной конгруэнцией 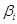 , если
, если 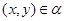 тогда и только тогда, когда существуют тогда и только тогда, когда существуют 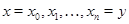 такие, что такие, что 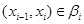 . .
Определение 3.4
Конгруэнцией Фраттини универсальной алгебры
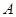 назовем конгруэнцию, порожденную всеми фраттиниевыми конгруэнциями алгебры назовем конгруэнцию, порожденную всеми фраттиниевыми конгруэнциями алгебры 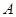 и будем обозначать и будем обозначать 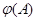 . .
Теорема
Конгруэнция Фраттини является фраттиниевой конгруэнцией.
Доказательство:
Из теоремы следует, что достаточно показать выполнимость следующего равенства 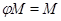 , где , где 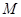 --- произвольная подалгебра алгебры --- произвольная подалгебра алгебры 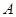 . Напомним, что . Напомним, что 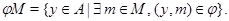
Так как 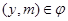 , то существует такая конечная последовательность фраттиниевых конгруэнций , то существует такая конечная последовательность фраттиниевых конгруэнций 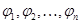 , что , что 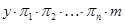 . Это означает, что существует последовательность элементов, что . Это означает, что существует последовательность элементов, что 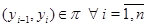 . .
Так как 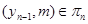 и и 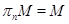 , то , то 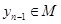 . Аналогичным образом получаем, что . Аналогичным образом получаем, что 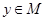 . .
Следовательно, 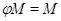 . .
Теорема доказана.
Напомним следующее определение из книги.
Определение 3.5
Пусть 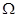 --- множество всех максимальных подалгебр алгебры --- множество всех максимальных подалгебр алгебры 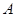 , , 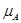 --- конгруэнция алгебры --- конгруэнция алгебры 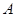 , порожденная всеми такими конгруэнциями , порожденная всеми такими конгруэнциями 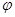 на на 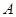 , что , что 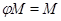 , , 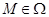 . .
Лемма 3.1
Конгруэнция 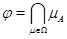 является фраттиниевой конгруэнцией на является фраттиниевой конгруэнцией на 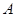 и всякая фраттиниева конгруэнция на и всякая фраттиниева конгруэнция на 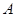 входит в входит в 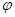 . .
Доказательство:
Пусть 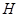 --- произвольная собственная подалгебра алгебря --- произвольная собственная подалгебра алгебря 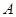 . Тогда найдется такая максимальная в . Тогда найдется такая максимальная в 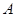 подалгебра подалгебра 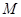 , что , что 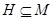 . Значит, . Значит, 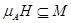 и тем более и тем более 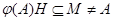 . Следовательно, . Следовательно, 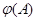 фраттиниева конгруэнция на фраттиниева конгруэнция на 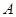 . .
Пусть теперь 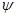 --- произвольная фраттиниева алгебры --- произвольная фраттиниева алгебры 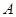 , , 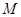 --- произвольная максимальная подалгебра из --- произвольная максимальная подалгебра из 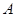 . Тогда . Тогда 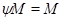 , т.е. , т.е. 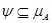 . Следовательно, . Следовательно, 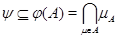 . Лемма доказана. . Лемма доказана.
Определение 3.6
Подалгебра Фраттини
универсальной алгебры 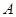 называется пересечение всех максимальных подалгебр из называется пересечение всех максимальных подалгебр из 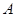 , и обозначается через , и обозначается через 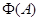 . .
Теорема
Пусть 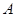 --- алгебра. Тогда --- алгебра. Тогда 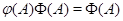 . .
Доказательство:
От противного. Предположим, что 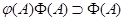 . Тогда существует элемент . Тогда существует элемент 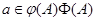 такой, что такой, что 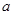 не принадлежит не принадлежит 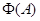 . Так как . Так как 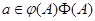 , то существует , то существует 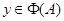 и, следовательно, и, следовательно, 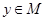 для любой максимальной подалгебры для любой максимальной подалгебры 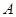 и и 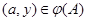 --- фраттиниева. Значит, --- фраттиниева. Значит, 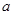 принадлежит любой максимальной подалгебре из принадлежит любой максимальной подалгебре из 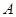 . Следовательно, . Следовательно, 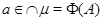 . Теорема доказана. . Теорема доказана.
Лемма 3.2
Пусть 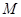 --- максимальная подалгебра алгебры --- максимальная подалгебра алгебры 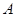 такая, что такая, что 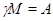 , где , где 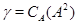 , тогда , тогда 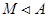 . .
Доказательство:
Определим бинарное отношение 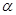 на алгебре на алгебре  следующим образом: следующим образом: 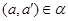 тогда и только тогда, когда существует элементы тогда и только тогда, когда существует элементы 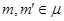 и и 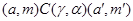 . .
Как показано в работе 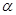 --- конгруэнция на алгебре --- конгруэнция на алгебре 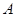 . .
Покажем, что 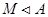 , т.е. , т.е. 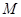 является смежным классом по конгруэнции является смежным классом по конгруэнции 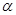 . .
Пусть 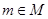 и пусть и пусть  . В силу определения . В силу определения 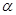 найдутся такие элементы найдутся такие элементы 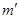 и и 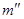 , что , что 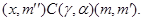
Применим мальцевский оператор 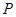 . Отсюда получаем . Отсюда получаем 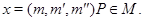
Следовательно, 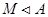 . .
Лемма доказана.
Лемма 3.3
Пересечение нормальных подалгебр алгебры 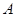 является нормальной подалгеброй алгебры является нормальной подалгеброй алгебры 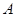 . .
Теорема
Подалгебра Фраттини нильпотентной алгебры 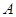 нормальна в нормальна в 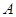 . .
Доказательство:
Пусть алгебра 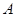 --- нильпотентна, тогда она обладает таким рядом конгруэнций, --- нильпотентна, тогда она обладает таким рядом конгруэнций, 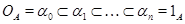 , где , где 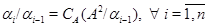 . Очевидно, что для любой максимальной подалгебры . Очевидно, что для любой максимальной подалгебры 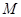 алгебры алгебры 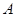 всегда найдется такой номер всегда найдется такой номер 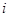 , что , что 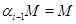 и и 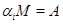 . .
По лемме 3.2. 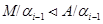 . Отсюда следует, что . Отсюда следует, что 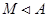 . Так как пересечение нормальных подалгебр является нормальной подалгеброй, то . Так как пересечение нормальных подалгебр является нормальной подалгеброй, то 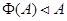 . .
Теорема доказана.
Заключение
В данной курсовой работе приведены с доказательствами результаты работ[2], касающееся свойств централизаторов конгруэнций. А также на основе введенного здесь понятия - конгруэнции Фраттини, устанавливаются некотоые свойства подалгебры Фраттини - универсальной алгебры. В частности, доказано, что подалгебра Фраттини нильпотентной алгебры 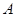 нормальна в нормальна в 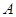 . .
Список использованной литературы
Шеметков Л. А., Скиба А. Н., Формации алгебраических систем. --- М.: Наука, 1989. -- 256с.
Ходалевич А. Д., Универсальные алгебры с 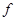 -центральными рядами конгруэнций// Известия АН Беларуси. Сер. физ.-мат. наук, 1994. N1. с.30--34 -центральными рядами конгруэнций// Известия АН Беларуси. Сер. физ.-мат. наук, 1994. N1. с.30--34
Smith J. D. Mal'cev Varieties // Lect. Notes Math. 1976. V.554.
Hodalevich A. D., Maximal Subalgebras of universal algebras --- Manuscript, 1994.
Кон П. М., Универсальная алгебра. М.:Мир, 1968.--351с.
|