| Цель работы:
изучить теорию и методы решения задач линейного программирования; пробрести навыки построения моделей линейного программирования и решения задач линейного программирования на ЭВМ.
Краткие теоретические сведения
Методы линейного программирования (ЛП) оказались весьма эффективными для решения задач из различных областей человеческой деятельности. Слово "программирование" понимается как планирование, и это определяет характер рассматриваемых приложений. Основные идеи линейного программирования возникли во время второй мировой войны в связи с поиском оптимальных стратегий при ведении военных операций. С тех пор они нашли широкое применение в промышленности, торговле и в управлении - как в местных, так и в государственных масштабах. Этими методами можно решить многие задачи, связанные с эффективным использованием ограниченных ресурсов.
Пример 1.
Фирма производит две модели (А
и В)
сборных книжных полок. Их производство ограничено наличием сырья (высококачественных досок) и временем машинной обработки. Для каждого изделия модели А
требуется 3 м2
досок, а для изделия модели В
- 4 м2
. Фирма может получить от своих поставщиков до 1 700 м2
досок в неделю. Для каждого изделия модели А
требуется 12 мин машинного времени, а для изделия модели 5-30 мин. В неделю можно использовать 160 ч машинного времени.
Сколько изделий каждой модели следует фирме выпускать в неделю, если каждое изделие модели А
приносит 2 дол. прибыли, а каждое изделие модели В-А
дол. прибыли?
Чтобы сформулировать эту задачу математически, обозначим через х{
количество выпущенных за неделю полок модели Л, а через х2
-количество выпущенных полок модели В.
Задача состоит в том, чтобы найти наилучшие
значения х\
и х2
.
Очевидно, наилучшими для данной задачи являются такие значения, которые максимизируют еженедельную прибыль.
Еженедельная прибыль составляет
Р
= 2x1
, + 4x2
.
Поскольку х1
и х2
выражают еженедельный объем выпускаемых изделий, то они не могут быть отрицательны, т.е.
х{
>
0, х2
>0 (1)
Теперь ограничения на наличие досок и машинное время могут быть записаны следующим образом: для досок -
Зх1
+ 4х2
< 1700 (2)
для машинного времени -
2X1
+ 5 х2
< 1600. (3)
Следовательно, задача состоит в том, чтобы найти значения х1
и х2
,
удовлетворяющие условиям неотрицательности (1) и ограничениям типа неравенства (2) - (3) и максимизирующие функцию Р.
Реклама

Это типичная двумерная задача линейного программирования. Целевая функция, которая должна быть максимизирована, является линейной функцией своих переменных. Ограничения на эти переменные тоже линейны (1).

Рис. 1 Линия уровня целевой функции и допустимое множество задачи ЛП
Условия неотрицательности позволяют ограничиться рассмотрением положительного квадранта. Границы определяются прямыми
3x1
+ 4х2
= 1700,
2х1
+ 5х2
= 1 600.
Стрелка на каждой границе указывает, с какой стороны прямой * выполняется ограничение. Заштрихованная область ОАВС,
содержащая точки, для которых соблюдены условия (2) и (3), является допустимой. Точки внутри и на границе этой области изображают допустимые решения. Допустимых решений много. Задача состоит в том, чтобы найти точку максимума функции Р.
Штриховыми линиями изображены прямые
2x1
+ 4x2
=0,
2x1
+ 4x2
= 800,
обозначенные а
и b
соответственно. Эти прямые параллельны и представляют собой две линии уровня функции Р
со значениями 0 и 800. Ясно, что значение функции Р
возрастает по мере того, как линии уровня удаляются от начала координат в положительном квадранте.
ми (2, 4), указывающий направление возрастания функции Р
перпендикулярен штриховым линиям и направлен в сторону, противоположную началу координат.
Линией уровня с наибольшим значением функции Р
имеющей хотя бы одну точку с допустимой областью, является прямая с, проходящая через вершину В;
на ней Р
принимает значение 1 400. Точка В,
в которой х1
= 300, х2
=
200, соответствует оптимальному решению задачи. Эти значения могут быть получены как решения уравнений.
2х1
+4х2
=1700,
2х1
+5х2
=1 600.
Следовательно, максимальная прибыль составляет 2*300 + 4*200 = 1400.
В точке максимума оба ограничения превращаются в равенства, что означает полное использование сырья и машинного времени.
Пример 1 показывает, как возникают задачи линейного программирования на практике и демонстрирует графический метод их решения.
Рассмотренная задача может быть расширена до трех и более ограничений и соответствующего количества неотрицательных переменных. Могут быть введены дополнительные ограничения, связанные с возможностями рынка, упаковкой и т.д. В этом случае задача по-прежнему заключается в максимизации линейной
функции от нескольких переменных при линейных
ограничениях.
Реклама

Порядок выполнения работы
Вариант № 2
-2х1
+ 3х2
→ max
Графический метод:
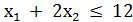
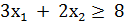
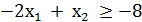
1) х1
+ 2х2
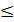 12 2) 3х1
+ 2х2 12 2) 3х1
+ 2х2
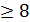
х1
> 0 x2
> 0 х1
> 0 x2
> 0
x1
= 0 x2
= 6 x1
= 0 x2
= 4
x1
= 12 x2
= 0 x1
= 8/3 x2
= 0
3) -2х1
+ х2
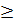 -8 -8
х1
> 0 x2
> 0
x1
= 0 x2
=-8
x1
= 4 x2
= 0
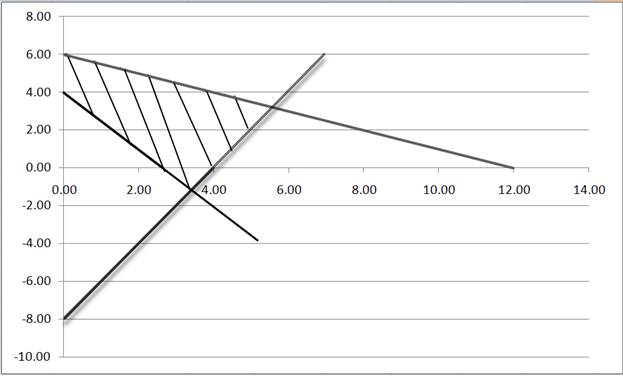
Таблица 1 – Начальное базисное решение
| Базисные переменные
|
Переменные
|
Постоянные
|
| х1
|
х2
|
х3
|
х4
|
х5
|
| х3
|
|
|
|
|
|
|
| х4
|
|
|
|
|
|
|
| х5
|
|
|
|
|
|
|
| с - строка
|
|
|
|
|
|
|
Опорная точка: х1
= 0, х2
= 0, х3
= 12, х4
= 8, х5
= -8, G = 0.
Таблица 2 – Правило минимальных отношений
| № строки
|
Базисные переменные
|
Отношение
|
| 1
|
|
|
| 2
|
|
|
| 3
|
|
|
Таблица 3 – Сложное базисное решение
| Базисные переменные
|
Переменные
|
Постоянные
|
| х1
|
х2
|
х3
|
х4
|
х5
|
| x3
|
|
|
|
|
|
|
| x4
|
|
|
|
|
|
|
| x2
|
|
|
|
|
|
|
| с - строка
|
|
|
|
|
|
|
|