Контрольная работа: Решение нелинейных уравнений

Задание №1

Отделить корни уравнения

графически и уточнить один из них:

· методом половинного деления;

· методом хорд;

· методом касательных;

· методом секущих;

· методом простой итерации;

с точностью ε=0,001.

Создать функции, реализующие указанные методы, построить графическую иллюстрацию методов, результаты проверить с помощью встроенных функций, оценить точность полученных значений.

1. Метод бисекции (деления отрезка пополам)

Метод бисекции или метод деления отрезка пополам — простейший численный метод для решения нелинейных уравнений вида F(x)=0. Предполагается только непрерывность функции F(x).

Графическое представление метода бисекций

Решим задание в пакете Маткад:

2. Метод хорд (метод линейной интерполяции)

Идея метода состоит в том, что по двум точкам и построить прямую (то есть хорду, соединяющую две точки графика) и взять в качестве следующего приближения абсциссу точки пересечения этой прямой с осью Ox .

Графическое представление метода хорд

Решим задание в пакете Маткад:

3. Метод касательных (Ньютона)

Графическое представление метода касательных

Решим задание в пакете Маткад:

4. Метод секущих

Графическое представление метода секущих

Решим задание в пакете Маткад:

5. Метод простой итерации

Введем функцию:

Графическое представление метода простой итерации

Решим задание в пакете Маткад:

Задание №2

Решить задачу Коши для дифференциального уравнения на отрезке [a,b] при начальном заданном условии и шаге интегрирования h:

1. методом Эйлера;

2. методом Рунге – Кутта 4 – го порядка точности.

3. проверить решение с помощью встроенных функций пакета MathCAD.

В решении оставлять 5 цифр после запятой.

1. Метод Эйлера

Решим задание в пакете Маткад:

2. Метод Рунге – Кутта 4 – го порядка точности

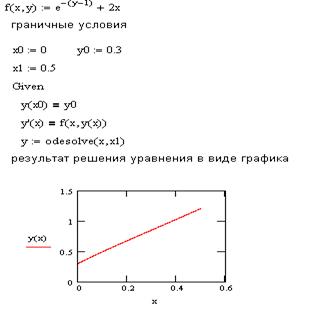
Проверим решение с помощью встроенных функций пакета MathCAD