| Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Кафедра «Летательные аппараты»
Курсовая работа
по курсу «Строительная механика»
Руководитель
__________________
«____»____________200г.
Автор работы
студент группы
__________________
«____»____________200г.
Работа защищена
с оценкой
__________________
«____»____________200г.
Содержание
1 Расчет подредукторной фермы вертолета
1.1 Геометрические параметры фермы
1.2 Расчетная схема фермы
1.3 Определение усилий в стержнях фермы
1.4 Проектировочный расчет стержней
2 Расчет кругового кольца при плоском изгибе
2.1 Уравновешивание кольца
2.2 Определение внутренних силовых факторов
2.3 Определение перемещений с помощью тригонометрических рядов
2.4 Определение размеров поперечного сечения шпангоута
1. Расчет подредукторной фермы вертолета
Определить усилия в стержнях подредукторной фермы вертолета (рисунок 1.1), оставшихся после разрушения передней левой опоры, при действии нагрузок:
Тх
= 1кН; Тy
= 10кН; Мр
= 0.1кН∙м.
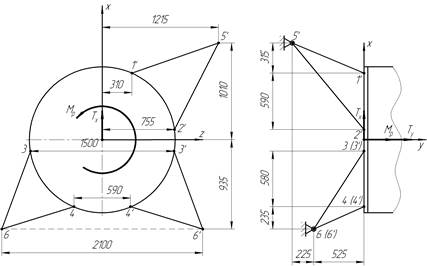
Рисунок 1.1 – Геометрия подредукторной фермы вертолета
1.1 Геометрические параметры фермы
Геометрические параметры фермы представлены в таблице 1.1.
Таблица 1.1 – Геометрические параметры фермы
| Наименование
|
Проекции, мм
|
l, мм
|
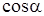
|
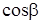
|
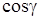
|
| lx
, мм
|
ly
, мм
|
lz
, мм
|
| 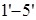
|
315
|
750
|
905
|
1216.86
|
0.259
|
0.616
|
0.744
|
| 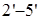
|
905
|
750
|
460
|
1262.19
|
0.717
|
0.594
|
0.364
|
| 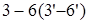
|
815
|
525
|
300
|
1014.82
|
0.803
|
0.517
|
0.296
|
| 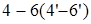
|
235
|
525
|
755
|
949.14
|
0.248
|
0.553
|
0.795
|
1.2 Расчетная схема фермы
Расчетная схема фермы представлена на рисунке 1.2.
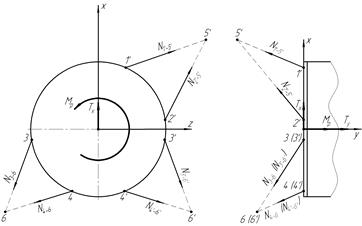
Рисунок 1.2 – Расчетная схема подредукторной фермы вертолета
1.3 Определение усилий в стержнях фермы
Составляем для данной статически определимой стержневой системы 6 уравнений равновесия:
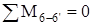 : :
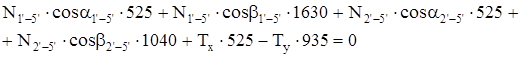
После подстановки значений косинусов углов и сокращения на меньший из коэффициентов при неизвестных усилиях получим:
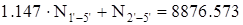 . (1.1) . (1.1)
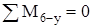 : :
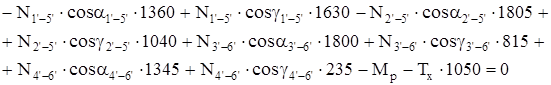
После преобразований получим:
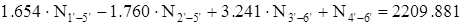 . (1.2) . (1.2)
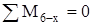 : :
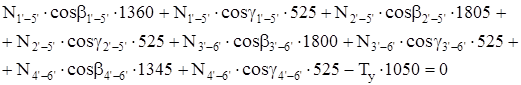
После преобразований получим:
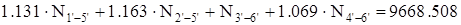 . (1.3) . (1.3)
 : :
 (1.4) (1.4)
 : :
 (1.5) (1.5)
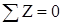 : :
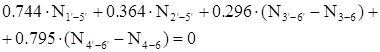 (1.6) (1.6)
Из уравнений (1.1), (1.2), (1.3), (1.4), (1.5), (1.6) составим систему, которую решим с помощью вычислительного пакета MathCAD (приложение 1). Для упрощения счета в MathCAD примем:
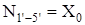 ; ; 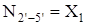 ; ; 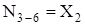 ; ;
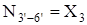 ; ; 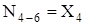 ; ; 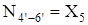 . .
После решения системы получим:
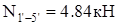 ; ;
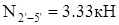 ; ;
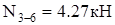 ; ;
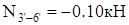 ; ;
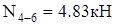 ; ;
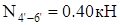 . .
Представим полученные результаты на диаграмме (рисунок 1.3).
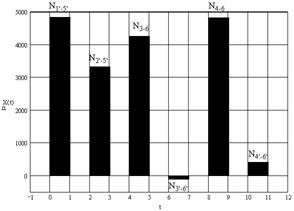
Рисунок 1.3 – Диаграмма усилий в стержнях подредукторной фермы вертолета
Реклама

Как видно из диаграммы, все стержни, кроме стержня 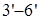 , растянуты. Наиболее нагружены стержни , растянуты. Наиболее нагружены стержни 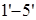 , , 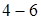 и и 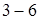 , менее нагружены стержни , менее нагружены стержни 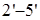 , , 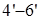 и и 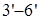 . Поэтому в первую очередь будут разрушаться стержни . Поэтому в первую очередь будут разрушаться стержни 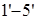 и и 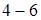 (силы, растягивающие их, почти одинаковы), а уже потом остальные. (силы, растягивающие их, почти одинаковы), а уже потом остальные.
1.4 Проектировочный расчет стержней
Проектировочный расчет проведем для самого нагруженного стержня – 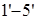 . Выберем стержень круглого поперечного сечения. Найдем диаметр этого сечения, если стержень изготовлен из сплава В95 [2, с. 43], для которого с учетом коэффициента запаса по пределу текучести ( . Выберем стержень круглого поперечного сечения. Найдем диаметр этого сечения, если стержень изготовлен из сплава В95 [2, с. 43], для которого с учетом коэффициента запаса по пределу текучести (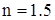 ) допускаемые напряжения ) допускаемые напряжения 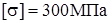 . .
Диаметр стержня вычисляется по формуле:
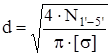 , мм; (1.7) , мм; (1.7)
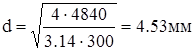 . .
После округления до нормального линейного размера по ряду Ra 40 [5, с. 481] получим:
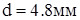 . .
Для подредукторной фермы вертолета необходимо взять стержни круглого поперечного сечения диаметром d = 4.8мм, изготовленные из сплава В95.
2. Расчет кругового кольца при плоском изгибе
Предварительно уравновесив кольцо потоком касательных сил (рисунок 2.1), найти:
силовые факторы M, Q, N методом сопряжения участков кольца;
перемещения v и w методом разложения нагрузки в ряд;
построить эпюры M, Q, N, v, w;
определить форму деформированного кольца и размеры поперечного сечения шпангоута.
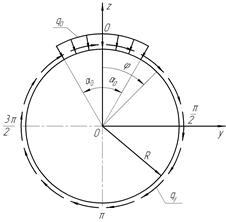
Рисунок 2.1 – Расчетная схема кольца, 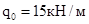 , , 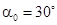 , , 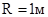
2.1 Уравновешивание кольца
Для уравновешивания внешней погонной радиальной нагрузки 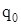 , равномерно распределенной в секторе , равномерно распределенной в секторе 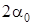 , определим значения коэффициентов в выражении для касательных погонных сил: , определим значения коэффициентов в выражении для касательных погонных сил:
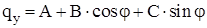 . (2.1) . (2.1)
При уравновешивании кольца целесообразно положительное направление для уравновешивающих касательных сил связывать с положительным направлением отсчета угла 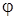 , так как в этом случае не нужно помнить о том, соответствует или нет положительное направление сил , так как в этом случае не нужно помнить о том, соответствует или нет положительное направление сил 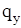 принятому для них положительному направлению при выводе дифференциальных уравнений изгиба кольца. принятому для них положительному направлению при выводе дифференциальных уравнений изгиба кольца.
Составим уравнения равновесия кольца, спроецировав все силы на направления осей y и z и взяв сумму моментов сил относительно центра кольца:
на ось y
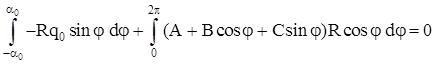 ; ;
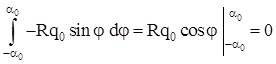 ; ;
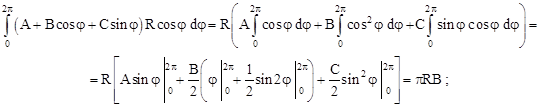
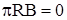 ; ; 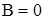 ; ;
на ось z:
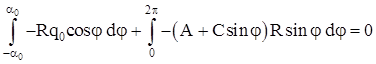 ; ;
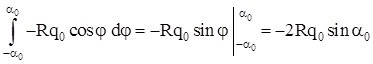 ; ;
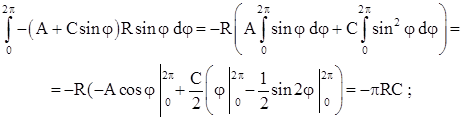
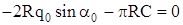 ; ;
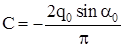 ; ;
относительно точки О:
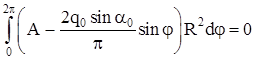 ; ;
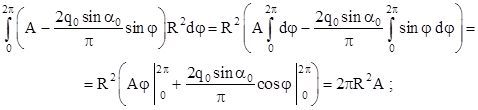
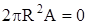 ; ;  . .
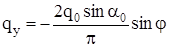 . (2.2) . (2.2)
2.2 Определение внутренних силовых факторов
Воспользуемся способом непосредственного интегрирования дифференциальных уравнений равновесия для кольца [1, с. 105]. Вследствие имеющей место симметрии ограничимся рассмотрением половины кольца ( ). По характеру нагружения здесь выделяются два участка. ). По характеру нагружения здесь выделяются два участка.
Уравнения равновесия для первого участка ( ): ):
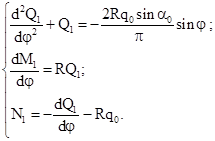 (2.3) (2.3)
Перед последним слагаемым в третьем уравнении системы (2.3) стоит знак «–», так как погонные нормальные силы 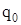 , направлены в сторону, противоположную принятому при выводе этих уравнений положительному направлению для , направлены в сторону, противоположную принятому при выводе этих уравнений положительному направлению для 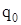 . .
Реклама

Уравнение равновесия для второго участка (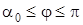 ): ):
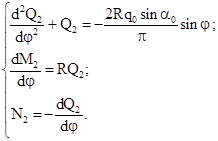 (2.4) (2.4)
Рассмотрим решение первого дифференциального уравнения системы (2.3).
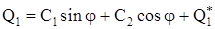 , (2.5) , (2.5)
где 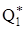 – частное решение. – частное решение.
Найдем это частное решение. Для простоты записи примем:
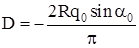 ; ; 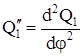 . .
Получили уравнение:
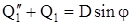 . (2.6) . (2.6)
Составляем характеристическое уравнение:
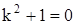 ; ;  . .
Частное решение имеет вид:
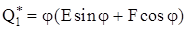 . (2.7) . (2.7)
Определим константы 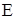 и и 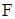 , для чего найдем , для чего найдем 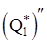 : :
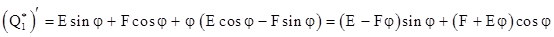 ; ;
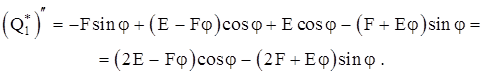
Подставив 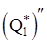 и и 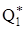 в уравнение (2.6): в уравнение (2.6):
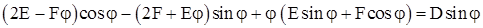 ; ;
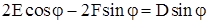 ; ;
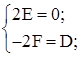 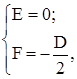
получим:
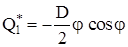 . (2.8) . (2.8)
Окончательно имеем:
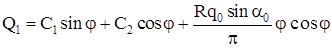 ; ;
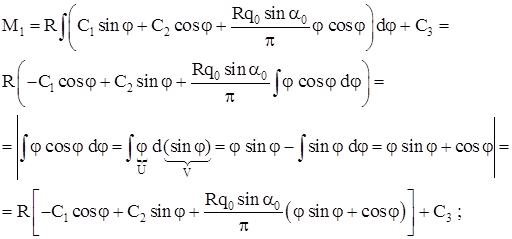
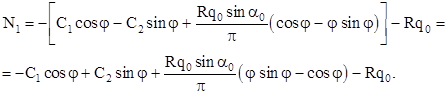
Для второй системы дифференциальных уравнений решение проводится аналогично.
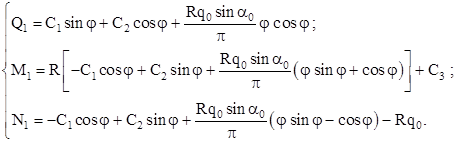 (2.9) (2.9)
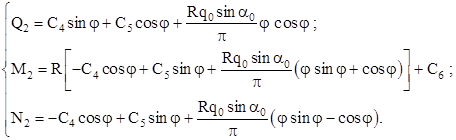 (2.10) (2.10)
Для определения неизвестных констант интегрирования воспользуемся граничными условиями и условиями сопряжения участков кольца:
при 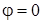 : 1) : 1) 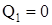 ; ;
при 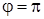 : 2) : 2) 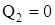 ; ;
при 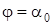 : 3) : 3) 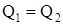 ; (2.11) ; (2.11)
4) 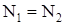 ; ;
5) 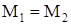 . .
Первые два условия из (2.11) справедливы, так как при симметричном нагружении кососимметричные факторы на оси симметрии равны нулю.
Для решения применим прикладной вычислительный пакет MathCAD (приложение 2). После того как неизвестные константы найдены, получим две системы уравнений:
первая система (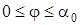 ): ):
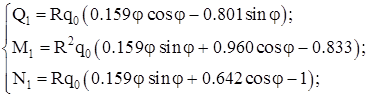 (2.12) (2.12)
вторая система (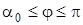 ): ):
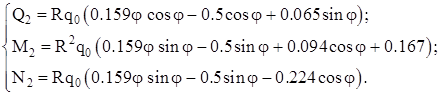 (2.13) (2.13)
Для построения эпюр безразмерных силовых факторов
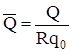 , , 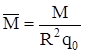 , , 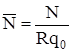
воспользуемся пакетом MathCAD (приложение 3). Результаты приведены в таблице 2.1 и представлены на рисунке 2.2.
Как видно из рисунка 2.2 опасными являются сечения при 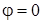 (действует максимальный изгибающий момент (действует максимальный изгибающий момент 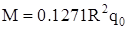 , нормальная сжимающая сила , нормальная сжимающая сила 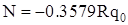 , а перерезывающая сила , а перерезывающая сила  ) и при ) и при 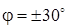 ( (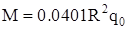 , , 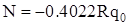 , , 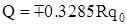 ). ).
2.3 Определение перемещений с помощью тригонометрических рядов
Внешнюю нагрузку, приложенную к кольцу, представим в виде ряда:
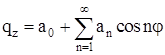 . (2.14) . (2.14)
Коэффициенты ряда (2.14) определяются при интегрировании левой и правой его частей в пределах от 0 до 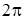 : :
Таблица 2.1 – Безразмерные силовые факторы и перемещения для кольца
| φ, °
|
Q
|
M
|
N
|
v
|
w
|
| 0.00
|
0.0000
|
0.1271
|
-0.3579
|
0.0000
|
-0.0346
|
| 10.00
|
-0.1118
|
0.1173
|
-0.3628
|
0.0059
|
-0.0322
|
| 20.00
|
-0.2218
|
0.0882
|
-0.3776
|
0.0110
|
-0.0253
|
| 30.00
|
-0.3285
|
0.0401
|
-0.4022
|
0.0145
|
-0.0149
|
| 40.00
|
-0.2563
|
-0.0110
|
-0.4215
|
0.0161
|
-0.0029
|
| 50.00
|
-0.1825
|
-0.0493
|
-0.4206
|
0.0156
|
0.0088
|
| 60.00
|
-0.1106
|
-0.0748
|
-0.4006
|
0.0131
|
0.0189
|
| 70.00
|
-0.0437
|
-0.0882
|
-0.3637
|
0.0091
|
0.0261
|
| 80.00
|
0.0155
|
-0.0905
|
-0.3124
|
0.0042
|
0.0299
|
| 90.00
|
0.0648
|
-0.0833
|
-0.2500
|
-0.0011
|
0.0300
|
| 100.00
|
0.1024
|
-0.0686
|
-0.1800
|
-0.0061
|
0.0268
|
| 110.00
|
0.1274
|
-0.0483
|
-0.1061
|
-0.0103
|
0.0206
|
| 120.00
|
0.1394
|
-0.0249
|
-0.0324
|
-0.0132
|
0.0124
|
| 130.00
|
0.1389
|
-0.0004
|
0.0375
|
-0.0145
|
0.0030
|
| 140.00
|
0.1267
|
0.0229
|
0.1001
|
-0.0142
|
-0.0065
|
| 150.00
|
0.1045
|
0.0433
|
0.1522
|
-0.0123
|
-0.0151
|
| 160.00
|
0.0744
|
0.0590
|
0.1914
|
-0.0090
|
-0.0219
|
| 170.00
|
0.0386
|
0.0689
|
0.2157
|
-0.0048
|
-0.0263
|
| 180.00
|
0.0000
|
0.0723
|
0.2239
|
0.0000
|
-0.0278
|
| 190.00
|
-0.0386
|
0.0689
|
0.2157
|
0.0048
|
-0.0263
|
| 200.00
|
-0.0744
|
0.0590
|
0.1914
|
0.0090
|
-0.0219
|
| 210.00
|
-0.1045
|
0.0433
|
0.1522
|
0.0123
|
-0.0151
|
| 220.00
|
-0.1267
|
0.0229
|
0.1001
|
0.0142
|
-0.0065
|
| 230.00
|
-0.1389
|
-0.0004
|
0.0375
|
0.0145
|
0.0030
|
| 240.00
|
-0.1394
|
-0.0249
|
-0.0324
|
0.0132
|
0.0124
|
| 250.00
|
-0.1274
|
-0.0483
|
-0.1061
|
0.0103
|
0.0206
|
| 260.00
|
-0.1024
|
-0.0686
|
-0.1800
|
0.0061
|
0.0268
|
| 270.00
|
-0.0648
|
-0.0833
|
-0.2500
|
0.0011
|
0.0300
|
| 280.00
|
-0.0155
|
-0.0905
|
-0.3124
|
-0.0042
|
0.0299
|
| 290.00
|
0.0437
|
-0.0882
|
-0.3637
|
-0.0091
|
0.0261
|
| 300.00
|
0.1106
|
-0.0748
|
-0.4006
|
-0.0131
|
0.0189
|
| 310.00
|
0.1825
|
-0.0493
|
-0.4206
|
-0.0156
|
0.0088
|
| 320.00
|
0.2563
|
-0.0110
|
-0.4215
|
-0.0161
|
-0.0029
|
| 330.00
|
0.3285
|
0.0401
|
-0.4022
|
-0.0145
|
-0.0149
|
| 340.00
|
0.2218
|
0.0882
|
-0.3776
|
-0.0110
|
-0.0253
|
| 350.00
|
0.1118
|
0.1173
|
-0.3628
|
-0.0059
|
-0.0322
|
| 360.00
|
0.0000
|
0.1271
|
-0.3579
|
0.0000
|
-0.0346
|
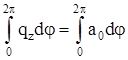 ; ;
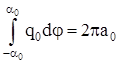 ; ; 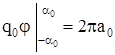 ; ;
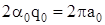 ; ; 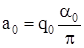 . .
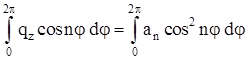 ; ;
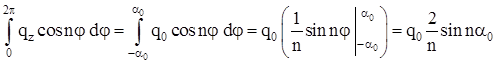 ; ;
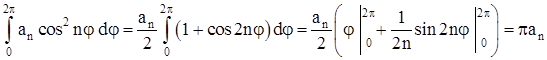 ; ;
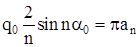 ; ;
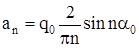 . .
В результате ряд для 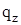 принимает вид: принимает вид:
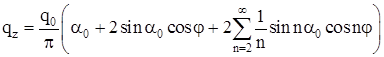 . (2.15) . (2.15)
Дифференциальное уравнение для перемещения v имеет вид [1, с. 108]:
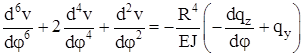 . (2.16) . (2.16)
Перед слагаемым 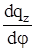 стоит знак «–», так как погонные нормальные силы стоит знак «–», так как погонные нормальные силы 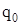 , направлены в сторону, противоположную принятому при выводе этого уравнения положительному направлению для , направлены в сторону, противоположную принятому при выводе этого уравнения положительному направлению для 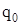 . .
Подставляя в уравнение (2.16)
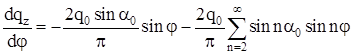 , ,
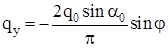 , ,
получим:
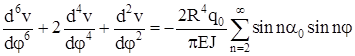 . (2.17) . (2.17)
Подставив в это уравнение выражение для перемещения v в виде ряда
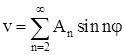
и приравняв коэффициенты при соответствующих функциях в уравнении
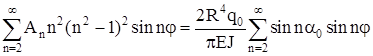 , ,
получим:
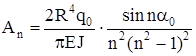 ; ;
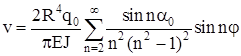 . (2.18) . (2.18)
Из условия нерастяжимости кольца
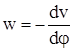 ; ;
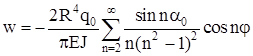 . (2.19) . (2.19)
Представим эти перемещения в безразмерном виде
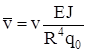 и и 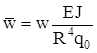 . .
Окончательно
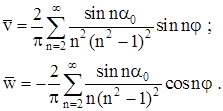 (2.20) (2.20)
Эпюры безразмерных перемещений и форму деформированного кольца построим с помощью пакета MathCAD (приложение 4). Результаты приведены в таблице 2.1 и представлены на рисунках 2.2 и 2.3.
2.4 Определение размеров поперечного сечения шпангоута
Выберем [3, с. 304] поперечное сечение шпангоута в виде двутаврового профиля (рисунок 2.4). Определим размеры этого сечения, если кольцо изготовлено из сплава В95 [2, с. 43], для которого с учетом коэффициента запаса
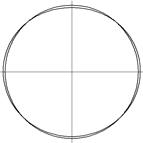
Рисунок 2.3 – Форма деформированного кольца
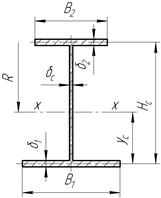
Рисунок 2.4 – Геометрические параметры сечения шпангоута
по пределу текучести (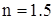 ) допускаемые напряжения ) допускаемые напряжения 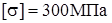 . Расчет проведем для сечения шпангоута при . Расчет проведем для сечения шпангоута при 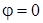 (приложение 5). Здесь (приложение 5). Здесь
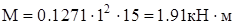 ; ;
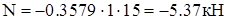 ; ;
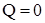 . .
Задаемся [3, с. 306]:
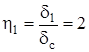 ; ; 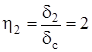 ; ;
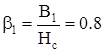 ; ; 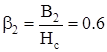 . .
Площадь сечения шпангоута
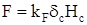 ; ;
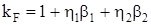 , ,
расстояние до нейтральной оси
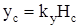 ; ;
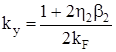 , ,
собственный момент инерции сечения
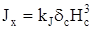 ; ;
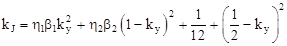 . .
Напряжения в наружной полке
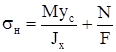 , (2.21) , (2.21)
во внутренней полке
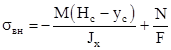 . (2.22) . (2.22)
M и N подставляются в формулы (2.21) и (2.22) с теми знаками, которые получаются при их вычислении.
Назначим толщину стенки 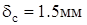 и найдем и найдем 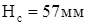 . .
Теперь толщина и ширина полок:
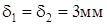 ; ; 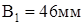 ; ; 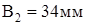 . .
Сечение шпангоута в масштабе 1:1 изображено на рисунке 2.5.
Нормальные напряжения в полках:
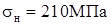 ; ; 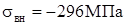 . .
Определим максимальные касательные напряжения в стенке шпангоута для сечения при 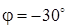 ( (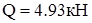 ): ):
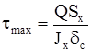 . (2.23) . (2.23)
Статический момент части площади сечения, расположенной выше нейтральной оси, относительно этой оси
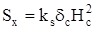 ; ;
 . .
После расчета получим
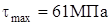 . .
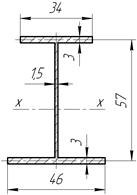
Рисунок 2.5 – Сечение шпангоута в масштабе 1:1
|